当前位置：文档之家 › 作业：第五章 树和二叉树

作业：第五章 树和二叉树

  • 格式：doc
  • 大小：567.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第5章二叉树与树

第5章二叉树与树

5.1.2 主要性质
性质1 在非空二叉树的i层上至多有2i个结点(i≥0)。 证明：用归纳法来证。
性质2 高度为k的二叉树中最多有2k+1 - 1个结点 (k≥0)。 证明：假设第i层上的最大结点个数是mi，由性质1 可知，深度为k的二叉树中最大结点个数M为:
k
k
M mi＝ 2i 2k1 1
如果2i＋1≤n－1，则下标为i的结点的左子结点的下标为2i ＋1；否则，下标为i的结点没有左子结点：
如果2i+2≤n－1，则下标为i的结点的右子结点的下标为2i+2； 否则，下标为i的结点没有右子结点。
性质6 在满二叉树中，叶结点的个数比分支结点个数多1。
性质7 扩充二叉树中，外部结点的个数比内部结点的个数多1。
i0
i0
性度为质23的对结于点任个何数一为棵n非2，空则的有二：叉n0树= ，n2 如+ 果1 。叶结点个数为n0，
证明：设一棵非空二叉树中有n个结点，度为1的结点个数为
n1，因为二叉树中所有结点的度均不大于2，所以
n = n0 + n1 + n2
(1)
在二叉树中，除根结点外，其余每个结点都有一个分支进入，
二叉树的高度：二叉树中结点的最大层数称为二叉树的高度。
树叶、分支结点：左（右）子树均为空二叉树的节点称作树 叶；否则称为分支节点。
特殊的二叉树
满二叉树：如果一棵二叉树的任何结点或者是树叶，或有两棵 非空子树，则此二叉树称作满二叉树（离散数学中称此树是正 则的)。
完全二叉树：如果一棵二叉树至多只有最下面的两层结点度数 可以小于2，其余各层结点度数都必须为2，并且最下面一层的 结点都集中在该层最左边的若干位置上，则此二叉树称为完全 二叉树。

《数据结构及其应用》笔记含答案 第五章_树和二叉树

《数据结构及其应用》笔记含答案 第五章_树和二叉树

第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。

二、判断题1、二叉树是树的特殊形式。

（）2、完全二叉树中，若一个结点没有左孩子，则它必是叶子。

（）3、对于有N个结点的二叉树，其高度为。

（）4、满二叉树一定是完全二叉树，反之未必。

（）5、完全二叉树可采用顺序存储结构实现存储，非完全二叉树则不能。

（）6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点，则它必是该子树的后序遍历序列中的第一个结点。

（）7、不使用递归也可实现二叉树的先序、中序和后序遍历。

（）8、先序遍历二叉树的序列中，任何结点的子树的所有结点不一定跟在该结点之后。

（）9、赫夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近。

（）110、在赫夫曼编码中，出现频率相同的字符编码长度也一定相同。

（）三、单项选择题1、把一棵树转换为二叉树后，这棵二叉树的形态是（A）。

A．唯一的Ｂ．有多种C．有多种，但根结点都没有左孩子Ｄ．有多种，但根结点都没有右孩子解释：因为二叉树有左孩子、右孩子之分，故一棵树转换为二叉树后，这棵二叉树的形态是唯一的。

2、由3个结点可以构造出多少种不同的二叉树？（D）A．2 B．3 C．4 D．5解释：五种情况如下：3、一棵完全二叉树上有1001个结点，其中叶子结点的个数是（D）。

A．250 B． 500 C．254 D．501解释：设度为0结点（叶子结点）个数为A，度为1的结点个数为B，度为2的结点个数为C，有A=C+1，A+B+C=1001，可得2C+B=1000，由完全二叉树的性质可得B=0或1，又因为C为整数，所以B=0，C=500，A=501，即有501个叶子结点。

4、一个具有1025个结点的二叉树的高h为（C）。

A．11 B．10 C．11至1025之间 D．10至1024之间解释：若每层仅有一个结点，则树高h为1025；且其最小树高为⎣log21025⎦ + 1=11，即h在11至1025之间。

第5章 树与二叉树

第5章 树与二叉树
20
树的抽象数据类型的定义
基本操作： InitTree(Tree)：将Tree初始化为一棵空树。 DestoryTree(Tree)：销毁树Tree。 CreateTree(Tree)： 创建树Tree。 TreeEmpty(Tree) ： 若 Tree 为 空 ， 则 返 回 TRUE，否则返回FALSE。 Root(Tree)：返回树Tree的根。 Parent(Tree,x)：树Tree存在，x是Tree中的某 个结点。若x为非根结点，则返回它的双亲，否 则返回“空”。
27
第五章 树和二叉树
树的定义与基本概念 二叉树(Binary Tree)
二叉树的定义与基本操作 二叉树的性质 二叉树的存储结构
二叉树的遍历与线索化 树、森林和二叉树的关系 哈夫曼树及其应用 要点小结
28
二叉树的性质
性质1：在二叉树的第i层上至多有2i-1个结点 (i≥1)。 证明：归纳基础：当i=1时，整个二叉树只有 一根结点，此时2i-1=20=1，结论成立。
『数据结构 ·DATA STRUCTURES』
第五章 树和二叉树
第五章 树和二叉树
本章要求
熟练掌握二叉树的结构特性(五个性质)，了解相应的证明 方法； 熟悉二叉树的各种存储结构的特点及适用范围； 遍历二叉树是二叉树各种操作的基础，熟练掌握各种遍历 策略的递归算法，了解其非递归算法； 熟悉树的各种存储结构及其特点，掌握树和森林与二叉树 之间的相互转换方法； 了解Huffman树的特性，掌握建立Huffman树和Huffman 编码的算法。
4
Organization structure
5
数据结构的内容
逻辑结构
指数据元素之间的逻辑关系 描述。
数据结构的形式定义为：

第5章 树与二叉树习题参考答案【VIP专享】

第5章 树与二叉树习题参考答案【VIP专享】

2. 一棵具有 n 个结点的二叉树，其深度最多为 n ，最少为 [log2n]+1 。 3. 一棵具有 100 个结点的完全二叉树，其叶结点的个数为 50 。37 4. 以{5，9，12，13，20，30}为叶结点的权值所构造的哈夫曼树的带权路径长度是 217
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

数据结构 第五章树答案

数据结构 第五章树答案

第五章 树(答案)一、选择题1、二叉树的第i 层最多有（ ）个结点。

A ．2i B. 2i C. 2i-1 D.2i -12.对于一棵满二叉树，高度为h ，共有n 个结点，其中有m 个叶子结点，则（ ）A ．n=h+m B.h+m=2n C.m=h-1 D.n=2h -1 3.在一棵二叉树中，共有16个度为2的结点，则其共有（ ）个叶子结点。

A ．15 B.16 C.17 D.184. 一棵完全二叉树中根结点的编号为1，而且编号为23的结点有左孩子但没有右孩子，则此树中共有（ ）个结点。

A ．24 B.45 C.46 D.47 5.下述编码那一组不是前缀码（ ）A ．00,01,10,11 B.0,1,00,11 C.0,10,110,111 D.1,01,001,000 6.某二叉树的中序序列和后序序列相同，则这棵二叉树必然是（ ）A ．空树B ．空树或任一结点均无左孩子的非空二叉树C ．空树或任一结点均无右孩子的非空二叉树D ．空树或仅有一个结点的二叉树7.设n,m 为一棵二叉树上的两个结点，在中序遍历时，n 在m 前的条件是（ ）A ．n 在m 的右边 B.n 是m 的祖先C ．n 在m 的左边 D.n 是m 的子孙8、假定中根遍历二叉树的定义如下：若二叉树为非空二叉树，则中根遍历根的右子树；访问根结点；中根遍历根的左子树。

按此定义遍历下图所示的二叉树，遍历的结果为： A 、 DBEAFHGC A B 、 C GHFADBE B C C 、 E BDAFHGC E D FD 、 FHGCADBE GH9、文中出现的字母为A 、B 、C 、D 和E ，每个字母在电文中出现的次数分别为9、27、3、5和11。

按哈夫曼编码（构造时左小右大），则字母C 的编码应是：A 、10B 、0110C 、1110D 、1100 10、设树T 的度为4，其中度为1，2，3和4的结点个数分别为4，2，1，1 则T 中的叶子数为（ ）A ．5B ．6C ．7D ．8 11．算术表达式a+b*（c+d/e ）转为后缀表达式后为（ ）A ．ab+cde/*B ．abcde/+*+C ．abcde/*++D ．12. 设有一表示算术表达式的二叉树（见下图），它所表示的算术表达式是（ ）A. A*B+C/(D*E)+(F-G)B. (A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+（F-G ）)D. A*B+C/D*E+F-G13．已知一算术表达式的中缀形式为 A+B*C-D/E ，后缀形式为ABC*+DE/-，其前缀形式为( ) A ．-A+B*C/DE B. -A+B*CD/E C ．-+*ABC/DE D. -+A*BC/DE14．若一棵二叉树具有10个度为2的结点，5个度为1的结点，则度为0的结点个数是（ ）A ．9B ．11C ．15D ．不确定15．树的后根遍历序列等同于该树对应的二叉树的( ).A. 先序序列B. 中序序列C. 后序序列16．已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历的结果为（ ）。

第5章 树和二叉树共148页文档

第5章 树和二叉树共148页文档
5.2 树的存储结构
实现树的存储结构，关键是什么? 如何表示树中结点之间的逻辑关系。
什么是存储结构? 数据元素以及数据元素之间的逻辑关系在存储器 中的表示。
树中结点之间的逻辑关系是什么?
思考问题的出发点：如何表示结点的双亲和孩子
5.2 树的存储结构
双亲表示法
数据结构（C＋＋版）
基本思想：用一维数组来存储树的各个结点（一般 按层序存储），数组中的一个元素对应树中的一个 结点，包括结点的数据信息以及该结点的双亲在数 组中的下标。
树的双亲表示法实质上是一个静态链表。
数据结构（C＋＋版）
5.2 树的存储结构
双亲表示法
A
B
C
DEF G H
I
下标 data
0A
1B
2C
3D
4E
5F
6G
7H
8
I
parent
-1 0 0 1 1 1 2 2 4
data parent
data：存储树中结点的数据信息 parent：存储该结点的双亲在数组中的下标
5.2 树的存储结构
双亲表示法
数据结构（C＋＋版）
data parent
template <class T> struct PNode {
T data; //数据域 int parent; //指针域，双亲在数组中的下标 };
数据结构（C＋＋版）
树的基本术语
同构：对两棵树，若通过对结点适当地重命名， 就可以使这两棵树完全相等（结点对应相等，结 点对应关系也相等），则称这两棵树同构。
A
B
C
D
E
A
DEF G
GBF C
5.1 树的逻辑结构

第5章+树与二叉树习题解析(答)

第5章+树与二叉树习题解析(答)

习题五树与二叉树一、选择题1、一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足。

A、所有的结点均无左孩子B、所有的结点均无右孩子C、只有一个叶子结点D、是任意一棵二叉树2、一棵完全二叉树上有1001个结点，其中叶子结点的个数是。

A、250B、500C、254D、505E、以上答案都不对3、以下说法正确的是。

A、若一个树叶是某二叉树前序遍历序列中的最后一个结点，则它必是该子树后序遍历序列中的最后一个结点B、若一个树叶是某二叉树前序遍历序列中的最后一个结点，则它必是该子树中序遍历序列中的最后一个结点C、在二叉树中，具有两个子女的父结点，在中序遍历序列中，它的后继结点最多只能有一个子女结点D、在二叉树中，具有一个子女的父结点，在中序遍历序列中，它没有后继子女结点4、以下说法错误的是。

A、哈夫曼树是带权路径长度最短得数，路径上权值较大的结点离根较近B、若一个二叉树的树叶是某子树中序遍历序列中的第一个结点，则它必是该子树后序遍历序列中的第一个结点C、已知二叉树的前序遍历和后序遍历并不能唯一地确定这棵树,因为不知道树的根结点是哪一个D、在前序遍历二叉树的序列中,任何结点其子树的所有结点都是直接跟在该结点之后的5、一棵有124个叶结点的完全二叉树，最多有个结点。

A、247B、248C、249D、250E、2516、任何一棵二叉树的叶结点在前（先）序、中序和后序遍历序列中的相对次序。

A、不发生变化B、发生变化C、不能确定7、设a、b为一棵二叉树上的两个结点。

在中序遍历时，a在b前面的条件是。

A、a在b的右方B、a在b的左方C、a是b的祖先D、a 是b的子孙8、设深度为k的二叉树上只有度为0和度为2的结点，则这类二叉树上所含的结点总数为。

A、不确定B、2kC、2k-1D、2k+19、设有13个值，用它们组成一棵哈夫曼树，则该哈夫曼树共有个结点。

A、13B、12C、26 D、2510、下面几个符号串编码集合中，不是前缀编码的是。

第5章 树和二叉树

第5章 树和二叉树
A
B A
C
D
E
F
G
H
I
J
K
L
T1
T2
M
2015年10月20日
T3
树的其它表示方式
A D K L F C G E B H M J I
A
A B E K L F C G
B C D
嵌套集合
E
D H M
F
G
H
I
J
I J
K
L
M
凹入表示
(A(B(E(K,L),F),C(G),D(H(M),I,J)))
广义表
2015年10月20日
北京林业大学信息学院
2015年10月20日
二叉树的链式存储
PARENT
lchild
data
rchild
DATA
lchild
data
parent rchild
LCHILD
RCHILD
北京林业大学信息学院
2015年10月20日
二叉链表
A A ^ B D lchild data rchild
B
C
E
G
F
二叉树的五种不同形态
2015年10月20日
练习
具有3个结点的二叉树可能有几种不同形态？普通树呢？ 5种/2种
2015年10月20日
二叉树的抽象数据类型定义
ADT BinaryTree{ 数据对象D: D是具有相同特性的数据元素的集合。 数据关系R: 若D=Φ，则R= Φ ； 若D≠Φ，则R= {H}；存在二元关系： ① root 唯一 //关于根的说明 ② Dj∩Dk= Φ //关于子树不相交的说明 ③ …… //关于数据元素的说明 ④ …… //关于左子树和右子树的说明 //至少有20个 基本操作 P： }ADT BinaryTree

第五章习题

第五章习题

三、填空题
9． n个结点的各棵树中，其深度最小的那棵树的深度 是 2 。它共有 n-1 个叶子结点和 1 个非叶子结点， 其中，深度最大的那棵树的深度是 n ，它共有 1 个 叶子结点和 n-1 个非叶子结点。
10．先根遍历树林正好等同于 先序 遍历对应的二叉树，后 根遍历树林正好等同于按 中序 遍历对应的二叉树。 11．若一个二叉树的叶子结点是某子树的中序遍历序列中的 前序 最后一个结点，则它必是该子树的______序列中的最后一个 结点。
C,E,F,G,
二、判断题
× 1.二叉树是度为2的有序树。
× 2. 完全二叉树一定存在度为1的结点。 √
√
3．深度为K的二叉树中结点总数≤2k-1。 4. 一个树的叶结点，在前序遍历和后序遍历 下，皆以相同的相对位置出现。 但是，如果我们还知道该树的根结点是哪一个， 则可以确定这棵二叉树。 一个栈。
C A
10．深度为h的满m叉树的第k层有（ ）个结 点。(1=<k=<h) A．mk-1 B．mk-1 C．mh-1 D．mh-1
一、选择题
11．高度为 K的二叉树最大的结点数为（ A．2k B．2k-1 C．2k -1 D．2k-1-1 12. 一棵树高为K的完全二叉树至少有（ A．2k –1 B. 2k-1 –1 C. 2k-1 D. 2k ）。
第五章 树和二叉树
习题讨论
、选择题
1．已知一算术表达式的中缀形式为 A+B*C-D/E，后缀形式 为ABC*+DE/-，其前缀形式为( ) A．-A+B*C/DE B. -A+B*CD/E C．-+*ABC/DE D. -+A*BC/DE
D
C
2. 设有一表示算术表达式的二叉树（见下图），它所表示的算 术表达式是（ ） A. A*B+C/(D*E)+(F-G) / B. (A*B+C)/(D*E)+(F-G) + + C * C. (A*B+C)/(D*E+（F-G）) * D E F G D. A*B+C/D*E+F-G A B

数据结构 第五章 树和二叉树

数据结构 第五章 树和二叉树

2.3 二叉树的性质



完全二叉树(Complete Binary Tree)：如果深度为 k，由n个结点的二叉树，当且仅当其每一个结点 都与深度为k的满二叉树中编号从 1到n的结点一 一对应，该二叉树称为完全二叉树。 或深度为k的满二叉树中编号从1到n的前n个结点 构成了一棵深度为k的完全二叉树。 其中2k-1 ≦ n≦2k-1 。 完全二叉树是满二叉树的一部分，而满二叉树是 完全二叉树的特例。
输入数据 { 53, 78, 65, 17, 87, 09, 81, 15 }
4.3 二叉搜索树的删除




删除叶结点，只需将其双亲结点指向它的指针清 零，再释放它即可。 被删结点右子树为空，可以拿它的左子女结点顶 替它的位置，再释放它。 被删结点左子树为空，可以拿它的右子女结点顶 替它的位置，再释放它。 被删结点左、右子树都不为空，可以在它的右子 树中寻找中序下的第一个结点(关键码最小),用它 的值填补到被删结点中，再来处理这个结点的删 除问题。
⑴ 若i=1：则结点i是二叉树的根，无双亲结点；否则， 若i>1，则其双亲结点编号是 i/2 。
⑵ 如果2i>n：则结点i为叶子结点，无左孩子；否则， 其左孩子结点编号是2i。 ⑶ 如果2i+1>n：则结点i无右孩子；否则，其右孩子 结点编号是2i+1。

性质6：给定N个节点，能构成CN种不同的 二叉树，其中为卡塔兰数（ Catalan ）。

3.4 根据遍历结果构建二叉树


由二叉树的前序序列和中序序列可唯一地 确定一棵二叉树。 例, 前序序列 { A B H F D E C K G } 和中序序 列 { H B D F A E K C G }, 构造二叉树过程如 下：

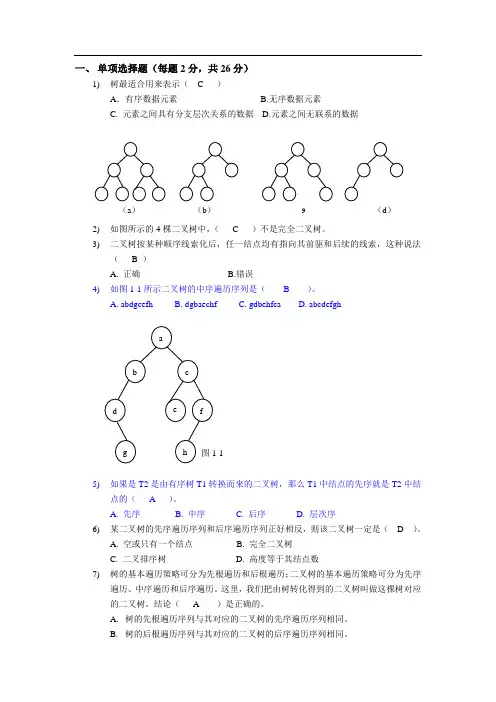
第五章-树-练习-答案

第五章-树-练习-答案

一、 单项选择题（每题2分，共26分）1) 树最适合用来表示（ C ）A ．有序数据元素 B.无序数据元素C. 元素之间具有分支层次关系的数据D.元素之间无联系的数据2) 如图所示的4棵二叉树中，（ C ）不是完全二叉树。

3) 二叉树按某种顺序线索化后，任一结点均有指向其前驱和后续的线索，这种说法（ B ）A. 正确B.错误4) 如图1-1所示二叉树的中序遍历序列是（ B ）。

A. abdgcefhB. dgbaechfC. gdbehfcaD. abcdefgh5) 如果是T2是由有序树T1转换而来的二叉树，那么T1中结点的先序就是T2中结点的（ A ）。

A. 先序B. 中序C. 后序D. 层次序6) 某二叉树的先序遍历序列和后序遍历序列正好相反，则该二叉树一定是（ D ）。

A. 空或只有一个结点B. 完全二叉树C. 二叉排序树D. 高度等于其结点数7) 树的基本遍历策略可分为先根遍历和后根遍历；二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。

这里，我们把由树转化得到的二叉树叫做这棵树对应的二叉树。

结论（ A ）是正确的。

A. 树的先根遍历序列与其对应的二叉树的先序遍历序列相同。

B. 树的后根遍历序列与其对应的二叉树的后序遍历序列相同。

（a ） （b ） 9 （d ）C. 树的先根遍历序列与其对应的二叉树的中序遍历序列相同。

D. 以上都不对8) 如图所示的T2是由森林T1转换而来的二叉树，那么森里T1有（ C ）个叶子结点。

A. 4B. 5C. 6D. 79) 深度为5的二叉树至多有（ C ）个结点。

A. 16B. 32C. 31D. 1010) 在一非空二叉树的中序遍历序列中，根结点的右边（ A ）。

A. 只有右子树上的所有结点B. 只有右子树的部分结点C. 只有左子树上的部分结点D. 只有左子树上的所有结点11) 设n ，m 为一棵二叉树上的两个结点，在中序遍历时，n 在m 前的条件是（ C ）。

王道 数据结构 第五章 树与二叉树思维导图

王道 数据结构 第五章 树与二叉树思维导图

在含有n个带权叶结点的二叉树中，其中带权路径长度（WPL）最小的二叉树称 为哈夫曼树，也称最优二叉树
哈夫曼树的构造
每次选两个根节点权值最小的树合并，并将二者权值之和作为新的根节点的权值
哈夫曼树的特点 哈夫曼编码
每个初始结点最终都成叶结点，且权值最小的结点到根节点的路径长度越长 哈夫曼树的结点总数为2n-1（n为叶结点数，也为初始结点数） 哈夫曼树中不存在度为1的结点 哈夫曼树不唯一，但WPL必然相同且为最优 固定长度编码——每个字符用相等长度的二进制位表示 可变长度编码——允许对不同字符用不等长的二进制位表示 前缀编码——没有一个编码是另一个编码的前缀 将字符频次作为字符结点权值，构造哈夫曼树，按照左0右1构造编码，即可得哈 夫曼编码，可用于数据压缩
平衡二叉树
常见考点
考点1 考点2 考点3
考点4
树上任一结点的左子树和右子树的深度之差不超过1
平衡二叉树能有更高的搜索效率
设非空二叉树中度为0、1和2的结点个数分别为n0
n, 1 ​
n 和​
2
，​ 则n0
​
=
n2 ​
+
1（叶子
结点比二分支结点多一个）
二叉树第i层至多有2i−1 个结点（i≥1）
高度为h的二叉树至多有2h − 1个结点（满二叉树）
树和森林的遍历
森林的遍历
先序遍历 中序遍历
若森林为非空，则按如下规则进行遍历： 访问森林中第一棵树的根结点。 先序遍历第一棵树中根结点的子树森林。 先序遍历除去第一棵树之后剩余的树构成的森林。
效果等同于依次对各个树进行先根遍历
若森林为非空，则按如下规则进行遍历： 中序遍历森林中第一棵树的根结点的子树森林。 访问第一棵树的根结点。 中序遍历除去第一棵树之后剩余的树构成的森林。

第五章树与二叉树

第五章树与二叉树
第五章 树和二叉树
5.1 树与树林 5.2 树和树林的存储表示 5.3 二 叉 树 5.4 二叉树的存储表示 5.5 哈夫曼算法及其应用
1
线性结构和非线性结构。
树形结构是以分支关系定义的层次结构， 在现实世界中广泛存在，在计算机领域中也 有广泛应用。
本章重点讨论二叉树的存储结构及其各 种操作，并研究树和森林与二叉树之间的转 换关系。
19
（II）按宽度方向周游 先访问层数为0的结点，然后从左到右逐个访
问层数为1的结点，依此类推，直到访问完树中 的全部结点。 层次序列（1，2，3，4，5，6，7，8，9，10）
20
5.1.6 树林的周游
1. 先根（A, B, C, K, D, E, H, F, J, G ) 2. 后根 ( B, K, C, A, H, E, J, F, G, D )
例如在图5.2中，按无序树的概念t和t'是同一棵树，按有序 树的概念则是不同的树，本章讨论的树一般是有序树。
➢ 结点的次序
在有序树中可以从左到右地规定结点的次序。按从 左到右的顺序，我们可以把一个结点的最左边的子 结点简称为最左子结点，或直接称为长子，而把长 子右边的结点称为次子。
例如在t中结点B是结点A的长子，结点C是结点A的次子，是 结点B的兄弟。
2. 周游的方法：按深度方向和按宽度方向周游。 （I）按深度方向（以右图为例） a. 先根次序 b. 中根次序 c. 后根次序
18
a. 先根次序 (1,2,3,5,8,9,6,10,4,7) （1） 访问根结点； （2）从左到右按先根次序周游根结点的每棵子树。 b. 中根次序 (2,1,8,5,9,3,10,6,7,4) （1）按中根次序周游根结点的最左子树； （2）访问根结点； （3）从左到右按中根次序周游根结点的其它各子树。 c. 后根次序 (2,8,9,5,10,6,3,7,4,1) （1）从左到右按后根次序周游根结点的每棵子树; （2）访问根结点。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章树和二叉树
一、单项选择题
1．关于二叉树的下列说法正确的是 (1)。

A．二叉树的度为2 B．二叉树的度可以小于2
C．每一个结点的度都为2 D．至少有一个结点的度为
2．设深度为h(h>0)的二叉树中只有度为0和度为2的结点，则此二叉树中所含的结点总数至少为（2）。

A．2h B．2h-1 C．2h+1 D．h+1
3．在树中，若结点A有4个兄弟，而且B是A的双亲，则B的度为 (3) 。

A．3 B．4 C．5 D．6
4．若一棵完全二叉树中某结点无左孩子，则该结点一定是 (4) 。

A.度为1的结点 B．度为2的结点 C．分支结点 D．叶子结点
5．深度为k的完全二叉树至多有 (5) 个结点，至少有 (6) 个结点。

A．2k-1-1 B．2k-1 C．2k-1 D．2k
6．前序序列为ABC的不同二叉树有 (7) 种不同形态。

A．3 B．4 C．5 D．6
7．若二叉树的前序序列为DABCEFG，中序序列为BACDFGE，则其后序序列为 (8) ，层次序列为 (9) 。

A．BCAGFED B．DAEBCFG C．ABCDEFG D．BCAEFGD
8．在具有200个结点的完全二叉树中，设根结点的层次编号为1，则层次编号为60的结点，其左孩子结点的层次编号为 (10) ，右孩子结点的层次编号为 (11) ，双亲结点的层次编号为 (12)。

A．30 B．60 C．120 D．121
9．遍历一棵具有n个结点的二叉树，在前序序列、中序序列和后序序列中所有叶子结点的相对次序 (13) 。

A.都不相同 B．完全相同 C．前序和中序相同 D．中序与后序相同
10．在由4棵树组成的森林中，第一、第二、第三和第四棵树组成的结点个数分别为30，10，20，5，当把森林转换成二叉树后，对应的二叉树中根结点的左子树中结点个数为（14），根结点的右子树中结点个数为 (15) 。

A．20 B．29 C．30 D．35
11.具有n个结点(n>1)的二叉树的前序序列和后序序列正好相反，则该二叉树中除叶子结点外每个结点 (16) 。

A.仅有左孩子 B．仅有右孩子 C．仅有一个孩子 D．都有左、右孩子
12．判断线索二叉树中p结点有右孩子的条件是 (17) 。

A.p!=NULL B．p->rchild!=NULL C．p->rtag=0 D．p->rtag=1
13．将一棵树转换成二叉树，树的前根序列与其对应的二叉树的 (18) 相等。

树的后根序列与其对应的二叉树的 (19)相同。

A．前序序列 B．中序序列 C．后序序列 D．层次序列
14．设数据结构(D，R)，D={dl，d2，d3，d4，d5，d6}，R={<d4，d2>，<d2，d1>，<d2，d3>，<d4，d6>，<d6，d5>}，这个结构的图形是 (20) ；用 (21) 遍历方法可以得到序列{d1，d2，d3，d4，d5，d6}。

(20)： A．线性表 B．二叉树C．队列 D．栈
(21)：A．前序 B．中序 C．后序 D．层次
15．对于树中任一结点x，在前根序列中序号为pre(x)，在后根序列中序号为post(x)，
若树中结点x是结点y的祖先，下列（22）条件是正确的。

A.pre(x)<pre(y)且post(x)<post(y)
B．pre(x)<pre(y)且post(x)>post(y)
C. pre(x)>pre(y)且post(x)<post(y)
D．pre(x)>pre(y)且post(x)>post(y)
16．每棵树都能惟一地转换成对应的二叉树，由树转换的二叉树中，一个结点N的左孩子是它在原树对应结点的 (23) ，而结点N的右孩子是它在原树里对应结点的 (24) 。

A．最左孩子 B．最右孩子 C．右邻兄弟 D．左邻兄弟17．二叉树在线索化后，仍不能有效求解的问题是 (25) 。

A．前序线索树中求前序直接后继结点
B．中序线索树中求中序直接前驱结点
C．中序线索树中求中序直接后继结点
D．后序线索树中求后序直接后继结点
18．一棵具有124个叶子结点的完全二叉树，最多有 (26)个结点。

A．247 B．248 C．249 D．250 。

二、填空题
1.树中任意结点允许有（1）孩子结点，除根结点外，其余结点（2）双亲结点。

2.若一棵树的广义表表示为A(B(E，F)，C(C(H，I，J，K)，L)，D(M(N)))。

则该树的度为 (3) ，树的深度为 (4) ，树中叶子结点个数为 (5) 。

3．若树T中度为1、2、3、4的结点个数分别为4、3、2、2，则T中叶子结点的个数是 (6) 。

4．一棵具有n个结点的二叉树，若它有m个叶子结点，则该二叉树中度为1的结点个数是 (7) 。

5．深度为k(k>0)的二叉树至多有 (8) 个结点，第i层上至多有 (9) 个结点。

6．已知二叉树有52个叶子结点，度为1的结点个数为30则总结点个数为 (10) 。

7．已知二叉树中有30个叶子结点，则二叉树的总结点个数至少是（11）。

8．高度为6的完全二叉树至少有 (12) 个结点。

9．一个含有68个结点的完全二叉树，它的高度是 (13) 。

10．已知一棵完全二叉树的第6层上有6个结点(根结点的层数为1)，则总的结点个数至少是 (14) ，其中叶子结点个数是（15）。

11．已知完全二叉树第6层上有10个叶子结点，则这棵二叉树的结点总数最多是（16）。

12．一棵树转换成二叉树后，这棵二叉树的根结点一定没有 (17) 孩子，若树中有m 个分支结点，则与其对应的二叉树中无右孩子的结点个数为（18）。

13．若用二叉链表示具有n个结点的二叉树，则有（19）个空链域。

14．具有m个叶子结点的哈夫曼树，共有（20）个结点。

15．树的后根遍历序列与其对应的二叉树的（21）遍历序列相同。

16．线索二叉树的左线索指向其（22），右线索指向其（23）。

三、应用题
1．具有n个结点的满二叉树的叶子结点个数是多少?
2．列出前序遍历序列是ABC的所有不同的二叉树。

3．已知二叉树的层次遍历序列为ABCDEFGHIJK，中序序列为DBGEHJACIKF，请构造一棵二叉树。

4．已知二叉树的中序遍历序列是ACBDGHFE，后序遍历序列是ABDCFHEG，请构造一棵二
叉树。

5．已知二叉树的前序、中序和后序遍历序列如下，其中有一些看不清的字母用*表示，请先填写*处的字母，再构造一棵符合条件的二叉树，最后画出带头结点的中序线索链表。

(1)前序遍历序列是：*BC***G*
(2)中序遍历序列是：CB*EAGH*
(3)后序遍历序列是：*EDB**FA
6．将下图所示的森林转换成一棵二叉树，并画出这棵二叉树的顺序存储结构。

7．将下图所示的二叉树还原成森林。

8．对于给定的一组权值{3，5，6，7，9}，请构造相应的哈夫曼树，并计算其带权路径长度。

四、算法设计题
1．请设计一个算法，求以孩子兄弟链表表示的树中叶子结点个数。

2．请编写一个算法，实现将以二叉链表存储的二叉树中所有结点的左、右孩子进行交换。

3．请编写一个算法，将以二叉链表存储的二叉树输出其广义表表示形式。

4．请编写一个算法，判断以二叉链表存储的二叉树是否为完全二叉树。

5．假设二叉树采用链接存储方式存储，编写一个二叉树先序遍历和后序遍历的非递归算法。

..
6．已知一棵二叉树用二叉链表存储，t指向根结点，p指向树中任一结点。

请编写一个非递归算法，实现求从根结点t到结点p之间的路径。