高一数学指数与指数函数

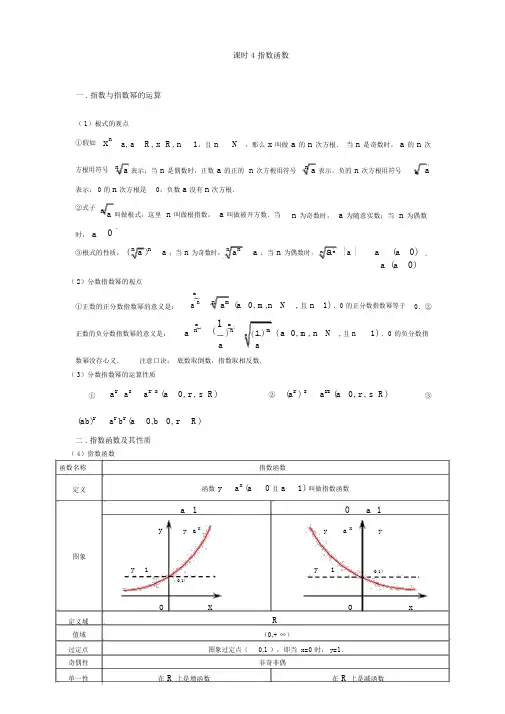
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

考点12指数运算和指数函数1、正确区分n a n与(n a)n(1)(n a)n已暗含了n a有意义，根据n的奇偶性可知a的范围．(2)n a n中的a可以是全体实数，n a n的值取决于n的奇偶性．2、有限制条件根式的化简(1)有限制条件根式的化简问题，是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简．(2)有限制条件根式的化简经常用到配方的方法．当根指数为偶数时，在利用公式化简时，要考虑被开方数或被开方的表达式的正负．3、根式与分数指数幂互化的规律(1)根指数分数指数的分母，被开方数(式)的指数分数指数的分子．(2)在具体计算时，通常会把根式转化成分数指数幂的形式，然后利用有理数指数幂的运算性质解题．4、指数幂运算的常用技巧(1)有括号先算括号里的，无括号先进行指数运算．(2)负指数幂化为正指数幂的倒数．(3)底数是小数，先要化成分数；底数是带分数，要先化成假分数，然后要尽可能用幂的形式表示，便于运用指数幂的运算性质．5、利用整体代换法求分数指数幂(1)整体代换法是数学变形与计算常用的技巧方法，分析观察条件与结论的结构特点，灵活运用恒等式是关键．(2)利用整体代换法解决分数指数幂的计算问题，常常运用完全平方公式及其变形公式．x2＋x－2＝(x±x－1)2∓2，x＋x－1＝(12x±12x-)2∓2，12x＋12x-＝(14x±14x-)2∓2.6、判断一个函数是否为指数函数的方法(1)底数的值是否符合要求．(2)a x前的系数是否为1.(3)指数是否符合要求．7、求指数函数的解析式或函数值(1)求指数函数的解析式时，一般采用待定系数法，即先设出函数的解析式，然后利用已知条件，求出解析式中的参数，从而得到函数的解析式，其中掌握指数函数的概念是解决这类问题的关键．(2)求指数函数的函数值的关键是掌握指数函数的解析式．8、解决有关增长率问题的关键和措施(1)解决这类问题的关键是理解增长(衰减)率的意义：增长(衰减)率是所研究的对象在“单位时间”内比它在“前单位时间”内的增长(衰减)率，切记并不总是只和开始单位时间内的比较．(2)分析具体问题时，应严格计算并写出前3～4个单位时间的具体值，通过观察、归纳出规律后，再概括为数学问题，最后求解数学问题即可．(3)在实际问题中，有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数函数模型表示，通常可以表示为y＝N(1＋p)x(其中N为基础数，p为增长率，x为时间)的形式．9、函数y＝a f(x)定义域、值域的求法(1)定义域：形如y＝a f(x)形式的函数的定义域是使得f(x)有意义的x的取值集合．(2)值域：①换元，令t＝f(x)；②求t＝f(x)的定义域x∈D；③求t＝f(x)的值域t∈M；④利用y＝a t的单调性求y＝a t，t∈M的值域．注意：(1)通过建立不等关系求定义域时，要注意解集为各不等关系解集的交集．(2)当指数型函数的底数含字母时，在求定义域、值域时要注意分类讨论．10、处理函数图象问题的策略(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的x，y的值，即可得函数图象所过的定点．(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)．(3)利用函数的性质：奇偶性与单调性．11、比较幂值大小的3种类型及处理方法12、简单的指数不等式的解法(1)利用指数型函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式．(2)解不等式a f(x)>a g(x)(a>0，a≠1)的依据是指数型函数的单调性，要养成判断底数取值范围的习惯，若底数不确定，就需进行分类讨论，即a f(x)>a g(x)⇒f(x)>g(x)(a>1)或f(x)<g(x)(0<a<1)．13、指数型复合函数的单调性(1)求复合函数的单调区间，首先求出函数的定义域，然后把函数分解成y＝f(u)，u＝φ(x)，通过考察f(u)和φ(x)的单调性，利用同增异减原则，求出y＝f(φ(x))的单调性．(2)关于指数型函数y＝a f(x)(a>0，且a≠1)的单调性由两点决定，一是底数a>1还是0<a<1；二是f(x)的单调性，它由两个函数y＝a u，u＝f(x)复合而成．考点一指数与指数幂的运算（一）根式化简求值1．（2022·西藏·拉萨中学高一期末）若a=b=a b+的值为（）π-A．1B．5C．1-D．25x<时，化简x__________. 2．（2022·上海长宁·高一期末）当03．（2022·全国·=_______．（二）利用分数指数幂的运算性质化简求值4．（2022·河南洛阳·高一期末）计算：22332728-⎛⎫⎛⎫⋅+⎪ ⎝⎭⎝⎭______．5．（2022·全国·04(1=___________________．6．（2022·江西·景德镇一中高一期末）化简)()146230.251624820229-=⎛⎫⨯+-⨯+- ⎪⎝⎭____________.7．（2022·全国·高一单元测试）计算：(1)21023213(2)(9.6)(3(1.5)48-----+；10421()0.252-+⨯.（三）整体代换法求分数指数幂8．（2022·江西省铜鼓中学高一期末）已知223x x --=，求44x x -+的值；9．（2022·广东汕头·高一期末）已知11223x x -+=，求1x x --的值．10．（2022·辽宁·大连二十四中高一期末）已知11223a a --=，求33221122a a a a----的值；考点二指数函数的概念（一）指数函数的概念11．（2022·青海·大通回族土族自治县教学研究室高一期末）若()233xy a a a =-+是指数函数，则有（）A ．1a =或2B ．1a =C ．2a =D ．0a >且1a ≠12．（2022·甘肃·甘南藏族自治州合作第一中学高一期末）已知函数()()33x f x k a b ⋅=++-(0a >，且1a ≠)是指数函数.(1)求k ，b 的值；(2)求解不等式()()2743f x f x ->-.（二）求指数函数的解析式或函数值13．（2022·湖南·高一课时练习）已知函数()f x 是指数函数，且35225f ⎛⎫-= ⎪⎝⎭，则()3f =________.14．（2022·浙江大学附属中学高一期末）已知函数1(),02()0xx f x x ⎧≤⎪=⎨⎪>⎩，则[(4)]f f =________.15．（2022·陕西·铜川阳光中学高一期末）设0a >且1a ≠，函数()1,0,0x x x f x a x -≤⎧=⎨>⎩，若()()11f f =-，则a 的值为________．16．（2022·福建·厦门一中高一期末）已知函数()221,1,,1,x x f x x ax x ⎧+<=⎨+≥⎩若()()03f f a =，则a 的值为______．17．（2022·云南昆明·高一期末）已知函数()x f x a =，()xg x b =，若()()115f g +=，()()111f g -=．(1)求()f x ，()g x 的解析式；(2)若()()f m g n =，试比较m ，n 的大小．18．（2022·广东汕头·高一期末）已知函数()1x f x a =-（0a >，且1a ≠）满足()()14129f f +=-.(1)求a 的值；(2)解不等式()2f x >.考点三指数函数的定义域和值域（一）指数函数的定义域19．（2022·全国·高一课时练习）函数y =的定义域为（）A．(-∞B．(-∞C ．[)3,+∞D ．()3,+∞20．（2022·广东广州·高一期末）函数1()1f x x =-的定义域为______．21．（2022·全国·高一课时练习）函数()f x =______________．22．（2022·全国·高一单元测试）已知函数()f x =[)2,+∞，则=a _________．（二）指数函数的值域23．（2022·吉林·长春外国语学校高一期末）已知集合{}2320A x x x =-+≥，{}3,1x B y y x ==≥，那么A B =（）A ．[]2,3B ．[](]2,3,1-∞C ．()3,+∞D ．[)3,+∞24．（2022·湖南邵阳·高一期末）函数2212x y -⎛⎫= ⎪⎝⎭的值域为______．25．（2022·浙江省义乌中学高一期末）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的美誉，用其名字命名的“高斯函数":设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，也称取整函数，例如:][1.32 3.43⎡⎤-=-=⎣⎦，，已知11()313x f x =-+，则函数[]()y f x =的值域为（）A ．{}0B ．{}10-，C ．{}01，D ．{}101-，，26．（2022·天津南开·高一期末）定义运算a b *为：,(){,(),a ab a b b a b ≤*=>如121*=，则函数()22x x f x -=*的值域为（）A ．RB ．(]0,1C ．()0,∞+D ．[)1,+∞27．（2022·辽宁鞍山·高一期末）若函数()f x =的值域为[0,)+∞，则实数a 的取值范围是（）A ．12⎧⎫⎨⎬⎩⎭B ．1,2⎡⎫+∞⎪⎢⎣⎭C ．1,2⎛⎤-∞ ⎥⎝⎦D ．[0,)+∞28．（2022·山东烟台·高一期末）已知函数()()112,03,0x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ，则实数a 的取值范围为___________.29．（2022·广东湛江·高一期末）已知函数()(0,1)x f x a b a a =+>≠的定义域和值域都是[1,0]-，则a b +=（）A ．32-B ．1-C ．1D ．32考点四指数函数的图象及应用（一）判断指数型函数图象的形状30．（2022·湖北黄石·高一期末）函数()2||24x x f x =-的图象大致为（）A ．B ．C ．D ．31．（2022·陕西咸阳·高一期末）函数()241x x xf x =+的大致图像为（）A ．B ．C ．D ．32．（2022·福建·莆田一中高一期末）函数3()22x xx xf x --=+的部分图象大致为（）A ．B ．C ．D ．33．（2022·河南安阳·高一期末）函数()22xf x x -=⋅在区间[]22-,上的图象可能是（）A ．B ．C ．D ．34．（2022·云南玉溪·高一期末）函数||()2x f x =，4()g x x =，则函数()()y f x g x =+的图象大致是（）A ．B ．C ．D ．35．（2022·陕西渭南·高一期末）函数y x a =+与x y a -=（0a >且1a ≠）在同一坐标系中的图象可能是（）A ．B ．C ．D ．36．【多选】（2022·吉林吉林·高一期末）已知函数()()()f x x a x b =--的图象如图所示，则()x g x a b =-的图象可能是（）A ．B ．C ．D ．（二）根据指数型函数图象判断参数范围37．（2022·全国·高一课时练习）已知113xy ⎛⎫= ⎪⎝⎭，23x y =，310x y -=，410x y =，则在同一平面直角坐标系内，它们的图象大致为（）A ．B ．C ．D ．38．（2022·全国·高一单元测试）函数①x y a =；②x y b =；③x y c =；④x y d =的图象如图所示，a ，b ，c ，d 分别是下列四个数：5413，12中的一个，则a ，b ，c ，d 的值分别是（）A ．5413，12B 54，13，12C ．12，1354，D ．13，12，5439．【多选】（2022·全国·高一期末）(多选)已知函数()x f x a b =-的图象如图所示，则（）A ．a >1B ．0<a <1C ．b >1D ．0<b <140．（2022·湖南·长沙市雨花区教育科学研究所高一期末）若函数(01,1)x y a a a m =>-≠+的图像在第一、三、四象限内，则（）A ．1a >B ．1a >，且0m <C ．01a <<，且0m >D ．01a <<41．（2022·上海交大附中高一期末）已知函数()()1201x f x a a a +=->≠，，的图象不经过第四象限，则a 的取值范围为__________．42．（2022·全国·高一课时练习）若函数32x y m =-+的图象不经过第二象限，则实数m 的取值范围是（）A ．（-∞，-2）B ．（-∞，-2]C ．（3，+∞）D ．[3，+∞）43．（2022·全国·高一期末）已知函数f (x )＝ax ＋b (a >0，且a ≠1)．(1)若()f x 的图象如图①所示，求a ，b 的值；(2)若()f x 的图象如图②所示，求a ，b 的取值范围；(3)在(1)中，若|()|f x ＝m 有且仅有一个实数解，求出m 的取值范围．（三）指数型函数过定点问题44．（2022·四川泸州·高一期末）函数3x y a =+（0a >且1a ≠）的图象恒过定点（）A ．()1,0B ．()0,4C ．()4,0D ．()3,345．（2022·江西省铜鼓中学高一期末）函数11x y a -=+，（0a >且1a ≠）的图象必经过一个定点，则这个定点的坐标是（）A ．()0,1B ．()1,2C ．()2,3D ．()3,446．（2022·安徽芜湖·高一期末）已知函数23x y a -=+（0a >且1a ≠）过定点P ，且P 点在幂函数()f x 的图象上，则(3)f 的值为_________．47．（2022·河南焦作·高一期末）已知函数()25x f x a -=-（0a >且1a ≠）的图象过定点(),m n ，则不等式210x mx n +++<的解集为（）A ．()1,3B ．()3,1--C ．()(),31,-∞-⋃+∞D ．()3,1-48．（2022·河南·永城市苗桥乡重点中学高一期末）已知函数42x y a +=+（0a >，且1a ≠）的图象恒过点P ，若角α的终边经过点P ，则cos α的值为（）A ．45-B ．223-C ．23D ．3549．（2022·广东揭阳·高一期末）已知0a >且1a ≠，函数()22x f x a -=-的图象恒经过定点(),m n ，正数b 、c 满足b c m n +=+，则14bc+的最小值为____________.（四）指数函数图象应用50．（2022·全国·高一课时练习）（1）若曲线21x y =-与直线y a =有两个公共点，则实数a的取值范围是______；（2）若曲线21xy =+与直线y b =没有公共点，则实数b 的取值范围是______．51．【多选】（2022·全国·高一课时练习）已知函数()21xf x =-，实数a ，b 满足()()f a f b =()a b <，则（）A ．222a b +>B ．a ∃，b ∈R ，使得01a b <+<C ．222a b +=D ．0a b +<52．（2022·辽宁·高一阶段练习）函数()|21|x f x =-(1)请在下面坐标系中画出函数()f x 的图像．(2)不等式13()44f x x <+的解集为________．（写出结果即可，不需写过程）(3)若()(),m n f m f n <=，求m n +的取值范围．考点五指数型函数的单调性（一）判断指数函数的单调性53．（2022·广西南宁·高一期末）设函数()122xx f x ⎛⎫=- ⎪⎝⎭，则()f x （）A ．是偶函数，且在()0,+∞单调递增B ．是偶函数，且在()0,+∞单调递减C ．是奇函数，且在()0,+∞单调递增D ．是奇函数，且在()0,+∞单调递减54．（2022·吉林·长春外国语学校高一期末）下列函数中，在其定义域内既是奇函数又是减函数的是（）A ．y x=-B ．12xy ⎛⎫= ⎪⎝⎭C ．3y x x =--D ．1y x=-55．（2022·浙江金华第一中学高一期末）已知函数()f x 的定义域为R ，且满足对任意12x x <，有()()12121f x f x x x ->--，则函数()f x =（）A ．xe -B ．2x x+C ．x e x-D x（二）由指数（型）函数的单调性求参数56．（2022·河北廊坊·高一期末）指数函数()()1xf x a =-在R 上单调递减，则实数a 的取值范围是（）A ．()2,1--B ．()2,+∞C ．(),2-∞-D ．()1,257．（2022·安徽·歙县教研室高一期末）若函数22113x mx y +-⎛⎫= ⎪⎝⎭在区间[]1,1-上为增函数，则实数m 的取值范围为______.58．【多选】（2022·重庆市巫山大昌中学校高一期末）若函数,0()3(1),0x a a x f x a x x ⎧+≥=⎨+-<⎩（0a >且1a ≠）在R 上为单调函数，则a 的值可以是（）A ．13B ．23C D ．259．（2022·湖北·沙市中学高一期末）已知函数(),0()23,0x a x f x a x a x ⎧<⎪=⎨-+≥⎪⎩，满足对任意x 1≠x 2，都有()()1212f x f x x x -<-0成立，则a 的取值范围是（）A ．a ∈(0,1)B ．a ∈[34,1)C ．a ∈(0,13]D ．a ∈[34,2)60．（2022·江苏南通·高一期末）已知指数函数()xf x a -=（0a >，且1a ≠），且()()23f f ->-，则a 的取值范围（）A ．()0,1B ．()1,+∞C ．()0,∞+D ．(),0∞-（三）比较指数幂的大小61．（2022·云南丽江·高一期末）若221333111,,252a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则a ､b ､c 的大小关系是（）A ．b a c <<B ．b c a<<C ．c a b<<D ．c b a<<62．（2022·广东汕尾·高一期末）若1312a ⎛⎫= ⎪⎝⎭，1314b ⎛⎫= ⎪⎝⎭，1412c ⎛⎫= ⎪⎝⎭，则（）A ．c a b >>B ．c b a >>C ．b c a >>D ．a b c>>63．（2022·全国·高一专题练习）设函数()21xf x =-，c b a <<，且()()()f c f a f b >>，则22a c +与2的大小关系是（）A ．222a c +>B ．222a c +≥C ．222a c +≤D ．222a c +<（四）解简单的指数不等式64．（2022·黑龙江·哈尔滨市第一六二中学校高一期末）不等式11(93x -≤的解集为_____________.65．（2022·河北张家口·高一期末）已知x R ∈，那么“4x >”是“124x -<”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件66．（2022·云南·昆明一中高一期末）设函数2,2()2,2x x x f x x ≤⎧=⎨>⎩，若2(2)(8)f t f t >-，则t 的取值范围是___________.67．（2022·湖南衡阳·高一期末）设函数()1e ,11,1x x x f x x x x -⎧+≤⎪=⎨+>⎪⎩，则满足()()12xf x f ->的x 的取值范围是（）A ．(],1-∞-B ．()0,∞+C ．()1,0-D ．(),0∞-考点六指数函数的最值（一）求已知指数型函数的最值68．（2022·甘肃·兰州一中高一期末）已知02x ≤≤，则函数124325x x y -=-⨯+的最大值为__________.69．（2022·河南开封·高一期末）已知函数()2x f x =的定义域是[]0,3，设()()()22g x f x f x =-+，(1)求()g x 的定义域；(2)求函数()g x 的最大值和最小值.（二）根据指数函数的最值求参数70．（2022·湖北·武汉市第十五中学高一期末）函数()21x x f x a a =++（0a >，且1a ≠）在[]1,1-上的最大值为13，则实数a 的值为___________.71．（2022·上海·高一单元测试）指数函数(0,1)x y a a a =>≠在区间[0,4]上的最大值与最小值之和为17，则=a ______;72．（2022·上海徐汇·高一期末）已知函数()()1,1,,1x a x x f x a x ⎧-≤=⎨>⎩（0a >且1a ≠）在x ∈R 上有最大值，那么实数a 的取值范围为__________73．（2022·全国·高一单元测试）已知242,0()1,0x x m x f x x x x +⎧-+≤⎪=⎨+>⎪⎩的最小值为2，则m 的取值范围为______________74．（2022·湖南·高一期末）已知函数()245x xf x a a =+-.(1)求()f x 的值域；(2)当[]1,2x ∈-时，()f x 的最大值为7，求a 的值.（三）指数函数的最值与不等式的综合问题75．（2022·江苏·无锡市教育科学研究院高一期末）已知函数()24,[2,1]x x f x x =-∈-.(1)求()f x 的值域；(2)若对[2,1]x ∀∈-，不等式()22x f x m >-⋅恒成立，求实数m 的取值范围.76．（2022·浙江宁波·高一期中）已知函数()212xxf x a=++(1)若()f x 是奇函数，求a 的值；(2)若()0f x ≥在[]1,1x ∈-上恒成立，求a 的取值范围．77．（2022·全国·高一课时练习）已知函数()()240,12x x a af x a a a a-+=>≠+是定义在R 上的奇函数．(1)求a 的值；(2)求函数()f x 的值域；(3)当()1,2x ∈时，()220xmf x +->恒成立，求实数m 的取值范围．考点七指数型函数的奇偶性（一）已和函数奇偶性求值78．（2022·内蒙古包头·高一期末）()f x 是定义域为R 的函数，且2()f x x -为奇函数，()2x f x +为偶函数，则(2)f 的值是（）A ．178B ．174C ．478D ．47479．（2022·广东广州·高一期末）已知函数()()2,0,x x f x g x x ⎧<⎪=⎨>⎪⎩为奇函数，则(2)g =______．（二）由函数的奇偶性求解析式80．（2022·福建福州·高一期末）已知函数()f x 是定义在R 上的偶函数，当0x ≥时，()23x f x =+．求()f x 的解析式；81．（2022·江西新余·高一期末）已知定义在R 上的偶函数f （x ）和奇函数g （x ）满足()()124x f x g x +-=(1)求函数f （x ）和g （x ）的表达式；(2)当1,02x ⎛⎫∈- ⎪⎝⎭时，不等式()()210f x ag x -+≥恒成立，求实数a 的取值范围.（三）已和函数奇偶性求参数82．（2022·辽宁丹东·高一期末）已知函数()22x x af x a-=+是奇函数．(1)求实数a 的值；(2)求()f x 的值域．83．（2022·天津南开·高一期末）已知函数()f x =122xx a b+⋅+是奇函数，并且函数()f x 的图像经过点()1,3.(1)求实数a ，b 的值；(2)求函数()f x 在0x <时的值域.84．（2022·浙江师范大学附属中学高一期中）已知函数()31xx a f x =+（0a >）为偶函数，则函数()f x 的值域为__________．（四）函数的单调性和奇偶性的综合85．（2022·河南·新乡市第一中学高一期末）已知定义在R 上的函数()22x xf x k -=-⋅是奇函数．(1)求实数k 的值；(2)若对任意的R x ∈，不等式()()240f x tx f x ++->恒成立，求实数t 的取值范围．86．（2022·云南丽江·高一期末）已知函数()333x xf x x -=+-，若2(2)(54)0f a a f a -+-<，则实数a 的取值范围为（）A ．(4)(4)-∞-+∞，，B ．(41)-，C ．(1)(4)-∞-+∞，，D ．(14)-，考点八指数函数的综合问题87．【多选】（2022·全国·高一课时练习）（多选）已知函数()24312x x f x ++⎛⎫= ⎪⎝⎭，则（）A ．函数()f x 的定义域为RB ．函数()f x 的值域为(]0,2C ．函数()f x 在[)2,-+∞上单调递增D ．函数()f x 在[)2,-+∞上单调递减88．（2022·辽宁·大连二十四中高一期末）已知指数函数()()01xf x a a a =>≠,过点()1,2，函数()()()11f xg x x f x -=⋅+.(1)求()1g ，()1g -的值；(2)判断函数()g x 在R 上的奇偶性，并给出证明；(3)已知()g x 在[)0,+∞上是单调函数，由此判断函数()y g x =，R x ∈的单调性（不需证明），并解不等式()1213g x +>.89．（2022·山东·德州市第一中学高一期末）已知定义域为R 的函数()22x x b nf x b +=--是奇函数，且指数函数x y b =的图象过点(2,4)．（Ⅰ）求()f x 的表达式；（Ⅱ）若方程()23()0f x x f a x ++-+=，(4,)x ∈-+∞恰有2个互异的实数根，求实数a 的取值集合；（Ⅲ）若对任意的[1,1]t ∈-，不等式()22(1)0f t a f at -+-≥恒成立，求实数a 的取值范围．考点九指数增长型和指数衰减型函数的实际应用90．（2022·全国·高一课时练习）当生物体死亡后，它机体内原有的碳14含量每经过5730年衰减为原来的一半，这个时间称为“半衰期”.当死亡生物体内的碳14的含量不足死亡前的万分之一时，用一般的放射性探测器就测不到碳14了.若用一般的放射性探测器不能测到碳14，那么死亡生物体内的碳14至少经过的“半衰期”个数是（参考数据：1328192=）（）A ．15B ．14C ．13D ．1291．（2022·全国·高一单元测试）企业在生产中产生的废气要经过净化处理后才可排放，某企业在净化处理废气的过程中污染物含量P （单位：mg /L ）与时间t （单位：h ）间的关系为0ektP P -=（其中0P ，k 是正的常数）．如果在前10h 消除了20%的污染物，则20h 后废气中污染物的含量是未处理前的（）A ．40%B ．50%C ．64%D ．81%92．（2022·全国·高一学业考试）某医药研究所开发一种新药，如果成年人按规定的剂量服用，据监测，服药后每毫升血液中的含药量()g μy 与时间()h t 之间近似满足如图所示的图象，则y 关于t 的函数解析式为______；据进一步测定，每毫升血液中含药量不少于0.25g μ时，治疗疾病有效，则服药一次治疗疾病有效的时间为______h ．93．（2022·重庆·高一期末）基本再生数0R 与世代间隔T 是流行病学基本参数，基本再生数是指一个感染者传染的平均人数，世代间隔指两代间传染所需的平均时间，在α型病毒疫情初始阶段，可以用指数函数模型(e )rt I t =描述累计感染病例数()I t 随时间t （单位：天）的变化规律，指数增长率r 与0R 、T 近似满足01R rT =+，有学者基于已有数据估计出0 3.22R =，10T =.据此，在α型病毒疫情初始阶段，累计感染病例数增加至(0)I 的4倍，至少需要（）（参考数据：ln 20.69≈）A ．6天B ．7天C ．8天D ．9天。

课时4指数函数一. 指数与指数幂的运算（1）根式的概念 ①如果,,,1nxa a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n表示；当n 是偶数时，正数a 的正的nn次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当na =；当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m naa m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数． （3）分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质（4）指数函数a 变化对图象影响在第一象限内，a 越大图象越高，越靠近y 轴； 在第二象限内，a 越大图象越低，越靠近x 轴． 在第一象限内，a 越小图象越高，越靠近y 轴； 在第二象限内，a 越小图象越低，越靠近x 轴．三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析：A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析：当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=［f(x)］n D.f ［(xy)n ］=［f(x)］n ［f(y)］n (n ∈N *) 解析：易知A 、B 、C 都正确. 对于D,f ［(xy)n］=a(xy)n,而［f(x)］n·［f(y)］n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析：a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析：令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析：因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明：∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.［1,+∞)C.(0,+∞)D.(-∞,+∞)解析：当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1］;当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析：可利用函数图象的对称性来判断两图象的关系.10.当x ∈［-1,1］时,函数f(x)=3x -2的值域为_______［-35,1］___________. 解析：f(x)在［-1,1］上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析：(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩［2,+∞］=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈［-3,2］的最大值和最小值. 解：设2-x =t,由x ∈［-3,2］得t ∈［41,8］,于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解：∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.［1,2］B.［2,3］C.(-∞,2]D.［2,+∞)解析：因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈［2,+∞)上递增,故所求的递增区间为［2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.［-1,+∞)B.［-1,63) C.［0,+∞)D.(0,63］解析：由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=［f(x)-1］2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈［1,9］. ∴所求值域为［-1,63］.2.1指数函数练习1．下列各式中成立的一项（）A ．7177)(m n mn= B ．31243)3(-=-C ．43433)(y x y x +=+D ．3339=2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 6B ．a -C ．a 9-D ．29a3．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确的是（） A ．f (x +y )=f(x )·f (y ) B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)(+∈=N n y f x f xy f n n n4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数x a y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于 （）A ．251+B ．251+- C ．251± D ．215± 6．当a ≠0时，函数y ax b =+和y b ax =的图象只可能是 （）7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围 （）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．函数22)21(++-=x x y 得单调递增区间是 （）A ．]21,1[-B ．]1,(--∞C ．),2[+∞D ．]2,21[10．已知2)(xx e e x f --=，则下列正确的是 （）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 11．已知函数f (x )的定义域是（1，2），则函数)2(x f 的定义域是. 12．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点. 三、解答题：13．求函数y x x =--1511的定义域.14．若a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）证明f (x )在(－∞，+∞)上是增函数.16．函数f(x)＝a x(a>0，且a ≠1)在区间[1,2]上的最大值比最小值大，求a 的值．参考答案一、DCDDDAADDA二、11．(0,1)；12．(2，－2)； 三、13．解：要使函数有意义必须：∴定义域为：{}x x R x x ∈≠≠且01,14．解：rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+，其中10,10<<<<cbc a . 当r ＞1时，1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr，所以a r +b r ＜c r； 当r ＜1时，1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ，所以a r +b r ＞c r . 15．解：(1)是奇函数.(2)设x 1＜x 2，则1111)()(221121+--+-=-x x x x a a a a x f x f 。

高一数学指数和函数知识点引言：数学是一门抽象而又实用的学科，在我们的日常生活中无处不在。

数学中的指数和函数是我们学习数学的基础知识点之一，它们具有广泛的应用和重要性。

本文将分析高一数学中涉及指数和函数的几个重要知识点，并探讨其实际应用。

1. 指数的基本概念与运算：在数学中，指数是表示一个数被乘若干次的方法。

例如，2²表示2被乘以2，即2的平方。

指数具有重要的运算法则，如指数相乘时底数相同，则指数相加。

此外，指数还可以是分数或负数，分别代表幂次的开平方和倒数。

2. 指数函数的性质与图像：指数函数是以指数为自变量的函数。

常见的指数函数有f(x) = a^x，其中a为底数，x为指数。

指数函数具有独特的性质，如当底数大于1时，函数呈现增长趋势；当底数介于0和1之间时，函数呈现衰减趋势。

指数函数的图像通常具有一条曲线，并根据底数的不同而呈现不同的形状。

3. 对数的定义与运算：对数是指一个数在某个底数下所得到的指数。

例如，log₂8表示以2为底数，求得8的对数，结果为3。

对数也具有运算法则，如对数相除时，底数相同，则指数相减。

4. 对数函数的性质与图像：对数函数是以对数为自变量的函数。

常见的对数函数有f(x) = logₐx，其中a为底数，x为对数。

对数函数具有特殊的性质，如当底数大于1时，函数呈现增长趋势；当底数介于0和1之间时，函数呈现衰减趋势。

对数函数的图像通常具有一条曲线，并根据底数的不同而呈现不同的形状。

5. 指数方程与对数方程的求解：指数方程和对数方程是数学中常见的方程类型，它们的求解对于解决实际问题非常重要。

求解指数方程和对数方程的关键是运用指数和对数的运算法则，将方程转化为简化形式后进行求解。

6. 指数增长与复利计算：指数增长是指以某个固定比例增长的现象，如人口增长、物质衰变等。

在实际生活中，我们常常需要计算指数增长的结果，这时可以借助指数函数的概念进行计算。

特别是在金融领域，复利的概念与指数增长密切相关。

高一指数基本知识点引言：在数学的学习过程中，指数是一种非常重要且基础的概念。

在高中阶段，指数的学习更加深入和系统化，掌握好指数的基本知识点对于学习后续数学知识是至关重要的。

本文将介绍高一指数的基本知识点，帮助读者理解和掌握指数的概念、性质和应用。

一、指数的概念指数是数学中常用的一种表示形式，也被称为幂。

指数表示有一个数（底数）连乘若干次自身所得的结果。

指数的定义：若a是任意一个不等于零且不等于1的实数，b是一个自然数（包括零），那么指数b就是以a为底的指数，记作a^b。

例如，2^3表示2的3次方，即2乘以2乘以2，结果为8。

二、指数的性质1. 同底数幂相乘：在指数运算中，如果底数相同，幂相加。

例如，2^3 * 2^4 = 2^(3+4) = 2^7。

2. 同底数幂相除：在指数运算中，如果底数相同，幂相减。

例如，3^5 / 3^2 = 3^(5-2) = 3^3。

3. 幂的指数相乘：在指数运算中，一个数的幂再求幂，指数相乘。

例如，(2^3)^4 = 2^(3*4) = 2^12。

4. 幂的指数相除：在指数运算中，一个数的幂再求幂，指数相除。

例如，(2^4)^3 = 2^(4/3) = 2^(4*3)。

5. 指数为0：任何数的0次方均为1。

例如，3^0 = 1。

6. 指数为负数：如果指数为负数，那么可以将其化为倒数的正指数。

例如，4^-2 = 1 / 4^2。

三、指数的应用在实际生活和学习中，指数有许多重要的应用。

以下介绍两个常见的指数应用。

1. 指数函数：指数函数是一种以常数e为底的指数，记为f(x) = e^x。

指数函数在数学和科学领域中有广泛的应用，如在物理学中描述指数增长、在概率论中描述随机过程等。

2. 科学计数法：科学计数法是一种使用指数来表示较大或较小的数字的方法。

将一个数表示成一个在1和10之间的数与某个幂的乘积的形式。

例如，300,000可表示为3×10^5，0.000002可表示为2×10^-6。

高一数学指数与指数函数试题答案及解析1.若，则在，，，中最大值是（）A．B．C．D．【答案】C【解析】由指数函数的性质，得，；由幂函数的性质得，因此最大的是.【考点】指数函数和幂函数的性质.2.设，，，则（）A．b<a<c B．c<a<b C．c<b<a D．a<c<b【答案】B【解析】,,【考点】指数函数和对数函数的性质.3.设均为正数，且，，.则（）A．B．C．D．【答案】C【解析】分别为方程的解，由图可知.【考点】函数图像4.若函数的图像与轴有公共点，则的取值范围是（）A．B．C．D．【答案】B【解析】函数与轴有公共点，即设函数,,有交点，函数如图:,即,故选B.【考点】函数图像5.已知函数和函数，其中为参数，且满足.（1）若，写出函数的单调区间（无需证明）；（2）若方程在上有唯一解，求实数的取值范围；（3）若对任意，存在，使得成立，求实数的取值范围.【答案】（1）的单调增区间为，，单调减区间为；（2）或；（3）.【解析】（1）当时，，由二次函数的图像与性质可写出函数的单调区间；（2）先将在上有唯一解转化为在上有唯一解，进而两边平方得到或，要使时，有唯一解，则只须或即可，问题得以解决；（3）对任意，存在，使得成立的意思就是的值域应是的值域的子集，然后分别针对与两种情形进行讨论求解，最后将这两种情况求解出的的取值范围取并集即可.试题解析：（1）时， 1分函数的单调增区间为，，单调减区间为 4分（2）由在上有唯一解得在上有唯一解 5分即，解得或 6分由题意知或即或综上，的取值范围是或 8分（3）则的值域应是的值域的子集 9分①时，在上单调递减，上单调递增，故 10分在上单调递增，故 11分所以，即 12分②当时，在上单调递减，故在上单调递减，上单调递增，故所以，解得.又，所以 13分综上，的取值范围是 14分.【考点】1.二次函数的图像与性质；2.指数函数的图像与性质；3.函数的单调性与最值.6.已知指数函数（且）的图像过点，则实数___________.【答案】【解析】因为指数函数（且）的图像过点，则，得.【考点】指数函数的定义.7.将函数的图像向左平移一个单位，得到图像，再将向上平移一个单位得到图像，作出关于直线对称的图像，则的解析式为 .【答案】【解析】根据平移口诀“上加下减”可得函数解析式为，函数解析式为，因为图像与图像关于直线对称，所以函数与函数互为反函数。

高一数学指数及指数函数1•根式的性质(3)负数没有偶次方根 (4)零的任何正次方根都是零2•幕的有关概念 (1)正整数指数幕：naa a a ..… n...... a (n N )(2)零指数幕a 01(a 0)1⑶负整数指数幕 a p-(a 0.p N )a pm(4)正分数指数幕a nnma (a0, m, n N ,且 n 1) (5)负分数指数幕a m1 nm(a0, m, n N ,且 n 1)a 石(6)0的正分数指数幕等于0，0的负分数指数幕无意义3•有理指数幕的运算性质rr s⑶(ab) a a ,(a0,b 0, r Q)4、指数函数的定义：函数y a% 0且a °叫做指数函数，其中x 是自变量，函数定义域是R 。

① 若a 0，则当x 0时，『0；当x 0时，a x 无意义.1 1② 若a 0，则对于X 的某些数值，可使a 无意义•如(2)，这时对于 4，2，等等，在实数范围内函数值不存在•③ 若a 1，则对于任何x R ，a x 1，是一个常量，没有研究的必要性• 对于任何x R ，「都有意义，且『0.因此指数函数的定义域是R ，值域是(°)有些函数貌似指数函数，实际上却不是，如y 『k (a 0且 a 1，k Z )；x有些函数看起来不像指数函数，实际上却是，如y a (a 0且a 1)，因为它可 x1 1 1 0 1 a ，其中a ，且a(1)当n 为奇数时，有n a na(2)当n 为偶数时，有；a" a a, (a 0) a, (a 0)r sr s .八 亠、(1) a a a ,(a 0, r, s Q)/ r、srs , -亠、⑵(a )a ,(a 0,r,s Q)以化为y5、函数的图象(1)①特征点：指数函数y = a x (a > 0且a ^ 1) 的图象经过两点(0 , 1)和(1,a).②指数函数y = a x (a > 0且a 工1)的图象中，y = 1 反映了它的分布特征；而直线x = 1 与指数函数图象的交点(1,a)的纵坐 标则直观反映了指数函数的底数特 征，称直线x = 1和y = 1为指数函 数的两条特征线•(2)、函数的图象单调性当a > 1时，函数在定义域范围内 呈单调递增； 当0v a v 1时，函数在定义域范围 内呈单调递减； 推论：(1)底互为倒数的两个函数图像关于y 轴对称(2)当a > 1时，底数越大，函数图象越靠近丫轴；当0v a v 1时，底数越小， 函数图象越靠近丫轴。

高一数学指数与指数函数试题答案及解析1.设，则的大小关系是（）.A．B．C．D．【解析】，，，因此.【考点】指数函数和对数函数的性质.2.若点在函数的图象上，则的值为．【答案】【解析】由点在函数的图象上得，所以，故应填入．【考点】指数函数及特殊角的三角函数．3.设，则下列不等式成立的是（）A．若，则B．若，则C．若，则D．若，则【答案】A【解析】对于A,B考查函数f（x）=2x+2x，g（x）=2x+3x的单调性与图象：可知函数f（x）、g（x）在R上都单调递增，若2a+2a=2b+3b，则a＞b，因此A正确；对于C,D分别考查函数u（x）=2x-2x，v（x）=2x-3x单调性与图象：当时，u′（x）＜0，函数u（x）单调递减；当时，u′（x）＞0，函数u（x）单调递增．故在x=取得最小值．当0＜x＜时，v′（x）＜0，函数v（x）单调递减；当x＞时，v′（x）＞0，函数v （x）单调递增．故在x＝取得最小值，据以上可画出图象．据图象可知：当2a-2a=2b-3b，a＞0，b＞0时，可能a＞b或a＜b．因此C,D不正确．综上可知：只有A正确．故答案为A．【考点】用导数研究函数的单调性和图象；命题的真假判断与应用．4.若，则（）A．B．C．D．【答案】D【解析】由得，所以.【考点】指对数式的互化，指数运算法则.5.若函数的图像与轴有公共点，则的取值范围是（）A．B．C．D．【答案】B【解析】函数与轴有公共点，即设函数,,有交点，函数如图: ,即,故选B.【考点】函数图像6.三个数的大小关系为（）A．B．C．D．【答案】D【解析】；；。

所以，故D正确。

【考点】指数对数函数的单调性。

7.已知幂函数的图象过点，则．【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算8.如图，在平面直角坐标系中，过原点O的直线与函数的图象交于A，B两点，过B作y轴的垂线交函数的图象于点C，若AC平行于y轴，则点A的坐标是．【答案】【解析】设，则，因为AC平行于y轴，所以，因此.又三点三点共线，所以由得，因此.【考点】指数函数运算，向量共线.9.已知指数函数（且）的图像过点，则实数___________.【答案】【解析】因为指数函数（且）的图像过点，则，得.【考点】指数函数的定义.10.我国大西北某地区荒漠化土地面积每年平均比上一年增长，专家预测经过年可能增长到原来的倍，则函数的图像大致为（）【答案】D【解析】设初始年份的荒漠化土地面积为，则1年后荒漠化土地面积为，2年后荒漠化土地面积为，3年后荒漠化土地面积为，所以年后荒漠化土地面积为，依题意有即，，由指数函数的图像可知，选D.【考点】1.指数函数的图像与性质；2.函数模型及其应用.11.若，则下列结论正确的是（）A．B．C．D．【答案】C【解析】指数函数、对数函数的底数大于1 时,函数为增函数,反之,为减函数，对于幂函数而言，当时，在上递增，当时，在上递减，而，所以，故选C.【考点】1.指数函数；2.对数函数；3.幂函数的性质.12.设函数,如果，求的取值范围.【答案】【解析】对分段函数需分情况讨论，再解指数及对数不等式时，需将实数转化为同底的指数或对数，然后根据指数、对数的单调性解不等式。

高一必修一数学指数知识点在高一的数学课程中，指数是一个重要的概念和工具。

指数是数学中用来表示乘法的简化形式，常用于科学计数法、复利计算、指数函数等领域。

本文将探讨高一必修一数学课程中的指数知识点，以帮助同学们更深入地理解和掌握这一概念。

一、指数的基本概念指数是数学中用来表示乘法的一个重要概念。

在指数表示中，我们使用一个高于基线的小数字表示乘法中的重复几次，称之为指数。

例如，2³表示2乘以自身3次，即2的立方。

指数的一般形式可以表示为aⁿ，其中a称为底数，n称为指数。

在指数中，指数n表示底数a重复相乘的次数。

二、指数的基本运算在高一数学课程中，我们学习了指数的基本运算规则，包括指数幂次运算、指数相乘和指数相除。

对于指数幂次运算，我们有以下规则：1. 任何数的0次幂都是1，即a^0=1。

2. 对于同一个底数的两个指数相乘，我们可以将底数保持不变，指数相加，即a^m * a^n = a^(m+n)。

3. 对于同一个底数的两个指数相除，我们可以将底数保持不变，指数相减，即a^m / a^n = a^(m-n)。

4. 对于指数的指数，我们可以将指数相乘，即(a^m)^n =a^(m*n)。

三、指数的负指数与倒数在指数运算中，指数可以是负数。

一个数的负指数表示将其取倒数后，再按指数幂次运算。

例如，2⁻³表示2的倒数的立方，即1/(2³)。

指数的负指数规则如下：1. 一个数的负指数可以通过取倒数再按照正指数计算。

即a⁻ⁿ= 1/(aⁿ)。

2. 底数为0的数没有意义，因此0的任何负指数都是没有意义的。

四、指数方程与指数函数除了上述基本概念和运算，高一数学课程还涵盖了指数方程和指数函数的知识。

指数方程是含有指数项的方程，形式一般为aⁿ=b。

解指数方程的关键是将其转化为相等底数的指数表达式，然后通过等式的性质来解方程。

指数函数是一个以指数为自变量的函数，通常形式为y=aⁿ，其中a是常数，n是变量。

1.4指数&指数函数
）和两种不同对于指数式来说，式子
）正整数指数幂
）无理指数幂：
定义若（，
为奇数，用符号表示次方根，这时．
，用符号表示
①
②
③（
④（
一般地，指数函数在底数a>1及0<a<1这两种情况下的图象和性质如下表所示：
6.利用函数单调性比较两实数大小，首先要通过观察分析，构造出适当的函数来，对于幂形数，若同指数不同底数，则考虑幂函数，若同底数不同指数，则考虑指数函数；其次比较大小时不仅要注意函数的单调性，还要注意幂形数比大小的两数是否都在同一函数的同一单调区间内，否则无法比较大小．
三、典型例题剖析
例1. (1)化简.
(2)计算.
例2．若的值．
例3．如图是指数函数（1）（2），（3）（4）的图象，则a,b,c,d与1的大小关系是（）
A．B．
C．D．
例4．已知，求函数的最大值和最小值.
例5．已知f(x)＝（a>0且）．
（1）求f(x)的定义域、值域．
（2）讨论f(x)的奇偶性．
（3）讨论f(x)的单调性．。

高中高一数学必修1知识点：指数函数、函数奇
偶性
数学是利用符号语言研究数量、结构、变化以及空间模型等概念的一门学科。

以下是为大家整理的高一数学必修1知识点，希望可以解决您所遇到的相关问题，加油，一直陪伴您。

指数函数的一般形式为，从上面我们对于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得
如图所示为a的不同大小影响函数图形的情况。

可以看到：
(1)指数函数的定义域为所有实数的集合，这里的前提是a 大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。

(2)指数函数的值域为大于0的实数集合。

(3)函数图形都是下凹的。

(4)a大于1，则指数函数单调递增;a小于1大于0，则为单调递减的。

(5)可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中(当然不能等于0)，函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y 轴的正半轴与X轴的负半轴的单调递增函数的位置。

其中水
平直线y=1是从递减到递增的一个过渡位置。

(6)函数总是在某一个方向上无限趋向于X轴，永不相交。

(7)函数总是通过(0，1)这点。

(8)显然指数函数无界。

最后，希望小编整理的高一数学必修1知识点对您有所帮助，祝同学们学习进步。