化工原理例题

三 计算题1 （15分）在如图所示的输水系统中，已知管路总长度（包括所有当量长度，下同）为 100m ，其中压力表之后的管路长度为80m ， 管路摩擦系数为0.03，管路内径为0.05m ， 水的密度为1000Kg/m 3，泵的效率为0.85， 输水量为15m 3/h 。

求：（1）整个管路的阻力损失，J/Kg ； （2）泵轴功率，Kw ； （3）压力表的读数，Pa 。

解：（1）整个管路的阻力损失，J/kg ； 由题意知，s m A Vu s /12.2)405.03600(152=⨯⨯==π 则kg J u d l h f /1.135212.205.010003.0222=⨯⨯=⋅⋅=∑λ （2）泵轴功率，kw ；在贮槽液面0-0´与高位槽液面1-1´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++10,121020022f e h p u gH W p u gH ρρ 其中， ∑=kg J h f /1.135, u 0= u 1=0， p 1= p 0=0（表压）, H 0=0， H=20m 代入方程得： kg J h gH W f e /3.3311.1352081.9=+⨯=+=∑又 s kg V W s s /17.41000360015=⨯==ρ 故 w W W N e s e 5.1381=⨯=， η=80%， kw w N N e 727.11727===η2 （15分）如图所示，用泵将水从贮槽送至敞口高位槽，两槽液面均恒定不变，输送管路尺寸为φ83×3.5mm ，泵的进出口管道上分别安装有真空表和压力表，真空表安装位置离贮槽的水面高度H 1为4.8m ，压力表安装位置离贮槽的水面高度H 2为5m 。

当输水量为36m 3/h 时，进水管道全部阻力损失为1.96J/kg ，出水管道全部阻力损失为4.9J/kg ，压力表读数为2.452×105Pa ，泵的效率为70%，水的密度ρ为1000kg/m 3，试求： （1）两槽液面的高度差H 为多少？ （2）泵所需的实际功率为多少kW ？ （3）真空表的读数为多少kgf/cm 2？解：（1）两槽液面的高度差H在压力表所在截面2-2´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，得：∑-+++=++32,323222222f h p u gH p u gH ρρ 其中， ∑=-kg J h f /9.432,, u 3=0, p 3=0,p 2=2.452×105Pa, H 2=5m, u 2=Vs/A=2.205m/s代入上式得： m H 74.2981.99.481.9100010452.281.92205.2552=-⨯⨯+⨯+= （2）泵所需的实际功率在贮槽液面0-0´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++30,323020022f e h p u gH W p u gH ρρ 其中， ∑=-kg J h f /9.864.630,, u 2= u 3=0, p 2= p 3=0, H 0=0， H=29.4m代入方程求得： W e =298.64J/kg ， s kg V W s s /101000360036=⨯==ρ 故 w W W N e s e 4.2986=⨯=， η=70%， kw N N e 27.4==η（3）真空表的读数在贮槽液面0-0´与真空表截面1-1´间列柏努利方程，有：∑-+++=+++10,1211020022f h p u gH p u gH ρρ 其中，∑=-kg J hf /96.110,, H 0=0， u 0=0, p 0=0, H 1=4.8m,u 1=2.205m/s代入上式得， 2421/525.01015.5)96.12205.28.481.9(1000cm kgf Pap -=⨯-=++⨯-= 3 用离心泵把20℃的水从储槽送至水洗塔顶部，槽内水位维持恒定。

柏努利方程应用例题：1、20℃的空气在直径为80mm 的水平管流过。

现于管路中接一文丘里管，如图：文丘里管的上游接一水银U 管压差计，在直径为20mm 的喉颈处接一细管，其下部插入水槽中。

空气流过文求里管的能量损失可忽略不计。

当U 管压差计读数R=25mm ，h=0.5m 时，试求此时空气的流量为若干m 3/h 。

当地大气压强为101.33kPa 。

文丘里管上游测压口处的表压强为p 1=ρHg g R =13600×9.81×0.025=3335Pa(表压)喉颈处的表压强为p 2=－ρgh =－1000×9.81×0.5=－4905Pa （表压） 空气流经截面1-1'与2-2'的压强变化为（绝对压强） ()()%20%9.7079.0333510133049051013303335101330121<==+--+=-p p p 故可按不可压缩流体来处理。

两截面间的空气平均密度为()300 1.20kg/m 10133029349053335211013302734.22294.22=⨯⎥⎦⎤⎢⎣⎡-+⨯===Tp p T M m m ρρ 在截面1-1'与2-2'之间列柏努利方程式，以管道中心线作基准水平面。

两截面间无外功加入，即W e =0；能量损失可忽略，即f h ∑=0。

据此，柏努利方程式可写为:ρρ2222121122p u gZ p u gZ ++=++式中 Z 1=Z 2=0所以 2.1490522.1333522221-=+u u简化得 137332122=-u u （a ）据连续性方程 u 1A 1=u 2A 2得 212211211202.008.0⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==u d d u A A u u u 2=16u 1 （b ）以式（b ）代入式（a ），即（16u 1）2－21u =13733 解得 u 1=7.34m/s空气的流量为/h m 8.13234.708.0436004360032121=⨯⨯⨯=⨯=ππu d Vs用泵将贮液池中常温下的水送至吸收塔顶部，贮液池水面维持恒定，各部分的相对位置如图所示。

化工原理习题答案问题一：质量守恒及干燥问题问题描述：一种含有30%水分的湿煤经过加热后，其水分含量降低到15%。

问：为了使1000kg湿煤的水分含量降到15%，需要排除多少千克水分？解答：根据质量守恒原则，该问题可以通过计算质量的变化来求解。

设湿煤的初始质量为m1，水分含量为w1，加热后的质量为m2，水分含量为w2。

根据题意可得到以下关系：m1 = m2 + m水分 w1 = (m水分 / m1) × 100% w2 = (m水分 / m2) × 100%根据题意可得到以下关系： w2 = 15% = 0.15 w1 = 30% = 0.30将以上关系代入计算，可得到： 0.15 = (m水分 / m2) × 100% 0.30 = (m水分 / m1) × 100%解得：m水分 = 0.15 × m2 = 0.30 × m1代入具体数值进行计算： m水分 = 0.15 × 1000kg = 150kg因此，需要排除150千克水分。

问题二：能量守恒问题问题描述：一个装有100升水的水箱，水温为20°C。

向该水箱中加热10000千卡的热量，水温升高到40°C。

问：热容量为1千卡/升·°C的水箱的温度升高了多少度？解答：根据能量守恒原理，可以通过计算热量的变化来求解。

热量的变化可表示为：Q = mcΔT其中，Q为热量的变化量，m为物体的质量，c为物体的比热容，ΔT为温度的变化。

根据题意可得到以下关系： Q = 10000千卡 = 10000 × 1000卡 m = 100升 = 100升 × 1千克/升 = 100 × 1千克 c = 1千卡/升·°C 代入公式计算温度的变化ΔT：10000 × 1000 = (100 × 1) × (ΔT) ΔT = (10000 × 1000) / (100 × 1) = 1000000 / 100 = 10000°C 因此，热容量为1千卡/升·°C的水箱的温度升高了10000度。

《化工原理》课程习题集一、单选题1.因次分析法的目的在于( )。

A 得到各变量间的确切定量关系B 得到各无因次数群的确切定量关系C 用无因次数群代替变量，使实验与关联工作简化D 用无因次数群代替变量，使实验结果更可靠2.某物体的质量为1000 kg，则其重量为( )。

A 1000 NB 9810 NC 9810 kgfD 1000/9.81 kgf3.某系统的绝对压力为0.04 MPa，若当地大气压力为0.1 MPa，，则该系统的真空度为（）。

A.0.1 MpaB.0.14 MpaC.0.04 MpaD.0.06 MPa4. 4 ℃水在SI制中密度为( )，重度为( )。

A 1000 kgf·m-3B 1000 kg·m-3C 102 kgf·s2·m-4D 9810 N·m-35. 4 ℃水在在工程单位制中密度为( )，重度为（）。

A 1000 kgf·m-3B 1000 kg·m-3C 102 kgf·s2·m-4D 9810 N·m-36.将含晶体10％的悬浮液送往料槽宜选用（）。

Ａ离心泵Ｂ往复泵Ｃ齿轮泵Ｄ喷射泵7.某泵在运行１年后发现有气缚现象，应（）。

Ａ停泵，向泵内灌液Ｂ降低泵的安装高度Ｃ检查进口管路有否泄漏现象Ｄ检查出口管路阻力是否过大8.离心通风机的铭牌上标明的全风压为100 mmH2O意思是( )。

A 输任何条件的气体介质全风压都达100 mmH2OB 输送空气时不论流量多少，全风压都可达100 mmH2OC 输送任何气体介质当效率最高时，全风压为100 mmH2OD 输送20 ℃，101325 Pa的空气，在效率最高时，全风压为100 mmH2O9.离心泵的实际安装高度( )允许安装高度，就可防止气蚀现象发生。

A 大于B 小于C 等于D 近似于10.操作条件下允许吸上真空高度为H s，允许的最大安装高度为H g,max，泵的入口速度为u1，S H f,0-1为吸入管路单位重量液体的阻力损失，则( )。

第一章 流体流动【例1-1】 已知硫酸与水的密度分别为1830kg/m 3与998kg/m 3，试求含硫酸为60%（质量）的硫酸水溶液的密度为若干。

解：根据式1-49984.018306.01+=m ρ=（3.28+4.01）10-4=7.29×10-4ρm =1372kg/m 3【例1-2】 已知干空气的组成为：O 221%、N 278%和Ar1%（均为体积%），试求干空气在压力为9.81×104Pa 及温度为100℃时的密度。

解：首先将摄氏度换算成开尔文100℃=273+100=373K 再求干空气的平均摩尔质量M m =32×0.21+28×0.78+39.9×0.01 =28.96kg/m3根据式1-3a 气体的平均密度为：3kg/m 916.0373314.896.281081.9=⨯⨯⨯=m ρ【例1-3 】 本题附图所示的开口容器内盛有油和水。

油层高度h 1=0.7m 、密度ρ1=800kg/m 3，水层高度h 2=0.6m 、密度ρ2=1000kg/m 3。

（1）判断下列两关系是否成立，即 p A =p'A p B =p'B （2）计算水在玻璃管内的高度h 。

解：（1）判断题给两关系式是否成立 p A =p'A 的关系成立。

因A 与A '两点在静止的连通着的同一流体内，并在同一水平面上。

所以截面A-A'称为等压面。

p B =p'B 的关系不能成立。

因B 及B '两点虽在静止流体的同一水平面上，但不是连通着的同一种流体，即截面B-B '不是等压面。

（2）计算玻璃管内水的高度h 由上面讨论知，p A =p'A ，而p A =p'A 都可以用流体静力学基本方程式计算，即p A =p a +ρ1gh 1+ρ2gh 2 p A '=p a +ρ2gh于是 p a +ρ1gh 1+ρ2gh 2=p a +ρ2gh简化上式并将已知值代入，得 800×0.7+1000×0.6=1000h 解得 h =1.16m【例1-4】 如本题附图所示，在异径水平管段两截面（1-1'、2-2’）连一倒置U 管压差计，压差计读数R =200mm 。

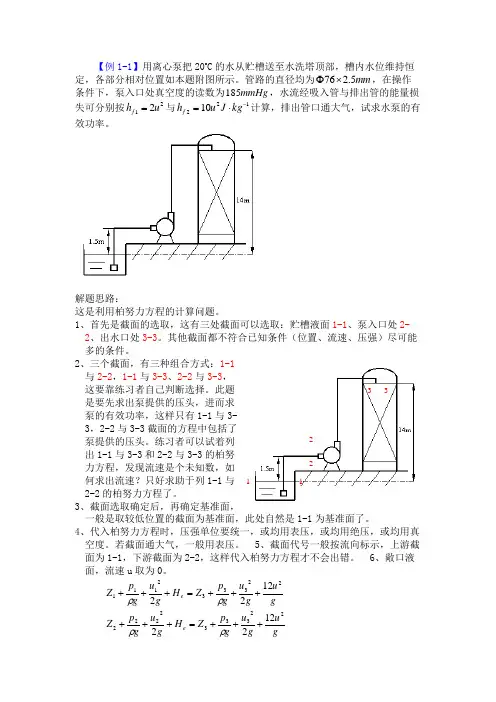
【例1-1】用离心泵把20o C 的水从贮槽送至水洗塔顶部，槽内水位维持恒定，各部分相对位置如本题附图所示。

管路的直径均为mm 5.276⨯Φ，在操作条件下，泵入口处真空度的读数为mmHg 185，水流经吸入管与排出管的能量损失可分别按212u h f =与12210-⋅=kg J u h f 计算，排出管口通大气，试求水泵的有效功率。

解题思路：这是利用柏努力方程的计算问题。

1、首先是截面的选取，这有三处截面可以选取：贮槽液面1-1、泵入口处2-2、出水口处3-3。

其他截面都不符合已知条件（位置、流速、压强）尽可能多的条件。

2、三个截面，有三种组合方式：1-1与2-2，1-1与3-3、2-2与3-3，这要靠练习者自己判断选择。

此题是要先求出泵提供的压头，进而求泵的有效功率，这样只有1-1与3-3，2-2与3-3截面的方程中包括了泵提供的压头。

练习者可以试着列出1-1与3-3和2-2与3-3的柏努力方程，发现流速是个未知数，如何求出流速？只好求助于列1-1与2-2的柏努力方程了。

3、截面选取确定后，再确定基准面，一般是取较低位置的截面为基准面，此处自然是1-1为基准面了。

4、代入柏努力方程时，压强单位要统一，或均用表压，或均用绝压，或均用真空度。

若截面通大气，一般用表压。

5、截面代号一般按流向标示，上游截面为1-1，下游截面为2-2，这样代入柏努力方程才不会出错。

6、敞口液面，流速u 取为0。

gug u g p Z H g u g p Z gu g u g p Z H g u g p Z e e 22333222222333211112221222+++=++++++=+++ρρρρ1 1 3 32 2求解过程：在贮槽液面1-1截面和泵入口处2-2截面，以1-1为基准面列柏努力方程。

(A) 22122221211⋅⋅⋅⋅⋅⋅+++=++f h p u g z p u g z ρρ122211212121 222100024666-9.811.5000 A , 2 , u , 0 , 5.1z , 0 ( 2466101330760185, ( 0-⋅=∴+++⨯=++=====-=⨯-==s m u u uu h u u m z p p p f a ）得代入式（表压）表压）(B) 222132331211⋅⋅⋅⋅⋅⋅++++=+++f f e h h p u g z w p u g z ρρ在1-1截面和出水口出3-3截面列柏努力方程 Ww Q N kg J B u u h h s m u m z p p e e f f 148010001872)071.0(418725.12081.914 w , 12)202( , 2u , 0 , 14z , 0 , ( 0212e 22211313131=⨯⨯⨯⨯=⋅⋅=∴⋅=⨯++⨯==+=+⋅======--πρ）得代入式（表压）点评：此题重点是复习柏努利方程的截面选取问题。

1.用连续精馏方法分离乙烯、乙烷混合物。

已知进料中含乙烯0.88（摩尔分数，下同），流量为200kmol/h。

今要求馏出液中乙烯的回收率为99.5%，釜液中乙烷的回收率为99.4%，试求所得馏出液、釜液的流量和组成。

2.例题：设计一精馏塔，用以分离双组分混合物，已知原料液流量为100kmol/h，进料中含轻组分0.2（摩尔分数，下同），要求馏出液和釜液的组成分别为0.8和0.05。

泡点进料（饱和液体），物系的平均相对挥发度α=2.5，回流比R=2.7。

试求：1）精馏段和提馏段操作线方程；2）从塔顶数第二块板下降的液相组成。

3.例题用一常压精馏塔分离某二元理想溶液，进料中含轻组分0.4（摩尔分数，下同），进料量为200kmol/h饱和蒸汽进料，要求馏出液和釜液的组成分别为0.97和0.02。

已知操作回流比R=3.0，物系的平均相对挥发度α=2.4，塔釜当作一块理论板处理。

试求：（1）提馏段操作线方程；（2）塔釜以上第一块理论板下降的液相组成。

（从塔底向上计算）4.例题：常压下分离丙酮水溶液的连续精馏塔，进料中丙酮50%（摩尔分数，下同），其中气相占80%，要求馏出液和釜液中丙酮的组成分别为95%和5%，回流比R=2.0，若进料流量为100kmol/h，分别计算精馏段和提馏段的气相和液相流量，并写出相应的两段操作线方程和q线方程。

5.在连续精馏塔中分离苯—甲苯混合液。

原料液组成为0.4（摩尔分数，下同），馏出液组成为0.95。

汽--液混合进料，其中汽相占1/3（摩尔数比），回流比为最小回流比的2倍，物系的平均相对挥发度为2.5，塔顶采用全凝器。

试求:(1)精馏段操作线方程；（2）从塔顶往下数第二层理论板的上升气相组成。

6.在常压连续精馏塔中分离苯-甲苯混合液，原料液流量为1000kmol/h，组成为含苯0.4（摩尔分数，下同），馏出液组成为含苯0.9，苯在塔顶的回收率为90%，泡点进料(q=1)，操作回流比为最小回流比的1.5倍，物系的平均相对挥发度为2.5。

化工原理第一章 练习1． 湍流流动的特点是 脉动 ，故其瞬时速度等于 时均速度 与 脉动速度 之和。

2．雷诺准数的物理意义是 黏性力和惯性力之比 。

3．当地大气压为755mmHg ，现测得一容器内的绝对压力为350mmHg ，则其真空度为405 mmHg 。

4．以单位体积计的不可压缩流体的机械能衡算方程形式为ρρρρρρf s w p u gz w p u gz +++=+++2222121122。

5．实际流体在管道内流动时产生阻力的主要原因是 黏性 。

6．如图所示，水由敞口恒液位的高位槽流向压力恒定的反应器，当管道上的阀门开度减小后，管路总阻力损失（包括所有局部阻力损失）将 （1） 。

(1)不变 (2)变大 (3)变小 (4)不确定7．如图所示的并联管路，其阻力关系是 （C ） 。

（A ）(h f )A1B (h f )A2B （B ）(h f )AB =(h f )A1B +(h f )A2B （C ）(h f )AB =(h f )A1B =(h f )A2B（D ）(h f )AB (h f )A1B =(h f )A2B8．孔板流量计和转子流量计的最主要区别在于：前者是恒 截面 、变 压头 ，而后者是恒 压头 、变 截面 。

9．如图所示，水从槽底部沿内径为100mm 的水平管子流出，阀门前、后的管长见图。

槽中水位恒定。

今测得阀门全闭时，压力表读数p=。

现将阀门全开，试求此时管内流量。

已知阀门（全开）的阻力系数为，管内摩擦因数=。

答：槽面水位高度m g p H 045.681.91000103.593=⨯⨯==ρ在槽面与管子出口间列机械能衡算式，得：24.60.15.01.0203081.9045.62u⎪⎭⎫ ⎝⎛++++=⨯λ解得：s m u /65.2=反应 器题7附图 1AB2题8附图p30m 20m题1附图h m s m u d V /9.74/0208.065.21.041413322==⨯⨯==ππ1．水以70m 3/h 的流量流过倾斜的异径管通。

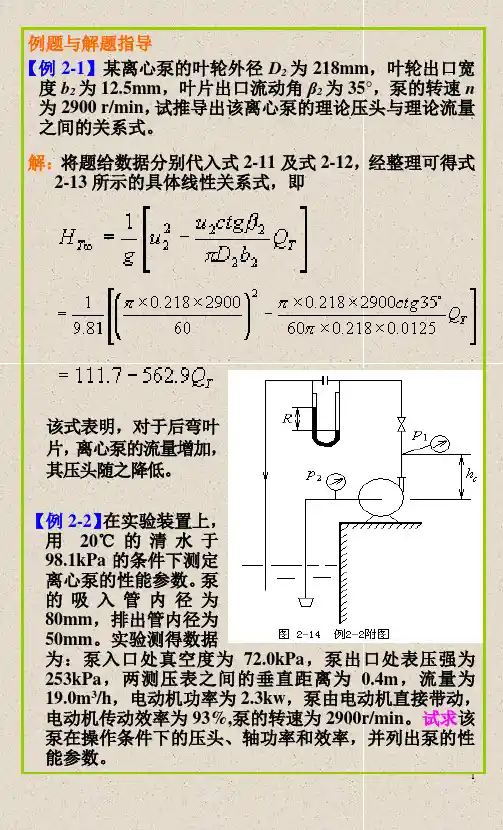
例题与解题指导【例2-1】某离心泵的叶轮外径D2为218mm，叶轮出口宽度b2为12.5mm，叶片出口流动角β2为35°，泵的转速n 为2900 r/min，试推导出该离心泵的理论压头与理论流量之间的关系式。

解：将题给数据分别代入式2-11及式2-12，经整理可得式2-13所示的具体线性关系式，即该式表明，对于后弯叶片，离心泵的流量增加，其压头随之降低。

【例2-2】在实验装置上，用20℃的清水于98.1kPa的条件下测定离心泵的性能参数。

泵的吸入管内径为80mm，排出管内径为50mm。

实验测得数据为：泵入口处真空度为72.0kPa，泵出口处表压强为253kPa，两测压表之间的垂直距离为0.4m，流量为19.0m3/h，电动机功率为2.3kw，泵由电动机直接带动，电动机传动效率为93%,泵的转速为2900r/min。

试求该泵在操作条件下的压头、轴功率和效率，并列出泵的性能参数。

解：(1) 泵的压头 在泵入口的真空表和泵出口压强表两截面之间列柏努利方程式，在忽略两测压口之间流动阻力下，可得测量泵压头的一般表达式为2201221()/2H h H H u u g =+++- (a) 式中h 0--泵的两测压截面之间的垂直距离，m ；H 1--与泵入口真空度对应的静压头，m ；H 1＝p 1/(ρg) (p 1为真空度)H 2 --与泵出口表压对应的静压头，m ；H 2＝p 2/(ρg)u 1、u 2--泵的入口和出口液体的流速，m/s ；m/sm/s取水的密度ρ＝1000kg/m 3，将已知条件代入式a ，得m(2) 泵的轴功率0.93 2.3 2.139N =⨯= kW(3) 泵的效率η 泵的有效功率为31934.45109.8117843600Ne HQ g ρ==⨯⨯⨯= W 故 / 1.784/2.1390.834Ne N η=== 即83.4% 泵性能参数：转速n 为2900r/min ，流量Q 为19m 3/h ，压头H 为34.45m ，轴功率N 为2.139kw ，效率η为83.4%。

化工原理试题库（一）一：填空题（18分）1、 某设备上，真空度的读数为80mmHg ，其绝压=________02mH =__________Pa. 该地区的大气压为720mmHg 。

2、 常温下水的密度为10003mKg ，粘度为1cp ，在mm d 100=内的管内以s m3 速度流动，其流动类型为 ______________。

3、 流体在管内作湍流流动时，从中心到壁可以__________.___________.__________________.4、 气体的粘度随温度的升高而_________，水的粘度随温度的升高_______。

5、 水在管路中流动时，常用流速范围为_______________sm,低压气体在管路中流动时，常用流速范围为_______________________sm。

6、 离心泵与往复泵的启动与调节的不同之处是：离心泵_________________. __________________.往复泵___________________.__________________.7、 在非均相物糸中，处于____________状态的物质，称为分散物质，处于 __________状态的物质，称为分散介质。

8、 间歇过滤操作包括_____ _._______.________._________.__________。

9、 传热的基本方式为___________.______________.__________________。

工业上的换热方法有_________.__________.__________.____________。

10、 α称为_______________，其物理意义为____________________________.__________________________，提高管内α值的有效方法____________.11、 提高管外α值的有效方法______________________________________。

三 计算题1 （15分）在如图所示的输水系统中，已知管路总长度（包括所有当量长度，下同）为 100m ，其中压力表之后的管路长度为80m ， 管路摩擦系数为0.03，管路径为0.05m ， 水的密度为1000Kg/m 3，泵的效率为0.85， 输水量为15m 3/h 。

求：（1）整个管路的阻力损失，J/Kg ； （2）泵轴功率，Kw ； （3）压力表的读数，Pa 。

解：（1）整个管路的阻力损失，J/kg ； 由题意知，s m A Vu s /12.2)405.03600(152=⨯⨯==π 则kg J u d l h f /1.135212.205.010003.0222=⨯⨯=⋅⋅=∑λ （2）泵轴功率，kw ；在贮槽液面0-0´与高位槽液面1-1´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++10,121020022f e h p u gH W p u gH ρρ 其中， ∑=kg J h f /1.135, u 0= u 1=0， p 1= p 0=0（表压）, H 0=0， H=20m 代入方程得： kg J h gH W f e /3.3311.1352081.9=+⨯=+=∑又 s kg V W s s /17.41000360015=⨯==ρ 故 w W W N e s e 5.1381=⨯=， η=80%， kw w N N e 727.11727===η2 （15分）如图所示，用泵将水从贮槽送至敞口高位槽，两槽液面均恒定不变，输送管路尺寸为φ83×3.5mm ，泵的进出口管道上分别安装有真空表和压力表，真空表安装位置离贮槽的水面高度H 1为4.8m ，压力表安装位置离贮槽的水面高度H 2为5m 。

当输水量为36m 3/h 时，进水管道全部阻力损失为1.96J/kg ，出水管道全部阻力损失为4.9J/kg ，压力表读数为2.452×105Pa ，泵的效率为70%，水的密度ρ为1000kg/m 3，试求： （1）两槽液面的高度差H 为多少？ （2）泵所需的实际功率为多少kW ？ （3）真空表的读数为多少kgf/cm 2？解：（1）两槽液面的高度差H在压力表所在截面2-2´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，得：∑-+++=++32,323222222f h p u gH p u gH ρρ 其中， ∑=-kg J h f /9.432,, u 3=0, p 3=0,p 2=2.452×105Pa, H 2=5m, u 2=Vs/A=2.205m/s代入上式得： m H 74.2981.99.481.9100010452.281.92205.2552=-⨯⨯+⨯+= （2）泵所需的实际功率在贮槽液面0-0´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++30,323020022f e h p u gH W p u gH ρρ 其中， ∑=-kg J h f /9.864.630,, u 2= u 3=0, p 2= p 3=0, H 0=0， H=29.4m代入方程求得： W e =298.64J/kg ， s kg V W s s /101000360036=⨯==ρ 故 w W W N e s e 4.2986=⨯=， η=70%， kw N N e 27.4==η（3）真空表的读数在贮槽液面0-0´与真空表截面1-1´间列柏努利方程，有：∑-+++=+++10,1211020022f h p u gH p u gH ρρ 其中，∑=-kg J hf /96.110,, H 0=0， u 0=0, p 0=0, H 1=4.8m,u 1=2.205m/s代入上式得， 2421/525.01015.5)96.12205.28.481.9(1000cm kgf Pap -=⨯-=++⨯-= 3 用离心泵把20℃的水从储槽送至水洗塔顶部，槽水位维持恒定。

例1-1 若某地大气压为100kPa ，（1）若真空度为30kPa ，表压、绝压为多少？（2）若表压为170kPa ，绝压、真空度为多少？（3）若绝压为200kPa ，表压、真空度为多少？（4）若绝压为50kPa ，表压、真空度为多少？例1-2 某台离心泵进口真空表读数为220mmHg(真空度) 、出口压力表读数为1.7kgf/cm2(表压)。

若当地大气压力为760mmHg ，试求： 它们的绝对压力各为若干，进出口压力差为多少？例1-3 如图所示，常温水在管道中流过。

为测定a 、b 两点的压力差，安装一U 型压差计，指示剂R 的读数为100mm 。

试计算a 、b 两点的压力差为若干？已知水与汞的密度分别为1000kg/m3及13600kg/m3。

例1-4 直径为800mm 的流化床反应器底部装有分布板，其上开有640个直径为10mm 的小孔，空气从分布板下部送入。

反应器的流速为0.5m/s ，求空气通过分布板小孔的流速。

例1-5 水从高位槽通过出口管流出。

高位槽液面上的压力为大气压。

高位槽液面与出口管中心线间的垂直高度为4.2m ，管子规格为Φ114⨯4的无缝钢管，设水在管内能量损失为39.2 J/kg （不包括出口能量损失），试求管路中水的体积流量为多少m3/h ？例1-6如图所示一输水系统，管路尺寸为Φ57⨯3.5。

已知全部流动阻力为 (u 为管内流速）。

试求：水的流量为多少？例1-7 从高位槽向塔内加料，高位槽上方为大气压，塔内压力为0.2kgf/cm2（表压），要求料液在管内以0.5m/s 的速度流动，若料液在管内的总压头损失为1.2m 液柱（ρ=800kg/m3）试求：高位槽的液面应比塔入口处高出多少米？例1-8 如图所示，水流经由小至大的管段，小管尺寸为Φ38⨯2.5，大管尺寸为Φ54⨯3.5，水在小管内的流速为2.5 m/s ，从截面1到截面2的阻力损失为2 J/kg ，水的密度为1000 kg/m3，指示剂密度为1594 kg/m3，试求：压差计的读数。

三 计算题1 （15分）在如图所示的输水系统中，已知 管路总长度（包括所有当量长度，下同）为 100m ，其中压力表之后的管路长度为80m ，管路摩擦系数为0.03，管路内径为0.05m ， 水的密度为1000Kg/m 3，泵的效率为0.85， 输水量为15m 3/h 。

求：（1）整个管路的阻力损失，J/Kg ； （2）泵轴功率，Kw ； （3）压力表的读数，Pa 。

解：（1）整个管路的阻力损失，J/kg ； 由题意知，s m A V u s /12.2)405.03600(152=⨯⨯==π 则kg J u d l h f /1.135212.205.010003.0222=⨯⨯=⋅⋅=∑λ （2）泵轴功率，kw ；在贮槽液面0-0´与高位槽液面1-1´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++10,121020022f e h p u gH W p u gH ρρ 其中， ∑=kg J h f /1.135, u 0= u 1=0， p 1= p 0=0（表压）, H 0=0， H=20m 代入方程得： kg J h gH W f e /3.3311.1352081.9=+⨯=+=∑又 s kg V W s s /17.41000360015=⨯==ρ 故 w W W N e s e 5.1381=⨯=， η=80%， kw w N N e 727.11727===η2 （15分）如图所示，用泵将水从贮槽送至敞口高位槽，两槽液面均恒定不变，输送管路尺寸为φ83×3.5mm ，泵的进出口管道上分别安装有真空表和压力表，真空表安装位置离贮槽的水面高度H 1为4.8m ，压力表安装位置离贮槽的水面高度H 2为5m 。

当输水量为36m 3/h 时，进水管道全部阻力损失为 1.96J/kg ，出水管道全部阻力损失为 4.9J/kg ，压力表读数为 2.452×H=20m H 1=2m105Pa ，泵的效率为70%，水的密度ρ为1000kg/m 3，试求： （1）两槽液面的高度差H 为多少？ （2）泵所需的实际功率为多少kW ？ （3）真空表的读数为多少kgf/cm 2？解：（1）两槽液面的高度差H在压力表所在截面2-2´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，得：∑-+++=++32,323222222f h p u gH p u gH ρρ 其中， ∑=-kg J h f /9.432,, u 3=0, p 3=0,p 2=2.452×105Pa, H 2=5m, u 2=Vs/A=2.205m/s代入上式得： m H 74.2981.99.481.9100010452.281.92205.2552=-⨯⨯+⨯+= （2）泵所需的实际功率在贮槽液面0-0´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++30,323020022f e h p u gH W p u gH ρρ 其中， ∑=-kg J h f /9.864.630,, u 2= u 3=0, p 2= p 3=0, H 0=0， H=29.4m代入方程求得： W e =298.64J/kg ， s kg V W s s /101000360036=⨯==ρ 故 w W W N e s e 4.2986=⨯=， η=70%， kw N N e 27.4==η（3）真空表的读数在贮槽液面0-0´与真空表截面1-1´间列柏努利方程，有：∑-+++=+++10,1211020022f h p u gH p u gH ρρ 其中，∑=-kg J hf /96.110,, H 0=0， u 0=0, p 0=0, H 1=4.8m,u1=2.205m/s代入上式得，24 21/525.01015.5)96.12205.28.481.9( 1000cm kgf Pap -=⨯-=++⨯-=3 用离心泵把20℃的水从储槽送至水洗塔顶部，槽内水位维持恒定。

化工原理第一章 练习1． 湍流流动的特点是 脉动 ，故其瞬时速度等于 时均速度 与 脉动速度 之和。

2．雷诺准数的物理意义是 黏性力和惯性力之比 。

3．当地大气压为755mmHg ，现测得一容器内的绝对压力为350mmHg ，则其真空度为405 mmHg 。

4．以单位体积计的不可压缩流体的机械能衡算方程形式为ρρρρρρf s w p u gz w p u gz +++=+++2222121122。

5．实际流体在管道内流动时产生阻力的主要原因是 黏性 。

6．如图所示，水由敞口恒液位的高位槽流向压力恒定的反应器，当管道上的阀门开度减小后，管路总阻力损失（包括所有局部阻力损失）将 （1） 。

(1)不变 (2)变大(3)变小(4)不确定7．如图所示的并联管路，其阻力关系是 （C ） 。

（A ）(∑h f )A1B >(∑h f )A2B（B ）(∑h f )AB =(∑h f )A1B +(∑h f )A2B （C ）(∑h f )AB =(∑h f )A1B =(∑h f )A2B（D ）(∑h f )AB >(∑h f )A1B =(∑h f )A2B 8．孔板流量计和转子流量计的最主要区别在于：前者是恒 截面 、变 压头 ，而后者是恒 压头 、变截面 。

9．如图所示，水从槽底部沿内径为100mm 的水平管子流出，阀门前、后的管长见图。

槽中水位恒定。

今测得阀门全闭时，压力表读数p=59.3kPa 。

现将阀门全开，试求此时管内流量。

已知阀门（全开）的阻力系数为6.4，管内摩擦因数λ=0.018。

答：槽面水位高度mgpH045.681.91000103.593=⨯⨯==ρ在槽面与管子出口间列机械能衡算式，得：24.60.15.01.0203081.9045.62u⎪⎭⎫ ⎝⎛++++=⨯λ 解得：sm u /65.2=hm s m u d V /9.74/0208.065.21.041413322==⨯⨯==ππ题8附图题1附图1．水以70m3/h的流量流过倾斜的异径管通。

第一章流体流动例1.高位槽内的水面高于地面8m，水从φ108×4mm的管道中流出，管路出口高于地面2m。

在本题特定条件下，水流经系统的能量损失可按∑ｈf = 6.5 u2计算，其中u为水在管道的流速。

试计算：⑴ A—A'截面处水的流速；⑵水的流量，以m3/h计。

解：处列柏Z1ｇ（Z1q例2.49J／kg，103Pa 时，B解：（1? ?? ?0+u? ???由B? ?? ?? ???∴W=（P A-P B）/ρ- Z B g+49=98.1+49=147.1J/kg? ?? ?∴q m=q vρ=36/3600×1100=11kg/s? ?? ?Pe= q m×W=147.1×11=1618.1w? ?? ?泵的抽功率N= Ne /76%=2311.57W=2.31kw（2）由第一个方程得（P A-PB）/ρ=Z B g+9.81得??P B=P A-ρ（Z B g+9.81）=245.2×103-1100×(7×9.81+98.1)=6.2×104Pa例3.用离心泵把20℃的水从贮槽送至水洗塔顶部，槽内水位维持恒定，各部分相对位置如本题附图所示。

管路的直径均为Ф76×2.5mm ，在操作条件下，泵入口处真空表的读数为24.66×103Pa,水流经吸入管与排处管（不包括喷头）的能量损失可分别按∑ｈf,1=2u2，∑h f,2=10u 2计算，由于管径不变，故式中u 为吸入或排出管的流速ｍ/s 。

排水管与喷头连接处的压强为98.07×103Pa （表压）。

试求泵的有效功率。

解：总能量损失∑hf=∑h f,1+∑h f ，2在截面与真空表处取截面作方程： z 0g+u 02/2+P 0/ρ=z 1g+u 2/2+P 1/ρ+∑h f ，1（∴q ∴ 例4. f ，BC =1.18u 2P 1∴P 1 P B +ρg （x+R 1）=P c +ρg （h BC +x ）+ρ水银R 1gP B +1100×9.81×（0.045+x ）=P c +1100×9.81×（5+x ）+13.6×103×9.81×0.045 P B -P C =5.95×104Pa在B ，C 处取截面列柏努力方程0+u B 2/2+P B /ρ=Zg+u c 2/2+P C /ρ+∑ｈf ，BC∵管径不变，∴u b =u cP B -P C =ρ（Zg+∑ｈf ，BC ）=1100×（1.18u 2+5×9.81）=5.95×104Pau=4.27m/s压缩槽内表压P1=1.23×105Pa（2）在B，D处取截面作柏努力方程0+u2/2+P B/ρ= Zg+0+0+∑ｈf，BC+∑ｈf，CDP B=（7×9.81+1.18u2+u2-0.5u2）×1100=8.35×104PaP B-ρgh=ρ水银R2g8.35×104-1100×9.81×0.2=13.6×103×9.81×R2R2=609.7mm例5.物质。