反比例函数(Word版习题)

反比例函数练习（1）一、判断题1．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数（ ） 2．如果一个函数不是正比例函数，就是反比例函数 （ ）3．y 与2x 成反比例时y 与x 并不成反比例（ ） 二．填空题4．已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________； 5．如果y 与x 成反比例，z 与y 成正比例，则z 与x 成_______； 6．如果函数222-+=k kkx y 是反比例函数，那么k =________，此函数的解析式是____ ____；7． 有一面积为60的梯形，其上底长是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是______________；三、选择题： 8．如果函数12-=m x y 为反比例函数，则m 的值是 （ ）A1- B 0 C 21 D 19．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校。

在课堂上，李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图，同学们画出的示意图如下，你认为正确的是（ ）10、下列函数中，y 是x 反比例函数的是（ ） （A ）12+=x y （B ）22x y =（C ）x y 51=（D ）x y =2四．辨析题（1）兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式（不要求写xy 的取值范围）.￥②虽然当弟吃的饺子个数增多时，兄吃的饺子数(y )在减少，但y 与x 是成反例吗（2）水池中有水若干吨，若单开一个出水口，水流速v 与全池水放光所用时t 如下表：①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系. ②这是一个反比例函数吗③与（1）的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决.。

反比例函数考试题(含答案)1. 对于反比例函数 $y = \frac{k}{x}$，已知 $y = 3$ 时，$x = 6$，求 $k$ 的值。

解答：当 $y=3$，$x=6$ 时，代入原函数得：$$3 = \frac{k}{6}$$解出 $k=18$，因此反比例函数为 $y=\frac{18}{x}$。

2. 已知反比例函数 $y=\frac{6}{x}$ 的图像和 $y=-12$ 的水平渐近线，求该反比例函数图像的方程和垂直渐近线方程。

解答：由于已知 $y=-12$ 是反比例函数的水平渐近线，因此 $y$ 趋向于 $0$ 时，$x$ 的值趋近于无穷大或负无穷大，即垂直于 $x$ 轴。

反比例函数的图像为双曲线，因此垂直渐近线分别为 $x=0$ 和$y=0$。

同时，已知 $y=\frac{6}{x}$，可得 $x=\frac{6}{y}$。

将其化简可得反比例函数的图像方程为 $xy=6$。

因此该反比例函数的图像方程为 $xy=6$，垂直渐近线方程为$x=0$ 和 $y=0$。

3. 已知反比例函数 $y=\frac{12}{x-1}$ 的图像和点 $P(5, 2)$，求 $P$ 点在反比例函数图像上的对称点 $Q$ 的坐标。

解答：首先，求出点$P$ 关于直线$x=1$ 的对称点$P'(p,q)$ 的坐标。

由于直线 $x=1$ 为反比例函数 $y=\frac{12}{x-1}$ 的渐近线，因此$P$ 点到该直线的距离为 $0$。

点 $P$ 到直线 $x=1$ 的距离公式为：$$d(P, x=1)=\frac{|\ ax+by+c\ |}{\sqrt{a^2+b^2}}$$将反比例函数化为标准形式 $y=\frac{12}{x-1}$，可得：$$d(P, x=1)=\frac{|\ x-1\ |}{\sqrt{1+0}}=5-1=4$$因此，点 $P$ 到直线 $x=1$ 的距离为 $4$。

点 $P'$ 在直线$x=1$ 上，因此其 $x$ 坐标为 $1$，根据点 $P$ 和 $P'$ 的对称性，其 $y$ 坐标应该等于 $2-4=-2$。

中考数学《反比例函数》专题 复习试题命题点1 图象与性质1．一台印刷机每年可印刷的书本数量 y(万册)与它的使用时间x(年)成反比例关系，当x ＝2时，y ＝20.则y 与x 的函数图象大致是(C)A B C D2．反比例函数y ＝mx的图象如图所示，以下结论：①常数m ＜－1；②在每个象限内，y 随x的增大而增大；③若A(－1，h)，B(2，k)在图象上，则h ＜k ；④若P(x ，y)在图象上，则P ′(－x ，－y)也在图象上．其中正确的是(C)A ．①②B ．②③C ．③④D ．①④3．如图，函数y ＝⎩⎪⎨⎪⎧1x （x ＞0），－1x （x ＜0）的图象所在坐标系的原点是(A)A ．点MB ．点NC ．点PD ．点Q4．定义新运算：a ⊕b ＝⎩⎪⎨⎪⎧a b （b ＞0），－ab （b ＜0）. 例如：4⊕5＝45，4⊕(－5)＝45.则函数y ＝2⊕x(x≠0)的图象大致是(D)A B C D5．如图，若抛物线y ＝－x2＋3与x 轴围成的封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ，则反比例函数y ＝kx(x ＞0)的图象是(D)A B CD命题点2 反比例函数、一次函数与几何图形综合6．如图，四边形ABCD 是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y ＝mx(x＞0)的图象经过点D ，点P 是一次函数y ＝kx ＋3－3k(k ≠0)的图象与该反比例函数图象的一个公共点．(1)求反比例函数的解析式；(2)通过计算说明一次函数y ＝kx ＋3－3k(k ≠0)的图象一定经过点C ；(3)对于一次函数y ＝kx ＋3－3k(k ≠0)，当y 随x 的增大而增大时，确定点P 横坐标的取值范围．(不必写出过程)解：(1)∵B(3，1)，C(3，3)，四边形ABCD 是平行四边形， ∴AD ＝BC ＝2，AD ∥BC ，BC ⊥x 轴．∴AD ⊥x 轴． 又∵A(1，0)，∴D(1，2)．∵点D 在反比例函数y ＝mx的图象上，∴m ＝1×2＝2.∴反比例函数的解析式为y ＝2x.(2)当x ＝3时，y ＝kx ＋3－3k ＝3，∴一次函数y ＝kx ＋3－3k(k ≠0)的图象一定过点C.(3)设点P 的横坐标为a ，则23＜a ＜3.命题点3 反比例函数的实际应用(8年2考)7．(2019·杭州)方方驾驶小汽车匀速地从A 地行驶到B 地，行驶里程为480千米，设小汽车的行驶时间为t(单位：小时)，行驶速度为v(单位：千米/小时)，且全程速度限定为不超过120千米/小时．(1)求v 关于t 的函数解析式；(2)方方上午8点驾驶小汽车从A 地出发．①方方需在当天12点48分至14点(含12点48分和14点)间到达B 地，求小汽车行驶速度v 的范围；②方方能否在当天11点30分前到达B 地？说明理由．解：(1)∵vt ＝480，且全程速度限定为不超过120千米/小时，∴v 关于t 的函数解析式为v ＝480t (t ≥4)．(2)①8点至12点48分时间长为245小时，8点至14点时间长为6小时．将t ＝6代入v ＝480t，得v ＝80；将t ＝245代入v ＝480t，得v ＝100.∴小汽车行驶速度v 的范围为80≤v ≤100.②方方不能在当天11点30分前到达B 地．理由如下：8点至11点30分时间长为72小时，将t ＝72代入v ＝480t ，得v ＝9607.∵9607＞120，超速了． 故方方不能在当天11点30分前到达B 地．基础训练1．(2019·柳州)反比例函数y ＝2x的图象位于(A)A ．第一、三象限B ．第二、三象限C ．第一、二象限D ．第二、四象限2．(2019·哈尔滨)点(－1，4)在反比例函数y ＝kx的图象上，则下列各点在此函数图象上的是(A)A ．(4，－1)B ．(－14，1)C ．(－4，－1)D ．(14，2)3．(2019·邢台模拟)已知甲圆柱型容器的底面积为30 cm 2，高为8 cm ，乙圆柱型容器底面积为x cm 2.若将甲容器装满水，全部倒入乙容器中(乙容器没有水溢出)，则乙容器水面高度y(cm)与x(cm 2)之间的大致图象是(C)A B C D4．(2019·唐山乐亭县模拟)若点(x 1，y 1)，(x 2，y 2)都是反比例函数y ＝－6x图象上的点，并且y 1＜0＜y 2，则下列结论中正确的是(A)A ．x 1＞x 2B ．x 1＜x 2C ．y 随x 的增大而减小D ．两点有可能在同一象限5．(2019·唐山滦南县一模)如图，正比例函数y ＝x 与反比例函数y ＝4x的图象交于A ，B 两点，其中A(2，2)，当y ＝x 的函数值大于y ＝4x的函数值时，x 的取值范围为(D)A ．x ＞2B ．x ＜－2C ．－2＜x ＜0或0＜x ＜2D ．－2＜x ＜0或x ＞26．(2019·石家庄模拟)已知反比例函数y ＝kx的图象过第二、四象限，则一次函数y ＝kx ＋k的图象大致是(B)A B C D7．(2019·唐山路北区模拟)已知点P(m ，n)是反比例函数y ＝－3x图象上一点，当－3≤n ＜－1时，m 的取值范围是(A)A ．1≤m ＜3B ．－3≤m ＜－1C ．1＜m ≤3D ．－3＜m ≤－18．(原创)(2017·河北T15变式)将九年级某班40名学生的数学测试成绩分为5组，第1～4组的频率分别为0.3，0.25，0.15，0.2，第5组的频数记为k ，则反比例y ＝kx(x ＞0)的图象是(D)A B C D9．(原创)(2019·河北T12变式)如图，函数y ＝⎩⎪⎨⎪⎧mx（x ＞0），－mx（x<0）的图象如图所示，以下结论：①常数m ＞0；②在每个象限内，y 随x 增大而减小；③若点A(－2，a)，B(3，b)在图象上，则a ＜b ；④若P(x ，y)在图象上，则P ′(－x ，y)也在图象上，其中正确的是(D)A ．①②B ．②③C ．③④D ．①④10．(2019·兰州)如图，矩形OABC 的顶点B 在反比例函数y ＝kx(x ＞0)的图象上，S 矩形OABC＝6，则k ＝6．11．(2019·北京)在平面直角坐标系xOy 中，点A(a ，b)(a ＞0，b ＞0)在双曲线y ＝k 1x上，点A 关于x 轴的对称点B 在双曲线y ＝k 2x，则k 1＋k 2的值为0．12．(2019·盐城)如图，一次函数y ＝x ＋1的图象交y 轴于点A ，与反比例函数y ＝kx(x ＞0)的图象交于点B(m ，2)．(1)求反比例函数的解析式； (2)求△AOB 的面积．解：(1)∵点B(m ，2)在直线y ＝x ＋1上， ∴2＝m ＋1，解得m ＝1. ∴点B 的坐标为(1，2)．∵点B(1，2)在反比例函数y ＝kx(x ＞0)的图象上，∴2＝k1，解得k ＝2.∴反比例函数的解析式是y ＝2x.(2)将x ＝0代入y ＝x ＋1，得y ＝1，则点A 的坐标为(0，1)． ∵点B 的坐标为(1，2)，∴△AOB 的面积为12×1×1＝12.能力提升13．(2019·石家庄新华区模拟)如图，在平面直角坐标系中，点A(0，2)，点P 是双曲线y ＝kx(x ＞0)上的一个动点，作PB ⊥x 轴于点B ，当点P 的横坐标逐渐减小时，四边形OAPB 的面积将会(C)A ．逐渐增大B ．不变C ．逐渐减小D ．先减小后增大14．(2019·陕西)如图，D 是矩形AOBC 的对称中心，A(0，4)，B(6，0)．若一个反比例函数的图象经过点D ，交AC 于点M ，则点M 的坐标为(32，4)．16．(2019·秦皇岛海港区模拟)如图，在平面直角坐标系中，▱ABCD 的顶点A(1，b)，B(3，b)，D(2，b ＋1)．(1)点C 的坐标是(4，b ＋1)(用b 表示)；(2)双曲线y ＝kx过▱ABCD 的顶点B 和D ，求该双曲线的解析式；(3)如果▱ABCD 与双曲线y ＝4x(x ＞0)总有公共点，求b 的取值范围．解：(2)∵双曲线y ＝kx过▱ABCD 的顶点B(3，b)和D(2，b ＋1)，∴3b ＝2(b ＋1)，解得b ＝2，即B(3，2)，D(2，3)．则该双曲线解析式为y ＝6x .(3)将A(1，b)代入y ＝4x ，得b ＝4；将C(4，b ＋1)代入y ＝4x ，得b ＋1＝1，即b ＝0.则▱ABCD 与双曲线y ＝4x(x ＞0)总有公共点时，b 的取值范围为0≤b ≤4.17．如图为某公园“水上滑梯”的侧面图，其中BC 段可看成是一段双曲线，建立如图的直角坐标系后，其中，矩形AOEB 为向上攀爬的梯子，OA ＝5米，进口AB ∥OD ，且AB ＝2米，出口C 点距水面的距离CD 为1米，则B ，C 之间的水平距离DE 的长度为(D)A ．5米B ．6米C ．7米D ．8米18．(1)探究新知：如图1，已知△ABC 与△ABD 的面积相等，试判断AB 与CD 的位置关系，并说明理由．(2)结论应用：①如图2，点M ，N 在反比例函数y ＝kx(x ＞0)的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E ，F ，试证明：MN ∥EF ；②若①中的其他条件不变，只改变点M ，N 的位置，如图3所示，请判断MN 与EF 是否平行？解：(1)AB ∥CD.理由：过点C 作CG ⊥AB 于点G ，过点D 作DH ⊥AB 于点H ， ∴∠CGA ＝∠DHB ＝90°.∴CG ∥DH. ∵△ABC 和△ABD 的面积相等， ∴CG ＝DH.∴四边形CGHD 是矩形．∴AB ∥CD.(2)①证明：连接MF ，NE ，设M(x 1，y 1)，N(x 2，y 2)，∵点M ，N 在反比例函数y ＝kx(x ＞0)的图象上，∴x 1y 1＝k ，x 2y 2＝k. ∵ME ⊥y 轴，NF ⊥x 轴，∴EM ＝x 1，OE ＝y 1，OF ＝x 2，NF ＝y 2.∴S △EFM ＝12x 1·y 1＝12k ，S △EFN ＝12x 2y 2＝12k.∴S △EFM ＝S △EFN ，由(1)中的结论可知，MN ∥EF.②MN ∥EF ，理由：连接MF ，NE ，设M(x 1，y 1)，N(x 2，y 2)．∵M ，N 在反比例函数y ＝kx(k ＞0)的图象上，∴x 1y 1＝k ，x 2y 2＝k. ∵ME ⊥y 轴，NF ⊥x 轴，∴EM ＝x 1，OE ＝y 1，OF ＝－x 2，NF ＝－y 2.∴S △EFM ＝12x 1·y 1＝12k ，S △EFN ＝12(－x 2)(－y 2)＝12k.∴S △EFM ＝S △EFN .由(1)中的结论可知，MN ∥EF.反比例函数中的面积问题1．(2019·枣庄)如图，在平面直角坐标系中，等腰Rt △ABC 的顶点A ，B 分别在x 轴、y 轴的正半轴上，∠ABC ＝90°，CA ⊥x 轴，点C 在函数y ＝kx(x ＞0)的图象上．若AB ＝1，则k的值为(A)A ．1B.22C. 2 D ．22．如图，A ，B 两点在双曲线y ＝4x(x ＞0)上，分别经过A ，B 两点向x 轴作垂线段，已知S阴影＝1，则S 1＋S 2＝(D)A ．3B ．4C ．5D ．63．(2019·黄冈)如图，一直线经过原点O ，且与反比例函数y ＝kx(k>0)相交于点A ，B ，过点A 作AC ⊥y 轴，垂足为C ，连接BC.若△ABC 面积为8，则k ＝8．4．如图，A ，B 是反比例函数y ＝2x的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，△ABC 的面积记为S ，则(B)A ．S ＝2B ．S ＝4C ．2＜S ＜4D ．S ＞45．(2019·郴州)如图，点A ，C 分别是正比例函数y ＝x 与反比例函数y ＝4x的图象的交点，过A 点作AD ⊥x 轴于点D ，过C 点作CB ⊥x 轴于点B ，则四边形ABCD 的面积为8．6．如图，AB 是反比例函数y ＝3x在第一象限内的图象上的两点，且A ，B 两点的横坐标分别是1和3，则S △AOB ＝4．7．(2019·鸡西)如图，在平面直角坐标系中，点O 为坐标原点，▱OABC 的顶点A 在反比例函数y ＝1x (x ＞0)的图象上，顶点B 在反比例函数y ＝5x(x ＞0)的图象上，点C 在x 轴的正半轴上，则▱OABC 的面积是(C)A.32B.52C ．4D ．68．如图，在平面直角坐标系中，点A 是x 轴上任意一点，BC 平行于x 轴，分别交反比例函数y ＝3x (x ＞0)，y ＝kx(x ＜0)的图象于B ，C 两点．若△ABC 的面积为2，则k 的值为－1．9．(2019·株洲)如图所示，在平面直角坐标系xOy 中，点A ，B ，C 为反比例函数y ＝k x(k ＞0)图象上不同的三点，连接OA ，OB ，OC ，过点A 作AD ⊥y 轴于点D ，过点B ，C 分别作BE ，CF 垂直x 轴于点E ，F ，OC 与BE 相交于点M ，记△AOD ，△BOM ，四边形CMEF 的面积分别为S 1，S 2，S 3，则(B)A ．S 1＝S 2＋S 3B ．S 2＝S 3C ．S 3＞S 2＞S 1D ．S 1S 2＜S 2310．(2019·本溪)如图，在平面直角坐标系中，等边△OAB 的边OA 和菱形OCDE 的边OE 都在x 轴上，点C 在OB 边上，S △ABD ＝3，反比例函数y ＝kx (x ＞0)的图象经过点B ，则k 的值。

第17章反比例函数姓名 分数 一、精心选一选（每题3分，共30分）1．下列函数中，当x ＞0时，y 随x 的增大而减小的是（ ）A ．y ＝3x +4B ．y ＝13x －2C ．y ＝－4xD ．y ＝12x2.若反比例函数y=xk的图象过第二、四象限，则函数y=k(x –1)的图象不经过（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 3. 下列函数，①y=2x，②y=x，③y=x -1，④y=11x 是反比例函数的个数有（ ）． A ．0个 B ．1个 C ．2个 D ．3个 4．函数y=kx 与y=-kx在同一直角坐标系中的图象可能是图（ ）．5．QQ 牌气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P （kPa ）是气体体积V （m 3）的反比例函数，其图象如图所示，当气球内的气压大于140kPa 时，•气球将爆炸，为了安全起见，气体体积应（ ）．A ．不大于2435m 3 B ．不小于2435m 3 C ．不大于2437m 3 D ．不小于2437m 36．已知点（3，1）是双曲线y=kx（k≠0）上一点，则下列各点中在该图象上的点是（ ）．A ．（13，-9）B ．（3，1）C ．（-1，3）D ．（6，-12）7．用电器的输出功率P 与通过的电流I 及电阻R 之间的关系是2P I R =，下面说法正确的是（ ） A ．P 为定值，I 与R 成反比例 B ．P 为定值，2I 与R 成反比例 C ．P 为定值，I 与R 成正比例D ．P 为定值，2I 与R 成正比例8．函数y=1x与函数y=x 的图象在同一平面直角坐标系内的交点个数是（ ）． A ．1个 B ．2个 C ．3个 D ．0个 9．若点（x 1，y 1），（x 2，y 2），（x 3，y 3）都是反比例函数y=-1x的图象上的点，并且x 1<0<x 2<x 3，则下列各式中正确的是（ ）．A ．y 1<y 2<y 3B ．y 2<y 3<y 1C ．y 3<y 2<y 1D ．y 1<y 3<y 2 10．反比例函数y=kx（k>0）在第一象限的图象上有一点P ，PQ ⊥x 轴，垂足为Q ，连PO ，设Rt △POQ 的面积为S ，则S 的值与k 之间的关系是（ ）． A ．S=.42kkB S =C ．S=kD ．S>k 二、细心填一填（每题3分，共18分）11．一个反比例函数y=kx（k≠0）的图象经过点P （-2，-1），则该反比例函数的解析式是________． 12．已知关于x 的一次函数y=kx+1和反比例函数y=6x的图象都经过点（2，m ），则一次函数的解析式是________．13．已知反比例函数y=2kx 的图象位于第二、四象限，且经过点（k-1，k+2），则k=_____． 14．若反比例函数y=21m x+的图象在第一、三象限，那么m 取值范围是______，•在第一象限内，y 随x 增大而_________． 15. 若函数y x =4与y x=1的图象有一个交点是（12，2），则另一个交点坐标是_________。

反比例函数一、选择题1、某闭合电路中，电源的电压为定值，电流I (A)与 电阻R (Ω)成反比例．如图表示的是该电路中电流I 与电阻R 之间函数关系的图象，则用电阻R 表示 电流I 的函数解析式为( )A ．I ＝2RB ．I ＝3RC ．I ＝6R D ．I ＝－6R 2、对于函数y ＝6x ，下列说法错误的是( )A ．它的图象分布在第一，三象限B ．它的图象既是轴对称图形又是中心对称图形C ．当x ＞0时，y 的值随x 的增大而增大D ．当x ＜0时，y 的值随x 的增大而减小3、若双曲线y ＝ kx 与直线y ＝2x ＋1的一个交点的横坐标为－1， 则k 的值为( )A ．－1B ．1C ．－2D ．24、已知反比例函数y ＝m －1x 的图象如图所示， 则实数m 的取值范围是( )A ．m ＞1B ．m ＞0C ．m ＜1D ．m ＜05．函数y ＝2x 与函数y ＝－1x 在同一坐标系中的大致图象是 ( )6、在反比例函数y ＝k x (k <0)的图象上有两点()－1，y 1，⎝ ⎛⎭⎪⎫－14，y 2，则y 1－y 2的值是 ( )A ．负数B ．非正数C ．正数D ．不能确定7、如图，正比例函数y1＝k 1x 和反比例函数 y 2＝k 2x 的图象交于A (－1，2)，B (1，－2)两点， 若y 1＜y 2，则x 的取值范围是( )A ．x <－1或x >1B ．x <－1或0<x <1C ．－1<x <0或0<x <1D ．－1<x <0或x >1 8、在同一直角坐标系中，正比例函数y ＝2x的图象与反比例函数y ＝4－2kx 的图象没有交点，则实数k 的取值范围在数轴上表示为 ( )二、填空题9、下列函数：①y ＝2x －1；②y ＝－5x ；③y ＝x 2＋8x －2；④y ＝3x 3；⑤y ＝12x ； ⑥y ＝ax 中，y 是x 的反比例函数的有__ __(填序号)．10、近视眼镜的度数y (度)与镜片焦距x (m)成反比例[即y ＝kx (k ≠0)]，已知200度近视眼镜的镜片焦距为0.5 m ，则y 与x 之间的函数关系式是_ _．11、如图，是反比例函数y ＝k －2x 的图象的一个分支，对于给出的下列说法：①常数k 的取值范围是k >2； ②另一个分支在第三象限；③在函数图象上取点A ()a 1，b 1和B ()a 2，b 2，当a 1>a 2时，b 1<b 2；④在函数图象的某一个分支上取点A ()a 1，b 1和B ()a 2，b 2，当a 1>a 2时，b 1<b 2. 其中正确的是__ __(在横线上填出正确的序号)．12、反比例函数y ＝kx 的图象与一次函数y ＝2x ＋1的图象的一个交点是(1，k )，则反比例函数的解析式是 __.13、若点A(m，－2)在反比例函数y＝4x的图象上，则当函数值y≥－2时，自变量x的取值范围是__．14、在平面直角坐标系xOy中，已知反比例函数y＝2kx(k≠0)满足：当x＜0时，y随x的增大而减小．若该反比例函数的图象与直线y＝－x＋3k都经过点P，且|OP|＝7，则实数k＝___．三、解答题15、蓄电池的电压为定值．使用此电源时，电流I(A)是电阻R(Ω)的反比例函数，其图象如图所示．(1)求这个反比例函数的表达式；(2)当R＝10 Ω时，电流能是4 A吗？为什么？16、如图，一次函数y＝－2x＋b(b为常数)的图象与反比例函数y＝kx(k为常数，且k≠0)的图象交于A，B两点，且点A的坐标为(－1，4)．(1)分别求出反比例函数及一次函数的表达式；(2)求点B的坐标．17、如图，已知双曲线y＝kx经过点D(6，1)，点C是双曲线第三象限分支上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连结AB，BC.(1)求k的值；(2)若△BCD的面积为12，求直线CD的解析式；(3)判断AB与CD的位置关系，并说明理由．。

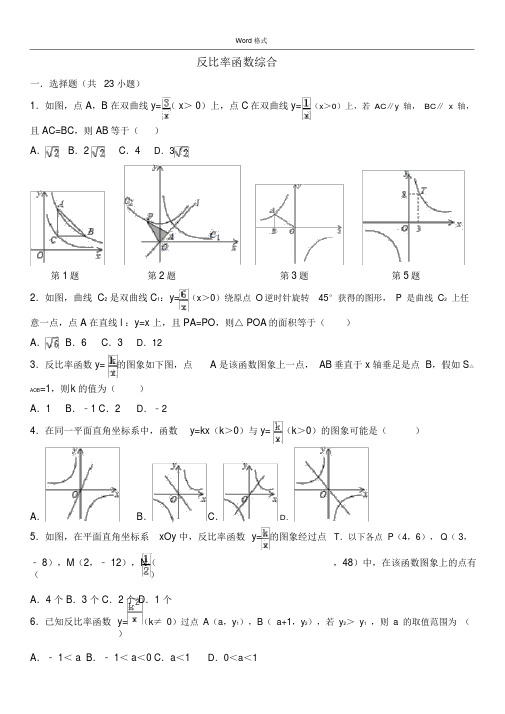
Word 格式反比率函数综合一．选择题（共23 小题）1．如图，点 A，B 在双曲线 y= （ x＞ 0）上，点 C在双曲线 y=（x＞0）上，若AC∥y轴，BC∥ x轴，且 AC=BC，则 AB等于（）A．B．2C．4D．3第1题第2题第3题第5题2．如图，曲线 C2是双曲线 C1：y=（x＞0）绕原点O逆时针旋转45°获得的图形，P是曲线C2上任意一点，点 A 在直线 l ：y=x 上，且 PA=PO，则△ POA的面积等于（）A．B．6C．3D．123．反比率函数 y=的图象如下图，点 A 是该函数图象上一点， AB垂直于 x 轴垂足是点 B，假如 S△AOB=1，则k 的值为（）A．1B．﹣1 C．2D．﹣24．在同一平面直角坐标系中，函数y=kx（k＞0）与 y=（k＞0）的图象可能是（）A．B．C．D．5．如图，在平面直角坐标系xOy 中，反比率函数y=的图象经过点T．以下各点 P（4，6）， Q（ 3，﹣ 8），M（2，﹣ 12），N（，48）中，在该函数图象上的点有（）A．4 个 B．3 个 C．2 个 D．1 个6．已知反比率函数y=（k≠ 0）过点A（a，y1），B（a+1，y2），若y2＞y1，则a的取值范围为（）A．﹣ 1＜ a B．﹣ 1＜ a＜0 C．a＜1D．0＜a＜1完满整理Word 格式7．如图，双曲线 y=与直线y=kx+b交于点M，N，而且点M的坐标为（1，3），点N的纵坐标为﹣1．根据图象信息可得对于x 不等式＜kx+b的解为（）A．x＜﹣ 3 B ．﹣ 3＜x＜0 C ．﹣ 3＜x＜1 D ．﹣ 3＜ x＜0 或 x ＞ 1第 7 题第 9 题第11题第 12题8．点 A（x1，y1），B（x2，y2），C（x3，y3）在反比率函数 y=的图象上，若 x1＜ x2＜0＜ x3，则 y1，y2，y3的大小关系是（）A．y ＜ y＜y3B ．y ＜y＜y1C ．y ＜y＜ y D．y ＜y＜ y31223321219．如图， A、B 是双曲线 y=（ k＞ 0）上的点， A、 B 两点的横坐标分别是a、3a，线段 AB的延伸线交 x 轴于点 C，若 S=3．则 k 的值为（）△AOCA．2B．1.5 C ．4D．610．已知点 A （ x1， y1），B（ x2，y2），C（ x3，y 3）在反比率函数y=（k＜0）的图象上，若x1＜x2＜0＜ x3，则 y1，y2，y3的大小关系是（）A．y ＜ y＜y3B ．y ＜y＜y3C ．y ＜y＜ y D．y ＜y＜ y212213213111．如图，点 A（m，1），B（ 2，n）在双曲线 y=（k≠0），连结 OA，OB．若 S=8，则 k 的值是（）△ABOA．﹣ 12B．﹣ 8 C ．﹣6D．﹣ 412．如图，反比率函数与正比率函数的图象交于A、B 两点，过点 A 作 AC⊥x 轴于点 C．若△ ABC的面积是 8，则这个反比率函数的分析式是（）A．y= B．y= C． y= D．y=13．如图，在平面直角坐标系中，函数y= 的图象与函数 y=x 的图象订交于 A，B 两点，点 C 是函数 y=的图象右支上一点，连结AC， BC，若∠ C=90°，则点C的坐标为（）A．（2，4） B．（3，6） C．（4，2） D．（，）Word 格式第13题第14题第15题第16题14．如图，直线 y= x﹣3 与 x 轴交于点 A，与双曲线 y=（k≠0）在第一象限内交于点B，过点 A 作AC⊥x 轴，交该双曲线于点C，若 AB=AC，则 k 的值是（）A．B．C．D．15．如图，在平面直角坐标系中，点A、B 分别在第二象限和第一象限，AB与 x 轴平行，∠ AOB=90°，OA=3，OB=4，函数 y=（x＜0）和y=（x＞0）的图象分别经过点AB，则的值为（）A．B．﹣C．D．﹣16．如图，在平面直角坐标系中，反比率函数y=（k≠ 0）经过? ABCD的极点B、D，点A的坐标为（ 0，﹣ 1）， AB∥x 轴， CD经过点（ 0， 2），? ABCD的面积是 18，则点 D 的坐标是（）A．（﹣2，2）B．（3，2） C．（﹣3，2）D．（﹣ 6，1）17．如图，点 M是反比率函数 y=（x＞0）图象上随意一点，MN⊥ y轴于N，点P是x轴上的动点，则△ MNP的面积为（）A．1B．2C． 4D．不可以确立第 17题第18题18．如图，已知点 A（ 0，4），B （ 1，4），点 B 在双曲线 y=（k ＞0）上，在AB的延伸线上取一点C，过 C 的直线交双曲线于点D，交 x 轴正半轴于点 E，且 CD=DE，则线段 CE长度的取值范围是（）A．4≤CE＜4B．4≤CE＜2C．2＜CE＜4D．4＜CE＜219．如图，已知点 A（2，3）和点 B（0，2），点 A 在反比率函数 y= 的图象上，作射线 AB，交反比率函数图象于另一点 M，再将射线 AB 绕点 A 按逆时针方向旋转 45°，交反比率函数图象于点 C，则Word 格式CM的长度为（）A．5B．6C．4D．5第19题第20题第21题第23题20．如图，在平面直角坐标系中，点 A 是 x 轴正半轴上的一个定点，点P 是双曲线 y= （x＞0）上的一个动点， PB⊥ y 轴于点 B，当点 P 的横坐标渐渐增大时，四边形OAPB的面积将会（）A．渐渐增大B．不变C．渐渐减小D．先增大后减小21．如图，一次函数 y1=x+1 的图象与反比率函数y2=的图象交于A、B两点，过点A作AC⊥ x轴于点C，过点 B 作 BD⊥ x 轴于点 D，连结 AO、BO，以下说法正确的选项是（）A．点 A 和点 B 对于原点对称B．当x＜1时，y1＞y2C．S△AOC=S△BOD D．当 x＞0 时， y1、y2都随 x 的增大而增大22．函数 y=k（x﹣1）与 y=﹣在同向来角坐标系内的图象大概是（）A．B．C．D．23．如图，点 A，C都在函数 y=（x＞0）的图象上，点B，D都在x轴上，且使得△ OAB，△ BCD 都是等边三角形，则点 C 的坐标是（）A．（+1，﹣）B．（+1，﹣1）C．（+1，﹣）D．（+1，﹣）二．填空题（共9 小题）24．如图，点 M是函数图象上的一点，直线l ：y=x，过点 M分别作 MA⊥y 轴， MB⊥l ，A，B 为垂足，则 MA? MB=．完满整理Word 格式第 24题第25题第30题第31题25．如图将直线向左平移 m 个单位，与双曲线交于点 A，与 x 轴交于点 B，则2 OB﹣22．OA+AB=26．假如反比率函数 y=（m﹣3）的图象在第二、四象限，那么 m=．27．已知双曲线 y= （ k≠ 0）上有一点 P，PA⊥ x 轴于 A，点 O为坐标原点，且 S=12，则此反比率△ PAO函数的分析式为．28．反比率函数的图象同时过 A（﹣ 2，a）、B（﹣ 3，b）、C（1，c ）三点，则 a、b、c 的大小关系是．2m2﹣ 3m+1，它的图象散布在象限，在29．函数 y=（ m﹣m）x是反比率函数，则 m 的值是每一个象限内， y 随 x 的增大而．30．如图， A、B 是反比率函数 y=上两点， AC⊥y 轴于 C，BD⊥x 轴于 D， AC=BD= OC，S 四边形ABDC=14，则 k=．31．如图， B 为双曲线 y=22（x＞0）上一点，直线 AB平行于 y 轴交直线 y=x 于点 A，若 OB﹣AB=12，则 k=．32．如图，正比率函数 y=x 与反比率函数 y=的图象订交于A，C 两点， AB⊥x 轴于 B，CD⊥x 轴于 D，则四边形 ABCD的面积为．完满整理Word 格式三．解答题（共8 小题）33．如图 1，在平面直角坐标系中，四边形AOBC是矩形，点 C 的坐标为（ 4，3），反比率函数 y=（k＞ 0）的图象与矩形 AOBC的边 AC、 BC分别订交于点 E、 F，将△ CEF沿 EF 对折后， C 点恰巧落在OB 上．（1）求证：△ AOE与△ BOF的面积相等；（2）求反比率函数的分析式；（3）如图 2， P 点坐标为（ 2，﹣ 3），在反比率函数 y= 的图象上能否存在点 M、 N（ M在 N 的左边），使得以 O、P、M、N为极点的四边形是平行四边形？若存在，求出点 M、N的坐标；若不存在，请说明原因．34．如图，在直角坐标系中，矩形 OABC的极点 O与坐标原点重合，极点 A、C 分别在座标轴上，极点B 的坐标为（ 4，2）， M、N 分别是 AB、BC的中点．（ 1）若反比率函数y=（x＞0）的图象经过点M，求该反比率函数的分析式，并经过计算判断点N能否在该函数的图象上；（ 2）若反比率函数y=（x＞0）的图象与△ MNB（包含界限）有公共点，请直接写出m的取值范围．35．如图，反比率函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点．完满整理Word 格式（1）求 A、B 两点的坐标；（2）察看图象，直接写出 x 为什么值时，一次函数值大于反比率函数？（3）求△ AOB的面积．36．如图，反比率函数 y1 = 的图象与一次函数 y2=kx+b 的图象交于 A（ m， 3），B（﹣ 3， n）、两点．（ 1）求一次函数的分析式及△ AOB的面积；（ 2）依据图象直接写出不等式的解集；（ 3）若点 P 是坐标轴上的一点，且知足△PAB面积等于△ AOB的面积的 2 倍，直接写出点P 的坐标．37．如图，若直线y=kx+b（ k≠0）与 x 轴交于点，与双曲线在第二象限交于点B，且 OA=OB，△ OAB的面积为完满整理（1）求直线 AB的分析式及双曲线的分析式；（2）求 tan ∠ ABO的值．38．已知反比率函数y=和一次函数y=2x﹣ 1，此中一次函数的图象经过（a，b），（ a+k，b+k+2）两点．（1）求反比率函数的分析式？（2）已知 A 在第一象限，是两个函数的交点，求 A 点坐标？（3）利用②的结果，请问：在 x 轴上能否存在点 P，使△ AOP为等腰三角形？39．如图，双曲线y=在第一象限的一支上有一点C（ 1， 5），过点 C 的直线 y=﹣kx+b（k＞0）与 x 轴交于点 A（a，0）．（ 1）求点 A 的横坐标 a 与 k 的函数关系式（不写自变量取值范围）．（ 2）当该直线与双曲线在第一象限的另一个交点 D 的横坐标是 9 时，求△ COA的面积．40．如图，一次函数y=ax+b 的图象与反比率函数的图象交于M、N两点．（1）利用图中条件，求反比率函数和一次函数的分析式；（2）连结 OM、ON，求三角形 OMN的面积．（3）连结 OM，在 x 轴的正半轴上能否存在点 Q，使△ MOQ是等腰三角形，若存在，请直接写出全部切合条件的点 Q的坐标，若不存在，说明原因．参照答案一．选择题（共23 小题）1．如图，点 A，B 在双曲线 y= （ x＞ 0）上，点 C在双曲线 y= （x＞0）上，若 AC∥y 轴， BC∥ x 轴，且 AC=BC，则 AB等于（ B ）Word 格式A ．B．2C．4D．3设 C（a，），则B（3a，），A（a，），∵ AC=BC，∴﹣=3a﹣a，解得a=1，（负值已舍去）∴C（ 1， 1），B（3，1），A（1， 3），∴ AC=BC=2，∴ Rt△ ABC中， AB=2 ，2．如图，曲线 C2是双曲线 C1：y=（x＞0）绕原点O逆时针旋转45°获得的图形，P是曲线C2上任意一点，点 A 在直线 l ：y=x 上，且 PA=PO，则△ POA的面积等于（B）A．B．6C．3D．12解：如图，将 C2及直线 y=x 绕点 O逆时针旋转 45°，则获得双曲线C3，直线 l 与 y 轴重合．双曲线 C3，的分析式为 y=﹣过点P作PB⊥ y轴于点B∵PA=PB∴B为OA中点．∴ S△PAB=S△POB由反比率函数比率系数△POBk 的性质， S =3∴△ POA的面积是 63．反比率函数 y=的图象如下图，点 A 是该函数图象上一点， AB垂直于 x 轴垂足是点 B，假如 S△=1，则 k 的值为（ D ）AOBA ．1 B．﹣1 C．2D．﹣ 24．在同一平面直角坐标系中，函数y=kx（k＞0）与 y=（k＞0）的图象可能是（C）A．B．C．D．5．如图，在平面直角坐标系xOy 中，反比率函数y=的图象经过点T．以下各点 P（4，6）， Q（ 3，完满整理Word 格式A．4个B．3个 C．2个 D．1个第5题第7题第9题6．已知反比率函数y=（k≠ 0）过点A（a，y1），B（a+1，y2），若y2＞y1，则a的取值范围为（B ）A．﹣ 1＜ a B．﹣ 1＜ a＜0 C．a＜1D．0＜a＜17．如图，双曲线 y=与直线y=kx+b交于点M，N，而且点M的坐标为（1，3），点N的纵坐标为﹣1．根据图象信息可得对于x 不等式＜kx+b的解为（D）A． x＜﹣ 3 B．﹣ 3＜x＜0 C ．﹣ 3＜ x＜ 1 D．﹣ 3＜x＜0 或 x ＞18．点 A（x1，y1），B（x2，y2），C（x3，y3）在反比率函数 y=的图象上，若 x1＜ x2＜0＜ x3，则 y1，y2，y3的大小关系是（D）A．y ＜ y＜y3B． y＜y＜y1C． y＜y＜y1D．y ＜y＜ y3122332219．如图， A、B 是双曲线 y=（ k＞ 0）上的点， A、 B 两点的横坐标分别是a、3a，线段 AB的延伸线交 x 轴于点 C，若 S=3．则 k 的值为（B）△AOCA．2 B．1.5 C ．4D．6解：如图，分别过点 A、B 作 AF⊥ y 轴于点∵ k＞ 0，点 A 是反比率函数图象上的点，∴F，AD⊥ x 轴于点 D， BG⊥y 轴于点 G， BE⊥x 轴于点 E，S△AOD=S△AOF= |k| ，∵ A、 B 两点的横坐标分别是 a、3a，∴ AD=3BE，∴点 B 是 AC的三均分点，∴ DE=2a，CE=a，∴S△AOC=S梯形ACOF﹣S△AOF= （OE+CE+AF）×OF﹣|k|=× 5a×﹣|k|=3，解得k=1.5．10．已知点 A （ x ， y），B（ x，y），C（ x，y ）在反比率函数 y=（k ＜0）的图象上，若 x＜ x＜0 11223312＜ x3，则 y1，y2，y3的大小关系是（D）A．y1＜ y2＜y3B． y2＜y1＜y3C． y3＜y2＜y1D．y3＜y1＜ y211．如图，点 A（ m，1），B（2，n）在双曲线 y= （ k≠ 0），连结 OA，OB．若 S△ABO=8，则 k 的值是（C）完满整理第11题第12题解：过 A 作 y 轴的垂线，过 B 作 x 轴的垂线，交于点C，连结 OC，设 A（k，1），B（2，k），则AC=2﹣k， BC=1﹣ k，∵ S△ABO=8，∴ S△ABC﹣ S△ACO﹣S△BOC=8，即（2﹣k）（ 1﹣ k）﹣（2﹣k）× 1﹣（1﹣k）× 2=8，解得 k=±6，∵ k＜0，∴ k=﹣6，12．如图，反比率函数与正比率函数的图象交于A、B 两点，过点 A 作 AC⊥x 轴于点 C．若△ ABC的面积是 8，则这个反比率函数的分析式是（C）A．y= B．y= C． y=D．y=13．如图，在平面直角坐标系中，函数y=的图象与函数y= x 的图象订交于 A，B 两点，点 C 是函数 y=的图象右支上一点，连结AC， BC，若∠ C=90°，则点 C的坐标为（A）A．（2，4）B．（3，6） C．（4，2） D．（，）解：函数 y=的图象与函数y=x 的图象订交于 A，B 两点，解方程组，可得，，∴B（4，2），A（﹣4，﹣2），∴OB=AO=2，又∵∠ ACB=90°，∴ OC= AB=2，设C（a，），则OC==2，解得a=2，或a=4（舍去），∴ C（2，4），14．如图，直线 y= x﹣3 与 x 轴交于点 A，与双曲线 y=（k≠0）在第一象限内交于点B，过点 A 作AC⊥x 轴，交该双曲线于点C，若 AB=AC，则 k 的值是（D）A．B．C．D．解：如图，过 B 作 BD⊥OA于 D，则∠ ADB=∠AOE=90°，由直线 y=x﹣3，可得 A（ 4，0），E（0，﹣3），∴ AO=4， OE=3， AE=5，设点 C 的坐标为（ 4，），则AC=AB=，由△ AOE∽△ ADB，可得= =，即= =，∴AD=，BD=，∴B（4+，），∵双曲线y=（k≠ 0）经过点B，∴（4+）×k=k，解得 k= ，15．如图，在平面直角坐标系中，点A、B 分别在第二象限和第一象限，AB与 x 轴平行，∠ AOB=90°，OA=3，OB=4，函数 y=（x＜0）和y=（x＞0）的图象分别经过点AB，则的值为（D）A ．B．﹣C．D．﹣解：∵ AB与 x 轴平行，∴ AB⊥ y 轴，即∠ AHO=∠OHB=90°，∵∠ AOB=90°，∴∠ AOH+∠BOH=∠AOH+∠OAH=90°，∴∠ OAH=∠BOH，∴△ AOH∽△ OBH，∴=，即=，又∵ k1＜0，∴=﹣，16．如图，在平面直角坐标系中，反比率函数y=（k≠ 0）经过? ABCD的极点B、D，点A的坐标为（ 0，﹣ 1）， AB∥x 轴， CD经过点（ 0， 2），? ABCD的面积是 18，则点 D 的坐标是（C）完满整理Word 格式A ．（﹣ 2， 2）B．（3，2） C．（﹣ 3，2）D．（﹣ 6， 1）解：如图，∵点 A 的坐标为（ 0，﹣ 1），AB∥x 轴，反比率函数 y= （k≠0）经过 ? ABCD的极点 B，∴点 B 的坐标为（﹣ k，﹣ 1），即 AB=﹣k，又∵点 E（0，2），∴ AE=2+1=3，又∵平行四边形ABCD的面积是 18，∴ AB×AE=18，∴﹣ k×3=18，∴ k=﹣6，∴ y=﹣，∵ CD经过点（ 0， 2），∴令 y=2，可得 x=﹣3，∴点 D的坐标为（﹣ 3， 2），17．如图，点 M是反比率函数 y= （x＞0）图象上随意一点， MN⊥ y 轴于 N，点 P 是 x 轴上的动点，则△ MNP的面积为（ A ）A．1B．2C．4D．不可以确立第17题第18题18．如图，已知点 A（ 0，4），B （ 1，4），点 B 在双曲线 y=（k ＞0）上，在AB的延伸线上取一点C，过 C 的直线交双曲线于点D，交 x 轴正半轴于点 E，且 CD=DE，则线段 CE长度的取值范围是（A）A．4≤CE＜4B．4≤CE＜2C．2＜CE＜4D．4＜CE＜2解：如图 1，过 D作 DF⊥OA于 F，∵点 A（0，4）， B （1，4），∴ AB⊥ y 轴， AB=1，OA=4，∵ CD=DE，∴AF=OF=2，∵点 B 在双曲线 y= （ k＞ 0）上，∴k=1×4=4，∴反比率函数的分析式为： y=，∵过点 C 的直线交双曲线于点D，∴ D 点的纵坐标为 2，把 y=2 代入 y=得，x=2，∴D（2，2），当 O与 E 重合时，如图 2，∵DF=2，∴AC=4，∵OA=4，∴CE=4 ，当 CE⊥ x 轴时，CE=OA=4，∴4≤CE＜4 ，19．如图，已知点A（2，3）和点B（0，2），点A 在反比率函数y= 的图象上，作射线AB，交反比率完满整理A．5B．6C．4D．5第19题第20题第21题解：如图，过 A 作 AD⊥y 轴于 D，将 AB绕着点 B 顺时针旋转 90°，获得 A'B，过 A' 作 A'H⊥y 轴于 H，由 AB=BA'，∠ ADB=∠BHA'=90°，∠ BAD=∠A'BH，可得△ ABD≌△ BA'H，∴ BH=AD=2，又∵ OB=2，∴点 H与点 O重合，点 A' 在 x 轴上，∴ A' （1，0），又∵等腰 Rt△ABA'中，∠ BAA'=45°，而∠ BAC=45°，∴点 A' 在 AC上，由 A（2，3），A' （ 1， 0），可得直线 AC的分析式为 y=3x﹣3，解方程组，可得或，∴ C（﹣1，﹣6），由点A（2，3）和点B（0，2），可得直线AB 的解析式为y= x+2 ，解方程组，可得或，∴ M（﹣6，﹣1），∴CM==5 ，20．如图，在平面直角坐标系中，点 A 是 x 轴正半轴上的一个定点，点P 是双曲线 y= （x＞0）上的一个动点， PB⊥ y 轴于点 B，当点 P 的横坐标渐渐增大时，四边形OAPB的面积将会（C）A．渐渐增大B．不变C．渐渐减小D．先增大后减小21．如图，一次函数 y1=x+1 的图象与反比率函数y2=的图象交于A、B两点，过点A作AC⊥ x轴于点C，过点 B 作 BD⊥ x 轴于点 D，连结 AO、BO，以下说法正确的选项是（ C ）A．点 A 和点 B 对于原点对称B．当 x＜1 时， y ＞ y12C．S△AOC=S△BOD D．当 x＞ 0 时， y1、 y2都随 x 的增大而增大解： A、，∵把①代入②得： x+1=，解得： x2+x﹣2=0，（ x+2）（ x﹣ 1） =0，x1=﹣2，x2=1，代入①得： y1=﹣1，y2=2，∴ B（﹣ 2，﹣ 1），A（1，2），∴ A、B 不对于原点对称，故本选项错误；B、当﹣ 2＜x＜0 或 x＞ 1 时， y1＞y2，故本选项错误；C、∵ S△AOC=×1×2=1，S△BOD=× |﹣2|×|﹣1|=1，∴ S△BOD=S△AOC，故本选项正确；完满整理D、当 x＞0 时， y1随 x 的增大而增大， y2随 x 的增大而减小，故本选项错误；22．函数 y=k（x﹣1）与 y=﹣在同向来角坐标系内的图象大概是（A）A．B．C．D．23．如图，点 A，C都在函数 y=（x＞0）的图象上，点B，D都在x轴上，且使得△ OAB，△ BCD都是等边三角形，则点 C 的坐标是（A）A．（+1，﹣）B．（+1，﹣1）C．（+1，﹣）D．（+1，﹣）第23题第24题解：如图，作 AE⊥OB于 E，CF⊥BD于 F，∵△ OAB，△ BCD均为正三角形， A 在反比率函数y=，∴ A 的横坐标是 1，纵坐标是，∴ OE=EB=1，OA=2OE=2，AE= ，设 BF=m，则 C（ 2+m， m），代入 y=2，，得： m+2m﹣ 1=0，解得： m=﹣1±，∵ m＞ 0，∴ m=﹣ 1+ ，∴点 C的坐标为：（1+）．二．填空题（共9 小题）24．如图，点 M是函数图象上的一点，直线l ：y=x，过点 M分别作 MA⊥y 轴， MB⊥l ，A，B 为垂足，则 MA? MB=．解：延伸 AM，交直线 y=x 于点 D，设 M（ x， x+）则△ AOD是等腰直角三角形，即∠ADO=45°，∴OA=AD=x+，AM=x，∴ MD=AD﹣AM= ，∵ MB⊥l ，∴ MB=BD，∴△ BDM是等腰直角三角形，222∴ MB+BD=MD，∴ MB= MD，∴ MB= × = ，∴ MA? MB=x?= ．25．如图将直线向左平移 m个单位，与双曲线222交于点 A，与 x 轴交于点 B，则 OB﹣OA+ AB=．完满整理Word 格式解：由题意知：平移后的直线分析式为：y=（x+m）；设 A（x，y），易知： B（﹣ m， 0），则有：22222222OB﹣OA+ AB=m﹣（ x+y ） +[ （m+x） +y ] ，联立 y=（ x+m），整理得：原式 =﹣2x2﹣2mx；因为直线 y=（x+m）与交于点 A，联立两个函数分析式得：（x+m） =﹣，即x2+mx+2=0，得﹣ x2﹣mx=2；2故所求代数式 =﹣2x ﹣2mx=4．26．假如反比率函数y=（m﹣3）的图象在第二、四象限，那么m= 1．2【解答】解：依据题意 m﹣6m+4=﹣ 1，解得 m=1或 5，又 m﹣3＜0，m＜3，因此 m=1．故答案为： 1．27．已知双曲线 y=（k≠ 0）上有一点P，PA⊥ x轴于A，点O为坐标原点，且S△PAO=12，则此反比率函数的分析式为y=﹣或y=．【解答】解：设点 P 的坐标为（ x， y）．∵P（x，y）在反比率函数y=kx（k≠0）的图象，∴ k=xy，∵S△PAO=12，∴|xy|=12 ，完满整理Word 格式∴ |xy|=24 ，∴ xy=±24，∴ k=±24，∴ y=﹣或y=．故答案为： y=﹣或y=．28．反比率函数的图象同时过A（﹣2，a）、B（﹣3，b）、C（1，c）三点，则a、b、c的大小关系是a＞b＞c．【解答】解：∵ k＜ 0，∴此函数的图象在二、四象限，∵﹣ 2＜0，﹣ 3＜0，1＞0，∴A、 B 两点在第二象限， C 点在第三象限，∴a＞ 0， b＞ 0， c＜ 0，∵﹣ 2＞﹣ 3，∴ a＞ b＞ 0，∴ a＞ b＞ c．故答案为 a＞b＞c．2m2﹣ 3m+129．函数 y=（ m﹣m）x是反比率函数，则 m的值是2 ，它的图象散布在第一、三象限，在每一个象限内， y 随 x 的增大而减小．22【解答】解：由题意得： m﹣3m+1=﹣ 1，且 m﹣ m≠ 0，解得： m=2，2∵ m﹣m=4﹣2=2＞ 0，∴图象散布在第一、三象限，在每一个象限内， y 随 x 的增大而减小，故答案为： 2；第一、三；减小．30．如图， A、B 是反比率函数 y=上两点，AC⊥y轴于C，BD⊥x轴于D，AC=BD= OC，S四边形ABDC=14，则 k= 16．完满整理Word 格式【解答】解：如图，分别延伸CA，DB交于点 E，依据 AC⊥y 轴于 C，BD⊥x 轴于 D，AC=BD= OC，知△ CED为直角三角形，且点A 与点 B 的纵横坐标正好相反，设点 A 的坐标为（ x A，y A），则点 B 的坐标为（ y A，x A），点 E 的坐标为（ y A，y A），四边形 ACDB的面积为△ CED的面积减去△ AEB的面积．CE=ED=y， AE=BE=y﹣y ，A A∴ S ACDB=S△CED﹣S△AEB= [y A? y A﹣（ y A﹣ y A）（y A﹣ y A）]=2=14，y A∵y A＞0，∴ y A=8，点 A 的坐标为（ 2， 8），∴ k=2×8=16．故答案为： 16．22 31．如图， B 为双曲线 y=（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，若OB﹣AB=12，则 k= 6 ．【解答】解：如图，延伸 AB交 x 轴于点 C，设点 C的横坐标为 a，完满整理则点 B 的纵坐标为，点A的纵坐标为a，因此， AB=a﹣，∵ AB平行于 y 轴，∴AC⊥OC，22222在 Rt△ BOC中， OB=OC+BC=a +（），2 2∵OB﹣ AB=12，∴ a2+（）2﹣（a﹣）2=12，整理得， 2k=12，解得 k=6．故答案为： 6．32．如图，正比率函数 y=x 与反比率函数 y= 的图象订交于 A，C 两点， AB⊥x 轴于 B，CD⊥x 轴于 D，则四边形 ABCD的面积为 2 ．【解答】解：依据反比率函数的对称性可知：OB=OD，AB=CD，∵四边形 ABCD的面积等于 S△ADB+S△BDC，∵A（1，1），B（1，0），C（﹣1，﹣1），D（﹣1，0）∴ S△ADB= （DO+OB）× AB= ×2×1=1，S△BDC=（DO+OB）× DC=×2×1=1，∴四边形 ABCD的面积 =2．完满整理故答案为： 2．三．解答题（共8 小题）33．如图 1，在平面直角坐标系中，四边形AOBC是矩形，点 C 的坐标为（ 4，3），反比率函数 y=（k＞ 0）的图象与矩形 AOBC的边 AC、 BC分别订交于点 E、 F，将△ CEF沿 EF 对折后， C 点恰巧落在OB 上．（1）求证：△ AOE与△ BOF的面积相等；（2）求反比率函数的分析式；（3）如图 2， P 点坐标为（ 2，﹣ 3），在反比率函数 y= 的图象上能否存在点 M、 N（ M在 N 的左边），使得以 O、P、M、N为极点的四边形是平行四边形？若存在，求出点 M、N的坐标；若不存在，请说明原因．【解答】解：（1）∵点 E、 F 均是反比率函数 y=上的点，四边形AOBC是矩形，∴AE⊥y 轴， BC⊥ x 轴，∴S△AOE=S△BOF=；（2）∵ C坐标为（ 4，3），∴设E（， 3），F（4，），如图 1，将△ CEF沿 EF 对折后， C点恰巧落在 OB边上的 G点，作 EH⊥OB，垂足为 H，∵∠ EGH+∠HEG=90°∠ EGH+∠FGB=90°，∴∠ HEG=∠FGB，又∵∠ EHG=∠GBF=90°，∴△ EGH∽△ GFB，∴=，完满整理Word 格式∴GB==，222222在 Rt△ GBF中， GF=GB+BF，即（ 3﹣） =（） +（），解得 k=，∴反比率函数的分析式为：y=；（ 3）存在．当 OP是平行四边形的边时，如图 2 所示：平行四边形 OPMN，能够当作线段 PN沿 PO的方向平移至OM地方得．设 N（a，），∵P（ 2，﹣ 3）的对应点 O（0，0），∴ M（ a﹣ 2， +3），代入反比率分析式得：（a﹣2）（+3）=，整理得 4a2﹣ 8a﹣7=0，解得 a=，当 a=时，==，﹣2=，+3=，∴ N（，），M（，）（舍去）或N（，），M（，）．当 OP为对角线时，如图3 所示：设 M（a，）， N（ b，），∵ P（ 2，﹣ 3），∴，解得，，∴M（，），N（，）（舍去）或M（，），N（，完满整理Word 格式），综上所述： M（，）N（，）；或M（，），N（，）．34．如图，在直角坐标系中，矩形 OABC的极点 O与坐标原点重合，极点 A、C 分别在座标轴上，极点B 的坐标为（ 4，2）， M、N 分别是 AB、BC的中点．（ 1）若反比率函数y=（x＞0）的图象经过点M，求该反比率函数的分析式，并经过计算判断点N 能否在该函数的图象上；（ 2）若反比率函数y=（x＞0）的图象与△ MNB（包含界限）有公共点，请直接写出m的取值范围．完满整理Word 格式【解答】解：（1）∵极点 B 的坐标为（ 4， 2），M、N分别是 AB、BC的中点，∴ M点的坐标为（ 2， 2），把 M（2，2）代入反比率函数y=（m≠0）得，m=2×2=4，∴反比率函数的分析式为y=；∵M、 N分别为矩形 OABC的边 AB、BC的中点，且 M（ 2， 2），B 点坐标为（ 4，2），∴ N点坐标为（ 4，1），∵4× 1=4，∴点 N 在函数 y=的图象上；（2） 4≤ m≤ 8．35．如图，反比率函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点．（1）求 A、B 两点的坐标；（2）察看图象，直接写出 x 为什么值时，一次函数值大于反比率函数？（3）求△ AOB的面积．【解答】解：（1）联立两函数分析式得：，解得：或，即 A（﹣ 2，4），B（4，﹣ 2）；（3）令 y=﹣x+2 中 x=0，获得 y=2，即D（0，2），∴ OD=2，∴ S△AOB=S△AOC+S△BOC= ×2×2+ × 2× 4=6．36．如图，反比率函数 y1 = 的图象与一次函数 y2=kx+b 的图象交于 A（ m， 3），B（﹣ 3， n）、两点．（ 1）求一次函数的分析式及△ AOB的面积；（ 2）依据图象直接写出不等式的解集；（ 3）若点 P 是坐标轴上的一点，且知足△PAB面积等于△ AOB的面积的 2 倍，直接写出点P 的坐标．【解答】解：（ 1）∵反比率函数 y1= 的图象与一次函数 y2=kx+b 的图象交于 A（m，3），B（﹣ 3，n）、两点，将A 与B 坐标代入反比率分析式得：m=1，n=﹣1，∴ A（ 1， 3）、B（﹣ 3，﹣ 1），代入一次函数分析式得：，解得： k=1， b=2，∴一次函数的分析式为y=x+2，∵直线 y=x+2 与 x 轴、 y 轴的交点坐标为（﹣ 2，0）、（ 0，2），∴S△AOB= ×2×（ 1+3） =4；（ 2）∵ A（1，3）， B（﹣ 3，﹣ 1），察看图象可知，当x＜﹣ 3 或 0＜x＜1 时，一次函数的图象在反比率函数图象的下方，∴不等式的解集是 x＜﹣ 3 或 0＜x＜1．∴S△PAB=2S△AOB=8，设 P1（p，0），即 OP1=|p+2| ，S△ABP1=S△AP1C+S△P1BC= |p+2| ×3+ |p+2| ×1=8，解得： p=﹣6 或 p=2，则 P1（﹣ 6，0）、P2（2，0），同理可得 P3（0，6）、P4（0，﹣ 2）．37．如图，若直线y=kx+b（ k≠0）与 x 轴交于点，与双曲线在第二象限交于点B，且 OA=OB，△ OAB的面积为（1）求直线 AB的分析式及双曲线的分析式；（2）求 tan ∠ ABO的值．【解答】解：（1）∵直线 y=kx+b（k≠0）与 x 轴交于点 A，∴OA= ，又∵ OA=OB，∴OB= ，过点 B 作 BM⊥ x 轴于点 M，∵△ OAB的面积为，即OA? BM= ，∴BM=2，在 Rt △OBM中可求 OM=1.5，∴B（﹣ 1.5 ，2），再依据待定系数法可得：，解得： k=﹣，b=，∴直线 AB的分析式为： y=﹣x+；再将点 B 代入函数 y=得：m=﹣3，∴双曲线的分析式为：y=﹣；（2）∵ OA=OB，∴∠ ABO=∠BAM，在 Rt△ ABM中， BM=2，∴ MO= ，AM= + =4，∴tan ∠ABO=tan∠BAM= = ．38．已知反比率函数y=和一次函数y=2x﹣ 1，此中一次函数的图象经过（a，b），（ a+k，b+k+2）两点．（1）求反比率函数的分析式？（2）已知 A 在第一象限，是两个函数的交点，求 A 点坐标？（3）利用②的结果，请问：在 x 轴上能否存在点 P，使△ AOP为等腰三角形？Word 格式【解答】解：（1）∵一次函数 y=2x﹣ 1 的图象经过（ a， b），（a+k，b+k+2）两点，代入得：，解得： k=2，代入反比率函数的分析式得：y= = ，∴反比率函数的分析式是y=．（ 2）解方程组得：，，∴两函数的交点坐标是（﹣，﹣ 2），（1，1），∵交点 A 在第一象限，∴A（1，1）．（ 3）在 x 轴上存在点 P，使△ AOP为等腰三角形，原因是：分为三种状况：①以O为圆心，以 OA为半径作圆，交x 轴于两点 C、D，此时 OA=0C=0D，∴当 P 于 C 或 D 重合时，△ AOP是等腰三角形，此时 P 的坐标是（，0），（﹣，0）；②以 A 为圆心，以 OA为半径作圆，交 x 轴于点 E，此时 OA=AE，∴当P 于 E 重合时，△ AOP是等腰三角形，此时 P 的坐标是（ 2，0）；③作 OA的垂直均分线交 x 轴于 F，此时 AF=OF，∴当 P 于 F 重合时，△ AOP是等腰三角形，此时P 的坐标是（ 1，0）；∴存在 4 个点 P，使△ AOP是等腰三角形．Word 格式39．如图，双曲线y=在第一象限的一支上有一点C（ 1， 5），过点 C 的直线 y=﹣kx+b（k＞0）与 x 轴交于点 A（a，0）．（ 1）求点 A 的横坐标 a 与 k 的函数关系式（不写自变量取值范围）．（ 2）当该直线与双曲线在第一象限的另一个交点 D 的横坐标是 9 时，求△ COA的面积．【解答】解：（1）把 C（1，5）代入直线 y=﹣ kx+b（ k＞ 0）得：﹣ k+b=5，则 b=5+k；把（ a，0）代入直线 y=﹣kx+b（k＞0）得：﹣ ak+b=0，把 b=5+k 代入﹣ ak+b=0，得：﹣ ak+5+k=0，解得： a=；（2）把 x=9 代入 y= 得： y= ，则 D 的坐标是（ 9，），设直线 AC的分析式是 y=﹣ kx+b，把 C、D两点代入，得，解得：，则 AC的分析式是： y=﹣x+．令 y=0，解得：x=10．则 OA=10，则△ COA的面积 = ×10×5=25．Word 格式40．如图，一次函数y=ax+b 的图象与反比率函数的图象交于M、N两点．（1）利用图中条件，求反比率函数和一次函数的分析式；（2）连结 OM、ON，求三角形 OMN的面积．（3）连结 OM，在 x 轴的正半轴上能否存在点 Q，使△ MOQ是等腰三角形，若存在，请直接写出全部切合条件的点 Q的坐标，若不存在，说明原因．【解答】解：（1）把 N（﹣ 1，﹣ 4）代入 y=得：k=4，∴y= ，把M（2，m）代入得：m=2，∴M（2，2），把 N（﹣ 1，﹣ 4），M（2，2）代入 y=ax+b 得：，解得： a=2， b=﹣2，∴ y=2x﹣ 2，答：反比率函数的分析式是y=，一次函数的分析式是y=2x﹣2．（ 2）设 MN交 x 轴于 C，y=2x﹣2，Word 格式∴C（1，0），OC=1，∴△ MON的面积是 S=S△MOC+S△NOC=×1×2+×1×|﹣4|=3，答：三角形 MON的面积是 3．（ 3）当 OM=OQ时， Q的坐标是（ 2，0）；当 OM=MQ时， Q的坐标是（ 4，0）；当 OQ=QM时， Q的坐标是（ 2，0）；答：在 x 轴的正半轴上存在点 Q，使△ MOQ是等腰三角形，全部切合条件的点Q的坐标是（ 2，0）或（ 4，0）或（ 2， 0）．完满整理。

专题08 反比例函数一．选择题（共14小题）1．（2021•江岸区校级自主招生）如图，点A在反比例函数y1＝（x＞0）的图象上，过点A作AB⊥x轴，垂足为B，交反比例函数y2＝（x＞0）的图象于点C，P为y轴上一点，连接P A，PC，则△APC的面积为（）A．6B．8C．12D．20 2．（2020•江岸区校级自主招生）直线y＝kx+1与双曲线y＝有两个交点均在直线y＝x的同侧，则k的取值范围为（）A．＜k＜B．﹣＜k＜0或＜k＜C．k＜﹣或k＞D．﹣＜k＜0或0＜k＜3．（2020•温江区校级自主招生）已知点A（﹣4，m），B（﹣，n）都在反比例函数y＝的图象上，则m与n的大小关系是（）A．m＞n B．m＜n C．m＝n D．不能确定4．（2020•淄博）如图，在直角坐标系中，以坐标原点O（0，0），A（0，4），B（3，0）为顶点的Rt△AOB，其两个锐角对应的外角角平分线相交于点P，且点P恰好在反比例函数y＝的图象上，则k的值为（）A．36B．48C．49D．64 5．（2020•南岸区自主招生）如图，点A与点B关于原点对称，点C在第四象限，∠ACB＝90°．点D是x轴正半轴上一点，AC平分∠BAD，E是AD的中点，反比例函数y＝（k＞0）的图象经过点A，E．若△ACE的面积为6，则k的值为（）A．4B．6C．8D．12 6．（2020•巴南区自主招生）如图，点A，B分别在x轴，y轴的正半轴上，且△ABO的面积为8，若双曲线y＝（k≠0）经过边AB的中点C，则k的值为（）A．4B．6C．8D．12 7．（2020•浙江自主招生）如图，点A是函数y＝的图象上的点，点B，C的坐标分别为B （﹣，﹣），C（，）．试利用性质：“函数y＝的图象上任意一点A都满足|AB﹣AC|＝2”求解下面问题：作∠BAC的角平分线AE，过B作AE的垂线交AE于F，已知当点A在函数y＝的图象上运动时，点F总在一条曲线上运动，则这条曲线为（）A．直线B．抛物线C．圆D．反比例函数的曲线8．（2019•永春县校级自主招生）如图，点A、B是反比例函数y＝（k≠0）图象上的两点，延长线段AB交y轴于点C，且点B为线段AC中点，过点A作AD⊥x轴于点D，点E 为线段OD的三等分点，且OE＜DE．连接AE、BE，若S△ABE＝7，则k的值为（）A．﹣12B．﹣10C．﹣9D．﹣6 9．（2015•湖州）如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y＝（x＜0）图象上一点，AO的延长线交函数y＝（x＞0，k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x轴的对称点为C′，交于x轴于点B，连接AB，AA′，A′C′．若△ABC的面积等于6，则由线段AC，CC′，C′A′，A′A所围成的图形的面积等于（）A．8B．10C．3D．4 10．（2018•市北区校级自主招生）如图，△OA1B1，△B1A2B2为等边三角形，△OA1B1的面积为，点A1，A2在反比例函数y＝的图象上，则B2点的坐标为（）A．（2，0）B．（+1，0）C．（3，0）D．（2，0）11．（2020•江汉区校级自主招生）已知点A是双曲线在第一象限上的一动点，连接AO 并延长交另一分支于点B，以AB为一边作等边三角形ABC，点C在第四象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式是（）A．（x＞0）B．（x＞0）C．（x＞0）D．（x＞0）12．（2020•赫山区校级自主招生）如图，反比例函数的图象经过点A（2，1），若y≤1，则x的范围为（）A．x≥1B．x≥2C．x＜0或0＜x≤1D．x＜0或x≥213．（2019•南岸区自主招生）如图，点A和点B都是反比例函数在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1，连接AB，以线段AB为边的矩形ABCD 的顶点D，C恰好分别落在x轴，y轴的负半轴上，连接AC，BD交于点E，若△ABC的面积为6，则k的值为（）A．2B．3C．6D．12 14．（2018•镇江）如图，一次函数y＝2x与反比例函数y＝（k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为，则k的值为（）A．B．C．D．二．填空题（共6小题）15．（2020•渝中区校级自主招生）如图所示，在平面直角坐标系xOy中，函数y＝（x＞0）的图象P经过点A（3，﹣1），直线l：y＝x+k与图象P交于点B，与y轴交于点C．记图象P在点A、B之间的部分与线段OA、OC、BC围成的区域（不含边界）为W，且区域W内恰有3个整数点（即横、纵坐标均为整数的点），则k的取值范围为．16．（2020•武昌区校级自主招生）过原点的直线与双曲线y＝分别交于A、B两点，过点B作x轴的垂线，垂足为点C（如图），则△ABC的面积为．17．（2020•衡阳县自主招生）如图，直线y＝x+1与x轴交于点A，与函数y＝（k＞0，x＞0）的图象交于点B，BC⊥x轴于点C，平移直线y＝x+1，使其经过点C，且与函数y＝（k＞0，x＞0）的图象交于点D，若AB＝2CD，则k的值为．18．（2020•温江区校级自主招生）在平面直角坐标系xOy中，记反比例函数y＝（k＜0，x＜0）的图象为C1，将C1沿x轴翻折得到C2（如图所示）．若点A（m，2）在C1上，将线段AO绕点A顺时针方向旋转90°后，点O恰好落在C2上点B的位置，则k ＝．19．（2020•武昌区校级自主招生）如图，已知直线y＝kx（k＞0）分别交反比例函数y＝和y＝在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交y＝的图象于点C，连接AC．若△ABC是等腰三角形，则k的值是．20．（2020•汉阳区校级自主招生）如图，平面直角坐标系xOy中，矩形OABC的边OA、OC 分别落在x、y轴上，点B坐标为（6，4），反比例函数的图象与AB边交于点D，与BC边交于点E，连接DE，将△BDE沿DE翻折到△B'DE处，点B'恰好落在正比例函数y＝kx图象上，则k的值是．三．解答题（共5小题）21．（2021•浦东新区校级自主招生）点A在y＝（x＞0）上，点B、C在y＝（x＞0）上，AB∥y轴，AC∥x轴，且＝，求BC的长．22．（2021•黄州区校级自主招生）如图，在平面直角坐标系中已知四边形ABCD为菱形，且A（0，3），B（﹣4，0）．（1）求过点C的反比例函数表达式；（2）设直线l与（1）中所求函数图象相切，且与x轴，y轴的交点分别为M，N，O为坐标原点．求证：△OMN的面积为定值．23．（2020•温江区校级自主招生）如图，在平面直角坐标系xOy中，一次函数y＝x+b的图象经过点C（0，2），与反比例函数y＝（x＞0）的图象交于点A（1，a）．（1）求一次函数和反比例函数的表达式；（2）设M是反比例函数y＝（x＞0）图象上一点，N是直线AB上一点，若以点O、M、C、N为顶点的四边形是平行四边形，求点N的坐标．24．（2020•北碚区自主招生）某数学小组对函数y1＝图象和性质进行探究．当x＝4时，y1＝0．（1）当x＝5时，求y1的值；（2）在给出的平面直角坐标系中，补全这个函数的图象，并写出这个函数的一条性质；（3）进一步探究函数图象并解决问题：已知函数y2＝﹣的图象如图所示，结合函数y1的图象，直接写出不等式y1≥y2的解集．25．（2020•汉阳区校级自主招生）如图1，平面直角坐标系xOy中，A（﹣4，3），反比例函数y＝（k＜0）的图象分别交矩形ABOC的两边AC，BC于E，F（E，F不与A重合），沿着EF将矩形ABOC折叠使A，D重合．（1）①如图2，当点D恰好在矩形ABOC的对角线BC上时，求CE的长；②若折叠后点D落在矩形ABOC内（不包括边界），求线段CE长度的取值范围．（2）若折叠后，△ABD是等腰三角形，请直接写出此时点D的坐标．专题08 反比例函数参考答案与试题解析一．选择题（共14小题）1．【解答】解：连接OA和OC，∵点P在y轴上，AB∥y轴，则△AOC和△APC面积相等，∵点A在反比例函数y1＝（x＞0）的图象上，点C在反比例函数y2＝（x＞0）的图象上，AB⊥x轴，∴S△OAB＝×20＝10，S△OBC＝＝4，∴S△AOC＝S△OAB﹣S△OBC＝6，∴△APC的面积为6，故选：A．2．【解答】解：因为双曲线y＝与直线y＝x的交点为A（2，2），B（﹣2，﹣2）．当函数y＝kx+1的图象过点A（2，2）时，k＝；当函数y＝kx+1的图象过点B（﹣2，﹣2）时，k＝．当k＞0时，又因为直线y＝kx+1与双曲线y＝有两个交点均在直线y＝x的同侧，所以实数k的取值范围是：＜k＜，令kx+1＝得到方程kx2+x﹣4＝0，当k＜0时，△＝1+16k＞0解得：﹣＜k＜0，综上，实数k的取值范围是＜k＜或﹣＜k＜0，故选：B．3．【解答】解：∵k＝2＞0，∴函数的图象在一、三象限，根据函数性质，函数在一、三象限y随x的增大而减小，∵﹣4＜﹣，∴m＞n，故选：A．4．【解答】解：过P分别作AB、x轴、y轴的垂线，垂足分别为C、D、E，如图，∵A（0，4），B（3，0），∴OA＝4，OB＝3，∴AB＝＝5，∵△OAB的两个锐角对应的外角角平分线相交于点P，∴PE＝PC，PD＝PC，∴PE＝PC＝PD，设P（t，t），则PC＝t，∵S△P AE+S△P AB+S△PBD+S△OAB＝S矩形PEOD，∴×t×（t﹣4）+×5×t+×t×（t﹣3）+×3×4＝t×t，解得t＝6，∴P（6，6），把P（6，6）代入y＝得k＝6×6＝36．故选：A．5．【解答】解：连接OC，在Rt△ABC中，点O是AB的中点，∴OC＝AB＝OA，∴∠OAC＝∠OCA，∵AC是∠BAD的角平分线，∴∠OAC＝∠EAC，∴∠OCA＝∠EAC，∴AE∥OC∴S△AEC＝S△AOE，过A作AM⊥x轴于M，过E作EN⊥x轴于N，∵A、E都在反比例函数y＝的图象上，∴S△AOM＝S△EON，∴S梯形AMNE＝S△AOE，∵AM∥EN，∴△DAM∽△DEN，∵AE＝DE，S梯形AMNE＝S△AOE＝S△AEC＝6，∴S△AOD＝12，延长DA交y轴于P，易得△DAM∽△DPO，设EN＝a，则AM＝2a，∴ON＝，OM＝，∴MN＝，DN＝，∴DM：OM＝2：1，∴S△DAM：S△AOM＝2：1，∴S△AOM＝4，∴k＝8．故选：C．6．【解答】解：设点A（a，0），点B（0，b），∴OA＝a，OB＝b，∵△ABO的面积为8，∴ab＝8，∴ab＝16，∵点C是AB中点，∴点C（，），∵点C在双曲线y＝（k≠0）上，∴k＝×＝4，故选：A．7．【解答】解：如图：延长AC交BF的延长线于G，连接OF．∵AF⊥BG，∴∠AFB＝∠AFG＝90°，∴∠BAF+∠ABF＝90°，∠G+∠GAF＝90°，∵AE为∠BAG的平分线，∴∠BAF＝∠F AG，∴∠ABF＝∠G，∴AB＝AG，∵AF⊥BG，∴BF＝FG，∵B（﹣，﹣），C（，），∴OB＝OC，∴OF＝CG，∵AC＝AG﹣CG，AB＝AG，∴AB﹣AC＝CG，∵|AB﹣AC|＝2，∴CG＝2，∴OF＝，∴点F在以O为圆心为半径的圆上运动．故选：C．8．【解答】解：设A（m，），C（0，n），则D（m，0），E（m，0），∵AB＝BC，∴B（，），∵点B在y＝上，∴•＝k，∴k+mn＝4k，∴mn＝3k，连接EC，OA．∵AB＝BC，∴S△AEC＝2•S△AEB＝14，∵S△AEC＝S△AEO+S△ACO﹣S△ECO，∴14＝•（﹣m）•+•n•（﹣m）﹣•（﹣m）•n，∴14＝﹣k﹣+，∴k＝﹣12．解法二：过点B作BM⊥DE于M，设A（a，），则B（，）．由题意，OE＝﹣a，DE＝﹣a，ME＝﹣a，BM＝，DM＝﹣a，∵S△ABE＝S梯形ADMB+S△BEM﹣S△ADE＝7，∴（+）×（﹣a）+×（﹣a）×（）﹣××（﹣a）＝7，解得k＝﹣12．故选：A．9．【解答】解：过A作AD⊥x轴于D，连接OA′，∵点A是函数y＝（x＜0）图象上一点，∴设A（a，），∵点C在函数y＝（x＞0，k是不等于0的常数）的图象上，∴设C（b，），∵AD⊥BD，BC⊥BD，∴△OAD∽△OCB，∴＝＝，∵S△ADO＝，S△BOC＝，∴k2＝，∵S△ABC＝S△AOB+S△BOC＝（﹣）•b+＝6，∴k2﹣＝12，①当k＞0时，k＝﹣，∴k2+k﹣12＝0，解得：k＝3，k＝﹣4（不合题意舍去），②当k＜0时，k＝，∴k2﹣k﹣12＝0，解得：k＝﹣3，k＝4（不合题意舍去），∴k2＝9∵点A关于y轴的对称点为A′，点C关于x轴的对称点为C′，∴∠1＝∠2，∠3＝∠4，∴∠1+∠4＝∠2+∠3＝90°，∴OA′，OC′在同一条直线上，∴S△OBC′＝S△OBC＝＝，∵S△OAA′＝2S△OAD＝1，∴由线段AC，CC′，C′A′，A′A所围成的图形的面积＝S△OBC+S△OBC′+S△OAA′＝10．故选：B．10．【解答】解：分别过A1、A2作x轴的垂线，垂足分别为D、E，如图，设OD＝m，B1E＝n（m＞0，n＞0）．∵△OA1B1，△B1A2B2是等边三角形，∴∠OA1D＝∠B1A2E＝30°，OD＝DB1＝OB1，B1E＝EB2＝B1B2，A1D＝m，A2E ＝n，则A1（m，m），A2（2m+n，n）∴S△A1OD＝S△A1OB1＝＝|k|，∴k＝（k＞0），∴反比例函数的关系式为：y＝，把A1（m，m），A2（2m+n，n）代入得，m•m＝，（2m+n）•n＝，∴m＝1，n＝﹣1，∴OB2＝2m+2n＝2，∴B2点的坐标为（2，0），故选：A．11．【解答】解：设A（a，），∵点A与点B关于原点对称，∴OA＝OB，∵△ABC为等边三角形，∴AB⊥OC，OC＝AO，∵AO＝，∴CO＝，过点C作CD⊥x轴于点D，则可得∠AOD＝∠OCD（都是∠COD的余角），设点C的坐标为（x，y），则tan∠AOD ＝tan∠OCD，即＝，解得：y＝﹣x，在Rt△COD中，CD2+OD2＝OC2，即y2+x2＝3a2+，将y＝﹣x代入，可得：x2＝，故x＝，y＝﹣x＝﹣a，则xy＝﹣9，故可得：y＝﹣（x＞0）．故选：C．12．【解答】解：在第一象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为x≥2；在第三象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为x＜0．故选：D．13．【解答】解：∵点A和点B都是反比例函数在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1∴A（1，k）、B（k，1）E为矩形ABCD对角线的交点，∴E（，）∵D，C恰好分别落在x轴，y轴的负半轴上，设D（a，0）、C（0，b）E为点A、C的中点∴a＝1﹣k，b＝1﹣k∴D（1﹣k，0），C（0，1﹣k）且1﹣k＜0在等腰直角△COD中，OD＝OC＝k﹣1，由勾股定理得：DC2＝OD2+OC2DC2＝（k﹣1）2+（k﹣1）2DC＝（k﹣1）A（1，k）、D（1﹣k，0），AD2＝（1﹣k﹣1）2+k2＝k∴k2﹣k﹣6＝0解得：k＝3，k＝﹣2（不符合题意，舍去）故选：B．14．【解答】解：连接BP，由对称性得：OA＝OB，∵Q是AP的中点，∴OQ＝BP，∵OQ长的最大值为，∴BP长的最大值为×2＝3，如图，当BP过圆心C时，BP最长，过B作BD⊥x轴于D，∵CP＝1，∴BC＝2，∵B在直线y＝2x上，设B（t，2t），则CD＝t﹣（﹣2）＝t+2，BD＝﹣2t，在Rt△BCD中，由勾股定理得：BC2＝CD2+BD2，∴22＝（t+2）2+（﹣2t）2，t＝0（舍）或﹣，∴B（﹣，﹣），∵点B在反比例函数y＝（k＞0）的图象上，∴k＝﹣＝；故选：C．二．填空题（共6小题）15．【解答】解：∵函数y＝（x＞0）的图象P经过点A（3，﹣1），∴m＝3×（﹣1）＝﹣3，∴直线l为：y＝﹣x+k，如图1，直线l在OA的下方时，当直线l：y＝﹣x+k过（1，﹣2）时，k＝﹣，区域W内有两个点整点，当直线l：y＝﹣x+k过（1，﹣3）时，k＝﹣，区域W内有三点整点，∴区域W内恰有3个整点，b的取值范围是﹣≤k＜﹣．如图2，直线l在OA的上方时，当直线l：y＝﹣x+k过（0，1）时，k＝1，区域W内有两个点整点，当直线l：y＝﹣x+k过（1，1）时，k＝，区域W内有三个点整点，∴区域W内恰有3个整点，k的取值范围是1＜k≤．综上所述，区域W内恰有3个整点，k的取值范围是﹣≤k＜﹣或1＜k≤．故答案为﹣≤k＜﹣或1＜k≤．16．【解答】解：设点A坐标为（a，b），则点B的坐标为（﹣a，﹣b），∴b＝，即ab＝﹣2，根据题意可知，S△BOC＝＝＝＝1，＝＝＝1，S△ABC＝S△BOC+S△AOC＝1+1＝2．故答案为：2．17．【解答】解：由直线y＝x+1可知A（﹣2，0），∴OA＝2，设B（m.m+1），∴OC＝m，BC＝，∴AC＝2+m，由题意可知，△ABC∽△CDE，∴＝，即，∴CE＝1+m，DE＝m+，∴OE＝OC+CE＝1+m，∴D（1+m，m+），∵函数y＝（k＞0，x＞0）的图象过点B、点D，∴k＝m（m+1）＝（1+m）（m+），解得m＝2（负数舍去），∴k＝2×（＝4，故答案为4．18．【解答】解：作AE⊥x轴于E，作BD∥x轴，交AE于D，∵点A（m，2）在C1上，∴OE＝﹣m，AE＝2，根据题意C2的函数关系式为y＝﹣，∵∠BAO＝90°，∴∠BAD+∠OAE＝90°，∵∠OAE+∠AOE＝90°，∴∠BAD＝∠AOE，∵∠AEO＝∠BDA＝90°，AB＝OA，∴△ABD≌△OAE（AAS），∴BD＝AE＝2，AD＝OE＝﹣m，∴B（m﹣2，﹣m+2），∵点A（m，2）在C1上，点B（m﹣2，﹣m+2）在C2上，∴k＝2m，﹣k＝（m﹣2）（﹣m+2），∴2m+（m﹣2）（m+2）＝0，整理得：m2+2m﹣4＝0，解得m1＝﹣1﹣，m2＝﹣1+，∵k＜0，x＜0，∴m＝﹣1﹣，∴k＝2m＝﹣2﹣2，故答案为﹣2﹣2．19．【解答】解：∵点B是y＝kx和y＝的交点，y＝kx＝，∴点B坐标为（，2），同理可求出点A的坐标为（，），∵BD⊥x轴，∴点C横坐标为，纵坐标为，∴BA＝，AC＝，BC＝，∴BA2﹣AC2＝k＞0，∴BA≠AC，若△ABC是等腰三角形，①当AB＝BC时，则＝，解得：k＝±（舍去负值）；②当AC＝BC时，同理可得：k＝；故答案为：或．20．【解答】解：∵四边形ABCD为矩形，B（6，4），∴E点的纵坐标为4，D点的横坐标为6，当x＝6时，y＝＝1，则D（6，1）；当y＝4时，＝4，解得x＝，则E（，4），∴BE＝，BD＝3，AD＝1，∵△BDE沿DE翻折到△B'DE处，∴EB′＝EB＝，DB′＝DB＝3，∠EB′D＝∠B＝90°，作B′M⊥AB于M，EN⊥B′M于N，如图，则MN＝BE＝，EN＝BM，∵∠EB′N+∠DB′M＝90°，∠EB′N+∠B′EN＝90°，∴∠B′EN＝∠DB′M，∴Rt△EB′N∽Rt△B′DM，∴＝＝＝＝，设B′N＝t，则DM＝t，∴EN＝3+t，∴B′M＝EN＝（3+t），∵B′N+B′M＝，∴t+（3+t）＝，解得t＝，∵AM＝DM﹣AD＝×﹣1＝，而+NB′＝+＝，∴B′点的坐标为（，﹣），把B′（，﹣）代入y＝kx得k＝﹣，解得k＝﹣．故答案为﹣．三．解答题（共5小题）21．【解答】解：∵点A在反比例函数y＝（x＞0）的图象上，点B、C在y＝（x＞0）上，∴设A（a，），∵AB∥y轴，AC∥x轴，∴B（a，），C（3a，），∴AB＝﹣＝，AC＝3a﹣a＝2a，又∵＝，∴＝，∴a＝，∴B（，2），C（，），∴BC＝＝．22．【解答】（1）解：∵点A的坐标为（0，3），点B的坐标为（﹣4，0），∴OA＝3，OB＝4．在Rt△AOB中，OA＝3，OB＝4，∴AB＝＝5.∵四边形ABCD为菱形，∴BC∥y轴，且BC＝AB＝5，∴点C的坐标为（﹣4，﹣5）．∵点C在反比例函数y＝的图象上，∴k＝（﹣4）×（﹣5）＝20，∴过点C的反比例函数表达式为y＝．（2）证明：设直线l的解析式为y＝mx+n（m≠0），将y＝mx+n代入y＝得：mx+n＝，整理得：mx2+nx﹣20＝0．∵直线l与反比例函数y＝的图象相切，∴△＝n2﹣4×m×（﹣20）＝0，∴n2＝﹣80m．当x＝0时，y＝m×0+n＝n，∴点N的坐标为（0，n）；当y＝0时，mx+n＝0，解得：x＝﹣，∴点M的坐标为（﹣，0）．∴S△OMN＝|n|×|﹣|＝||＝40，∴△OMN的面积为定值．23．【解答】解：（1）∵点C（0，2）在直线y＝x+b上，∴b＝2，∴一次函数的表达式为y＝x+2；∵点A（1，a）在直线y＝x+2上，∴a＝3，∴点A（1，3），∵点A（1，3）在反比例函数y＝（x＞0）的图象上，∴k＝1×3＝3，∴反比例函数的表达式为y＝；（2）由（1）知，直线AB的表达式为y＝x+2，反比例函数的表达式为y＝，设点M（m，），N（n，n+2），若以点O、M、C、N为顶点的四边形是平行四边形，则①以OC和MN为对角线时，∴＝0，，∴m＝，n＝﹣或m＝﹣（此时，点M不在第一象限，舍去），n＝，∴N（﹣，﹣+2），②以CN和OM为对角线时，∴＝，＝，∴m＝n＝﹣2+或m＝n＝﹣2﹣（此时，点M不在第一象限，舍去），∴N（﹣2+，），③以CM和ON为对角线时，∴＝，＝，∴m＝n＝或m＝n＝﹣（此时，点M不在第一象限，舍去），∴N（，2+），即满足条件的点N的坐标为（﹣，﹣+2）或（﹣2+，）或（，2+）．24．【解答】解：（1）由题意x＝0时，y1＝0，∴16+4b+8＝0，∴b＝﹣6，∴x＝5时，y1＝25﹣6×5+8＝3．（2）函数图象如图所示：性质：x＜3时，y1随x的增大而减小，x＞3时，y1随x的增大而增大．（3）观察图形可知：不等式y1≥y2的解集为：x≤﹣2或x＞0．25．【解答】解：（1）①如图2中，连接AD交EF于H．∵四边形ABOC是矩形，A（﹣4，3），∴∠A＝90°，OB＝AC＝4，AB＝OC＝3，∵E，F在y＝时，∴可以假设E（，3），F（﹣4，），∴AE＝4+，AF＝3+，∴AE：AF＝4：3，∵AC：BC＝4：3，∴＝，∵∠EAF＝∠CAB，∴△EAF∽△CAB，∴∠AEF＝∠ACB，∴EF∥BC，∵A，D关于EF对称，点D落在BC上，∴EF垂直平分线段AD，∴AH＝DH，∵EF∥BC，∴＝，∴AE＝EC＝2．②如图3中，当点D落在OB上时，连接AD交EF于H．∵∠EAF＝∠ABD＝90°，∠AEF＝∠BAD，∴△AEF∽△BAD，∴＝，则＝＝，∴BD＝AB÷＝，设AF＝x，则FB＝3﹣x，FD＝AF＝x在Rt△BDF中，∵FB2+BD2＝DF2，∴（3﹣x）2+（）2＝x2，解得x＝，∴AF＝，∴AE＝AF＝，∴EC＝4﹣AE＝4﹣＝，∴＜CE＜4时，折叠后点D落在矩形ABOC内（不包括边界），线段CE长度的取值范围为：＜CE＜4．（2）∵△ABD是等腰三角形，F与B不重合，∴AB≠BD．①如图4中，当AD＝BD时，∠BAD＝∠ABD，由（1）可知∠BAD＝∠AEF，∴∠ABD＝∠AEF．作DM∥OB交AB于M，交OC于N．则DM⊥AB，MN＝AC＝4，∴∠BMD＝∠EAF＝90°，BM＝AB＝，∴△AEF∽△MBD，∴＝，则＝＝，∴MD＝BM÷＝，∴DN＝MN﹣MD＝4﹣＝，∴D（﹣，）．②如图5中，当AD＝AB时，作DM∥OB交AB于M，交OC于N．则DM⊥AB，MN＝AC＝4，∴∠AMD＝∠EAF＝90°，由（1）可得∠BAD＝∠AEF，∴△AEF∽△MAD，∴＝，则＝＝，设AM＝4a，则MD＝3a，在Rt△MAD中，∵AM2+DM2＝AD2，∴（4a）2+（3a）2＝32，∴a＝，∴AM＝，MD＝，∴BM＝AB＝AM＝3﹣＝，DN＝MN﹣MD＝4﹣＝，∴D（﹣，）．综上所述，满足条件的点D的坐标为（﹣，）或（﹣，）．。

完整版)反比例函数练习题含答案测试1 反比例函数的概念一、填空题1.一般的，形如 y=k/x 的函数称为反比例函数，其中x是自变量，y是因变量。

自变量x的取值范围是x≠0.2.写出下列各题中所要求的两个相关量之间的函数关系式，并指出函数的类别。

1) 商场推出分期付款购电脑活动，每台电脑元，首付4000元，以后每月付y元，x个月全部付清，则y=(8000+)/x，是反比例函数。

2) 某种灯的使用寿命为1000小时，它的使用天数y与平均每天使用的小时数x之间的关系式为 y=1000/x，是反比例函数。

3) 设三角形的底边、对应高、面积分别为a、h、S。

当a=10时，S与h的关系式为 S=10h/2，是正比例函数；当S=18时，a与h的关系式为 h=36/a，是反比例函数。

4) 某工人承包运输粮食的总数是w吨，每天运x吨，共运了y天，则 y=w/x，是反比例函数。

3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x和y=3x-1 中，是y关于x的反比例函数的有：①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。

4.若函数 y=m/(x-1) (m是常数) 是反比例函数，则 m=1，解析式为 y=1/(x-1)。

5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜片的焦距为0.25m，则 y=1000/x。

二、选择题6.已知函数 y=3x/(kx+1)，当x=1时，y=-3，那么这个函数的解析式是 y=3x/(3k+1)。

(解析：由 y=-3=3/(3k+1) 可得 k=-1/3，代入原式得 y=3x/(3x-1)。

)7.已知 y 与 x 成反比例，当 x=3 时，y=4，那么 y=3 时，x 的值等于 4/3.三、解答题8.已知 y 与 x 成反比例，当 x=2 时，y=3.1) 求y 与x 的函数关系式：y=k/x，代入已知条件得k=6，因此函数关系式为 y=6/x。

反比例函数综合一．选择题（共23小题）1．如图，点A，B在双曲线y=（x＞0）上，点C在双曲线y=（x＞0）上，若AC∥y轴，BC∥x 轴，且AC=BC，则AB等于（）A．B．2C．4 D．3第1题第2题第3题第5题2．如图，曲线C2是双曲线C1：y=（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（）A．B．6 C．3 D．123．反比例函数y=的图象如图所示，点A是该函数图象上一点，AB垂直于x轴垂足是点B，如果S△AOB=1，则k的值为（）A．1 B．﹣1 C．2 D．﹣24．在同一平面直角坐标系中，函数y=kx（k＞0）与y=（k＞0）的图象可能是（）A．B．C．D．5．如图，在平面直角坐标系xOy中，反比例函数y=的图象经过点T．下列各点P（4，6），Q（3，﹣8），M（2，﹣12），N（，48）中，在该函数图象上的点有（）A．4个B．3个C．2个D．1个6．已知反比例函数y=（k≠0）过点A（a，y1），B（a+1，y2），若y2＞y1，则a的取值范围为（）A．﹣1＜a B．﹣1＜a＜0 C．a＜1 D．0＜a＜17．如图，双曲线y=与直线y=kx+b交于点M，N，并且点M的坐标为（1，3），点N的纵坐标为﹣1．根据图象信息可得关于x不等式＜kx+b的解为（）A．x＜﹣3 B．﹣3＜x＜0 C．﹣3＜x＜1 D．﹣3＜x＜0 或x＞1第7题第9题第11题第12题8．点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y=的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y3＜y1C．y3＜y2＜y1D．y2＜y1＜y39．如图，A、B是双曲线y=（k＞0）上的点，A、B两点的横坐标分别是a、3a，线段AB的延长=3．则k的值为（）线交x轴于点C，若S△AOCA．2 B．1.5 C．4 D．610．已知点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y=（k＜0）的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y2＜y1D．y3＜y1＜y211．如图，点A（m，1），B（2，n）在双曲线y=（k≠0），连接OA，OB．若S△ABO=8，则k的值是（）A．﹣12 B．﹣8 C．﹣6 D．﹣412．如图，反比例函数与正比例函数的图象交于A、B两点，过点A作AC⊥x轴于点C．若△ABC 的面积是8，则这个反比例函数的解析式是（）A．y=B．y=C．y=D．y=13．如图，在平面直角坐标系中，函数y=的图象与函数y=x的图象相交于A，B两点，点C是函数y=的图象右支上一点，连结AC，BC，若∠C=90°，则点C的坐标为（）A．（2，4）B．（3，6）C．（4，2）D．（，）第13题第14题第15题第16题14．如图，直线y=x﹣3与x轴交于点A，与双曲线y=（k≠0）在第一象限内交于点B，过点A 作AC⊥x轴，交该双曲线于点C，若AB=AC，则k的值是（）A．B．C．D．15．如图，在平面直角坐标系中，点A、B分别在第二象限和第一象限，AB与x轴平行，∠AOB=90°，OA=3，OB=4，函数y=（x＜0）和y=（x＞0）的图象分别经过点AB，则的值为（）A．B．﹣C．D．﹣16．如图，在平面直角坐标系中，反比例函数y=（k≠0）经过▱ABCD的顶点B、D，点A的坐标为（0，﹣1），AB∥x轴，CD经过点（0，2），▱ABCD的面积是18，则点D的坐标是（）A．（﹣2，2）B．（3，2）C．（﹣3，2）D．（﹣6，1）17．如图，点M是反比例函数y=（x＞0）图象上任意一点，MN⊥y轴于N，点P是x轴上的动点，则△MNP的面积为（）A．1 B．2 C．4 D．不能确定第17题第18题18．如图，已知点A（0，4），B （1，4），点B在双曲线y=（k＞0）上，在AB的延长线上取一点C，过C的直线交双曲线于点D，交x轴正半轴于点E，且CD=DE，则线段CE长度的取值范围是（）A．4≤CE＜4B．4≤CE＜2C．2＜CE＜4 D．4＜CE＜219．如图，已知点A（2，3）和点B（0，2），点A在反比例函数y=的图象上，作射线AB，交反比例函数图象于另一点M，再将射线AB绕点A按逆时针方向旋转45°，交反比例函数图象于点C，则CM的长度为（）A．5 B．6 C．4D．5第19题第20题第21题第23题20．如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线y=（x＞0）上的一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小21．如图，一次函数y1=x+1的图象与反比例函数y2=的图象交于A、B两点，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，连接AO、BO，下列说法正确的是（）A．点A和点B关于原点对称B．当x＜1时，y1＞y2C．S△AOC=S△BOD D．当x＞0时，y1、y2都随x的增大而增大22．函数y=k（x﹣1）与y=﹣在同一直角坐标系内的图象大致是（）A．B．C．D．23．如图，点A，C都在函数y=（x＞0）的图象上，点B，D都在x轴上，且使得△OAB，△BCD 都是等边三角形，则点C的坐标是（）A．（+1，﹣）B．（+1，﹣1）C．（+1，﹣）D．（+1，﹣）二．填空题（共9小题）24．如图，点M是函数图象上的一点，直线l：y=x，过点M分别作MA⊥y轴，MB⊥l，A，B为垂足，则MA•MB=．第24题第25题第30题第31题25．如图将直线向左平移m个单位，与双曲线交于点A，与x轴交于点B，则OB2﹣OA2+AB2=．26．如果反比例函数y=（m﹣3）的图象在第二、四象限，那么m=．27．已知双曲线y=（k≠0）上有一点P，PA⊥x轴于A，点O为坐标原点，且S△PAO=12，则此反比例函数的解析式为．28．反比例函数的图象同时过A（﹣2，a）、B（﹣3，b）、C（1，c）三点，则a、b、c 的大小关系是．29．函数y=（m2﹣m）x m2﹣3m+1是反比例函数，则m的值是，它的图象分布在象限，在每一个象限内，y随x的增大而．30．如图，A、B是反比例函数y=上两点，AC⊥y轴于C，BD⊥x轴于D，AC=BD=OC，S四边形=14，则k=．ABDC31．如图，B为双曲线y=（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，若OB2﹣AB2=12，则k=．32．如图，正比例函数y=x与反比例函数y=的图象相交于A，C两点，AB⊥x轴于B，CD⊥x轴于D，则四边形ABCD的面积为．三．解答题（共8小题）33．如图1，在平面直角坐标系中，四边形AOBC是矩形，点C的坐标为（4，3），反比例函数y=（k＞0）的图象与矩形AOBC的边AC、BC分别相交于点E、F，将△CEF沿EF对折后，C点恰好落在OB上．（1）求证：△AOE与△BOF的面积相等；（2）求反比例函数的解析式；（3）如图2，P点坐标为（2，﹣3），在反比例函数y=的图象上是否存在点M、N（M在N的左侧），使得以O、P、M、N为顶点的四边形是平行四边形？若存在，求出点M、N的坐标；若不存在，请说明理由．34．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A、C分别在坐标轴上，顶点B的坐标为（4，2），M、N分别是AB、BC的中点．（1）若反比例函数y=（x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上；（2）若反比例函数y=（x＞0）的图象与△MNB（包括边界）有公共点，请直接写出m的取值范围．35．如图，反比例函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点．（1）求A、B两点的坐标；（2）观察图象，直接写出x为何值时，一次函数值大于反比例函数？（3）求△AOB的面积．36．如图，反比例函数y1=的图象与一次函数y2=kx+b的图象交于A（m，3），B（﹣3，n）、两点．（1）求一次函数的解析式及△AOB的面积；（2）根据图象直接写出不等式的解集；（3）若点P是坐标轴上的一点，且满足△PAB面积等于△AOB的面积的2倍，直接写出点P的坐标．37．如图，若直线y=kx+b（k≠0）与x轴交于点，与双曲线在第二象限交于点B，且OA=OB，△OAB的面积为（1）求直线AB的解析式及双曲线的解析式；（2）求tan∠ABO的值．38．已知反比例函数y=和一次函数y=2x﹣1，其中一次函数的图象经过（a，b），（a+k，b+k+2）两点．（1）求反比例函数的解析式？（2）已知A在第一象限，是两个函数的交点，求A点坐标？（3）利用②的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？39．如图，双曲线y=在第一象限的一支上有一点C（1，5），过点C的直线y=﹣kx+b（k＞0）与x 轴交于点A（a，0）．（1）求点A的横坐标a与k的函数关系式（不写自变量取值范围）．（2）当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△COA的面积．40．如图，一次函数y=ax+b的图象与反比例函数的图象交于M、N两点．（1）利用图中条件，求反比例函数和一次函数的解析式；（2）连接OM、ON，求三角形OMN的面积．（3）连接OM，在x轴的正半轴上是否存在点Q，使△MOQ是等腰三角形，若存在，请直接写出所有符合条件的点Q的坐标，若不存在，说明理由．参考答案一．选择题（共23小题）1．如图，点A，B在双曲线y=（x＞0）上，点C在双曲线y=（x＞0）上，若AC∥y轴，BC∥x 轴，且AC=BC，则AB等于（B）A．B．2C．4 D．3设C（a，），则B（3a，），A（a，），∵AC=BC，∴﹣=3a﹣a，解得a=1，（负值已舍去）∴C（1，1），B（3，1），A（1，3），∴AC=BC=2，∴Rt△ABC中，AB=2，2．如图，曲线C2是双曲线C1：y=（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（B）A．B．6 C．3 D．12解：如图，将C2及直线y=x绕点O逆时针旋转45°，则得到双曲线C3，直线l与y轴重合．双曲线C3，的解析式为y=﹣过点P作PB⊥y轴于点B∵PA=PB∴B为OA中点．∴S△PAB=S△POB=3∴△POA的面积是6由反比例函数比例系数k的性质，S△POB3．反比例函数y=的图象如图所示，点A是该函数图象上一点，AB垂直于x轴垂足是点B，如果S△AOB=1，则k的值为（D）A．1 B．﹣1 C．2 D．﹣24．在同一平面直角坐标系中，函数y=kx（k＞0）与y=（k＞0）的图象可能是（C）A．B．C．D．5．如图，在平面直角坐标系xOy中，反比例函数y=的图象经过点T．下列各点P（4，6），Q（3，﹣8），M（2，﹣12），N（，48）中，在该函数图象上的点有（C）A．4个B．3个C．2个D．1个第5题第7题第9题6．已知反比例函数y=（k≠0）过点A（a，y1），B（a+1，y2），若y2＞y1，则a的取值范围为（B）A．﹣1＜a B．﹣1＜a＜0 C．a＜1 D．0＜a＜17．如图，双曲线y=与直线y=kx+b交于点M，N，并且点M的坐标为（1，3），点N的纵坐标为﹣1．根据图象信息可得关于x不等式＜kx+b的解为（D）A．x＜﹣3 B．﹣3＜x＜0 C．﹣3＜x＜1 D．﹣3＜x＜0 或x＞18．点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y=的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（D）A．y1＜y2＜y3B．y2＜y3＜y1C．y3＜y2＜y1D．y2＜y1＜y39．如图，A、B是双曲线y=（k＞0）上的点，A、B两点的横坐标分别是a、3a，线段AB的延长线交x轴于点C，若S△AOC=3．则k的值为（B）A．2 B．1.5 C．4 D．6解：如图，分别过点A、B作AF⊥y轴于点F，AD⊥x轴于点D，BG⊥y轴于点G，BE⊥x轴于点E，∵k＞0，点A是反比例函数图象上的点，∴S△AOD =S△AOF=|k|，∵A、B两点的横坐标分别是a、3a，∴AD=3BE，∴点B是AC的三等分点，∴DE=2a，CE=a，∴S△AOC =S梯形ACOF﹣S△AOF=（OE+CE+AF）×OF﹣|k|=×5a×﹣|k|=3，解得k=1.5．10．已知点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y=（k＜0）的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（D）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y2＜y1D．y3＜y1＜y211．如图，点A（m，1），B（2，n）在双曲线y=（k≠0），连接OA，OB．若S△ABO=8，则k的值是（C）A．﹣12 B．﹣8 C．﹣6 D．﹣4第11题第12题解：过A作y轴的垂线，过B作x轴的垂线，交于点C，连接OC，设A（k，1），B（2，k），则AC=2﹣k，BC=1﹣k，∵S△ABO=8，∴S△ABC﹣S△ACO﹣S△BOC=8，即（2﹣k）（1﹣k）﹣（2﹣k）×1﹣（1﹣k）×2=8，解得k=±6，∵k＜0，∴k=﹣6，12．如图，反比例函数与正比例函数的图象交于A、B两点，过点A作AC⊥x轴于点C．若△ABC 的面积是8，则这个反比例函数的解析式是（C）A．y=B．y=C．y=D．y=13．如图，在平面直角坐标系中，函数y=的图象与函数y=x的图象相交于A，B两点，点C是函数y=的图象右支上一点，连结AC，BC，若∠C=90°，则点C的坐标为（A）A．（2，4）B．（3，6）C．（4，2）D．（，）解：函数y=的图象与函数y=x的图象相交于A，B两点，解方程组，可得，，∴B（4，2），A（﹣4，﹣2），∴OB=AO=2，又∵∠ACB=90°，∴OC=AB=2，设C（a，），则OC==2，解得a=2，或a=4（舍去），∴C（2，4），14．如图，直线y=x﹣3与x轴交于点A，与双曲线y=（k≠0）在第一象限内交于点B，过点A 作AC⊥x轴，交该双曲线于点C，若AB=AC，则k的值是（D）A．B．C．D．解：如图，过B作BD⊥OA于D，则∠ADB=∠AOE=90°，由直线y=x﹣3，可得A（4，0），E（0，﹣3），∴AO=4，OE=3，AE=5，设点C的坐标为（4，），则AC=AB=，由△AOE∽△ADB，可得==，即==，∴AD=，BD=，∴B（4+，），∵双曲线y=（k≠0）经过点B，∴（4+）×k=k，解得k=，15．如图，在平面直角坐标系中，点A、B分别在第二象限和第一象限，AB与x轴平行，∠AOB=90°，OA=3，OB=4，函数y=（x＜0）和y=（x＞0）的图象分别经过点AB，则的值为（D）A．B．﹣C．D．﹣解：∵AB与x轴平行，∴AB⊥y轴，即∠AHO=∠OHB=90°，∵∠AOB=90°，∴∠AOH+∠BOH=∠AOH+∠OAH=90°，∴∠OAH=∠BOH，∴△AOH∽△OBH，∴=，即=，又∵k1＜0，∴=﹣，16．如图，在平面直角坐标系中，反比例函数y=（k≠0）经过▱ABCD的顶点B、D，点A的坐标为（0，﹣1），AB∥x轴，CD经过点（0，2），▱ABCD的面积是18，则点D的坐标是（C）A．（﹣2，2）B．（3，2）C．（﹣3，2）D．（﹣6，1）解：如图，∵点A的坐标为（0，﹣1），AB∥x轴，反比例函数y=（k≠0）经过▱ABCD的顶点B，∴点B的坐标为（﹣k，﹣1），即AB=﹣k，又∵点E（0，2），∴AE=2+1=3，又∵平行四边形ABCD的面积是18，∴AB×AE=18，∴﹣k×3=18，∴k=﹣6，∴y=﹣，∵CD经过点（0，2），∴令y=2，可得x=﹣3，∴点D的坐标为（﹣3，2），17．如图，点M是反比例函数y=（x＞0）图象上任意一点，MN⊥y轴于N，点P是x轴上的动点，则△MNP的面积为（A）A．1 B．2 C．4 D．不能确定第17题第18题18．如图，已知点A（0，4），B （1，4），点B在双曲线y=（k＞0）上，在AB的延长线上取一点C，过C的直线交双曲线于点D，交x轴正半轴于点E，且CD=DE，则线段CE长度的取值范围是（A）A．4≤CE＜4B．4≤CE＜2C．2＜CE＜4 D．4＜CE＜2解：如图1，过D作DF⊥OA于F，∵点A（0，4），B （1，4），∴AB⊥y轴，AB=1，OA=4，∵CD=DE，∴AF=OF=2，∵点B在双曲线y=（k＞0）上，∴k=1×4=4，∴反比例函数的解析式为：y=，∵过点C的直线交双曲线于点D，∴D点的纵坐标为2，把y=2代入y=得，x=2，∴D（2，2），当O与E重合时，如图2，∵DF=2，∴AC=4，∵OA=4，∴CE=4，当CE⊥x轴时，CE=OA=4，∴4≤CE＜4，19．如图，已知点A（2，3）和点B（0，2），点A在反比例函数y=的图象上，作射线AB，交反比例函数图象于另一点M，再将射线AB绕点A按逆时针方向旋转45°，交反比例函数图象于点C，则CM的长度为（D）A．5 B．6 C．4D．5第19题第20题第21题解：如图，过A作AD⊥y轴于D，将AB绕着点B顺时针旋转90°，得到A'B，过A'作A'H⊥y轴于H，由AB=BA'，∠ADB=∠BHA'=90°，∠BAD=∠A'BH，可得△ABD≌△BA'H，∴BH=AD=2，又∵OB=2，∴点H与点O重合，点A'在x轴上，∴A'（1，0），又∵等腰Rt△ABA'中，∠BAA'=45°，而∠BAC=45°，∴点A'在AC上，由A（2，3），A'（1，0），可得直线AC的解析式为y=3x﹣3，解方程组，可得或，∴C（﹣1，﹣6），由点A（2，3）和点B（0，2），可得直线AB 的解析式为y=x+2，解方程组，可得或，∴M（﹣6，﹣1），∴CM==5，20．如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线y=（x＞0）上的一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（C）A．逐渐增大B．不变C．逐渐减小D．先增大后减小21．如图，一次函数y1=x+1的图象与反比例函数y2=的图象交于A、B两点，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，连接AO、BO，下列说法正确的是（C）A．点A和点B关于原点对称B．当x＜1时，y1＞y2C．S△AOC=S△BOD D．当x＞0时，y1、y2都随x的增大而增大解：A、，∵把①代入②得：x+1=，解得：x2+x﹣2=0，（x+2）（x﹣1）=0，x1=﹣2，x2=1，代入①得：y1=﹣1，y2=2，∴B（﹣2，﹣1），A（1，2），∴A、B不关于原点对称，故本选项错误；B、当﹣2＜x＜0或x＞1时，y1＞y2，故本选项错误；C、∵S△AOC=×1×2=1，S△BOD=×|﹣2|×|﹣1|=1，∴S△BOD=S△AOC，故本选项正确；D、当x＞0时，y1随x的增大而增大，y2随x的增大而减小，故本选项错误；22．函数y=k（x﹣1）与y=﹣在同一直角坐标系内的图象大致是（A）A．B．C．D．23．如图，点A，C都在函数y=（x＞0）的图象上，点B，D都在x轴上，且使得△OAB，△BCD都是等边三角形，则点C的坐标是（A）A．（+1，﹣）B．（+1，﹣1）C．（+1，﹣）D．（+1，﹣）第23题第24题解：如图，作AE⊥OB于E，CF⊥BD于F，∵△OAB，△BCD均为正三角形，A在反比例函数y=，∴A的横坐标是1，纵坐标是，∴OE=EB=1，OA=2OE=2，AE=，设BF=m，则C（2+m，m），代入y=，得：m2+2m﹣1=0，解得：m=﹣1±，∵m＞0，∴m=﹣1+，∴点C的坐标为：（1+，）．二．填空题（共9小题）24．如图，点M是函数图象上的一点，直线l：y=x，过点M分别作MA⊥y轴，MB⊥l，A，B为垂足，则MA•MB=．解：延长AM，交直线y=x于点D，设M（x，x+）则△AOD是等腰直角三角形，即∠ADO=45°，∴OA=AD=x+，AM=x，∴MD=AD﹣AM=，∵MB⊥l，∴MB=BD，∴△BDM是等腰直角三角形，∴MB2+BD2=MD2，∴MB=MD，∴MB=×=，∴MA•MB=x•=．25．如图将直线向左平移m个单位，与双曲线交于点A，与x轴交于点B，则OB2﹣OA2+AB2=．解：由题意知：平移后的直线解析式为：y=（x+m）；设A（x，y），易知：B（﹣m，0），则有：OB2﹣OA2+AB2=m2﹣（x2+y2）+[（m+x）2+y2]，联立y=（x+m），整理得：原式=﹣2x2﹣2mx；由于直线y=（x+m）与交于点A，联立两个函数解析式得：（x+m）=﹣，即x2+mx+2=0，得﹣x2﹣mx=2；故所求代数式=﹣2x2﹣2mx=4．故答案为：4．26．如果反比例函数y=（m﹣3）的图象在第二、四象限，那么m=1．【解答】解：根据题意m2﹣6m+4=﹣1，解得m=1或5，又m﹣3＜0，m＜3，所以m=1．故答案为：1．27．已知双曲线y=（k≠0）上有一点P，PA⊥x轴于A，点O为坐标原点，且S△PAO=12，则此反比例函数的解析式为y=﹣或y=．【解答】解：设点P的坐标为（x，y）．∵P（x，y）在反比例函数y=kx（k≠0）的图象，∴k=xy，=12，∵S△PAO∴|xy|=12，∴|xy|=24，∴xy=±24，∴k=±24，∴y=﹣或y=．故答案为：y=﹣或y=．28．反比例函数的图象同时过A（﹣2，a）、B（﹣3，b）、C（1，c）三点，则a、b、c的大小关系是a＞b＞c．【解答】解：∵k＜0，∴此函数的图象在二、四象限，∵﹣2＜0，﹣3＜0，1＞0，∴A、B两点在第二象限，C点在第三象限，∴a＞0，b＞0，c＜0，∵﹣2＞﹣3，∴a＞b＞0，∴a＞b＞c．故答案为a＞b＞c．29．函数y=（m2﹣m）x m2﹣3m+1是反比例函数，则m的值是2，它的图象分布在第一、三象限，在每一个象限内，y随x的增大而减小．【解答】解：由题意得：m2﹣3m+1=﹣1，且m2﹣m≠0，解得：m=2，∵m2﹣m=4﹣2=2＞0，∴图象分布在第一、三象限，在每一个象限内，y随x的增大而减小，故答案为：2；第一、三；减小．30．如图，A、B是反比例函数y=上两点，AC⊥y轴于C，BD⊥x轴于D，AC=BD=OC，S四边形=14，则k=16．ABDC【解答】解：如图，分别延长CA，DB交于点E，根据AC⊥y轴于C，BD⊥x轴于D，AC=BD=OC，知△CED为直角三角形，且点A与点B的纵横坐标正好相反，设点A的坐标为（x A，y A），则点B的坐标为（y A，x A），点E的坐标为（y A，y A），四边形ACDB的面积为△CED的面积减去△AEB的面积．CE=ED=y A，AE=BE=y﹣y A，∴S ACDB=S△CED﹣S△AEB=[y A•y A﹣（y A﹣y A）（y A﹣y A）]=y A2=14，∵y A＞0，∴y A=8，点A的坐标为（2，8），∴k=2×8=16．故答案为：16．31．如图，B为双曲线y=（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，若OB2﹣AB2=12，则k=6．【解答】解：如图，延长AB交x轴于点C，设点C的横坐标为a，则点B的纵坐标为，点A的纵坐标为a，所以，AB=a﹣，∵AB平行于y轴，∴AC⊥OC，在Rt△BOC中，OB2=OC2+BC2=a2+（）2，∵OB2﹣AB2=12，∴a2+（）2﹣（a﹣）2=12，整理得，2k=12，解得k=6．故答案为：6．32．如图，正比例函数y=x与反比例函数y=的图象相交于A，C两点，AB⊥x轴于B，CD⊥x轴于D，则四边形ABCD的面积为2．【解答】解：根据反比例函数的对称性可知：OB=OD，AB=CD，∵四边形ABCD的面积等于S△ADB +S△BDC，∵A（1，1），B（1，0），C（﹣1，﹣1），D（﹣1，0）∴S△ADB=（DO+OB）×AB=×2×1=1，S△BDC=（DO+OB）×DC=×2×1=1，∴四边形ABCD的面积=2．故答案为：2．三．解答题（共8小题）33．如图1，在平面直角坐标系中，四边形AOBC是矩形，点C的坐标为（4，3），反比例函数y=（k＞0）的图象与矩形AOBC的边AC、BC分别相交于点E、F，将△CEF沿EF对折后，C点恰好落在OB上．（1）求证：△AOE与△BOF的面积相等；（2）求反比例函数的解析式；（3）如图2，P点坐标为（2，﹣3），在反比例函数y=的图象上是否存在点M、N（M在N的左侧），使得以O、P、M、N为顶点的四边形是平行四边形？若存在，求出点M、N的坐标；若不存在，请说明理由．【解答】解：（1）∵点E、F均是反比例函数y=上的点，四边形AOBC是矩形，∴AE⊥y轴，BC⊥x轴，∴S△AOE =S△BOF=；（2）∵C坐标为（4，3），∴设E（，3），F（4，），如图1，将△CEF沿EF对折后，C点恰好落在OB边上的G点，作EH⊥OB，垂足为H，∵∠EGH+∠HEG=90°∠EGH+∠FGB=90°，∴∠HEG=∠FGB，又∵∠EHG=∠GBF=90°，∴△EGH∽△GFB，∴=，∴GB==，在Rt△GBF中，GF2=GB2+BF2，即（3﹣）2=（）2+（）2，解得k=，∴反比例函数的解析式为：y=；（3）存在．当OP是平行四边形的边时，如图2所示：平行四边形OPMN，可以看成线段PN沿PO的方向平移至OM处所得．设N（a，），∵P（2，﹣3）的对应点O（0，0），∴M（a﹣2，+3），代入反比例解析式得：（a﹣2）（+3）=，整理得4a2﹣8a﹣7=0，解得a=，当a=时，==，﹣2=，+3=，∴N（，），M（，）（舍去）或N（，），M（，）．当OP为对角线时，如图3所示：设M（a，），N（b，），∵P（2，﹣3），∴，解得，，∴M（，），N（，）（舍去）或M（，），N（，），综上所述：M（，）N（，）；或M（，），N（，）．34．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A、C分别在坐标轴上，顶点B的坐标为（4，2），M、N分别是AB、BC的中点．（1）若反比例函数y=（x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上；（2）若反比例函数y=（x＞0）的图象与△MNB（包括边界）有公共点，请直接写出m的取值范围．【解答】解：（1）∵顶点B的坐标为（4，2），M、N分别是AB、BC的中点，∴M点的坐标为（2，2），把M（2，2）代入反比例函数y=（m≠0）得，m=2×2=4，∴反比例函数的解析式为y=；∵M、N分别为矩形OABC的边AB、BC的中点，且M（2，2），B点坐标为（4，2），∴N点坐标为（4，1），∵4×1=4，∴点N在函数y=的图象上；（2）4≤m≤8．35．如图，反比例函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点．（1）求A、B两点的坐标；（2）观察图象，直接写出x为何值时，一次函数值大于反比例函数？（3）求△AOB的面积．【解答】解：（1）联立两函数解析式得：，解得：或，即A（﹣2，4），B（4，﹣2）；（2）根据图象得：当x＜﹣2或0＜x＜4时，一次函数值大于反比例函数值．（3）令y=﹣x+2中x=0，得到y=2，即D（0，2），∴OD=2，∴S△AOB =S△AOC+S△BOC=×2×2+×2×4=6．36．如图，反比例函数y1=的图象与一次函数y2=kx+b的图象交于A（m，3），B（﹣3，n）、两点．（1）求一次函数的解析式及△AOB的面积；（2）根据图象直接写出不等式的解集；（3）若点P是坐标轴上的一点，且满足△PAB面积等于△AOB的面积的2倍，直接写出点P的坐标．【解答】解：（1）∵反比例函数y1=的图象与一次函数y2=kx+b的图象交于A（m，3），B（﹣3，n）、两点，将A与B坐标代入反比例解析式得：m=1，n=﹣1，∴A（1，3）、B（﹣3，﹣1），代入一次函数解析式得：，解得：k=1，b=2，∴一次函数的解析式为y=x+2，∵直线y=x+2与x轴、y轴的交点坐标为（﹣2，0）、（0，2），∴S△AOB=×2×（1+3）=4；（2）∵A（1，3），B（﹣3，﹣1），观察图象可知，当x＜﹣3或0＜x＜1时，一次函数的图象在反比例函数图象的下方，∴不等式的解集是x＜﹣3或0＜x＜1．（3）∵S△AOB=4，∴S△PAB =2S△AOB=8，设P1（p，0），即OP1=|p+2|，S△ABP1=S△AP1C+S△P1BC=|p+2|×3+|p+2|×1=8，解得：p=﹣6或p=2，则P1（﹣6，0）、P2（2，0），同理可得P3（0，6）、P4（0，﹣2）．37．如图，若直线y=kx+b（k≠0）与x轴交于点，与双曲线在第二象限交于点B，且OA=OB，△OAB的面积为（1）求直线AB的解析式及双曲线的解析式；（2）求tan∠ABO的值．【解答】解：（1）∵直线y=kx+b（k≠0）与x轴交于点A，∴OA=，又∵OA=OB，∴OB=，过点B作BM⊥x轴于点M，∵△OAB的面积为，即OA•BM=，∴BM=2，在Rt△OBM中可求OM=1.5，∴B（﹣1.5，2），再根据待定系数法可得：，解得：k=﹣，b=，∴直线AB的解析式为：y=﹣x+；再将点B代入函数y=得：m=﹣3，∴双曲线的解析式为：y=﹣；（2）∵OA=OB，∴∠ABO=∠BAM，在Rt△ABM中，BM=2，∴MO=，AM=+=4，∴tan∠ABO=tan∠BAM==．38．已知反比例函数y=和一次函数y=2x﹣1，其中一次函数的图象经过（a，b），（a+k，b+k+2）两点．（1）求反比例函数的解析式？（2）已知A在第一象限，是两个函数的交点，求A点坐标？（3）利用②的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？【解答】解：（1）∵一次函数y=2x﹣1的图象经过（a，b），（a+k，b+k+2）两点，代入得：，解得：k=2，代入反比例函数的解析式得：y==，∴反比例函数的解析式是y=．（2）解方程组得：，，∴两函数的交点坐标是（﹣，﹣2），（1，1），∵交点A在第一象限，∴A（1，1）．（3）在x轴上存在点P，使△AOP为等腰三角形，理由是：分为三种情况：①以O为圆心，以OA为半径作圆，交x轴于两点C、D，此时OA=0C=0D，∴当P于C或D重合时，△AOP是等腰三角形，此时P的坐标是（，0），（﹣，0）；②以A为圆心，以OA为半径作圆，交x轴于点E，此时OA=AE，∴当P于E重合时，△AOP是等腰三角形，此时P的坐标是（2，0）；③作OA的垂直平分线交x轴于F，此时AF=OF，∴当P于F重合时，△AOP是等腰三角形，此时P的坐标是（1，0）；∴存在4个点P，使△AOP是等腰三角形．39．如图，双曲线y=在第一象限的一支上有一点C（1，5），过点C的直线y=﹣kx+b（k＞0）与x 轴交于点A（a，0）．（1）求点A的横坐标a与k的函数关系式（不写自变量取值范围）．（2）当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△COA的面积．【解答】解：（1）把C（1，5）代入直线y=﹣kx+b（k＞0）得：﹣k+b=5，则b=5+k；把（a，0）代入直线y=﹣kx+b（k＞0）得：﹣ak+b=0，把b=5+k代入﹣ak+b=0，得：﹣ak+5+k=0，解得：a=；（2）把x=9代入y=得：y=，则D的坐标是（9，），设直线AC的解析式是y=﹣kx+b，把C、D两点代入，得，解得：，则AC的解析式是：y=﹣x+．令y=0，解得：x=10．则OA=10，则△COA的面积=×10×5=25．40．如图，一次函数y=ax+b的图象与反比例函数的图象交于M、N两点．（1）利用图中条件，求反比例函数和一次函数的解析式；（2）连接OM、ON，求三角形OMN的面积．（3）连接OM，在x轴的正半轴上是否存在点Q，使△MOQ是等腰三角形，若存在，请直接写出所有符合条件的点Q的坐标，若不存在，说明理由．【解答】解：（1）把N（﹣1，﹣4）代入y=得：k=4，∴y=，把M（2，m）代入得：m=2，∴M（2，2），把N（﹣1，﹣4），M（2，2）代入y=ax+b得：，解得：a=2，b=﹣2，∴y=2x﹣2，答：反比例函数的解析式是y=，一次函数的解析式是y=2x﹣2．（2）设MN交x轴于C，y=2x﹣2，当y=0时，x=1，∴C（1，0），OC=1，∴△MON的面积是S=S△MOC +S△NOC=×1×2+×1×|﹣4|=3，答：三角形MON的面积是3．（3）当OM=OQ时，Q的坐标是（2，0）；当OM=MQ时，Q的坐标是（4，0）；当OQ=QM时，Q的坐标是（2，0）；答：在x轴的正半轴上存在点Q，使△MOQ是等腰三角形，所有符合条件的点Q的坐标是（2，0）或（4，0）或（2，0）．第31页（共31页）。

反比例函数练习题 一、精心选一选！（30分）1．下列函数中，图象经过点(11)-，的反比例函数解析式是（ ） A ．1y x=B ．1y x-=C ．2y x=D ．2y x-=2．反比例函数2k y x=-（k 为常数，0k ≠）的图象位于（ ）Ａ．第一、二象限 Ｂ．第一、三象限 Ｃ．第二、四角限 Ｄ．第三、四象限3．已知反比例函数y ＝x2k -的图象位于第一、第三象限，则k 的取值范围是（ ）． （A ）k ＞2 （B ） k ≥2 （C ）k ≤2 （D ） k ＜24．反比例函数xky =的图象如图所示，点M 是该函数图象上一点，MN 垂直于x 轴，垂足是点N ，如果S △MON ＝2，则k 的值为（ ） (A)2 (B)-2 (C)4 (D)-4 5．对于反比例函数2y x=，下列说法不正确．．．的是（ ） A ．点(21)--，在它的图象上B ．它的图象在第一、三象限C ．当0x >时，y 随x 的增大而增大D ．当0x <时，y 随x 的增大而减小6．反比例函数22)12(--=m xm y ，当x ＞0时，y 随x 的增大而增大，则m 的值时（ ）A 、±1B 、小于21的实数 C 、－1 D 、1 7．如图，P 1、P 2、P 3是双曲线上的三点，过这三点分别作y 轴的垂线，得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O ，设它们的面积分别是S 1、S 2、S 3，则（ ）。

A 、S 1＜S 2＜S 3B 、S 2＜S 1＜S 3C 、S 3＜S 1＜S 2D 、S 1=S 2=S 38．在同一直角坐标系中，函数xy 2-=与x y 2=图象的交点个数为（ ） A ．3 B ．2 C ．1 D ．0 9．已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（ ）10．如图，直线y=mx 与双曲线y=xk交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM,若ABM S ∆=2，则k 的值是（ ）A ．2B 、m-2C 、mD 、4OA 1 A 2 A 3 P 1 P 2 P 3xy11．在反比例函数xky =(k <0)的图象上有两点A (x 1，y 1)，B (x 2，y 2)，且1x >2x >0，则12y y -的值为（ ） (A)正数 (B)负数 (C)非正数 (D)非负数 二、细心填一填！（30分）11．写出一个图象在第一、三象限的反比例函数的解析式 ． 12．已知反比例函数8y x=-的图象经过点P （a+1，4），则a=_____． 13．反比例函数6y x=-图象上一个点的坐标是 ． 14．一个函数具有下列性质：①它的图像经过点（－1，1）；②它的图像在二、四象限内； ③在每个象限内，函数值y 随自变量x 的增大而增大．则这个函数的解析式可以为 ．15．已知反比例函数的图象经过点（m ，2）和（-2，3）则m 的值为 ．15．3-； 16．在ABC △的三个顶点(23)(45)(32)A B C ----，，，，，中，可能在反比例函数(0)ky k x=>的图象上的点是 ． 17．在对物体做功一定的情况下，力F (牛)与此物体在力的方向上移动的距离s (米)成反比例函数关系，其图象如图所示，P (5，1)在图象上，则当力达到10牛时，物体在力的方向上移动的距离是 米． 18．已知点P 在函数2y x=(x ＞0)的图象上，PA⊥x 轴、PB⊥y 轴，垂足分别为A 、B ，则矩形OAPB 的面积为__________． 19．已知直线mx y =与双曲线xky =的一个交点A 的坐标为（-1，-2）．则m =_____；k =____；它们的另一个交点坐标是______．20．如图，过原点的直线l 与反比例函数1y x=-的图象交于M ，N 两点，根据图象猜想线段MN 的长的最小值是___________． 三、用心解一解！（60分）21.在平面直角坐标系xOy 中，直线y x =-绕点O 顺时针旋转90o得到直线l ．直线l 与反比例函数ky x=的图象的一个交点为(3)A a ，，试确定反比例函数的解析式．（5分）22．如图，点A 是反比例函数图象上的一点，自点A 向y 轴作垂线，垂足为T ，已知S △AOT ＝4，求此函数的表达式. （5分）OyMNl23.已知点P （2，2）在反比例函数xky =（0≠k ）的图象上， （Ⅰ）当3-=x 时，求y 的值；（Ⅱ）当31<<x 时，求y 的取值范围．（7分）24．如图，已知双曲线ky x=（0x >）经过矩形OABC 的边AB BC ，的中点F E ，，且四边形OEBF 的面积为2，求k 的值．（7分）25．若一次函数y ＝2x －1和反比例函数y ＝2kx的图象都经过点（1，1）． （1）求反比例函数的解析式；（2）已知点A 在第三象限，且同时在两个函数的图象上，求点A 的坐标；（8分）26.已知点A （2，6）、B （3，4）在某个反比例函数的图象上. （1）求此反比例函数的解析式；（2）若直线mx y =与线段AB 相交，求m 的取值范围. （8分）27.如图正方形OABC 的面积为4，点O 为坐标原点，点B 在函数ky x=(0,0)k x << 的图象上，点P(m ，n)是函数ky x=(0,0)k x <<的图象上异于B 的任意一点，过点P 分别作x 轴、y 轴的垂线，垂足分别为E 、F ． (1)设矩形OEPF 的面积为S l ，判断S l 与点P 的位置是否有关(不必说理由)．(2)从矩形OEPF 的面积中减去其与正方形OABC 重合的面积，剩余面积记为S 2，写出S 2与m 的函数关系，并标明m 的取值范围．（8分）A B CO y x y xOFAB EC参考答案：一、1．B 2．C 3．A 4．D 5．C 6．C 7．D 8．D 9．C 10．A ；三、21．解：依题意得，直线l 的解析式为y x =．因为(3)A a ，在直线y x =上，则3a =． 即(33)A ，．又因为(33)A ，在k y x =的图象上，可求得9k =．所以反比例函数的解析式为9y x=． 22．解：设所求反比例函数的表达式为x ky =，因为S △AOT ＝k 21，所以k 21＝4，即8±=k ，又因为图象在第二、四象限，因此8-=k ，故此函数的表达式为8y x =-；又反比例函数xy 4=在0>x 时y 值随x 值的增大而减小， ∴当31<<x 时，y 的取值范围为434<<y ．24.设B 点的坐标为（2a ，2b ），则E 点的坐标为（a ，2b ），F 点的坐标为（2a ，b ），所以k =2ab .因为4ab －21×2ab ×2=2，所以2ab =2. 25．(1) ∵反比例函数y =2k x的图象经过点(1，1)，∴1=2k解得k=2，∴反比例函数的解析式为y=1x．∵点A 在第三象限，且同时在两个函数图象上， ∴A(12-，–2)．26.解：（1）设所求的反比例函数为xky =，依题意得: 6 =2k ，∴k=12． ∴反比例函数为x y 12=．（2） 设P （x ，y ）是线段AB 上任一点，则有2≤x≤3，4≤y ≤6．∵m =xy， ∴34≤m ≤26．所以m 的取值范围是34≤m ≤3．27.(1) 没有关系；(2) 当P 在B 点上方时，242(20)S m m =+-<<；当P 在B 点下方时，284(2)S m m=+<-。

反比例函数测试题（含答案）（时间90分钟满分100分）班级学号姓名得分一、选择题(每小题3分，共24分)1．如果x、y之间的关系是10(0)ax y a-+=≠,那么y是x的( ）A．正比例函数B．反比例函数C．一次函数D．二次函数2．函数y＝－错误!的图象与x轴的交点的个数是（）A．零个B．一个C．两个D．不能确定3．反比例函数y＝－错误!的图象在（）A．第一、三象限B．第二、四象限C．第一、二象限D．第三、四象限4．已知关于x的函数y＝k（x+1）和y＝－kx（k≠0）它们在同一坐标系中的大致图象是（• ）5．已知反比例函数y＝xk的图象经过点(m，3m），则此反比例函数的图象在（)A．第一、二象限B．第一、三象限C．第二、四象限D．第三、四象限6．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa ）是气体体积V（m3 ）的反比例函数,其图象如图所示．当气球内的气压大于120 kPa时，气球发将爆炸．为了安全起见,气球的体积应（）A．不小于54m3B．小于54m3 C．不小于45m3 D．小于45m37．如果点P为反比例函数xy4=的图象上一点，PQ⊥x轴，垂足为Q,那么△1.660O V (m3)P (kPa)(1.6，60)第6题POQ 的面积为 （ ）A ．2B ． 4C ．6D ． 8 8．已知：反比例函数xmy 21-=的图象上两点A （x 1，y 1），B （x 2， y 2）当x 1＜0＜x 2时，y 1＜y 2，则m 的取值范围（ ） A ．m ＜0 B ．m ＞0 C ．m ＜21D ．m ＞21二、填空题（每小题2分，共20分)9．有m 台完全相同的机器一起工作,需m 小时完成一项工作,当由x 台机器（x 为不大于m 的正整数）完成同一项工作时,所需的时间y 与机器台数x 的函数关系式是____。

10．已知y 与x 成反比例,且当x 32=-时，y =5，则y 与x 的函数关系式为__________。

反比例函数一、选择题1．（2016·黑龙江大庆）已知A（x1，y1）、B（x2，y2）、C（x3，y3）是反比例函数y=上的三点，若x1＜x2＜x3，y2＜y1＜y3，则下列关系式不正确的是（）A．x1•x2＜0 B．x1•x3＜0 C．x2•x3＜0 D．x1+x2＜0【考点】反比例函数图象上点的坐标特征．【分析】根据反比例函数y=和x1＜x2＜x3，y2＜y1＜y3，可得点A，B在第三象限，点C在第一象限，得出x1＜x2＜0＜x3，再选择即可．【解答】解：∵反比例函数y=中，2＞0，∴在每一象限内，y随x的增大而减小，∵x1＜x2＜x3，y2＜y1＜y3，∴点A，B在第三象限，点C在第一象限，∴x1＜x2＜0＜x3，∴x1•x2＜0，故选A．【点评】本题考查了反比例函数图象上点的坐标特征，解答此题的关键是熟知反比例函数的增减性，本题是逆用，难度有点大．2．（2016·湖北十堰）如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y=上（k＞0，x＞0），则k的值为（）A．25B．18C．9D．9【考点】反比例函数图象上点的坐标特征；平行线的性质；等边三角形的性质．【分析】过点A作AE⊥OB于点E，根据正三角形的性质以及三角形的边长可找出点A、B、E 的坐标，再由CD⊥OB，AE⊥OB可找出CD∥AE，即得出，令该比例=n，根据比例关系找出点D、C的坐标，利用反比例函数图象上点的坐标特征即可得出关于k、n的二元一次方程组，解方程组即可得出结论．【解答】解：过点A作AE⊥OB于点E，如图所示．∵△OAB为边长为10的正三角形，∴点A的坐标为（10，0）、点B的坐标为（5，5），点E的坐标为（，）．∵CD⊥OB，AE⊥OB，∴CD∥AE，∴．设=n（0＜n＜1），∴点D的坐标为（，），点C的坐标为（5+5n，5﹣5n）．∵点C、D均在反比例函数y=图象上，∴，解得：．故选C．【点评】本题考查了反比例函数图象上点的坐标特征、平行线的性质以及等边三角形的性质，解题的关键是找出点D、C的坐标．本题属于中档题，稍显繁琐，解决该题型题目时，巧妙的借助了比例来表示点的坐标，根据反比例函数图象上点的坐标特征找出方程组是关键．3. (2016·新疆)已知A（x1，y1），B（x2，y2）是反比例函数y=（k≠0）图象上的两个点，当x1＜x2＜0时，y1＞y2，那么一次函数y=kx﹣k的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【考点】反比例函数图象上点的坐标特征；一次函数图象与系数的关系．【分析】首先根据x1＜x2＜0时，y1＞y2，确定反比例函数y=（k≠0）中k的符号，然后再确定一次函数y=kx﹣k的图象所在象限．【解答】解：∵当x1＜x2＜0时，y1＞y2，∴k＞0，∴﹣k＜0，∴一次函数y=kx﹣k的图象经过第一、三、四象限，∴不经过第二象限，故选：B．【点评】此题主要考查了反比例函数图象上点的坐标特征以及一次函数图象与系数的关系，解决此题的关键是确定k的符号．4. (2016·云南)位于第一象限的点E在反比例函数y=的图象上，点F在x轴的正半轴上，O是坐标原点．若EO=EF，△EOF的面积等于2，则k=（）A．4 B．2 C．1 D．﹣2【考点】反比例函数系数k的几何意义．【分析】此题应先由三角形的面积公式，再求解k即可．【解答】解：因为位于第一象限的点E在反比例函数y=的图象上，点F在x轴的正半轴上，O是坐标原点．若EO=EF，△EOF的面积等于2，所以，解得：xy=2，所以：k=2，故选：B【点评】主要考查了反比例函数系数k的几何意义问题，关键是由三角形的面积公式，再求解k．5. （2016·四川达州·3分）下列说法中不正确的是（）A．函数y=2x的图象经过原点B．函数y=的图象位于第一、三象限C．函数y=3x﹣1的图象不经过第二象限D ．函数y=﹣的值随x 的值的增大而增大【考点】正比例函数的性质；一次函数的性质；反比例函数的性质． 【分析】分别利用正比例函数以及反比例函数的定义分析得出答案． 【解答】解：A 、函数y=2x 的图象经过原点，正确，不合题意； B 、函数y=的图象位于第一、三象限，正确，不合题意； C 、函数y=3x ﹣1的图象不经过第二象限，正确，不合题意；D 、函数y=﹣的值，在每个象限内，y 随x 的值的增大而增大，故错误，符合题意． 故选：D ．6. （2016·四川乐山·3动时，点C 图象上运动，若tan ()A 2 ()C 6答案：D解析：连结CO 所以，CO ⊥AB ，因为tan 作AE ⊥x 轴，CD ⊥x 轴于则有△OCD ∽△OEA 设C （m ，n ），则有A 所以，k n m =①， 2解①②得：k ＝87. （2016·四川凉山州·4分）二次函数y=ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是（）A．B．C．D．【考点】反比例函数的图象；一次函数的图象；二次函数的图象．【分析】根据二次函数的图象找出a、b、c的正负，再结合反比例函数、一次函数系数与图象的关系即可得出结论．【解答】解：观察二次函数图象可知：开口向上，a＞0；对称轴大于0，﹣＞0，b＜0；二次函数图象与y轴交点在y轴的正半轴，c＞0．∵反比例函数中k=﹣a＜0，∴反比例函数图象在第二、四象限内；∵一次函数y=bx﹣c中，b＜0，﹣c＜0，∴一次函数图象经过第二、三、四象限．故选C．8. （2016,湖北宜昌，15，3分）函数y=的图象可能是（）A．B．C．D．【考点】反比例函数的图象．【分析】函数y=是反比例y=的图象向左移动一个单位，根据反比例函数的图象特点判断即可．【解答】解：函数y=是反比例y=的图象向左移动一个单位，即函数y=是图象是反比例y=的图象双曲线向左移动一个单位．故选C【点评】此题是反比例函数的图象，主要考查了反比例函数的图象是双曲线，掌握函数图象的平移是解本题的关键．9. （2016吉林长春，8，3分）如图，在平面直角坐标系中，点P（1，4）、Q（m，n）在函数y=（x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（）A．减小B．增大C．先减小后增大D．先增大后减小【考点】反比例函数系数k的几何意义．【分析】首先利用m和n表示出AC和AQ的长，则四边形ACQE的面积即可利用m、n 表示，然后根据函数的性质判断．【解答】解：AC=m﹣1，CQ=n，=AC•CQ=（m﹣1）n=mn﹣n．则S四边形ACQE∵P（1，4）、Q（m，n）在函数y=（x＞0）的图象上，∴mn=k=4（常数）．∴S四边形ACQE=AC•CQ=4﹣n，∵当m＞1时，n随m的增大而减小，∴S四边形ACQE=4﹣n随m的增大而增大．故选B．【点评】本题考查了二次函数的性质以及矩形的面积的计算，利用n表示出四边形ACQE 的面积是关键．10. (2016兰州，2,4分)反比例函数的图像在（）。

x新人教版反比例函数单元测试题一、选择题（每小题3分，共30分）1、反比例函数y = ^5图象经过点（2, 3）,则n的值是（）.xA、一2B、一1C、0D、1k2、若反比例函数y = —（k工0）的图象经过点（一1, 2）,则这个函数的图象一x定经过点（）.3、（08双柏县）已知甲、乙两地相距s （km））,汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h）与行驶速度v （km/h）的函数关系图象大致是（）4、若y与x成正比例，xB与z成反比例，则y与z之间的关系是（D ）.A、成正比例B、成反比例C、不成正比例也不成反比例D、无法确k5、一次函数y = kx —k ,y随x的增大而减小，那么反比例函数y = 满足（）.xA、当x>0时，y>0B、在每个象限内，y随x的增大而减小C、图象分布在第一、三象限D、图象分布在第二、四象限6如图，点P是x轴正半轴上一个动点，过点P作x轴的垂1线PQ交双曲线y=—于点Q,连结OQ，点P沿x轴正方向x运动时，Rt △ QOP的面积（）.A、逐渐增大B、逐渐减小C、保持不变D、无法确定A、 (2,- 1)1B、(- 2 , 2)1C、(一2,- 1)D、( , 2)7、在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积P与V在一定范围内满足pV时，气体的密度p也随之改二m，它的图象如图所示，则该气体的质量m为（A、1.4kg8、若A （—3,).B、5 kgy1), B ( —2,C、6.4kgD、7kg1y2), C (—1, y3)三点都在函数y —的图象x上，贝U y1，y2，A、y1 >y2>y39、已知反比例函数y =v/(km/h)y3的大小关系是（）.B、y1V y2V y3C、y1 = y2 = y3D、y1V y3V y2口巴的图象上有A （X1, y1）、B （x2, y2）两点，当x1 xv X 2V 0时，y i v y 2,则m 的取值范围是（）.111. 某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 ___________ . _________k12、 已知反比例函数y k 的图象分布在第二、四象限，则在一次函数y kx bx中，y 随x 的土 ---------- （填“增大”或“减小”或“不变”） 13、若反比例函数y = 口和一次函数y = 3x + b 的图象有两个交点，且有一个x交点的纵坐标为6，则b = __________ .2 “14、 反比例函数y =（m + 2） x m 10的图象分布在第二、四象限内，贝U m 的值 为 ___________ .115、 有一面积为S 的梯形，其上底是下底长的1，若下底长为x ,高为y ，则y3与x 的函数关系是 ________________ .16、 如图，点M 是反比例函数y = a （0）的图象上一点，d 7过M 点作x 轴、y 轴的平行线，若S 阴影二5,贝吐匕反比例函数解析电 £式为 ____________ .「217、 使函数y =（ 2m 2 — 7m — 9） x m— 9m +19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程（不等式组）为 ____________________ . 18、过双曲线y 二k （k 丰0） 上任意一点引x 轴和y 轴的垂线，所得长方形的面x积为 ______ .4.. 19. 如图，直线y = kx （k >0）与双曲线y —交于A （X 1，y 1）， xB （x 2，y 2）两点，贝u 2x 1y 2 — 7x 2y 1 =20、如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上，点B 的坐标为B （—号，5），D 是AB 边上的一点,D / V 将厶ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的打泪 点E 处，若点E 在一反比例函数的图象上，那么该函数的解町 斗° 式是.c 1 C 、m v —210、如图，一次函数与反比例函数的图象相交于 点，则图中使反比例函数的值小于一次函数的值的 是（ ）• A 、x v — 1 B 、x > 2 C 、— 1 v x v 0或 x >2 D 、x v — 1 或 0v x v 2 二、填空题（每小题3分，共30分） A 、 m v 0B 、m > 0 D 、m > -2A 、B 两—x 的取值范围三、解答题(共60分)21、( 8分)如图，P是反比例函数图象上的一点，且点P到x轴的距离为3，到y轴的距离为2，求这个反比例函数的解析式0厂?k23、( 10分)如图，已知A (x i, y i), B (x2, y2)是双曲线y =仝在第一象限内x的分支上的两点，连结OA、OB. (1)试说明y i v OA v y i「+ k; (2)过B作BC丄x轴于C,当m= 4时，•-求厶BOC的面积. '824、( 10分)如图，已知反比例函数y二一8与一次函数x 萤纵坐标都是一2.求：(1) 一次函数的解析式;y = kx + b的图象交于A、B两点，且点A的横坐标和点B的25、( 11分)如图，一次函数y= ax+ b的图象与反比例(2)^ AOBWk _函数y =-的图象交于M、N两点.x(1)求反比例函数与一次函数的解析式；(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.(1) 求这两个函数的解析式；(2)求厶MON 的面积；(3) 请判断点P (4, 1)是否在这个反比例函数的图象上, 并说明理由.、选择题 1、D ； 2、3、C ；4、B ；5、 D ；6、C7、D ；& B ；9、D ；10、D .二、填空题 (1000)11、 y =12 、减小； 13、514、- -3； 15、y =3sx2x5m 29m 19116、y =— _;17、218、|k|;19、20；20、yx2m 7m 9> 012x三、解答题621、 y = .x22、 举例：要编织一块面积为2米2的矩形地毯，地毯的长x (米)与宽y (米)2之间的函数关系式为y 二-(x >0).x23、 (1)过点 A 作 AD 丄x 轴于 D ，贝U OD = x 1, AD = y 1,因为点 A ( X 1, y 1)kk在双曲线y = 上，故X 1=，又在Rt △ OAD 中，AD v OA v AD + OD ，所以x y 1k y 1 v OA v y 〔 +y 124、( 1)由已知易得 A (-2, 4), B (4,— 2),代入 y = kx + b 中，求得 y =— x + 2;(2) 当 y = 0 时，x = 2,则 y = — x + 2 与 x 轴的交点 M (2, 0),即 |OM| = 2, =-|OM| • |y A |+ 丄|OM| • |y B |= - X 2X 4+ 1 X 2X2 2 2 22 = 6.(2)^ BOC 的面积为2.于是 S A AOB = S A AOM + S A BOMx25、( 1)将N (— 1,— 4)代入y =-，得k = 4.二反比例函数的解析式为 yx4 4=4 .将 M ( 2, m )代入 y = 4，得 m = 2.将 M (2, 2), N (— 1,— 4)代 x x 2a b 2 a 2入y 二ax + b ,得 b 2,解得a 2, •次函数的解析式为y 二2x — 2. a b 4. b 2. (2)由图象可知，当x v — 1或O v x v 2时，反比例函数的值大于一次函数的 值. k 426、解(1)由已知，得一4= , k = 4,二y =.又•图象过M (2, m )点,1 x 4 ••• m = - = 2, v y = ax + b 图象经过 M 、N 两点,2• y = 2x — 2.(2) 如图，对于 y = 2x — 2,y = 0 时，x = 1 ,• A (1, 0), OA =1 ,• S ^MON1 11 1=S A MOA + S A NOA = -OA • MC + -OA• ND = - X 1X 2+ —X 1 X 4 = 3.2 2224(3) 将点P (4, 1)的坐标代入y = 4，知两边相等，• P 点在反比例函数图象 2a K Q,解之得4上x。

第 17 章反比率函数综合检测题一、选择题 〔每题 3 分，共 30 分〕1、反比率函数y ＝n5图象经过点〔 2， 3〕，那么 n 的值是〔〕．xA 、－ 2B 、－ 1C 、 0D 、12、假设反比率函数 y ＝ k〔 k ≠ 0〕的图象经过点 〔－ 1，2〕，那么这个函数的图象必然经过点〔 〕．x1，2〕D 、〔 1，2〕A 、〔 2，－ 1〕B 、〔－C 、〔－ 2，－ 1〕223、 (08 双柏县 ) 甲、乙两地相距s 〔 km 〕，汽车从甲地匀速行驶到乙地，那么汽车行驶的时间 t 〔 h 〕与行驶速度 v 〔 km/h 〕的函数关系图象大体是〔〕t/ht/ht/ht/hOv/(km/h)Ov/(km/h)Ov/(km/h)Ov/(km/h)A ．B ．C ．D ．4、假设 y 与 x 成正比率， x 与 z 成反比率，那么 y 与 z 之间的关系是〔 〕．A 、成正比率B 、成反比率C 、不行正比率也不行反比率D 、无法确定5、一次函数 y ＝ kx － k ， y 随 x 的增大而减小，那么反比率函数y ＝ k满足〔〕．xA 、当 x ＞ 0 时， y ＞ 0B 、在每个象限内， y 随 x 的增大而减小C 、图象分布在第一、三象限D 、图象分布在第二、四象限6、如图，点 P 是 x 轴正半轴上一个动点，过点P 作 x 轴的垂y 线 PQ 交双曲线 y ＝ 1于点 Q ，连结 OQ ，点 P 沿 x 轴正方向运动时，xQRt △ QOP 的面积〔 〕．A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定opx7、在一个可以改变容积的密闭容器内，装有必然质量m 的某种气体，当改变容积V 时，气体的密度 ρ 也随之改变．ρ与 V 在必然范围内满足ρ＝m，它的图象以以下图，那么该气体的质量 m 为〔V〕．A 、B 、5kgC 、D 、 7kg8、假设 A 〔－ 3， y 1〕， B 〔－ 2， y 2〕， C 〔－ 1，y 3〕三点都在函数 y ＝－ 1的图象上，那么y 1，y ， yx的大小关系是〔〕．23A 、 y ＞ y ＞ y3B 、y ＜ y 2 ＜ y3C 、 y ＝ y ＝ y3D 、 y ＜ y ＜ y212112139、反比率函数 y ＝12m的图象上有 A 〔 x 1，y 1〕、B 〔x 2，y 2〕两点，当 x 1 ＜ x 2＜0 时，xy1＜ y2，那么 m 的取值范围是〔〕．A 、 m ＜ 0B 、 m ＞ 0C 、 m ＜1D 、 m ＞ 12 210、如图，一次函数与反比率函数的图象订交于 A 、B 两点，那么图中使反比率函数的值小于一次函数的值的 x 的取值范围是〔〕．A 、 x ＜－ 1B 、 x ＞ 2C 、－ 1＜x ＜ 0 或 x ＞ 2D 、 x ＜－ 1 或 0＜ x ＜ 2二、填空题 〔每题 3 分，共 30 分〕11. 某种灯的使用寿命为 1000小时，它的可使用天数 y 与平均每天使用的小时数 x 之间的函数关系式为.12、反比率函数yk 四象限， 那么在一次函数 y kx b 中， y 随的图象分布在第二、 x 的增大而x〔填“增大〞或“减小〞或“不变〞 〕．13、假设反比率函数y ＝b3和一次函数 y ＝3x ＋ b 的图象有两个交点， 且有一个交点的纵坐x标为 6，那么 b ＝．14、反比率函数 y ＝〔 m ＋ 2〕x m2－10 的图象分布在第二、 四象限内， 那么 m 的值为．15、有一面积为S 的梯形，其上底是下底长的1，假设下底长为 x ，高为 y ，那么 y 与 x 的函数3关系是．16、如图，点 M 是反比率函数y ＝ a〔 a ≠ 0〕的图象上一点，x过 M 点作 x 轴、 y 轴的平行线，假设 S 阴影 ＝ 5，那么此反比率函数剖析式为．2m2－ 9m ＋ 19是反比率函数，且图象在每个象限内y 随 x 的增17、使函数 y ＝〔 2m － 7m － 9〕x 大而减小，那么可列方程〔不等式组〕为．18、过双曲线 y ＝ k〔 k ≠ 0〕上任意一点引x 轴和 y 轴的垂线， 所得长方形的面积为 ______．x419. 如图，直线 y ＝ kx(k ＞ 0)与双曲线 y 交于 A 〔 x 1，y 1〕，xB 〔 x ， y 〕两点，那么 2xy －7x1 2 y ＝ ___________．222120、如图，长方形 AOCB 的两边 OC 、 OA 分别位于 x 轴、20 y 轴上，点 B 的坐标为 B 〔－3， 5〕， D 是 AB 边上的一点，将△ ADO 沿直线 OD 翻折，使 A 点恰好落在对角线 OB 上的点 E 处，假设点 E 在一反比率函数的图象上，那么该函数的剖析式是．三、解答题 〔共 60 分〕21、〔 8 分〕如图， P 是反比率函数图象上的一点，且点P 到 x 轴的距离为3，到 y 轴的距离为2，求这个反比率函数的剖析式．22、〔 9 分〕请你举出一个生活中能用反比率函数关系描述的实例，写出其函数表达式，并画出函数图象．举例：函数表达式：23、〔 10 分〕如图， A 〔 x1， y1〕， B 〔 x2， y2〕是双曲线y＝k在第一象限内的分支上x 的两点，连结OA 、 OB ．〔1〕试说明y1＜ OA ＜ y1＋k ；y1（2〕过 B 作 BC ⊥ x 轴于 C，当 m＝ 4 时，求△ BOC 的面积．24、〔 10 分〕如图，反比率函数y＝－8与一次函数xy＝ kx ＋ b 的图象交于 A 、B 两点，且点 A 的横坐标和点 B 的纵坐标都是－ 2．求：〔 1〕一次函数的剖析式；〔2〕△ AOB 的面积．25、〔 11 分〕如图，一次函数 y＝ ax＋ b 的图象与反比率函数k y＝的图象交于 M 、 N 两点．x 〔1〕求反比率函数与一次函数的剖析式；〔2〕依照图象写出使反比率函数的值大于一次函数的值的x 的取值范围．26、〔 12 分〕如图，反比率函数y＝k的图象与一次函x数 y＝ ax＋b 的图象交于 M 〔 2， m〕和 N〔－ 1，－ 4〕两点．〔1〕求这两个函数的剖析式；〔2〕求△ MON 的面积；〔3〕请判断点 P〔 4， 1〕可否在这个反比率函数的图象上，并说明原由．参照答案 :一、选择题1、D；2、A；3、C；4、B；6、C7、D；8、B；9、D；二、填空题1 1 、 y ＝1000；12、减小；13、 5；14、－ 3；15、y＝3s x2x5、D；10、D ．；16、 y＝－ 5；17、 m29m 191 ； 18、 |k|； 19、 20； 20、y ＝－12．x2 m2m ＞ 0 x7 9三、解答题21、 y ＝－ 6 ．x2 米 2 的矩形地毯，地毯的长22、举例：要编织一块面积为 x 〔米〕与宽 y 〔米〕之间的函数关系式为 y ＝ 2〔 x ＞ 0〕．xx11 322 2y42 413〔只若是生活中吻合反比率函数关系的实例均可〕 画函数图象如右图所示．23、〔 1〕过点 A 作 AD ⊥ x 轴于 D ，那么 OD ＝ x 1， AD ＝ y 1，因为点 A 〔 x 1， y 1〕在双曲线 y＝ k 上，故 x 1＝k，又在 Rt △ OAD 中， AD ＜ OA ＜AD ＋ OD ，所以 y 1＜ OA ＜ y 1 ＋k；x y 1 y 1〔2〕△ BOC 的面积为 2．24、〔 1〕由易得 A 〔－ 2， 4〕，B 〔 4，－ 2〕，代入 y ＝kx ＋ b 中，求得 y ＝－ x ＋ 2； 〔2〕当 y ＝0 时， x ＝ 2，那么 y ＝－ x ＋2与 x 轴的交点 M 〔 2， 0〕，即 |OM|＝ 2，于是 S △ AOB ＝SAOM ＋S BOM ＝1 11×2×4＋ 1× 2×2＝ 6．AB|＝△ △|OM| · |y |＋|OM| · |y222225、〔 1〕将 N 〔－ 1，－ 4〕代入 y ＝k，得 k ＝ 4．∴反比率函数的剖析式为y ＝ 4．将 Mxx〔2，m 〕代入 y ＝ 4，得 m ＝ 2．将 M 〔 2，2〕，N 〔－ 1，－ 4〕代入 y ＝ ax ＋ b ，得2a b 2,xa b 4.解得 a 2,y ＝ 2x － 2．∴一次函数的剖析式为b2.（ 2〕由图象可知，当 x ＜－ 1 或 0＜ x ＜2 时，反比率函数的值大于一次函数的值．26、解 〔1〕由，得－4＝k，k ＝ 4，∴ y ＝4．又∵图象过M 〔2， m 〕点，∴ m ＝41x2＝2，∵ y ＝ ax ＋ b 图象经过 M 、N 两点，∴2a b2,解之得 a 2, ∴ y ＝ 2x － 2．a b4 b2〔2〕如图，对于 y ＝ 2x － 2， y ＝ 0 时， x ＝ 1，∴ A 〔 1， 0〕， OA ＝ 1，∴ S △MON ＝S △ MOA ＋ S △NOA＝1OA ·MC＋1OA ·ND ＝1×1×2＋1× 1×4＝ 3．2222〔3〕将点 P〔 4， 1〕的坐标代入y＝4，知两边相等，∴P 点在反比率函数图象上．x。

第 _______ 象限•3n m19•如果一次函数 y=mx+n 与反比例函数y=的图象相交于点（，2），那么该直线x2与双曲线的另一个交点的坐标为 ____________ •210 •已知一次函数 y=kx+b 的图象与双曲线 y=- 交于点（1,,且过点（0, 1） , ?求此x一次函数的解析式•初中数学反比例函数精华练习题（含答案）1 •反比例函数y=m的图象两支分布在第二、四象限，则点（ m, m-2）在（） x B •第二象限 C •第三象限 k y= 的图象经过点（-2 , -1） x B •第二象限 C •第三象限 A •第一象限 D •第四象限 2 •如果反比例函数，那么当x>0时, 图象所在象限是（？ ?） A •第一象限 3.下列函数中，当 • y= - x-2 C 3 4 •如图，某个反比例函数的图象经过点 A • y=3x+4 B D •第四象限 x>0时，y 随x 的增大而减小的是（ ） 4 厂 1 • y=- D • y=-x 2x则它的解析式为（ ） P,k i 、 k 2、 k 3?的大小关系为（ A • k i >k 2>k 3 B ) • k 3>k 2>k i 6.如图，正比例函数 C • k 2>k 3>k i D • k 3>k i >k 2 k y=x 和y=mx （m>0的图象与反比例函数 y=— （k>0）的图象分别交 x 于第一象限内的 A 、C 两点，过A 、C 两点分别向x 轴作垂线，垂足分别为 BD, ?若Rt △ AOB 与Rt △ COD 的面积分别为 S 和S ，则S 与S 的关系为（ A • S>S 2 B • Si<S a C7•如果点（a , -2a ）在双曲线）• S=S D .与m k 值有关ky=°上，那么双曲线在第 _______x象限.&当x>0时，反比例函数 y=m x 22m 3m 6随x 的减小而增大，则m 的值为,?图象在n 111. ------------------------------------------------------------------------ 关于x的一次函数y=-2x+m和反比例函数y= ------------------------------------------------------------------------- 的图象都经过点A（ -2 , 1）.求：（1）x一次函数和反比例函数的解析式；（2）两函数图象的另一个交点B的坐标；（3）A AOB的面积.k12. 如图，点A、B在反比例函数y= 的图象上，且点A B的横坐标分别为a, 2a （a>0）,xAC垂直x轴于6且厶AOC的面积为2.（1）求该反比例函数的解析式.（2）若点（-a , y1）,（-2a , y2）在该反比例函数的图象上，试比较y1与y2的大小.13.如图, 已知Rt△ ABC的锐角顶点A在反比例函数OB=3求：（1 ）点A的坐标;2 8y= x+ ，求△ ABC的面积？7 7 2）函数y=m的解析式; 3）直线AC的函数关系式为3,.cn14. 某地上年度电价为0.8元，年用电量为1亿度，本年度计划将电价调至0.55 —0.75元之间，经测算，若电价调至x元，则本年度新增用电量y （亿度）与（x-0.4 ）成反比例，又当x=0.65时，y=0.8 .求：（1）y与x之间的函数关系式；（2）若电价调至0.6元时，本年度的用电量是多少？15. 某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时，？室内每立方米空气中的含药量y （毫克）与时间x （分钟）成正比例，药物燃烧后，y与x成反比例（？如图所示），现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg ?请你根据题中所提供的信息，解答下列问题.（1）药物燃烧时y关于x的函数关系式为_________ ，自变量x的取值范围是_______ ;药物燃烧后y与x的函数关系式为_____________ .（2）研究表明，当空气中每立方米的含药量低于 1.6mg时学生方可进教室，那么从消毒开始，至少多少分钟后学生才能回到教室？（3）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时, 才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？ly/mg.c n1即y 与x 之间的函数关系式为y=5x 27. 二、四 8 . 1 ------- '9 . ( -1 , -1 ) 10 . y=-3x+111(1) y=-2x-3 ,y =2； ( 2)13 B ( , -4 );( 3)=3 ?x2 4 12(1)4 y=_; (2) y 1<y 2 13 .6(1) A (3, 2);( 2) y=— ; ( 3) (=7xx14(1)设y=k _ ,因为当 x=0.65 时 y=0.8 , x 0.4k所以有0.8=-0.65 0.4/• k=0.2 ,••• y=0.2 = 1x 0.4 5x 2=1.答案: 1. C 2 . A 3D 4 . D 5 . B 6 . C1 1（2）把x=0.6代入y=中，得y=5x 25 0.6 2所以本年度的用电量为 1 + 1=2 （亿度）.15.（ 1）设正比例函数的解析式为y=k 1x ,反比例函数的解析式为 y=邑,将（8, 6） ?分别代入这两个解析式中求出k 1=— , k 2=48,x43•••正比例函数的解析式为 y= x （0<x w 8）（ ?即燃烧时的关系式）；4反比例函数（即药物燃烧后）的关系式为y=48348 (3)将y=3分别代入y= x 和y= 中，得x=?4和x=16.4x••• 16-4>10 ,•此次消毒有效.=1。