下载文档原格式
习题七67习题七7-1试证明两串联的互感线圈不可能出现0221≤-+M L L 。
7-2试求图7-2电路中ab 端口的等值参数。
7-3 试求图7-3电路中对于工频的输入阻抗， 答：Ω∠=65.2354.809i Z 7-4图7-4电路中已知V 314sin 210t u s =，H 11=L ，H 42=L ，H 5.0=M ，Ω=5001R ，Ω=10002R ，试求①各支路电流、输入阻抗；②等效去耦电路。
答：A 41.27018.01-∠=I ；A 83.380072.02-∠=I ；A 65.30025.0-∠=I Ω∠=65.30400i Z解314.7515.195096.1884500616.3145001∠=+=⨯+=j j Z图7-2习题7-2题图图7-3 习题7-3题图图7-4 习题7-4题图习题七Ω∠=∠∠=+∠=++∠⨯=65.2354.80949.5196.240814.75195015096.1884150014.751950150100096.188450014.7515.19501000j j Z i解4 等效去耦电路 回路法求解()[]()[]SSU I M M L j R I M j U I M j I M M L j R =-+++-=--++22212111ωωωω[][]010431410005.03140105.03143145002121∠=⨯++⨯-∠=⨯-+I j I j I j I j[][]01047.5147.160515701015713.3242.5902121∠=∠+-∠=-∠I I j I j I [][][]A 41.27018.012.8273.95096471.5453.173102.94199458.13031071.5453.173********.94199458.1056613.1412986.10000246496.836.94790115703.1255986.100002464947.5147.160513.3242.5901015747.5147.1605101-∠=∠∠=+∠=+++=+∠++=+∠∠⨯+∠⨯=j j j j j j I [][][]A 83.380072.012.8273.95096429.4309.6869246492.94199458.1056611.471093.4999246496.836.94790115701.314093.49992464947.5147.160513.3242.5901015713.3242.590102-∠=∠∠=+++=+∠++=+∠∠⨯+∠⨯=j j j j j I()()A65.30025.00128.00216.00045.00056.00083.0016.083.380072.041.27018.021 -∠=-=-+-=-∠+-∠=+=j j j I I I Ω∠=-∠∠=65.3040065.30025.0010i Z习题七7-5试写出图7-4电路中2U 、3U 、4U 的表达式。
第七章 直流电路二、填空题1、0S j dS ⋅=⎰⎰或0j ∇⋅=2、非静电力3、充电，放电4、串联时，两导线的电流强度相等，即12I I =，因截面积12:3:1S S =，所以电流密度大小121212::1:3I I j j S S ==，再由欧姆定律的微分形式j E σ=（其中σ是导体的电导率，通常仅与导体材料和温度有关，此处12σσ=），可得两导线的电场之比为121212::1:3j j E E σσ==；若将二导线并联，接上同一电池，则12εε=，因导线长度12l l =，注意到导线电动势与电场满足关系El ε=，所以两导线的电场之比为121212::1:1E E l l εε== 因导线的电阻满足l R S ρ=（其中1ρσ=是导体的电阻率，此处12ρρρ==）。
所以两导线的电阻之比为 12121212::1:3l l R R S S ρρ== 不妨记01R R =，则203R R =，当两导线串联时，总电阻1204R R R R =+=，电源输出功率为221=4P I R R εεε==串 当两导线并联时，由11112R R R ---=+，可得总电阻034R R =，电源输出功率为 2204=3P R R εε=并所以，电池供给的总电功率之比为220014:=:=3:1643P P R R εε串串5、零6、升高，降低。
三、选择题1、选A2、选C3、选B4、质量为m ，电量为q 的油滴静止时，设其所在位置的电场强度大小为E ，则有qE mg =当电荷量减小时，为维持该油滴仍处于静止状态，需要增大其所在位置处的电场强度。
因平行板电容器内电场是匀强场，由课本平行板电容器的电容一节可知两极板电势差为0AB Qd V Ed Sε== 由此可得电容内部电场强度0Q E Sε= 因所给选项均无法改变电场强度大小，故不选。
5、选D 。
四、计算题1、解：记四个灯泡的通电电阻为12340 6.0R R R R R =====Ω，电源电动势和内阻分别为ε和r 。
第1章1.1.11. 单项选择题1）A 2）C 3）B 4）A 5）C 6）A2.多项选择题1）AB 2）AB 3）ABCD 4）ABD 5）ABCD 6）ABC 3.判断题1）F 2）F1.1.21. 单项选择题1）A 2）B 3）A 4）C 5）D 6）D 7）A 8）A 9）C 2. 多项选择题1）ABCDE 2）ABC 3）ABCD 4）AB 5）ABCD 6）ABCD3. 判断题1）F 2）T 3）F 4）F 5）F 6）T7）F1.1.31. 单项选择题1）A 2）D 3）A 4）B 5）A 6）D 7）C 8）A 9）A10）D 11）A 12）D2. 多项选择题1）ABE 2）ABCD 3）ABCD 4）ABC3. 判断题1）T 2）T 3）F 4）F 5）T 6）T 7）T1.1.41. 单项选择题1）A 2）C 3）D 4）A 5）B 6）C 7）A 8）C2. 多项选择题1）ABCD 2）ABCD 3）ABE 4）ABC 5）ABCD3. 判断题1）T 2）T 3）T 4）T 5）T 6）F7）F 8）F4. 填空题1）操作码地址码2）操作系统3）算术运算逻辑运算4）输入设备5）控制器运算器6）编译程序1.1.51. 单项选择题1）A 2）C 3）D 4）A 5）B 6）D 7）D 8）A2. 多项选择题1）ABC 2）ABD 3）ABD 4）ABD 5）ABDE3. 判断题1）F 2）T 3）T 4）T 5）T6）F 7）F 8）T 9）F4. 填空题1）CD-ROM 2）CPU 3）Personal Computer（个人计算机）4）AGP 5）分辨率6）采样7）LCD8）显示分辨率颜色质量刷新速度1.1.61. 单项选择题1）A 2）C 3）A 4）D 5）E2. 填空题1）MPEG-2 2）JPEG 3）MPEG视频MPEG音频MPEG系统4）专用芯片1.3一、单项选择题1. A 世界上第一台真正意义上的计算机ENIAC是1946年2月在美国宾夕法尼亚大学诞生的，故应选A2. A 显示器是输出设备，磁盘驱动器既可以看作输入设备也可以作为输出设备，而鼠标器是输入设备，故应选A。
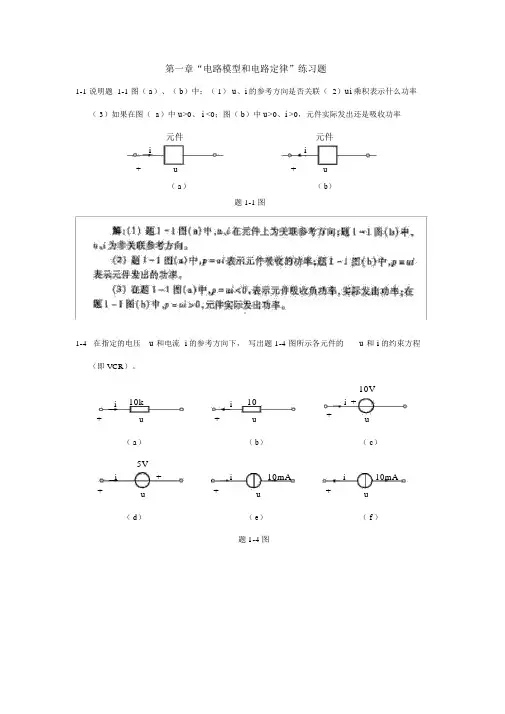
第一章“电路模型和电路定律”练习题1-1 说明题 1-1 图（ a）、（ b）中：（ 1）u、i的参考方向是否关联（2）ui乘积表示什么功率（ 3）如果在图（ a）中u>0、i <0；图（ b）中u>0、i >0，元件实际发出还是吸收功率元件元件i i+ u + u（ a）（ b）题1-1图1-4在指定的电压u 和电流 i 的参考方向下，写出题1-4图所示各元件的u 和 i 的约束方程（即 VCR）。
10k 10 i 10Vi i +++ u + u u （ a）（ b）（ c）i 5Vi 10mA i 10mA++ u + u + u （ d）（ e）（ f ）题1-4图1-5试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。
52A + ++15V 5 15V 5 15V 2A 2A（ a）（b）（c）题1-5图1-16 电路如题 1-16 图所示，试求每个元件发出或吸收的功率。
A0.5A 2 I 122I1+ + +1U 2U 2VI 2（a）（ b）题 1-16 图1-20试求题1-20图所示电路中控制量u1及电压 u。
1k10k++ + +u 1u10u 12V题 1-20 图第二章“电阻电路的等效变换”练习题2-1 电路如题2-1 图所示，已知u S=100V ， 1=2k ， 2=8k 。
试求以下 3 种情况下的电压 2RRu和电流 i 2、 3：（ 1） 3=8k ；（2） 3 = （3处开路）；（ 3） 3=0（ 3 处短路）。
i RRRRRi 2 i 3R 1 ++R 2u2 R 3u S题2-1 图2-5 用△— Y 等效变换法求题2-5 图中 a、b 端的等效电阻：（1）将结点①、②、③之间的三个 9 电阻构成的△形变换为 Y 形；（2）将结点①、③、④与作为内部公共结点的②之间的三个 9 电阻构成的 Y 形变换为△形。
①a999②③99b④题 2-52-11利用电源的等效变换，求题2-11 图所示电路的电流i 。
大学电路原理习题答案大学电路原理习题答案电路原理是大学电子工程专业的一门重要课程，它是电子工程师必备的基础知识。
在学习电路原理的过程中，习题是帮助学生巩固知识、提高能力的重要途径。
本文将给出一些大学电路原理习题的答案，帮助学生更好地理解和掌握电路原理。
一、基础电路习题答案1. 串联电阻电路问题：已知电阻R1=10Ω，R2=20Ω，R3=30Ω，求串联电阻的阻值。
答案：串联电阻的阻值等于各电阻阻值之和，即R=R1+R2+R3=10Ω+20Ω+30Ω=60Ω。
2. 并联电阻电路问题：已知电阻R1=10Ω，R2=20Ω，R3=30Ω，求并联电阻的阻值。
答案：并联电阻的阻值等于各电阻阻值的倒数之和的倒数，即1/R=1/R1+1/R2+1/R3=1/10Ω+1/20Ω+1/30Ω=1/60Ω，所以R=60Ω。
3. 电压分压问题：已知电源电压为12V，电阻R1=10Ω，R2=20Ω，求电阻R1上的电压。
答案：根据电压分压定律，R1上的电压等于电源电压乘以R1与总电阻之比，即U1=U*(R1/(R1+R2))=12V*(10Ω/(10Ω+20Ω))=4V。
4. 电流分流问题：已知电源电压为12V，电阻R1=10Ω，R2=20Ω，求电阻R1上的电流。
答案：根据电流分流定律，电阻R1上的电流等于电源电流乘以R2与总电阻之比，即I1=I*(R2/(R1+R2))=12V/(10Ω+20Ω)=0.4A。
二、交流电路习题答案1. 交流电阻电路问题：已知电阻R=10Ω，电源电压为V=220V，求电路中的电流。
答案：根据欧姆定律，电路中的电流等于电压除以电阻，即I=V/R=220V/10Ω=22A。
2. 交流电容电路问题：已知电容C=10μF，电源电压为V=220V，求电路中的电流。
答案：根据电容电流公式，电路中的电流等于电容的导数乘以电压的正弦频率，即I=C*dv/dt，其中dv/dt是电压的变化率。
由于电源电压是交流的，所以电压可以表示为V=V0*sin(ωt)，其中V0是电压的峰值，ω是角频率。
习题77-2 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A 与C 相距2.0 mm ．B ，C 都接地，如题7-2图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题7-2图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题7-2图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 7-3 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q(1)(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题7-3图⎰⎰∞∞==⋅=22020π4π4d d R R R qr r q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q '；则外壳内表面带电量为q '-，外壳外表面带电量为+-q q ' (电荷守恒)，此时内球壳电势为零，且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=7-4 半径为R 的金属球离地面很远，并用导线与地相联，在与球心相距为R d 3=处有一点电荷+q ，试求：金属球上的感应电荷的电量．解: 如题8-24图所示，设金属球感应电荷为q '，则球接地时电势0=O U7-4图由电势叠加原理有：=O U 03π4π4'00=+RqR q εε得 -='q 3q 7-5有三个大小相同的金属小球，小球1，2带有等量同号电荷，相距甚远，其间的库仑力为0F ．试求：(1)用带绝缘柄的不带电小球3先后分别接触1，2后移去，小球1，2之间的库仑力；(2)小球3依次交替接触小球1，2很多次后移去，小球1，2解: 由题意知 2020π4rq F ε=(1)小球3接触小球1后，小球3和小球1均带电2q q =', 小球3再与小球2接触后，小球2与小球3均带电q q 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后，每个小球带电量均为32q.∴ 小球1、2间的作用力00294π432322F r qq F ==ε7-6如题7-6图所示，一平行板电容器两极板面积都是S ，相距为d ，分别维持电势A U =U ，B U =0不变．现把一块带有电量q 的导体薄片平行地放在两极板正中间，片的面积也是S ，片的厚度略去不计．求导体薄片的电势． 解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ，2σ，3σ，4σ,5σ,6σ如图所示．由静电平衡条件，电荷守恒定律及维持U U AB =可得以下6个方程题7-6图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A 解得 Sq261==σσS q d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 Sqd U E 00422εεσ+==)2d (212d 02Sq U E U U CB C ε+=== 注意：因为C 片带电，所以2U U C ≠，若C 片不带电，显然2U U C = 7-7 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强；(2)电介质层内、外的电势； (3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εε ==内; 介质外)(2R r <场强303π4,π4rrQ E r Qr D ε ==外 (2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞外介质内)(21R r R <<电势rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内2020π4)11(π4R QR r qr εεε+-=)11(π420R r Q r r -+=εεε(3)金属球的电势r d r d 221 ⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Q r r -+=εεε7-8如题7-8图所示，在平行板电容器的一半容积内充入相对介电常数为r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题7-8图所示，充满电介质部分场强为2E ，真空部分场强为1E，自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得11σ=D ，22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题7-8图7-9 金属球壳A 和B 的中心相距为r ，A 和B 原来都不带电．现在A 的中心放一点电荷1q ，在B 的中心放一点电荷2q ，如题8-30图所示．试求： (1) 1q 对2q 作用的库仑力，2q 有无加速度；(2)去掉金属壳B ，求1q 作用在2q 上的库仑力，此时2q 有无加速度． 解: (1)1q 作用在2q 的库仑力仍满足库仑定律，即2210π41r q q F ε=但2q 处于金属球壳中心，它受合力．．为零，没有加速度． (2)去掉金属壳B ，1q 作用在2q 上的库仑力仍是2210π41rq q F ε=，但此时2q 受合力不为零，有加速度．题7-9图7-10 半径为1R =2.0cm 的导体球，外套有一同心的导体球壳，壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ，当内球带电荷Q =3.0×10-8C(1)整个电场储存的能量；(2)此电容器的电容值．解: 如图，内球带电Q ，外球壳内表面带电Q -，外表面带电Q题7-10图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r rQ E ε= 3R r >时 302π4r rQ E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε ∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F。
7-1 图 (a)、(b) 所示电路中开关S 在 0t = 时动作，试求电路在 0t +=时刻电压、电流的初始值。
1210-+V 5c u V2L∙（a ） (b)题7-1图解：(a)设S 在1处闭合的时间已足够，则电路已达稳态，故C 开路，V 10=c u ，即V 10)0(=-c u换路后，S 在2处闭合，则有换路定则：)0()0(-+=c c u u ，C 可看作是电压源，于是由KVL 定律： 0)0()0(=++++R i u u c s cV 15510)0()0(-=--=--=-+s c c u u R i.5A 1)0(-=+c i故V 10)0(=+c u .5A 1)0()0(-==++i i c V 15)0()0(-=⨯=++R i u R (b) S 在1处闭合，设已达稳态，故L 已视短路。
()A 155V10)0(=Ω+=-L i0=t 时刻发生短路，有换路定则得：A 1)0()0(==-+L L i i故在+=0t 时刻，L 可看作电流源，于是，由欧姆定律：V 551)0()0(=⨯=⨯=++R i u L R由KVL 定律：)0()0(++-=L R u u ，故V 5)0(-=+L u7-2 图示各电路中开关S 在 0t =时动作，试求各电路在0t +=时刻电压、电流。
已知图(d)中的()100sin()3e t t πω=+V ，(0)20c u -=V 。
F2S∙2Ω15H10(a) (b)+-V 10Ω5∙∙Fμ1.(c) (d)题7-2图解：(1)对图7-2 (a)电路，在换路前两个电容相当于开路，可求的两个电容电压为V 5V 336320)0(1=⎪⎭⎫⎝⎛⨯++=-uV 10V 636320)0(2=⎪⎭⎫⎝⎛⨯++=-u在+=0t 时，两个电容均用电压源代替，则+=0t 时的等效电路如图7-2 (a ')所示，其中V 5)0()0(11==-+u u ，V 10)0()0(22==-+u u 。
可解出各初始值为 A 34)0(1=+i ，1A )0(2=+i ，A 37)0(=+iF2S20ΩS)0(2+i +图7-2（a ） 图7-2 (a ')(2)对图7-2（b ）电路，在换路前电感相当于短路，可求得A 56A 3020203)0(=⎪⎭⎫ ⎝⎛+⨯=-L i在+=0t 时，电感元件用电流为A 6)0()0(==-+L L i i 的电流源代替，则+=0t 时的等效电路如图7-2 (b ')所示，解得A 3)0(1=+i ，V 18)0(15-)0(-==++L i u ，()V 6.21)0(153)0(-=+-=++L L i u∙215H 103()+0L图7-2（b ） 图7-2(b ')(3)对图7-2（c ）电路，在换路前电容相当于开路，求出15V V 1055151030)0(=⎪⎭⎫⎝⎛+⨯+-=-c u在+=0t 时，电容用电压为V 51)0()0(==-+c c u u 的电压源代替，作出+=0t 时的等效电路如图7-2 (c ')所示，可求得A 61525)0(10)0(-=+-=++c c u iA 61)0()0(1=-=++c i i+-V 10Ω5∙∙()+0c )+图7-2（c ） 图7-2 (c ')(4)对图7-2（d ）电路， 在+=0t 时，将电容用电压为V 20)0()0(==-+c c u u 的电压源代替，得+=0t 时的等效电路如图7-2 (d ')所示，其中电源)0(+e 的值为V 6.86V 3sin 100)0(=⎪⎭⎫ ⎝⎛=+πe可求出A 33.320)0()0()0(=-=+++c c u e iA 6.66)0(20)0(==++c i uFμ1.0Ω20()+0c )+图7-2（d ） 图7-2 (d ')7-3 开关S 原在位置1已久，0t =时合向位置2，求()c u t 和()i t 。
+-cu S ∙∙Ωk题7-3图解：设0<t 时，电路已达稳态，故电容C 上的电流0=c i ，故V 455425100100)0(=⨯=+=-s c u u在0=t 时，发生换路，由换路定理，故V 4)0()0(==-+c c u u所以有V 4)0()(1t RCc c e eu t u --+==()mA e C dtt du t i t c -=∙=04.0)( 7-4 一个高压电容器原先已充电，其电压为10 kV ，从电路中断开后，经过15 min ， 它的电压降低为kV ，问：（1）再经过15 min 电压将降低为多少（2）如果电容C = 15μF ，那么它的绝缘电阻是多少 （3）需经多少时间，可使电压将至30 V 以下（4）如果以一根电阻为Ω的导线将电容接地放电，最大放电电流是多少若认为在5τ时间内放电完毕，那么放电的平均功率是多少（5）如果以100 k Ω的电阻将其放电，应放电多少时间并重答（4）。
解：由题意知，这个高压电容器为非理想电容，其电路模型如图7-4所示。
R图7-4已知，kV 10)0(=-c u ，所以，由换路定则kV 10)0(=+c u ，由于是一所RC 电路的零输入响应：RCtc c eu t u -+=)0()(已知：经过15min ，)(t u c 由 3.2kV kV 10)0(→=+c u ，于是可求RC ：RCe601510.23⨯-=故s 87.7892.310ln 6015=⨯=RC （1） 再过15min ，)6030(e)6015(ee)0(e)0(6015601560156030⨯=⨯=∙=⨯-⨯-⨯-+⨯-+c RCc RCRCc RCc u u u u所以RCe601510.23⨯-=，故2.306015=⨯-RCe已知：kV 24.012.30.232.30)6015()6030(=⨯=⨯⨯=⨯c c u u （2）s 87.789=RC ，F 10156-⨯=C ，于是，Ω⨯=⨯=66106.652101587.789R （3）要求V 30)(≤t u c V 30)0(<-+RCt c eu33103101030--⨯=⨯<RCt es 44.458831000ln 87.7891031ln3==⨯≥-RC t即需经过至少，才能使V 30)(≤t u c 。
（4）用导线将电容接地，总电阻Ω≈⨯=='2.02.0//1066.52//6W R R R ，时间常数s 10310152.066--⨯=⨯⨯=RC由于)0()(+≤c c u t u ，即()kA 502.0k100)0()(=='=≤++R u i t i c 在+=0t 时，电容储能：[]J 7501010101521)0(214462=⨯⨯⨯⨯==-+c c u C Wτ5=t 时，电容储能：0='c W故对外输出能量：t p W c ∙-=∆，p 为平均功率，τ5=t故W 100.5s1035J 750076--⨯=⨯⨯--=p （5）若Ω=k 100W R ，则()()Ω⨯≈⨯⨯=='566100.1100.1//1065.52//R R R W于是，有时间常数：s 5.11015101065=⨯⨯⨯='-C R故放电时间：s 5.755='=C R τ所以平均功率：W 5100.5s7J750=-=p 最大放大电流： ()A 1.0101010053max =⨯='=+R u I c 7-5 图示电路中，若0=t 时开关S 闭合，求电流i 。
题7-5图解：设0<t 时，S 打开且保持足够长的时间，因此，电路已达稳态，有L 短路，C 开路，见图7-5（a ）。
()0uci图7-5（a ） 图7-5（b ）于是，由KVL 定律A 24.010015060)0(=+=-L iV 246V 3V 60)0(150V 60)0(=-=⨯-=--L c i u0=t 时，S 闭合，发生换路，电路如图7-5（b ）所示，由换路定则有A 24.0)0()0(==-+L L i i ，V 24)0()0(==-+c c u u由于短路，L 和C 分别组成互不相关的回路，因此，在0>t 时，仍然为一阶零输入回路：RC 回路：V 24)0(500t RCt c c e eu u --+==RL 回路：A 24.0)0(1000t t LR L L e ei i --+==由于()()A 24.0A 500241020)(5005006t t c c e e dtt du Ct i ----=-⨯⨯⨯= 因此，由KCL 定律：()()()A 24.01000500t tc L e et i t i i ---=--= 7-6 图示电路中开关S 打开前已处稳定状态。
0=t 开关S 打开，求0≥t 时的)(t u L 和电压源发出的功率。
0Ls ∙题7-6图解：当0<t 时，电感支路被短路，故有0)0()0(==-+L L i i ，这是一个求零状态响应问题。
当∞→t 时，电感相当于短路。
则应用叠加定理可求得)(∞L i 为.4A 15322253210)(=++⨯+++=∞L i从电感两端向电路看去的等效电阻为Ω=++=105320R 所以时间常数s 501102.00===R L τ 故0>t 后的电感电流为()A e 14.1e 1)()(500t t L L i t i ---=⎪⎪⎭⎫⎝⎛-∞=τ电感电压V e 4.1)()(500t L L dtt di Lt u -== 电压源中的电流()A e4.16.0250tL i i ---=-= 电压源发出的功率为()W e1461050ti p ---=⨯=因此，电压源吸收功率，作为电路的负载。
7-7 图示电路中开关闭合前电容无初始储能，0=t 时开关S 闭合，求0≥t 时的电容电压)(t u C 。
Lu Ω0(t题7-7图Ω215sci i -=1图7-7（a ） 图7-7（b ）解：由题意知0)0()0(==-+c c u u ，这是一个求零状态响应问题。
当∞→t 时，电容看作开路，受控电流源的电流为零，亦看作开路电路如图7-7（a ）所示。
故有V 2)(=∞c u 求a 、b 端口的等效电阻。
用开路短路法求。
图7-7（b ）所示电路中()2214=+⨯+sc sc sc i i i解得A 72=sc i 则等效电阻()Ω==∞==77220scc sc oc i u i u R故时间常数s 10211037660--⨯=⨯⨯==C R τ所以0>t 后，电容电压()()V 12121106⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-∞=--t t c c e e u t u τ7-8 图示电路中0=t 时开关S 闭合，求L i 和电源发出的功率。
