水的相图2

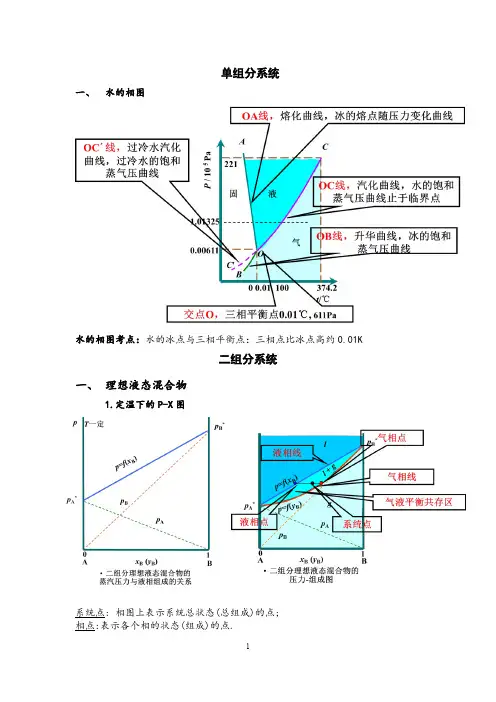
单组分系统一、水的相图水的相图考点：水的冰点与三相平衡点：三相点比冰点高约0.01K二组分系统一、理想液态混合物1.定温下的P-X图系统点: 相图上表示系统总状态(总组成)的点;相点:表示各个相的状态(组成)的点.结线:两个平衡相点的连结线.系统点总是在结线上2.定压下的T-X图泡点: 液相升温至开始起泡沸腾的温度;露点: 气相降温至开始凝结的温度.两点之间为相变温度区间, 与系统总组成有关.精馏原理：将液态混合物同时经多次部分气化和部分冷凝而使之分离的操作称为精馏。

同一层隔板上, 自下而上的有较高温度的气相与反方向的较低温度的液相相遇. 通过热交换,气相部分冷凝, 液相则部分气化.二、非理想液态混合物1.二组分真实液态混合物的4种类型的P-X图关于正偏差:若两组分分子间的吸引力小于各纯组分分子间吸引力,形成混合物后,分子就容易逸出液面而产生正偏差.若纯组分有缔合作用,在形成混合物后发生离解,因分子数增多而产生正偏差.混合时常有吸热及体积增大现象.关于负偏差:若两组分分子间的吸引力大于各纯组分分子间吸引力,形成混合物后,分子就较难逸出液面而产生负偏差.若形成混合物后分子发生缔合,因分子数减少而产生负偏差.混合时常有放热及体积缩小现象.2. 二组分真实液态混合物的4种类型的T-X图恒沸点处气相组成和液相组成相同。

此点对应的自由度数为0.一般正偏差和一般负偏差系统的温度-组成相图与理想系统的类似.3.部分互溶系统部分互溶的情况:系统会以两个饱和溶液平衡共存,这两个液层称为共轭溶液. 当混合物组成未达到两组分的相互溶解度时, 系统都以均相存在。

将具有两个液层的系统升高或降低至某个温度，两个液层的界面消失而成为一个液相，这个温度叫做最高或最低会溶温度。

4. 二组分液态完全互溶向部分互溶过渡5. 二组分液态部分互溶向完全不互溶过渡6. 完全不互溶三、二组分固-液平衡体系1.固态完全不互溶系统2.热分析法冷却曲线出现平台的原因：释放的凝固热抵消了因冷却而散失的热量出现最低点：因最初非常微细的晶体难以析出，过冷现象导致斜率变小的原因：固态Bi析出所释放的凝固热部分抵消了降温过程散失的热量低共熔温度、低共熔混合物3.溶解度法4.固态部分互熔系统5.固态完全互熔系统晶内偏析：退火：淬火：6.生成稳定化合物的系统注：若化合物数目有N种，则其相图就被看作是由（N+1）个简单低共熔点的固态不互溶系统的相图组合而成。

水的相图在通常压力下，水的相图为单组分系统中最简单的相图。

在此系统中只有一个相存在时，即水以气相或液相或固相存在时，系统的自由度数f=2，即温度、压力均可变更。

因此，在T-p图上有三个面各代表这三个相。

在此系统中可能存在的两相平衡有三种情形，即（1）液-气平衡，（2）固-气平衡，（3）固-液平衡；此时系统的自由度数f=1，即T和p 只有一个能任意变更。

因此，在T-p图上有三条线各代表上述三种两相平衡。

在此系统中可能存在的三相平衡为固-液-气三相平衡；此时系统的自由度数f=0，即T和p均已一定，不能变更。

因此，在T-p图上有一个三相点。

虽然根据相律指出了水的相图的大概情况只是所有的线和点的具体位置却不能由相律指出，必须依靠实验来测定。

水的相图的具体形状见下图。

其中OA线是液-气平衡线，即水的蒸气压曲线；OB线是固-气平衡线，即冰的蒸气压曲线；OB线是固-气平衡线，即冰的蒸气压曲线；OC线是固-液平衡线；O点是冰-水-气三相平衡的三相点，从图可以看出，此时的温度和压力均已一定，温度为0.0098℃压力为609Pa。

此图与相律所指示的完全一致，即有三个单相面，三条两相平衡线，一个三相点。

水的蒸气压曲线OA向上不能无限地延伸，只能延伸到水的临界点，因为在该点以上，液态水将不复存在。

水的临界点的温度为374℃；压力为2.23×107Pa。

OA线超过三相点O向下延伸所形成的OF线代表过冷水与蒸气的平衡，因此OF线为不稳定的液-气平衡线，此种液-气平衡系统处于介稳状态，只要稍受干扰，如受到搅动或有小冰块投入系统，立即就会有冰析出。

由上图可以看出，过冷水的饱和蒸气压大于冰的饱和蒸气压，即OF线比OB线略高。

OB线向下可延伸到绝对零度。

向上延伸不能超过三相点O，因为不存在过热的冰。

OC线向上可延伸到2×108Pa和-20℃左右。

压力再增加，将出现另外的冰晶型，本图中不再介绍由图可以看出，OA、OB线的斜率为正值，而OC线的斜率为负值。

§1水的相变及相图返回概述1.水蒸气是热力工程中最为常见的工质在18世纪发明的蒸气机，水蒸气是唯一的工质，直到内燃机发明，才有了燃气工质。

尽管在各种热力设备或系统中，已采用了其他物质作为工质，如空气、各种制冷剂、燃气等等，但水蒸气目前仍是暖通、火力发电、核电、化工等行业热力设备或系统中最为普遍采用的工质。

作为工质，水蒸气具备：来源丰富，耗资少，无毒无味，比热容大，传热好，良好的膨胀和载热性能等优点。

2.水蒸气是实际气体水蒸气在工程应用中，一般处于离液态不远的状态，是一种实际气体。

只有在空气中，由于其含量极小，可视作理想气体处理。

在热力设备或系统工作过程中，涉及到物质的聚集态主要是液态和气态。

那么，对于非理想气体的性质及其热力过程如何分析呢？本章将以水蒸汽为例，说明实际气体热力性质的基本特点和确定方法、参数计算以及基本热力过程分析的基本方法。

重点内容：了解实际气体热力性质的基本特点，与理想气体的区别所在。

一、纯物质聚集态的变化纯物质通常以三种聚集态固相、液相及气相状态存在。

1.纯物质聚集态的变化融解与凝固→固态与液态；汽化与凝结→液态与气态；升华与凝华→固态与气态。

2.聚集态变化的影响因素纯物质种类、压力、温度二、纯物质的p-t相图1. p-t相图指在p-t图上，纯物质在发生聚集态变化时压力及温度的变化规律。

如图7-2所示。

注意：(1)三相点是三条相平衡曲线的交点。

(2)临界点以上区域（虚线以上区域，即温度及压力均高于临界点温度及压力）为气液相不分或共存区域，只体现流体的特性。

(3)多数物质压力增大将使凝固点温度增加。

但对于水等少数物质，压力的增大将使其凝固点温度降低。

图7-2 纯物质的p-t相图2.几个基本概念(1)三相点与临界点（每种纯物质的三相点与临界点的压力和温度都是唯一确定的。

）临界状态(临界点)：临界点（状态）是气-液共存的状态，而且气、液的状态参数值相同，例如具有相同的比容、密度等等。

2 液、固相化学势表达式 纯液体（或固体）物质B 的标准状态规定为同温度，标准压力时纯液体（或固体）物质B 的状态。

即O Bμ（l, T ）= *B μ(l, T, O p ) (2—23a) 于是纯液体（或固体）物质B 的化学势为*B μ(l, T , p ) =O B μ（l, T ）+p V pp d )l (O m B,⎰ (2—23b) 实际上，在处理液体（或固体）问题时常用与液相平衡的气相化学势来表示。

考虑纯物质气-液、气-固两相平衡系统，根据两相平衡时化学势相等的关系，可以用气相的化学势来表示液相或固相的化学势。

如果将气体视为理想气体其化学势为O Oln ) (g,), (g,p p RT T p T **+=μμ 与之平衡的液相或固相的化学势为=*), (l ,p T μO Oln ) (g,),(g,p p RT T p T **+=μμ （2—24a ） =*), (s ,p T μO Oln ) (g,), (g,p p RT T p T **+=μμ （2—24b ） 上式中p *是与液(或固)相平衡的蒸气的压力，称为饱和蒸气压，此两相平衡系统中在液体(或固体)上面除了其蒸气外别无他物，这时系统的压力就是蒸气压p *。

3* 外压对蒸气压的影响 如果气相中混有其它惰性气体，这时系统的压力p ＞p *，由于μ(T , p , l) -μ(T , p *, l)=⎰*pp p V (l)d m若以*e p 表示外压为p 时的饱和蒸气压，则利用上面液相化学势表达式可得**pp RT e ln =⎰*p p p V (l)d m ， 如果V m (l)与p 无关则 )((l)ln m ***-=p p RT V p p e （2—25） 由于V m (l)很小，所以在外压增加时，液体(或固体)的蒸气压会略有上升。

二 两相平衡时温度与压力的关系1 Clapeyron 方程 在T 、p 一定的条件下，纯物质两相平衡系统 , βμ=αμ 。

水的相图众所周知，水有三种不同的聚集状态。

在指定的温度、压力下可以互成平衡，即在特定条件下还可以建立其的三相平衡体系。

表５－１的实验数据表明了水在各种平衡条件下，温度和压力的对应关系。

水的相图（图５－２）就是根据这些数据描绘而成的。

表５－１水的压力～温度平衡关系温度（℃）体系的水蒸气压力(kPa)(kPa) (kPa) (kPa)-20 -15 -10-5 0.00989 +20 +100 374--0.1910.2860.4210.6102.338101.32.204x1040.1030.1650.2590.4010.610------1.996x1051.611x1051.145x1046.18x1040.610１.两相线：图中三条曲线分别代表上述三种两相平衡状态，线上的点代表两相平衡的必要条件，即平衡时体系温度与压力的对应关系。

在相图中表示体系（包含有各相）的总组成点称为"物系点"，表示某一相的组成的点称为"相点"，但两者常通称为"状态点"。

OA 线是冰与水气两相平衡共存的曲线，它表示冰的饱和蒸气压与温度的对应关系，称为"升华曲线"，由图可见，冰的饱和蒸气压是随温度的下降而下降。

OC 线是（蒸）气与液（水）两相平衡线，它代表气～液平衡时，温度与蒸气压的对应关系，称为"蒸气压曲线"或"蒸发曲线"。

显然，水的饱和蒸气压是随温度的增高而增大，Ｆ点表示水的正常沸点，即在敞开容器中把水加热到100℃时，水的蒸气压恰好等于外界的压力（），它就开始沸腾。

在压力下液体开始沸腾的温度称其为"正常沸点"。

OB 线是固（冰）与液（水）两相平衡线，它表示冰的熔点随外压变化关系，故称之为冰的"熔化曲线"。

熔化的逆过程就是凝固，因此它又表示水的凝固点随外压变化关系，故也可称为水的"凝固点曲线"。