理论力学复习 运动学自测题

运动学自测题一、概念题（40分）1、点的运动方程的直角坐标形式为t x 4sin 3=，t y 3cos 4=，其中x ，y ，以m 计，t 以s 计，求点在s 3π=t 时的切向加速度和法向加速度大小。

6分2/324s m a t =，2/36s m a n =2、21//O O AB ，21O O AB =，轮心速度v 不变，试画出AB 杆上M 点速度和加速度的方向。

（轮纯滚动）6分A 点速度方向垂直AP ；A 点加速度方向沿AO 1M 点速度和加速度方向与A 相同。

3、偏心轮半径为R ，以匀角速度1ω绕O 轴转动，并带动AB 杆以角速度2ω绕A 轴转动。

在图示瞬时，AB 水平，AD =2R ，O 、C 在同一水平线上。

若以偏心轮轮心C 为动点，动系在AB 杆上，求动点C 的牵连速度。

（并图示牵连速度和科氏加速度方向）。

6分25ωR v e =，方向垂直AC 斜向上。

科氏加速度方向铅垂向下4、曲柄OA 以匀角速0ω绕轴O 转动，取套筒A 为动点，直角杆O 1BC 为动系，求牵连速度和科氏加速度并图示方向。

6分02ωL v e =，方向沿AC 指向O ；204ωL a C =，方向竖直向上5、半径为r 的圆盘在半径为R 的圆弧轨道作纯滚动，中心连线O O ′与铅垂线的夹角为()t Ω=sin 0ϕϕ，其中，0ϕ、Ω为常数。

则求圆盘O 的角速度和角加速度。

6分t r r R ΩΩ−=cos 0ϕω t rr R ΩΩ−−=sin 20ϕα 6、已知在曲柄连杆机构中AO = r ，AB = L ，当OA 与AB 成一水平直线时，杆OA 有角速度ω。

图示AB 杆的速度瞬心，并求连杆AB 的角速度和AB 中点C 的速度需图示方向。

5分B 为速度瞬心。

L r AB ωω=顺时针；C 点速度铅垂向上。

7、半径为R 的圆轮以匀角速度ω 转动，动点M 沿轮缘以相对速度R v r ω=运动 求 M 点的加速度。

第五章运动学基础一、是非题1．已知直角坐标描述的点的运动方程为X=f1（t），y=f2（t），z=f3（t），则任一瞬时点的速度、加速度即可确定。

（）2．一动点如果在某瞬时的法向加速度等于零，而其切向加速度不等于零，尚不能决定该点是作直线运动还是作曲线运动。

（）3．切向加速度只表示速度方向的变化率，而与速度的大小无关。

（）4．由于加速度a永远位于轨迹上动点处的密切面内，故a在副法线上的投影恒等于零。

（）5．在自然坐标系中，如果速度υ=常数，则加速度α=0。

（）6．在刚体运动过程中，若其上有一条直线始终平行于它的初始位置，这种刚体的运动就是平动。

（）7．刚体平动时，若刚体上任一点的运动已知，则其它各点的运动随之确定。

（）8．若刚体内各点均作圆周运动，则此刚体的运动必是定轴转动。

（）9．定轴转动刚体上点的速度可以用矢积表示为v=w×r，其中w是刚体的角速度矢量，r是从定轴上任一点引出的矢径。

（）10、在任意初始条件下，刚体不受力的作用、则应保持静止或作等速直线平动。

（）二、选择题1、已知某点的运动方程为S=a+bt2（S以米计,t以秒计，a、b为常数），则点的轨迹。

①是直线；②是曲线；③不能确定。

2、一动点作平面曲线运动，若其速率不变，则其速度矢量与加速度矢量。

①平行；②垂直；③夹角随时间变化。

3、刚体作定轴转动时，切向加速度为，法向加速度为。

①r×ε②ε×r③ω×v④v×ω4、杆OA绕固定轴O转动，某瞬时杆端A点的加速度α分别如图（a）、（b）、（c）所示。

则该瞬时的角速度为零，的角加速度为零。

①图（a）系统；②图（b）系统；③图（c）系统。

三、填空题1、点在运动过程中，在下列条件下，各作何种运动？①aτ=0，a n=0（答）：；②aτ≠0，a n=0（答）：；③aτ=0，a n≠0（答）：；④aτ≠0，a n≠0（答）：；2、杆O1B以匀角速ω绕O1轴转动，通过套筒A带动杆O2A绕O2轴转动，若O1O2=O2A=L，α=ωt，则用自然坐标表示（以O1为原点，顺时针转向为正向）的套筒A 的运动方程为s=。

《运动学》自测试卷班级：姓名：学号：题号一二三四五六总分得分100阅卷教师一、选择题（每小题3分，共36分）1、点M沿螺线自外向内运动，如图所示，它走过的弧长与时间的一次方成正比，则该点 C 。

A. 越跑越快B. 越跑越慢C. 加速度越来越大D. 加速度越来越小2、点作直线运动，运动方程，x的单位为米，t的单位为秒。

则点在t＝0到t＝7s的时间间隔内走过的路程为 B 。

A．154 mB．262 mC．54 mD．208 m3、绳子的一端绕在滑轮上，另一端与置于水平面上的物块B相连，若物B的运动方程为x=kt2,其中k为常数，轮子半径为R。

则轮缘上A点的加速度的大小为 C 。

A．2kB．C．D．4、每段长度相等的直角折杆在图示的平面内绕O轴转动，角速度为顺时针转向，M点的速度方向如图中的 A 所示。

5、曲柄OA在图示瞬时以ω0绕轴O转动，并带动直角曲杆O1BC在图示平面内运动。

若取套筒A为动点，杆O1BC为动系，则相对速度大小为 C ，牵连速度大小为 B 。

（将正确答案的序号填入划线内）A. dω0B.C. 2dω0D.6、图示直角弯杆OAB以匀角速度ω绕O轴转动，并带动小环M沿OD杆运动。

已知OA=，取小环M为动点，OAB杆为动系，当? = 60o时，M点牵连速度ve的大小为： D 。

A. lω/2B. lωC.lωD. 2lω7、直角杆OAB以角速度ω绕O转动，并带动套在其上的小环M沿固定铅直杆CD 滑动，已知OC＝OA＝a，图示位置OA⊥OC，则该瞬时小环的绝对速度为aω。

8、半径为R的圆轮以匀角速度ω作纯滚动，带动杆AB绕B作定轴转动，D是轮与杆的接触点。

若取轮心C为动点，杆AB为动系，则动点的牵连速度为 C 。

A.，方向垂直ABB. ve = Rω，方向平行BEC.，方向垂直BCD. ve = Rω，方向平行BA9、图示各平面图形的速度分布为：(a) vA＝- vB ，vA不垂直AB，这种速度分布是 B 。

理论⼒学⾃测复习题（全）理论⼒学⾃测复习题静⼒学部分⼀、填空题：（每题2分）1、作⽤于物体上的⼒的三要素是指⼒的、和。

2、当物体处于平衡状态时，作⽤于物体上的⼒系所满⾜的条件称为，此⼒系称为⼒系，并且⼒系中的任⼀⼒称为其余⼒的。

3、⼒的可传性原理适⽤于，加减平衡⼒系公理适⽤于。

4、将⼀平⾯⼒系向其作⽤⾯内任意两点简化，所得的主⽮相等，主矩也相等，且主矩不为零，则此⼒系简化的最后结果为。

5、下列各图为平⾯汇交⼒系所作的⼒多边形，试写出各⼒多边形中⼏个⼒之间的关系。

A、B、C、D、。

6、某物体只受三个⼒的作⽤⽽处于平衡状态，已知此三⼒不互相平⾏，则此三⼒必并且。

7、⼀平⾯⼒系的汇交点为A，B为⼒系作⽤⾯内的另⼀点，且满⾜⽅程∑m B＝0。

若此⼒系不平衡，则其可简化为。

、q2、q3、q4的均匀分布荷载（亦8、长⽅形平板如右图所⽰。

荷载集度分别为q称剪流）作⽤在板上，欲使板保持平衡，则荷载集度间必有如下关系：。

9、平⾯⼀般⼒系平衡⽅程的⼆⼒矩式为，其适⽤条件是。

10、平⾯⼀般⼒系平衡⽅程的三⼒矩式为，其适⽤条件是。

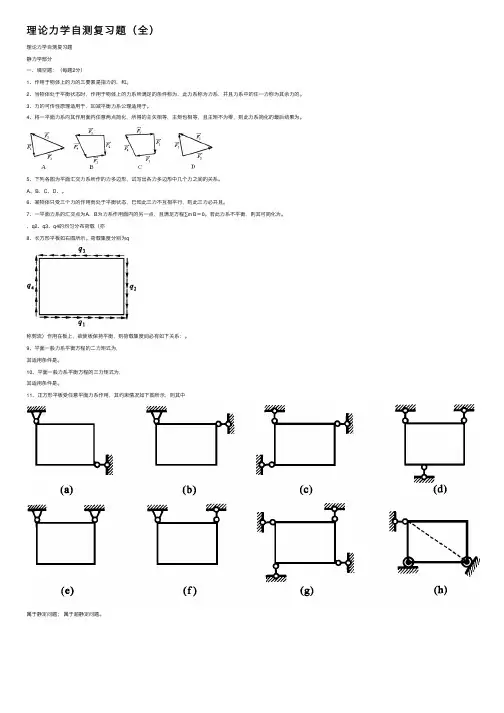
11、正⽅形平板受任意平⾯⼒系作⽤，其约束情况如下图所⽰，则其中属于静定问题；属于超静定问题。

12、已知平⾯平⾏⼒系的五个⼒（下左图⽰）分别为F 1 = 10 N ， F 2 = 4 N ，F 3 = 8 N ，F 4 = 8 N和F 5 = 10 N ，则该⼒系简化的最后结果为。

13、平⾯⼒系如右图，已知F 1 =F 2 = F 3 = F 4 =F ，则：⑴⼒系合⼒的⼤⼩为；⑵⼒系合⼒作⽤线距O 点的距离为（合⼒的⽅向和作⽤位置应在图中画出）。

14、⼆⼒构件是指，作⽤在⼆⼒体上的两个⼒的作⽤线必与相重合。

15、在下图所⽰的平⾯平衡问题中，属于静定问题的有，属于超静定问题的有。

16、置于铅垂⾯内的均质正⽅形簿板（下左⼀图所⽰）重P = 100kN ，与地⾯间的摩擦系数f = 0.5，欲使簿板静⽌不动，则作⽤在点A 的⼒F 的最⼤值应为。

第二篇 运动学一、判断题（每题2分，共10分）1．刚体作平移时，某瞬时体内各点不但有相同的速度，而且有相同的加速度。

（ ） 2．刚体作定轴转动时，垂直于转动轴的同一直线上的各点，不但速度的方向相同而且其加速度的方向也相同。

（ ）3．刚体作平面运动时，绕基点转动的角速度和角加速度与基点的选取有关。

（ ） 4．某刚体作平面运动时，若A 和B 是其平面图形上的任意两点，则速度投影定理AB B AB A v v )()(=永远成立。

（ ）5．因为不同的瞬时，速度瞬心的位置不同，所以刚体的平面运动可以看成是绕一系列的速度瞬心所作的瞬时转动。

（ ） 二、选择题（每题2分，共20分）1．半径为r 的车轮沿固定圆弧面作纯滚动，若某瞬时轮子的角速度为ω，角加速度为α，则轮心O 的切向加速度和法向加速度的大小分别为（ ）。

（A ）2n ωr a o =，αr a o =t ；（B ）2n )(ωr R a o +=，α)(tr R a o +=；（C ）rR r r R v a o+=+=2220n ω，α)(tr R a o +=； （D ）rR r r R v a o+=+=2220n ω，αr a o =t。

题1 题2 题32．圆盘某瞬时以角速度ω，角加速度α绕O 轴转动，其上A ，B 两点的加速度分别为A a 和B a，与半径的夹角分别为θ 和ϕ，若OA =R ，OB =2R，则（ ）。

（A ）a A =a B ，θ=ϕ； （B ） a A =a B ，θ=2ϕ； （C ） a A =2a B ，θ=ϕ； （D ） a A =2a B ，θ=2ϕ。

3．圆盘作定轴转动，若某瞬时其边缘上A ，B ，C 三点的速度，加速度如图所示，则（ ）的运动是不可能的。

（A ）点A ，B ； （B ）点A ，C （C ）点B ，C ； （D ）点A ，B ，C 。

4．在图示机构中，已知OA =3m ，O 1B =4m ，ω=10rad/s ，图示瞬时O 1A =2m ，则该瞬时B 点的速度v B =（ ）m/s 。

一、选择题（将正确答案的序号填入划线内）1、点M 沿螺线自外向内运动，如图所示，它走过的弧长与时间的一次方成正比，则该点 。

A . 越跑越快 B . 越跑越慢 C . 加速度越来越大D . 加速度越来越小2、点作直线运动，运动方程327t t x -=，x 的单位为米，t 的单位为秒。

则点在t ＝0到t ＝7s 的时间间隔内走过的路程为 。

A ．154 m B ．262 m C ．54 m D ．208 m3、绳子的一端绕在滑轮上，另一端与置于水平面上的物块B 相连，若物B 的运动方程为x =kt 2,其中k 为常数，轮子半径为R 。

则轮缘上A 点的加速度的大小为 。

A ．2kB ．21222)/4(R t k C ．212442)/164(R t k k + D ．R t k k /4222+4、每段长度相等的直角折杆在图示的平面内绕O 轴转动，角速度ω为顺时针转向，M 点的速度方向如图中的 所示。

MxABM Ov M ω(A)M Ov ω(B)M Ov M ω(C)M Ov M ω(D)5、曲柄OA 在图示瞬时以ω0绕轴O 转动，并带动直角曲杆O 1BC 在图示平面内运动。

若取套筒A 为动点，杆O 1BC 为动系，则相对速度大小为 ，牵连速度大小为 。

（将正确答案的序号填入划线内） A . d ω0 B . 02ωdC . 2d ω0D . 022ωd6、图示直角弯杆OAB 以匀角速度ω绕O 轴转动，并带动小环M 沿OD 杆运动。

已知OA =l ，取小环M 为动点，OAB 杆为动系，当ϕ = 60º时，M 点牵连速度v e 的大小为： 。

A. l ω/2B. l ωC. 3l ωD. 2l ω7、直角杆OAB 以角速度ω绕O 转动，并带动套在其上的小环M 沿固定铅直杆CD 滑动，已知OC ＝OA ＝a ，图示位置OA ⊥OC ，则该瞬时小环的绝对速度为 。

8、半径为R 的圆轮以匀角速度ω作纯滚动，带动杆AB 绕B 作定轴转动，D 是轮与杆的接触点。

理论力学测试题及答案一、单项选择题（每题2分，共10分）1. 牛顿第一定律描述的是：A. 物体在没有外力作用下的运动状态B. 物体在受到平衡力作用下的运动状态C. 物体在受到非平衡力作用下的运动状态D. 物体在任何力作用下的运动状态答案：A2. 以下哪个不是惯性参考系的特点？A. 牛顿第一定律在其中成立B. 牛顿第二定律在其中成立C. 牛顿第三定律在其中成立D. 物体在其中不受任何力的作用答案：D3. 动量守恒定律适用于：A. 只有重力作用的系统B. 只有弹力作用的系统C. 只有摩擦力作用的系统D. 只有保守力作用的系统答案：D4. 以下哪个是矢量？A. 质量B. 速度C. 时间D. 温度答案：B5. 以下哪个是标量？A. 力B. 位移C. 功D. 速度答案：C二、填空题（每空1分，共10分）1. 牛顿第二定律的数学表达式为：\[ F = ma \]，其中\( F \)代表______，\( m \)代表______，\( a \)代表______。

答案：力；质量；加速度2. 根据牛顿第三定律，作用力和反作用力大小相等，方向______，作用在______。

答案：相反；不同物体上3. 动量的定义是质量与______的乘积。

答案：速度4. 功的定义是力与力的方向上的______的乘积。

答案：位移5. 动能的定义是\( \frac{1}{2}mv^2 \)，其中\( m \)代表______，\( v \)代表______。

答案：质量；速度三、简答题（每题10分，共20分）1. 简述牛顿第二定律的物理意义。

答案：牛顿第二定律表明，物体的加速度与作用在物体上的合外力成正比，与物体的质量成反比，即力是改变物体运动状态的原因。

2. 描述动量守恒定律在碰撞过程中的应用。

答案：在没有外力作用的系统中，两个或多个物体发生碰撞时，碰撞前后系统的总动量保持不变。

这意味着碰撞前后各物体动量的矢量和相等。

四、计算题（每题15分，共30分）1. 一辆质量为1500kg的汽车以20m/s的速度行驶，突然刹车，经过5秒后停止。

运动学自测1、是非题（10分）（1）刚体作定轴转动，则该刚体上总有一直线静止不动。

（ ）（2）动系作定轴转动，动点的科氏加速度一定不为零。

（ ）（3）平面图形作瞬时平动时，其上任意两点的加速度在这两点连线上的投影相等。

（ ）（4）如果刚体上各点的轨迹都是圆，则刚体一定作定轴转动。

（ ）（5）刚体作瞬时平动时，刚体上各点的速度和加速度都相同（ ）（6）两齿轮传动时，两齿轮接触点的速度相同，加速度也相同。

（ ）（7）凡是刚体平移，其上各点的法向加速度始终为零。

（ ）（8）相对速度和牵连角速度均不为零时，并不能肯定科氏加速度为零。

（ ）（9）轮子作平面运动时，如轮上与地面接触点 C 的速度不等于零，即相对地面有滑动，则此时轮子一定不存在瞬时速度瞬心。

（ ）2、选择题（20分）（1）点M 沿螺线自外向内运动，走过的弧长与时间的一次方成正比，则该点（ ）A 、加速度越来越大 B 、加速度越来越小 C 、加速度保持不变 D 、越跑越快（2）图示机构中，O 1A=O 2B ，角速度，角加速度如图示，当O 1A//O 2B 时，有（ ）A B 2121,ααωω==2121,ααωω=≠C D 2121,ααωω≠=2121,ααωω≠≠（3）两个几何尺寸相同、绕线方向不同的绕线轮，在绳的拉动下沿平直固定轨道作纯滚动，设绳端的速度都是v ，在图（a ），（b ），两种情况下，轮的角速度及轮心的速度分别用ω1、v C1与ω2、v C2表示，则（ ）A 且转向相同B 且转向相同 2121,C C v v ==ωω2121,C C v v <<ωωC 且转向相反D 且转向相反2121,C C v v >>ωω2121,C C v v <<ωω（4）圆轮A 做纯滚动，其中其角速度为常数，则轮心A 的加速度大小为（ ）A 、0 B 、 C 、 D 、 2ωr 22ωr Rr +()22ωr R r R R ++（5）偏心轮半径为R ，以匀角速度绕O 轴转动，并带动AB 杆以角速度绕A 轴转1ω2ω动。

一、判断题：1. 在自然坐标系中，如果速度v = 常数，则加速度a = 0。

（ ） 2、在分析点的合成运动时，动点的绝对速度一定不能恒等于零。

( ) 3、对于平动刚体，任一瞬时，各点速度大小相等而方向可以不同。

( )4、在刚体运动过程中，若刚体内任一平面始终与某固定平面平行，则这种运动就是刚体的平面运动。

( )5、加速度d d v t 的大小为d d vt。

（ ） 6、点的法向加速度与速度大小的改变率无关。

( ) 7、速度瞬心的速度为零，加速度也为零。

（ ）8、火车在北半球上自东向西行驶，两条铁轨的磨损程度是相同的。

( ) 9、平动刚体上各点运动状态完全相同。

( )10、某瞬时动点的加速度等于零，则其速度可能为零。

( ) 11、不论点作什么运动，点的位移始终是一个矢量。

( )12、某动点如果在某瞬时法向加速度为零，而切向加速度不为零，则该点一定做直线运动。

（ ）13、在研究点的合成运动时，所选动点必须相对地球有运动（ ）14、已知自然法描述的点的运动方程为S=f(t)，则任意瞬时点的速度、加速度即可确定。

（ ）15、科氏加速度的大小等于相对速度与牵连角速度之大小的乘积的两倍。

（ ） 16、作平面运动的平面图形可以同时存在两个或两个以上的速度瞬时中心。

( ) 17、在自然坐标系中，如果速度v = 常数，则加速度0a 。

（ ） 18、在有摩擦的情况下，全约束力与法向约束力之间的夹角称为摩擦角。

（ ） 19、在分析点的合成运动时，动点的绝对速度一定不能恒等于零。

( ) 20、若动系的牵连运动为定轴转动，则肯定存在哥氏加速度C a。

( )21、在直角坐标系中，如果一点的速度v 在三个坐标上的投影均为常数，其加速度a 必然为零。

（ ）22、刚体平行移动时，其上各点的轨迹一定是相互平行的直线。

二.填空题1.点M 沿螺旋线自外向内运动，如图所示。

它走过的弧长与时间的一次方成正比。

试分析它的加速度越来越__________ (填大或小)2．图所示平板绕AB 轴以匀角速度ω定轴转动，动点M 在板上沿圆槽顺时针运动，运动方程为t v s ⋅=0。

一、选择题（将正确答案的序号填入划线内）1、点M 沿螺线自外向内运动，如图所示，它走过的弧长与时间的一次方成正比，则该点 。

A . 越跑越快 B . 越跑越慢 C . 加速度越来越大D . 加速度越来越小2、点作直线运动，运动方程327t t x -=，x 的单位为米，t 的单位为秒。

则点在t ＝0到t ＝7s 的时间间隔内走过的路程为 。

A ．154 m B ．262 m C ．54 m D ．208 m3、绳子的一端绕在滑轮上，另一端与置于水平面上的物块B 相连，若物B 的运动方程为x =kt 2,其中k 为常数，轮子半径为R 。

则轮缘上A 点的加速度的大小为 。

A ．2kB ．21222)/4(R t kC ．212442)/164(R t k k +D ．R t k k /4222+4、每段长度相等的直角折杆在图示的平面内绕O 轴转动，角速度ω为顺时针转向，M 点的速度方向如图中的 所示。

M(A)(B)(C)(D)5、曲柄OA 在图示瞬时以ω0绕轴O 转动，并带动直角曲杆O 1BC 在图示平面内运动。

若取套筒A 为动点，杆O 1BC 为动系，则相对速度大小为 ，牵连速度大小为 。

（将正确答案的序号填入划线内） A . d ω0 B . 02ωdC . 2d ω0D . 022ωd6、图示直角弯杆OAB 以匀角速度ω绕O 轴转动，并带动小环M 沿OD 杆运动。

已知OA =l ，取小环M 为动点，OAB 杆为动系，当ϕ = 60º时，M 点牵连速度v e 的大小为： 。

A. l ω/2B. l ωC. 3l ωD. 2l ω7、直角杆OAB 以角速度ω绕O 转动，并带动套在其上的小环M 沿固定铅直杆CD 滑动，已知OC ＝OA ＝a ，图示位置OA ⊥OC ，则该瞬时小环的绝对速度为 。

8、半径为R 的圆轮以匀角速度ω作纯滚动，带动杆AB 绕B 作定轴转动，D 是轮与杆的接触点。

理论力学I —2自测试卷一答案一、填空题(每题5分)1、在图示机构中，杆B O A O 21//=，杆D O C O 32//=，且，，，若杆以角速度cm 201=A O cm 402=C O cm 30==MD CM A O 1rad/s 3=ω匀速转动，则点的速度大小为______D 120__cm/s ，M 点的加速度大小为___360_____cm/s 2题一.1图 题一.2图2、半径为R ，质量为的均质圆盘在其自身平内作平面运动。

在图示位置时，若已知图形上、m A B 两点的速度方向如图示。

°=45α，且知B 点的速度大小为，则圆轮的动能为_____B v 1632B mv ____________________。

3、质量为、半径为m R 的匀质圆轮，在力偶的作用下沿粗糙水平直线作纯滚动。

已知轮心的加速度为，则圆轮所受的摩擦力大小为_a ma _____；力偶矩M 的大小为_____mRa 5.1________。

题一.3图 题一.4图4、小车以速度沿直线运动，车上一轮以角速度v ω转动，若以轮缘上一点M 为动点，车厢为动坐标，则M 点的科氏加速度大小为_________0__________。

二、计算题(本题10分)图示机构由五根连杆与固定边AB 形成正六边形。

已知各杆长及AB 边长均为L ，角φ也已知，受三力作用。

试用虚位移原理求机构平衡时，力P 与力Q 之间的关系。

解：以中点为原点建立坐标系，则各主动力作用点的相关坐标为AB ϕϕϕsin 2cos 5.0cos 5.0L x L L x L L x Q D C =+=−−=取虚位移ϕδ，相应坐标的变分为ϕϕϕϕϕϕδcos 2δδsin δδsin δ⋅=⋅−=⋅=L x L x L x Q D C根据虚功原理0δ)cos sin (2δδδ=−=−−ϕϕϕL Q P x Q x P x P Q D C最后3tan ==ϕP Q三、计算题(本题10分)质量为m 的平板A 置于光滑的水平面上, 相同质量且半径为r 的均质圆柱B 可沿斜面无滑动的滚动。

理论力学复习题及答案理论力学复习题及答案理论力学是物理学中的一门基础课程，它研究物体的运动规律和相互作用。

在学习理论力学的过程中，复习题是非常重要的一环，它可以帮助我们巩固知识，提高解题能力。

本文将为大家提供一些理论力学的复习题及答案，希望能对大家的学习有所帮助。

1. 什么是理论力学？答案：理论力学是研究物体的运动规律和相互作用的科学。

它包括牛顿力学、拉格朗日力学和哈密顿力学等分支，通过数学方法描述物体的运动和受力情况。

2. 牛顿第一定律是什么？答案：牛顿第一定律，也称为惯性定律，指出一个物体如果没有外力作用，将保持静止或匀速直线运动的状态。

3. 牛顿第二定律的公式是什么？答案：牛顿第二定律可以用公式F=ma表示，其中F表示物体所受的合力，m表示物体的质量，a表示物体的加速度。

根据牛顿第二定律，物体的加速度与所受的力成正比，与质量成反比。

4. 什么是动量？答案：动量是物体运动的一种性质，它等于物体的质量乘以速度。

动量的守恒是指在一个孤立系统中，物体的总动量在没有外力作用下保持不变。

5. 什么是功？答案：功是力对物体运动所做的功率乘以时间的积分。

它表示力在物体运动过程中所做的总功。

6. 什么是势能？答案：势能是物体由于位置或状态而具有的能量。

常见的势能有重力势能、弹性势能和化学势能等。

7. 什么是角动量？答案：角动量是物体绕某一轴旋转时的动量，它等于物体的质量乘以速度与距离轴的距离的乘积。

8. 什么是刚体？答案：刚体是指物体在运动过程中，各部分之间的相对位置保持不变的物体。

刚体的运动可以分为平动和转动两种。

9. 什么是牛顿万有引力定律？答案：牛顿万有引力定律是描述物体之间引力相互作用的定律。

它表明任何两个物体之间的引力与它们的质量成正比，与它们之间的距离的平方成反比。

10. 什么是开普勒定律？答案：开普勒定律是描述行星运动规律的三个定律。

第一定律称为椭圆轨道定律，第二定律称为面积定律，第三定律称为调和定律。

运动学1、图示滚子传送带中滚子做匀角速转动，已知滚子的直径m 2.0=d ，转速为min /r 2.0=n 。

试求钢板A 运动的速度和加速度，并求滚子上与钢板接触点P 的加速度。

2、飞轮边缘上的点按t s 4πsin4=的规律运动，飞轮的半径cm 20=r 。

试求时间s t 10=该点的速度和加速度。

3、图示曲柄滑道机构中，曲柄长r OA =，并以匀角速度ω绕O 轴转动。

装在水平杆上的滑槽DE 与水平线成60角。

试求当曲柄与水平轴的交角分别为0=ϕ，30时，杆BC 的速度。

4、图示凸轮推杆机构中，偏心圆凸轮的偏心距e OC =，半径e r 3=。

若凸轮以匀角速度ω绕轴O 作逆时针转动，且推杆AB 的延长线通过轴O ，试求当OC 与CA 垂直时杆AB 的速度。

5、铰接四边形机构，cm B O A O 1021==, AB O O =21且A O 1杆以匀角速度s rad /2=ω绕1O 轴转动。

求060=θ时，CD 杆的速度。

6、刨床急回机构如图所示。

曲柄OA 的角速度为ω，通过套筒A 带动摇杆B O 1摆动。

已知OA =r ，l OO =1，求当OA 水平时B O 1的角速度1ω。

7、半圆形凸轮半径为R ,已知凸轮的平动速度为v , 加速度为a ,杆AB 被凸轮推起. 求杆AB 的速度和加速度。

该瞬时凸轮中心 C 与 A 点的连线与水平线之夹角为ϕ。

8、图示曲柄滑道机构，圆弧轨道的半径R ＝OA ＝10 cm ，已知曲柄绕轴 O 以匀速n ＝120 r/min 转动，求当030=ϕ时滑道BCD 的速度和加速度。

9、曲柄OA 长为R ，通过滑块A 使导杆BC 和DE 在固定滑道内上下滑动，当030=ϕ时，OA 杆的角速度为ω、角加速度为ε。

试求该瞬时点B 的速度与加速度。

10、OA 由L 形推杆BCD 推动而在图面内绕O 轴转动。

假定推杆以匀速u 沿水平方向运动，试用合成运动的方法，求OA 杆的角速度和角加速度。

理论力学考试试题理论力学考试试题理论力学作为物理学的基础学科，是研究物体运动规律的重要分支。

在物理学考试中，理论力学常常是一个重要的考点。

下面我们来看一些关于理论力学的考试试题。

1. 一个质点在一维直线上运动，其位移与时间的关系可以表示为：$x(t) =A\sin(\omega t + \phi)$，其中A、$\omega$和$\phi$都是常数。

试问该质点的速度与时间的关系是什么？解析：我们知道速度是位移对时间的导数。

所以，通过对位移函数求导，我们可以得到速度与时间的关系。

对$x(t)$关于$t$求导，得到$v(t) =A\omega\cos(\omega t + \phi)$。

因此，该质点的速度与时间的关系是$v(t) = A\omega\cos(\omega t + \phi)$。

2. 一个质点在一个平面上做匀速圆周运动，半径为R。

试问该质点的加速度大小是多少？解析：在匀速圆周运动中，质点的速度大小是恒定的，但方向会不断改变。

由于加速度是速度对时间的导数，所以在匀速圆周运动中，质点的加速度大小是恒定的，等于速度大小除以转动周期。

转动周期T等于2πR/v，其中v是质点的速度大小。

因此，该质点的加速度大小是v/T，即v/(2πR/v)，即v²/R。

3. 一个质点在一个斜面上滑动，斜面的角度为θ。

试问质点的加速度大小是多少？解析：在斜面上滑动的质点，受到重力和斜面的支持力两个力的作用。

我们可以将重力分解为平行于斜面和垂直于斜面的两个分力。

平行于斜面的分力为mg*sinθ，垂直于斜面的分力为mg*cosθ。

由于斜面的支持力与垂直于斜面的分力相等且反向，所以质点的净受力为mg*si nθ。

根据牛顿第二定律，质点的加速度等于净受力除以质量，即a = (mg*sinθ)/m，即a = g*sinθ。

4. 一个质点在一个半径为R的圆环上做匀速圆周运动，试问质点的角速度是多少？解析：在匀速圆周运动中，质点的角速度等于速度大小除以半径。