2016-2017年北京市通州区初三第一学期期中

2016-2017学年北京市通州区九年级（上）期中数学试卷一、选择题（每小题3分，共30分）1．（3分）已知3x=4y，则的值为（）A．B．C．D．2．（3分）函数y=x2﹣1中自变量x的取值范围（）A．x≠1 B．x=1 C．x＞1 D．全体实数3．（3分）相似三角形的概念是（）A．对应角相等、对应边成比例的两个三角形B．两角分别相等的两个三角形C．三边对应成比例的两个三角形D．两边对应成比例且夹角相等的两个三角形4．（3分）下列图形中有可能与图相似的是（）A．B．C．D．5．（3分）在平面直角坐标系xOy中，二次函数y=ax2的图象经过点A、B、O，则下列对二次项系数a判断正确的是（）A．a＞0 B．a=0 C．a＜0 D．a≥06．（3分）黄金矩形的宽与长的比值更接近于（）A．3.14 B．2.71 C．0.62 D．0.577．（3分）一次函数y=ax2+c在平面直角坐标系xOy中的图象如图所示，则可判断（）A．a＞0，c＞0 B．a＞0，c＜0 C．a＜0，c＞0 D．a＜0，c＜08．（3分）已知点A（﹣1，﹣2），B关于抛物线y=a（x﹣1）2的对称轴对称，则点B的坐标为（）A．（1，﹣2）B．（﹣1，2）C．（2，﹣2）D．（3，﹣2）9．（3分）过点A（﹣3，2），B（﹣1，2），C（﹣1，﹣1）的抛物线有（）A．0条 B．1条 C．2条 D．至少3条10．（3分）如图，线段AC和直线l分别垂直线段AB于点A，B．点P是线段AB 上的一个动点，由A移动到B，连接CP，过点P作PD⊥CP交l于点D，设线段AP的长为x，BD的长为y，在下列图象中，能大致表示y与x之间函数关系的是（）A．B．C．D．二、填空题（共6小题，每小题4分，共24分）11．（4分）如果=，那么=．12．（4分）如图，直线a∥b∥c，度量线段AB≈1.89，BC≈3.80，DE≈2.02，则线段EF的长约为．13．（4分）如图，线段AB=2，过点B作BD⊥AB，使BD=AB，连接AD，在AD 上截取DE=DB．在AB上截取AC=AE．那么线段AC的长为．14．（4分）如图，点B，D在∠A的一条边上，点C，E在∠A的另一条边上，且DE∥BC，请你写出图中能够成立的一组比例式．15．（4分）二次函数y=x2﹣bx+c的图象如图所示，根据图象信息，求出关于x 的方程x2﹣bx+c=0的解为．16．（4分）如图，在反比例函数y=（x＞0）的图象上，有点P1，P2，P3，P4…P n （n为正整数，且n≥1）．它们的横坐标依次为1，2，3，4…n（n为正整数，且n≥1），分别过这些点作x轴与y轴的垂线，连接相邻两点，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3…S n﹣1（n为正整数，且n≥2），那么S2+S3+S4+…S7=．三、解答题（共46分）17．（4分）用配方法把二次函数y=x2+4x﹣5化成y=a（x﹣h）2+k的形式并写出顶点坐标．18．（4分）如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．（1）求证：△CBD∽△CAB；（2）若D是AC中点，CD=3，求BC的长．19．（4分）已知反比例函数y=的图象经过点P（﹣1，﹣1）．（1）求此函数的表达式；（2）画出此函数在第一象限内的图象．（3）根据函数图象写出此函数的一条性质．20．（4分）如图，四边形ABCD∽四边形EFGH，连接相应的对角线AC，EG．（1）求证△ABC∽△EFG；（2）若=，直接写出四边形ABCD与四边形EFGH的面积比为．21．（6分）已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：（1）求此函数的表达式；（2）画出此函数的示意图．22．（6分）如图，在平面直角坐标系xOy中，过坐标原点O的直线l与双曲线y=相交于点A（m，3）．（1）求直线l的表达式；（2）过动点P（n，0）且垂于x轴的直线与l及双曲线的交点分别为B，C，当点B位于点C上方时，写出n的取值范围．23．（6分）若平面直角坐标系中的点作如下平移：沿x轴方向平移的数量为a （向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．（1）若动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为，点G的坐标为．（2）若动点P从坐标原点出发，先按照“平移量”m平移到B，再按照“平移量”n 平移到C；最后按照“平移量”q平移回到点O．当△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，请你直接写出“平移量”m，n，q．（3）在（1）、（2）的前提下，请你在平面直角坐标系中画出△OBC与△MNG．24．（6分）已知二次函数y=mx 2+（3m +1）x +3．（1）当m 取何值时，此二次函数的图象与x 轴有两个交点；（2）当抛物线y=mx 2+（3m +1）x +3与x 轴两个交点的横坐标均为整数，且m 为正整数时，求此抛物线的表达式．25．（6分）在△ABC 中，D 是BC 边上的点（不与点B 、C 重合），连结AD ．（1）如图1，当点D 是BC 边上的中点时，S △ABD ：S △ACD = ；（2）如图2，当AD 是∠BAC 的平分线时，若AB=m ，AC=n ，求S △ABD ：S △ACD 的值（用含m ，n 的代数式表示）（3）如图3，AD 平分∠BAC ，延长AD 到E ，使得AD=DE ，连接BE ，如果AC=2，AB=4，S △BDE =6，那么S △ABC = ．2016-2017学年北京市通州区九年级（上）期中数学试卷参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）已知3x=4y，则的值为（）A．B．C．D．【解答】解：∵3x=4y，∴=．故选：B．2．（3分）函数y=x2﹣1中自变量x的取值范围（）A．x≠1 B．x=1 C．x＞1 D．全体实数【解答】解：函数y=x2﹣1中自变量x的取值范围全体实数．故选：D．3．（3分）相似三角形的概念是（）A．对应角相等、对应边成比例的两个三角形B．两角分别相等的两个三角形C．三边对应成比例的两个三角形D．两边对应成比例且夹角相等的两个三角形【解答】解：A、对应角相等、对应边成比例的两个三角形相似，正确；B、两角对应相等的两个三角形相似，错误；C、三边对应成比例的两个三角形相似，错误；D、两边对应成比例且夹角相等的两个三角形相似，错误；故选：A．4．（3分）下列图形中有可能与图相似的是（）A．B．C．D．【解答】解：原图为四边形，与之相似的只可能是四边形，故选：B．5．（3分）在平面直角坐标系xOy中，二次函数y=ax2的图象经过点A、B、O，则下列对二次项系数a判断正确的是（）A．a＞0 B．a=0 C．a＜0 D．a≥0【解答】解：∵二次函数y=ax2的图象过点A，B、O，∴ax2≥0，∵x=0时，y=0；x≠0时，y≠0，∴a＞0．故选：A．6．（3分）黄金矩形的宽与长的比值更接近于（）A．3.14 B．2.71 C．0.62 D．0.57【解答】黄金矩形的宽与长的比=≈0.618，四选项中更接近于这一比值的是0.62，7．（3分）一次函数y=ax2+c在平面直角坐标系xOy中的图象如图所示，则可判断（）A．a＞0，c＞0 B．a＞0，c＜0 C．a＜0，c＞0 D．a＜0，c＜0【解答】解：由函数图象可知，抛物线的开口向上，顶点（0，c）在y轴的负半轴，∴a＞0，c＜0，故选：B．8．（3分）已知点A（﹣1，﹣2），B关于抛物线y=a（x﹣1）2的对称轴对称，则点B的坐标为（）A．（1，﹣2）B．（﹣1，2）C．（2，﹣2）D．（3，﹣2）【解答】解：∵y=a（x﹣1）2，∴对称轴为x=1，∵点A、B关于对称轴对称，∴A、B两点到对称轴的距离相等，且纵坐标相同，∴B点横坐标为x=2×1﹣（﹣1）=3，纵坐标为﹣2，∴B（3，﹣2），故选：D．9．（3分）过点A（﹣3，2），B（﹣1，2），C（﹣1，﹣1）的抛物线有（）A．0条 B．1条 C．2条 D．至少3条【解答】解：∵B（﹣1，2），C（﹣1，﹣1），一个横坐标对应2个函数值，∴过点A（﹣3，2），B（﹣1，2），C（﹣1，﹣1）的抛物线有0条．10．（3分）如图，线段AC和直线l分别垂直线段AB于点A，B．点P是线段AB 上的一个动点，由A移动到B，连接CP，过点P作PD⊥CP交l于点D，设线段AP的长为x，BD的长为y，在下列图象中，能大致表示y与x之间函数关系的是（）A．B．C．D．【解答】解：∵AC⊥AB，BD⊥AB，PD⊥CP，∴∠A=∠B=∠CPD=90°，∴∠C+∠APC=∠APC+∠BPD=90°，∴∠C=∠BPD，∴△ACP∽△BPD，∴，设AC=a，AB=b，则BP=b﹣x，即=，∴y=﹣+x，∴y是x的二次函数，故选：C．二、填空题（共6小题，每小题4分，共24分）11．（4分）如果=，那么=．【解答】解：=，那么=，故答案为：．12．（4分）如图，直线a∥b∥c，度量线段AB≈1.89，BC≈3.80，DE≈2.02，则线段EF的长约为 4.04．【解答】解：∵a∥b∥c，∴=，即=，解得，EF≈4.04，故答案为：4.04．13．（4分）如图，线段AB=2，过点B作BD⊥AB，使BD=AB，连接AD，在AD上截取DE=DB．在AB上截取AC=AE．那么线段AC的长为﹣1．【解答】解：∵AB=2，BD=AB，∴BD=1，由勾股定理得：AD=，∵DE=BD=1，∴AC=AE=AD﹣DE=﹣1．故答案为：﹣1．14．（4分）如图，点B，D在∠A的一条边上，点C，E在∠A的另一条边上，且DE∥BC，请你写出图中能够成立的一组比例式（答案不唯一）．【解答】解：∵DE∥BC，∴；故答案为：（答案不唯一）．15．（4分）二次函数y=x2﹣bx+c的图象如图所示，根据图象信息，求出关于x 的方程x2﹣bx+c=0的解为﹣1或5．【解答】解：由图象可知，抛物线y=x2﹣bx+c与x轴的交点为（﹣1，0）和（5，0），∴方程x2﹣bx+c=0的解为x=﹣1或5，故答案为﹣1或5．16．（4分）如图，在反比例函数y=（x＞0）的图象上，有点P1，P2，P3，P4…P n （n为正整数，且n≥1）．它们的横坐标依次为1，2，3，4…n（n为正整数，且n≥1），分别过这些点作x轴与y轴的垂线，连接相邻两点，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3…S n﹣1（n为正整数，且n≥2），那么S2+S3+S4+…S7=．【解答】解：当x=1时，P1的纵坐标为4，当x=2时，P2的纵坐标为2，当x=3时，P 3的纵坐标为，当x=4时，P4的纵坐标为1，当x=5时，P5的纵坐标为，…则S1=×1×（4﹣2）=1=2﹣1；S2=×1×（2﹣）==1﹣；S3=×1×（﹣1）==﹣；S4=×1×（1﹣）==﹣；…S n=﹣；∴S2+S3+S4+…+S7=1﹣+﹣+…+﹣=1﹣=，故答案为：．三、解答题（共46分）17．（4分）用配方法把二次函数y=x2+4x﹣5化成y=a（x﹣h）2+k的形式并写出顶点坐标．【解答】解：y=x2+4x﹣5=x2+4x+4﹣9=（x+2）2﹣9，∴二次函数y=x2+4x﹣5的顶点坐标为（﹣2，﹣5）．18．（4分）如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．（1）求证：△CBD∽△CAB；（2）若D是AC中点，CD=3，求BC的长．【解答】（1）证明：∵∠CBD=∠A，∠C是公共角，∴△CBD∽△CAB；（2）解：∵D是AC中点，CD=3，∴AC=2AD=6．∵△CBD∽△CAB，∴=，即BC2=AC•CD=6×3=18，∴BC=3．19．（4分）已知反比例函数y=的图象经过点P（﹣1，﹣1）．（1）求此函数的表达式；（2）画出此函数在第一象限内的图象．（3）根据函数图象写出此函数的一条性质．【解答】解：（1）∵反比例函数y=的图象经过点P（﹣1，﹣1）．∴﹣1=，解得k=1．∴此函数的表达式为y=；（2）函数在第一象限内的图象如图：（2）函数在第一象限，y随x的增大而减小．20．（4分）如图，四边形ABCD∽四边形EFGH，连接相应的对角线AC，EG．（1）求证△ABC∽△EFG；（2）若=，直接写出四边形ABCD与四边形EFGH的面积比为．【解答】解：（1）∵四边形ABCD∽四边形EFGH，∴，∠B=∠F，∴△ABC∽△EFG；（2）=（）2=，故答案为：．21．（6分）已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：（1）求此函数的表达式；（2）画出此函数的示意图．【解答】解：（1）把（﹣2，5）、（1，﹣4）、（2，﹣3）代入y=ax2+bx+c得，解得，所以抛物线解析式为y=x2﹣2x﹣3；（2）如图，22．（6分）如图，在平面直角坐标系xOy中，过坐标原点O的直线l与双曲线y=相交于点A（m，3）．（1）求直线l的表达式；（2）过动点P（n，0）且垂于x轴的直线与l及双曲线的交点分别为B，C，当点B位于点C上方时，写出n的取值范围﹣1＜n＜0或n＞1．【解答】解：（1）∵双曲线y=过点A（m，3），∴3=3m，解得：m=1，∴点A的坐标为（1，3）．设直线l的表达式为y=kx，将（1，3）代入y=kx中，3=k，∴直线l的表达式为y=3x．（2）由正、反比例函数的对称性可知：直线l与双曲线y=的两交点坐标为（﹣1，﹣3）和（1，3）．观察函数图象可知：当﹣1＜x＜0或x＞1时，一次函数图象在双曲线的上方，∴n的取值范围为﹣1＜n＜0或n＞1．故答案为：﹣1＜n＜0或n＞1．23．（6分）若平面直角坐标系中的点作如下平移：沿x轴方向平移的数量为a （向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．（1）若动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为（3，1），点G 的坐标为（4，3）．（2）若动点P从坐标原点出发，先按照“平移量”m平移到B，再按照“平移量”n 平移到C；最后按照“平移量”q平移回到点O．当△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，请你直接写出“平移量”m{4，0}或{4，0}或{﹣4，0}或{﹣4，0} ，n{2，4}或{2，﹣4}或{﹣2，4}或{2，4} ，q{﹣6，﹣4}或{﹣6，4}或{6，4}或{6，﹣4} ．（3）在（1）、（2）的前提下，请你在平面直角坐标系中画出△OBC与△MNG．【解答】解：（1）动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为（3，1），点G的坐标为（4，3），故答案为（3，1），（4，3）．（2）△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，①当△OB1C1∽△MNG时，m{4，0}，n{2，4}，q{﹣6，﹣4}，②当△OB1C2∽△MNG时，m{4，0}，n{2，﹣4}，q{﹣6，4}，③当△OB2C3∽△MNG时，m{﹣4，0}，n{﹣2，4}，q{6，4}，④当△OB2C4∽△MNG时，m{﹣4，0}，n{2，4}，q{6，﹣4}，故答案为{4，0}或{4，0}或{﹣4，0}或{﹣4，0}；{2，4}或{2，﹣4}或{﹣2，4}或{2，4}；{﹣6，﹣4}或{﹣6，4}或{6，4}或{6，﹣4}．（3）如图所示△OB1C1，△OB1C2，△OB2C3，△OB2C4都满足条件．24．（6分）已知二次函数y=mx2+（3m+1）x+3．（1）当m取何值时，此二次函数的图象与x轴有两个交点；（2）当抛物线y=mx2+（3m+1）x+3与x轴两个交点的横坐标均为整数，且m为正整数时，求此抛物线的表达式．【解答】解：（1）由题意可知，△=b2﹣4ac=（3m+1）2﹣4m×3=（3m﹣1）2＞0，解得：m≠，∵二次函数的图象与x轴有两个交点，∴m≠0，∴当m≠且m≠0时，此二次函数的图象与x轴有两个交点；（2）有求根公式，得：x==，∴x1=﹣3，x2=﹣，∵抛物线与x 轴两个交点的横坐标均为整数，且m 为正整数， ∴m=1，∴抛物线的解析式为：y=x 2+4x +3；25．（6分）在△ABC 中，D 是BC 边上的点（不与点B 、C 重合），连结AD ． （1）如图1，当点D 是BC 边上的中点时，S △ABD ：S △ACD = 1：1 ；（2）如图2，当AD 是∠BAC 的平分线时，若AB=m ，AC=n ，求S △ABD ：S △ACD 的值（用含m ，n 的代数式表示）（3）如图3，AD 平分∠BAC ，延长AD 到E ，使得AD=DE ，连接BE ，如果AC=2，AB=4，S △BDE =6，那么S △ABC = 9 ．【解答】解：（1）过A 作AE ⊥BC 于E ， ∵点D 是BC 边上的中点， ∴BD=DC ，∴S ABD ：S △ACD =（×BD ×AE ）：（×CD ×AE ）=1：1， 故答案为：1：1；（2）过D 作DE ⊥AB 于E ，DF ⊥AC 于F ， ∵AD 为∠BAC 的角平分线，∴DE=DF，∵AB=m，AC=n，∴S ABD：S△ACD=（×AB×DE）：（×AC×DF）=m：n；（3）∵AD=DE，∴由（1）知：S△ABD ：S△EBD=1：1，∵S△BDE=6，∴S△ABD=6，∵AC=2，AB=4，AD平分∠CAB，∴由（2）知：S△ABD ：S△ACD=AB：AC=4：2=2：1，∴S△ACD=3，∴S△ABC=3+6=9，故答案为：9．。

2016—2017学年度第一学期期中测试卷九年级(初三)英语听力材料、参考答案及评分意见一、听力测试 (每小题1分，共25分)A）请听下面6段对话。

每段对话后有一小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都将会有10秒钟的时间回答有关小题和阅读下一小题。

每段对话读两遍。

1. M: How do you learn English so well, Lin Tao?W: I learn English from a foreigner who is my neighbor.2. M: Excuse me. Do you know where I can get some food?W: Yes. Go to the top floor. You can find many restaurants there.3. W: Do you remember me, Bill?M: Oh, wow. You’re Kate, aren’t you? You used to be very quiet. But you are outgoing now.4. M : I wonder why you bought such an expensive dress.W : Expensive? Maybe, but it’s fascinating.5. W: What bad weather!M: It’s always rainy these days. I really miss the sunshine.6.W: We’re going to Yunnan.M: Sounds great. This is the time of the Water Festival.B）请听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前,你将有时间阅读各小题，每小题5秒钟；听完后，各小题给出5秒钟的作答时间。

北京市通州区九年级上学期期中物理试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）对生活中物理量的认识，下列数据最接近实际的是（）A . 教室里课桌的高度约为75dmB . 一节新干电池的电压约为36VC . 九年级学生100m短跑的成绩约为15sD . 我们正常步行的速度大约是12m/s2. （2分） (2016九上·东港期中) 甲、乙两种物质，它们的质量之比是3：1，吸收热量之比是2：1，那么它们升高的温度之比和比热容之比分别可能是（）A . 2：3 10：1B . 3：2 1：10C . 3：5 5：2D . 5：3 2：53. （2分）在“用电流表、电压表小灯泡测电阻”的实验中，滑动变阻器不能起到的作用是（）A . 改变电路中的电流B . 改变被测电阻的阻值C . 改变被测电阻两端的电压D . 保护电路4. （2分） (2020九上·嘉陵期末) 如图甲所示电路，闭合开关后，两个电流表指针偏转均为图乙所示，则通过L1与L2的电流分别是（）A . 2．2A 0．44AB . 1．76A 0．44AC . 0．44A 1．76AD . 0．42A 2．2A5. （2分）如图是四冲程汽油机工作的示意图，其中不是靠惯性完成的是（）A .B .C .D .6. （2分）通常情况下，下列用品中属于绝缘体的是（）A . 玻璃杯B . 金属汤勺C . 大地D . 盐水7. （2分）(2019·辽阳) 酿酒是人类神奇的发明，如图是将谷物倒入锅中熬制酒料的过程。

下列说法正确的是（）A . 用火种引燃木柴的过程与钻木取火的原理相同B . 灶台下木柴燃烧的过程，将内能转化成了化学能C . 锅能向酒料传递热量，是因为锅的温度高于酒料的温度D . 熬制过程中需要不断地搅拌，这是为了通过做功的方式增加物体内能8. （2分） (2017九上·山西期中) 在用电压表测某电阻两端的电压时，若选用0—3V的量程，测得的电压值为2.2V；若使用0—15V的量程，测得的电压值为2.0V，那么该电阻两端的电压大小应该是（）A . 2.2VB . 2.0ＶC . 2.1VD . 都正确9. （2分） (2017九上·简阳期中) 将肉片直接放入热油锅里爆炒，会将肉炒焦或炒糊，大大失去鲜味．厨师预先将适量的淀粉拌入肉片中，再放到热油锅里爆炒，炒出的肉片既鲜嫩味美又营养丰富，对此现象说法不正确的是（）A . 在炒肉片过程中，肉片的温度升高，内能增加B . 附着在肉片外的淀粉糊有效防止了肉片里水分的蒸发C . 在炒肉片过程中，肉片内能增加主要通过做功实现的D . 附近能闻到肉香体现了分子在不停地做无规则的运动10. （2分）(2013·盐城) 小明将酒精气体传感器、电阻R与电压表组成如图所示电路，闭合开关，将传感器逐渐靠近装有酒精的杯口上方，发现电压表示数逐渐增大，此过程中（）A . 通过传感器的电流逐渐减小B . 传感器两端的电压逐渐增大C . 传感器的电阻逐渐减小D . 传感器的电阻逐渐增大11. （2分） (2018九上·太原期中) 小明根据如表提供的几种物质的比热容得出了以下四个结论，其中正确的是（）A . 一杯水比一桶煤油的比热容小B . 液体一定比固体的比热容大C . 比热容只和物质种类有关D . 水吸热或放热的本领较强，常用作冷却剂12. （2分）(2020·东莞模拟) 如图所示，是创新小组设计的汽车油量显示仪的电路原理图，其中电源电压恒为 6V，定值电阻 R0 为5Ω，油量表实质量程是 0～3V 的电压表。

北京市通州区第三中学九年级上册期中试卷检测题一、初三数学一元二次方程易错题压轴题（难）1．阅读与应用：阅读1：a，b为实数，且a＞0，b＞0，因为()2≥0，所以a﹣2+b≥0，从而a+b≥2(当a＝b时取等号)．阅读2：若函数y＝x+(m＞0，x＞0，m为常数)，由阅读1结论可知：x+≥2，所以当x＝，即x＝时，函数y＝x+的最小值为2．阅读理解上述内容，解答下列问题：问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为2(x+)，求当x＝时，周长的最小值为；问题2：汽车的经济时速是汽车最省油的行驶速度，某种汽车在每小时70～110公里之间行驶时(含70公里和110公里)，每公里耗油()L．若该汽车以每小时x公里的速度匀速行驶，1h的耗油量为yL．(1)求y关于x的函数关系式(写出自变量x的取值范围)；(2)求该汽车的经济时速及经济时速的百公里耗油量．【答案】问题1：2，8；问题2：(1)y=；(2)10.【解析】【分析】（1）利用题中的不等式得到x+=4，从而得到x=2时，周长的最小值为8；（2）根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可，经济时速就是耗油量最小的形式速度．【详解】(1)∵x+≥2＝4，∴当x＝时，2(x+)有最小值8．即x＝2时，周长的最小值为8；故答案是：2；8；问题2：，当且仅当，即x ＝90时，“＝”成立，所以，当x ＝90时，函数取得最小值9， 此时，百公里耗油量为，所以，该汽车的经济时速为每小时90公里，经济时速的百公里耗油量为10L ． 【点睛】本题考查了配方法及反比例函数的应用，最值问题，解题的关键是读懂题目提供的材料，易错点是了解“耗油总量=每公里的耗油量×行驶的速度”，难度中等偏上．2．机械加工需用油进行润滑以减小摩擦，某企业加工一台设备润滑用油量为90kg ，用油的重复利用率为60%，按此计算，加工一台设备的实际耗油量为36kg ，为了倡导低碳，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关． （1）甲车间通过技术革新后，加工一台设备润滑油用油量下降到70kg ，用油的重复利用率仍然为60%，问甲车间技术革新后，加工一台设备的实际油耗量是多少千克？ （2）乙车间通过技术革新后，不仅降低了润滑油用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1kg ，用油的重复利用率将增加1.6%，例如润滑用油量为89kg 时，用油的重复利用率为61.6%． ①润滑用油量为80kg ，用油量的重复利用率为多少？②已知乙车间技术革新后实际耗油量下降到12kg ，问加工一台设备的润滑用油量是多少千克？用油的重复利用率是多少？ 【答案】（1）28（2）①76%②75，84% 【解析】试题分析：（1）直接利用加工一台设备润滑油用油量下降到70kg ，用油的重复利用率仍然为60%，进而得出答案；（2）①利用润滑用油量每减少1kg ，用油的重复利用率将增加1.6%，进而求出答案； ②首先表示出用油的重复利用率，进而利用乙车间技术革新后实际耗油量下降到12kg ，得出等式求出答案．试题解析：（1）根据题意可得：70×（1﹣60%）=28（kg ）； （2）①60%+1.6%（90﹣80）=76%； ②设润滑用油量是x 千克，则 x{1﹣[60%+1.6%（90﹣x ）]}=12， 整理得：x 2﹣65x ﹣750=0， （x ﹣75）（x+10）=0， 解得：x 1=75，x 2=﹣10（舍去）， 60%+1.6%（90﹣x ）=84%，答：设备的润滑用油量是75千克，用油的重复利用率是84%． 考点：一元二次方程的应用3．如图，∠ AOB ＝90°，且点A ，B 分别在反比例函数1k y x =（x ＜0），2ky x=（x ＞0）的图象上，且k1，k2分别是方程x2－x－6＝0的两根．（1）求k1，k2的值；（2）连接AB，求tan∠OBA的值．【答案】（1）k1＝－2，k2＝3．（2）tan∠OBA＝63．【解析】解：（1）∵k1，k2分别是方程x2－x－6＝0的两根，∴解方程x2－x－6＝0，得x1＝3，x2＝－2．结合图像可知：k1＜0，k2＞0，∴k1＝－2，k2＝3．（2）如图，过点A作AC⊥x轴于点C，过点B作BD⊥y轴于点D．[来源:学&科&网Z&X&X&K]由（1）知，点A，B分别在反比例函数2yx=-（x＜0），3yx=（x＞0）的图象上，∴S△ACO＝12×2-＝1 ，S△ODB＝12×3＝32．∵∠ AOB＝90°，∴∠ AOC＋∠ BOD＝90°，∵∠ AOC＋∠ OAC＝90°，∴∠ OAC＝∠ BOD．又∵∠ACO＝∠ODB＝90°，∴△ACO∽△ODB．∴SSACOODB∆∆＝2OAOB⎛⎫⎪⎝⎭＝23，∴OAOB6OAOB6∴在Rt△AOB中，tan∠OBA＝OAOB6．4．已知x1、x2是关于x的﹣元二次方程（a﹣6）x2+2ax+a=0的两个实数根．（1）求a的取值范围；（2）若（x1+1）（x2+1）是负整数，求实数a的整数值．【答案】（1）a≥0且a≠6;（2）a的值为7、8、9或12．【解析】 【分析】（1）根据一元二次方程的定义及一元二次方程的解与判别式之间的关系解答即可；（2）根据根与系数的关系可得x 1+x 2=﹣2-6a a ，x 1x 2=-6a a ，由（x 1+1）（x 2+1）=x 1x 2+x 1+x 2+1=﹣66a - 是是负整数，即可得66a -是正整数．根据a 是整数，即可求得a 的值2． 【详解】（1）∵原方程有两实数根，∴260(2)4(6)*0a a a a -≠⎧⎨∆=-->⎩， ∴a≥0且a≠6．（2）∵x 1、x 2是关于x 的一元二次方程（a ﹣6）x 2+2ax+a=0的两个实数根， ∴x 1+x 2=﹣26a a -，x 1x 2=6aa -， ∴（x 1+1）（x 2+1）=x 1x 2+x 1+x 2+1=-6a a ﹣26a a -+1=﹣66a -． ∵（x 1+1）（x 2+1）是负整数， ∴﹣66a -是负整数，即66a -是正整数． ∵a 是整数，∴a ﹣6的值为1、2、3或6， ∴a 的值为7、8、9或12． 【点睛】本题考查了根的判别式和根与系数的关系，能根据根的判别式和根与系数的关系得出关于a 的不等式是解此题的关键．5．已知关于x 的一元二次方程（x ﹣3）（x ﹣4）﹣m 2=0． （1）求证：对任意实数m ，方程总有2个不相等的实数根； （2）若方程的一个根是2，求m 的值及方程的另一个根．【答案】（1）证明见解析；（2）m 2，方程的另一个根是5． 【解析】 【分析】（1）先把方程化为一般式，利用根的判别式△=b 2-4ac 证明判断即可；（2）根据方程的根，利用代入法即可求解m 的值，然后还原方程求出另一个解即可. 【详解】 （1）证明：∵（x ﹣3）（x ﹣4）﹣m 2=0， ∴x 2﹣7x+12﹣m 2=0，∴△=（﹣7）2﹣4（12﹣m 2）=1+4m 2， ∵m 2≥0， ∴△＞0，∴对任意实数m ，方程总有2个不相等的实数根； （2）解：∵方程的一个根是2， ∴4﹣14+12﹣m 2=0，解得m=±，∴原方程为x 2﹣7x+10=0，解得x=2或x=5，即m 的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b 2-4ac ＞0时，方程有两个不相等的实数根； 当△=b 2-4ac=0时，方程有两个相等的实数根； 当△=b 2-4ac ＜0时，方程没有实数根.二、初三数学 二次函数易错题压轴题（难）6．在平面直角坐标系中，二次函数22y ax bx =+-的图象与x 轴交于点(4,0)A -，(1,0)B ，与y 轴交于点C ．（1）求此抛物线的解析式；（2）点P 是抛物线22y ax bx =+-上的任意一点，过点P 作x 轴的垂线PD ，直线PD交直线AC 于点D ．①是否存在点P ，使得PAC ∆的面积是ABC ∆面积的45？若存在，求出点P 的坐标；若不存在，请说明理由．②点Q 是坐标平面内的任意一点，若以O ，C ，Q ，D 为顶点的四边形是菱形时，请直接写出点Q 的坐标． 【答案】(1)213222y x x =+- (2)①存在，点P的坐标为(2-+-，(2--+，(2,3)--②1816,55Q ⎫⎛-- ⎪⎝⎭，2(2,1)Q -，355Q ⎛- ⎝⎭，455Q ⎛- ⎝⎭【解析】 【分析】(1)将(4,0)A -，(1,0)B 两点坐标代入解析式中求解即可； (2)①先求出△PAC 的面积为4，再求出直线AC 的解析式为122y x =--．设点P 的横坐标为(t ,213222t t +-)，利用21442∆∆∆=-=⋅=+=PAC PDC PDA S S S OA PD t t 即可求解； ②先设出D 点坐标，然后再按对角线分成三种情况讨论即可求解． 【详解】解：(1)由题意得,将(4,0)A -，(1,0)B 两点坐标代入解析式中：1642020a b a b --=⎧⎨+-=⎩，解得：1232a b ⎧=⎪⎪⎨⎪=⎪⎩． ∴此抛物线的解析式为213222y x x =+-， 故答案为213222y x x =+-． (2)①存在点P ，使得PAC ∆的面积是ABC ∆面积的45．理由如下： 作出如下所示示意图：∵点(4,0)A -，(1,0)B ， ∴4OA =，5AB =， 令0x =，则2y =-， ∴(0,2)C -，∴2OC =， ∴1152522ABC S AB OC ∆=⋅=⨯⨯=， ∴445545PAC ABC S S ∆∆==⨯=， 设直线AC 的解析式为y mx n =+，则有402m n n -+=⎧⎨=-⎩，解得：122m n ⎧=-⎪⎨⎪=-⎩，∴直线AC 的解析式为122y x =--． 设点P 的横坐标为t ，则其纵坐标为213222t t +-， 即213,222P t t t ⎫⎛+- ⎪⎝⎭． ∵PD x ⊥轴，则点D 的坐标为1,22t t ⎫⎛-- ⎪⎝⎭． ∴2213112222222PD t t t t t ⎫⎛=+----=+ ⎪⎝⎭． ∵22111424222PAC PDC PDA S S S OA PD t t t t ∆∆∆=-=⋅=⨯⨯+=+． ∴244t t +=，即2440t t +-=或2440t t ++=，解得：1222t =-+，2222t =--，32t =-．∴点P 的坐标为(222,12)-+-，(222,12)--+，(2,3)--， 故答案为：(222,12)-+-或(222,12)--+或(2,3)--． ②分类讨论：情况一：当OC 为菱形的对角线时，此时DO=DC ，即D 点在线段OC 的垂直平分线， ∴D 点坐标(-2,-1)，将△OCD 沿y 轴翻折，此时四边形ODCQ 为菱形，故此时Q 点坐标为(2,-1)，如下图一所示，情况二：当OQ 为对角线时，DO=DQ ，如下图二所示，DQ=OC=OD=2，设D 点坐标1,22⎛⎫-- ⎪⎝⎭x x ，则EO=-x ，DE=122x +，在Rt △EDO 中，由勾股定理可知：EO²+ED²=DO²， 故221(2)42++=x x ，解得80(),5舍==-x x ，此时Q 点坐标为816,55⎛⎫-- ⎪⎝⎭，情况三：当OD 为对角线时，OC=OQ=2，如下图三所示：设D 点坐标1,22⎛⎫-- ⎪⎝⎭m m ，则EO=|m|，DE=122m +，QE=2-(122m +)=12m ， 在Rt △QDO 中，由勾股定理可知：QE²+EO²=QO²， 故221()()42+=m m ，解得124545,==-m m ，此时Q 点坐标为4525,⎛⎫- ⎪ ⎪⎝⎭或4525,55⎛⎫- ⎪ ⎪⎝⎭， 综上所述，Q 点的坐标为1816,55Q ⎫⎛-- ⎪⎝⎭，2(2,1)Q -，34525,55Q ⎫⎛-⎪ ⎝⎭，44525,Q ⎫⎛-⎪ ⎝⎭．故答案为1816,55Q ⎫⎛-- ⎪⎝⎭，2(2,1)Q -，34525,Q ⎫⎛-⎪ ⎝⎭，44525,Q ⎫⎛-⎪ ⎝⎭．【点睛】本题考查了待定系数法求二次函数解析式，三角形的面积问题，菱形的存在性问题等，属于综合题，具有一定的难度，熟练掌握二次函数的图形及性质是解决本题的关键．7．如图所示，在平面直角坐标系中，抛物线2(0)y ax bx c a =++≠的顶点坐标为()3, 6C ，并与y 轴交于点()0, 3B ，点A 是对称轴与x 轴的交点．(1)求抛物线的解析式;(2)如图①所示, P 是抛物线上的一个动点,且位于第一象限，连结BP 、AP ,求ABP ∆的面积的最大值;(3)如图②所示，在对称轴AC 的右侧作30ACD ∠=交抛物线于点D ,求出D 点的坐标;并探究:在y 轴上是否存在点Q ,使60CQD ∠=?若存在，求点Q 的坐标;若不存在，请说明理由．【答案】（1）21233y x x =-++；（2）当92n =时，PBA S ∆最大值为818；（3）存在，Q 点坐标为((0,-或，理由见解析【解析】 【分析】(1)利用待定系数法可求出二次函数的解析式；(2)求三角形面积的最值，先求出三角形面积的函数式.从图形上看S △PAB=S △BPO+S △APO-S △AOB,设P 21,233n n n ⎛⎫-++ ⎪⎝⎭求出关于n 的函数式，从而求S △PAB 的最大值. (3) 求点D 的坐标，设D 21,233t t t ⎛⎫-++ ⎪⎝⎭,过D 做DG 垂直于AC 于G,构造直角三角形，利用勾股定理或三角函数值来求t 的值即得D 的坐标;探究在y 轴上是否存在点Q ,使60CQD ∠=?根据以上条件和结论可知∠CAD=120°,是∠CQD 的2倍，联想到同弧所对的圆周角和圆心角，所以以A 为圆心，AO 长为半径做圆交y 轴与点Q,若能求出这样的点，就存在Q 点. 【详解】解：()1抛物线顶点为()3,6∴可设抛物线解析式为()236y a x =-+将()0,3B 代入()236y a x =-+得396a =+ 13a ∴=-∴抛物线()21363y x =--+，即21233y x x =-++ ()2连接,3, 3OP BO OA ==，PBA BPO PAO ABO S S S S ∆∆∆∆=+- 设P 点坐标为21,233n n n ⎛⎫-++⎪⎝⎭1133222BPO x S BO P n n ∆=== 2211119323322322PAO y S OA P n n n n ∆⎛⎫==-++=-++ ⎪⎝⎭11933222ABO S OA BO ∆==⨯⨯=22231991919813222222228PBAS n n n n n n ∆⎛⎫⎛⎫=+-++-=-+=--+ ⎪ ⎪⎝⎭⎝⎭ ∴当92n =时，PBA S ∆最大值为818()3存在，设点D 的坐标为21,233t t t ⎛⎫-++ ⎪⎝⎭过D 作对称轴的垂线，垂足为G , 则213,6233DG t CG t t ⎛⎫=-=--++ ⎪⎝⎭30ACD ∠=2DG DC ∴=在Rt CGD ∆中有222243CG CD DG DG DG DG =+=-=)21336233t t t ⎛⎫-=--++ ⎪⎝⎭化简得(1133303t t ⎛⎫---= ⎪⎝⎭13t ∴=（舍去），2333t =+∴点D(333+3,33AG GD ∴==连接AD ，在Rt ADG ∆中229276AD AG GD ++=6,120AD AC CAD ∴==∠=Q ∴在以A 为圆心，AC 为半径的圆与y 轴的交点上此时1602CQD CAD ∠=∠=设Q 点为(0,m), AQ 为A 的半径则AQ ²=OQ ²+OA ², 6²=m ²+3²即2936m +=∴1233,33m m ==-综上所述，Q 点坐标为()()0,330,33-或 故存在点Q ，且这样的点有两个点.【点睛】(1)本题考查了利用待定系数法求二次函数解析式，根据已知条件选用顶点式较方便； (2)本题是三角形面积的最值问题，解决这个问题应该在分析图形的基础上，引出自变量，再根据图形的特征列出面积的计算公式，用含自变量的代数式表示面积的函数式,然后求出最值.(3)先求抛物线上点的坐标问题及符合条件的点是否存在.一般先假设这个点存在，再根据已知条件求出这个点.8．已知抛物线2(0)y ax bx c a =++≠过点(0,2)A -． （1）若点(2,0)-也在该抛物线上，请用含a 的关系式表示b ；（2）若该抛物线上任意不同两点()11,M x y 、()22,N x y 都满足：当120x x <<时，()()12120x x y y --<；当120x x <<时，()()12120x x y y -->；若以原点O 为圆心，OA 为半径的圆与抛物线的另两个交点为B 、C （点B 在点C 左侧），且ABC ∆有一个内角为60，求抛物线的解析式；（3）在（2）的条件下，若点P 与点O 关于点A 对称，且O 、M 、N 三点共线，求证：PA 平分MPN ∠．【答案】（1）21b a =-；（2）22y x =-；（3）见解析.【解析】 【分析】（1）把点()0,2-、()2,0-代入抛物线解析式，然后整理函数式即可得到答案． （2）根据二次函数的性质可得出抛物线的对称轴为y 轴、开口向上，进而可得出0b =，由抛物线的对称性可得出ABC ∆为等腰三角形，结合其有一个60︒的内角可得出ABC ∆为等边三角形，设线段BC 与y 轴交于点D ，根据等边三角形的性质可得出点C 的坐标，再利用待定系数法可求出a 值，此题得解；（3）由（1）的结论可得出点M 的坐标为1(x ，212)x -+、点N 的坐标为2(x ，222)x -+，由O 、M 、N 三点共线可得出212x x =-，进而可得出点N 及点'N 的坐标，由点A 、M 的坐标利用待定系数法可求出直线AM 的解析式，利用一次函数图象上点的坐标特征可得出点'N 在直线PM 上，进而即可证出PA 平分MPN ∠． 【详解】解：（1）把点()0,2-、()2,0-分别代入，得2420c a b c =-⎧⎨-+=⎩． 所以21b a =-．（2），如图1，当120x x <<时，()()12120x x y y --<，120x x ∴-<，120y y ->， ∴当0x <时，y 随x 的增大而减小；同理：当0x >时，y 随x 的增大而增大，∴抛物线的对称轴为y 轴，开口向上，0b ∴=．OA 为半径的圆与拋物线的另两个交点为B 、C ， ABC ∴∆为等腰三角形，又ABC ∆有一个内角为60︒， ABC ∴∆为等边三角形．设线段BC 与y 轴交于点D ，则BD CD =，且30OCD ∠=︒， 又2OB OC OA ===，·303CD OC cos ∴=︒=，·301OD OC sin =︒=． 不妨设点C 在y 轴右侧，则点C 的坐标为(3，1)． 点C 在抛物线上，且2c =-，0b =，321a ∴-=，1a ∴=，∴抛物线的解析式为22y x =-．（3）证明：由（1）可知，点M 的坐标为1(x ，212)x -，点N 的坐标为2(x ，222)x -．如图2，直线OM 的解析式为()110y k x k =≠．O 、M 、N 三点共线，10x ∴≠，20x ≠，且22121222x x x x --=，121222x x x x ∴-=-， ()1212122x x x x x x -∴-=-，122x x ∴=-，即212x x =-， ∴点N 的坐标为12(x -，2142)x -． 设点N 关于y 轴的对称点为点'N ，则点'N 的坐标为12(x ，2142)x -． 点P 是点O 关于点A 的对称点，24OP OA ∴==，∴点P 的坐标为()0,4-．设直线PM 的解析式为24y k x =-，点M 的坐标为1(x ，212)x -，212124x k x ∴-=-，21212x k x +∴=，∴直线PM 的解析式为21124x y x x +=-．()222111221111224224·42x x x x x x x +-+-==-， ∴点'N 在直线PM 上，PA ∴平分MPN ∠． 【点睛】本题考查了待定系数法求一次（二次）函数解析式、二次函数的性质、等边三角形的性质以及一次（二次）函数图象上点的坐标特征，解题的关键是：（1）利用二次函数图象上点的坐标特征求出a 、b 满足的关系式；（2）①利用等边三角形的性质找出点C 的坐标；②利用一次函数图象上点的坐标特征找出点'N 在直线PM 上．9．如图①抛物线y ＝ax 2+bx +4（a ≠0）与x 轴，y 轴分别交于点A （﹣1，0），B （4，0），点C 三点．（1）试求抛物线的解析式；（2）点D （3，m ）在第一象限的抛物线上，连接BC ，BD ．试问，在对称轴左侧的抛物线上是否存在一点P ，满足∠PBC ＝∠DBC ？如果存在，请求出点P 点的坐标；如果不存在，请说明理由；（3）点N 在抛物线的对称轴上，点M 在抛物线上，当以M 、N 、B 、C 为顶点的四边形是平行四边形时，请直接写出点M 的坐标． 【答案】（1）y ＝﹣x 2+3x +4；（2）存在．P （﹣34，1916）．（3）1539(,)24M --21139(,)24M - 3521(,)24M【解析】【分析】（1）将A,B,C三点代入y＝ax2+bx+4求出a,b,c值，即可确定表达式；（2）在y轴上取点G，使CG＝CD＝3，构建△DCB≌△GCB，求直线BG的解析式，再求直线BG与抛物线交点坐标即为P点，（3）根据平行四边形的对边平行且相等，利用平移的性质列出方程求解，分情况讨论.【详解】解：如图：（1）∵抛物线y＝ax2+bx+4（a≠0）与x轴，y轴分别交于点A（﹣1，0），B（4，0），点C三点．∴4016440a ba b-+=⎧⎨++=⎩解得13ab=-⎧⎨=⎩∴抛物线的解析式为y＝﹣x2+3x+4．（2）存在．理由如下：y＝﹣x2+3x+4＝﹣（x﹣32）2+254．∵点D（3，m）在第一象限的抛物线上，∴m＝4，∴D（3，4），∵C（0，4）∵OC＝OB，∴∠OBC＝∠OCB＝45°．连接CD，∴CD∥x轴，∴∠DCB＝∠OBC＝45°，∴∠DCB＝∠OCB，在y轴上取点G，使CG＝CD＝3，再延长BG交抛物线于点P，在△DCB和△GCB中，CB＝CB，∠DCB＝∠OCB，CG＝CD，∴△DCB≌△GCB（SAS）∴∠DBC＝∠GBC．设直线BP解析式为y BP＝kx+b（k≠0），把G（0，1），B（4，0）代入，得k＝﹣14，b＝1，∴BP解析式为y BP＝﹣14x+1．y BP＝﹣14x+1，y＝﹣x2+3x+4当y＝y BP时，﹣14x+1＝﹣x2+3x+4，解得x1＝﹣34，x2＝4（舍去），∴y＝1916，∴P（﹣34，1916）．（3）1539 (,)24M--21139 (,) 24M-3521 (,) 24M理由如下，如图B(4，0),C(0，4) ，抛物线对称轴为直线32x=，设N(32，n)，M(m, ﹣m2+3m+4)第一种情况：当MN与BC为对边关系时，MN∥BC,MN=BC,∴4-32=0-m，∴m=52-∴﹣m2+3m+4=39 4 -,∴1539 (,)24M--；或∴0-32=4-m，∴m=11 2∴﹣m2+3m+4=39 4 -,∴21139 (,) 24M-；第二种情况：当MN与BC为对角线关系，MN与BC交点为K,则K(2,2)，∴322 2m∴m=5 2∴﹣m2+3m+4=21 4∴3521(,)24M 综上所述，当以M 、N 、B 、C 为顶点的四边形是平行四边形时，点M 的坐标为1539(,)24M -- 21139(,)24M - 3521(,)24M .【点睛】本题考查二次函数与图形的综合应用，涉及待定系数法，函数图象交点坐标问题，平行四边形的性质，方程思想及分类讨论思想是解答此题的关键.10．如图，在平面直角坐标系中，抛物线2(0)y ax bx c a =++≠交x 轴于点(2,0),(3,0)A B -，交y 轴于点C ，且经过点(6,6)D --，连接,AD BD ．（1）求该抛物线的函数关系式；（2）△ANM 与ABD ∆是否相似?若相似，请求出此时点M 、点N 的坐标；若不存在，请说明理由；（3）若点P 是直线AD 上方的抛物线上一动点(不与点,A D 重合)，过P 作//PQ y 轴交直线AD 于点Q ，以PQ 为直径作⊙E ，则⊙E 在直线AD 上所截得的线段长度的最大值等于 ．（直接写出答案）【答案】（1）2113442y x x =--+；（2）点M （0，32）、点N （34，0）或点M （0，32），N （-3，0）或点M （-1，32）、点N （-3，0）或N （14-，0）、M （-1，32）；（3）QH 有最大值，当x=2-时，其最大值为125． 【解析】 【分析】（1）用交点式函数表达式得：y=a （x-2）（x+3），将点D 坐标代入上式即可求解； （2）分∠MAB=∠BAD 、∠MAB=∠BDA ，两种大情况、四种小情况，分别求解即可； （3）根据题意，利用二次函数的性质和三角函数，QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+=23392055x x --+，即可求解． 【详解】解：（1）用交点式函数表达式得：y=a （x-2）（x+3）， 将点D 坐标代入上式并解得：14a =-， 故函数的表达式为：2113442y x x =--+…①， 则点C （0，32）；（2）由题意得：AB=5，AD=10，BD=， ①∠MAN=∠ABD 时， （Ⅰ）当△ANM ∽△ABD 时， 直线AD 所在直线的k 值为34，则直线AM 表达式中的k 值为34-，则直线AM 的表达式为：3(2)4y x =--，故点M （0，32），AD AB AM AN =，则AN=54，则点N （34，0）； （Ⅱ）当△AMN ∽△ABD 时，同理可得：点N （-3，0），点M （0，32），故点M （0，32）、点N （34，0）或点M （0，32），N （-3，0）；②∠MAN=∠BDA 时，（Ⅰ）△ABD ∽△NMA 时，∵AD ∥MN ，则tan ∠MAN=tan ∠BDA=12，AM ：y=12-（x-2），则点M （-1，32）、点N （-3，0）； （Ⅱ）当△ABD ∽△MNA 时， AD BD AM AN =，即3535=， 解得：AN=94， 故点N （14-，0）、M （-1，32）； 故：点M （-1，32）、点N （-3，0）或N （14-，0）、M （-1，32）； 综上，点M （0，32）、点N （34，0）或点M （0，32），N （-3，0）或点M （-1，32）、点N （-3，0）或N （14-，0）、M （-1，32）； （3）如图所示，连接PH ，由题意得：tan ∠PQH=43，则cos ∠PQH=35， 则直线AD 的表达式为：y=3342x -， 设点P （x ，2113442x x --+），则点Q （x ，3342x -）， 则QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+ =23392055x x --+ =2312(2)205x -++， ∵3020-<，故QH有最大值，当x=2时，其最大值为125．【点睛】本题考查的是二次函数综合应用，涉及到一次函数、圆的基本知识，解直角三角形，相似三角形的判定和性质，其中（2）需要分类求解共四种情况，避免遗漏．三、初三数学旋转易错题压轴题（难）11．综合与实践问题情境在一节数学活动课上，老师带领同学们借助几何画板对以下题目进行了研究.如图1，MN是过点A的直线，点C为直线MN外一点，连接AC，作∠ACD=60°，使AC=DC，在MN上取一点B，使∠DBN=60°．观察发现（1）根据图1中的数据，猜想线段AB、DB、CB之间满足的数量关系是；（2）希望小组认真思考后提出一种证明方法：将CB所在的直线以点C为旋转中心，逆时针旋转60°，与直线MN交于点E，即可证明（1）中的结论. 请你在图1中作出线段CE，并根据此方法写出证明过程；实践探究（3）奋进小组在继续探究的过程中，将点C绕点A逆时针旋转，他们发现当旋转到图2和图3的位置时，∠DBN=120°，线段AB、BD、CB的大小发生了变化，但是仍然满足一定的数量关系，请你直接写出这两种关系：在图2中，线段AB、DB、CB之间满足的数量关系是；在图3中，线段AB、DB、CB之间满足的数量关系是；提出问题（4）智慧小组提出一个问题：若图3中BC⊥CD于点C时，BC=2，则AC为多长？请你解答此问题.【答案】（1）AB+DB=CB；（2）见解析；（3）AB－DB=CB；DB－AB=CB；（4）23【解析】【分析】（1）根据图中数据直接猜想AB+DB=CB（2）在射线AM上一点E，使得∠ECB=60°，证明△ACE≌△DCB，推出EB=CB从而得出（1）中的结论；（3）利用旋转的性质和线段的和差关系以及全等三角形的性质得出线段关系；（4）过点C作∠BCE=60º，边CE与直线MN交于点E，设AC与BD交于点F.证明△ACE≌△DCB，得出BC=EC，结合△ECB为等边三角形，得出∠ECA=90°，在Rt△AEC中根据边长计算出AC的长度.【详解】综合与实践（1）AB+DB=CB（2）线段CE如图所示.证明：∵∠ECB=∠ACD=60º，∴∠2+∠ACB=∠1+∠ACB，∴∠2=∠1.∵∠ACD=∠DBN=60º, ∠ABD+∠DBN=180º，∴∠ABD+∠ACD=180º，∴在四边形ACDB中，∠CAB+∠3=180º.∵∠CAB+∠4=180º，∴∠4=∠3.又∵AC=DC，∴△ACE≌△DCB（ASA）∴EA=BD，EC=BC.又∵∠ECB=60°，∴△ECB为等边三角形,∴EB=CB.而EB=EA+AB=DB+AB,∴CB=DB+AB.（3） AB－DB=CB；DB－AB=CB；（4）证明：如图，过点C作∠BCE=60º，边CE与直线MN交于点E，设AC与BD交于点F.∵∠DCA=60º∴∠ECB+∠BCA=∠DCA+∠BCA即∠ECA=∠BCD∵∠DBN=120º∴∠DBA=60º又∵∠AFB=∠DFC∴∠EAF=∠BDC又∵AC=DC∴△ACE≌△DCB（ASA）∴BC=EC∴△ECB为等边三角形∴∠CEB=60º∵BC⊥CD∴∠ECA=∠BCD=90º∴在Rt△AEC中，∠CAE=30º∵BC=2，EC=BC∴AC=EC·tan60º= 23【点睛】本题考查了全等三角形的判定和性质，旋转的性质，根据题中条件适当添加辅助线构造全等三角形，利用全等的性质得出线段关系是本题的关键.12．如图，△ABC和△DEC都是等腰三角形，点C为它们的公共直角顶点，连接AD、BE，F 为线段AD的中点，连接CF．（1）如图1，当D点在BC上时，BE与CF的数量关系是__________；（2）如图2，把△DEC绕C点顺时针旋转90°，其他条件不变，问（1）中的关系是否仍然成立？请说明理由；（3）如图3，把△DEC绕C点顺时针旋转一个钝角，其他条件不变，问（1）中的关系是否仍然成立？如成立，请证明；如果不成立，请写出相应的正确的结论并加以证明．【答案】（1）BE=2CF；（2）（1）中的关系是仍然成立，理由见解析；（3）（1）中的关系是仍然成立，理由见解析.【解析】试题分析：（1）根据“SAS”证明△ACD≌△BCE，可得AD=BE，又因为AD=2CF，从而BE=2CF；（2）由点F是AD中点，可得AD=2DF，从而AC= 2DF+CD，又由△ABC和△CDE是等腰直角三角形，可知BC=2DF+CE，所以BE= 2（DF+CE），CF= DF+CD，从而BE=2CF；（3）延长CF至G使FG=CF，即：CG=2CF，可证△CDF≌△GAF，再证明△BCE≌△ACG，从而BE=CG=2CF成立.解：（1）∵△ABC是等腰直角三角形，∴AC=BC，∵△CDE是等腰直角三角形，∴CD=CE，在△ACD和△BCE中，，∴△ACD≌△BCE，∴AD=BE，在Rt△ACD中，点F是AD中点，∴AD=2CF，∴BE=2CF，故答案为BE=2CF；（2）（1）中的关系是仍然成立，理由：∵点F是AD中点，∴AD=2DF，∴AC=AD+CD=2DF+CD，∵△ABC和△CDE是等腰直角三角形，∴AC=BC，CD=CE，∴BC=2DF+CE，∴BE=BC+CE=2DF+CE+CE=2（DF+CE），∵CF=DF+CD=DF+CD，∴BE=2CF；（3）（1）中的关系是仍然成立，理由：如图3，延长CF至G使FG=CF，即：CG=2CF，∵点F是AD中点，∴AF=DF，在△CDF和△GAF中，，∴△CDF≌△GAF，∴AG=CD=CE，∠CDF=∠GAF，∴∠CAG=∠CAD+∠GAF=∠CAD+∠ADC=180°﹣∠ACD，∵∠ACB=∠DCE=90°，∴∠BCE=360°﹣∠ACB﹣∠DCE﹣∠ACD=180°﹣∠ACD，∴∠CAG=∠BCE，连接BE，在△BCE和△ACG中，，∴△BCE≌△ACG，∴BE=CG=2CF，即：BE=2CF．点睛：本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质和旋转的性质，考查了学生综合运用知识的能力，熟练掌握旋转的性质、全等三角形的判定与性质是解答本题的关键．13．已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．（1）如图1，求证：△CDE是等边三角形．（2）设OD＝t，①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．②求t为何值时，△DEB是直角三角形（直接写出结果即可）．【答案】(1)见解析;(2)①见解析;②t＝2或14.【解析】【分析】（1）由旋转的性质得到∠DCE=60°，DC=EC，即可得到结论；（2）①当6＜t＜10时，由旋转的性质得到BE=AD，于是得到C△DBE=BE+DB+DE=AB+DE=4+DE，根据等边三角形的性质得到DE=CD，由垂线段最短得到当CD⊥AB时，△BDE的周长最小，于是得到结论；②存在，当点D与点B重合时，D，B，E不能构成三角形；当0≤t＜6时，由旋转的性质得到∠ABE=60°，∠BDE＜60°，求得∠BED=90°，根据等边三角形的性质得到∠DEB=60°，求得∠CEB=30°，求得OD=OA-DA=6-4=2=t；当6＜t＜10时，此时不存在；当t＞10时，由旋转的性质得到∠DBE=60°，求得∠BDE＞60°，于是得到t=14．【详解】（1）∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；（2）①存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝，∴△BDE的最小周长＝CD+4＝；②存在，∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意；当0≤t＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴t＝2；当6＜t＜10时，由∠DBE＝120°＞90°，∴此时不存在；当t＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴t＝14，综上所述：当t＝2或14时，以D、E、B为顶点的三角形是直角三角形．【点睛】本题考查了旋转的性质，等边三角形的判定和性质，三角形周长的计算，直角三角形的判定，熟练掌握旋转的性质是解题的关键．14．两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为______和位置关系为______；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．【答案】（1）相等，垂直．（2）成立，证明见解析；（3）成立，结论是FH=FG，FH⊥FG．【解析】试题分析：（1）证AD=BE，根据三角形的中位线推出FH=12AD，FH∥AD，FG=12BE，FG∥BE，即可推出答案；（2）证△ACD≌△BCE，推出AD=BE，根据三角形的中位线定理即可推出答案；（3）连接BE、AD，根据全等推出AD=BE，根据三角形的中位线定理即可推出答案．试题解析：（1）解：∵CE=CD，AC=BC，∠ECA=∠DCB=90°，∴BE=AD，∵F是DE的中点，H是AE的中点，G是BD的中点，∴FH=12AD，FH∥AD，FG=12BE，FG∥BE，∴FH=FG，∵AD⊥BE，∴FH⊥FG，故答案为相等，垂直．（2）答：成立，证明：∵CE=CD，∠ECD=∠ACD=90°，AC=BC，∴△ACD≌△BCE∴AD=BE ，由（1）知：FH=12AD ，FH ∥AD ，FG=12BE ，FG ∥BE ， ∴FH=FG ，FH ⊥FG ， ∴（1）中的猜想还成立．（3）答：成立，结论是FH=FG ，FH ⊥FG ．连接AD ，BE ，两线交于Z ，AD 交BC 于X ，同（1）可证∴FH=12AD ，FH ∥AD ，FG=12BE ，FG ∥BE ， ∵三角形ECD 、ACB 是等腰直角三角形，∴CE=CD ，AC=BC ，∠ECD=∠ACB=90°，∴∠ACD=∠BCE ， 在△ACD 和△BCE 中AC BC ACD BCE CE CD ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ACD ≌△BCE ，∴AD=BE ，∠EBC=∠DAC ，∵∠DAC+∠CXA=90°，∠CXA=∠DXB ，∴∠DXB+∠EBC=90°，∴∠EZA=180°﹣90°=90°，即AD ⊥BE ，∵FH ∥AD ，FG ∥BE ，∴FH ⊥FG ，即FH=FG ，FH ⊥FG ，结论是FH=FG ，FH ⊥FG.【点睛】运用了等腰直角三角形的性质、全等三角形的性质和判定、三角形的中位线定理，旋转的性质等知识点的理解和掌握，能熟练地运用这些性质进行推理是解此题的关键．15．已知ABC ∆是边长为4的等边三角形，点D 是射线BC 上的动点，将AD 绕点A 逆时针方向旋转60得到AE，连接DE．(1).如图，猜想ADE∆是_______三角形；（直接写出结果）(2).如图，猜想线段CA、CE 、CD之间的数量关系，并证明你的结论；(3).①当BD=___________时，30DEC∠=；（直接写出结果）②点D在运动过程中，DEC∆的周长是否存在最小值？若存在．请直接写出DEC∆周长的最小值；若不存在，请说明理由．【答案】（1）等边三角形；（2）AC CD CE+=，证明见解析；（3）①BD为2或8时，30DEC∠=；②最小值为423+【解析】【分析】（1）根据旋转的性质得到,60AD AE DAE=∠=，根据等边三角形的判定定理解答；（2）证明ABD ACE∆≅∆，根据全等三角形的性质得到BD CE=，结合图形计算即可；（3）①分点D在线段BC上和点D在线段BC的延长线上两种情况，根据直角三角形的性质解答；②根据ABD ACE∆≅∆得到CE BD=，根据垂线段最短解答．【详解】解：（1）由旋转变换的性质可知，,60AD AE DAE=∠=，ADE∴∆是等边三角形，故答案为等边三角形；（2）AC CD CE+=，证明：由旋转的性质可知，60,DAE AD AE∠==，ABC∆是等边三角形60AB AC BC BAC∴∠︒＝＝，＝，60BAC DAE∴∠∠︒＝＝，BAC DAC DAE DAC∴∠+∠∠+∠＝，即BAD CAE∠∠＝，在ABD∆和ACE∆中，AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩,ABD ACE SAS∴∆∆≌（）BD CE∴=，CE BD CB CD CA CD∴++＝＝＝；（3）①BD 为2或8时，30DEC ∠=，当点D 在线段BC 上时，3060DEC AED ∠︒∠︒＝，＝，90AEC ∴∠︒＝，ABD ACE ∆∆≌，9060ADB AEC B ∴∠∠︒∠︒＝＝，又＝，30BAD ∴∠︒＝，122BD AB ∴＝＝， 当点D 在线段BC 的延长线上时，3060DEC AED ∠︒∠︒＝，＝，30AEC ∴∠︒＝，ABD ACE ∆∆≌，3060ADB AEC B ∴∠∠︒∠︒＝＝，又＝，90BAD ∴∠︒＝，28BD AB ∴＝＝，BD ∴为2或8时，30DEC ∠︒＝；②点D 在运动过程中，DEC ∆的周长存在最小值，最小值为423+，理由如下：ABD ACE ∆∆≌，CE BD ∴＝，则DEC ∆的周长DE CE DC BD CD DE BC DE +++++＝＝＝，当CE 最小时，DEC ∆的周长最小，ADE ∆为等边三角形，DE AD ∴=， AD 的最小值为23，DEC ∴∆的周长的最小值为423+．【点睛】本题考查的是旋转变换的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键．四、初三数学 圆易错题压轴题（难）16．已知圆O 的半径长为2，点A 、B 、C 为圆O 上三点，弦BC=AO ，点D 为BC 的中点，(1)如图，连接AC 、OD ，设∠OAC=α，请用α表示∠AOD ；。

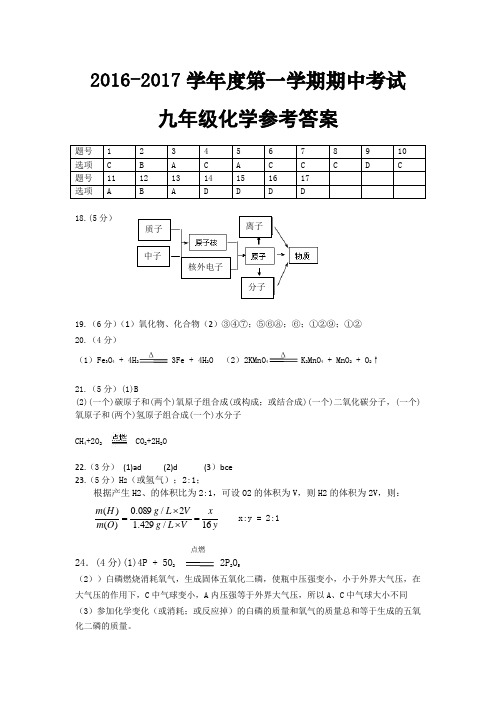
2016-2017学年度第一学期期中考试九年级化学参考答案18.(5分）19.（6分）（1）氧化物、化合物（2）③④⑦；⑤⑥⑧；⑥；①②⑨；①② 20.（4分）（1）Fe 3O 4 + 4H 2O （2）2KMnO 2MnO 4 + MnO 2 + O 2↑21.（5分）(1)B(2)(一个)碳原子和(两个)氧原子组合成(或构成；或结合成)(一个)二氧化碳分子，(一个)氧原子和(两个)氢原子组合成(一个)水分子CH 4+2O 2 CO 2+2H 2O 22.（3分） (1)ad (2)d (3）bce 23.（5分）H 2（或氢气）；2:1；根据产生H2、的体积比为2:1，可设O2的体积为V ，则H2的体积为2V ，则：质子 核外电子中子分子离子25.（6分）（1）长颈漏斗； （2）2H 2O 2↑ （3） AD （4）80.0；注射器内原有的10mL 液体占据了试管的一部分体积。

26.（5分）四种化肥氮元素质量分数分别为：尿素CO(NH 2)2：6028×100% ≈ 46.7% 硝酸铵NH 4NO 3：8028×100% =35% 碳铵NH 4HCO 3：7914×100% ≈ 17.7% 氯化铵NH 4Cl ：5.5314×100% ≈ 26.2%如用200元分别购买上述四种化肥，其中氮元素含量分别为： 尿素：吨元元/1200200× 46.7% = 0.078吨，硝酸铵：：吨元元/900200×35% =0.078吨碳铵：吨元元/350200×17.7%=0.101吨， 氯化铵：吨元元/450200×126.2%=0.116吨对以上计算结果进行比较，可知该农民应购买氯化铵。

96149 = gx96.0 .............1分 x = 1.49g.............1分MnO 2的质量为2.49g - 1.49g=1g .............1分答：制得的氧气我0.96g ，2.49g 固体中有氯化钾1.49g ，二氧化锰1g。

北京市2015~2016学年度第一学期初三英语期中考试 成绩听力理解(共25分)一、 听对话，选择与内容相符的图片，每段对话读两遍。

（共4分，每小题1分） ( ) 1. A B C( )2. A BC( )3. A BC(ABC二、听对话或独白，选择最佳答案。

每段对话或独白读两遍。

（共12分，每小题1分） 请听一段对话，完成第5至第6小题。

( ）5. How does John know something about ancient elephants?A. From movies.B. From books.C. From the Internet.( ) 6. When will they meet?A. At 9:00 on Sunday morning.B. At 8:00 on Saturday morning.C. At 9:00 on Saturday morning.请听一段对话，完成第7至第8小题。

( ) 7. What is the woman's size?A. Size 7.B. Size 8.C. Size 9. ( )8. What did the woman buy at last?A. An expensive silk dress.B. A less expensive dress.C. A cotton dress. 请听一段对话，完成第9至第10小题。

( )9. What is the tradition for the festival?A. People make cakes.B. People plant a tree.C. People give things away.( )10. What collection does Mr. Green have?A. A collection of food.B. A collection of music.C. A collection of games. 请听一段对话，完成第11至第12小题。

北京市通州区九年级语文上学期期中模拟检测试卷（附答案）一(6分。

每小题2分)1．下列词语中，没有错别字的一组是（）A．娴熟默守成规扪心自问B．杀戮栩栩如生支撑门户C．带挈扣人心弦舍身取义D．阔绰腐草为萤一愁莫展2．下列各句中，加点的成语使用恰当的一项是（）A、庆幸在那风雪路上，与那车老板相遇，就在要各奔东西、南辕北辙．．．．的瞬间，他对我说了句话。

B、孙雯的表现可圈可点．．．．，尽显球星风范。

C、市数百名警察倾巢出动．．．．。

D、春节晚会上，杜老振振有词．．．．地诵诗一首。

3．下列各句中，没有语病的一句是（）A．最近一次模拟考试中，全班同学的数学平均成绩都超过了80分。

B．我不但支持他，而且连反对过他的人也支持他了。

C．这种平等、团结、互助的社会主义民族关系已经确定。

D．一些发达国家的建筑业，新技术应用之迅速，见效之广泛，都是我们所不及的。

二(6分。

每小题3分)阅读下面两段文言文。

完成4--7题。

(甲)予观夫巴陵胜状，在洞庭一湖。

衔远山，吞长江，浩浩荡荡，横无际涯；朝晖夕阴，气象万千。

此则岳阳楼之大观也。

前人之述备矣。

然则北通巫峡，南极潇湘，迁客骚人，多会于此，览物之情，得无异乎？嗟夫！予尝求．古仁人之心，或异二者之为，何哉？不以物喜，不以己悲；居．庙堂之高则忧其民；处江湖之远则忧其君。

是进亦忧，退亦忧。

然则何时而乐耶？其必曰“先天下之忧而忧，后天下之乐而乐”乎。

噫！微斯人，吾谁与归？(乙) 风烟俱净，天山共色。

从流飘荡，任意东西。

自富阳至桐庐，一百许里，奇山异水，天下独绝。

水皆缥碧，千丈见底。

游鱼细石，直视无碍。

急湍甚箭，猛浪若奔。

夹岸高山，皆生寒树。

负势竞上，互相轩邈；争高直指，千百成峰。

泉水激石，泠泠作响；好鸟相鸣，嘤嘤成韵。

蝉则千转不穷，猿则百叫无绝。

鸢飞戾天者，望峰息心；经纶世务者，窥谷忘反。

横柯上蔽，在昼犹昏；疏条交映，有时见日。

4、下列划线字注音错误的一项是（）（3分）A、浩浩汤汤（ tānɡ）B、衔远山（ xián ）C、互相轩邈（ miǎo ）D、泠泠作响（ líng ）5、下列几组加点字意义相同的一组是（）（3分）A、奇山异．水始指异．之B、吾谁与．归呼尔而与．之C、朝晖夕阴春和景明D、此则岳阳楼之大观．也以俟夫观．人风者得焉第II卷(共118分)三(22分)6、翻译句子。

2015-2016学年北京市通州区重点中学九年级（上）期中物理模拟试卷一、下列各小题均有四个选项，其中只有一个符合题意（共30分，每小题2分）1．在国际单位制中，电荷[量]的单位是（）A．库仑（C）B．安培（A）C．欧姆（Ω）D．焦耳（J）2．下列物体在通常情况下属于绝缘体的是（）A．人体 B．金属棒C．塑料棒D．食盐水溶液3．下列几种现象中，属于光的反射现象的是（）A．影子的形成B．海上出现海市蜃楼C．平静的湖水映出桥的倒影D．日食、月食的形成4．下列数据中，符合一般中学生实际情况的是（）A．质量约为50kg B．正常体温约为38℃C．正常步行的速度约为10m/s D．身高约为1.8dm5．如图所示的四种情景中，人对物体做功的是（）A．拉着重物静止不动B．用力推石头，石头没动C．用力搬起箱子D．背着书包在等车6．下列说法错误的是（）A．电压是电路中形成电流的原因B．金属导线中电流方向与自由电子定向移动方向相同C．电路中有电流时，电路两端就一定有电压D．同种电荷相斥，异种电荷相吸7．下列现象中不属于空气中水蒸气液化的是（）A．冬天人在室外呼出“白气”B．闷热的夏天自来水管上出现水珠C．冬天戴眼镜的人进入温暖的屋内，眼镜片上出现一层“雾”D．夏天，打开冰棍的包装纸，看见冰棍旁出现“白气”8．能量转化是非常普遍的现象，下列关于能量转化的叙述中正确的是（）A．洗衣机甩干衣服时，将机械能转化为电能B．电动机工作时，将电能转化为机械能C．发电机工作时，将电能转化为机械能D．电热水器烧水时，将内能转化为电能9．在如图所示的电路中，开关闭合后，三个电阻并联的电路是（）A．B．C．D．10．医护人员用体温计给病人测量体温时，体温计中的水银在测量过程中始终不变的是（）A．质量 B．体积 C．密度 D．温度11．下列说法正确的是（）A．小磁针通常指南北，是因为受到地磁场的作用B．同名磁极互相吸引，异名磁极互相排斥C．磁场对放入其中的导体一定有力的作用D．导体做切割磁感线的运动时，导体中就一定产生感应电流12．生活中处处有物理，李亮同学养成了观察生活的好习惯，他对观察到的一些现象做了以下解释，其中解释错误的是（）A．夏天，家里保险丝易熔断，是因为同时使用几个大功率的用电器造成电流过大B．电饭锅用三脚插头和三孔插座，是为了防止锅体漏电造成触电事故C．冬天家里的“暖气”中用水做循环介质，是由于水的比热容大D．在海中游泳，从岸边向深处走去，感到越来越轻，是由于人所受重力变小13．如图所示电路，电源两端的电压一定，开关S1闭合，如果使电压表示数减小，电流表的示数增大，则下列操作一定可行的是（）A．滑动变阻器的滑片P向下移B．滑动变阻器的滑片P向上移C．开关S2闭合，滑动变阻器的滑片P向下移D．开关S2闭合，断开开关S1，滑动变阻器的滑片P不动14．如图所示的电路中，电源电压为4.5V．开关S闭合后，电流表的示数为0.5A，电压表的示数为3V．当把滑动变阻器的滑片P移到最右端时，电流表的示数为0.3A．滑动变阻器的最大电阻值是（）A．9ΩB．12Ω C．10Ω D．4.5Ω15．用如图所示滑轮组，将质量为48kg的物体以0.3m/s的速度匀速提起，绳子自由端的拉力为200N；若用该滑轮组将重570N的物体匀速提升2m时，不计绳重、绳子的伸长和滑轮内部的摩擦，（g=10N/kg），则（）A．前、后两次滑轮组的机械效率相同B．后一次绳端拉力做的功为1380JC．动滑轮受到的重力是40ND．前一次绳端拉力的功率是144W二、下列各小题均有四个选项，其中符合题意的选项均多于一个．（共6分，每小题3分，不选、错选该小题不得分，漏选该小题得2分）16．图所示的电动自行车，从它的结构和使用来看，应用了许多物理知识．下列说法中正确的是（）A．车座的设计应用了压强的知识B．脚蹬上刻有凹凸不平的花纹，是为了增大摩擦C．车喇叭应用了声音发生和传播的知识D．它工作时，将机械能转化为电能17．给某物质组成的一个物体均匀加热，设物体吸收的热量与加热时间成正比，得到其温度随时间变化的曲线如图所示，下列说法中正确的是（）A．该物质是非晶体B．该物质是晶体，它的熔点是60℃C．该物质在固态时的比热容与液态时的比热容之比是2：1D．该物质在固态时的比热容与液态时的比热容之比是1：4三、填空题（共14分，每空2分）18．图中的茶壶、锅炉水位计、乳牛自动喂水器，它们都是利用的原理工作的．19．汽油机是由四个冲程不断循环而工作的，图的三个冲程中表示内能转化为机械能的是（选填图中字母）．20．室内洁白的墙壁能将照射在墙壁上的太阳光变成散射光，达到保护视力的目的，这是利用了光的（选填：“镜面反射”或“漫反射”）．21．我国在今年要整体打捞古代沉船“南海I号”．沉船在珠江口以西，距阳江海陵岛30多海里海面下20m深处．若海水的密度为1.03×103kg/m3，g取10N/kg，沉船受到海水的压强是Pa．22．中国救援队在某国地震灾害的救援行动中使用了一种气袋．受力面积为100dm2的气袋可顶起质量为68t的楼板，此时楼板对气袋的压强是Pa．（g=10N/kg）23．一盏白炽灯上标有“220V 100W”字样．若用长导线把这盏白炽灯接到远处的电源上，该电源的供电电压为220V且不变，这时白炽灯的实际电功率为8lW，则导线上损耗的电功率为W（设灯丝的电阻不变）．24．如图所示，电源电压保持不变，三个电阻的阻值分别是R1、R2、R3．当闭合开关S后，电流表A1、A2、A3的示数分别为I1、I2、I3，则R1：R2= ．四、作图、实验探究题（共34分）25．图中体温计的示数是℃．26．图中，重20N的物体被拉上斜面．请你画出此物体受重力的示意图．27．在图中的虚线框内填入适当的透镜．28．请你画出图中拉力F对支点O的力臂l．29．自行车尾灯的部分结构如图所示，请在图上画出所给射入光线经两个反射面反射的光路．30．小明家有两盏墙壁灯，由一个开关控制，其元件符号如图所示，试将其连接成电路图．31．两个同学做“测平均速度”实验，图是小车滑下过程的示意图．下表是他们未完成的实验记录．（l）请你将表补填完整．（2）由表中数据可知小车前半程和后半程速度大小的关系是．路程/cm 运动时间/s 平均速度/m•s﹣1S1=80.00 t1=2.8 V1≈0.29S2=40.00 t2=2.0 V2=0.20S3=S1﹣S2=40.00 t3=t1﹣t2=0.8 V3=32．图是探究凸透镜成像规律的实验装置示意图，MN为凸透镜的主光轴，F1、F2为凸透镜的焦点，将点燃的蜡烛放在凸透镜的左侧时，通过移动凸透镜右侧的光屏，在光屏上得到清晰放大的像，烛焰应位于凸透镜左侧A、B、C、D四点中的点处；当烛焰移动到D点时，在光屏上就看不到烛焰的实像了，这时怎样观察烛焰的虚像，请写出你的观察方法．33．如图所示的均匀杠杆，相邻刻度线之间的距离都是相等的．使杠杆在水平位置平衡后，在杠杆的A刻线处挂2个钩码．为了使杠杆在水平位置重新平衡，那么应该在B刻线处挂个钩码．（每个钩码的质量都相等）34．西藏学校的丹增同学在拉萨家中做“观察水的沸腾”实验时，绘出了温度随时间变化的图象如图所示，请你根据表1、表2填写丹增同学实验时的气压标准大气压（选填：“高于”、“等于”或“低于”），其原因是．1个标准大气压下几种物质的沸点：物质沸点（℃）酒精78水100煤油1501个标准大气压下几种物质的熔点：物质熔点（℃）海波48萘80.5铅32835．在研究“水和煤油的比热容”实验中，两个同样的烧杯里分别装着质量和温度都相同的水和煤油，用两个同样的电热器给它们加热如图所示，李红所在小组记录了如下一组数据．通过分析表中的实验数据，可以得到的初步结论是：．加热时间/min 0 2 4 6 8 10水的温度/℃20 21 22 23 24 25煤油的温度/℃20 22 24 26 28 3036．为了探究实心圆柱体对水平地面压力的作用效果与哪些因素有关，韩磊同学用若干个不同的圆柱体竖直放置在同一水平细沙面上，进行了三组实验，并记录有关数据分别如表一、表二、表三所示．表一实验序号材料高度（cm）底面积（cm2）1 铜20 102 铜20 203 铜20 30表二实验序号材料高度（cm）底面积（cm2）4 铁20 105 铁20 206 铁20 30表三实验序号材料高度（cm）底面积（cm2）7 铜10 108 铜10 209 铜10 30实验时，他仔细观察沙面的凹陷程度，并通过比较，发现每一组沙面的凹陷程度相同，而各组却不同，第一组凹陷程度最大，第二组其次，第三组最小．请你完成：（1）分析比较表一、表二中的数据及观察到的现象，可初步得出：．（2）分析比较表一和表三中的数据及观察到的现象，可初步得出：．37．北京市某中学初三（5）班学生分成两组在实验中探究“电阻消耗电功率与电阻阻值的关系”．实验室提供了符合实验要求的实验器材：电源一个，电流表和电压表各一只，开关一个，各种不同阻值的定值电阻5个，导线若干．小明同学所在小组很快通过实验找到了当通电电流保持一定时，电阻消耗的电功率与该电阻的阻值成正比的关系．但小红同学所在小组却在实验中遇到了困难．她们小组探究的是“当加在电阻两端电压一定时，电阻消耗的电功率与该电阻阻值的关系．”请你也参与小红小组的探究活动，画出设计的实验电路（在方框中），写出实验步骤，并简要说明你的分析方法．（l）实验电路：．（2）实验步骤：．（3）分析方法：．五、简答、计算题（共16分）计算题要求：（1）写出必要的文字说明和依据的主要公式；（2）代入数据；（3）凡有数字运算的题目，运算过程和结果都要写明单位．38．如图所示的漫画十分形象的表示了这位汽车驾驶员在开车时，因未使用安全带造成的严重后果．请你用学过的物理知识解释为什么会发生这种情况？39．装有50kg水的太阳能热水器，在阳光照射下，水温从20℃上升到50℃．该热水器中水吸收的热量是多少？[C水=4.2×103J/（kg•℃）]．40．电烙铁在使用时，如果不断通电会使烙铁头的温度不断升高，影响焊接．有一种变阻电热丝控温电烙铁，其结构示意图和电路示意图分别如图甲、乙所示．电阻丝R1是主电热丝，是用电阻基本不随温度变化的镍铬合金绕制，用于对烙铁头进行加热．电阻丝R2为控温电热丝，是用铁铬铝合金绕制，当温度低时R2阻值小，温度升高阻值变大．工作时，闭合开关接通家庭电路，电压是220V，且保持不变．R1的电功率为100W，电烙铁的总功率为160W．通电30s后烙铁头的温度可以达到300℃左右．这个过程中由于R2的阻值变大，电路中电流减小为0.4A，使R1的电功率下降，烙铁头的温度不会继续上升．求：（l）刚接通电路时，R2的电功率；（2）在使用电烙铁的过程中R2阻值的变化范围（计算过程和结果保留1位小数）．41．用起重机吊重物，在起重机吊臂前端安装着滑轮组，滑轮组的连接方式如图所示，不计绳重及伸长、滑轮轮与轴间的摩擦．当动滑轮下的重物是边长为1m的正方体，质量是2.4t 时，绳子拉力是1000N，重物保持静止，此时重物对水平地面的压强为2.15×104Pa．g取10N/kg，求：（1）重物对水平地面的压力是多少？（2）仍用此滑轮组吊起重为2500N的物体，要使重物匀速上升，绳子的拉力应是多大？此时滑轮组的机械效率是多少？（计算结果百分数保留整数）2015-2016学年北京市通州区重点中学九年级（上）期中物理模拟试卷参考答案与试题解析一、下列各小题均有四个选项，其中只有一个符合题意（共30分，每小题2分）1．在国际单位制中，电荷[量]的单位是（）A．库仑（C）B．安培（A）C．欧姆（Ω）D．焦耳（J）【考点】电量及其计算．【专题】电流和电路．【分析】根据对各物理量单位的掌握分析答题．【解答】解：A、库伦是电荷量的单位，符号：C；B、安培是电流的单位，符号A；C、欧姆是电阻的单位；D、焦耳是功的单位；故选A．【点评】本题考查了电荷量的单位，是一道基础题，掌握基础知识即可正确解题．2．下列物体在通常情况下属于绝缘体的是（）A．人体 B．金属棒C．塑料棒D．食盐水溶液【考点】绝缘体．【专题】应用题．【分析】根据导电性的不同，材料可分为导体，半导体，绝缘体三大类，容易导电的物体叫导体，不容易导电的物体叫绝缘体，导电性能介于导体与绝缘体之间的叫半导体．【解答】解：常见的导体有：金属、人体、大地、各种酸、碱、盐的水溶液等．题中的四个选项中，人体、金属棒、食盐水溶液是导体，塑料棒是绝缘体．故选C．【点评】本题考查了导体和绝缘体的概念．属于识记性的东西，对于常见的导体和绝缘体可以联系它们在日常生活和工业生产中的应用来记忆，不要死记硬背．3．下列几种现象中，属于光的反射现象的是（）A．影子的形成B．海上出现海市蜃楼C．平静的湖水映出桥的倒影D．日食、月食的形成【考点】光的反射．【专题】光的传播和反射、平面镜成像．【分析】解答此题要从以下知识点入手：①平面镜成像，成因是光的反射．②光的折射现象．由物体发出的光透过不同介质时，会发生折射，使光路发生改变，因此我们看到的是物体的虚像．③光的直线传播．知道光在同一均匀介质中是沿直线传播的．【解答】解：A、影子是光的直线传播现象．不符合题意；B、海市蜃楼是光在不均匀的空气中发生的光的折射现象，不符合题意；C、平静湖面上呈现山的倒影，是平面镜成像，成因是光的反射．符合题意；D、日食月食是由于光的直线传播形成的，不符合题意；故选C．【点评】本题考查了光的反射现象、光的折射现象、与光的直线传播原理属于常见的考题．4．下列数据中，符合一般中学生实际情况的是（）A．质量约为50kg B．正常体温约为38℃C．正常步行的速度约为10m/s D．身高约为1.8dm【考点】质量的估测；温度；长度的估测；速度与物体运动．【专题】估算综合应用题．【分析】不同物理量的估算，有的需要凭借生活经验，有的需要简单的计算，有的要进行单位的换算，最后判断最符合实际的是哪一个．【解答】解：A、成年人的质量在65kg左右，中学生比成年人的质量小一些，在50kg左右．符合实际；B、正常情况下人体体温在37℃左右，变化幅度很小．不符合实际；C、中学生步行的速度在4km/h=4×m/s≈1.1m/s左右．不符合实际；D、成年人的身高在170cm左右，中学生的身高比成年人小一些，在160cm=16dm左右．不符合实际．故选A．【点评】对于生活中数据的估测，应从实际的角度出发进行判断，也可从自己的角度出发判断，如自己的身高、自己的体重、自己正常时的体温及正常行走的速度等方面来与题目中的数据比较，只要相差不大，即该数据就是合理的．5．如图所示的四种情景中，人对物体做功的是（）A．拉着重物静止不动B．用力推石头，石头没动C．用力搬起箱子D．背着书包在等车【考点】力是否做功的判断．【专题】应用题；功、功率、机械效率．【分析】本题要抓住做功的两个必要因素：作用在物体上的力；物体在力的方向上通过的距离．二者缺一不可．【解答】解：A、拉着重物静止不动，给重物一个向上的力，重物向上没有移动距离，对重物没有做功．不符合题意．B、用力推石头，石头没动，故人给石头一个推力，石头在推力作用下没有移动距离，故人对石头没有做功．不符合题意．C、将箱子从地面搬起，人给箱子一个向上的力，箱子向上移动了距离，小丽对箱子做功．符合题意；D、学生背着书包在等车，学生给书包一个向上的力，书包向上没有移动距离，故学生对书包没有做功．不符合题意．故选C．【点评】有力有距离，力对物体不一定做功，物体必须在力的作用下通过了距离，力对物体才做功．6．下列说法错误的是（）A．电压是电路中形成电流的原因B．金属导线中电流方向与自由电子定向移动方向相同C．电路中有电流时，电路两端就一定有电压D．同种电荷相斥，异种电荷相吸【考点】电流的方向；电荷间的相互作用规律．【专题】电流和电路．【分析】①电压促使电荷发生定向移动，从而形成电流；②正电荷定向移动的方向为电流方向；③同种电荷相互排斥，异种电荷相互吸引．【解答】解：A、电压可以使电荷发生定向移动形成电流，故A正确；B、自由电子带负电，故电流的方向与自由电子定向移动的方向相反，故B错误；C、只有存在电压，电荷才能发生定向移动，故C正确；D、同种电荷相互排斥，异种电荷相互吸引，故D正确；故选B．【点评】本题考查了电流的成因，电流的方向以及正负电荷间的相互作用，属于中考中常见的电学综合题目，难度不大．7．下列现象中不属于空气中水蒸气液化的是（）A．冬天人在室外呼出“白气”B．闷热的夏天自来水管上出现水珠C．冬天戴眼镜的人进入温暖的屋内，眼镜片上出现一层“雾”D．夏天，打开冰棍的包装纸，看见冰棍旁出现“白气”【考点】液化及液化现象．【专题】汽化和液化、升华和凝华．【分析】物质由气态变成液态的现象叫做液化，根据物质变化前后的状态分析答题．【解答】解：A、冬天人在室外呼出“白气”，是口中呼出的温度较高的水蒸气遇冷液化的小水滴，符合题意；B、闷热的夏天自来水管上出现水珠，是空气中的水蒸气遇到温度较低的水管凝结成的小水滴，不符合题意；C、冬天戴眼镜的人进入温暖的屋内，眼镜片上出现一层“雾”，是室内空气中的水蒸气遇到温度较低的镜片液化成的小水滴，不符合题意；D、夏天，打开冰棍的包装纸，看见冰棍旁出现“白气”，是空气中的水蒸气遇到温度较低的冰棒液化成的小水滴，不符合题意．故选A．【点评】本题考查了学生对液化现象的分析，知道液化是温度较高的水蒸气遇冷凝结成的小水滴．8．能量转化是非常普遍的现象，下列关于能量转化的叙述中正确的是（）A．洗衣机甩干衣服时，将机械能转化为电能B．电动机工作时，将电能转化为机械能C．发电机工作时，将电能转化为机械能D．电热水器烧水时，将内能转化为电能【考点】能量的相互转化．【专题】应用题；机械能及其转化．【分析】判断能量的转化，我们主要看它要消耗什么能量，得到什么能量，总是消耗的能量转化为得到的能量．【解答】解：A、洗衣机甩干衣服时，消耗电能，产生机械能，故是将电能转化为机械能的过程，故错误；B、电动机工作时，消耗电能，产生机械能，故是将电能转化为机械能的过程，故正确；C、发电机工作时，消耗机械能，产生电能，故是将机械能转化为电能的过程，故错误；D、电热水器烧水时，消耗电能，产生内能，故是将电能转化为内能的过程，故错误；故选B．【点评】能量转化的过程都是有规律可循的，在平常的学习中要注意总结归纳是解决这一类问题的关键，例如燃料燃烧都是将化学能转化为内能，该类题目比较简单，要掌握做题的思路与方法．9．在如图所示的电路中，开关闭合后，三个电阻并联的电路是（）A．B．C．D．【考点】串联电路和并联电路的辨别．【专题】电流和电路．【分析】并联电路中，电流有多条路径，各用电器是并列连接的，结合电路图可做出判断．【解答】解：A、图中下方的两个电阻是串联关系，再与另一个并联，属混联，不合题意；B、三个电阻依次连接，属串联，不合题意；C、电路中有三个支路，三个电阻并列连接，符合题意；D、两电阻并联后与另一个电阻串联，属混联，不合题意．故选C．【点评】明确串并联电路的基本连接特点，能对照电路图进行判断电路的串并联关系，这是电学的基本能力．10．医护人员用体温计给病人测量体温时，体温计中的水银在测量过程中始终不变的是（）A．质量 B．体积 C．密度 D．温度【考点】质量及其特性；密度公式的应用．【分析】体温计内的水银属于液体，而且水银具有热胀冷缩的性质；用公式ρ=判断密度的变化；质量不随物体温度的升高而变化．【解答】解：体温计示数升高时，关于体温计内的水银温度随之升高，体积变大，质量不变，由公式ρ=得密度变小．故选A．【点评】质量是物体的一种属性，不随物体的位置、状态、形状、温度的变化而变化，只有物体所含物质的多少变化，质量才会变化．11．下列说法正确的是（）A．小磁针通常指南北，是因为受到地磁场的作用B．同名磁极互相吸引，异名磁极互相排斥C．磁场对放入其中的导体一定有力的作用D．导体做切割磁感线的运动时，导体中就一定产生感应电流【考点】地磁场；磁场对通电导线的作用；电磁感应．【分析】磁场的性质：对放入其中的磁体产生磁力的作用．磁极间的作用规律：同名磁极互相排斥，异名磁极互相吸引．感应电流的产生条件：闭合电路的一部分导体在磁场中做切割磁感线运动时，导体中就会产生感应电流．【解答】解：A、小磁针处在地磁场中，受到地磁场的作用而指示南北．故A正确；B、磁极间的作用规律：同名磁极互相排斥，异名磁极互相吸引．故B错误；C、磁场的性质：对放入其中的磁体产生磁力的作用．故C错误；D、闭合电路的一部分导体做切割磁感线运动时，导体中就会产生感应电流．故D错误．故选A【点评】此题考查的知识点有三个：一是磁场的性质；二是磁极间的作用规律；三是感应电流产生的条件﹣﹣闭合电路的一部分导体在磁场中做切割磁感线运动．12．生活中处处有物理，李亮同学养成了观察生活的好习惯，他对观察到的一些现象做了以下解释，其中解释错误的是（）A．夏天，家里保险丝易熔断，是因为同时使用几个大功率的用电器造成电流过大B．电饭锅用三脚插头和三孔插座，是为了防止锅体漏电造成触电事故C．冬天家里的“暖气”中用水做循环介质，是由于水的比热容大D．在海中游泳，从岸边向深处走去，感到越来越轻，是由于人所受重力变小【考点】水的比热容的特点及应用；阿基米德原理；插座的构造与工作方式；家庭电路电流过大的原因．【分析】（1）知道保险丝熔断的原因有，家庭电路中的用电器功率过大或发生短路时引起的电流过大．（2）三孔插座的地线的作用是外壳万一带电，电流会通过地线导入大地，防止造成触电事故的发生．（3）因为水的比热容较大：相同质量的水和其它物质比较，吸收或放出相同的热量，水的温度升高或降低的少；升高或降低相同的温度，水吸收或放出的热量多．（4）人从岸边向深处走去，排开的液体体积增大，根据阿基米德原理分析即可．【解答】解：A、同时使用几个大功率的用电器造成电流过大会使保险丝熔断，但也可能是某处发生短路，造成电路中电流过大，该项说法错误，符合题意；B、电饭锅用三脚插头和三孔插座，这样锅体万一带电，电流会通过地线导入大地，防止造成触电事故的发生．造成触电事故，该项说法正确，不符合题意C、因水的比热容最大，相同质量的水和其它物质比较，降低相同的温度，水放出的热量多，所以暖气装置中用水来供热．该项说法正确，不符合题意；D、由阿基米德原理可知：液体密度不变，但人从浅水区向深水区走去，排开的液体体积增大，所受浮力增大，所以不是重力变小的缘故．该项说法错误，符合题意；故选A、D．【点评】本题考查电路电流过大的原因、三孔插座中地线的作用、水的比热容大的利用和浮力的产生，知识点较多．但本题联系实际生活，学生都有切身的体会，运用所学知识解决实际问题，增强学生学习的积极性．13．如图所示电路，电源两端的电压一定，开关S1闭合，如果使电压表示数减小，电流表的示数增大，则下列操作一定可行的是（）A．滑动变阻器的滑片P向下移B．滑动变阻器的滑片P向上移C．开关S2闭合，滑动变阻器的滑片P向下移D．开关S2闭合，断开开关S1，滑动变阻器的滑片P不动【考点】电路的动态分析．【专题】电路变化分析综合题．【分析】图中开关S1闭合时，R1与R2串联，电压表测R2两端电压．根据串联电压分配与电阻关系特点来分析，要使电压表示数减小，只能是R2的阻值减小，即滑片P向下移，且电流表的示数增大，而开关S2闭合后，R1被短路，电压表测量电源电压，示数会增大，故C错误．若开关S2闭合，断开开关S1，电压表串在电路中，示数会增大，电流表的示数几乎为零，不可行．。

北京市2016—2017学年度第一学期九年级英语期中考试试卷听力理解（共30分）一、听对话，从下面各题所给的A、B、C三幅图片中选择与对话内容相符的图片。

每段对话你将听两遍。

（共5分，每小题1分）二、听对话或独白，根据对话或独白内容，从下面各题所给的A、B、C三个选项中选择最佳选项。

每段对话或独白你将听两遍。

（共15分，每小题1.5分）请听一段对话，完成第6至第7小题。

6. Where’re the speakers going during this winter holiday?A．The Wonderland． B．The Great Wall. C．The Story House．7. Who’ll take the speakers there?A．Tony’s father． B．Tony’s mother． C．Tony’s sister．请听一段对话，完成第8至第9小题。

8. Where’re they?A．In a garden． B．In a classroom． C．In a museum．9. When are they leaving?A．At 10:40． B．At 10:30． C．At 10:00．请听一段对话，完成第10至第11小题。

10. What’re they talking about?A．Some famous places． B．A photo competition．C．Their good friends．11. Who’ll help to decide?A．Peter． B．Lily． C．Miss Wu．请听一段独白，完成第12至第13小题。

12. What’s Love and Care?A．An old people’s home． B A friend’s home． C．A student’s home．13. What happened at Love and Care?A．Some old people did performances．B．Some good friends held a party there．C．Some students visited with their songs．请听一段对话，完成第14至第15小题。

通州区初三物理期末质量检测2017年1月小题2分）1. 通常情况下，下列物体中属于绝缘体的是A ．干燥的竹木筷子B ．不锈钢尺C ．2B 铅笔芯D ．酱油 2. 在国际单位制中，电功率的单位是A．瓦特B ．焦耳C ．库仑D ．千瓦时 3. 图1所示的家用电器中，利用电流热效应工作的是4. 图2所示的滑动变阻器连入电路的四种接法中，当滑片P 向左滑动时，滑动变阻器接入电路部分的电阻减小．．．．的是5. 当温度一定时，比较两根镍铬合金丝电阻的大小，下列说法中正确的是 A. 长的合金丝的电阻大 B. 长度相同时，粗的合金丝的电阻大 C. 细的合金丝的电阻大 D. 粗细相同时，长的合金丝的电阻大6. 图3所示的四种情景中，符合安全用电原则的是A. 洗衣机 Ｂ. 电饭锅 Ｃ. 家用电风扇 Ｄ. 笔记本电脑图2BP CPAPDS 1S 2 铃灯7. 在图4中，涂有深颜色的一端表示小磁针的N 极，将它们放在磁体周围，小磁针静止不动时，小磁针N 极指向正确的是 8. 现有两只普通白炽灯泡L 1、L 2，其中L 1标有"220 V 40 W"、L 2标有"110 V 40 W"。

两灯都正常发光时A. L 2比L 1亮B. L 1比L 2亮C. L 1、L 2一样亮D. 无法判断 9. 图5所示为一种声光报警器的电路图，闭合开关S 1和S 2后，会出现的现象是A ．灯亮，铃响B ．灯亮，铃不响C ．灯不亮，铃响D ．灯不亮，铃不响10. 图6所示的四个实验中，说明电动机工作原理的实验是11. 图7所示的各个电路中的电源完全相同，已知R 1>R 2>R 3。

当电路中的开关S 闭合后，电流表示数最大的是12.如图8所示，当甲电路中的开关S 闭合时，两个电压表的指针位置均为图乙所示，则电阻R 1、R 2两端的电压分别为 A ．6V ，1.2V B ．1.2V ，6V C ．4.8V ，1.2V D ．1.2V ，4.8V图6A B C D ISS电动机M电热器～ 电源a bR 0图4SNAN S CN S DNSB图7 A B C DSAR 3 R 2 R 1 SAR 1 R 2SR 1AR 2SR 1AR 2R 3SR 1V 1V 213. 如图9所示，电源电压为6V 且保持不变，定值电阻R 0=20Ω，在开关S 闭合的情况下，下列说法中正确的是A ．在a 、b 两点间接入一个“3V 0.5A ”的小灯泡，小灯泡能正常发光B ．在a 、b 两点间接入一个量程为0~0.6A 的电流表，电流表的示数为0.2AC ．在a 、b 两点间接入一个阻值为10Ω的定值电阻R ，则R 0两端的电压为4VD ．在a 、b 两点间接入一个阻值为10Ω的定值电阻R ，电路消耗的总电功率为1.8W 14. 如图10所示，闭合开关S ，当滑动变阻器滑片P 向右移动时，下列说法中正确的是A. 电压表的示数不变，电流表A 1的示数变大，A 2的示数变小B. 电压表的示数不变, 电流表A 1的示数不变，A 2C. 电压表的示数与A 1的示数的比值变大，A 2 的示数变小D. 电压表的示数与A 1的示数的比值不变，A 2 的示数变小15. 图11所示电路，电源电压不变。

2015-2016学年北京市通州区普通中学九年级（上）期中物理试卷一．下列各小题均有四个选项，其中只有一个符合题意．（每小题2分，共38分）1．（2分）下列现象中，不能说明分子在永不停息地运动的是（）A．香水瓶盖子打开后，满屋充满香味B．糖放入水中后，整杯水都变甜了C．太阳光下扫地时，能看到尘土飞扬D．衣箱里的卫生球不断变小，衣箱内充满卫生球的味道2．（2分）关于内能，下列说法中正确的是（）A．内能是每个分子作无规则运动具有的能B．内能是物体中所有分子做无规则运动的动能和分子势能的总和C．内能是物体具有的动能和势能的总和D．0℃时物体具有的内能为零3．（2分）液体和固体很难被压缩，这是因为（）A．分子间没有间隙 B．分子在不停地做无规则运动C．分子间存在着引力D．分子间存在着斥力4．（2分）物体的温度升高，说明（）A．一定是物体放出了热量B．一定是物体吸收了热量C．一定是外界对物体做了功D．物体的内能一定增加了5．（2分）一瓶酒精用掉一半，剩下的酒精（）A．比热容、热值都变为原来的一半B．比热容不变，热值变为原来的一半C．热值不变，比热容变为原来的一半D．比热容、热值都不变6．（2分）下列各现象中，能说明物体吸收的热量跟物质种类有关的是（）A．体积相同的两块铜，分别升高5℃和10℃时，它们吸收的热量不同B．铁块和铜块，都升高5℃时，它们吸收的热量不同C．质量相同的铁块和铜块，都升高10℃时，它们吸收的热量不同D．质量相同的铁块和铜块，分别升高5℃和10℃时，它们吸收的热量不同7．（2分）下列事例中，利用热传递改变物体内能的是（）A．工人打铁时，铁块的温度升高B．用暖水袋暖手，手会感到暖和C．用两手来回弯折铁丝，弯折处会烫手D．用砂轮打磨刀具，迸出火星8．（2分）关于太阳能，下面说法中错误的是（）A．太阳核心发生的是聚变反应B．太阳核心发生的是裂变反应C．利用化石能源实际是利用上亿年前的太阳能D．人类可以通过将太阳能转化为电能的方式利用太阳能9．（2分）有四个带电小球，已知甲、乙相斥，乙、丙相吸，丙、丁相斥，若甲带正电，则丁带（）A．正电B．负电C．可能带正电，也可能带负电D．无法判断10．（2分）关于电流、电流的方向，下列说法正确的是（）A．电荷的移动形成电流B．负电荷定向移动不能形成电流C．负电荷定向移动的方向为电流的方向D．正、负电荷的定向移动都能形成电流11．（2分）通常情况下，下列物质中属于导体的是（）A．玻璃B．煤油C．盐水D．橡胶12．（2分）街上的路灯总是同时亮同时灭，它们之间的连接方式是（）A．都是串联B．都是并联C．有的串联，有的并联D．无法判断13．（2分）如图所示的电路中，开关闭合后，三盏灯属于并联的是（）A．B．C．D．14．（2分）如图所示为四冲程汽油机的一个冲程，下列说法正确的是（）A．这是压缩冲程，机械能转化为内能B．这是压缩冲程，内能转化为机械能C．这是做功冲程，机械能转化为内能D．这是做功冲程，内能转化为机械能15．（2分）如图所示的电路，要使灯L1和L2并联，应当（）A．闭合S1和S2，断开S3B．闭合S1和S3，断开S2C．闭合S2和S3，断开S1D．闭合S1、S2和S316．（2分）如图所示的电路中，电流表A1、A2、A3的示数分别为I1、I2、I3，它们的关系是（）A．I1＞I2＞I3B．I1＜I2＜I3C．I1=I2=I3D．I3=I1+I217．（2分）如图所示的电路中开关闭合后两灯均能发光，则（）A．表1、表2均为电压表B．表1、表2均为电流表C．表1为电压表、表2为电流表D．表1为电流表、表2为电压表18．（2分）如图所示，将滑动变阻器连入电路，当滑片P向A端移动时，电路中的电阻变大，则应连接的接线柱是（）A．C和D B．D和A C．A和B D．B和C19．（2分）当温度一定时，关于导体电阻的大小，下列说法正确的是（）A．长度相同的两条导线，细导线的电阻大B．长度相同的两条铜导线，粗导线的电阻大C．粗细相同的两条导线，长导线的电阻大D．粗细相同的两条铜导线，长导线的电阻大二．下列各小题均有四个选项，其中符合题意的选项均多于一个．（每小题2分，共6分）20．（2分）下列物理量中的单位是焦耳的是（）A．比热容B．热量C．功D．能量21．（2分）下列事例中，用做功的方法使物体的内能增加的是（）A．用气筒给自行车胎打气时，气筒会发热B．用锯条锯木头时，锯条会发烫C．冬天，在房间内用暖气取暖，室内空气温度升高D．冰块在阳光下熔化成水22．（2分）用电流表测通过灯L1的电流，则如图所示的电路中，能测出灯L1电流的是（）A．B．C．D．三．填空题．（每空1分，共19分）23．（1分）现象说明分子不停地做无规则运动。

2016北京市通州区玉桥中学初三（上）期中物理一、单项选择题（每题3分，共30分）1．下列说法中正确的是（）A．足球在草坪上沿水平方向向前滚动，重力对足球做了功B．石块从高处下落，重力对石块做了功C．举重运动员把杠铃在空中停留3s，人对杠铃做了功D．推出去的铅球在空中运动过程中，推力对铅球做了功2．运汽油的汽车都有一条铁链子拖地，它的作用是（）A．发出声响，让路人注意B．作为运油车的统一标志C．通过它向空气和大地散热D．通过与地相连的铁链将汽油和铁罐因摩擦起电所带的电荷导入大地，从而避免危害发生3．热水和冷水混合时，不计热量损失，下面说法正确的是（）A．热水降低的温度一定等于冷水升高的温度B．热水初温度高，它降低的温度一定多C．热水放出的热量一定等于冷水吸收的热量D．冷水初温度低，它吸收的热量一定多4．下面四幅图中，属于利用热传递改变物体内能的是（）A．搓手取暖B．烧水C．锯木头D．钻木取火5．汽油机的一个工作循环中，内能转化为机械能的是（）A．吸气冲程 B．压缩冲程 C．做功冲程 D．排气冲程6．关于摩擦起电，下列说法正确的是（）A．用丝绸和玻璃棒摩擦后，玻璃棒带正电B．用丝绸和玻璃棒摩擦后，丝绸带正电C．用毛皮和橡胶棒摩擦后，毛皮带负电D．用两根铁棒互相摩擦后，两铁棒均带正电7．如图所示，m A＞m B＞m C，三个物体在同样大小的力F的作用下，都沿着力F的方向移动距离s，比较F对三个物体所做的功，结论是（）A．三次做功一样多B．对A做的功多C．对B做的功多 D．对C做的功多8．一杯水，温度由30℃加热到50℃时吸收的热量为Q1，再由50℃加热到70℃时吸收的热量为Q2，Q1与Q2的大小关系为（）A．Q1＞Q2B．Q1=Q2 C．Q1＜Q2D．无法判断9．下列器件中，不能称之为用电器的是（）A．电灯 B．电炉 C．电熨斗D．电线10．一瓶酒精用去一半后，剩下的酒精（）A．热值不变，比热容减小一半 B．热值不变，比热容不变C．热值和比热容都减小一半D．热值减小一半，比热容不变二、选择说理题：（选出唯一正确答案并说明理由，10分，每小题5分）11．教室屋顶有四盏照明电灯，由一个开关控制，合上开关，它们都亮，断开开关，它们都灭．则这四盏灯的连接方式是；A：串联 B：并联 C：既有串联又有并联 D：以上都不是．理由是．12．下列说法正确的是A．温度高的物体内能一定大；B．比热容跟物体吸收或放出的热量有关；C．做功和热传递都可以改变物体的内能；D．热机的压缩冲程将内能转化为机械能．理由：．三、填空题（每空1分，共20分）13．用砂轮磨刀具，刀具会发烫，这是利用的形式来改变刀具的内能．14．电视机的荧光屏上经常粘有灰尘，这是因为电视机工作时，屏幕上带，而具有了的性质．15．以同样速度行驶的大卡车和小轿车，的动能大，故在同样道路上，不同车型限速是不同的，大卡车的最大行驶速度应比小轿车要（填“大”或“小”）16．古诗文中有许多描述自然现象的优美诗句．如“无边落木萧萧下，不尽长江滚滚来”，从物理学的角度看，滚滚奔流的长江具有巨大的．17．水的比热容是，其物理含义是．18．在下面的三句话中，“热”字的含义各指的是什么？（填“温度”、“热量”或“内能”）（1）今天天气很热，这里的“热”是指；（2）摩擦生热，这里的“热”是指；（3）物体吸热升温，这里的“热”是指．19．已知A球带负电，如图所示现象可知，B球带电，C 球可能带电，也可能不带电．20．电路中最常见的连接方式有两种，三个灯泡连成一串后，再接入电路，这三个灯泡的连接方式是；三个灯泡的两端分别连在一起，然后再接入电路中，这三个灯泡的连接方式叫做．家庭用的各种电器设备采取的是方式连接．21．燕子在高空飞行时，动能25J，重力势能15J，它的机械能为J，它从高空匀速飞落下来衔泥时机械能（选填“增大，减小或不变”）．22．在受太阳照射条件相同时，沿海地区比内陆地区温度变化小，这是因为水与干沙土相比的较大．四、实验题：（10分，每空1分）23．用图甲所示装置比较不同液体吸热升温特点．在两个相同烧杯中分别加入初温、体积相同的水和食盐水，用相同酒精灯加热直到沸腾．（1）分别测量出水和食盐水的沸点，发现食盐水的沸点比水高．其中水沸腾时温度计的局部放大图如乙图所示，水的沸点为℃．（2）实验中加热食盐水到沸腾需要的时间长，说明食盐水吸收的热量比水（填“多，或“少，）．（3）能否仅由“加热食盐水到沸腾需要的时间长”得出食盐水比热容大的结论？答：；其原因是：．24．如图所示，下面是某同学做探究“斜面的机械效率与斜面的粗糙程度、斜面的倾斜程度的关系”实验时，得到如下实验数据．斜面与水平面夹角小车的重力G/N斜面的粗糙程度斜面的高度h/m沿斜面拉力F/N斜面长S/m有用功W有/J总功W总/J机械效率%20° 2.1 玻璃面0.09 0.6 0.5 0.189 0.30 63 30° 2.1 玻璃面0.21 1.1 0.5 0.441 0.55 80.2 45° 2.1 玻璃面0.36 1.8 0.545° 2.1 棉布面0.36 2.0 0.5 0.756 1.00 75.6 （1）此探究实验是采用了的物理研究方法．（2）请将上表中空格补充完整．（3）请你根据表中的实验数据，得出要探究的实验结论：结论一：．结论二：．五．计算题：（要有计算公式和计算过程，15分）25．一辆汽车在平直公路上匀速行驶160m，在此过程中，汽车牵引力做功8.0×104J，这辆汽车的牵引力有多大？26．某举重运动员在0.8s内将140kg的杠铃从地上举到1.6m的高度，他在这个过程中做功的平均功率是多少？（g=10N/Kg）27．王小聪同学的家住在新农村建设示范村里，他父亲年前拉回了一套液化石油气灶具．液化石油气热值为3.5×107J/kg，燃烧放出的热量只有60%被水吸收．（1）将质量为5kg，初温为20℃的水加热到100℃，水吸热多少J？（2）需燃烧液化石油气多少Kg？物理试题答案一、单项选择题（每题3分，共30分）1．【考点】功的计算．【分析】根据做功的两个必要条件判断：一是有力作用在物体上，二是物体在力的方向上有通过的距离．【解答】解：A、足球在草坪上沿水平方向向前滚动，可以判断球只是在水平方向上运动，在竖直方向上移动的距离为0，所以重力对足球做的功为0．故A选项错误．B、重力方向是竖直向下，且物体在重力的作用下下落了一段距离高度，所以重力对石块做了功；故B选项正确；C、运动员给杠铃一个力，但杠铃在空中停留，没有通过距离，所以，他对杠铃没有做功．故C错误．D、推出去的铅球在空中运动过程中受到竖直向下的重力作用，不再受到推力作用，所以推力没有对铅球做功，故D 选项错误．故选B．2．【考点】摩擦起电；导体．【分析】为了防止由于摩擦产生的静电造成事故，要把产生的静电用铁链导入大地．【解答】解：当汽车开动的时候，汽油与油槽不断摩擦，会使汽油和油槽带上等量异种电荷．由于汽车的轮胎是橡胶绝缘体，电荷不会传到地面，而是越积越多，当达到一定的程度时，会使空气电离，发生放电现象，产生电火花，使汽油燃烧甚至爆炸．只有在车尾上装一根铁链，使油槽里的电荷通过铁链传到地面，才能避免事故，所以，在汽车上装有铁链拖在地上，是运输易燃物品的必要安全措施．故选D．3．【考点】热传递．【分析】要解答本题需掌握：热传递过程中高温物体放出热量，低温物体吸收热量，直到最后温度相同．【解答】解：冷水和热水混合后，如果不计热损失，冷水吸收热量，内能增加，温度升高；热水放出热量，内能减小，温度降低．直到温度相同．热水降低的温度不一定等于冷水升高的温度，因为不知道水的质量，但是热水放出的热量一定等于冷水吸收的热量．故选C．4．【考点】热传递改变物体内能．【分析】改变物体内能的方式有两种：做功和热传递，热传递过程是能量的转移过程，做功过程是能量的转化过程．【解答】解：A、搓手取暖，是克服摩擦做功，因此是通过做功改变物体内能的，故A不符合题意；B、用火烧水时，水从火吸热，使水的内能增加、温度升高，是热传递改变物体的内能，故B符合题意；C、锯木材时，锯与木头摩擦，摩擦生热这是利用做功来改变物体内能的，故C不符合题意；D、钻木取火，是克服摩擦做功，因此是通过做功改变物体的内能，故D不符合题意．故选B．5．【考点】内燃机的四个冲程．【分析】汽油机的一个工作循环有吸气冲程、压缩冲程、做功冲程、排气冲程四个冲程组成，将机械能转化为内能的是压缩冲程，将内能转化为机械能的是做功冲程；只有做功冲程对外输出功，其它三个冲程依靠飞轮惯性完成．【解答】解：汽油机的一个工作循环包括：吸气、压缩、做功、排气四个冲程．压缩冲程活塞向下运动，压缩燃料混合物做功，将机械能转化为内能；做功冲程是高温高压的燃气推动活塞做功，是将内能转化为机械能的过程，带动曲轴转动，对外提供动力．故选C．6．【考点】摩擦起电．【分析】摩擦起电的实质是电子发生了转移．【解答】解：A、说法正确，用丝绸摩擦玻璃棒后，玻璃棒带正电；B、说法错误，丝绸与玻璃棒摩擦，有电子从玻璃棒转移到丝绸上，故丝绸带负电；C、说法错误，用毛皮摩擦橡胶棒后，有负电荷从毛皮转移到橡胶棒，毛皮带正电；D、说法错误，用两根铁棒互相摩擦后，没有发生电子的转移．故选A．7．【考点】功的计算．【分析】已知力F的大小和沿着力F的方向移动的距离s，根据功的计算公式W=FS可判断F对三个物体所做功的大小．【解答】解：因为对三个物体的作用力都是大小相等的力F，三个物体在力F的方向上移动的距离都是s，根据功的计算公式W=FS可知，F对三个物体所做的功一样多．故选A．8．【考点】热量的计算．【分析】需要根据热量的计算公式，Q=cm△t，求出热量之比．【解答】解：由题意知，同一杯水质量相同，m1=m2，比热也相同，c1=c2，两次加热升高的温度也相同，△t1=△t2，由热量公式：Q=cm△t很容易得知，Q1=Q2．故选B．9．【考点】电路的组成．【分析】电路组成包括四部分：电源、用电器、导线和开关；用电器是用电来工作的装备．【解答】解：电灯、电炉、电熨斗用电来工作，将电能转化为其它形式的能，它们是用电器；电线是用来连接各电路元件的，不属于用电器．故选D．10．【考点】燃料的热值；比热容的概念．【分析】比热容是物质的特性，热值是燃料的特性，只要物质或燃料确定，这些特性是不变的．【解答】解：把一瓶酒精用去一半后，所含的酒精减少，质量变为原来的一半，但是燃烧值和比热容是不会改变的，酒精的热值和比热容与质量无关．故A、C、D错．故选B．二、选择说理题：（选出唯一正确答案并说明理由，10分，每小题5分）11．【考点】串联电路和并联电路的辨别．【分析】在串联电路中，开关控制整个电路；在并联电路中，干路上的开关可以控制整个电路，支路上的开关只控制支路．在并联电路中，各用电器之间是互不影响的，而串联电路中各用电器互相影响．【解答】解：一只开关同时控制四盏照明电灯，但是当其中任意一盏坏掉后，其它照明电灯仍能正常发光，即它们之间的工作互不影响，所以它们之间一定是并联的．故答案为：B；这四盏灯的工作互不影响，所以它们之间一定是并联的．【考点】温度、热量与内能的关系；物体内能的改变；内燃机的四个冲程．【分析】（1）内能的大小与物体的质量、温度有关；（2）比热容是物质本身的一种性质；（3）做功和热传递都能改变物体的内能；（4）热机的压缩冲程将机械能转化为内能．【解答】解：A、内能的大小与物体的质量、温度有关，故温度高的物体内能不一定大，故A错误；B、比热容是物质本身的一种性质，与物体吸收或放出的热量无关，故B错误；C、做功和热传递都可以改变物体的内能，故C正确；D、热机的压缩冲程将机械能转化为内能，故D错误；故选C．故答案为：C；内能的大小与物体的质量、温度有关，故温度高的物体内能不一定大，故A错误；比热容是物质本身的一种性质，故B错误；做功和热传递都可以改变物体的内能，故C正确；热机的压缩冲程将机械能转化为内能，故D错误．三、填空题（每空1分，共20分）13．【考点】做功改变物体内能．【分析】改变物体内能的途径：一是做功，二是热传递，二者在改变内能方面是等效的．【解答】解：用砂轮磨刀具，克服摩擦做功，消耗机械能转化为内能，使刀具的内能增加、温度升高，这是通过做功的方法使刀具的内能增加．故答案为：做功．14．【考点】静电现象．【分析】根据带电体有吸引轻小物体的性质回答．【解答】解：电视机工作时，由于电子运动到了屏幕上，而使屏幕带静电，而带电体有吸引轻小物体的性质，故把灰尘吸引到了屏幕上．故本题答案为：静电；吸引轻小物体．15．【考点】动能的影响因素．【分析】物体动能的大小跟质量和速度有关，质量越大、速度越大，动能就越大．【解答】解：以同样速度行驶的大卡车和小轿车，因为大卡车的质量大，所以，大卡车的动能就大．在同样的道路上，不同车型限制车速不同，因为大卡车质量比小轿车的大，所以大卡车的最大速度应比小轿车小．故答案为：大卡车；小．16．【考点】机械能．【分析】滚滚流动的长江水具有动能，长江水由地势高的地方流向地势低的地方，地势越高，水具有的重力势能越大；动能和势能的总和称为机械能；可见从物理学的角度看，滚滚奔流的长江具有巨大机械能．【解答】解：流动的长江水具有动能；水位的高低显示了水的重力势能大小；重力势能的总和称为机械能；故答案为：机械能．17．【考点】比热容的概念．【分析】单位质量的某种物质，温度升高1℃吸收的热量，叫这种物质的比热容．比热容是物质本身的一种特性．【解答】解：水的比热容是4.2×103J/（kg•℃），它的物理含义是质量为1kg的水温度升高1℃，吸收的热量为4.2×103J．故答案为：4.2×103J/（kg•℃）；质量为1kg的水温度升高1℃，吸收的热量为4.2×103J．18．【考点】温度、热量与内能的关系．【分析】物理中的“热”有三种含义：温度、热量、内能．天气很热，其中的热指温度高；吸收热量，温度升高，其中的热指热量；摩擦生热其中的热指内能．【解答】解：（1）今天天气很热说明气温高，这里的“热”是指温度．（2）摩擦生热是机械能转化为内能，这里的“热”是指内能．（3）物体吸热升温是热传递过程中吸收热量温度升高，这里的“热”是指热量．故答案为：（1）温度；（2）内能；（3）热量．19．【考点】物体带电情况的判断．【分析】物体相互排斥时，物体带同种电荷．带电的物体吸引不带电的物体．【解答】解：如图，A和B球相互排斥，两个球一定带同种电荷，A球带负电荷，B球一定带负电荷．如图，B和C球相互吸引，两个可能带异种电荷，可能带电体吸引不带电体，所以C球可能带正电或不带电．故答案为：负；正．20．【考点】电路的基本连接方式．【分析】电路的连接的两种方式：串联和并联；串联是指将用电器首尾相连接入电源两端；而并联是将用电器的两端分别连在一起后，再接入电路．【解答】解：三个灯泡连成一串后，再接入电路，这三个灯泡的连接方式是串联；三个灯泡的两端分别连在一起，然后再接入电路中，这三个灯泡的连接方式叫做并联．家庭用的各种电器都可以单独工作，互不影响，因此家庭电路中各用电器设备采取的是并联方式连接．故答案为：串联；并联；并联．21．【分析】（1）物体的速度越大，质量越大，具有的动能就越大；物体的质量越大，高度越高，它的重力势能也越大．（2）物体的动能与重力势能之和是物体的机械能．【解答】解：（1）因为物体的动能与重力势能之和是物体的机械能，所以燕子的机械能E=25J+15J=40J；（2）它从高空匀速飞落下来衔泥时，速度不变，动能不变；高度降低，重力势能变小，所在机械能减小．故答案为：40；减小．22．【考点】比热容解释简单的自然现象．【分析】要解答本题需掌握：水的比热容大，在同样吸放热条件下，水的温度变化小．【解答】解：沿海地区多水，水的比热容大，在同样吸放热条件下，水的温度变化小，所以昼夜温度变化不大．故答案为水，比热容．四、实验题：（10分，每空1分）23．【考点】探究比热容的实验．【分析】（1）根据图乙读出温度计的示数，即可得出水的沸点；（2）在相同的酒精灯下，向相同的烧杯加热，要比较吸收热量的多少，就得比较加热时间的多少，而实验中加热食盐水所用时间多，则其吸收的热量也多；（3）要比较比热容的大小，必须得控制其他物理量不变，保证质量不变，还有一个因素，得使两者的温度差相同，才可以比较比热容的大小．【解答】解：（1）根据图中所示，90℃﹣100℃中间有10个格，则1个格表示1℃，图中液面在90℃以上第8个小格，所以温度计示数为98℃，所以水的沸点为98℃；（2）用相同的酒精灯对两相同的烧杯加热，要比较吸收热量的多少，就得比较加热时间的多少，而实验中加热食盐水所用时间多，说明食盐水吸收的热量也多；（3）要比较比热容的大小，根据Q吸=cm△t可知，必须控制质量相同、两者升高的温度相同，才可以比较比热容的大小；水和食盐水的密度不同，体积相同，则二者的质量不同；因为食盐水的沸点比水的沸点高，所以它们升高的温度不相等，不能得出食盐水比热容大的结论．故答案为：（1）98；（2）多；（3）不能；没有控制质量和升高的温度相同．24．【考点】斜面机械效率的测量实验；机械效率；机械效率的计算；斜面的机械效率．【分析】（1）斜面的机械效率与斜面的高度、斜面的长度、斜面的粗糙程度等多个因素有关，研究斜面机械效率与其中某个因素的关系时必须采用控制变量法的思想；（2）斜面的有用功是克服小车重力做的功，用公式W有用=Gh计算，总功是拉力做的功，用公式W总=FS计算，机械效率等于有用功和总功的比值，用公式η=计算；（3）采用控制变量法思想探究的实验，在得实验结论时，找准变量和不变量，然后根据控制变量法结论的一般形式“在（）一定时，（）越（），（）越（）”归纳总结．【解答】解：（1）从实验记录表中可以看出，实验的因素比较多有斜面的夹角、斜面的粗糙程度、斜面的高度、斜面的长度等多个因素，有些因素相同，有些因素不同，这正是控制变量法思想的体现．（2）有用功W有用=Gh=2.1N×0.36m=0.756J，总功W总=FS=1.8N×0.5m=0.9J，机械效率η==×100%=84%；（3）斜面的倾斜程度通过斜面与水平面的夹角体现，夹角越大斜面的倾斜程度越大，分析第1、2、3组实验数据可知，斜面的光滑程度相同时，斜面的斜面的倾斜角度越大，机械效率越高；分析第3、4两组实验数据可知，斜面的倾斜角度相同时，斜面的表面越粗糙，机械效率越低．故答案为：（1）控制变量法；（2）0.756、0.9、84；（3）结论一：斜面的光滑程度相同时，斜面的倾斜角度越大（小），机械效率越高（低）；结论二：斜面的倾斜角度相同时，斜面的表面越粗糙（光滑），机械效率越低（高）．五．计算题：（要有计算公式和计算过程，15分）25．【考点】功的计算公式的应用．【分析】已知牵引力所做的功和汽车行驶路程，由W=Fs计算牵引力的大小．【解答】解：由题知，牵引力所做的功：W=8.0×104J，汽车行驶路程：s=160m，由W=Fs可得，牵引力：F===500N．答：汽车的牵引力为500N．26．【考点】功率的计算．【分析】（1）知道杠铃的质量m，根据公式G=mg可以计算出杠铃的重力；（2）已知杠铃的重力和杠铃被举高的高度，根据公式W=Gh可求对杠铃做的功．（3）知道对杠铃做的功和时间t，根据公式P=求他在这个过程中做功的平均功率．【解答】解：杠铃的重力：G=mg=140kg×10N/kg=1400N；运动员对杠铃做的功：W=Gh=1400N×1.6m=2240J；他在这个过程中做功的平均功率：P===2800W．答：他在这个过程中做功的平均功率是2800W．27．【考点】热量的计算．【分析】（1）已知水的质量、比热容、初温和末温，利用Q吸=c水m水（t﹣t0）计算水吸收的热量．（2）已知热效率，根据η=可求出燃烧液化石油气放出的热量Q放，再根据Q放=m气q变形可求得需燃烧液化石油气的质量．【解答】解：（1）水吸收的热量：Q吸=c水m水（t﹣t0）=4.2×103J/（kg•℃）×5kg×=1.68×106J；（2）由η=可得，完全燃烧液化石油气放出的热量：Q放===2.8×106J；由Q放=mq可得，需燃烧液化石油气的质量：m===0.08kg．答：（1）将质量为5kg，初温为20℃的水加热到100℃，水吸热1.68×106J；（2）需燃烧液化石油气0.08kg．。

通州区初三语文期末学业水平质量检测1．《大众电影》杂志创刊60余年，以图文并茂的形式普及电影文化，娱乐大众，拥有广泛的读者群体。

下面四幅书法作品，你认为哪幅不适合作为《大众电影》的标题，请写出书体名称并说明理由。

（3分）我认为第___幅不适合。

书体：____理由：_______________________________________________________________2．阅读下面的文字，完成第（1）—（3）题。

（7分）汉字，你承载．着文明的曙光，从远古走来。

【甲】 、白露时节的蒹葭，因你而走进《诗经》的抑扬顿挫；东篱采菊的独处．、 【乙】 ，因你而淡泊成最美的风景； 【丙】 ，烽火三月的痛楚，因你而伴着诗人的忧愤zh èn 聋发聩；桃园结义的豪情，鞠躬尽瘁的叹息，因你而随勾栏瓦社的茗香流传。

时间的长河，奔涌不息，五千年的文化，在你的舞蹈里，源远流长。

（1）下列成语中加点字与文段中加点字读音相同的一项是( )（2分）A ．载．歌载舞设身处．地 B ．一年半载．处．心积虑C．怨声载．道 恰到好处． D ．厚德载．物 绝处．逢生 （2）对拼音处字形与画线字笔顺判断全部正确的一项是( )（2分）A ．震“五”的笔顺为：B ．震 “五”的笔顺为：第一幅：第二幅： 第三幅：第四幅：C ．振 “五”的笔顺为：D ．振 “五”的笔顺为：（3）请将下面三句话分别填入文中【甲】【乙】【丙】处。

（只填序号）（3分）①石壕村中的夜啼 ②黄发垂髫的悠然 ③河畔婉转的雎鸠【甲】______ 【乙】______ 【丙】______3．依据语境与节气特点，用节气名称补全下面对联，最恰当的一项是( )（2分）上联：昨夜大寒， ① 茅屋如 ②下联：今朝惊蛰，春分时雨到 ③A ．①霜降②清明③小雪B ．①小雪②霜降③清明C ．①霜降②小雪③清明D ．①清明②小雪③霜降4．下列成语全部出自古诗词的一项是( )（2分）A ．无可奈何温故知新无人问津B ．悲欢离合柳暗花明万紫千红C ．门庭若市乘风破浪犬牙交错D ．辗转反侧似曾相识病入膏肓5．“长亭外，古道边，芳草碧连天……”循着这熟悉的旋律，同学们走进了卓越艺术家、教育家李叔同的故居。