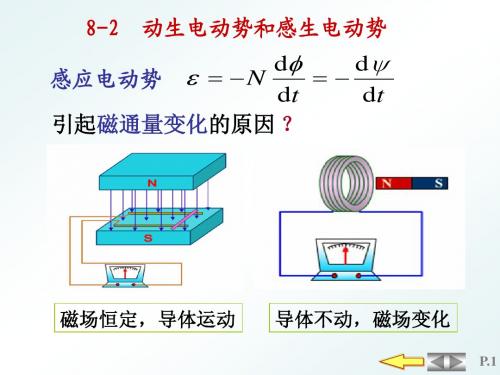
当前位置：文档之家 › 动生电动势和感生电动势

动生电动势和感生电动势

  • 格式：ppt
  • 大小：3.34 MB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

动生电动势和感生电动势

动生电动势和感生电动势

§6-2 动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。

感生电动势：仅由磁场的变化而产生的感应电动势。

一 动生电动势图6 - 5 动生电动势动生电动势的产生可以用洛伦兹力来解释。

长为l 的导体棒与导轨构成矩形回路abcd 平放在纸面内，均匀磁场B 垂直纸面向里。

当导体棒ab 以速度v 沿导轨向右滑动时，导体棒内自由电子也以速度v 随之一起向右运动。

每个自由电子受到的洛伦兹力为B v F ⨯-)(=e ,方向从b 指向a ，在其作用下自由电子向下运动。

如果导轨是导体，在回路中将形成沿着abcd 逆时针方向的电流。

如果导轨是绝缘体，则洛伦兹力将使自由电子在a 端累积，从而使a 端带负电，b 端带正电，在ab 棒上产生自上而下的静电场。

当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab 间电压达到稳定值，b 端电势比a 端高。

这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。

电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力K 所作的功，即B v F K ⨯=-=e.动生电动势为ε⎰⎰+-⋅⨯=⋅=l B v l K d )(d ba .(6.4)均匀磁场情况：若v ⊥ B , 则有ε = B l v ；若导体顺着磁场方向运动，v // B ，则有 v ⨯ B = 0，没有动生电动势产生。

因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。

普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈L (闭合的或不闭合的)在运动或发生形变时，各个线元d l 的速度v 的大小和方向都可能是不同的。

这时，在整个线圈L 中产生的动生电动势为ε l B v d )()(⋅⨯=⎰L .(6.5)图6 - 6 洛伦兹力不作功洛伦兹力对电荷不作功：洛伦兹力总是垂直于电荷的运动速度，即v ⊥F v ，因此洛伦兹力对电荷不作功。

第19讲动生电动势与感生电动势

第19讲动生电动势与感生电动势

解：由 B 0, 与B同向 感生电场沿逆时针。 t
取逆时针回路, r < R 时
l Ei dl
B dS S t
l
Ei
dl
cos
0
B t
dS
cos
Ei
2
r
dB dt
r2
r dB Ei 2 dt
××××× ×××××××
r × × × × × × ×
×××××××
×R× × × × B
r > R时，
3. 动生电动势的计算
作为电源的这段运动导体杆，其中的洛仑兹力 是非静电力。
非静电力 对应的非静电场强 由电动势定义
Fk e(v B)
Ek
Fk e
v
B
i Ek dl
运动导线ab产生的动生电动势为
i
(v B) dl
l
例题1 有一半圆形金属导线在匀强磁场中作切 割磁力线运动。已知 v, B, R. 求动生电动势.
解：
d (v B)dl
dl Rd v B
vB sin900 dl cos
2
vBR cos d 2 vB2R 有效段！
b dl
d
v
0：与假定的方向相同
R
B
方向：a b
a
例题2 如图，长为L 的铜棒在匀强磁场中以角速度 ω绕 o 轴转动。求：棒中感应电动势的大小 和方向。
解：取如图所示微元(此微元暗示了假定的正方向)
C × × ×O× ×
B t
Ei Dx
L
d Ei dx cos
r dB dx cos
2 dt
r dB Ei 2 dt
逆时针
r cos h

12.2 动生电动势和感生电动势

12.2 动生电动势和感生电动势

此时电荷积累停止， 两端形成稳定的电势差 两端形成稳定的电势差。 此时电荷积累停止，ab两端形成稳定的电势差。 洛仑兹力是产生动生电动势的根本原因 洛仑兹力是产生动生电动势的根本原因. 是产生动生电动势的根本原因
动生电动势的公式
非静电力
f = −e(v × B)
f 定义 Ek为非静电场强 Ek = = v ×B −e
S
A B ××× ×
ω ××v × ×
非均匀磁场
例 一直导线CD在一无限长直电流磁场中作 一直导线 在一无限长直电流磁场中作 切割磁力线运动。 切割磁力线运动。求：动生电动势。 动生电动势。 解：方法一
dε = ( v × B )⋅ dl I l dl µ0I 0 0 D sin90 dl cos180 =v C 2πl b a µ0vI dl =− 方向 D→C → 2πl µ0vI a+b dl µ0vI a + b ε =− ∫a l = − 2π ln a 2π
×××× ⊗ o ×××× B ×××× h
C
∂B ∂t
××
L
D
解:
ε i = ∫ E涡 • dl
L
r dB E涡 = 2 dt
dε = E涡 • dl r dB dl cosθ = 2 dt
h dB dl = 2 dt
⊗o
B
⊗
θ
∂B ∂t
E涡
r h
l dl
L
θ
C
D
h dB 1 dB εCD = ∫L dl = 2hL dt 2 dt
O
解：方法一 取微元
dε = ( v × B )⋅ dl
= Bvdl = Blωdl
εi = ∫ dεi = ∫0 Blωdl

动生电动势与感生电动势

动生电动势与感生电动势

【解】由于金属棒处在通电导线的非均匀磁场中，因此必
须将金属棒分成很多长度元dx，规定其方向由A指向B。这样 在每一dx处的磁场可以看作是均匀的，其磁感应强度的大小为
B 0I
2x
根据动生电动势的公式可知，dx小段上的动生电动势为
d动
(v
B)
dl
Bv
cos
dx
0I
2x
vdx
由于所有长度元上产生的动生电动势的方向都相同，所以金
d
dt
d dt
S
B
dS
又根据电动势的定义可得
L EK dl
式中，EK为感生电场的电场强度。感生电场的电场强度是 非静电性场强。
则有
L EK
dl
d dt
B dS B dS
s
s t
dB
s
S t
若闭合回路是静止的，即所包围面积S不随时间变化，即
S 0 ，则上式可写成
t
B L EK dl s t dS
性场强为
Ek
fL (e)
vB
根据电动势的定义可得，动生电动势为
a
动
L Ek
dl
(v B) dl
b
上式是动生电动势的一般表达式。由上式可知，动生电动势
的方向是非静电性场强 Ek v B 在运动导线上投影的指向。
【例9-2】如下图所示，长直导线 中通有电流I＝10A，有一长l＝0.1m的 金属棒AB，以v＝4m·s-2的速度平行于 长直导线作匀速运动，棒离导线较近的 一端到导线的距离a＝0.1m，求金属棒 中的动生电动势。
1861年，英国物理学家麦克斯韦提出感生电场的假设，认为 由于磁场变化而产生一种电场，是这个电场使导体中自由电子作 定向运动而形成电流。麦克斯韦还认为，即使没有导体，这种电 场同样存在。这种由变化磁场激发的电场称为感生电场。

动生电动势和感生电动势

动生电动势和感生电动势

动生电动势和感生电动势§6-2动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。

感生电动势：仅由磁场的变化而产生的感应电动势。

一动生电动势图6-5动生电动势动生电动势的产生可以用洛伦兹力来解释。

长为l的导体棒与导轨构成矩形回路abcd平放在纸面内，均匀磁场b垂直纸面向里。

当导体棒ab以速度v沿导轨向右滑动时，导体棒内自由电子也以速度v随之一起向右运动。

每个自由电子受到的洛伦兹力为f=（。

e）v。

b，方向从b指向a，在其作用下自由电子向下运动。

如果导轨是导体，在回路中将形成沿着abcd逆时针方向的电流。

如果导轨是绝缘体，则洛伦兹力将使自由电子在a端累积，从而使a端带负电，b端带正电，在ab棒上产生自上而下的静电场。

当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab间电压达到稳定值，b端电势比a端高。

这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。

电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力k所作的功，即k。

f。

e。

v。

b.动生电动势为。

k。

dl。

a（v。

b）。

dl.b（6.4）均匀磁场情况。

若v。

b，则有。

=blv；若导体顺着磁场方向运动，v。

b，则有v。

b=0，没有动生电动势产生。

因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。

普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈l（闭合的或不闭合的）1在运动或发生形变时，各个线元dl的速度v的大小和方向都可能是不同的。

这时，在整个线圈l中产生的动生电动势为。

（v。

b）。

dl.（l）（6.5）图6-6洛伦兹力不作功洛伦兹力对电荷不作功。

洛伦兹力总是垂直于电荷的运动速度，即fv。

v，因此洛伦兹力对电荷不作功。

然而，当导体棒与导轨构成回路时会有感应电流出现，这时感应电动势却是要作功的。

感应电动势作功能量的来源。

在运动导体中的自由电子不但具有导体本身的运动速度v，而且还具有相对于导体的定向运动速度u，与此相应的洛伦兹力fu。

动生电动势和感生电动势

动生电动势和感生电动势

Ek
1 2
B t
r
1 2
kr
2. r > R 区域
作半径为 r 的环形路径，并以逆
时针为回路绕向，则同理有
2rEk
S
B t
ds
R2k
R
o
r
r
B
1 B R2 1 R2
Ek 2 t
r
k 2r
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 9/33
随时间均匀增加， dB k dt
若铝圆盘的电导率为γ，求盘内 的感应电流。
见书P212页，例4
R
解： 取半径为r、宽为dr的圆环微 元，并以逆时针方向为正方向，则 微元环中元电动势为
d L Ek dl L Ek dl
1 kr 2r dl kr2
20
o
r
dr
B
微元环中的电阻为 dR 1 2r hdr
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 21/33
4) 电度表记录电量
电度表记录用电量，就是
利用通有交流电的铁心产生交
变的磁场，在缝隙处铝盘上产
o
生涡电流，涡电流的磁场与电
磁铁的磁场作用，表盘受到一
转动力矩，使表盘转动。
o’
Foundation - SJYGGF
感生电动势
1. 感生电动势——回路不动或不变，因磁场随时间变 化产生的电动势。相应的电流称为感生电流。
2. 感生电动势的起源——感生电场Ek 1) Maxwell感生电场（涡旋电场）假设
Maxwell 1861年首先从理论上预言感生电场的存在，后 被Hertz的电磁波实验所证实。Maxwell假设： 变化的磁场要在其周围空间激发一种电场——感生电场

感生电动势和动生电动势

感生电动势和动生电动势
VIP时长期间，下载特权不清零。
100W优质文档免费下 载
VIP有效期内的用户可以免费下载VIP免费文档，不消耗下载特权，非会员用户需要消耗下载券/积分获取。
ቤተ መጻሕፍቲ ባይዱ
部分付费文档八折起 VIP用户在购买精选付费文档时可享受8折优惠，省上加省；参与折扣的付费文档均会在阅读页标识出折扣价格。
在这种电场力的作用下定向移动,产生感应 电流,或者说产生感应电动势.变化的的磁
场能在周围空间激发电场,这种电场叫感应 电场,由感生电场产生的感应电动势称为感 生电动势.
感生电动势在电路中的作用就是 电源,其电路就是内电路,当它与 外电路连接后就会对外电路供电.
感应电场是产生感应电流或感应电动势 的原因,感应电场的方向同样可由楞次定 律判断.
X X CX
伦兹力为F洛=QVB,F洛方向向上,正 X X XF洛 电荷向上运动,使导体下端出现负电 X XL X V 荷,结果上端C的电势高于下端D的 X X XF电 电势,出现由C指向D的静电场,此时 X X DX 电场对正电荷的作用力是向下,与洛 伦兹力方向相反,当二力互相平衡时， ＣＤ两端随时随地彰显尊贵身份。
专属客服
VIP专属客服，第一时间解决你的问题。专属客服QQ：800049878
路漫部权益：1.海量精选书免费读2.热门好书抢先看3.独家精品资源4.VIP专属身份标识5.全站去广告6.名
VIP专享文档下载特权自VIP生效起每月发放一次， 每次发放的特权有效期为1个月，发放数量由您购买 的VIP类型决定。
每月专享9次VIP专享文档下载特权， 自VIP生效起每月发放一次，持续有 效不清零。自动续费，前往我的账号 -我的设置随时取消。
服务特 权
共享文档下载特权

动生电动势与感生电动势

动生电动势与感生电动势

Science &Technology Vision 科技视界1动生电动势如图1,一根金属棒在匀强磁场中沿与棒和磁场垂直的方向以速度V0向右运动。

自由电荷(电子)随棒运动。

必然受到洛仑磁力作用,而发生运动。

电子沿棒运动的速度为U。

这样自由电子具有随金属棒运动的速度V0同时还有沿棒运动的速度U,故自由电子相对磁场的合速度为V0。

金属棒ab 两端因正负电荷分别积累,而形成电动势,Uab>0。

图1由左手定则可知,由于自由电子相对磁场以速度V 运动,一定会受到洛仑磁力F 洛。

当F 洛的分力F1与F 外平衡,F 洛的另一分力F2与电场力FE 平衡时,金属棒两端建立了稳定的动生电动势。

F 洛=eBV 其分力F1=eBVcosα=eBu,F2=eBVsinα=eBV0金属棒ab 两端电动势U=BLV0,自由电子受到的电场力FE=eE=eBLV0/L=eBV0FE 与F2等大反向。

F 外与F1等大反向(图2)。

图2F E 与F 外的合力F'=eB V 02+U 2√=eBVH 合和F 洛等大反向。

此时自由电子受到的三个力F 洛、F 外、F E 作用达到平衡。

金属棒匀速垂直切割磁感线运动建立了稳定的电动势。

E=BLV 0从能量转化的观点来看:外力克服洛仑磁力的分力F1做功,机械能转化的电能。

在此过程中洛仑磁力起到中转能量的作用。

使机械能和电能之间发生转化。

那么洛仑磁力是否做功呢:F 洛的分力F 1与V 0反向做负功W1,另一分力F2与电子沿棒移动方向U 一致做正功W2,则有:W1=-F 1V 0t=-eBIV 0t W2=F 2Ut=eBV 0Ut W=W1+W1=0其实洛仑磁力F H 合与电子合速度V 垂直,其做功为零是肯定的。

我们可以看到动生电动势有以下几个特点:a.在能量转化上是机械能转化为电能。

b.洛仑磁力参与其全过程并传递能量,实现两种形式的能量转化。

c.因为洛仑磁力与自由电荷合速度方向垂直,洛仑磁力不做功。

动生和感生电动势

动生和感生电动势
动生和感生电动势
目录
• 动生电动势 • 感生电动势 • 比较动生和感生电动势 • 实例分析 • 问题与讨论
01
CATALOGUE
动生电动势
定义与原理
定义
动生电动势是指由导体在磁场中运动而产生的感应电动势。
原理
根据法拉第电磁感应定律，当导体在磁场中运动时，导体中 的电子会受到洛伦兹力的作用，从而在导体两端产生电动势 。
感生电动势的大小取决于磁场的变化率。如果磁场变化很快，那么产生的电动势就很大。
应用比较
动生电动势在电力生产和传输中起着关键作用。例如，发电机是通过动生电动势将机械能转化为电能 。
感生电动势在电子设备和磁性材料中有着广泛的应用。例如，变压器和电感器是通过感生电动势来改 变信号和传输能量。
04
CATALOGUE
电磁制动
在某些机械设备中，利用 动生电动势可以实现电磁 制动，达到减速或停止的 目的。
电磁感应现象
动生电动势是电磁感应现 象的一种表现形式，可以 用来解释和利用电磁感应 现象。
02
CATALOGUE
感生电动势
定义与原理
定义
感生电动势是指磁场变化时在导体中产生的电动势。
原理
根据法拉第电磁感应定律，当一个导体处于变化的磁场中时，导体中的自由电子 会受到洛伦兹力的作用，从而在导体两端产生电动势。
电子感应加速器
利用感生电动势加速带电粒子。
03
CATALOGUE
比较动生和感生电动势
产生方式比较
动生电动势
是由磁场和导线的相对运动引起的。当 导线切割磁力线时，导线两端会感应出 电动势。
VS
感生电动势
是由磁场的变化引起的。当磁场发生变化 时，附近的导体中会产生感应电流和电动 势。

动生电动势和感生电动势

动生电动势和感生电动势
8-2
动生电动势和感生电动势
d d 感应电动势 N dt dt 引起磁通量变化的原因 ？
磁场恒定，导体运动
导体不动，磁场变化
P.1
1、电动势定义
I
Ek
+
-
Ek : 非静电电场强度.



Ek dl
P.2
2、感应电动势的分类： （1）动生电动势 稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等。 （2）感生电动势： 导体不动，磁场变化。
OP
P.5
动生

OP
(v B) dl
混合积：(a b ) c
× × P ×
(vB sin ) cosdl
OP
×
× × ×
×
(v × B) ×
× ×
×
特例 B均匀，杆 l水平运动：
l×
×
× v×
× B
× O ×

OP
l
l (vB sin 900 )cos00 dl (v B) dl 0
vBl
vBdl vBl
0
P.6
2、计算方法
d动生 (v B) dl
动生
×
×
× P× B × dl
× ×

OP
(v B) dl
1 2 d BL 2 dt 1 2 BL 2
×
×
× P × × × ×
× ×
B ×
×
×
×
o
×
×
×
×
×
×
×

动生电动势与感生电动势

动生电动势与感生电动势

F(m e)vvBB
(e)
i
op Ek dl
(v B) dl
op
在磁场中运动的导线内的感应电动势
i
op Ek dl
(v B) dl
op
由上式可以看出，矢积
v与 B
成锐d l角时，
为i
正负为；之负成分时i 钝，，角则为时 表正， 示时i电，为动i表负势示。的电因方动此向势，逆方由着向上顺式的着算方出向d的。l的电方d动l向势；有正
C B B
通电导体棒AB在磁场中受到的安培力大小为Fm ，IlB
方向向左。为了使导体棒匀速向右运动，必须有外力
F外与Fm平衡，它们大小相等，方向相反。因此，外
力的功率为
P F v IilBv
这正好等于上面求得的感应电动势做功的功率。
在磁场中运动的导线内的感应电动势 例13—2 长为L的铜棒在磁感强度为B的均匀磁场中，以角
由于ab ,表0 明电动势的方向由a 指向b,b 端电势较高。
在磁场中运动的导线内的感应电动势
（2）应用电磁感应定律求解 设某时刻导线ab 到U 形
a
v
X b
框底边的距离为x，取顺时
针方向为回路的正方向,则
I
O
O
该时刻通过回路 abo的o磁a
r
通量为
dr
Φ
s
B
d
S
dL d
0I 2r
x
d
r
0Ix 2
由 B dS可知，取决于B、S以及B与S
S
的夹角三个因素，我们 把由于B变化而引起 的感
应电动势叫做感生电动 势；而把由于 S或B与S
的夹角的变化而引起的 感应电动势叫做动生电 动势。

动生电动势和感生电动势

动生电动势和感生电动势

m1
三、电子感应加速器
原理：在电磁铁的两磁极间放一个真空室，电磁铁是由
交流电来激磁的。
当磁场发生变化时，两极间任意闭合回路的磁通发生变化， 激起感生电场，电子在感生电场的作用下被加速，电子在 Lorentz力作用下将在环形室内沿圆周轨道运动。
轨道环内的磁场 等于它围绕面积 内磁场平均值的 一半。
解:法拉第电机可视为无数铜棒一 端在圆心，另一端在圆周上，即为 并联，因此其电动势类似于一根铜 棒绕其一端旋转产生的电动势。
w
B
o a
R
U0 Ua o Bwl dl
U0
Ua
1 2
BR2w
二、感生电动势
1、感生电动势
由于磁场的变化而在回路中产生的感应电 动势称为感生电动势.
2、感生电场
变化的磁场在其周围空间激发的一种能够产生感生电动势 的电场，这种电场叫做感生电场，或涡旋电场。
是以轴为圆心的一系列同心圆，同一同心圆
上任一点的感生电场的Ek大小相等，并且方
向必然与回路相切。于是沿L取Ek的线积分，
有：
L Ek dl Ek 2 r
EkΒιβλιοθήκη 2rr 2dB dt
若r<R，则 Br 2
L
Ek
dl
－ d dt
r 2
dB dt
r dB Ek 2 dt
若r≥R，则
BR2
2、涡流的热效应
电阻小，电流大，能 够产生大量的热量。
3、应用
高频感应炉 真空无按触加热
加热
4、涡流的阻尼作用
当铝片摆动时，穿过运动铝片的磁通量 是变化的，铝片内将产生涡流。根据楞 次定律感应电流的效果总是反抗引起感 应电流的原因。因此铝片的摆动会受到 阻滞而停止，这就是电磁阻尼。

动生和感生电动势

动生和感生电动势
动生和感生电动势
汇报人： 日期:
目录
• 动生电动势 • 感生电动势 • 动生与感生电动势的异同点 • 动生和感生电动势在电磁学中
的重要性
01
动生电动势
定义与产生机理
定义
动生电动势是由于导体在磁场中运动，导致导体中的自由电子受到洛伦兹力作 用，从而在导体内部形成电动势。
产生机理
当导体在磁场中运动时，导体中的自由电子受到洛伦兹力作用，产生定向移动 ，形成电流。这个电流在导体内部产生电动势，其方向与电流方向相反。
动生电动势的应用场景
电磁感应现象
电磁测量
动生电动势是电磁感应现象中的一种 表现形式，可以用来解释电磁感应现 象。
动生电动势可以用于电磁测量中，例 如测量磁场强度、电流强度等参数。
电机原理
电机是利用动生电动势的原理工作的 ，当电机中的导线在磁场中运动时， 导线中会产生动生电动势，从而驱动 电机转动。
动生电动势的计算方法
公式
动生电动势的大小可以通过计算洛伦兹力与导体运动速度的乘积得到。公式为： E =BLv，其中E为动生电动势，B为磁场强度，L为导体长度，v为导体运动速度 。
注意事项
在计算动生电动势时，需要确定磁场强度、导体长度和导体运动速度等参数。同 时，还需要注意洛伦兹力方向与电流方向的关系。
02
感生电动势
定义与产生机理
定义
感生电动势是由于磁场变化而产 生的电动势。当磁场发生变化时 ，会在导体中产生感应电流，从 而产生电动势。
产生机理
当磁场发生变化时，导体中的自 由电子受到洛伦兹力的作用，定 向移动形成电流，从而产生电动 势。
感生电动势的计算方法
计算公式
感生电动势的大小可以通过法拉第电磁感应定律来计算，即 E=nΔΦ/Δt，其中E为感生电动势，n为线圈匝数，ΔΦ为磁通 量的变化量，Δt为时间间隔。

动生电动势 感生电动势

动生电动势 感生电动势

bv
a
I
例10－6 由导线弯成的宽为a
高为b的矩形线圈，以不变速 率v平行于其宽度方向从无磁 场空间垂直于边界进入一宽为
3a
3a的均匀磁场中，线圈平面与 磁场方向垂直（如图），然后
又从磁场中出来，继续在无磁
场空间运动。设线圈右边刚进
入磁场时为t=0时刻，试在附
图中画出感应电流I与时间t的
ab中的感生电动势，并确定哪端电势高？解：Fra bibliotekl Er
dl
dm
dt
螺线管外感生电场的分布具有轴对 称性，取半径为r（r>R）的圆形环
R
o 0
Er b
rP
路与ab交于P点，Er沿P点的逆时针 切线方向。则
a
l
E r
dl
E r
2r
m B S 0nI R2 29
dm
dt
0n
dI dt
R2
，设t = 0 时线圈平面的法线方向n0
与B的夹角为 = 0，若线圈角速度为
，则 t时刻穿过该线圈的磁通为
m B s Bscos Bscos t
由法拉第电磁感应定律
0 b
c
no
B
a
d 0/
i
d dt
d dt
(NBscos t)
NBs sint m sin t m NBs
电动势的实质依然是动生电动势,上述为交流发电机的工作原理 14
uB v v B u
所以总的洛仑兹力的功率为零，即总的洛仑兹力仍然不做功。
但为维持导体棒以速度v作匀速运动，必须施加外力以克服
洛仑兹力的一个分力fmu=qu×B。
由前述可知
qu B v qv B u
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
3
已知 R1 1.2m ,
2R2
d 1.0 10 m , 5 2 π rad s 1
R2 2.0 10 m , T01 B
3

N dr R1 r
求
E i ?
R1，
o
.
B
（方法一） 解 因为 d 所以不计圆盘厚度.
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
例 3 设有一半径为R ,高度为 h 的铝圆盘, 其电导 率为 . 把圆盘放在磁感强度为 B 的均匀磁场中, 磁 场方向垂直盘面.设磁场随时间变化, 且 dB dt k 为一常量.求盘内的感应电流值.（圆盘内感应电流自 己的磁场略去不计） r dr
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
1 2 2 Φ B( R1 R2 ) 2R2 2 设 t 0 时点 M 与点 N 重合即 0 N' R1 则 t 时刻 t d o N B 1 2 2 Φ B( R1 R2 )t 2 M d Φ E i o' E B i dt 1 2 2 方向与回路 MNOM 绕向 B ( R1 R2 ) 相反,即盘缘的电势高于中心. 2
d Ei (v B) dl
vBdl
L
+ + P + + + + +
E i vBdl
0
B
o v + + +
Ei 方向 O P 1 2 E B L i （点 P 的电势高于点 O 的电
+ + + + + + +
13 - 2 动生电动势和感生电动势
动生电动势的非静电力场来源
洛伦兹力
+ + + P + + + + B ++ + + F+ + + + +
e
+ + + -+ + + + + + + -+ + + O+ +
Fm
+ v
+
+ + + +
E i
设杆长为
OP
Ek dl OP ( v B ) dl
2 2
2 2
方向沿 ox轴反向
N
则
dv B l v m dt R 2 2 v dv t B l v0 v 0 mR dt
R l
B
F
v
M
o
x
计算得棒的速率随时间变化的函数关系为
v v0 e
( B 2l 2 mR ) t
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
例2 一导线矩形框的平面与磁感强度为 B 的均 匀磁场相垂直.在此矩形框上,有一质量为 m长为 l 的 可移动的细导体棒 MN ; 矩形框还接有一个电阻 R , 其值较之导线的电阻值要大得很多 .若开始时,细导体 棒以速度 v0 沿如图所示的矩形框运动,试求棒的速率
第十三章电磁感应 电磁场
四 涡电流 感应电流不仅 能在导电回 路内出 现， 而且当大块导 体与磁场有相对运 动或处在变化的磁 场中时，在这块导 体中也会激起感应 电流.这种在大块导 体内流动的感应电 流,叫做涡电流 , 简 称涡流. 应用 热效应、电磁阻尼效应.
13 - 2 动生电动势和感生电动势
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
E R rBdr i
R2 1
o
.
B
1 2 2 B ( R1 R2 ) 2 226 V
圆盘边缘的电势高于 中心转轴的电势.
B
M
E i o'
..
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
3
1
已知 R1 1.2m ,
2R2
d 1.0 10 m , 5 2 π rad s
则圆环中的感生电动势的值为
r
dr
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
由计算得圆环中电流
kh dI rdr 2
于是圆盘中的感应电流为
r
dr
h
r
dr
kh R I dI rd r 2 0 1 2 kR h 4
13 - 2 动生电动势和感生电动势
h
R
h
r
dr
B
13 - 2 动生电动势和感生电动势
已知 求
R , h , , B , dB dt k
I
第十三章电磁感应 电磁场
r
dr
h
解 如图取一半径为 r ,宽度 为dr ,高度为 h 的圆环.
dB E i Ek dl ds L S dt d B 2 代入已知条件得 E ds k π r i dt S 1 2π r kh 又 dR rdr 所以 dI hdr 2
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
.
..
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
3
R2 2.0 10 m , T01 B

R1
求
E i ?
o
B
M

.
d N B
N'
（方法二） 解 取一虚拟的闭和 回路 MNOM 并去取其 绕向与 B 相同 . 则
E i o'
..
Φ B

1 2 2 B ( R1 R2 ) 2
2π
2 π ( R12 R2 )
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
引起磁通量变化的原因
1）稳恒磁场中的导体运动 , 或者回路面积
变化、取向变化等 动生电动势 感生电动势
2）导体不动，磁场变化
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
l
E i vBdl vBl
0
l
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
例1 的均匀 磁场中,以角速度 在与磁场方向垂直的平面上绕 棒的一端转动，求铜棒两端的感应电动势. 解
一长为 L 的铜棒在磁感强度为 B
+ + + + + + + + + + + + + + + dl + + +
E


Ek dl
13 - 2 动生电动势和感生电动势
闭合电路的总电动势
E E k dl
l
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
一 动生电动势
Fm (e)v B 平衡时 Fm Fe eEk Fm Ek v B e
如图取线元 dr
则
B
M
E i o'
..
dE i (v B) dr
vBdr rB dr
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
解
2R2
dE i ( v B) dr vBdr rBdr

N dr R1 r
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场

L
E静 dl 0
dΦ 感生电场是非保守场 L Ek dl dt 0
静电场由电荷产生；感生电场是由变化的磁 场产生 .
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
随时间变化的函数关系. 解 如图建立坐标 棒中
第十三章电磁感应 电磁场
N N
E i Blv
且由 M
2 2
棒所受安培力
R l
B
B l v F IBl R 方向沿 ox轴反向
F
I
M
v