2013年数学建模竞赛培训内容(新)
- 格式:doc
- 大小:26.50 KB
- 文档页数:1


2013年全国大学生数学建模比赛培训及比赛相关说明
1.培训时间:2013年8月5日—8月23日
2.培训流程:
(1)2013年8月5日—8月11日,基础培训。
培训内容:上午和下午数学建模比赛可能会用得到的数学知识,晚上机房(14号楼)上机操作,主要是Matlab。
培训说明:本周内应组队完成,如果自己最终还找不到,可向老师求助。
(2)2013年8月12日,休息一天
(3)2013年8月13日—2013年8月23日,比赛模拟训练。
第一阶段:老师出题,小组找一篇别人的论文读懂,参加答辩。
第二阶段:老师出题,小组找几篇别人的论文,总结出思路,写一篇论文,参加答辩。
第三阶段:老师出题,小组独立完成论文。
培训说明:以上完成时间均为3天。
PS;应该比高三还紧张,最好准备。
3.比赛时间:2013年9月13日8点—9月16日8点
比赛说明:13日早上8点下载题目,确定选题,9月16日8点前完成一篇学术论文。
PS:(1)建议论文尽早开始写。
不然,早16日早上8点可能无法完成;
(2)论文很注重格式,比如字体,首行缩进等等。
请在写作过程和论文完成后特别注意;
(3)论文的摘要请一定要写清楚。
推荐格式:本人针对XX问题,运用了XX方法,得到了XX结论,对于问题一,对于问题二,对于问题三。

数模培训计划一、培训背景和目的数学建模是一种将数学方法应用于实际问题求解的过程,通过建立数学模型,解决现实问题。
数学建模在工程、经济、生物、环境等领域都有广泛的应用。
为了提高学生的数学建模能力,培养学生的实际问题解决能力,学校决定组织开展数学建模的培训活动。
培训目的:通过培训,提高学生的数学建模能力和实际问题解决能力,培养创新思维和团队协作能力,为学生参加数学建模竞赛做好准备。
二、培训对象培训对象为高中或大学在校学生,年级不限。
三、培训内容1.数学建模基础知识:介绍数学建模的基本概念和方法,包括建模的基本流程、模型分类、建模误差及可行性分析等。
2.数学建模工具:介绍数学建模的常见工具,如Matlab、Python、R等编程语言和软件,在建模过程中的使用。
3.实例分析:通过一些经典的数学建模实例,讲解实际问题的数学建模和求解过程,帮助学生理解数学建模的实际应用。
4.团队合作:培养学生团队协作能力,通过小组讨论和合作实践,提高学生在团队中的沟通和协作能力。
5.竞赛技巧:介绍数学建模竞赛的常见题型和解题技巧,帮助学生提高在竞赛中的应试能力。
6.实践演练:组织学生实际参与数学建模竞赛,通过实际操作提高学生的数学建模能力。
四、培训方式1.线上课程:采用网络直播的方式进行培训课程,学生可以在家中通过网络参与培训课程。
2.线下实践:定期组织学生到实验室或企业进行实地参观和实践活动,帮助学生了解实际问题解决的流程和方法。
3.小组讨论:组织学生进行小组讨论,通过讨论和合作,提高学生的团队协作能力。
五、培训评估1.培训结束后,组织学生进行统一考试,考核学生的数学建模基础知识和实际问题解决能力。
2.培训过程中,定期对学生进行考核和评估,及时发现问题并进行指导和帮助。
3.定期组织学生进行实际项目的实践活动,评估学生的实际应用能力。
六、培训师资培训师资由学校优秀的数学教师和企业相关领域的专业人士组成,保证培训课程的专业性和实用性。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):甲所属学校(请填写完整的全名):曲阜师范大学日照校区参赛队员 (打印并签名) :1. 文志勇2. 周祥亮3. 步巧凤指导教师或指导教师组负责人 (打印并签名):邢丽红日期:2013年9月13 日编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):碎纸片的拼接复原摘要本文对文字(中文或者英文)碎片的自动拼接问题展开研究,介绍了文字碎片预处理及碎片拼接的理论与技术,并重点研究了碎片拼接的核心问题文字碎片匹配,文中提出了一种基于???匹配算法,用于获得文字碎片最可能的拼接结果,并将该算法与多尺度空间结合,提高计算效率与现有的曲率序列匹配算法相比,角序列匹配算法不但有效地解决了文字碎片在拼合过程中的模糊识别问题,且提高了计算效率,最后,本文应用Matlab程序设计,实现了文字碎片的自动拼接。
图像碎片拼接的方法很多,根据特征可以分为基于色彩!纹理!材质!轮廓等图像碎片拼接;根据形状特征又可以分为规则图像碎片和不规则图像碎片的拼接;根据空间特征还可分为二维图像碎片拼接和三维图像碎片拼接"图像碎片拼接的主要工作流程可概括为以下三个步骤:(l)对图像碎片进行预处理,即对物体碎片数字化,得到碎片的数字图像"(2)图像碎片匹配,通过匹配算法找到相互匹配的图像碎片"(3)图像碎片的拼接合并,将相互匹配的图像碎片拼接在一起得到最终的结果"其中,最重要的就是第二步图像碎片匹配"图像碎片匹配是图像碎片拼接的核心问题,是学术研究的前沿问题,这个问题的研究是模式识别技术的一个新的拓展,更好的促进模式识别方法的发展"因此图像碎片匹配的研究工作具有重要的理论和现实意义,也是本文的研究重点"提供了一种典型的解决平面图像碎片匹配算法"它定义一个判别式,把不符合判别式的一对对侯选匹配通过多尺度方法逐步从原可能匹配的集合中删除,最后剩下的少量匹配对可能就是真正匹配的图像碎片对对于问题1我们用。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A 我们的参赛报名号为(即电子文件名):所属学校(请填写完整的全名):玉林师范学院参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):日期: 2013年 9 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):车道被占用对城市道路通行能力的影响摘要本文研究发生交通事故时车道被占用对城市道路通行能力的影响问题。
可视作优化类问题,本题重点在于目标的选取和目标函数的建立。
可用排队论,模拟仿真,泊松定理等手段来建立函数模型;使问题迎刃而解。
具体分析如下:针对问题一,为更真实地反应在交通事故发生至撤离期间,事故所处于横断面实际通行能力的变化过程的实际情况,本文针对视频一得数据运用excel表格制图与Matlab 软件进行拟合,拟合曲线能够很直观地反映通行情况,具有较高实用性。
针对问题二,结合问题一以及对视频二的车辆通行情况的比较,可以运用与问题一相同的求法,把两视频拟合曲线相比较,即可判断出同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异。

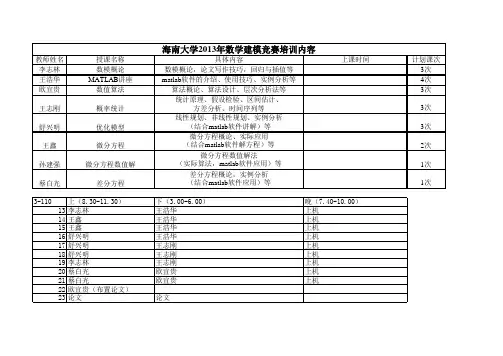
教师姓名授课名称具体内容
上课时间
计划课次李志林数模概论数模概论,论文写作技巧,回归与插值等3次王浩华MATLAB 讲座matlab 软件的介绍、使用技巧、实例分析等4次欧宜贵数值算法算法概论、算法设计、层次分析法等3次统计原理、假设检验、区间估计、
方差分析、时间序列等
线性规划、非线性规划、实例分析
(结合matlab
软件讲解)等微分方程概论、实际应用(结合matlab 软件解方程)等
微分方程数值解法
(实际算法,matlab 软件应用)等
差分方程概论,实例分析(结合matlab 软件应用)等海南大学2013年数学建模竞赛培训内容
王志刚概率统计3次王鑫微分方程2次舒兴明优化模型3次蔡白光差分方程
1次
孙建强微分方程数值解1次。

承诺书我们仔细阅读了南昌大学数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B中选择一项填写): B .报名序号是(没有或不清楚可不填):_____152__________.参赛队员(打印并签名) :所属院系(请填写完整的全名):日期: 2013 年 5 月 28 日编号专用页评阅编号:冠心病月就诊人数的预测模型摘要冠心病是目前威胁人类生命的严重疾病之一,对其发病环境因素进行分析,其目的是为了对其就诊人数的进行预测,掌握其发病率的规律,有效降低其危害。
本文建立了主成分分析模型对冠心病月就诊人数问题进行了研究。
问题一中,我们采用主成分分析法,利用s p s s数学软件分别算出各个影响因素的特征值和方差贡献率及累计方差贡献率,提取出累计方差贡献率为92.234%的y1,y2这两个新变量,并采用偏最小二乘回归方法对冠心病的发病率与影响因素之间的关系进行线性拟合,得出它们的关系式,z=0.1435*exp(0.00571*y1)+0.1237*exp(0.005843*y2)并进行检验,检验结果证明,模型有效。
为卫生行政部门和医疗机构提出预警和干预的建议方案做准备。
问题二中,我们根据用excel画平均气压与时间的关系,可认为气压随时间近似为正弦变化,根据利用m a t l a b中c f t o o l软件包拟合出影响最大的两个变量中,平均气压、最高气压与月份序号的关系,以便预测接下来的气压变化,利用傅里叶级数模型x=a0+a1*cos(w*t)+b1*sin(w*t)预测:第97月的第一个新变量为:885.15302064164732913081212563522,第97月的第二个新变量为:1023.1664276144538880403457721973。

2013高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):长春理工大学光电信息学院参赛队员(打印并签名) :1. 翁思远2. 赵潇婧3. 石国伟指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 9 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):S28033所属学校(请填写完整的全名):信息工程大学参赛队员(打印并签名) :1. 王丹菂2. 林雨准3. 秦剑琪指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 9 月 15 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):碎纸片的拼接与复原模型分析摘要本文研究的是碎纸片的拼接与复原问题。
利用碎纸片内字迹的连续性和行间距等特征,对纸片边缘进行相似度分析,以碎纸片边缘文字的灰度为依据进行匹配与拼接。
在此基础上,加上人工干预,采用半自动碎片拼接的方法,对碎纸片进一步进行比较与分析。
关于2013全国大学生数学建模竞赛培训的通知各学院:2013全国大学生数学建模竞赛将于2013年9月举行,为使我校学生在该项竞赛中取得较好成绩,尽早做好参赛的各项准备工作,现将数模培训的有关事项通知如下:一、本次将开设《数学建模实践与认识》相关培训课程,内容包括数学建模简介、MatLab与Lingo软件基础和部分常用数学建模方法介绍,具体安排见下表。
二、培训时间为本学期第三周(3月16日)至第十四周(6月1日)。
理论教学:每周六上午8:30—11:30,地点A01129教室。
实验教学:第四周(3月23日)、第五周(3月30日)的周六下午14:00—17:20和晚上6:30—21:40,地点在双福校区计算机中心二、三机房。
请各学院通知报名的学生按时参加培训。
(名单见附见1)。
三、参加的同学需参加选课,并记入选修课学分,按学分收费。
本课程计2学分,其中48学时理论,5学时上机,按学校规定,可试听二周后改选。
(选课学生名单第四周由教练组提交教务处,学生不需自行选课)附件:重庆交通大学2013年数学建模竞赛培训名单实践教学科 2013年3月11日附件:重庆交通大学2013数学建模竞赛培训名单土木建筑学院:赵亚宇马庆涛崔强陈畅薛轲庞琦李龙李瑞章曹晨阮鹿鸣贺俊玺王统井钱涛代飞廖晓璇杨云珲张杨郭宁刘杰夏润川谭书林蒋茂源谭涛刘相阳曾琢谢宏伟王松河海工程学院:刘洪王小蓉王磊李高攀伍灵晶邵帅何梦男吴骏逸王前邓睛许克勤刘杨廖方冉国全李雨霖楼聪李江涛黄丹张凤勇何佳威张鑫秦海涛刘瑶徐久洋甘林鹭管理学院:曾倩颖甄萌王金秋张雷孙亚平孙春兰李秋梅肖瑶郑光明王栋陈群叶圣侯刘爽王蕊刘玲刘承朋郑虹胡庆交通运输学院:刘源王媛媛赵艳花王杰邹方姿谢金倩张鑫郑桂桐安武军范峰马美娜吴丹刘永红张先波蔡文波杨博刘悦谭宇万柳玉凤刘皓王志恒陈嫣蕊张炳森练海洋机电学院:黄欢廖贞孔维茜郭凯黄林辉马帅祝冯火汪明明陆雪雯龚玉梅龚文兰陈浩熊德意夏于洋王先术向丽霞姚艺徐笑寒曾丹冯轲王泽坤刘绍龙尚琦焦科名王晓飞付毛锐王晓周琳信息科学与工程学院:杨杰刘亚梅汤璐霞陈永秋衣云飞刘秀财经学院:周杰马文灿李娟周先雯李阳李存佳罗玉群刘哲存田补祥刘雨丹陈凤英杨婷钰赵萍陈杨李鑫张选琴王岩强姜维航海学院:李银祥魏贺孙闯张萌田科刘彪吴攀陈健曾庆南理学院:李静代红艳王利敏周冬梅何建龙侯洋任音吉汪光裕张生辉张向欣李茜刘川陈科霖王林刘波张俊韬郑文华陈丹江利华张玉竹毛宪周廷苗成成盛超军陈屏。
2013年全国大学生数学建模竞赛培训计划一、说明随着石河子大学高等数学竞赛顺利落幕,2013年的全国大学生数学建模培训即将开始。
为了在2013年石河子大学数学建模队在全国大学生数学建模竞赛中取得更加优异的成绩,针对建模培训出现的问题和面临的挑战,总结前些年的数学建模竞赛的培训经验,结合数学建模指导组教师、理学院、数学系和教务处各方意见,给出今年的培训办法。
具体内容如下:二、培训内容主要为:队员间的协作、建模方法的学习、数学实验课程、资料查阅、自学能力培养、论文写作、实战模拟。
三、培训流程1、初选队员、动员、组队(1)初选队员。
来自老队员、高数竞赛获奖学生、任课老师推荐队学生,考虑到中途会有参加培训队员中途推出,为保证最终参赛队员质量,初选队员规模控制在200人到220人之间。
(2)动员。
5月31日召开颁奖动员大会,对获奖队员进行表彰,并召集老队员、高数竞赛获奖学生、任课老师推荐队学生,对数学建模竞赛培训进行动员,并由参加数学建模竞赛获奖的毕业生为大家介绍参赛经验。
(3)组队。
在确定总的参加人员后,将参赛学生分组,三人一组,根据以往经验,每组最好一名负责计算机计算的学生,三人专业不同。
计划选择50队(150人),未能选拨的其余学生作为替补队员,能全程坚持的将与正式队员一样获相同学分。
(4)纪律要求。
由于培训的人数较多,纪律方面必须严格,管理需有序安排。
2、培训(1)教材以姜启源《数学模型》为主,各位老师可以充分利用各种电子教案和课件(自备)。
(3)韩志全负责辅助其他老师在课程安排上的调整、学生作业布置、统计、考勤、教师课时统计、学生管理。
(4)韩志全出选拔题,结合作业、考勤选拔。
(5)唐红兵、姚斌负责机房的管理、软件的安装。
李双成负责摄像宣传。
(6)培训时间合计28天。
其中暑假前培训8天,主要利用周末时间,培训内容为初等模型;暑假集训14天(数学软件学习大模型为主);休息一天(自己练习),模拟比赛3天(综合训练),要求学生8月11日(待定)到校,开学后培训2天(利用周末时间,写作讲座为主)。
数学建模竞赛辅导资料
数学建模竞赛是一项旨在锻炼学生综合思维能力的比赛,需要参赛者在规定时间内,利用所学数学知识和建模技能解决实际问题。
为了帮助参赛者更好地备战数学建模竞赛,提供一些辅导资料,希望能对大家有所帮助。
首先,建议参赛者提前了解比赛规则和题型特点。
数学建模竞赛通常包含问题描述、问题分析、模型建立和结果展示等环节,在备战过程中要熟悉这些要素,做到心中有数。
其次,参赛者可以通过学习相关数学知识和建模方法来提升自己的竞赛水平。
数学建模竞赛涉及到概率统计、微积分、线性代数等多个学科领域,需要参赛者具备扎实的数学基础,学有余力者还可以深入了解一些高级数学知识。
第三,参赛者在解题过程中要注重团队合作和创新精神。
数学建模竞赛强调综合思维和团队合作能力,参赛者需要与队友密切配合,共同分析问题、构建模型,发挥各自优势,为团队取得好成绩而努力。
最后,参赛者要在竞赛前做好充分准备和心理调适。
数学建模竞赛时间紧、任务重,需要参赛者保持良好的心态和稳定的状态,做到临危不惧、沉着应对,为最终的竞赛成功打下坚实基础。
综上所述,数学建模竞赛辅导资料旨在帮助参赛者在备战过程中更好地应对挑战,提升竞赛能力,取得优异成绩。
希望以上提供的建议
和资料能够对大家有所启发,祝愿所有参赛者取得好成绩,享受竞赛的乐趣!。
2013年数学建模竞赛培训内容建模竞赛概论(论文撰写,论文评阅及其注意事项)
一、图论
图论算法(包括最短路、网络流、二分图等算法)
二、数学软件
1.Matlab
2. 优化模型建立与求解及lingo软件运用
3.统计软件
SPSS统计软件聚类分析的基本操作介绍
SPSS统计软件主成分分析、因子分析的基本操作介绍
三、数据处理
1.数据的统计分析与描述
2.基于matlab的海量数据的处理方法
3.近年来全国大学生数学建模竞赛中大型数据的处理范例分析
四、运筹学:线性规划、动态规划、排队论
五、多项式插值、最小二乘曲线拟合、微分方程数值解法及其在数学建模中的应用
1.多项式插值的基本原理及MATLAB的实现
2.数据插值建模案例的分析与求解
3.最小二乘曲线拟合的基本原理及MATLAB实现
4.曲线拟合建模案例的分析与求解
5.微分方程数值解法及其MATLAB实现
6.微分方程建模案例分析与求解
六、模糊数学理论简介、灰色系统理论
1.模糊综合评价方法及应用案例
2.数学建模中常用的预测方法
3.灰色预测模型及其应用
4.评价与决策的数学模型
5.长江水质的综合评价分析
七、优化智能算法
1.模拟退火法算法、神经网络算法、遗传算法的Matlab实现
2.真题模型的遗传算法求解。