七年级数学上册 综合训练 代数式求值(含字母的代数式化简、数位表示)天天练新人教版

代数式求值学生做题前请先回答以下问题问题1：整体代入的思考方向①求值困难，考虑_____________；②化简________________，对比确定________；③整体代入，化简．问题2：已知代数式2a2+3b=6，求代数式4a2+6b+8的值．①根据2a2+3b=6无法求出a和b的具体值，考虑_____________；②对比已知及所求，考虑把________作为整体；③整体代入，化简，最后结果为______．代数式求值（整体代入一）（人教版）一、单选题(共13道，每道7分)1.把看成一个整体，合并同类项的结果为( )A. B.C. D.2.把看成一个整体，合并同类项的结果为( )A. B.C.D.3.设，把用含的代数式表示并化简的结果为( )A. B.C. D.4.设，把用含的代数式表示并化简的结果为( )A. B.C. D.5.若，则代数式的值为( )A.0B.4C.6D.26.已知，则的值为( )A.-1B.0C.1D.37.若，则代数式的值为( )A.-1B.1C.-5D.58.已知代数式的值是4，则的值为( )A.1B.5C.9D.109.若代数式的值为5，则代数式的值为( )A.1B.9C.11D.2110.已知代数式的值为6，则的值为( )A.24B.18C.12D.911.若，则的值为( )A.0B.2C.5D.812.若，则的值为( )A.7B.-7C.1D.-113.若，则的值为( )A.-59B.-31C.41D.61感谢您的支持，我们会努力把内容做得更好！。

代数式求值专题1：已知：m=51,n=-1,求代数式3(m 2n+mn)-2(m 2n-mn)-m 2n 的值2：已知：x+x 1=3,求代数式(x+x 1)2+x+6+x1的值3：已知当x=7时,代数式ax 5+bx-8=8,求x=7时,8225++x bx a 的值.4：已知2x =3y =4z,则代数式yz yz xy z y x 3232+++-5：已知a=3b,c=4a 求代数式cb a cb a -++-65292的值6：已知a,b 互为相反数，c,d 互为倒数，x 的绝对值等于1，求代数式a+b+x 2-cdx 的值7：设a+b+c=0,abc ＞0,求ac b ++b a c ++c ba +的值9：5a 2－4a 2+a －9a －3a 2－4+4a ，其中a=－12；10：5ab －92a 2b+12a 2b －114ab －a 2b －5，其中a=1，b=－2；11：（3a 2－ab+7）－（5ab －4a 2+7），其中a=2，b=13；12：12x －2（x －13y 2）+3（－12x+19y 2），其中x=－2，y=－23；13：－5abc －{2a 2b －[3abc －2（2ab 2－12a 2b ）]}，其中a=－2，b=－1，c=314：证明多项式16+a －{8a －[a －9－3（1－2a ）]}的值与字母a 的取值无关．15：由于看错了符号，某学生把一个代数式减去x 2+6x －6误当成了加法计算，结果得到2x 2－2x+3，正确的结果应该是多少？16：当12,2x y ==时，求代数式22112x xy y +++的值。

17：已知x 是最大的负整数，y 是绝对值最小的有理数，求代数式322325315x x y xy y +--的值。

18：已知3613211⎪⎭⎫ ⎝⎛⨯⨯÷-=x ，求代数式1199719981999+++++x x x x Λ的值。

小学 +初中 +高中
代数式求值
学生做题前请先答复以下问题
问题 1：整体代入的思考方向
①求值困难，考虑_____________；
②化简 ________________ ，比照确定 ________；
③整体代入，化简．
问题 2：代数式2a2+3b=6，求代数式4a2+6b+8 的值．
①根据 2a2+3b=6 无法求出 a 和 b 的具体值，考虑_____________；
②比照及所求，考虑把________作为整体；
③整体代入，化简，最后结果为______ ．
代数式求值〔整体代入一〕〔人教版〕
一、单项选择题 ( 共 13 道，每道 7 分 )
1. 把看成一个整体，合并同类项的结果为 ( )
A. B.
C. D.
2. 把看成一个整体，合并同类项的结果为 ( )
A. B.
小学 +初中 +高中
C. D.
3. 设，把用含的代数式表示并化简的结果为( )
A. B.
C. D.
4. 设，把用含的代数式表示并化简的结果为( )
A. B.
C. D.
5. 假设，那么代数式的值为()
6. ，那么的值为()
7. 假设，那么代数式的值为()
小学 +初中 +高中
8. 代数式的值是4，那么的值为()
9. 假设代数式的值为5，那么代数式的值为()
10. 代数式的值为6，那么的值为()
11. 假设，那么的值为()
12. 假设，那么的值为()
小学 +初中 +高中
13. 假设，那么的值为()小学 +初中 +高中。

初中数学代数式化简求值练习题（含答案）1、已知x=1，求代数式x²+x（x-2）+（x+1）（x-1）的值。

2、已知x= -2，求代数式3（x-1）²+4x（x+2）-10的值。

3、先化简，再求值：2（x-3）（x+2）-（3+x）（3-x）-3（x-1）2，其中x=－2。

4、先化简再求值∶（2x³-2y²）-3（x³y²+x³）+2（y²+y²x³），其中x=-1，y=2。

5、先化简，再求值：(3x²y－2xy²)－2(xy²－2x²y)，其中x＝2，y＝－1。

6、先化简，再求值：5y（2x²y+3xy²）-3x（4xy²+3x²y），其中x＝1，y＝－1。

7、先化简，再求值：(3x²y-xy²)-2(xy²-3x²y)，其中x=-2，y=3。

8、先化简，再求值：(3x²y－2xy²)－2(xy²－2x²y)，其中x＝2，y＝－1。

9、若x²＋2y²＝5，求多项式(3x²－2xy＋y²)－(x²－2xy－3y²)的值。

10、先化简，再求值：5x²＋4－3x²－5x－2x²－5＋6x，其中x＝－3。

11、先化简，再求值：2(x＋x²y)－2/3(3x²y＋3/2x)－y²，其中x＝1，y＝－3。

12、先化简，再求值：（4x²y-3xy）+（-5x²y+2xy）-（2yx²-1），其中x=2，y=1/2。

13、先化简，再求值：2x²y－[2xy²－2(－x²y＋4xy²)]，其中x＝1/2，y＝－2。

3.2代数式的值拓展练习：代数式的化简求值问题人教版2024—2025学年七年级上册一、问题引入与归纳1.用具体的数值代替代数式中的字母所得的数值，叫做这个代数式的值。

注：一般来说，代数式的值随着字母的取值的变化而变化。

2.代数式的求值(整体代入法)：整体思想就是从问题的整体性质出发，突出对问题的整体结构的分析和改造，发现问题的整体结构特征，善于用“集成”的眼光，把某些式子或图形看成一个整体，把握它们之间的关联，进行有目的、有意识的整体处理。

二、典型例题解析例1．若多项式()x y x x x mx 537852222+--++-的值与x 无关，求])45(2[22m m m m +---的值.变式1．已知多项式（m ﹣3）x |m |﹣2y 3+x 2y ﹣2xy 2是关于x ，y 的四次三项式．（1）求m 的值；（2）当x ＝，y ＝﹣1时，求此多项式的值．例2．当代数式532++x x 的值为7时,求代数式2932-+x x 的值.变式2．已知x ﹣2y ＝3，则代数式6﹣2x +4y 的值为（ ）A ．0B ．﹣1C ．﹣3D ．3变式3．当x ＝1时，代数式ax 3﹣3bx +4的值是7，则当x ＝﹣1时，这个代数式的值是（ ）A ．7B ．3C ．1D ．﹣7变式4．若m ﹣n ＝﹣1，则（m ﹣n ）2﹣2m +2n 的值为（ ）A ．﹣1B ．1C ．2D ．3变式5．已知2a +3b ＝4，则整式﹣4a ﹣6b +1的值是（ ）A ．5B ．3C ．﹣7D ．﹣10变式6．当x ＝﹣2时，式子3x 2+ax +8的值为16，当x ＝﹣1时，这个式子的值为（ ）A ．2B ．9C ．21D ．3变式7．如果a 和﹣4b 互为相反数，那么多项式2（b ﹣2a +10）+7（a ﹣2b ﹣3）的值是（ ）A ．﹣3B ．﹣1C ．1D ．3变式8．若x 2﹣4x ﹣1＝0，则2x 2﹣8x ﹣（x 2﹣4x ）+2020的值为（ ）A ．2021B ．2022C ．2023D ．2024变式9．已知m +n ＝﹣2，mn ＝﹣4，则整式2（mn ﹣3m ）﹣3（2n ﹣mn ）的值为（ ）A ．8B ．﹣8C ．16D ．﹣16变式10．已知a +2b ＝3，则代数式2（2a ﹣3b ）﹣3（a ﹣3b ）﹣b 的值为（ ）A ．﹣3B ．3C ．﹣6D ．6变式11．已知代数式m 2+m ﹣1＝0，那么代数式2023﹣2m 2﹣2m 的值是（ ）A ．2021B ．﹣2021C ．2025D ．﹣2025 例3．x=-2时，代数式635-++cx bx ax 的值为8，求当x=2时，代数式635-++cx bx ax 的值。

七年级数学上册综合算式专项练习题代数式的计算与化简（解答方法）在七年级数学上册中，我们将学习代数式的计算与化简。

代数式是由数和字母通过运算符号组成的式子，其中字母代表某个数，也可以代表未知数。

这个章节给出了一系列的综合算式专项练习题，让我们掌握代数式的计算与化简的方法。

在解答这些综合算式专项练习题时，我们可以按照以下步骤进行：1. 观察式子，辨认运算符号：首先，我们要仔细观察算式中的各个运算符号，包括加号、减号、乘号与除号。

这样有助于我们准确理解整个算式。

2. 运用运算法则进行计算：接下来，我们根据运算法则进行计算。

运算法则包括加法法则、减法法则、乘法法则和除法法则。

- 加法法则：将同类项合并。

例如，3x + 2x可以合并为5x。

- 减法法则：将同类项合并。

例如，6a - 3a可以合并为3a。

- 乘法法则：对于两个字母相乘的情况，我们可以将字母相乘的结果写为一个指数大于1的字母。

例如，ax × bx可以合并为ab x^2。

- 除法法则：对于两个字母相除的情况，我们可以将字母相除的结果写为一个指数小于1的字母。

例如，(ax^2)/(bx)可以合并为a/bx。

3. 使用分配律进行化简：分配律是指将乘法运算分配到加法或减法运算的法则。

例如，对于式子3(a + b)，我们可以将乘法运算分配到加法运算，得到3a + 3b。

通过以上三个步骤，我们可以有效地进行代数式的计算与化简。

下面举例说明：例题1：计算表达式5x + 2x - 3x的值。

解答：首先，观察式子中的运算符号。

我们可以发现它们分别是加号、减号和减号。

接下来，根据减法法则合并同类项，得到4x - 3x。

最后，进行减法运算，得到x。

因此，式子5x + 2x - 3x的值为x。

例题2：化简表达式2a(b + c) + 3b(a + c)。

解答：首先，观察式子中的运算符号。

我们可以发现乘号、加号和加号。

接下来，利用分配律将乘法运算分配到加法运算，得到2ab +2ac + 3ab + 3bc。

七年级数学上册综合算式专项练习题代数式的运算代数式的运算是数学中的基础知识之一，在七年级数学上册中也是一个重要的内容。

通过对代数式的学习和练习，可以帮助学生掌握基本的代数运算规则，培养他们的逻辑思维和数学计算能力。

本文将介绍七年级数学上册中的综合算式专项练习题，通过具体例题的讲解和解答，帮助学生加深对代数式运算的理解。

1. 例题1：计算下列各式的值。

（1）$5a-2a$，其中$a=3$解答：将$a$的值代入代数式中，得到：$5a-2a=5\times3-2\times3=15-6=9$所以，$5a-2a$的值为9。

（2）$2b+4c$，其中$b=2$，$c=-1$解答：将$b$和$c$的值代入代数式中，得到：$2b+4c=2\times2+4\times(-1)=4-4=0$所以，$2b+4c$的值为0。

2. 例题2：计算下列各式的值。

（1）$(a-3)^2$，其中$a=2$解答：将$a$的值代入代数式中，得到：$(a-3)^2=(2-3)^2=(-1)^2=1$所以，$(a-3)^2$的值为1。

（2）$(2b+c)(b-2c)$，其中$b=-1$，$c=3$解答：将$b$和$c$的值代入代数式中，得到：$(2b+c)(b-2c)=(2\times(-1)+3)(-1-2\times3)=(1)(-7)=-7$所以，$(2b+c)(b-2c)$的值为-7。

3. 例题3：比较下列各组代数式的大小。

（1）比较$3a+4$和$2a+7$的大小，其中$a=2$解答：将$a$的值代入代数式中，得到：$3a+4=3\times2+4=10$$2a+7=2\times2+7=11$所以，$3a+4<2a+7$。

（2）比较$5b-2$和$3b+4$的大小，其中$b=-1$解答：将$b$的值代入代数式中，得到：$5b-2=5\times(-1)-2=-7$$3b+4=3\times(-1)+4=1$所以，$5b-2<3b+4$。

代数式求值专题12221：已知： m= ,n=-1, 求代数式 3(m n+mn)-2(m n-mn)-m n 的值2：已知： x+ 1 =3, 求代数式 (x+ 1) 2+x+6+ 1的值x x x3：已知当 x=7 时, 代数式 ax 5+bx-8=8, 求 x=7 时, ax 5bx 8的值 .224：已知x yz, 则代数式x 2 y 3z2==xy 2 yz 3 yz3 45：已知 a=3b,c=4a 求代数式2a9b2c的值5a 6b c6：已知 a,b 互为相反数， c,d 互为倒数， x 的绝对值等于 1，求代数式 a+b+x 2- cdx 的值7：设 a+b+c=0,abc ＞0, 求bc + c a + a b 的值abc22219：5a －4a +a － 9a －3a －4+4a ，此中 a=－ ；10：5ab － 9a 2b+ 1a 2b － 11ab － a 2b －5，此中 a=1， b=－2；2 2 422111：（ 3a － ab+7）－（ 5ab － 4a +7），此中 a=2， b=；12： 1 x －2（x － 1y 2）+3（－ 1 x+ 1y 2），此中 x=－2，y=－ 2；2 3 2 9 3221213：－ 5abc －{2a b － [3abc －2（2ab － a b ）]} ，此中 a=－2，b=－ 1， c14：证明多项式 16+a －{8a －[a －9－ 3（ 1－ 2a ）]} 的值与字母 a 的取值没15：因为看错了符号， 某学生把一个代数式减去 x 2 +6x －6 误看作了加法计算正确的结果应当是多少？16：当 x 2, y1时，求代数式 1 x 2 xy y 2 1 的值。

2217：已知 x 是最大的负整数， y 是绝对值最小的有理数，求代数式2 x3 5x。

1 3 1318：已知x1，求代数式 x1999x1998x1997x 1 的值。

初中《代数式求值》精选练习题及答案根据已知，求代数式的值：1、已知：x=√3 + √3 ，求代数式（x+1）（x-1）的值；2、已知x 2 +1= x ，求代数式x 1001 -x 1000的值；3、已知m =√493 +√563 +√643，求代数式 m - 1m 2 的值；4、已知a 2 = √2 √1+a 2 -1，求代数式a 2024 + a −2024的值；5、已知t ≠0，且 1t - t =1，求代数式t 3 +2t 2 +3003的值；6、已知9x2 +30x+23=0，求代数式（3x +4）2 + 1（3x+4）2 的值；7、已知m 2 -13m =n ，n 2 -13n =m ，求代数式√m 2+n 2+1 的值；8、已知2t +√2 =√3 ，求代数式t 6 -2t 4的值；9、已知3m 2 +5m -11=0，求代数式（4m+7）（2m-5）+m （m+21）+3 的值；10、已知x+√3 =2，求代数式4x 2-〔6x-（5x-8）-x 2〕+3x-〔5x-2（2x-1）〕的值。

参考答案1、已知：x=√3+√3，求代数式（x+1）（x-1）的值；解：已知x=√3+√3=√3+ √33=4√33那么x2=（4√33）2= 163----------①代数式（x+1）（x-1）=x2 -1将①代入= 163-1= 1332、已知x2 +1=x，求代数式x1001 -x1000的值；解：已知x2 +1=x变换一下，得x2-x= -1----------①再变换，得x2 =x -1------------②又x3=x2·x将②代入x3=（x -1）·x=x2-x将①代入故：x3= -1------------③代数式x1001 -x1000=x999+2 -x999+1=x999·x2 -x999·x=x 999（x 2 -x ）将①代入=x 999·（-1）= -x 999= -（x 3）333将③代入= -（−1）333 = -（-1）= 13、已知m =√493 +√563 +√643，求代数式 m - 1m 2 的值； 解：m =√493 +√563 +√643m=（√73）2 +√73 √83 + （√83）2-------------------① 将①等号两边同时取分母为1，得 m 1 =（√73）2 +√73 √83 + （√83）21等号右边分子分母同时乘以√83 -√73，得m 1 =[（√73）2 +√73 √83 + （√83）2]（√83 −√73）√83 −√73m 1 = √83）3√73）3√83 −√73 = √83 −√73 = √83 −√73 等号两边同时取倒数所以：1m = √83 -√73故： 1m 2 = （√73）2 -2√73 √83 + （√83）2-----------② 由① -②，得m - 1m 2 = 3√73 √833·2= 3√73=6√74、已知a2=√2√1+a2 -1，求代数式a2024+ a−2024的值；解：已知a2=√2√1+a2 -1变换一下，得a2+1=√2√1+a2等号两边同时平方，得a4+2a2+1= 2（1+a2）a4+2a2+1= 2+2a2化简，得a4=1代数式a2024+ a−2024=a4×506+ a4×（−506）=（a4）506+（a4）−506将a4=1代入= 1506+ 1−506=1+1=25、已知t≠0，且1- t =1，求代数式t3 +2t2 +3003的值；t解：已知t≠01- t =1t等号两边同时乘以t，得1 -t2=t变换一下，得t2=1 - t---------------------①代数式t3 +2t2 +3003=t2·t +2t2 +3003将①待入=（1 - t）·t +2（1 - t）+3003 =t -t2 +2-2t +3003再将①待入=t -（1- t） +2-2t +3003= t -1 +t +2 -2t +3003=（t +t -2t）+（-1 +2 +3003）=30046、已知9x2+30x+23=0，求代数式（3x+4）2+1（3x+4）2的值；解：设3x+4 =t则x= 13（t -4）---------------①已知9x2+30x+23=0将①代入9×[13（t−4）]2+30×[ 13（t−4）]+23=0（t−4）2+10（t -4）+23=0t2 -8t +16 +10t -40 +23=0 t2 +2t -1=0等号两边同时除以t，得t +2 - 1t=0变化一下，得1t- t =2等号两边同时平方，得1t2-2 + t2=4整理，得1t2+ t2= 6因为3x+4 =t故：（3x+4）2+1（3x+4）2=67、已知m2 -13m =n，n2 -13n =m，求代数式√m2+n2+1的值；解：m2 -13m=n，n2 -13n=m则变换一下，得m2 =13m +n----------------①n2 =m +13n----------------②① -②，得m2 -n2 =12（m-n）（m +n）（m -n）=12（m-n）（m +n）（m -n）-12（m-n）=0（m -n）〔（m +n）-12〕=0则有：m -n =0，或（m +n）-12=0即：m = n 或m +n =12（1）当m = n时已知m2 =13m +nm2 =13m +m=14m解得m=0，或m=14第一种情况：m=n=0代数式√m2+n2+1将m=n=0代入=√1=1第二种情况：m=n=14代数式√m2+n2+1将m=n=0代入=√142+142+1=√393（2）当m +n =12时① +②，得m2 +n2 =14（m+n）=14×12代数式√m2+n2+1=√14×12+1=√（13+1）（13−1）+1= √132−1+1=138、已知2t +√2=√3，求代数式t6 -2t4的值；解：2t +√2=√3t = √3−√22所以：t2= 5−2√64----------------①①两边同时平方，得t4= 49−20√616------------------------②代数式t6 -2t4=t4（t2 -2）将①，②代入= 49−20√616（5−2√64-2）= 49−20√616×−3−2√64=−3×49+（−20√6）×（−2√6）+（60√6−98√6）64= 93−38√6649、已知3m2 +5m -11=0，求代数式（4m+7）（2m-5）+m（m+21）+3 的值；解：3m2 +5m -11=0变换一下，得3m2 +5m =11------------①代数式（4m+7）（2m-5）+m（m+21）+3=8m2 -20m+14m -35 +m2 +21m+3=9m2 +15m -32=3（3m2 +5m）-32将①代入=3×11-32=110、已知x+√3=2，求代数式4x2-〔6x-（5x-8）-x2〕+3x-〔5x-2（2x-1）〕的值。

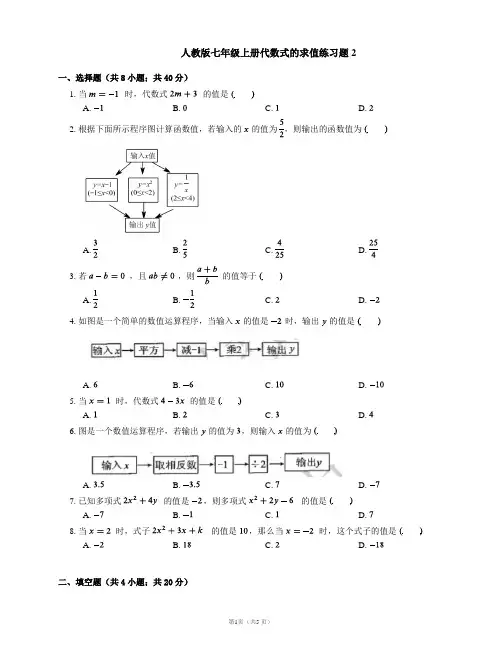
人教版七年级上册代数式的求值练习题2一、选择题（共8小题；共40分）1. 当时，代数式的值是B. C. D.2. 根据下面所示程序图计算函数值，若输入的的值为，则输出的函数值为A. B. C. D.3. 若，且的值等于A. B. C.4. 如图是一个简单的数值运算程序，当输入的值是时，输出的值是A. C. D.5. 当时，代数式的值是A. B. C. D.6. 图是一个数值运算程序，若输出的值为，则输入的值为A. C.7. 已知多项式的值是的值是C. D.8. 当时，式子的值是，那么当时，这个式子的值是B. C. D.二、填空题（共4小题；共20分）9. 如图是一台数值转换机的运算程序，若输出的结果为，则输入的的值为．10. 按照如图所示的计算程序，若，则输出的结果是．11. 若，则．12. 如图，是一个运算程序的示意图，若开始输入的值为，则第次输出的结果为．三、解答题（共4小题；共52分）13. 求下列代数式的值：（1），其中；（2），其中，．14. 已知，求代数式的值．15. 小玲在电脑中设置了一个程序，输入数，按键，再输入数，就可以运算．（1）求的值；（2）小华在运用程序时，屏幕显示“该操作无法进行”，你猜猜看，小华输入的数据有什么特征?16. 根据如图所示的程序计算，若输入的值为，求输出的的值．答案第一部分1. C 【解析】将代入，得．故选C．2. B3. C4. C5. A6. D7. A 【解析】，，，．8. A第二部分9.10.11.12.第三部分13. （1）（2）14. ，，，，，，，故代数式的值为．15. （1）．（2）第一个数的倍等于第二个数，即，导致除数为零，无法进行除法运算．16. 当时，，．所以输出的的值为．。

人教版七年级上册代数式的求值练习题8一、选择题（共8小题；共40分）1. 随着值的增大，代数式的值A. 增大B. 减小C. 不变D. 大于2. 下列说法正确的是A. 代数式的值与代数式中的字母无关B. 代数式的值是随着代数式中的字母的取值变化而变化的C. 代数式中的字母可以取任意的值D. 含有的代数式的值等于的值3.A. B. C. D.4. 如果代数式的值为，那么的值等于A. B.5. 若，则的值为A. B. C.6. 若，满足等式，且，则式子的值为A. B. C. D.7. 按如图所示的运算程序，能使输出的结果为的是A. ，B. ，C. ，D. ，8. 按如图所示的程序计算，若开始输入的数为，则最后输出的结果是A. B. C. D.二、填空题（共4小题；共20分）9. 已知代数式的值为，则的值为．10. 已知，，计算代数式．11. 按如图所示的程序流程计算，若开始输入的值为，则最后输出的结果是．12. 若，则．三、解答题（共4小题；共52分）13. 当，时，求下列代数式的值：（1）；（2）；（3）．14. 【概念学习】规定：求若干个相同的有理数（均不等于）的除法运算叫做除方．例如，记作，读作“的圈次方”；再例如，记作，读作" 的圈次方"；一般地，把记作，读作“的圈次方”．（1）【初步探究】①直接写出计算结果：，．②关于除方，下列说法错误的是．A．任何非零数的圈次方都等于1B．对于任何大于的整数，C．D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数（2）【深入思考】我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢?①依照上面的算式，将下列运算结果直接写成幂的形式：；．②将一个非零有理数的圈次方写成幂的形式为．③将（为大于等于的整数）写成幂的形式为．15. 根据如图所示的程序计算，若输入的值为，求输出的的值．16. 已知．（1）判断是否成立?请说明理由．（2）求的值（3）求的值．答案第一部分1. B 【解析】随着值的增大，代数式的值减小．故选B．2. B3. C 【解析】设，4. A 【解析】，，则，．5. B【解析】，，．6. C 【解析】，，，，，故选：C．7. C8. D第二部分9.10.11.12.第三部分13. （1）．（2）（3）．14. （1）；；C【解析】①，②A选项：任何非零数的圈次方都等于，故A正确；B选项：对于任何大于等于的整数，，故B正确；C选项：，故C错误；D选项：负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数，故D正确．（2）；；；【解析】①②③15. 当时，，．所以输出的的值为．16. （1）将代入，，故不成立．（2），．（3），，．。

七年级数学上册综合算式专项练习题带有字母的代数式的化简与还原数学上册综合算式专项练习题中，涉及到带有字母的代数式的化简与还原是一个需要重点关注和掌握的内容。

通过合理运用代数的基本运算法则和化简原则，可以将复杂的代数表达式化简为简单形式，使计算更加简便和准确。

在本篇文章中，将对这一内容进行详细的讲解和实例演示。

在数学上册综合算式专项练习题中，出现带有字母的代数式是为了让学生熟悉和掌握运用代数进行数字运算的方法。

代数式的化简和还原是掌握代数知识的基础，这种方法能够将复杂的代数式转化为更加简便和易于计算的形式。

首先，我们来看一个例子，对于代数式2x + 3y + x - y，我们可以根据代数的基本运算法则进行合并同类项。

同类项指的是具有相同字母部分的项，如2x和x就是同类项，3y和-y也是同类项。

合并同类项的方法是将它们的系数相加，即2x + x = 3x，3y + (-y) = 2y。

因此，化简后的代数式为3x + 2y。

在化简过程中，我们还需要注意符号的运用。

比如在上述例子中，2x + 3y + x - y的加号和减号都是相邻的，因此可以直接合并。

但是如果一个代数式中的加号和减号不是相邻的，我们就需要注意它们的符号运算了。

例如，对于代数式2x - 3y + x + y，我们需要先将加减号重新排列，变为2x + x - 3y + y，然后再合并同类项，得到3x - 2y。

除了合并同类项，我们还可以运用分配律、结合律和交换律等基本运算法则进行代数式的化简。

这些法则可以帮助我们更好地理解和处理代数式中的复杂运算。

另外，当我们需要还原代数式时，可以运用因式分解和提公因式等方法。

以代数式3x + 6y为例，我们可以把公因式3提到括号外面，得到3(x + 2y)。

这个过程称为提公因式，可以帮助我们找到代数式中的共同因子，从而更好地理解和计算代数式。

除了上述的方法，化简和还原代数式还需要考虑乘法和幂运算的操作。

七年级数学上册综合算式专项练习题代数式的计算与化简【正文】本文为七年级数学上册综合算式专项练习题代数式的计算与化简的详细解答。

一、计算与化简1. 计算下列算式的值：(1) 3 + 4 = 7(2) 5 - 2 = 3(3) 2 × 6 = 12(4) 8 ÷ 4 = 22. 计算下列算式的值：(1) 2 × (3 + 4) = 14(2) 5 + 2 × 3 = 11(3) 10 - (4 + 3) = 3(4) 15 ÷ (3 - 1) = 7.53. 化简下列代数式：(1) 3a + 2a = 5a(2) 4x - 2x + 3x = 5x(3) 5y - (2y + 3y) = 0(4) 6m + 4m - (2m - 1) = 13m + 14. 求下列代数式的值：(1) 当 x = 2 时，计算 3x - 5 的值：3x - 5 = 3 × 2 - 5 = 6 - 5 = 1(2) 当 y = 3 时，计算 2y + 4 的值：2y + 4 = 2 × 3 + 4 = 6 + 4 = 10(3) 当 m = 4 时，计算 5m - 8 的值：5m - 8 = 5 × 4 - 8 = 20 - 8 = 12二、综合练习1. 计算下列算式的值：(1) 2 + 3 × 4 - 5 ÷ 5 = 2 + 12 - 1 = 13(2) 7 × 3 - (5 - 2) ÷ 3 = 21 - 3 ÷ 3 = 21 - 1 = 20(3) 4 × (6 - 3) + 1 ÷ 2 = 4 × 3 + 0.5 = 12 + 0.5 = 12.5 2. 化简下列代数式：(1) 2a + 3a - 4a = a(2) 5x - 2x + 2x - 3x = 2x(3) 4y + (2y + 3y) - 3y = 6y(4) 3m + 5m - 7m + 2m = 3m3. 求下列代数式的值：(1) 当 a = 2 时，计算 3a - 4 的值：3a - 4 = 3 × 2 - 4 = 6 - 4 = 2(2) 当 x = 3 时，计算 2x + 5 的值：2x + 5 = 2 × 3 + 5 = 6 + 5 = 11(3) 当 y = 4 时，计算 5y - 2 的值：5y - 2 = 5 × 4 - 2 = 20 - 2 = 18(4) 当 m = 5 时，计算 4m + 3 的值：4m + 3 = 4 × 5 + 3 = 20 + 3 = 23三、练习题1. 计算下列代数式的值：(1) 3x + 4y，当 x = 2，y = 33x + 4y = 3 × 2 + 4 × 3 = 6 + 12 = 18 (2) 2a + 5b，当 a = 4，b = 12a + 5b = 2 × 4 + 5 × 1 = 8 + 5 = 13 2. 化简下列代数式：(1) 4a + 2b - 3a + b= (4a - 3a) + (2b + b)= a + 3b(2) 3x + 6y - 4x - 2y= (3x - 4x) + (6y - 2y)= -x + 4y3. 求下列代数式的值：(1) 2x + 3y，当 x = 5，y = 22x + 3y = 2 × 5 + 3 × 2 = 10 + 6 = 16(2) 3a - 4b，当 a = 3，b = 13a - 4b = 3 × 3 - 4 × 1 = 9 - 4 = 5通过本文的解析和大量练习题的计算，我们对七年级数学上册综合算式专项练习题代数式的计算与化简有了深入的了解。

七年级数学上册综合算式专项练习题含有字母的代数式求值数学是一门关于数字和运算的学科，它在我们日常生活中起着重要的作用。

在七年级数学上册中，综合算式是一种重要的内容，而其中涉及到字母的代数式求值更是考察我们对数学概念和运算方法的理解和应用能力。

本文将针对七年级数学上册综合算式专项练习题含有字母的代数式求值展开讨论。

一、代数式求值的基本概念在解答含有字母的代数式求值题目时，我们需要了解一些基本概念。

首先，字母通常代表某个未知数或变量，可以是任意一个数。

其次，求值是指在给定字母的取值范围内，计算代数式的结果。

通过将字母代入代数式中，进行运算得出具体的数值结果，这就是代数式求值的过程。

二、求值策略和方法为了准确求值含有字母的代数式，我们需要根据具体情况采取不同的求值策略和方法。

下面将就一些典型的情况进行具体说明。

1. 单个字母代数式的求值：对于只含有一个字母的代数式，我们可以将所给字母代入代数式中，进行运算求值。

例如，给定代数式：3x + 2，如果要求x = 4时的值，我们将x替换成4，得到3 * 4 + 2 = 14，即当x = 4时，代数式的值为14。

2. 多个字母代数式的求值：对于含有多个字母的代数式，我们需要根据题目给出的具体条件，将各个字母代入代数式中，并进行相应的运算求值。

例如，给定代数式：2x + 3y，如果要求x = 5，y = 2时的值，我们将x替换成5，y替换成2，得到2 * 5 + 3 * 2 = 17，即当x = 5，y= 2时，代数式的值为17。

3. 复杂代数式的求值：对于复杂的代数式，我们可以根据运算规则和优先级进行逐步计算，并且根据题目给出的具体条件将字母代入代数式中。

例如，给定代数式：2x + y^2，如果要求x = 3，y = 4时的值，我们先计算y^2，得到4^2 = 16，然后将x替换成3，得到2 * 3 + 16 = 22，即当x = 3，y = 4时，代数式的值为22。

初一数学上册综合算式专项练习题代数式简化在初一数学的学习中，代数式的简化是一个重要的内容，也是数学中基础的一部分。

代数式的简化指的是将代数式中的项合并、抵消，使其更加简洁明了。

本文将针对初一数学上册综合算式专项练习题中的代数式简化部分进行详细解答。

一、基础知识回顾在进行代数式简化之前，我们需要回顾一下基础的代数知识。

1. 代数式的定义代数式是由数字、字母和运算符号组成的表达式。

它可以包含一个或多个变量，并通过加、减、乘、除等运算符号进行计算。

2. 项和系数代数式中的每一部分称为一个项。

每个项由系数和字母的乘积组成，系数表示字母的倍数。

3. 合并同类项合并同类项是代数式简化的关键步骤。

同类项具有相同的字母和指数，我们可以将它们合并为一个项。

二、代数式简化解题步骤下面我们将根据初一数学上册综合算式专项练习题中的代数式简化题目进行解答。

请注意，由于无法输入数学符号，我将用符号“^”代替乘方。

练习题1：简化代数式：5x + 2y - 3x - 4y^2解答过程：首先，将代数式中相同的字母和指数的项合并在一起。

原式变为：(5x - 3x) + (2y - 4y^2)接下来，合并同类项：= 2x + (-4y^2 + 2y)最后，按照字母顺序进行排列：= 2x - 4y^2 + 2y练习题2：简化代数式：6a^2 - 3ab - 2a^2 + 4ab解答过程：首先，将代数式中相同的字母和指数的项合并在一起。

原式变为：(6a^2 - 2a^2) + (-3ab + 4ab)接下来，合并同类项：= 4a^2 + (4ab - 3ab)最后，进行进一步的合并操作：= 4a^2 + ab通过以上两个例题，我们可以看出代数式的简化其实就是将同类项合并，并将其按照字母顺序进行排列。

三、练习题探索以下是一些综合算式专项练习题中常见的代数式简化题目，我们将逐一进行解答。

1. 简化代数式：3x - 2x + 5y - 3y - 7z解答过程：首先，将代数式中相同的字母和指数的项合并在一起。

数学上册综合算式专项练习题代数式的化简与变形代数式的化简与变形在数学上册综合算式专项练习题中是一项重要的技能。

通过进行化简和变形，我们可以简化复杂的代数式，使其更易于计算和理解。

本文将介绍代数式的化简和变形的基本原则和方法，并通过综合算式专项练习题来讲解。

一、化简代数式的基本原则代数式的化简是指将复杂的代数式简化为更简单的形式。

化简代数式的基本原则有：1. 合并同类项：将含有相同字母和指数的项合并为一项。

例如，将3x + 2x化简为5x。

2. 移项：将含有未知数的项移至等号的另一侧，以求得未知数的值。

例如，将2x + 3 = 7中的2x移至等号的右侧，得到3 = 7 - 2x。

3. 分配律：将括号外的数与括号里的每一项相乘或相除。

例如，将2(x + 3)化简为2x + 6。

4. 括号内的化简：将括号内的代数式进行化简。

例如，将2x + 3 - (x - 1)化简为2x + 3 - x + 1。

二、化简代数式的方法化简代数式的方法因不同的题型而异。

下面以综合算式专项练习题为例，介绍几种常见的化简代数式的方法。

练习题一：化简代数式1. 将3ab + 2cd - 5ab - cd进行合并同类项，得到-2ab - cd。

2. 将4(x + 3) - 2(2x - 1)化简。

先使用分配律展开括号，得到4x + 12 - 4x + 2。

合并同类项，化简为14。

3. 将2x + 3(x - 1)化简。

使用分配律展开括号，得到2x + 3x - 3。

合并同类项，化简为5x - 3。

练习题二：移项1. 将3x + 2 = 7中的2移至等号的右侧，得到3x = 7 - 2，化简为3x = 5。

2. 将4(x - 2) + 3 = 2x + 5中的2x移至等号的左侧，得到4(x - 2) + 3 - 2x = 5。

练习题三：括号内的化简1. 将2(3x + 4) + 5(2x - 1)化简。

先使用分配律展开括号，得到6x + 8 + 10x - 5。

代数式求值学生做题前请先回答以下问题问题1：①若关于x的代数式mx+1的值不受x取什么值的影响，即与x无关，只需m_______，理由是__________________；②若关于x的代数式(m+1)x+1的值不受x取什么值的影响，即与x无关，只需m_______;③若关于x的代数式(2m-1)x+1的值不受x取什么值的影响，即与x无关，只需m_______．问题2：数位表示要先画_________，再乘以对应的_________．代数式求值（含字母的代数式化简、数位表示）（人教版）一、单选题(共11道，每道9分)1.若关于x的多项式ax+4的值与x无关，则下列说法正确的是( )A.a=1B.a=0C.x=1D.x=02.若关于x的多项式的值与x无关，则m的值为( )A.0B.1C.6D.-63.若关于x，y的多项式的值与y无关，则a的值为( )A.-1B.5C.0D.-54.若关于x的多项式的值与x无关，则( )A.m=1，n=3B.m=-1，n=3C.m=1，n=-3D.m=0，n=05.已知代数式的值与x无关，则的值为( )A.12B.-12C.24D.-246.若关于x，y的多项式的值与y无关，则的值为( )A.-46B.8C.26D.277.一个三位数，百位上的数字为，十位上的数字是百位上的数字的2倍，个位上的数字是5，用代数式表示这个三位数为( )A. B.C. D.8.若表示一个两位数，表示一个一位数，把放在的左边，则组成的三位数应表示为( )A. B.C. D.9.若表示一个三位数，表示一个一位数，把放在的左边，则组成的四位数应表示为( )A. B.C. D.10.若表示一个两位数，也表示一个两位数，把放在的右边，则组成的四位数应表示为( )A. B.C. D.11.若表示一个两位数，表示一个三位数，把放在的右边，则组成的五位数应表示为( )A. B.C. D.。

代数式化简求值专项训练1．先化简，再求值：（1）)1)(2(2)3(3)2)(1(-+++---x x x x x x ，其中31=x ．（2） （a ＋b ）（a －b ）＋（a ＋b ）2－a (2a ＋b )，其中a =23，b ＝－１12。

（3）22(3)(3)(5)(5)a b a b a b a b -++-+-，其中2a =-，1b =-．2.已知312=-y x ，2=xy ，求 43342y x y x -的值。

3.若x 、y 互为相反数，且4)1()2(22=+-+y x ，求x 、y 的值4．已知22==+ab b a ，，求32232121ab b a b a ++的值．5．已知x 2＋x －1＝0，求x 3＋2x 2＋3的值．6．已知：222450a b a b ++-+=，求2243a b +-的值．7．已知等腰△ABC 的两边长,a b 满足：222448160a ab b a -+-+=，求△ABC 的周长？8．若（x 2＋px ＋q ）（x 2－2x －3）展开后不含x 2，x 3项，求p 、q 的值．9、已知x 、y 都是正整数，且3722+=y x ，求x 、y 的值。

10、若182++ax x 能分解成两个因式的积，求整数a 的值？代数式典型例题30题参考答案：1．解：在1，a，a+b，，x2y+xy2，3＞2，3+2=5中，代数式有1，a，a+b，，x2y+xy2，共5个．故选C2．解：题中的代数式有：﹣x+1，π+3，共3个．故选C．3．解：①1x分数不能为假分数；②2•3数与数相乘不能用“•”；③20%x，书写正确；④a﹣b÷c不能出现除号；⑤，书写正确；⑥x﹣5，书写正确，不符合代数式书写要求的有①②④共3个．故选：C4．解：“负x的平方”记作（﹣x）2；“x的3倍”记作3x；“y与的积”记作y．故选B5．解：A、x是代数式，0也是代数式，故选项错误；B、表示a与b的积的代数式为ab，故选项错误；C、正确；D、意义是：a与b的和除y的商，故选项错误．故选C6．解：答案不唯一，如买一支钢笔5元，买x支钢笔共5x元7．解：（1）（x+2）2可以解释为正方形的边长为x+2，则它的面积为（x+2）2；（2）某商品的价格为n元．则80%n可以解释为这件商品打八折后的价格．故答案为：（1）正方形的边长为x+2，则它的面积为（x+2）2；（2）这件商品打八折后的价格8．解：根据题意得此三位数=2×100+x=200+x9．解：两位数x放在一个三位数y的右边相当于y扩大了100倍，那么这个五位数为（100y+x）10．解：这m+n个数的平均数=．故答案为：．11．解：小华第一天读了全书的，还剩下（1﹣）n=n；第二天读了剩下的，即（1﹣）n×=n．则未读完的页数是n12．解：（1）∵a﹣b=3，∴3a﹣3b=3，5﹣4a+4b=5﹣4（a﹣b）=5﹣4=1；（2）∵x+5y﹣2=0，∴x+5y=2，∴2x+3+10y=2（x+5y）+3=2×2+3=7；（3）∵3x2﹣6x+8=0，∴x2﹣2x=﹣，∴x2﹣2x+8=﹣+8=．故答案为：（1）3，1；（2）7；（3）13．解：因为a，b互为倒数，c，d互为相反数，所以ab=1，c+d=0，所以3c+3d﹣9ab=3（c+d）﹣9ab=0﹣9=﹣9，故答案为：﹣914．解：由题意知：﹣a﹣b=5所以a+b=﹣5；则当x=1时，ax3+bx=a+b=﹣515．解：开放题，答案无数个，只要所写同类项，所含字母相同且相同字母的指数也相同即可，同类项与字母的顺序无关．如5x3y，12x3y，20x3y．故答案为：5x3y，12x3y，20x3y16．解：由同类项的定义可知m=2，n=3，代入（﹣n）m，结果为9．答：（﹣n）m值是917．解：两个单项式的和是单项式，则它们是同类项，则2m+3=4，m=；n=3．则（4m﹣n）n=（4×﹣3）3=﹣1．答：（4m﹣n）n=﹣118．解：x5y n与﹣3x2m+1y3n﹣2是同类项，2m+1=5，n=3n﹣2，m=2，n=1，m+n=2+1=3，故答案为：319．解：（1）∵其余三面留出宽都是x米的小路，∴由图可以看出：菜地的长为18﹣2x米，宽为10﹣x米；（2）由（1）知：菜地的长为18﹣2x米，宽为10﹣x米，所以菜地的面积为S=（18﹣2x）•（10﹣x）；（3）由（2）得菜地的面积为：S=（18﹣2x）•（10﹣x），当x=1时，S=（18﹣2）（10﹣1）=144m2．故答案分别为：（1）18﹣2x，10﹣x；（2）（18﹣2x）（10﹣x）；（3）144m220．解：∵﹣3x4+m y与x4y3n是同类项，∴4+m=4，3n=1，∴m=0，n=，∴m100+（﹣3n）99﹣mn=0+（﹣1）﹣0=﹣121．解：∵多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项，即二次项系数为0，即m﹣2=0，∴m=2；∴2n+4=0，∴n=﹣2，把m、n的值代入n m中，得原式=422．解：∵6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项，∴5﹣2R=0，解得R=2.523．解：原式=x2+（﹣2k+6）xy﹣3y2﹣y，∵不含x，y的乘积项，∴x，y的乘积项的系数为0，∴﹣2k+6=0，∴2k=6，∴k=3．∴当k=3时，已知多项式不含x，y的乘积项24．（1）﹣3（2s﹣5）+6s=﹣6s+15+6s=15；（2）3x﹣[5x﹣（x﹣4）]=3x﹣[5x﹣x+4]=3x﹣5x+x﹣4=﹣x+4；（3）6a2﹣4ab﹣4（2a2+ab）=6a2﹣4ab﹣8a2﹣2ab=﹣2a2﹣6ab；（4）﹣3（2x2﹣xy）+4（x2+xy﹣6）=﹣6x2+3xy+4x2+4xy﹣24=﹣2x2+7xy﹣2425．（1）x+[﹣x﹣2（x﹣2y）]=x﹣x﹣2x+4y=﹣2x+4y；（2）原式=a﹣a﹣﹣+b2=；（3）2a﹣（5a﹣3b）+3（2a﹣b）=2a﹣5a+3b+6a﹣3b=3a；（4）﹣3{﹣3[﹣3（2x+x2）﹣3（x﹣x2）﹣3]}，=﹣3{9（2x+x2）+9（x﹣x2）+9}，=﹣27（2x+x2）﹣27（x﹣x2）﹣27，=﹣54x﹣27x2﹣27x+27x2﹣27，=﹣81x﹣2726．解：（1）﹣；（2）原式=1﹣+﹣++…+﹣=1﹣=27．解：（1）∵第n个数是（﹣1）n，∴第7个，第8个，第9个数分别是﹣，，﹣．（2），最后与0越来越接近28．解：通过图案观察可知，当n=1时，点的个数是12=1；当n=2时，点的个数是22=4；当n=3时，点的个数是32=9；当n=4时，点的个数是42=16，…∴第n个正方形点阵中有n2个点，∴第n个正方形点阵中的规律是=n2．29．解：根据图案可知，（1）第4个图案火柴有3×4+1=13；第6个图案中火柴有3×6+1=19；（2）当n=1时，火柴的根数是3×1+1=4；当n=2时，火柴的根数是3×2+1=7；当n=3时，火柴的根数是3×3+1=10；所以第n个图形中火柴有3n+1．（3）当n=2008时，3n+1=3×2008+1=602530．解：（1）在第1个图中，共有白色瓷砖1×（1+1）=2块，（2）在第2个图中，共有白色瓷砖2×（2+1）=6块，（3）在第3个图中，共有白色瓷砖3×（3+1）=12块，（4）在第10个图中，共有白色瓷砖10×（10+1）=110块，（5）在第n个图中，共有白色瓷砖n（n+1）块。

初一数学上册综合算式专项练习题代数式化简在初一数学上册中，综合算式是一个重要的内容，而代数式化简作为其中的一个专项练习题，更是需要我们加以重视和掌握的部分。

本文将围绕初一数学上册的综合算式专项练习题中代数式化简的方法和技巧展开论述，帮助同学们更好地理解和应用这一知识点。

一、基本概念在进行代数式化简之前，我们首先需要了解一些基本的概念和符号。

在代数式中，字母通常代表未知数或变量，而数字则表示已知数或常数。

常见的代数式运算符有加法、减法、乘法和除法，分别用"+"、"-"、"×"和"÷"表示。

此外，指数运算也是我们常见的代数式运算，用小数字表示。

二、代数式化简的基本方法1. 合并同类项合并同类项是代数式化简中的基本方法之一。

所谓同类项指的是具有相同字母部分的项，它们的指数可以不同。

合并同类项的关键是运用加法和减法的性质，将相同字母部分的项合并到一起。

如：3x + 4x = 7x2a^2b - 3ab^2 = ab(2a - 3b)注意，合并同类项时要注意正负号的运算。

2. 提取公因数提取公因数是代数式化简中的另一个常用方法。

当代数式中多个项都含有相同的公因子时，我们可以将这个公因子提取出来。

如：3x^2 + 6x = 3x(x + 2)2ab + 4ac = 2a(b + 2c)3. 拆分因式拆分因式是将复杂的代数式按照一定的规律进行拆分，使原来的式子更易于化简。

这一方法通常需要我们观察代数式中的特点，并运用一些常用的公式。

如：x^2 + 2x + 1 = (x + 1)(x + 1)a^2 - b^2 = (a + b)(a - b)三、代数式化简技巧除了基本的方法外，我们还可以运用一些技巧来更快速地进行代数式化简。

1. 奇异恒等式奇异恒等式是指当变量满足某种关系时出现的等式。

对于一些特定的奇异恒等式，我们可以直接使用，以节省时间和精力。