当前位置：文档之家 › 最新电工学电力学课程第八章《电路定律的相量形式》

最新电工学电力学课程第八章《电路定律的相量形式》

  • 格式：ppt
  • 大小：878.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

教学课件PPT电路定律的向量形式

教学课件PPT电路定律的向量形式

i u

eL i
N L i
或
N L i i
u
L为线圈的电感(或自感)，它是线圈 的结构参数。 进而：
eL
L
di u e L L dt
7.5 正弦交流电路的三种基本元件
二、正弦交流电路中的电感元件(Inductance)
1、瞬时分析 2、相量分析 3、相量电路 4、相量图 5、瞬时功率
容对电流的阻力情况，描述电容电路中电压、电流 有效值之间的关系，且只对正弦量有效。
I U C IX C C
7.5 正弦交流电路的三种基本元件
2、相量分析
i 2 I cos( t i ) 2 CU cos( t u u 2U cos( t u )
7.4
电路定律的相量形式
相量形式KCL
瞬时形式KCL ∑i=0
I 0
U 0
瞬时形式KVL
∑u=0
相量形式KVL
欧姆定律
u=Ri
相量形式
U RI
7.5 正弦交流电路的三种基本元件
7.5 正弦交流电路的三种基本元件
一、 正弦交流电路中的电阻元件
二、 正弦交流电路中的电感元件
i
u
i
R
根据 欧姆定律
u iR
2 RI cos t i ) （
则
u Ri
比较两个电压表达式得：
7.5 正弦交流电路的三种基本元件
结论：（1）U=RI
欧姆定律的有效值形式 电阻上电压、电流同相
（2） i u
u,i
0
t
7.5 正弦交流电路的三种基本元件
二、相量分析

84 电路定律的相量形式

84 电路定律的相量形式
§8.4 电路定律的相量形式
一. 基尔霍夫定律的相量形式 正弦电流电路中的各支路电流和支路电压都
是同频正弦量，所以可以用相量法将KCL和KVL转 换为相量形式。
•
i(t) 0 I 0
•
u(t) 0 U 0
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
相量模型
IL IC IR
jLIL
1
jC
IC
U S
RIR
1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例8-6：正弦电流源的电流，其有效值IS=5A，角频率 ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
ai
b
c
iS
+ uR - + uL - +
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R
相量形式：
I I
U R RI I
相量关系
U R R I
+
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
= 15 /0 °V
•
•
U L jL I = 5000 / 90°V
•
UC j
1
•
I
= 5000 / - 90 °V
C
•

电路原理课件 第8章 相量法

电路原理课件 第8章 相量法

三. 相位差 ：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则 相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。 不同频率的两个正弦量之间的相位差不再是一个常数，而是 随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的 复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二 复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A

第8章( 8.1-8.3) 相量及相量分析法

第8章( 8.1-8.3) 相量及相量分析法

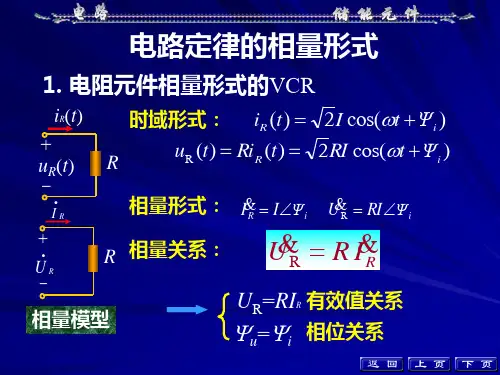
例
i(t)
+ u(t) -
R
已知： u( t ) U m sin(wt y u ) 解: L
求：稳态解 i(t)
1. 经典法: 一阶常系数 di(t ) Ri (t ) L U m sin(wt y u ) 线性微分方程 dt 自由分量(齐次方程通解)： A e-(R/L) t
全解：
第8章 相量及相量分析法 8.1-8.3 重点：
复数及其运算 相位差
相量和相量图 正弦量的相量表示
电路元件VCR 的相量形式
电路定律的相量形式
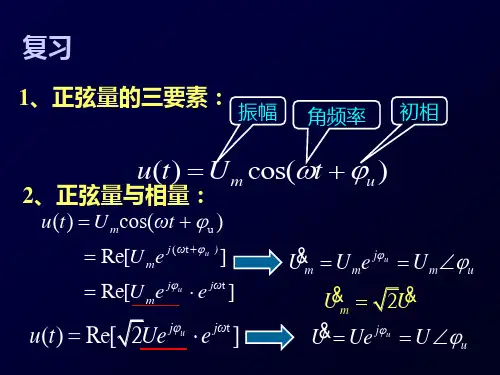
8 .1 .1 正弦量的基本概念 正弦交流电路
如果在电路中电动势的大小与方向均随时间按 正弦规律变化，由此产生的电流、电压大小和方向 也是正弦的，这样的电路称为正弦交流电路。

u (t ) 2U cos(wt y ) U Uy
例1. 已知
解： I 10030o A
o

i 141.4 cos(314t 30 ) A u 311.1cos(3 14t 60o )V
试用相量表示 i, u 。
U 220 60o V

14
例2. 已知 I 5015o A, f 50Hz . 试写出电流的瞬时值表达式。
y
Re
a
Re
A a jb
A A e jy | A | y
11
2. 复数运算
(1)加减运算——直角坐标
(2) 乘除运算——极坐标 3. 旋转因子
A1±A2=(a1±a2)+j(b1±b2)
A1 A2 A1 A2 y 1 y 2
复数 e jy = cos y + jsin y = 1∠y A e jy A逆时针旋转一个角度y ，模不变

电路原理第8章

电路原理第8章
0
10 0 I = ∠ 45 2
实数有效值
j45°
& I m = 10 e
45 0
？
0
已知： 已知：I& = 100 ∠ 50
最大值 I m = 2I = 100 2
则： i = 100 cos ( ω t + 50 0 )
2、相量运算
i = 2 I cos(ωt + ϕ ) = Re = Re
[ 2 Ie (
1 T
T
2
直流
则有
I =
∫ i
0
2
均方根值） dt （均方根值）
有效值
I= 1 T
∫ i
0
T
2
dt
均方根值） （均方根值）
当i
= I m cos(ω t + φ ) 时，
Im 2
可得： I = 可得：
i = 2 I cos(ω t + ϕ )
ωt
2、角频率： 角频率： 反映正弦量变化的快慢。 反映正弦量变化的快慢。
两个同频率的正弦电流： 如：两个同频率的正弦电流：
i1 = I m1 cos(ω t + ϕ 1 )
i2 = Im2 cos(ω t + ϕ 2 )
i1
ϕ2 ϕ1
1
i2
相位差： 相位差：ϕ = (ω t + ϕ
) − (ω t + ϕ 2 ) = ϕ 1− ϕ 2
计时起点不同，正弦量的初相位不同， 计时起点不同，正弦量的初相位不同，但同频 正弦量之间的相位差不会改变， 率正弦量之间的相位差不会改变，总是等于初相 位之差。 位之差。
•
关于正弦量表示符号的说明 瞬时值--小写（ 瞬时值--小写（u ,i） --小写 有效值--大写（ 有效值--大写（U , I） --大写 ）

电路定理的相量形式

电路定理的相量形式
返 回 上 页 下 页
2. 电阻元件相量形式的VCR
i(t) + uR(t)
瞬时表达式： i(t ) 2I sin(t Ψ i )
I
uR (t ) Ri(t ) 2RI sin(t Ψ i ) R UR u 相量形式： I IΨ i U R RIΨ i
4.已知：
U 100 15V
负号 U 100V ？ j15 U 100 e V ？
i 10 sin ( ω t 60 )A ？
最大值
例1 已知电流表读数：
A1 ＝8A
A2 ＝6A
若 1. Z1 R, Z 2 jX C
2. Z1 R, Z 2为何参数
返 回
上 页
下 页
正误判断
u 220 sin ( ω t 45 )V
220 U 45 V？ 2
有效值
j45 •
1.已知：
3.已知：
I 4e
j30
A
复数
4 2 sin ( ω t 30 )A？
瞬时值
220 e45 V？ Um
2.已知： I 10 60 A
I
+ UL -
相量关系： U L
j L
j L I
相量形式的欧姆定律 定义： X L L 2 f L 感抗(Ω )
相量模型
U L jL I jX L I
返 回 上 页 下 页
感抗的性质 XL
I U L
XL=L=2fL
①表示限制电流的能力； ②感抗和频率成正比。
注意：通常铭牌数据或测量的功率均指有功功率。
2. 电感元件相量形式的VCR

电工与电子技术电路定理的相量形式


i(t) =10 2 cos(5t + 36.90 )A
ɺ U _ ɺ I
+
ɺ I
1
-j10Ω 15Ω j20Ω
ɺ I2
返 回
ɺ I3
上 页 下 页
jω L 相量关系： 相量关系：
ɺ ɺ ɺ UL = jωL IL = jXL IL
Ψu=Ψi +90°
返 回 上 页 下 页
相量模型
有效值关系： UL=ω L IL 相位关系： 相位关系：
感抗和感纳
XL=ωL=2πfL，称为感抗，单位为 (欧姆) 称为感抗，单位为Ω 欧姆) BL=1/ω L =1/2πfL， 称为感纳，单位为 S 称为感纳 感纳，
ɺ IC
Ψu
ɺ UC
ωt
pC = uCiC = 2UC IC cos(ω t +Ψu ) sin( ω t +Ψu ) = UC IC sin 2(ω t +Ψu )
瞬时功率以2ω交变，有正有负， 瞬时功率以 交变，有正有负，一周期 交变 内刚好互相抵消，表明电容只储能不耗能。 内刚好互相抵消，表明电容只储能不耗能。 有功功率P 有功功率 P=0
1 ωC
ɺ IC
+ ɺ UC -
−j
相量模型
ɺ ɺ 相量关系： 相量关系： ɺC = 1 IC = −j 1 IC U jωC ωC 1 IC 有效值关系： UC = 有效值关系： ωC 相位关系： 相位关系： Ψu=Ψi -90°
返 回 上 页 下 页
容抗与容纳
XC=1/ω C， 称为容抗，单位为 Ω(欧姆) 称为容抗， (欧姆) Β C = ω C， 称为容纳，单位为 S 称为容纳，
返 回 上 页 下 页

电路第五版课件 第八章相量法


j 30 （ 105) 135
( 2) i1 ( t ) 5 cos(100π t 30 ) i2 ( t ) 3 cos(100π t 300 ) 3cos(100πt 150)
j 30 ( 150) 120
( 3) u1 ( t ) 10 cos(100π t 30 ) u2 ( t ) 10 cos(200π t 45 )
③正弦量对时间的导数、积分、几个同频率正弦量的
加减，其结果仍是同频率的正弦量，这不仅使电路 的分析计算变得简单，而且其结果还可以推广到非 正弦周期电流电路中。
正弦量的时域表达式有两种形式
i Imcos(wti) i Imsin(wti) 也称为瞬时值表达式 分析时不可混用，以免发生相位错误。 今后采用的形式以教材为准： i Imcos(wti)
i3
i3
i2
wt
复数
（2）正弦量的相量表示
由数学知识可知：任意一个正弦函数都有唯一
的复数与其对应。
可用复数表示正弦量 相量表示法的实质：用复数表示正弦量 相量的模 表示正弦量的有效值（或最大值）
相量的幅角
表示正弦量的初相位
如：uUmcos(wt) 相量 注意：
j U Ue U
2 2 2 2
三角函数式： F 10cos53 j10sin53
指数式：
极坐标式：
F 10e
j 53
F 1053
2. 复数的运算
（1）相等： 代数式：实部相等，虚部相等 极坐标式：模相等，辐角相等 （2）加、减：实部相加减，虚部相加减
如果是其他形式表示的复数，应先化成代数式
U
q
j
I

电路定律的向量形式资料


jωt Re[ 2 R Ie ] ]
故
可得
RI RI 或 U U m m
U R I 且
u i
3）u、i 的波形及相量图 波形图 i(t ) I u (t ) U
u ( t)

结论：
R
时域模型
相量模型
R
i( t)
00
1）电阻的 u , i 是同频率的正弦量；
k 1 k
n
对于线性时不变的正弦稳态电路（单一频率激 励）各支路电压、电流为同频率的正弦量。 设：
n
jωt ik (t ) I km cos(ωt ik ) Re[ I km e ]
n
n jωt jωt ik (t ) Re[I km e ] Re I kme k 1 k 1 k 1
i3
i1 i2
求：
i3 (t )
解：方法1）由KCL的时域形式： 1060
0
6.236.2
10 60 5 90 I3 I1 I 2
5 90
相量图
10 cos 60 10 j sin 60 j5

5 j3.66 6.236.2 A
复习
1、正弦量的三要素：
振幅
角频率
初相
2、正弦量与相量： u (t ) U mcos(ωt u )
u(t ) U m cos(t u )
U m U me ju U mu U m 2U U Ue ju U u
Re[U me j ( ωt u ) ] Re[U me ju e jωt ]
0
故有：

电路原理第8章1-2节

F1 F2 (a1 jb1 ) (a2 jb2 )
说明
(a1 a2 ) j(b1 b2 )
可以用平行四边形法则或多边形法则（首尾相
接法）实现复数的加减运算，如图所示。
j
F1 F2
j
F22
O
F1 F2
1 O
F1 F2
F1 F2
1
6
2. 复数的乘除运算：用指数形式或极坐标式
如：
i1 u2
相位差等于初相差
（主 值 范 围：j12 π）
16
讨论
（1）若j12 0，即i1 u2，则称i1超前u2； （2）若j12 0，即i1 u2，则称i1滞后u2；
i1 u2
u2
i1
i1 u2
u2
O
j12
t O
i1
t
(a)j12 0
(b)j12 0
（3）若j12 0，即i1 u2，则称i1和u2同相；
j b
j 1
虚单位
O
Re[F ] a，Im[F ] b
几何意义：坐标点（常用向量表示） 如图所示。
F
a 1
3
2. 三角式
F | F | (cos jsin )
|F|：复数的模
： arg F
（复数的辐角）
j b
O
F 和与a和b之 间 的 关 系：
F
a 1
a F cos 或 b F sin
12
7. 初相位（初相）
t=0时的相位，即 ( t i ) t0 i
注意 ①初相位的主值区间
i 180或i π
②可根据需要任意指定任一正弦量初相位的值，
但同一电路其他正弦量计时零点必须与之相同。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。



由相量形式KVL有 : V V 1 V 2 600 8090 (V)
（2）相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式


UR RIR


U L jL IL

1
UC

j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C

U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路（旁路作用）;

(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源（线性）的控制电压或电流是正弦量， 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示，反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°，当电容电压由负值增加经过零点时，其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义：
X
C
定义

1
C
(1) 表示限制电流的能力；
相量关系
+
U R R I
U R
-
有效值关系：UR = RI 相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)
L
dt
-
2L I sin t
时域模型 2L I cos(t 90o )
感抗
U= L I
XL= U/I = L= 2 f L， 单位: 欧姆
感抗的物理意义： (1) 表示限制电流的能力；
错误的写法
L u
i
L

U I
(2) 感抗和频率成正比。
XL
0(直流), X L 0, 短路;
, X L , 开路;

(3) 由于感抗的存在使电流落后电压。

IS
5 / 0


UR RI
= 15 /0 °V


U L jL I = 5000 / 90°V

UC


j
1
C

I
= 5000 / - 90 °V



U bd U L U C = 0



U ad U R U bd 15/ 0
ubd 0 uad 15 2 cos(103t) V
8-4 电路定律的相量形式
一. 基尔霍夫定律的相量形式
1. KCL：
时域: 对于任一集总参数电路，在任一时刻，流出（或流入）任 一节点的电流代数和等于零。
n

k 1
ik
(t)

0
n

k 1
2Ik cos(t ik ) 0
n
频域: 以相量表示正弦量，有 I k 0 k 1
在正弦稳态电路中，对于任一节点，流出（或流入）该 节点的电流相量代数和等于零。
2、KVL： 时域:
对于任一集总参数电路，在任一时刻，对任一回路，按 一定绕行方向，其电压降的代数和等于零。
m

k 1
uk
(t)

0
m

k 1
2Uk cos(t uk ) 0
频域:
m
以相量表示正弦量，有 U k 0 k 1
在正弦稳态电路中，对任一回路，按一定绕行方向，其
电压降相量的代数和等于零。
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R 相量形式：
I I U R RI I
下得到的；
如果为非关联参考方向，则以上各式要变号。
以上公式 既包含电压和电流的大小关系，
又包含电压和电流的相位关系。
四、相量法注意点：
1. 同频率的正弦量才能表示在同一个相量图中； 2. 正角度按逆时针计； 3. 应选定一个参考相量(设初相位为零。)
ai
b
c
iS
+ uR - + uL - +
u-C
d
解：画出所示电路相对应的相量形式表示的电路图 a I R b jωL c

+ - + -
IS
UR
UL
+

UC -
1
jC
d

a I R b jωL c

+ - + -
IS
UR
U L + UC -
1
jC
d
设电路的电流相量为参考相量

即令 I
ik 0

Ik 0
uk
uj
ij

Uk


Ij
Uj
i j guk
I j gUk
三. 电路的相量模型 :
L
iR
j L
I R
+ iL
iC
uS -
1
C2 R
+ IL
U S
-1
IC 2
1
R
jC
时域电路
iL iC iR
L diL 1 dt C
iCdt uS
R
3. 电容
时域
频域
i (t)
u(t) 2U cost
U U0o
+ u(t)
Ci(t)

C
du(t dt
)
-
2CU sin t
I jC U
有效值关系
时域模型 2CU cos(t 90o ) I= C U
I
+1
U jC
相量模型
相位关系
u, i i u
iR

1 C
iC dt
时域列写微分方程
相量模型
IL IC IR
jLIL

1
jC
IC
U S
RIR

1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例1：正弦电流源的电流，其有效值IS=5A，角频率ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
u, i u
i
0
t
波形图
I I0o
I
U jL I
有效值关系
+
U j L
-
U= L I
相量模型
相位关系
u 超前 i 90°U
I
相量图
电感元件的时域模型如图 (a)所示，反映电压电流瞬时 值关系的波形图如图 (b)所示。由此可以看出电感电压超前 于电感电流90°，当电感电流由负值增加经过零点时，其电 压达到正最大值。
例2：如图正弦稳态电路，已知交流电压表V1读数为60V ，V2读数为80V，求V读数。
i +
V -
R
+ -
V1
L
+ - V2

V

V2
100 80

V 1 60

I
相量图解法
解:（1）相量法求解

假设以电流为参考相量，即设： I I0 (A)


则 : V 1 600 (V) V 2 8090 (V)