电工学(少学时)课后规范标准答案全
- 格式:doc
- 大小:5.36 MB
- 文档页数:32

U2.1求阳113所示电坤:|切关S闭介和盼汕闻种佶况 J、b・c二点的电他.【龊】S匱仟时.K = ^V. l;=_3V・V c = 0 V.S 断开吋.V, = V; = 6 V, K =(6+3) V=9 V.1・3」冷田1 14所环:电拓•"・电诉电劝外虫一120 V・内电阻7^-03 述按导线电阻心/ =O2・・jX-ftftlSfl A L= 115 Q. 4<J( 1)遽路时的电沆•负载和电淅的电爪.侑载消克的电功沖、削滋产牛和输II]的电功屮:(2〉升略时的电加屯压和负找屯圧,(3)在负皴均和屯凍玳如滋时屯源的巳滄恵电压。
2 1.D LU 114【解】(1)通络时电険的电流E120I = ------------------ = ---------------------- A= 10 J A+• R、・+R L 0.3 + 0.2-t-11.5负我电圧U L■%】-11.5X1OV-115 V 屯折屯斥f/5=叫 * R X}1 = (0 2 + 11 5)x10 V =117 V 或者U s -£-&/-(120 - 0・3x10)V-117 V 负找消耗的电功冰^=^7 = 115x10 W = 1 150 W 或古化=R』=1 I 5xl0; W = 1 150 W 电源产生的电功率件二日“ 20x10 W 二 1 200 W电游城)出的电功率化一UJ -117X10 w-l 170 W(2>幵路时U、=£=120 V久-0⑶短幷吋S 二 O 二 0・2xZ4() V 二 4H V- E-/1.7- (120-0.3x240)V-48 V 1.5.1试分析图1.15所示西电路中电阳的电压刃电浹以&图(3)中电Ml 液的电压和IM M 中电压涯恂电盜.【解】的足为了理解Rih 游棚电浜・的待点•选择待求电压和屯讹 的參考方向如图1」5所示.(1》在阁1.15 <3)所禾电路中•山于二匕并联.屯压和问・故 〃•二 S =1 v K •>/ = ―— = A = 2 A R 0.5i/c =(/s =l V(2>右图l.M (b)所示电腔中,川丁「者皿段,电涼相I 町故= 7S = 1 A—pRI* =05x1 V =05 V人=4 = 1 A1.5.2 在町1丄6所示直淀屯册帀•乜知17十37 ■人二3A ;求41、b 、C 三点的电位C 【解】木题H 的是力了复习理母电経元件 的特点以及电位的槪念・ill T a 点电型就足a 点对卷為点c 们电压,M «=5・3 V由丁• b 点电位比4点电位高7?/fl ・a 点电位乂120 0.3 4-0.2 = 240 A孔卅)A 0.3R 05Q3)(b >1・8J 用叠加左理求BB 123所示电踣中的电流人和【解】 电朮源単独作用时,电路如图1.24 (a)所示.则1: = ——— 1、= | —-—x 5 IA = 3 A&F 〔2 + 3 /x5 A = 2 A比c 点岳U“故b 丘电位儿%=RS =0x3 + 3)V = 6 V c*;为翁考点.故c 点电位为v c = 01.7.1用支賂屯说注求图1.220详口跑中各支肉的电血•并说叨匕% 昆起电源作用还足起负栽作用“廉中(7SI =12 V,O S2 = 15 V , &=3a • = 1.5 Q, R ? = 9 □.【解】结血、回控标十图1.22屮。


第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注: U U例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示): 第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U 。



电工学习题少学时答案标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]2012年《电工学》习题(上)解答第1章直流电路习题一、单项选择题1.图示电阻元件R消耗电功率10W,则电压U为( A )。
A)5V B)5V C)20VU题1图2.在图示的电路中,A点的电位V A为( C )。
A)2 V B)4 V C) 2 V-2 k7 kΩΩ题2图3.在图示电路中,U、I的关系式正确的是( B )。
A)U= (I S + I )R0 B)U = (I S-I )R0C)U = (I I S )R0R L题3图2题4图4.图示电路中电流I2为( C )。
A )7AB )3AC )3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A )越高B )越低C )不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A )2A 的理想电流源B )2V 的理想电压源C )不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( B )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源B )理想电流源C )理想电压源与理想电流源U 4VS +题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3B )3和3C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用B )不可以用C )有条件地使用11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )18VB )18VC )6VU I SS题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。

电工学少学时1-4章课后习题答案第一章电路的基本概念和基本定律一、填空题1、电路的作用是实现电能的传输和转换,以及对电信号的传递和处理。
2、电流的实际方向规定为正电荷定向移动的方向,电压的实际方向规定为由高电位指向低电位。
3、电阻元件的伏安特性曲线是一条过原点的直线,其斜率表示电阻的大小。
4、电源的电动势是电源将其他形式的能转化为电能的能力的物理量,其方向规定为在电源内部由负极指向正极。
二、选择题1、已知空间有 a、b 两点,电压 Uab=10V,a 点电位为 Va=4V,则b 点电位 Vb 为()A 6VB -6VC 14VD -14V答案:B解析:Vb = Va Uab = 4 10 =-6V2、一电阻元件,当其电流减为原来的一半时,其功率为原来的()A 1/2B 1/4C 2 倍D 4 倍答案:B解析:P = I²R,当 I 变为原来的一半时,P' =(I/2)²R = 1/4 I²R三、计算题1、如图所示电路,已知 E1 = 18V,E2 = 12V,R1 =3Ω,R2 =6Ω,R3 =9Ω,求各支路电流。
解:首先设各支路电流方向如图所示。
根据基尔霍夫电压定律(KVL),对于回路①:E1 I1R1 I3R3 = 0即 18 3I1 9I3 = 0 (1)对于回路②:E2 I2R2 + I3R3 = 0即 12 6I2 + 9I3 = 0 (2)根据基尔霍夫电流定律(KCL),在节点 A 处:I1 = I2 + I3 (3)联立(1)、(2)、(3)式,解得:I1 = 3A,I2 = 1A,I3 = 2A第二章电路的分析方法一、填空题1、支路电流法是以支路电流为未知量,应用基尔霍夫定律列出方程组求解的方法。
2、网孔电流法是以网孔电流为未知量,列写网孔的 KVL 方程进行求解的方法。
3、节点电压法是以节点电压为未知量,列写节点的 KCL 方程进行求解的方法。
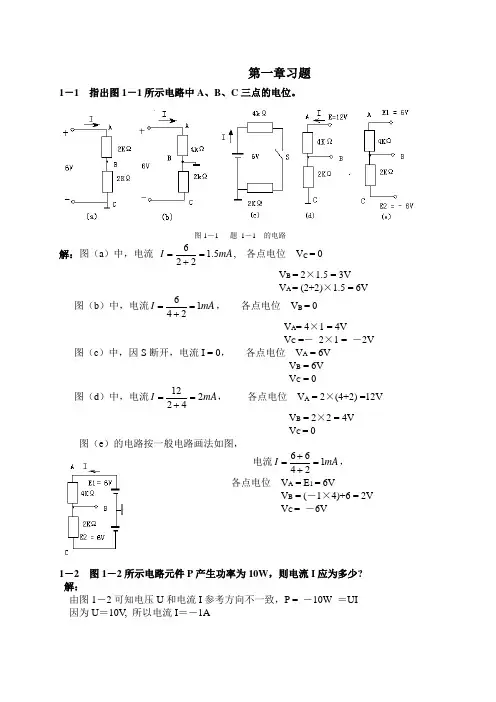
第一章习题1-1 指出图1-1所示电路中A 、B 、C 三点的电位。
图1-1 题 1-1 的电路解:图(a )中,电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图(b )中,电流mA I 1246=+=, 各点电位 V B = 0V A = 4×1 = 4VV C =- 2×1 = -2V图(c )中,因S 断开,电流I = 0, 各点电位 V A = 6V V B = 6VV C = 0图(d )中,电流mA I 24212=+=, 各点电位 V A = 2×(4+2) =12VV B = 2×2 = 4V V C = 0图(e )的电路按一般电路画法如图,电流mA I 12466=++=,各点电位 V A = E 1 = 6VV B = (-1×4)+6 = 2V V C = -6V1-2 图1-2所示电路元件P 产生功率为10W ,则电流I 应为多少? 解:由图1-2可知电压U 和电流I 参考方向不一致,P = -10W =UI 因为U =10V , 所以电流I =-1A图 1-2 题 1-2 的电路1-3 额定值为1W 、10Ω的电阻器,使用时通过电流的限额是多少? 解:根据功率P = I 2 R A R P I 3160101.===1-4 在图1-3所示三个电路中,已知电珠EL 的额定值都是6V 、50mA ,试问哪个电珠能正常发光?图 1-3 题 1-4 的电路解:图(a )电路,恒压源输出的12V 电压加在电珠EL 两端,其值超过电珠额定值,不能正常发光。
图(b )电路电珠的电阻Ω=Ω==120120506K R .,其值与120Ω电阻相同,因此电珠EL 的电压为6V ,可以正常工作。
图(c )电路,电珠与120Ω电阻并联后,电阻为60Ω,再与120Ω电阻串联,电珠两端的电压为V 4126012060=+⨯小于额定值,电珠不能正常发光。

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注: 图2-6(b)U例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示): 第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U 。
第三章 三相交流电路3.1基本要求(1)掌握对称三相电源及其相电压、线电压的表示方法。
(2)能计算三相负载星形接法电路。
(3)能计算三相负载三角形接法电路。
(4)掌握三相功率的计算。
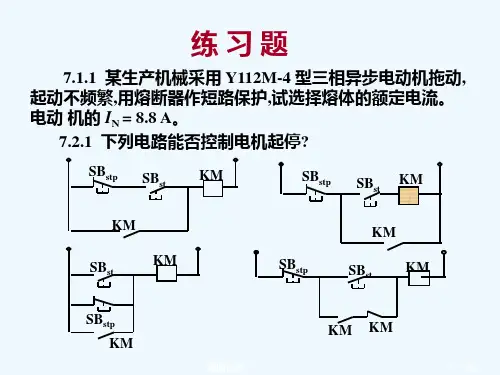
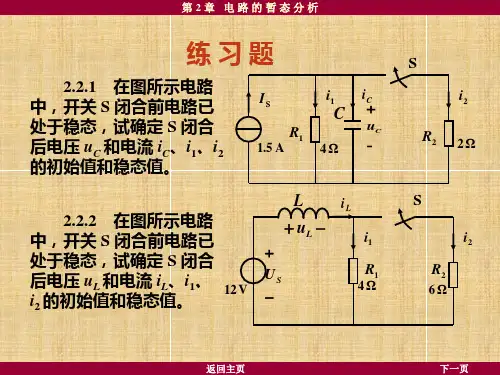
3.2基本内容3.2.1 对称三相电源(通常都为星型接法,如图3-1-1所示。
)对称三相电源是由三个同频率、等幅值、初相角依次落后120º的正弦电压构成。
三相电源的表示:瞬时值表达,波形表达,相量图表示,相量式表示,计算中常用的是相量图表示和相量式表示:1. 相电压:对称三相电源的相电压常以U P 表示:oo1100P U U U =∠=∠22120120P U U U =∠-︒=∠-︒24024033-∠=-∠=pUU U注: V 的单下标代表某点的电位,U 的双下标代表 图3-1-1 两点的电压,这里的1U 实质是电压1N U ,因为省略N ,故写作1U 。
2. 线电压:对称三相电源的线电压常以U L 表示:由相量图或复数可以证明:线电压U L 等于相电压P U 的3倍,且超前于相应相电压30º。
121211300333030P L U U U U =-=∠︒=∠⋅∠=⋅∠=∠,23232.........3090LU U U U =-==∠︒=∠-3131330......210LU U U U =-=∠︒==∠- 3.2.2 三相负载三相负载接入电源之前,首先核对每相负载的首端与尾端,每相负载在电路中施加的电压应符合本身的额定电压。
1. 三相负载的星形接法三相负载的首端分别接在三相电源上,其三个尾端的连结点N '接电源中线N 。
(1)若Z 1=Z 2=Z 3(大小相等,性质相同)是对称三相负载,以U U I I z Z==或求出各相电流,相量图求解或复数求解的结果,中线电流等于零( 1230NL L L I I I I =++= ),可以省去中线,变成三相三线制。
注:尽管中线省去,但每相负载两端电压依然等于电源相电压U P 。
电工学少学时1-4章课后习题答案第一章电路的基本概念和基本定律11 电路和电路模型(1)电路是电流的通路,是为了实现某种功能而将电气设备和元器件按照一定方式连接起来的整体。
(2)电路模型是由理想电路元件组成的,用于近似地描述实际电路的性能。
理想电路元件包括电阻、电感、电容、电源等。
12 电流和电压的参考方向(1)电流的参考方向是人为假定的电流流动的方向。
若实际电流方向与参考方向相同,电流为正值;反之,电流为负值。
(2)电压的参考方向也是假定的,通常规定从高电位指向低电位为电压的参考方向。
13 电源有载工作、开路与短路(1)电源有载工作时,电路中有电流通过,电源向外输出功率。
此时,电源的端电压等于电源电动势减去内阻上的压降。
(2)电源开路时,电路中没有电流,电源端电压等于电源电动势。
(3)电源短路时,电流很大,会损坏电源和电路。
14 基尔霍夫定律(1)基尔霍夫电流定律(KCL):在任一时刻,流入一个节点的电流之和等于流出该节点的电流之和。
(2)基尔霍夫电压定律(KVL):在任一时刻,沿任一闭合回路,各段电压的代数和为零。
课后习题答案:习题 11 一个手电筒电路,电池电动势为 3V,内阻为05Ω,灯泡电阻为5Ω。
求电路中的电流和灯泡两端的电压。
解:根据全电路欧姆定律,电路中的电流 I = E /(R + r) = 3 /(5 + 05) = 0545A灯泡两端的电压 U = IR = 0545 × 5 = 2725V习题 12 已知电路中某点的电位为 5V,若选择另一点为参考点,电位为 0V,两点之间的电压为 10V,求该点的电位。
解:因为两点之间的电压等于两点电位之差,所以该点的电位为 10 + 0 = 10V第二章电路的分析方法21 电阻串并联连接的等效变换(1)电阻串联时,总电阻等于各电阻之和。
(2)电阻并联时,总电阻的倒数等于各电阻倒数之和。
22 电源的两种模型及其等效变换(1)实际电源可以用电压源和电流源两种模型表示。
第一章习题1-1 指出图1-1所示电路中A 、B 、C 三点的电位。
图1-1 题 1-1 的电路解:图(a )中,电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图(b )中,电流mA I 1246=+=, 各点电位 V B = 0V A = 4×1 = 4VV C =- 2×1 = -2V图(c )中,因S 断开,电流I = 0, 各点电位 V A = 6V V B = 6VV C = 0图(d )中,电流mA I 24212=+=, 各点电位 V A = 2×(4+2) =12VV B = 2×2 = 4V V C = 0图(e )的电路按一般电路画法如图,电流mA I 12466=++=,各点电位 V A = E 1 = 6VV B = (-1×4)+6 = 2V V C = -6V1-2 图1-2所示电路元件P 产生功率为10W ,则电流I 应为多少? 解:由图1-2可知电压U 和电流I 参考方向不一致,P = -10W =UI 因为U =10V , 所以电流I =-1A图 1-2 题 1-2 的电路1-3 额定值为1W 、10Ω的电阻器,使用时通过电流的限额是多少? 解:根据功率P = I 2 R A R P I 3160101.===1-4 在图1-3所示三个电路中,已知电珠EL 的额定值都是6V 、50mA ,试问哪个电珠能正常发光?图 1-3 题 1-4 的电路解:图(a )电路,恒压源输出的12V 电压加在电珠EL 两端,其值超过电珠额定值,不能正常发光。
图(b )电路电珠的电阻Ω=Ω==120120506K R .,其值与120Ω电阻相同,因此电珠EL 的电压为6V ,可以正常工作。
图(c )电路,电珠与120Ω电阻并联后,电阻为60Ω,再与120Ω电阻串联,电珠两端的电压为V 4126012060=+⨯小于额定值,电珠不能正常发光。
1-5 图1-4所示电路中,已知电压U 1 = U 2 = U 4 = 5V ,求U 3和U CA 。
解:根据基尔霍夫电压定律,对回路ABCDA 可写出方程U 1+U 2-U 3+U 4 =0U 3= U 1+U 2+U 4 = 5+5+5=15V 对回路ACDA 可写出方程 U CA +U 3-U 4=0U CA =U 4-U 3=5-15=-10V1-6 欲使图1-5所示电路中的电流I=0,U S 应为多少?解:因为电流I=0,所以I 1=I 2=A 205154.=)+(U S =5×0.2=1V图1-5 题1-6的电路1-7 在图1-6所示三个电路中,R 1 = 5Ω,R 2 = 15Ω,U S = 100V ,I 1 = 5A ,I 2 = 2A 。
若R 2电阻两端电压U =30V ,求电阻R 3 。
解:A R U I 2153025===A I I I 725514=+=+= Ω=⨯--=--==++5172577010051433514.I R I U U R U U R I R I S S图 1-6 题1-7的电路1-8 求图1-7所示各电路中的未知量。
图 1-7 题1-8的电路解: (a)图 Ω=-=42816R (b) 图 V U 1020103=-⨯= (c) 图 A I 60101016.=-=1-9 在图1-8所示的电路中,R 1、R 2、R 3、R 4的额定值均为6.3V 、0.3A ,R 5额定值为6.3V 、0.45A ,U = 110V 。
为使上述各电阻元件均处于额定工作状态,则选配电阻R X 和R Y 的理想阻值应为多少?解: I 1 =0.3A I =0.45AI 2 = 0.45-0.3 = 0.15AΩ=⨯=168150436..Y RΩ=⨯-=4174450536110...X R图 1-8 题1-9的电路1-10 电路如图1-9所示,求A 点的电位。
(a)(b)图 1-9 题1-10的电路解: 图(a )的电路按一般电路画法如图(b), A I 2514410.=+=V A =-1.25×4=-5V 1-11 求图1-10所示电路中的电压U 、电流I 。
图 1-10 题1-11的电路解:(a )图 U 为恒压源的输出,U =10VI =10/2=5A(b )图 I 为恒流源的输出,I =5AU =5×10=50V1-12 简化图1-11所示各电路为一个等效的电压源或理想电流源。
图1-11 题1-12的电路解:(a)图两理想电流源合并为一个,电流I S=5-3=2A,如图(f)。
(b)图两理想电压源合并为一个,其值U S=6-4=2V,如图(g)。
(c)图与恒压源并联的电阻可以去掉,等效为一个理想电压源,如图(h)。
(d)图与恒流源串联的电阻可以去掉,等效为一个理想电流源,如图(j)。
(e)图与3A恒流源串联的电压源可以去掉,与5A恒流源串联的电阻可以去掉,等效为一个理想电流源,电流I S=5-3=2A,如图(k)。
1-13 在图1-12(a)(b)(c)所示的电路中,是哪些元件在提供功率?图1-12 题1-13的电路解:(a)图由1A电流源提供功率。
(b)图由10V电压源提供功率。
(c)图由U S电压源提供功率。
1-14 在图1-13(a)(b)(c)所示的电路中,电压U是多少?图1-13 题1-14的电路解:(a)图U=0(b)图U=1-3=-2V(c)图U=(1+2)×120=360V1-15 某实际电源的伏安特性如图1-14所示,试求它的电压源模型,并将其等效变换为电流源模型。
(a)图1-14 题1-15的电路解:U=U S-IR0(1)根据图(a)可知,当I=0时,U=9V;带入(1)式解得U S=9V当I=4时,U=6V;带入(1)式解得R0=3/4Ω电压源模型如图(b),电流源模型如图(c)。
第二章习题2-1 图2-1所示的电路中,U S=1V,R1=1Ω,I S=2A.,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中I S=2A,U S=2V,R1=3Ω,R2=R3=2Ω。
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。
2-5 图2-3所示电路中,已知U S1=6V,R1=2Ω,I S=5A,U S2=5V,R2=1Ω,求电流I。
2-6 图2-4所示电路中,U S1=30V,U S2=10V,U S3=20V,R1=5kΩ,R2=2kΩ,R3=10kΩ,I S=5mA。
求开关S在位置1和位置2两种情况下,电流I分别为多少?2-7 图2-5所示电路中,已知U AB=0,试用叠加原理求U S的值。
2-8 电路如图2-6所示,试用叠加原理求电流I。
2-9 电路如图2-7所示,试用叠加原理求电阻R4上电压U的表达式。
2-10电路如图2-8所示,已知R1=Ω,R2=R3=2Ω,U S=1V,欲使I=0,试用叠加原理确定电流源I S的值。
2-11 画出图2-9所示电路的戴维宁等效电路。
2-12 图2-10所示的电路接线性负载时,U 的最大值和I的最大值分别是多少?2-13 电路如图2-11所示,假定电压表的内阻无穷大,电流表的内阻为零。
当开关S处于位置1时,电压表的读数为10V,当S处于位置2时,电流表的读数为5mA。
试问当S处于位置3SHI 4,电压表和电流表的读数各为多少?2-14 图2-12所示电路中,各电源的大小和方向均未知,只知每个电阻均为6Ω,又知当R=6Ω时,电流I=5A。
今欲使R支路电流I=3A,则R应该多大?2-15 图2-13所示电路中,N为线性有源二端网络,测得AB之间电压为9V,见图(a);若连接如图(b)所示,可测得电流I=1A。
现连接如图(c)所示形式,问电流I为多少?2-16 电路如图2-14所示,已知R1=5Ω时获得的功率最大,试问电阻R是多大?2 u/V ,i /A ωt 310 iu 45° 90° O 图3-1 t rad f /3145014.322=⨯⨯==πωAt i Vt u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25At i i t At t i f )(,时,)(︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω本 章 小 结1、支路电流法是分析和计算电路的基本方法,适用于任何电路。
它是以电路中的支路电流为未知量,应用基尔霍夫定律列出电路方程,通过解方程得到各支路电流。
一般地,对于具有n 个节点、b 条支路的电路可列出(n-1)个独立的节点电流方程和[b-(n-1)] 个独立的回路电压方程。
2、叠加原理是反映线性电路基本性质的一条重要定理,它可将多个电源共同作用下产生的电压和电流,分解为各个电源单独作用时产生的电压和电流的代数和。
某电源单独作用时,将其它理想电压源短路,理想电流源开路,但电源内阻必须保留。
3、戴维宁定理适合于求解电路中某一条支路电压或电流的情况。
把待求支路(或元件)单独划出来,剩下的线性有源二端网络可用一个电压源来等效替代。
此电压源中理想电压源的电压U S 等于有源二端网络的开路电压,内阻R 0等于有源二端网络中所有电源均除去后所得无源二端网络的等效内阻。
对于待求元件不要求一定是线性的。
第三章习题3-1 已知正弦电压和正弦电流的波形如图3-1所示,频率为50Hz ,试指出它们的最大值、初相位以及它们之间的相位差,并说明哪个正弦量超前,超前多少度?超前多少时间?解: u 、i 的表达式为即:u 比i 超前135°,超前2-1 某正弦电流的频率为20Hz ,有效值为 A ,在t =0时,电流的瞬时值为5A ,且此时刻电流在增加,求该电流的瞬时值表达式。
解:︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=•••••89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===AI A I V U t i A t i tV u ︒-∠=︒∠=︒∠=︒-=︒+==•••45259010022045sin10)90sin(210sin 22202121)(ωωωAt i tA i Aj jX U I Aj jX U I A R U I Hz f V U R C C L L R )(时:当︒-==∴︒∠=-︒∠=-=︒-∠=︒∠==︒∠=︒∠===︒∠=•••••••90314sin 210314sin 2109010)22(0220)(9010220220010220220500220•R I •LI •CI •U 时Hz f 50=3-3 已知复数A 1=6+j8Ω,A 2=4+j4Ω,试求它们的和、差、积、商。