列一元二次方程解应用题之面积问题.doc

列一元二次方程解应用题解应用题的关键是：能够理解题目中所给条件的关系，找出题目中的等量关系，列出方程。

1.面积问题[提示：面积问题一定要画图分析]例1：穗园小区住宅设计，准备在每两幢楼房之间，开辟面积为875m2的一块长方形绿地，并且长比宽多10m，那么绿地的长和宽各为多少？例2如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方厘米.求截去正方形的边长.解：设截去正方形的边长为x厘米，根据题意，得(60－2x)（）＝800解得：x1= , x2= 答：截去正方形的边长为。

例3、有一面积为150m2的长方形鸡场，鸡场的一边靠墙（墙长为18m），另三边用竹篱笆围成。

如果竹篱笆的长为35m，求鸡场的长与宽各为多少？解：(1) 如果鸡场的靠墙一边为长，则设鸡场的宽为xm ，长为（35-2x）m，根据题意得：x( )=150整理得：2x2-35x+150=0解得：x1=________, x2=________________因为__________________________________,所以x=_________符合题意。

因为______________________=20>18，不符题意，所以舍去。

答：鸡场的长与宽各为15m,10m 。

（2）如果鸡场的靠墙一边为宽，则设鸡场的长为ym ，宽为（35-2y）m，根据题意得：y( )=150整理得：____________________________________-解得：y1= , y2=35-2y1= __________________________________,35-2y2=__________________________课堂练习1：学校中心大草坪上准备建两个相等的圆形花坛，要使花坛的面积是余下草坪面积的一半.已知草坪是长和宽分别为80米和60米的矩形，求花坛的半径.解：设_______________________ 列得方程_________________________________________2．根据科学分析，舞台上的节目主持人应站在舞台前沿的黄金分割点（即该点将舞台前沿这一线段分为两条线段，使较短线段与较长线段之比等于较长线段与全线段之比），视觉和音响效果最好.已知学校礼堂舞台宽20米，求举行文娱会演时主持人应站在何处？解：设_______________________ 列得方程_________________________________________3.要做一个容积是750cm2,高是6cm，底面的长比宽多5cm的长方形匣子，底面的长和宽应该是多少？4.要给一幅长30cm，宽25cm的照片配一个镜框，要求镜框的四条边宽度相等，•且镜框所占面积为照片面积的四分之一，求镜框边的宽度。

成共识6、（CAI动态演示）各图形中路的平行移动过程，师概括点明做此类题目的方法并板书过程。

7、观察图形⑸，能否用上述方法，又如何理解呢？同学们讨论得出将图⑹的路平行向四周移动可得图⑸（CAI动态演示）。

8、学生独立完成此题。

（CAI课件展示）例2、要设计一本书的封面，封面长27 cm ,宽21 cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上下边衬等宽，左右边衬等宽，应如何设计四周边衬的宽度（精确到0.1 cm）.1、讨论：此题与上题的图⑸有什么不同？又如何解答？2、师讲解：如何由封面及正中的长宽比例相同为9:7，得出上、下边衬宽与左、右边衬宽的比也是9：7.。

3、学生讨论得出直接设中央的长与宽的比9X:7X，从而列方程求解。

4、一人演板。

5、集体订正，强调结果验证。

1、如图，某中学为方便师生活动，准备在长30 m，宽20 m的矩形草坪上修两横两纵四条小路，横纵路的宽度之比为3∶2，若使余下的草坪面积是原来草坪面积的四分之三，则路宽应为多少？论形成的结果，易记熟且能灵活运用。

设疑，激发学生积极思考用题目之间的联系培养学生灵活处理问题的能力。

此方法不易理解，但可以借助图⑸，拓宽了学生的知识面。

设元的灵活性。

触类旁通，你有哪些心得体会。

拓展延伸总结反思2、有一面积是150平方米的长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边（门除外）用竹篱笆围成，篱笆总长33米．求鸡场的长和宽各多少米？归纳小结：系统地总结此类应用题的解法。

布置作业：（略）板书设计：12.6 一元二次方程的应用（二）例1．略例2．略解：设………解：………………………………课后反思，本节课的收获，还有没有需要老师帮助解决的问题。

18米2米。

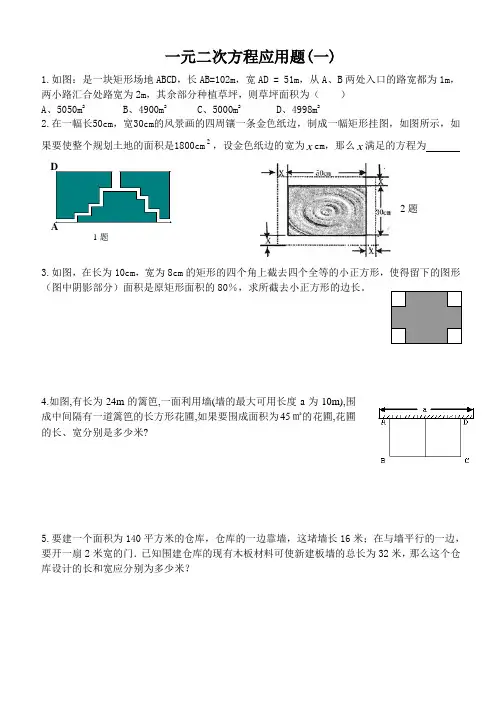
一元二次方程应用题(一)1.如图：是一块矩形场地ABCD ，长AB=102m ，宽AD = 51m ，从A 、B 两处入口的路宽都为1m ， 两小路汇合处路宽为2m ，其余部分种植草坪，则草坪面积为（ ）A 、5050m 2B 、4900m 2C 、5000m 2D 、4998m2 2.在一幅长50cm ，宽30cm 的风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个规划土地的面积是1800cm 2，设金色纸边的宽为x cm ，那么x 满足的方程为3.如图，在长为10cm ，宽为8cm 的矩形的四个角上截去四个全等的小正方形，使得留下的图形（图中阴影部分）面积是原矩形面积的80％，求所截去小正方形的边长。

4.如图,有长为24m 的篱笆,一面利用墙(墙的最大可用长度a 为10m),围成中间隔有一道篱笆的长方形花圃,如果要围成面积为45㎡的花圃,花圃的长、宽分别是多少米?5.要建一个面积为140平方米的仓库，仓库的一边靠墙，这堵墙长16米；在与墙平行的一边，要开一扇2米宽的门．已知围建仓库的现有木板材料可使新建板墙的总长为32米，那么这个仓库设计的长和宽应分别为多少米？A D1题2题6.如图,在一幅长90cm,宽40cm 的风景画四周镶上一条宽度相同的金色纸边,制成一幅挂画.如果要求挂画的面积是整个面积的72%,那么金边的宽应是多少?7.如图，利用一面墙（墙的长度不超过45m ），用80m 长的篱笆围一个矩形场地．⑴怎样围才能使矩形场地的面积为750m 2? ⑵能否使所围矩形场地的面积为810m 2，为什么?8.如图，在一块长为92m ，宽为60m 的矩形耕地上挖三条水渠,水渠的宽都相等，水渠把耕地分成面积均为885m 2的6个矩形小块，水渠应挖多宽？9.如图17①，在一幅矩形地毯的四周镶有宽度相同的花边． 如图17②，地毯中央的矩形图案长6米、宽3米，整个地毯的面积是40平方分米．求花边的宽．第21题图。

列一元二次方程解应用题之面积问题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（列一元二次方程解应用题之面积问题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为列一元二次方程解应用题之面积问题的全部内容。

《列一元二次方程解应用题之面积问题》教学目标:1.以面积的计算为载体，进一步培养学生运用方程的思想解决实际问题的意识，提高学生建立方程模型的能力2.体会变换在解决数学问题的作用，进一步强化学生问题转化的意识，进而形成解决问题的能力教学重点：构建方程模型教学难点：应用恰当等积变换，探索问题中隐含的等量关系教学过程：一、解方程（引入）（1）x2-52x+100=0 (2) x2—36x+35=0二、例题:某学校准备在一块长32米，宽20米的草地上修筑道路互相垂直的两条道路（道路的宽度相等)，使余下的草坪的面积为540平方米，求这个方案的道路的宽度。

变式1若改变道路的形状如下图（变式1），其他条件不变，那么应该怎么列方程？变式2。

若改变道路的条数如下图，且设计草坪的总面积是570平方米。

其他条件不变,那么应该怎么列方程?变式3。

方案设计问题：学校准备在一块长32米,宽20米的草地上修筑道路，决定在全校征集修改方案。

方案要求:①两条竖道保存不变.②横道不能是直道.③所有道路入口要相等，注明图形名称。

④使余下的草坪的面积仍然为570平方米。

你能帮学校修改这个方案吗?并标出入口的宽度三、小结（从数学思想的角度)四、效果反馈某小区中间有一块长方形的草地，长18米，宽10米,中间有两条均匀的小路（小路的人口相等）。

已知要求草地的面积为128平方米求，小路的入口的宽度。

列一元二次方程解应用题解应用题的关键是：能够理解题目中所给条件的关系，找出题目中的等量关系，列出方程。

1.面积问题[提示：面积问题一定要画图分析]例1：穗园小区住宅设计，准备在每两幢楼房之间，开辟面积为875m2的一块长方形绿地，并且长比宽多10m，那么绿地的长和宽各为多少？解：设宽为x m，则长为（）m，根据题意，得：____________________________＝875整理得－875＝0解这个方程，得 x1= , x2=-35∵ x2=-35<0，不合题意，舍去。

∴ x+10= 答：绿地得长和宽分别为，。

例2如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方厘米.求截去正方形的边长.解：设截去正方形的边长为x厘米，根据题意，得(60－2x)（）＝800解得：x1= , x2= 答：截去正方形的边长为。

例3、有一面积为150m2的长方形鸡场，鸡场的一边靠墙（墙长为18m），另三边用竹篱笆围成。

如果竹篱笆的长为35m，求鸡场的长与宽各为多少？解：(1) 如果鸡场的靠墙一边为长，则设鸡场的宽为xm ，长为（35-2x）m，根据题意得：x( )=150整理得：2x2-35x+150=0解得：x1=________, x2=________________因为__________________________________,所以x=_________符合题意。

因为______________________=20>18，不符题意，所以舍去。

答：鸡场的长与宽各为15m,10m 。

（2）如果鸡场的靠墙一边为宽，则设鸡场的长为ym ，宽为（35-2y）m，根据题意得：y( )=150整理得：____________________________________-解得：y1= , y2=35-2y1= __________________________________,35-2y2=__________________________答：鸡场的长与宽各为m, m课堂练习1：学校中心大草坪上准备建两个相等的圆形花坛，要使花坛的面积是余下草坪面积的一半.已知草坪是长和宽分别为80米和60米的矩形，求花坛的半径.解：设_______________________ 列得方程_________________________________________2．根据科学分析，舞台上的节目主持人应站在舞台前沿的黄金分割点（即该点将舞台前沿这一线段分为两条线段，使较短线段与较长线段之比等于较长线段与全线段之比），视觉和音响效果最好.已知学校礼堂舞台宽20米，求举行文娱会演时主持人应站在何处？解：设_______________________ 列得方程_________________________________________3.要做一个容积是750cm2,高是6cm，底面的长比宽多5cm的长方形匣子，底面的长和宽应该是多少？4.要给一幅长30cm，宽25cm的照片配一个镜框，要求镜框的四条边宽度相等，•且镜框所占面积为照片面积的四分之一，求镜框边的宽度。