下载文档原格式
曲率计算公式推导过程
曲率k=y''/[(1+(y')^2)^(3/2)]，其中y', y"分别为函数y对x的一阶和二阶导数(函数形式)。
曲率计算公式的推导过程如下：
曲线的曲率（curvature）就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。
数学上表明曲线在某一点的弯曲程度的数值。
曲率越大，表示曲线的弯曲程度越大。
曲率的倒数就是曲率半径。
扩展资料：
曲率是几何体不平坦程度的一种衡量。
平坦对不同的几何体有不同的意义。
在动力学中，一般的，一个物体相对于另一个物体做变速运动时也会产生曲率。
这是关于时空扭曲造成的。
结合广义相对论的等效原理，变速运动的物体可以看成处于引力场当中，因而产生曲率。
按照广义相对论的解释，在引力场中，时空的性质是由物体的“质量”分布决定的，物体“质量”的分布状况使时空性质变得不均匀，引起了时空的弯曲。
因为一个物体有质量就会对时空造成弯曲，而你可以认为有了速度，有质量的物体变得更重了，时空弯曲的曲率就更大了。
在物理中，曲率通常通过法向加速度（向心加速度）来求，具体请参见法向加速度。
未知驱动探索，专注成就专业
曲率公式
曲率公式是一种用于计算曲线的曲率的公式。
曲线的曲率
描述了曲线的弯曲程度。
曲率公式的一种常见形式是:
曲率(k) = |(dy/dx'') / (1+(dy/dx)^2)^(3/2)|
其中，dy/dx表示曲线在某一点处的斜率（即变化率），
dy/dx''表示曲线在这一点处的二阶导数（即曲率）。
以参
数方程表示的曲线，可以通过将x和y分别表示为参数t的函数来计算曲率。
曲率公式可以帮助我们衡量曲线的弯曲程度，从而在数学、物理、工程等领域中有广泛的应用。
通过计算曲线的曲率，我们可以判断曲线的凸、凹性，找到曲线的高低点，以及
解决各种与曲线相关的问题。
1。
曲率的公式
曲率分为数学曲率和物理曲率两大类。
数学曲率是指物体在物理坐标系上表示时所采用的曲率，它舍弃了物质特质，只考虑坐标系中的物体形状。
物理曲率描述物质在其他条件相同的情况下，物理空间中物体形状。
数学曲率和物理曲率之间有着密切的联系，例如，在物体空间中拥有相同的曲率的物体（椭圆体或球体），它们的数学曲率也是相等的。
物理曲率的计算公式是把形状和物理特性结合起来表示的：物体的物理曲率R为曲率半径的负值：R=−1／K，其中K为物体的曲率，又称为弧长所占的角度。
弧长所占的角度可以通过下面公式求得：Δφ＝s／R，而s则表示曲线上两点之间的弧长，故可以得出物理曲率公式：R＝−s／Δφ，当Δφ趋近于0时，R趋近于负无穷大，表明表面形状越来越接近直线。
总之，求物理曲率的公式是R＝−s／Δφ，其中K为曲率半径，s为曲线上两点之间的弧长，Δφ表示弧长所占的角度。
物理曲率的计算方法主要考虑物质在空间中的形状和物质特性，它与数学曲率有着千丝万缕的联系。
因为:1
■"-r 'Ax 令二;一〕，同时用1代替二
曲率的概念及计算公式
概念
来源：为了平衡曲线的弯曲程度。
平均曲率’厶，这个定义描述了 AB 曲线上的平均弯曲程度。
其中-「表示曲 线段AB 上切线变化的角度，-为AB 弧长。
计算公式的推导：
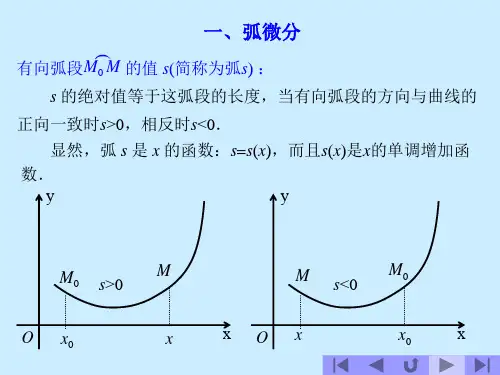
由于’ 丄，所以要推导「•与ds 的表示法，ds 称为曲线弧长的微分
MN\
具体表示； 仁y 叮⑴时，矗二±』1+丁%）必
2、 ◎厂加）时，d 汁士厶阳石西%
3、 彳=时，亦二±//（龙+孑（为刖（令厂內開肉厂"in 竹
再推导；，因为U ，所以mW ，两边对x 求导，得八 -'T' ， d^= ‘卩 dx
推出'0
即为曲率的计算公式
曲率半径:
般称.'为曲线在某一点的曲率半径
几何意义为在该点做曲线的法线（在凹的一侧），在法线上取圆心，以P为半径做圆，则此圆称为该点处的曲率圆。
曲率圆与该点有相同的曲率，切线及一阶、两阶稻树。
