东北师范大学 8-2 狭义相对论的时空观

狭义相对论的三个时空观
狭义相对论是爱因斯坦于1905年提出的一种物理学理论，它涉及到了时间和空间的观念。

狭义相对论的三个时空观如下：
1. 相对性原理：狭义相对论的第一个时空观是相对性原理，它认为物理定律在所有惯性参考系中都是相同的。

换句话说，物理定律在不同的观察者之间是不变的，无论他们的运动状态如何。

这意味着没有一个特定的参考系是绝对的，而是都是相对的。

2. 光速不变原理：狭义相对论的第二个时空观是光速不变原理，它指出光速在真空中是恒定不变的，无论观察者自身的运动状态如何。

这意味着光在不同的参考系中传播的速度始终是相同的。

这个原理对于理解狭义相对论中的时间和空间的变化至关重要。

3. 时空的相对性：狭义相对论的第三个时空观是时空的相对性。

根据狭义相对论，时间和空间是相互关联的，构成了一个四维时空的连续体。

观察者的运动状态会导致时间和空间的相对变化，即时间的流逝速度和空间的长度会随着观察者的运动状态而发生变化。

这个时空观对于理解相对论中的时间膨胀和长度收缩等效应至关重要。

4.3 狭义相对论的时空观4.3.1 同时的相对性光速相对于所有惯性系中的观测者以不变的速率传播，其惊人的结果是:时间一定是相对的。

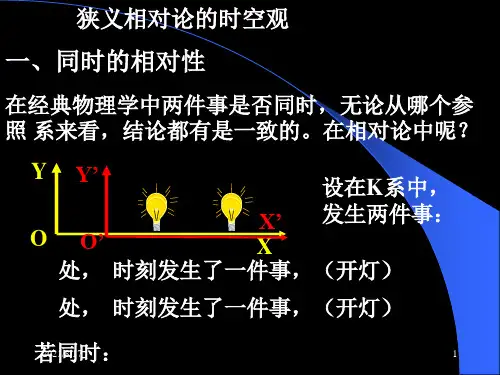
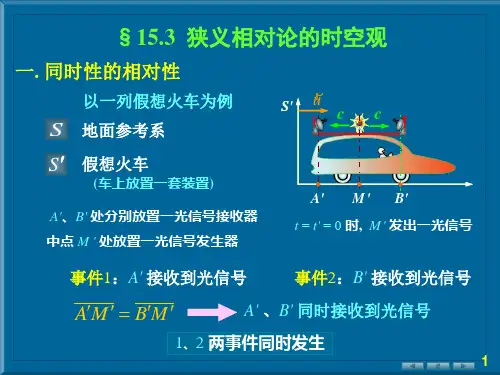
1 “同时”的定义设A 、B 两处发生两个事件，在事件发生的同时，发出两光信号，若在A 、B 的中心点同时收到两光信号，则A 、B 两事件是同时发生的。

这就是用光前进的路程来测量时间，而这样定义的理由就是光速不变，这样的定义适用于一切惯性系。

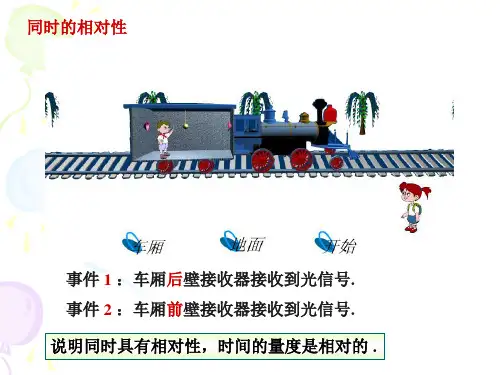
2 爱因斯坦理想的 “火车对钟实验”设有一列火车相对于站台以匀速向右运动，站台上的观测者测得当列车的首尾两点与站台上的A ，B 两点重合时，站台上的A ，B 两点同时发出一个闪光，所谓“同时”，就是两闪光同时传到站台上的中心点C 。

但对于列车来说，由于它向右行驶，车上的中点先接到来自车头方（即站台上的A 点）的闪光，后接到来自车尾方（即站台的B 点）的闪光。

于是对于列车上中点的观察者来说，A 点的闪光早于B 点。

就是说，对于站台参照系是同时的事件，对于列车参照系就不是同时的，即事件的同时性是相对的。

在一个惯性系中的两个同时事件，在另一个惯性系中观测不是同时的，这是时空均匀性和光速不变原理的一个直接结果。

3 同时的相对性设在惯性系S 中,在不同地点同时发生两事件,时空坐标分别为（x 1，0，0 ，t ）和（x 2，0，0，t ），则根据洛仑兹变换式（4-4a ），有2221'11c u c ux t t --=, 2222'21c u c ux t t --=，即()0122122'1'2≠---=-cu x x c ut t 讨论 1 从上可知，在某一惯性系同时不同地发生的两个事件，在另一惯性系中观测则是不同时发生, 这就是狭义相对论的同时相对性。

同时相对性的本质在于在狭义相对论中时间和空间是相互关联的。

若u 沿x 轴正方向，且12x x ->0,则0'1'2<-t t ,可得出结论，沿两个惯性系相对运动方向发生的两个事件,在其中一个惯性系中表现为同时的,在另一惯性系中观察,则总是在前一惯性系运动的后方那一事件先发生。

狭义相对论的四维时空观狭义相对论的四维时空观狭义相对论是建立在四维时空观上的一个理论，因此要弄清相对论的内容，要先对相对论的时空观有个大体了解。

在数学上有各种多维空间，但目前为止，我们认识的物理世界只是四维，即三维空间加一维时间。

现代微观物理学提到的高维空间是另一层意思，只有数学意义，在此不做讨论。

四维时空是构成真实世界的最低维度，我们的世界恰好是四维，至于高维真实空间，至少现在我们还无法感知。

我在一个帖子上说过一个例子，一把尺子在三维空间里（不含时间）转动，其长度不变，但旋转它时，它的各坐标值均发生了变化，且坐标之间是有联系的。

四维时空的意义就是时间是第四维坐标，它与空间坐标是有联系的，也就是说时空是统一的，不可分割的整体，它们是一种”此消彼长”的关系。

四维时空不仅限于此，由质能关系知，质量和能量实际是一回事，质量（或能量）并不是独立的，而是与运动状态相关的，比如速度越大，质量越大。

在四维时空里，质量（或能量）实际是四维动量的第四维分量，动量是描述物质运动的量，因此质量与运动状态有关就是理所当然的了。

在四维时空里，动量和能量实现了统一，称为能量动量四矢。

另外在四维时空里还定义了四维速度，四维加速度，四维力，电磁场方程组的四维形式等。

值得一提的是，电磁场方程组的四维形式更加完美，完全统一了电和磁，电场和磁场用一个统一的电磁场张量来描述。

四维时空的物理定律比三维定律要完美的多，这说明我们的世界的确是四维的。

可以说至少它比牛顿力学要完美的多。

至少由它的完美性，我们不能对它妄加怀疑。

相对论中，时间与空间构成了一个不可分割的整体——四维时空，能量与动量也构成了一个不可分割的整体——四维动量。

这说明自然界一些看似毫不相干的量之间可能存在深刻的联系。

在今后论及广义相对论时我们还会看到，时空与能量动量四矢之间也存在着深刻的联系。

--------------------------------------------------------------------------------狭义相对论基本原理物质在相互作用中作永恒的运动，没有不运动的物质，也没有无物质的运动，由于物质是在相互联系，相互作用中运动的，因此，必须在物质的相互关系中描述运动，而不可能孤立的描述运动。

狭义相对论的三个时空观
狭义相对论是爱因斯坦在1905年提出的一种新的时空观，它颠覆了牛顿力学的时空观，提出了三个新的时空观，分别是相对性原理、光速不变原理和等效原理。

相对性原理是狭义相对论的核心，它指出物理规律在所有惯性系中都是相同的。

也就是说，无论在哪个惯性系中观察，物理规律都是一样的。

这个原理的提出，打破了牛顿力学中绝对时空的观念，强调了时空的相对性。

光速不变原理是狭义相对论的另一个重要原理，它指出光速在任何惯性系中都是不变的。

也就是说，无论在哪个惯性系中观察，光速都是不变的。

这个原理的提出，引发了对时空的重新认识，强调了时空的相对性和不可分割性。

等效原理是狭义相对论的第三个重要原理，它指出惯性质量和引力质量是等效的。

也就是说，任何物体在重力场中的运动状态，都可以等效地看作在惯性系中匀速直线运动。

这个原理的提出，揭示了引力与惯性的本质联系，强调了物理规律的普适性和等效性。

总之，狭义相对论的三个时空观，相对性原理、光速不变原理和等效
原理，都是对时空的重新认识和理解，它们打破了牛顿力学中绝对时空的观念，强调了时空的相对性和不可分割性，揭示了物理规律的普适性和等效性。

这些时空观的提出，不仅推动了物理学的发展，也深刻影响了人们对世界的认识和理解。

一、同时的相对性（Relativity of Simultaneity ）： 狭义1．概念相对论的时空观认为：同时是相对的。

即在一个惯性系中不同地点同时发生的两个事件，在另一个惯性系中不一定是同时的。

例如：在地球上不同地方同时出生的两个婴儿，在一个相对地球高速飞行的飞船上来看，他们不一定是同时出生的。

2．例子：Einstein 列车：以u 匀速直线运动，车厢中央有一闪光灯发出信号，光信号到车厢前壁为事件1，到后壁为事件2；地面为S 系，列车为S'系。

在S'系中，A 以速度v 向光接近；B 以速度v 离开光，事件1与事件2同时发生。

在S 系中，光信号相对车厢的速度v ’1=c-v ，v ’2=c+v ，事件1与事件2不是同时发生。

即S'系中同时发生的两个事件，在S 系中观察却不是同时发生的。

因此，“同时”具有相对性。

说明：Lorentz 速度变换式中，是求某质点相对于某参考系的速度，不可能超过光速。

而在同一参考系中，两质点的相对速度应该按矢量合成来计算。

2．解释：在S'系中，不同地点x 1'与x 2'同时发生两件事 t 1'= t 2'，Δ t '= t 1'- t 2'=0，Δ x '=x 1' – x 2'在S 系中()221c v x c v t t -'∆+'∆=∆由于Δ t '=0。

Δ x '=x 1' – x 2'≠0，故Δ t ≠0。

可见，两个彼此间作匀速运动的惯性系中测得的时间间隔，一般来说是不相等的。

即不同地点发生的两件事，对S'来说是同时发生的，而在S 系中不一定是同时发生的。

若Δ x '=x 1' – x 2'=0，则Δ t =0，即是同一地点同时发生的两件事，则在不同的惯性中也是同时发生的。

爱因斯坦的时空观东南大学物理系董科牛顿的时空观在牛顿力学中，时间和长度的测量是绝对的伽利略变换公式CA CB B AC A C B B AC A C B B A→→→→→→→→→=+=+=+r r r v v v a a a 牛顿的相对性原理：对于所有的惯性系，牛顿力学的规律都应有相同的形式假想实验一:真空中光速的测量S参照系中观测S参照系中观测实验表明，真空中光速的测量不依赖于惯性系的选取，这是与由伽利略速度变换公式推出的结论相矛盾的。

有两种可能性电磁现象不遵守相对性原理伽利略速度变换公式光速测量实验伽利略速度变换公式不正确矛盾时间测量的绝对性不正确长度测量的绝对性不正确？？？？狭义相对论的两个基本假设爱因斯坦的相对性原理：所有物理规律在不同的惯性系中的表述都是一样的。

光速不变原理：真空中光速不依赖于惯性系的选取。

假想实验二:同时性的相对性结论：时间的测量是相对的。

参照系中观测S 参照系中观测S假想实验三:时间延缓效应参照系中观测S若两事件在某一惯性系的同一地点发生，则该惯性系中测得的时间间隔称为这两个事件的固有时。

参照系中观测S假设：在观测者看来，沿水平方向运动的物体的高度小于其静止不动时的高度静止不动时，火车与山洞等高结论：垂直于相对运动方向的长度测量不受相对运动的影响。

假想实验四:垂直于相对运动方向的长度测量假想实验五:平行于相对运动方向的长度测量l S ''=参照系中测得救护车的车身长度l S =参照系中静止不动的观测者测得的救护车的车身长度=相对于物体静止不动的参照系中测得的该物固有长度体的长度结论：相对于物体静止不动的惯性系中测得物体的长度最长。

总结200 1l l l β=-(2) （平行于相对运动方向）, 其中长为度收缩效应：固有长度；相对于物体静止不动的参照系中测得的该物体的长度为其固有长度若两事件在某惯性系中发生在同一坐标，则该参照系中测得的两事件的时间间隔为其固有时(3) 垂直于相对运动方向的长度测量不受相对运动的影响。