与动物有关的数学

题目：共有蛐蛐和蜘蛛6只，总共40条腿，问蛐蛐和蜘蛛各有多少只？
解题：蛐蛐每只6条腿，蜘蛛每只8条腿。

第一步：假设都是蛐蛐，画出6只蛐蛐和所有的36条腿：
111111 111111 111111 111111 111111 111111
第二步：总数40条腿减去第一步蛐蛐的36条腿，还剩4条腿，由于每只蜘蛛比蛐蛐多2条腿，因此多出来的是2个蜘蛛的腿数；
第三步：在图上找2只蛐蛐的腿数上各加2条腿，如下图红色部分：
1111111111111111111111 111111 111111 111111
第四步：既然前2只蛐蛐变成了8条腿，就应该变为蜘蛛，如下图：
1111111111111111111111 111111 111111 111111
第五步：数图就知道蜘蛛2只，蛐蛐4只。

其它鸡兔同笼的问题都可以这样解释，只是画的比较多一些。

等学了乘除法后，就更简单了：
1、用总腿数(40)-腿少的蛐蛐的数量乘腿数(6×6)÷腿数差（8-6）=腿多的动物的
个数（2只蜘蛛）；
2、那么蛐蛐=6-2=4只。

动物里的数学动物世界中的数学数学是一门抽象而又晦涩的学科，但你可能不知道，在动物世界中，也存在着各种各样的数学现象。

本文将介绍一些有趣的动物数学现象，带你一起探索动物世界中的数学之谜。

第一章：斐波那契数列与兔子繁殖斐波那契数列是一组无穷序列，其中每个数字是前两个数字之和。

这个数列在自然界中也有出现，最典型的例子就是兔子的繁殖。

假设一对兔子在出生后第三个月开始繁殖，每对兔子每个月可以生一对小兔子。

那么经过n个月，共有多少对兔子呢？答案就是斐波那契数列的第n+2个数字。

这是因为在第一个月，只有一对兔子；在第二个月，还是只有一对兔子；而在第三个月开始，每个月的兔子对数都等于前两个月兔子对数之和。

所以，通过斐波那契数列可以计算兔子繁殖的数量。

第二章：蜜蜂与六边形蜂巢蜜蜂建造的蜂巢是六边形的，这不仅是因为六边形的结构更加稳固，还因为它可以最大限度地利用空间。

如果用其他形状的图形来构建蜂巢，将会浪费更多的空间。

利用数学的知识，我们可以证明六边形是最有效的形状。

假设我们要用相同的面积来构建蜂巢，如果使用正方形，将会有更多的空隙；如果使用圆形，同样会浪费空间。

而六边形正好在这方面达到了最佳效果。

第三章：鸟群与V字队形当我们看到鸟群在天空中飞行时，它们往往排成一个字母V的队形。

这个队形背后也隐藏着一些数学的原理。

队形的V字形状可以减少空气阻力，让鸟群更加省力地飞行。

其次，队形中的每只鸟都能够看到前面的鸟，这样可以提高整个群体的反应速度和飞行效率。

队形中的每只鸟都可以利用空气上升的气流，从而节省体力。

这种利用气流的方式也遵循着数学中的一些原理，使得整个鸟群能够更好地适应飞行环境。

第四章：斑马与条纹斑马身上的条纹一直以来都是一个谜团。

科学家们通过数学的方法研究发现，斑马身上的条纹可以起到一种视觉欺骗的作用。

斑马条纹的密度和宽度可以使捕食者产生视觉上的干扰，使其难以判断斑马的精确位置和行动方向。

这种视觉干扰使得捕食者难以成功捕食，从而保护了斑马的安全。

动物中的数学知识
1、蚂蚁he丹顶鹤的算术
毫不起眼的蚂蚁的计算本领也十分高超。

英国科学家亨斯顿做过一个有趣的实验。

他把一只死蚱蜢切成三块，第二块比第一块大一倍，第三块比第二块大一倍。

在蚁群发现这三块食物40分钟后，聚集在最小一块蚱蜢处的蚂蚁有28 只，第二块有44 只，第三块有89 只，后一组差不多都较前一组多一倍。

看来蚂蚁的乘、除法算得相当不错。

产于我国的珍稀动物丹顶鹤总是成群结队地迁徙，而且排成“人”字形。

2、天才的数学家蜜蜂。

18世纪初，法国学者马拉尔奇曾经专门测量过大量蜂巢的尺寸，令他感到十分惊讶的是，这些蜂巢组成底盘的菱形的所有钝角都是109°28′，所有的锐角都是70°32′。

后来经过法国数学家克尼格he苏格兰数学家马克洛林从理论上的计算，如果要消耗最少的材料，制成最大的菱形容器正是这个角度。

从这个意义上说，蜜蜂称得上是“天才的数学家兼设计师”。

十二生肖数学知识十二生肖数学知识根据传统的十二生肖（鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪），我们可以探索一些与数学相关的知识。

1. 鼠鼠是十二生肖中最小的动物之一，但是它在数学中有着重要的地位。

鼠可以被用来表示分数，比如1/2、1/4、1/8等等。

2. 牛牛在数学中有着非常重要的作用，它是幂运算的一个例子。

如果将2的幂记作2^n，那么2的3次幂就是8，我们可以将其表示成“2的牛为3”。

3. 虎虎是一个很有力量的动物，这也让我们想起了整数的乘方运算。

如果我们将一个整数a乘以自己n次，那么可以表示成a^n。

4. 兔兔子是一个快速的动物，这也让我们想起了数列中的增长速度。

在数列中，如果每一项都是前一项的倍数，那么这个数列就被称为等比数列。

例如，1，2，4，8就是一个等比数列，每个数都是前面一个数的两倍。

5. 龙龙是中国文化中的一个非常重要的象征，但在数学中，我们通常用它来描述单位长度。

比如，一根龙的长度等于三个人的身高，可以用来测量长距离。

6. 蛇蛇在数学中可以用来描述曲线。

如果一个曲线在任何一点的斜率都相同，那么这条曲线就是一条直线。

但如果曲线的斜率在不同的点有所变化，那么就可以称之为弧线。

7. 马马是一个很快的动物，也是一个重要的数学元素。

在代数学中，马可以代表一种“变速度”的运动。

如果一个物体以不同的速度运动，它的速度就会在不同的时间和不同的地点发生变化。

8. 羊羊是一个温和的动物，但在数学中，羊可以用来描述一种“夹缝”的状态。

比如，如果一个物体被固定在两个不同的支点之间，那么它的位置就会受到夹缝的限制，只能在一个特定的区域内移动。

9. 猴猴是一个非常机智的动物，也是数学中的一个重要元素。

在计算机科学中，猴可以代表一种“随机性”。

比如，我们可以用猴子来模拟一个随机的过程，如抛硬币或掷骰子。

10. 鸡鸡是一个很有信仰的动物，但在数学中，它可以用来描述一种特殊的计数方法，被称为“二进制”。

动物中的数学知识动物王国是一个充满神奇与美妙的领域。

在动物世界中，数学原理在各种行为和特征中发挥着重要作用。

本文将探讨动物中的数学知识，包括鸟类的飞行路径、动物的对称性、动物的斐波那契数列、动物的空间感知与拓扑结构、昆虫的计数能力、生物演化的数学模型以及动物数量的周期性变化。

1.鸟类的飞行路径鸟类在飞行过程中，会利用几何原理来优化飞行路径。

例如，燕子在飞行时会采取最优化的路线，以最短的距离和时间完成迁徙。

这种最优路径的几何原理涉及到了曲率和弧度等概念。

通过研究鸟类的飞行路径，科学家们可以深入了解鸟类的导航和迁徙行为。

2.动物的对称性动物的对称性体现在许多方面，如蜜蜂、蚂蚁和蝴蝶等昆虫的身体结构。

这些动物的对称性不仅具有观赏价值，还涉及到数学原理。

例如，蜜蜂的蜂巢是一种典型的对称结构，体现了六边形的概念。

这种对称结构有助于蜜蜂节省空间和材料，同时也有助于加强蜂巢的结构强度。

3.动物的斐波那契数列斐波那契数列是一个在数学中常见的数列，同样也存在于动物的行为和结构中。

例如，金枪鱼在游动时划过的路径形成了一个斐波那契数列。

此外，蜜蜂在寻找食物和建造巢穴时，也会遵循斐波那契数列的规律。

这种数列在生物学中的应用，不仅体现了数学原理在自然界中的广泛应用，还为研究者提供了理解动物行为的视角。

4.动物的空间感知与拓扑结构动物在寻找食物、躲避天敌和迁徙过程中，需要精确地感知空间位置和方向。

许多动物利用几何学和拓扑学原理来识别周围环境。

例如，蚂蚁会使用直线和角的信息来构建最优路径。

此外，一些鸟类和鱼类也会利用地球的磁场来感知方向。

这些动物的空间感知能力，为拓扑学和几何学的研究提供了有趣的案例。

5.昆虫的计数能力昆虫的世界同样充满了数学原理。

一些昆虫具备计数能力，这在它们寻找食物、避开天敌和繁殖时非常重要。

例如，蚂蚁能够计算食物的数量，以便公平地分配给每一个成员。

这种计数能力涉及到分形和迭代函数等数学概念。

此外，蜜蜂的舞蹈也体现了对数学规律的理解，用于传递关于食物位置的信息。

生活中的10种数学动物1、灰鹦鹉生物学家佩珀伯格，曾在美国印第安纳州耐心训练一只6岁的非洲灰鹦鹉，让它学会了40个英文单词，还能计数，这只鹦鹉能用这些单词说出几十种物件的名称、颜色和形状，如果把这些东西各自分堆的话，还会说出这堆东西各自是多少。

2、珊瑚虫珊瑚虫的头脑不简单，据观察，珊瑚虫自身便是一个“日历”，它们每年在自己的体壁上“刻画”出365条斑纹，显然是一天“画”一条。

奇怪的是，古生物学家发现3亿5千万年前的珊瑚虫每年“画”出的是400幅水彩画，天文学家告诉我们，当时地球一天仅为21．9小时，一年不是365天，而是400天，这足以证明珊瑚虫的数字才能。

3、蛇类蛇在爬行时，走的是一个数字正弦函数图形，它的脊椎像火车一样，是一节一节连接起来的，节与节之间有较大的活动余地，如果把每一节的平面坐标固定下来，并已开始点为坐标原点，结果发现蛇是按着30°60°和90°的正弦函数曲线有规律地运动的。

4、蜘蛛蜘蛛结的“八卦”形网络是既复杂又美丽的八角形几何图案，人们即使用直尺和圆规等制图工具也很难画出像蜘蛛网那样匀称的图案来。

五、鸬鹚中国有些地方靠鸬鹚捕鱼，主人用一根细绳拴住鸬鹚的喉颈，当鸬鹚捉回6条鱼以后，允许它们吃第7条鱼，这是主人与鸬鹚之间长期形成的约定，科学家注意到，渔民偶尔数错了，没有解开鸬鹚脖子上的绳子时，鸬鹚则动也不懂，即使渔民打它们，它们也不出去捕鱼了，它们知道这第7条鱼应该是自己所得的。

6、蚂蚁的计数本领高超。

7、蜘蛛结的“八卦”形网是既复杂又美丽的八角形几何图案。

8、野猴和黑猩猩有数学脑瓜，会计量。

9、蜜蜂构巢。

10、小鸡；对新生的小鸡进行的试验显示，它们生来具有数字的意识。

意大利帕多瓦大学一个研究小组发现，那些把小球和碎纸片当成它们亲戚的小鸡能进行简单的加减法运算。

建筑师——蜜蜂和桦树卷叶象虫蜜蜂蜂房是严格的六角柱状体，它的一端是平整的六角形开口，另一端是封闭的六角菱锥形的底，由三个相同的菱形组成。

组成底盘的菱形的钝角为109度28分，所有的锐角为70度32分，这样既坚固又省料。

蜂房的巢壁厚0,073室米，误差极小。

桦树卷叶象虫能用桦树叶制成圆锥形的产房，它们是这样做的：雌象虫开始工作时，先爬到里叶柄不远的地方，用锐利的双颚咬透叶片，向后退去，咬出第一道弧形的裂口；然后爬到树叶的另一侧，咬出弯度小些的曲线；接下来又回到开头的地方，把下面的一半叶子卷成很细的锥形圆筒，卷5—7圈；最后把另一半朝向反方向卷成锥形圆筒。

这样，结实的产房就做成了。

图形设计师——蜘蛛和蛇蜘蛛结的”八卦”形网，是既复杂又美丽的八角形几何图案，人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案。

蛇在爬行时，走的是一个数字正弦函数图形。

它的脊椎像火车一样，是一节一节连接起来的，节与节之间有较大的活动余地。

如果把每一节的平面坐标固定下来，并以开始点为坐标原点，结果发现蛇是按着30度、60度和90度的正弦函数曲线有规律地运动的。

最佳团队——丹顶鹤丹顶鹤总是成群结队迁飞，而且排成“人“字形。

“人"字形的角度是110度。

更精确地计算还表明“人”字形夹角的一半一一即每边与鹤群前进方向的夹角为54度44分8秒！而金刚石结晶体的角度正好也是54度44分8秒！这是巧合还是某种大自然的“默契”呢？数学物理双学位——猫在赛冷的冬天，猫睡觉时总是把身体抱成一个球形，这其间也有数学，因为球形使露在冷空气中的身体表面积最小，从而散发的热量也最少，达到保暖的目的。

代数天才一一是珊瑚虫珊瑚虫懂得在自己的身上记下“日历”，它们每年在自己的体壁上“刻画"出365条斑纹，显然是一天“画”一条。

奇怪的是，古生物学家发现3亿5千万年前的珊瑚虫每年“画"出400幅”水彩画”。

天文学家告诉我们，当时地球一天仅21.9小时，一年不是365天，而是400天。

中班数学教案动物有多少中班数学教案：动物有多少？一、教学目标：1. 知识目标：通过本节课的学习，学生将学会使用简单的数学方法来计算动物数量。

2. 能力目标：培养学生观察和计数的能力，训练学生记数的顺序和准确性。

3. 情感目标：培养学生对动物的兴趣，提高学生的积极参与和合作意识。

二、教学重点和难点：重点：数数，加减法概念的初步形成。

难点：辨别不同的动物，进行正确的计数。

三、教学准备：1. 教具准备：动物图卡，卡片上分别有不同种类的动物。

2. 教材准备：教案、活动册。

四、教学过程：Step 1：引入新知1. 教师出示动物图片，引导学生观察，提问：“你们看到了哪些动物？”2. 学生积极回答，教师鼓励他们用手指指向图片上的每个动物，帮助学生记住不同的动物。

Step 2：认识不同的动物1. 教师拿出一张动物图卡，出示并说出动物的名称。

2. 教师让学生模仿并大声说出该动物的名称，帮助学生记忆和发音。

3. 教师反复出示不同的动物图卡，让学生逐个说出动物的名称。

4. 教师提问：“你们能用手指指出它们吗？”学生积极回答，教师鼓励他们正确指出动物的名称。

Step 3：学习数数1. 教师出示一个动物图卡，让学生集中注意并观察。

2. 教师问学生：“这个动物有几只？”学生可以用手指数数或直接说出数字。

3. 教师鼓励学生正确回答，并对回答错误的学生进行纠正和指导。

4. 教师逐个出示其他动物图卡，让学生计数动物的数量。

Step 4：加一加1. 教师出示两张相同的动物图卡，让学生观察。

2. 教师问学生：“这是同样的动物吗？有多少只？”学生可以用手指数数或直接说出数字。

3. 教师引导学生发现两张图卡上的动物数量相同，并指出两个数量可以通过加法来表示。

4. 教师出示其他两张相同数量的动物图卡，让学生加一加，并说出结果。

5. 教师反复练习加法运算，鼓励学生互相帮助和指导。

Step 5：减一减1. 教师出示两张不同数量的动物图卡，让学生观察。

一年级数学小动物分类的题
一、题目示例
1. 把下面的小动物分类，可以按腿的数量分，也可以按生活的地方分。

（小动物有：小鸡、兔子、小鱼、青蛙、小狗）
二、题目解析
1. 按腿的数量分
两条腿的小动物：小鸡。

四条腿的小动物：兔子、小狗。

没有腿（或者说靠鳍等游动的）小动物：小鱼。

青蛙比较特殊，它是两栖动物，幼体（蝌蚪）没有腿，成体有四条腿，在这里按照成体考虑的话可以分到四条腿的这一类。

2. 按生活的地方分
生活在陆地上的小动物：小鸡、兔子、小狗。

生活在水里的小动物：小鱼。

青蛙既能生活在水中也能生活在陆地上，不过如果按照常见的分类习惯，也可以把它归到既能生活在水里又能生活在陆地上这一特殊类（两栖类）。

这样的分类题有助于一年级学生初步建立分类的思想，学会根据不同的标准对事物进行分类，同时也能让他们对小动物的基本特征（腿的数量、生活环境等）有更清晰的认识。

幼小衔接数学题数一数动物一、数数小动物在我们周围，有许多可爱的小动物。

它们有一种独特的魅力，经常成为孩子们喜爱的对象。

我们通过一些有趣的数学题目来数一数不同种类的小动物吧！1. 小鸟在树上和天空中，时常可以看到小鸟在飞翔。

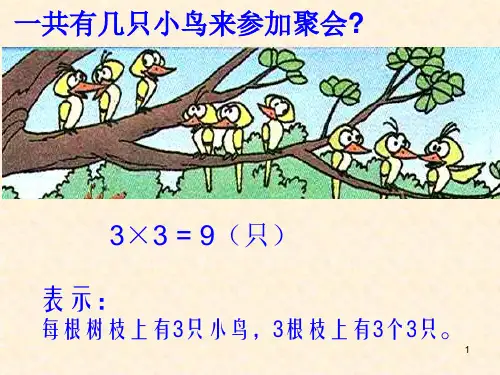
今天，我看到了5只小鸟在树上唱歌，还有3只小鸟在天空中飞翔。

请问一共有几只小鸟呢？2. 小猫和小狗在市区的巷子里，有3只小猫在玩耍，而在旁边的花园里，有7只小狗在追逐着小球。

请问一共有几只小动物呢？3. 小兔子在农田里，我看到了4只小兔子在欢快地跳跃。

突然，又有5只小兔子从草丛中出现。

请问一共有几只小兔子呢？4. 小鱼和小虾在清澈的河水中，许多小鱼不停地游来游去。

我数了一数，发现有6只小鱼在兴奋地畅游。

与此同时，7只小虾也在河底嬉戏。

请问一共有几只水中小生物呢？5. 小青蛙在池塘边，我看到了8只小青蛙在跳跃。

它们欢快地蹦蹦跳跳，给整个池塘带来了生机。

请问一共有几只小青蛙呢？二、解决数学题让我们来一起解决这些有趣的数学题目，帮助我们更好地理解数的概念和计算能力。

1. 小鸟5只小鸟在树上唱歌，3只小鸟在天空中飞翔。

那么一共有5只小鸟 + 3只小鸟 = 8只小鸟。

答案：一共有8只小鸟。

2. 小猫和小狗3只小猫在玩耍，7只小狗在追逐小球。

那么一共有3只小猫 + 7只小狗 = 10只小动物。

答案：一共有10只小动物。

3. 小兔子4只小兔子在农田中跳跃，5只小兔子从草丛中出现。

那么一共有4只小兔子 + 5只小兔子 = 9只小兔子。

答案：一共有9只小兔子。

4. 小鱼和小虾6只小鱼在河水中游动，7只小虾在河底嬉戏。

那么一共有6只小鱼 + 7只小虾 = 13只水中小生物。

答案：一共有13只水中小生物。

5. 小青蛙8只小青蛙在池塘边跳跃。

那么一共有8只小青蛙。

答案：一共有8只小青蛙。

三、小结通过这些有趣的数学题目，我们能够更好地理解数的概念，并培养我们的计算能力。

同时，通过数数不同种类的小动物，我们也能够了解到自然界中的多样性和生命的美妙。

用数学方法介绍一种动物
我将以数学的角度介绍一种动物，选择羚羊作为例子。

描述途径一：几何描述
羚羊是一种优美而灵活的动物，它们具有优秀的跑步能力和敏锐的观察力。

从几何的角度来看，羚羊的身躯可以近似地看作一个长方形，背部较为平坦，四肢细长而有力。

另外，羚羊的头部可以近似看作一个尖锐的三角形，与身体相连。

描述途径二：运动学描述
羚羊在奔跑时以惊人的速度移动，其奔跑过程可以通过运动学进行描述。

羚羊能够迅速加速并保持匀速直线奔跑，这表明它具有出色的加速度和速度控制能力。

羚羊的奔跑速度也可以用速度-时间图进行描述，表现出最大速度和平均速度的变化情况。

描述途径三：生态学描述
羚羊生活在广阔的草原和沙漠地区，它们通过适应环境来获取食物和保护自己。

数学模型可以用来描述羚羊种群的增长和数量的变化。

生态学模型可以利用随机和确定性方程来描述不同环境因素的影响，如食物供应、天敌的存在等。

综上所述，数学作为一门工具，可以从不同的角度对动物进行描述。

在羚羊的例子中，数学可以被应用于几何、运动学和生态学等方面，帮助我们更好地理解这
一动物的特征和行为。

幼儿园数学6只鸭子,2只小鸟
在我们生活的周围，数学无处不在。

即使是幼儿园的小朋友，也能通过生活中的小事锻炼数学思维。

今天，我们要解决的一个数学问题就是：6只鸭子和2只小鸟一共有多少只？
首先，我们要了解题目的背景。

题目中提到的6只鸭子和2只小鸟，是我们生活中常见的小动物。

孩子们可以通过数数的方法，计算出它们的总数量。

接下来，我们来分析一下题目的要求。

题目要求我们计算6只鸭子和2只小鸟的数量总和。

这是一个简单的加法运算，我们可以用数字6和2来表示。

现在，我们可以提出解决方案了。

将6只鸭子和2只小鸟的数量相加，即6+2=8。

所以，6只鸭子和2只小鸟一共有8只。

最后，我们来总结一下。

这个简单的数学问题，让孩子们学会了生活中简单的加法运算，培养了他们的数学思维。

在日常生活中，我们可以引导孩子关注这些细节，让他们在轻松愉快的氛围中学习数学。

久而久之，孩子们会发现，原来数学可以这么有趣！。

小学数学试卷动物题一、选择题（每题2分，共20分）1. 小明有5只兔子，小华有3只兔子，他们一共有几只兔子？A. 7只B. 8只C. 9只D. 10只2. 如果每只猫每天吃2条鱼，那么4只猫一天吃几条鱼？A. 6条B. 8条C. 10条D. 12条3. 小红有6只小鸡，她又买了2只，现在她有多少只小鸡？A. 7只B. 8只C. 9只D. 10只4. 一个动物园里有3只大象和5只老虎，大象和老虎一共有多少只？A. 6只B. 7只C. 8只D. 10只5. 小刚有4只小狗，他的朋友给了他3只，现在小刚有多少只小狗？A. 5只B. 6只C. 7只D. 8只二、填空题（每题2分，共20分）6. 如果每只猴子有4只香蕉，那么5只猴子一共有_________只香蕉。

7. 小明有3只小鸭子，如果他再得到2只，他将有_________只小鸭子。

8. 一个农场有7只羊和4只牛，农场里一共有_________只动物。

9. 每只狗每天吃3根骨头，那么5只狗一周吃_________根骨头。

10. 小红有10只小鸡，如果每只小鸡每天下一个蛋，那么一周小红可以得到_________个鸡蛋。

三、计算题（每题5分，共30分）11. 小明有10只小鸡，每只小鸡每天下一个蛋，那么小明一周可以得到多少个鸡蛋？12. 一个动物园有6只狮子和8只熊，如果每只狮子每天需要吃5公斤肉，每只熊每天需要吃3公斤肉，那么动物园一天需要准备多少公斤肉？13. 小华有4只小猫，每只小猫每天需要吃1罐猫粮，那么小华一个月（30天）需要准备多少罐猫粮？14. 小明有5只小兔子，每只小兔子每天需要吃0.2公斤的胡萝卜，那么小明一个月（30天）需要准备多少公斤的胡萝卜？四、应用题（每题10分，共30分）15. 小红家有一只小狗，小狗每天吃2个狗饼干。

如果小红要为小狗准备一个月的狗饼干，请问她需要准备多少个狗饼干？16. 一个农场有10只鸡和5只鸭，每只鸡每天下一个蛋，每只鸭两天下一个蛋。

动物的数学头脑（一）
科学家们经过多年的研究与探索发现，在自然界中有许多动物所具有的数学本领令人称奇，叫人折服。

说它们是名不见经传的“数学家”，一点也不为过。

蚂蚁的计算本领是十分高明的，堪称“计算专家”。

英国数学家亨斯顿曾经做过一个非常有趣的实验，他把一块糖按照下面的要求分成了3份：第二块的质量比第一块的质量大1倍，第三块的质量比第二块的质量大1倍，然后把它们散放在地面上。

当蚂蚁发现这些食物后，又过了大约半个小时左右，便有23只蚂蚁一起来搬运最小的一块食物，有45只蚂蚁一起齐心协力地搬运第二块食物，有89只蚂蚁通力合
作搬运第三块食物。

后一组蚂蚁数差
不多是前一组蚂蚁数的2倍。

蚂蚁的
这种“精确”的分工，如果没有一定
的“数学头脑”是难以办到的。

由此
可见，蚂蚁具有高超的计算本领。

丹顶鹤是我国的一级保护动物，也具有一定的“数学头脑”。

它们总是成群结队地迁徙，当它们在天空中飞行时，总是排成“人”字形，它们排列得是那么整齐，动作又是如此协调，令人叹为观止。

并且这个“人”字形的夹角总是保持着110°。

更为精确的计算表明，这个“人”字形的夹角的一半——即每边与丹顶鹤群的前进方向的夹角
为54°44′8″，恰好是金刚石结晶体的角度。

由此看来，
丹顶鹤的队形保持在110°飞行，这其中也潜藏着深奥
的数学之谜。

（作者单位：安徽省灵璧县黄湾中学）
44。

数学二年级动物爬几米又倒退的题
一只青蛙从井底向上爬，第一次向上爬了5米，下滑了3米，第二次向爬了4米，下滑了2米，第三次向上爬了6米，下滑了3米，则青蛙共向上爬了多少米？
分析：令向上爬为正，下滑为负，则第一次向上爬了5米记为+5米，下滑了3米记为-3米，第二次向爬了4米记为+4米，下滑了2米记为-2米，第三次向上爬了6米记为+6米，下滑了3米记为-3米，再根据有理数的加法求和即可。

解答：解：令向上爬为正，下滑为负，则青蛙共向上爬的距离为：5+（-3）+4+（-2）+6+（-3）=7（米）。

答：青蛙共向上爬了7米。

此题主要考查了有理数的加法，关键是掌握计算法则，注意结果符号的判断。