人教版九年级上册数学第二十四章达标测试卷

人教版数学九年级上册第二十四章测试卷(45分钟100分)一、选择题(每小题4分,共28分)1.已知☉O的半径为6,A为线段PO的中点,当OP=10时,点A与☉O的位置关系为( )A.在圆上B.在圆外C.在圆内D.不确定【解析】选C.∵点A为OP的中点,∴OA=OP÷2=5<6,∴点A在☉O内部.2.圆最长弦为12cm,如果直线与圆相交,且直线与圆心的距离为d,那么( )A.d<6cmB.6cm<d<12cmC.d≥6cmD.d>12cm【解析】选A.由题意知圆的直径为12cm,那么圆的半径为6cm.则当直线与圆相交时,直线与圆心的距离d<6cm.3.(2013·巴中中考)如图,已知☉O是△ABD的外接圆,AB是☉O的直径,CD是☉O 的弦,∠ABD=58°,则∠BCD等于( )A.16°B.32°C.58°D.64°【解析】选B.∵AB是☉O的直径,∴∠ADB=90°.∵∠ABD=58°,∴∠A=90°-∠ABD=32°,∴∠BCD=∠A=32°.4.(2013·河池中考)如图, AB为☉O的直径,C为☉O外一点,过C作☉O的切线,切点为B,连接AC交☉O于D,∠C=38°.点E在AB右侧的半圆周上运动(不与A,B 重合),则∠AED的大小是( )A.19°B.38°C.52°D.76°【解析】选B.如图,连接BE,则直径AB所对的圆周角∠AEB=90°,由切线BC可得直角△ABC中,∠BAC=90°-∠C=90°-38°=52°,因为∠BAC=∠BED=52°,所以∠AED=∠AEB-∠BED=90°-52°=38°.5.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a2B.3a2C.4a2D.5a2【解析】选A.由正方形和正八边形的性质知四个三角形为全等的等腰直角三角形,正好拼接成一个边长为a的正方形,又根据正方形的面积等于边长的平方,所以阴影部分的面积是2a2.6.(2013·德州中考)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )A.πB.π-C. D.π+【解析】选C.因为扇形AOB的半径为1,∠AOB=90°,所以AB=,△AOB的面积为,扇形AOB的面积为=,所以弓形的面积为-,又因为半圆的面积为,所以阴影部分的面积为:-=.【变式训练】(2013·东营中考)如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长a 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )A.πaB.2πaC.πaD.3a【解析】选A.方法一:∵四边形ABCD是正方形,∴∠B=∠D=90°.则扇形ABC的弧长为l==aπ,同理可求扇形ADC的弧长为aπ,所以树叶形图案的周长为aπ×2=πa;方法二:由题意知树叶形图案的周长为以a为半径的圆周长的一半,所以树叶形图案的周长为:×2πa=πa.7.如图,四边形ABCD内接于☉O,如果它的一个外角∠DCE=64°,那么∠BOD=( )A.128°B.100°C.64°D.32°【解析】选A.∵∠DCE=64°,∴∠BCD=116°,∵四边形ABCD内接于☉O,∴∠A+∠DCB=180°,∴∠A=64°,∴∠BOD=2∠A= 128°.二、填空题(每小题5分,共25分)8.如图,已知AB,CD是☉O的直径,=,∠AOE=32°,那么∠COE的度数为度.【解析】∵=,∴∠AOE=∠COA;又∠AOE=32°,∴∠COA=32°,∴∠COE=∠AOE+∠COA=64°.答案:649.(2013·衡阳中考)如图,要制作一个母线长为8cm,底面圆周长为12πcm的圆锥形小漏斗,若不计损耗,则所需纸板的面积是cm2.【解析】所需纸板的面积=×12π×8=48π(cm2).答案:48π10.如图,AB,AC,BD是☉O的切线,P,C,D为切点,如果AB=5,AC=3,则BD的长为.【解析】∵AC,AP为☉O的切线,∴AC=AP,∵BP,BD为☉O的切线,∴BP=BD,∴BD=PB=AB-AP=5-3=2.答案:211.(2013·哈尔滨中考)如图,直线AB与☉O相切于点A,AC,CD是☉O的两条弦,且CD∥AB,若☉O的半径为,CD=4,则弦AC的长为.【解析】连接AO并延长交CD于点E,连接OC,∵AB是圆O的切线,∴OA⊥AB,∵CD∥AB,∴∠AEC=90°,∴CE=CD=2,在Rt△OCE 中,由勾股定理得OE===,∴AE=4,在Rt△ACE中,由勾股定理得AC===2.答案:212.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是. 【解析】当已知长度分别为16和12的两边为直角边时,可知斜边长为20,此时直角三角形的外接圆半径是10.当斜边长为16时,此时直角三角形的外接圆半径是8.所以三角形的外接圆半径是10或8.答案:10或8三、解答题(共47分)13.(10分)如图,☉O的半径OC=10cm,直线l⊥CO,垂足为H,交☉O于A,B两点,AB=16cm,直线l平移多少厘米时能与☉O相切?【解析】如图,连接OA,延长CO交☉O于D,∵l⊥OC,∴OC平分AB.∴AH=8.在Rt△AHO中,OH===6,∴CH=4cm,DH=16cm.答:直线l向左平移4cm,或向右平移16cm时与圆相切.【一题多解】设直线l平移x cm时能与圆相切,(10-x)2+82=102,x1=16,x2=4,所以CH=4cm,DH=16cm.答:直线l向左平移4cm,或向右平移16cm时与圆相切.【易错提醒】直线l可能向左移动,也可能向右移动,不要只考虑一种情况.14.(12分)如图,AB是☉O的直径,=,∠COD=60°.(1)△AOC是等边三角形吗?请说明理由.(2)求证:OC∥BD.【解析】(1)△AOC是等边三角形.∵=,∴∠AOC=∠COD=60°.∵OA=OC,∴△AOC是等边三角形.(2)∵=,∴OC⊥AD,又∵AB是☉O的直径,∴∠ADB=90°,即BD⊥AD,∴OC∥BD.15.(12分)(2013·德州中考)如图,已知☉O的半径为1,DE是☉O的直径,过D作☉O的切线,C是AD的中点,AE交☉O于B点,四边形BCOE是平行四边形.(1)求AD的长.(2)BC是☉O的切线吗?若是,给出证明;若不是,说明理由.【解题指南】(1)连接BD,由ED为☉O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由四边形BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD 的长即可.(2)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.【解析】(1)连接BD,则∠DBE=90°.∵四边形BCOE是平行四边形,∴BC∥OE,BC=OE=1.在Rt△ABD中,C为AD的中点,∴BC=AD=1.∴AD=2.(2)连接OB,由(1)得BC∥OD,且BC=OD.∴四边形BCDO是平行四边形.又∵AD是☉O的切线,∴OD⊥AD.∴四边形BCDO是矩形.∴OB⊥BC,∴BC是☉O的切线.16.(13分)(2013·莆田中考)如图,▱ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE,AC,AE.(1)求证:△AED≌△DCA.(2)若DE平分∠ADC且与☉A相切于点E,求图中阴影部分(扇形)的面积.【解析】(1)∵AB=AE,∴∠ABE=∠AEB;在▱ABCD中,AB=CD,AD∥BC,∠ABE=∠ADC,∴DC=AE,∠DAE=∠AEB=∠ADC;在△ADE与△DAC中,DC=AE,∠DAE =∠ADC,AD=DA,∴△AED≌△DCA.(2)∵DE平分∠ADC且与☉A相切于点E,AE是☉A的半径,∴∠AED=90°,∠ADE=∠EDC,∵AD∥BC,∴∠ADE=∠DEC=∠CDE,∴CD=CE.由(1)中结论,可知∠AED=∠DCA=90°,DC=AE=CE, ∴∠ACE=∠EAC.∵∠CAE+∠BAE=90°,∠ACE+∠ABE=90°,∴∠BAE=∠ABE,∴BE=AE=AB,∴△ABE是等边三角形,∴∠BAE=60°.∴阴影部分的面积为:=π.。

第二十四章检测题时间：120分钟满分：120分一、选择题(每小题3分，共30分)1．下列说法中，错误的是( C )A．半圆是弧B．半径相等的圆是等圆C．过圆心的线段是直径D．直径是弦2．如图，在⊙O中，半径为r＝5 cm，弦AB＝8 cm，OC⊥AB于点C，则OC＝( A ) A．3 cm B．4 cm C．5cm D．6cm第2题图第3题图第4题图第5题图3．(2020·镇江)如图，AB是半圆的直径，C，D是半圆上的两点，∠ADC＝106°，则∠CAB等于( C )A．10°B．14°C．16°D．26°4．(2020·长春)如图，AB是⊙O的直径，点C，D在⊙O上，∠BDC＝20°，则∠AOC 的大小为( B )A．40°B．140°C．160°D．170°5．(2020·雅安)如图，△ABC内接于圆O，∠ACB＝90°，过点C的切线交AB的延长线于点P，∠P＝28°.则∠CAB＝( B )A．62°B．31°C．28°D．56°6．(德阳中考)已知圆内接正三角形的面积为3，则该圆的内接正六边形的边心距是( B )A．2 B．1 C．3D．3 27．(2020·黄石)如图，点A，B，C在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，若∠DCE＝40°，则∠ACB的度数为( C )A．140°B．70°C．110°D．80°第7题图第8题图第9题图第10题图8．(2020·永州)如图，已知P A ，PB 是⊙O 的两条切线，A ，B 为切点，线段OP 交⊙O 于点M .给出下列四种说法：①P A ＝PB ；②OP ⊥AB ；③四边形OAPB 有外接圆；④M 是△AOP 外接圆的圆心．其中正确说法的个数是( C )A ．1B ．2C ．3D ．49．(2020·泰州)如图，半径为10的扇形AOB 中，∠AOB ＝90°，C 为AB 上一点，CD ⊥OA ，CE ⊥OB ，垂足分别为D ，E .若∠CDE 为36°，则图中阴影部分的面积为( A )A ．10πB ．9πC ．8πD ．6π10．(2020·泰安)如图，点A ，B 的坐标分别为A (2，0)，B (0，2)，点C 为坐标平面内一点，BC ＝1，点M 为线段AC 的中点，连接OM ，则OM 的最大值为( B )A ．2 ＋1B ．2 ＋12C ．22 ＋1D ．22 ＋12二、填空题(每小题3分，共24分)11．已知圆的直径是13 cm ，圆心到某条直线的距离是6 cm ，那么这条直线与该圆的位置关系是__相交__.12．(2020·随州)如图，点A ，B ，C 在⊙O 上，AD 是∠BAC 的角平分线，若∠BOC ＝120°，则∠CAD 的度数为__30°__．第12题图 第13题图 第14题图第15题图13．如图，扇形OAB 的圆心角为122°，C 是AB 上一点，则∠ACB ＝__119__°.14．(湖州中考)如图，已知△ABC 的内切圆⊙O 与BC 边相切于点D ，连接OB ，OD .若∠ABC ＝40°，则∠BOD 的度数是__70°__．15．(2020·安顺)如图，△ABC 是⊙O 的内接正三角形，点O 是圆心，点D ，E 分别在边AC ，AB 上，若DA ＝EB ，则∠DOE 的度数是__120__度．16．在周长为26π的⊙O 中，CD 是⊙O 的一条弦，AB 是⊙O 的切线，且AB ∥CD ，若AB 和CD 之间的距离为18，则弦CD 的长为__24__．17．如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b ，然后把半圆沿直线b 进行无滑动滚动，直到半圆的直径与直线b 重合为止，则圆心O 运动路径的长度等于__5π__．第17题图第18题图18．(2020·贵港)如图，在扇形OAB中，点C在AB上，∠AOB＝90°，∠ABC＝30°，AD⊥BC于点D，连接AC，若OA＝2，则图中阴影部分的面积为3．三、解答题(共66分)19．(6分)如图，AB是⊙O的直径，点D，C是⊙O上两点，且AD＝DC＝CB，连接AD，AC，OC，求证：OC∥AD.解：∵AD＝DC＝CB，∴∠DAC＝∠BAC.∵∠BAC＝∠ACO，∴∠DAC＝∠ACO，∴OC∥AD20．(6分)如图所示，破残的圆形轮片上弦AB的垂直平分线交弧AB于点C，交弦AB 于点D.(1)求作此残片所在的圆；(不写作法，保留作图痕迹)(2)已知AB＝16，CD＝4，求(1)中所作圆的半径．解：(1)图略(2)∵AB＝16，CD＝4，CD⊥AB，∴AD＝BD＝8.设半径为x，得x2＝82＋(x－4)2，解得x＝1021．(6分)(2020·天津)在⊙O 中，弦CD 与直径AB 相交于点P ，∠ABC ＝63°.(1)如图①，若∠APC ＝100°，求∠BAD 和∠CDB 的大小；(2)如图②，若CD ⊥AB ，过点D 作⊙O 的切线，与AB 的延长线相交于点E ，求∠E 的大小．题图 答图解：(1)∵∠APC 是△PBC 的一个外角，∴∠C ＝∠APC －∠ABC ＝100°－63°＝37°，由圆周角定理得：∠BAD ＝∠C ＝37°，∠ADC ＝∠ABC ＝63°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠CDB ＝∠ADB －∠ADC ＝90°－63°＝27° (2)连接OD ，如图②所示：∵CD ⊥AB ，∴∠CPB ＝90°，∴∠PCB ＝90°－∠ABC ＝90°－63°＝27°，∵DE 是⊙O 的切线，∴DE ⊥OD ，∴∠ODE ＝90°，∵∠BOD ＝2∠PCB ＝54°，∴∠E ＝90°－∠BOD ＝90°－54°＝36°22．(8分)(2020·深圳)如图，AB 为⊙O 的直径，点C 在⊙O 上，AD 与过点C 的切线互相垂直，垂足为D .连接BC 并延长，交AD 的延长线于点E .(1)求证：AE ＝AB ；(2)若AB ＝10，BC ＝6，求CD 的长．(1)证明：连接AC ，OC ，如图，∵CD 为切线，∴OC ⊥CD ，又∵CD ⊥AD ，∴OC ∥AD ，∴∠OCB ＝∠E ，∵OB ＝OC ，∴∠OCB ＝∠B ，∴∠B ＝∠E ，∴AE ＝AB (2)解：∵AB 为直径，∴∠ACB ＝90°，∴AC ＝102－62 ＝8，∵AB ＝AE ＝10，AC ⊥BE ，∴CE ＝BC ＝6，∵12 CD ·AE ＝12 AC ·CE ，∴CD ＝6×810 ＝24523．(8分)如图所示，已知圆锥底面半径r ＝10 cm ，母线长为40 cm.(1)求它的侧面展开图的圆心角和表面积；(2)若一小虫从A 点出发沿着圆锥侧面运动到母线SA 的中点B 处，请你计算它所走的最短路线是多少？解：(1)依题意，得n π×40180＝2π×10，解得n ＝90.圆锥表面积为π×102＋π×10×40＝500π(cm 2) (2)如图，由圆锥的侧面展开图可知，所走的最短路线是线段AB 的长．在Rt △ASB 中，SA ＝40 cm ，SB ＝20cm ，∴AB ＝205 cm.故小虫走的最短路线的长度是205 cm.原因：两点之间线段最短24．(10分)(2020·扬州)如图，△ABC 内接于⊙O ，∠B ＝60°，点E 在直径CD 的延长线上，且AE ＝AC .(1)试判断AE 与⊙O 的位置关系，并说明理由；(2)若AC ＝6，求阴影部分的面积．(1)证明：连接OA ，AD ，如图，∵CD 为⊙O 的直径，∴∠DAC ＝90°，又∵∠ADC ＝∠B ＝60°，∴∠ACD ＝30°，又∵AE ＝AC ，OA ＝OD ，∴△ADO 为等边三角形，∴∠E ＝30°，∠ADO ＝∠DAO ＝60°，∴∠EAD ＝30°，∴∠EAD ＋∠DAO ＝90°，∴OA ⊥AE ，∴AE 为⊙O 的切线 (2)解：作OF ⊥AC 于F ，由(1)可知△AEO 为直角三角形，且∠E ＝30°，∵AE ＝AC ＝6，∴OA ＝23 ，∴阴影部分的面积为12 ×6×23 －60π×（23）2360＝6 3 －2π.故阴影部分的面积为(63 －2π)25．(10分)(2020·宜昌)如图，在四边形ABCD 中，AD ∥BC ，AB ＝23 a ，∠ABC ＝60°，过点B 的⊙O 与边AB ，BC 分别交于E ，F 两点．OG ⊥BC ，垂足为G ，OG ＝a .连接OB ，OE ，OF .(1)若BF ＝2a ，试判断△BOF 的形状，并说明理由；(2)若BE ＝BF ，求证：⊙O 与AD 相切于点A .(1)解：△BOF 为等腰直角三角形．理由如下：∵OG ⊥BC ，∴BG ＝FG ＝12BF ＝a ，∵OG ＝a ，∴BG ＝OG ，FG ＝OG ，∴△BOG 和△OFG 都是等腰直角三角形，∴∠BOG ＝∠FOG ＝45°，∴∠BOF ＝90°，而OB ＝OF ，∴△BOF 为等腰直角三角形(2)证明：连接EF ，如图，∵∠EBF ＝60°，BF ＝BE ，∴△BEF 为等边三角形，∴EB ＝EF ，∵OG 垂直平分BF ，∴点E ，O ，G 共线，即EG ⊥BF ，∵OG ＝a ，∠OBG ＝30°，∴BG ＝3 OG ＝3 a ，∴BE ＝2BG ＝23 a ，而AB ＝23 a ，∴点A 与点E 重合，∵AD ∥BC ，AG ⊥BF ，∴AG ⊥AD ，∴⊙O 与AD 相切于点A26．(12分)如图，已知⊙O 上依次有A ，B ，C ，D 四个点，AD ＝BC ，连接AB ，AD ，BD ，弦AB 不经过圆心O ，延长AB 到E ，使BE ＝AB ，连接EC ，F 是EC 的中点，连接BF .(1)若⊙O 的半径为3，∠DAB ＝120°，求劣弧BD 的长；(2)求证：BF ＝12BD ； (3)设G 是BD 的中点，探索：在⊙O 上是否存在点P (不同于点B )，使得PG ＝PF ？并说明PB 与AE 的位置关系．解：(1)连接OB ，OD ，∵∠DAB ＝120°，∴BCD 所对圆心角的度数为240°，∴∠BOD＝120°.∵⊙O 的半径为3，∴劣弧BD 的长为120180×π×3＝2π (2)连接AC ，∵AB ＝BE ，∴点B 为AE 的中点．∵F 是EC 的中点，∴BF 为△EAC 的中位线，∴BF ＝12AC .∵AD ＝BC ，∴AD ＋AB ＝BC ＋AB ，∴BD ＝CA ，∴BD ＝AC ，∴BF ＝12BD(3)过点B 作AE 的垂线，与⊙O 的交点即为所求的点P ，∵BF 为△EAC 的中位线，∴BF ∥AC ，∴∠FBE ＝∠CAE .∵AD ＝BC ，∴∠DBA ＝∠CAB ，∴∠FBE ＝∠DBA .由作法可知BP ⊥AE ，∴∠GBP ＝∠FBP .∵G 为BD 的中点，∴BG ＝12BD ，∴BG ＝BF .在△PBG 和△PBF 中，BG ＝BF ，∠PBG ＝∠PBF ，BP ＝BP ，∴△PBG ≌△PBF (SAS)，∴PG ＝PF .故在⊙O 上存在点P ，使得PG ＝PF ，此时PB ⊥AE。

人教版九年级上册数学第二十四章过关测试题含答案24.1.4圆周角一．选择题1．在同圆或等圆中，下列说法正确的有（）①平分弦的直径垂直于弦；②圆内接平行四边形是菱形；③一条弧所对的圆周角等于它所对的圆心角的一半；④如果两条弦相等，那么他们所对的圆周角相等．A．1个B．2个C．3个D．4个2．如图，⊙O中，若OA⊥BC、∠AOB＝66°，则∠ADC的度数为（）A．33°B．56°C．57°D．66°3．如图所示，四边形ABCD是圆O的内接四边形，∠A＝45°，BC＝4，CD＝2，则弦BD的长为（）A．2B．3C．D．24．如图，⊙O是四边形ABCD的外接圆，连接OB、OD，若四边形ABOD是平行四边形，则∠ABO的度数是（）A．50°B．55°C．60°D．65°5．如图，AB是⊙O的直径，点C，D在⊙O上．若∠D＝50°，则∠BAC等于（）A．25°B．40°C．50°D．55°6．如图，AB，BC为⊙O中异于直径的两条弦，OA交BC于点D，若∠AOC＝50°，∠C＝35°，则∠A的度数为（）A．35°B．50°C．60°D．70°7．如图，AB是半圆O的直径，C、D是上的两点，＝，点E为上一点，且∠CED＝∠COD，则∠DOB＝（）A．92°B．96°C．100°D．120°8．如图，五边形ABCDE内接于⊙O，若∠CAD＝35°，则∠B+∠E的度数是（）A．210°B．215°C．235°D．250°9．如图，AB是⊙O的直径，OC是⊙O的半径，点D是半圆AB上一动点（不与A、B 重合），连结DC交直径AB与点E，若∠AOC＝60°，则∠AED的范围为（）A．0°＜∠AED＜180°B．30°＜∠AED＜120°C．60°＜∠AED＜120°D．60°＜∠AED＜150°10．如图，BC为⊙O直径，弦AC＝2，弦AB＝4，D为⊙O上一点，I为AD上一点，且DC＝DB＝DI，AI长为（）A．B．C．D．二．填空题11．如图，已知C为上一点，若∠AOB＝100°，则∠ACB的度数为度．12．如图，AB是⊙O的直径，点C，D，E都在⊙O上，∠1＝55°，则∠2＝°．13．如图，AB是⊙O的直径，弦CD⊥AB，连接CO并延长交⊙O于点E，连接BD交CE于点F，若∠DBE＝32°，则∠DFE的度数是．14．如图，四边形ABCD内接于圆O，四边形ABCO是平行四边形，则∠ADC＝．15．如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB＝30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为8，则GE+FH 的最大值为．三．解答题16．如图，在△ABC中，AC＝BC，D是AB上一点，⊙O经过点A、C、D，交BC于点E，过点D作DF∥BC，交⊙O于点F．求证：（1）四边形DBCF是平行四边形；（2）AF＝EF．17．如图，BC是⊙O的直径，点A、D在⊙O上，DB∥OA，BC＝10，AC＝6．（1）求证：BA平分∠DBC；（2）求DB的长．参考答案1．解：①平分弦的直径垂直于弦，错误，此弦不是直径，才能成立．②圆内接平行四边形是菱形，错误，圆内接平行四边形是矩形．③一条弧所对的圆周角等于它所对的圆心角的一半，正确．④如果两条弦相等，那么他们所对的圆周角相等．错误，弦所对的圆周角有两个，也可能互补．故选：A．2．解：如图，连接OC，OB．∵OA⊥BC，∴＝，∴∠AOC＝∠AOB＝66°，∴∠ADC＝∠AOC＝33°，故选：A．3．解：如图，过点D作DE⊥BC交BC的延长线于E．∵∠A+∠BCD＝180°，∠A＝45°，∴∠BCD＝135°，∴∠DCE＝45°，∵∠E＝90°，CD＝2，∴CE＝ED＝2，BE＝CE+BC＝6，在Rt△BED中，∵∠E＝90°，BE＝6，DE＝2，∴BD＝＝＝2，故选：D．4．解：∵四边形ABOD是平行四边形，∴∠A＝∠BOD，∵∠BOD＝2∠C，∠A+∠C＝180°，∴∠C＝60°，∠A＝∠BOD＝120°，∵AD∥OB，∴∠ABO+∠DAB＝180°，∴∠ABO＝60°，故选：C．5．解：∵AB是直径，∴∠ACB＝90°，∵∠ABC＝∠ADC＝50°，∴∠BAC＝90°﹣50°＝40°，故选：B．6．解：∵∠C＝35°，∠AOC＝50°，∴∠ADC＝85°，∠B＝∠AOC＝25°，∴∠A＝∠ADC﹣∠B＝85°﹣25°＝60°，故选：C．7．解：设∠COD＝x，则∠CED＝x，∴，解得：x＝60°，∴∠COD＝60°，∴∠BOD+∠AOC＝180°﹣60°＝120°，∵＝，∴∠BOD＝4∠AOC，∴∠BOD＝120°×＝96°，故选：B．8．解：如图，连接CE，∵五边形ABCDE是圆内接五边形，∴四边形ABCE是圆内接四边形，∴∠B+∠AEC＝180°，∵∠CED＝∠CAD＝35°，∴∠B+∠E＝180°+35°＝215°．故选：B．9．解：如图1，当点E在线段AO上时，∵AB是⊙O的直径，∴∠ADB＝90°，∵∠AOC＝60°，∴∠ADC＝30°，∴∠BDE＝60°，∴∠AED＞∠BDE，∴∠AED＞60°；如图2，当点E在线段OB上时，∵∠ADE＝AOC＝30°，∴∠DEB＞30°，∵∠AED+∠DEB＝180°，∴∠AED＜150°，∴∠AED的范围为60°＜∠AED＜150°，故选：D．10．解：如图，连接IC，作IE⊥AC于E，IF⊥AB于F，IG⊥BC于G．∵DB＝DC，∴＝，∠DBC＝∠DCB，∴∠BAD＝∠CAD，∵DI＝DC，∴∠DIC＝∠DCI，∵∠DIC＝∠DAC+∠ACI，∠DCI＝∠DCB+∠ICB，∠DBC＝∠DAC，∴∠ICA＝∠ICB，∴点I为△ABC内心，∴IE＝IF＝IG，∵BC是直径，∴∠BAC＝90°，∴BC＝＝＝2，∵S△ABC＝•AB•AC＝•IE•（AB+AC+BC），∴IE＝3﹣，∵∠IAE＝∠AIE＝45°，∴AI＝IE＝3﹣，故选：D．11．解：在优弧AB上取一点D，连接AD、BD，∵∠AOB＝100°，∴∠D＝AOB＝50°，∵A、D、B、C四点共圆，∴∠D+∠ACB＝180°，∴∠ACB＝180°﹣∠D＝130°，故答案为：130．12．解：如图，连接AD．∵AB是直径，∴∠ADB＝90°，∵∠1＝∠ADE，∴∠1+∠2＝90°，∵∠1＝55°，∴∠2＝35°，故答案为35．13．解：如图，∵∠DBE＝32°，∴∠C＝∠DBE＝32°．∵弦CD⊥AB，∴∠1＝90°﹣32°＝58°．∴∠2＝∠1＝58°．∵OB＝OE，∴∠E＝∠OBE＝＝61°．∴∠DFE＝∠DBE+∠E＝32°+61°＝93°．故答案是：93°．14．解：设∠ADC的度数＝α，∠ABC的度数＝β；∵四边形ABCO是平行四边形，∴∠ABC＝∠AOC；∵∠ADC＝β，∠AOC＝α；而α+β＝180°，∴，解得：β＝120°，α＝60°，∠ADC＝60°，故答案为：60°．15．解：如图1，连接OA、OB，，∵∠ACB＝30°，∴∠AOB＝2∠ACB＝60°，∵OA＝OB，∴△AOB为等边三角形，∵⊙O的半径为8，∴AB＝OA＝OB＝8，∵点E，F分别是AC、BC的中点，∴EF＝AB＝4，要求GE+FH的最大值，即求GE+FH+EF（弦GH）的最大值，∵当弦GH是圆的直径时，它的最大值为：8×2＝16，∴GE+FH的最大值为：16﹣4＝12．故答案为：12．16．证明：（1）∵AC＝BC，∵DF∥BC，∴∠ADF＝∠B，∵∠BAC＝∠CFD，∴∠ADF＝∠CFD，∴BD∥CF，∵DF∥BC，∴四边形DBCF是平行四边形；（2）连接AE，∵∠ADF＝∠B，∠ADF＝∠AEF，∴∠AEF＝∠B，∵四边形AECF是⊙O的内接四边形，∴∠ECF+∠EAF＝180°，∵BD∥CF，∴∠ECF+∠B＝180°，∴∠EAF＝∠B，∴∠AEF＝∠EAF，∴AF＝EF．17．解：（1）∵OA∥BD，∴∠ABD＝∠OAB，∵OA＝OB，∴∠OAB＝∠OBA，∴∠OBA＝∠ABD，∴BA平分∠DBC．（2）如图，作AH⊥BC于H，OE⊥BD于E，则BD＝2BE，∵BC为直径，∴，∵，∴，在Rt△OAH中，，∵OA∥BD，∴∠AOH＝∠EBO，在△AOH和△OBE中，，∴△AOH≌△OBE（AAS），∴，∴．24.2 点和圆、直线和圆的位置关系一、选择题1. 下列说法中，正确的是()A．垂直于半径的直线是圆的切线B．经过半径的外端且垂直于这条半径的直线是圆的切线C．经过半径的端点且垂直于这条半径的直线是圆的切线D．到圆心的距离等于直径的直线是圆的切线2. (2019•益阳)如图，PA、PB为圆O的切线，切点分别为A、B，PO交AB于点C，PO 的延长线交圆O于点D，下列结论不一定成立的是A．PA=PB B．∠BPD=∠APDC．AB⊥PD D．AB平分PD3. 平面上⊙O与四条直线l1，l2，l3，l4的位置关系如图.若⊙O的半径为2 cm，且点O 到其中一条直线的距离为2.2 cm，则这条直线是()A．l l B．l2C．l3D．l44. 在Rt△ABC中，∠C＝90°，BC＝3 cm，AC＝4 cm，以点C为圆心，以2.5 cm为半径画圆，则⊙C与直线AB的位置关系是()A. 相交B. 相切C. 相离D. 不能确定5. 如图，一个边长为4 cm的等边三角形ABC的高与⊙O的直径相等．⊙O与BC相切于点C，与AC相交于点E，则CE的长为()A．4 cm B．3 cm C．2 cm D．1.5 cm6. 如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝7，点D在边BC上，CD＝3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D外，那么⊙D 的半径长r的取值范围是()A. 1＜r＜4B. 2＜r＜4C. 1＜r＜87. 2020·武汉模拟 在平面直角坐标系中，圆心为坐标原点，⊙O 的半径为10，则P (－10，1)与⊙O 的位置关系为( ) A ．点P 在⊙O 上 B ．点P 在⊙O 外 C ．点P 在⊙O 内D ．无法确定8. 如图0，在Rt △ABC 中，AB ⊥BC ，AB ＝6，BC ＝4，P 是△ABC 内部的一个动点，且满足∠PAB ＝∠PBC ，则线段CP 长的最小值为( )图0A.32B ．2C.81313D.121313二、填空题9. 如图，AT切⊙O 于点A ，AB 是⊙O 的直径．若∠ABT ＝40°，则∠ATB ＝________.10. 直角三角形的两条直角边分别是5和12，则它的内切圆半径为 .11. 如图1，已知△ABC 的外心为O ，BC ＝10，∠BAC ＝60°，分别以AB ，AC 为腰向三角形外作等腰直角三角形ABD 与ACE ，连接BE ，CD 交于点P ，则OP 长的最小值是________．12. 如图，在矩形ABCD 中，AB ＝6，BC ＝2.8，⊙O 是以AB 为直径的圆，则直线CD 与⊙O 的位置关系是________．13. 在周长为26π的⊙O 中，CD 是⊙O 的一条弦，AB 是⊙O 的切线，且AB ∥CD ，若AB 和CD 之间的距离为18，则弦CD 的长为________．14. 如图所示，在半圆O 中，AB 是直径，D 是半圆O 上一点，C 是AD ︵的中点，CE ⊥AB于点E ，过点D 的切线交EC 的延长线于点G ，连接AD ，分别交CE ，CB 于点P ，Q ，连接AC ，有下列结论：①∠BAD ＝∠ABC ；②GP ＝GD ；③点P 是△ACQ 的外心．其中正确的结论是________(只需填写序号)．15. 如图，⊙O 的半径为1，正方形ABCD 的对角线长为6，OA ＝4.若将⊙O 绕点A 按顺时针方向旋转360°，则在旋转的过程中，⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现( )A ．3次B ．4次C ．5次D ．6次16. 2019·兴化期中 已知等边三角形ABC 的边长为2，D 为BC 的中点，连接AD .点O 在线段AD 上运动(不与端点A ，D 重合)，以点O 为圆心，33为半径作圆，当⊙O 与△ABC 的边有且只有两个公共点时，DO 的取值范围为________．三、解答题17. 如图，MP切⊙O 于点M ，直线PO 交⊙O 于点A 、B ，弦AC ∥MP ，求证：MO ∥BC.18. 如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，P是CD的延长线上一点，且AP＝AC.(1)求证：P A是⊙O的切线；(2)若PD＝5，求⊙O的直径．19. 在△ABC中，AB＝AC＝10，BC＝16，⊙A的半径为7，判断⊙A与直线BC的位置关系，并说明理由．20. 2019·天津如图，已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为⊙O上一点．(1)如图①，求∠ACB的大小；(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．21. 如图，在平面直角坐标系中，以点O为圆心，5个单位长度为半径画圆．直线MN平行移动．按下列条件求m的值或取值范围．(1)⊙O上任何一点到直线MN的距离都不等于3；(2)⊙O上有且只有一点到直线MN的距离等于3；(3)⊙O上有且只有两点到直线MN的距离等于3；(4)随着m的变化，⊙O上到直线MN的距离等于3的点的个数还有哪些变化？请说明所有各种情形及对应m的值或取值范围．人教版九年级数学上册24.2 点和圆、直线和圆的位置关系同步训练-答案一、选择题1. 【答案】B2. 【答案】D【解析】∵PA，PB是⊙O的切线，∴PA=PB，所以A成立；∠BPD=∠APD，所以B成立；∴AB⊥PD，所以C成立；∵PA，PB是⊙O的切线，∴AB⊥PD，且AC=BC，只有当AD∥PB，BD∥PA时，AB平分PD，所以D不一定成立，故选D．3. 【答案】C[解析] 因为所求直线到圆心O的距离为2.2 cm＞半径2 cm，所以此直线与⊙O相离，所以这条直线为直线l3.4. 【答案】A【解析】如解图，在Rt△ABC中，AC＝4，BC＝3，由勾股定理得AB＝5.过C作CD⊥AB于D，则S△ABC ＝12AC·BC＝12AB·CD，解得CD＝2.4<2.5，∴直线AB与⊙C相交．解图5. 【答案】B [解析] 如图，连接OC ，并过点O 作OF ⊥CE 于点F .∵△ABC 为等边三角形，边长为4 cm ， ∴△ABC 的高为23 cm ，∴OC ＝ 3 cm.又∵⊙O 与BC 相切于点C ，∠ACB ＝60°， ∴∠OCF ＝30°.在Rt △OFC 中，可得FC ＝32 cm ， ∴CE ＝2FC ＝3 cm.6. 【答案】B【解析】连接AD ，则AD ＝AC 2＋CD 2＝42＋32＝5，∵⊙A与⊙D 相交，∴3－r <5<3＋r ，解得2＜r ＜8，又∵点B 在⊙D 外，∴r <BD ，即r <4.∴2<r <4，故选B.解图7. 【答案】B8. 【答案】B [解析] ∵∠ABC ＝90°，∴∠ABP ＋∠PBC ＝90°. ∵∠PAB ＝∠PBC ，∴∠ABP ＋∠PAB ＝90°，∴∠APB ＝90°，∴点P 在以AB 为直径的圆上，设圆心为O ，连接OC 交⊙O 于点P ，此时CP 最小． 在Rt △BCO 中，∵∠OBC ＝90°，BC ＝4，OB ＝3，∴OC ＝5，OP ＝OB ＝3，∴PC ＝OC －OP ＝5－3＝2，∴PC 的最小值为2.二、填空题9. 【答案】50°【解析】∵AT 是⊙O 的切线，AB 是⊙O 的直径，∴∠BAT10. 【答案】2 [解析]直角三角形的斜边==13，所以它的内切圆半径==2.11. 【答案】5－533 [解析] ∵∠BAD ＝∠CAE ＝90°，∴∠DAC ＝∠BAE .在△DAC 和△BAE 中， ⎩⎪⎨⎪⎧AD ＝AB ，∠DAC ＝∠BAE ，AC ＝AE ，∴△DAC ≌△BAE (SAS)， ∴∠ADC ＝∠ABE ，从而∠PDB ＋∠PBD ＝90°， 即∠DPB ＝90°，从而∠BPC ＝90°， ∴点P 在以BC 为直径的圆上．如图，过点O 作OH ⊥BC 于点H ，连接OB ，OC . ∵△ABC 的外心为O ，∠BAC ＝60°， ∴∠BOC ＝120°.又∵BC ＝10， ∴OH ＝53 3，∴OP 长的最小值是5－533.12. 【答案】相交 [解析] 设AB 的中点为O ，则点O 到CD 的距离为2.8.因为⊙O 的半径为3，3＞2.8，所以直线CD 与⊙O 的位置关系是相交．13. 【答案】24【解析】设AB 切⊙O 于点E ，如解图，连接EO 并延长交CD 于点M ，∵C ⊙O ＝26π＝2πr ，∴r ＝13，∵AB ∥CD ，且AB 与CD 之间的距离为18，∴OM ＝18－r ＝5，∵AB 为⊙O 的切线，∴∠CMO ＝∠AEO ＝90°，∴在Rt △CMO 中，CM ＝OC 2－OM 2＝12，∴CD ＝2CM ＝24.解图14. 【答案】②③ [解析] ∵在半圆O 中，AB 是直径，D 是半圆O 上一点，C 是AD ︵的中点，∴AC ︵＝DC ︵，但不一定等于DB ︵，∴∠BAD 与∠ABC 不一定相等，故①错误．如图，连接OD ，则OD ⊥GD ，∠OAD ＝∠ODA .∵∠ODA ＋∠GDP ＝90°，∠OAD ＋∠GPD ＝∠OAD ＋∠APE ＝90°，∴∠GPD ＝∠GDP ，∴GP ＝GD ，故②正确．补全⊙O ，延长CE 交⊙O 于点F .∵CE ⊥AB ，∴A 为FC ︵的中点，即AF ︵＝AC ︵.又∵C 为AD ︵的中点，∴CD ︵＝AC ︵，∴AF ︵＝CD ︵，∴∠CAP ＝∠ACP ，∴AP ＝CP .∵AB 为⊙O 的直径，∴∠ACQ ＝90°，∴∠ACP ＋∠PCQ ＝90°，∠CAP ＋∠PQC ＝90°，∴∠PCQ ＝∠PQC ，∴PC ＝PQ ，∴AP ＝PQ ，即P 为Rt △ACQ 的斜边AQ 的中点，∴点P 为Rt △ACQ 的外心，故③正确．15. 【答案】B [解析] ∵正方形ABCD 的对角线长为6，∴它的边长为3 2.如图，⊙O 与正方形ABCD 的边AB ，AD 只有一个公共点的情况各有1次，与边BC ，CD 只有一个公共点的情况各有1次，∴在旋转的过程中，⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现4次．16. 【答案】0<DO <33或2 33<DO <3 [解析] ∵等边三角形ABC 的边长为2，D 为BC的中点，∴AD ⊥BC ，BD ＝1，AD ＝ 3.分四种情况讨论：(1)如图①所示，当0<DO <33时，⊙O 与△ABC 的BC 边有且只有两个公共点，(2)如图②所示，当DO ＝33时，⊙O 与△ABC 的边有三个公共点；(3)如图③所示，当⊙O 经过△ABC 的顶点A 时，⊙O 与△ABC 的边有三个公共点，则当33<DO ≤2 33时，⊙O 与△ABC 的边有四个或三个公共点．(4)如图④所示，当2 33<DO <3时，⊙O 与△ABC 的边有两个公共点．综上，当0<DO <33或2 33<DO <3时，⊙O 与△ABC 的边只有两个公共点．故答案为0<DO <33或2 33<DO < 3.三、解答题17. 【答案】证明：∵AB 是⊙O 的直径，∴∠ACB ＝90°，∵MP 为⊙O 的切线， ∴∠PMO ＝90°，∵MP ∥AC ，∴∠P ＝∠CAB ，∴∠MOP ＝∠B,故MO ∥BC.18. 【答案】∵∠B＝60°，∴∠AOC＝2∠B＝120°.又∵OA＝OC，∴∠OAC＝∠OCA＝30°.又∵AP＝AC，∴∠P＝∠OCA＝30°，∴∠OAP＝∠AOC－∠P＝90°，∴OA⊥PA.又∵OA是⊙O的半径，∴PA是⊙O的切线．(2)在Rt△OAP中，∵∠P＝30°，∴PO＝2OA＝OD＋PD.又∵OA＝OD，∴PD＝OD＝OA.∵PD＝5，∴2OA＝2PD＝2 5，∴⊙O的直径为2 5.19. 【答案】解：⊙A与直线BC相交．理由：过点A作AD⊥BC于点D，则BD＝CD＝8.∵AB＝AC＝10，∴AD＝6.∵6＜7，∴⊙A与直线BC相交．20. 【答案】∵PA ，PB 是⊙O 的切线，∴∠OAP ＝∠OBP ＝90°，∴∠AOB ＝360°－90°－90°－80°＝100°.由圆周角定理，得∠ACB ＝12∠AOB ＝50°.(2)如图②，连接CE .∵AE 为⊙O 的直径，∴∠ACE ＝90°.∵∠ACB ＝50°，∴∠BCE ＝90°－50°＝40°，∴∠BAE ＝∠BCE ＝40°.∵AB ＝AD ，∴∠ABD ＝∠ADB ＝70°，∴∠EAC ＝∠ADB －∠ACB ＝20°.21. 【答案】解：(1)m ＜－8或m ＞8(2)m ＝－8或m ＝8(3)－8＜m ＜－2或2＜m ＜8(4)当m ＝－2或m ＝2时，⊙O 上有且只有三个点到直线MN 的距离等于3； 当－2＜m ＜2时，⊙O 上有且只有四个点到直线MN 的距离等于3.24.3正多边形和圆1．如图，四边形ABCD是⊙O的内接四边形，若∠D＝3∠B，则∠B的度数为（）A．30°B．36°C．45°D．60°2．如图，四边形ABCD是⊙O的内接四边形，BE平分∠ABC，若∠D＝110°，则∠ABE 的度数是（）A．30°B．35°C．50°D．55°3．对于以下说法：①各角相等的多边形是正多边形；②各边相等的三角形是正三角形；③各角相等的圆内接多边形是正多边形；④各顶点等分外接圆的多边形是正多边形．正确的有（）A．1个B．2个C．3个D．4个4．一个三角形的外接圆的圆心在这个三角形的外部，则该三角形一定是（）A、锐角三角形B、直角三角形C、钝角三角形D、等腰三角形5．如图，△ABC是半径为1的⊙O的内接正三角形，则圆的内接矩形BCDE的面积为（）A．3B．32C3D．326．如图，正五边形ABCDE内接于O，点P是劣弧BC上一点（点P不与点C重合），A．45︒B．36︒C．35︒D．30∠等于（）7．如图，四边形ABCD内接于⊙O ，110BOD︒∠=，那么BCDA．110°B．135°C．55°D．125°8．如图，△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ADC的度数是（）A．80°B．160°C．100°D．40°9．如图，将正五边形绕中心O顺时针旋转a角度，与原正五边形构成新的图形，若要使该图形既是轴对称又是中心对称图形，则a的最小角度为（）A．30B．36C．72D．90∠的度数是（）10．如图，正五边形ABCDE和等边AFG内接于O，则GFDA ．10︒B ．12︒C ．15︒D ．20︒二、填空题 11．如图，四边形ABCD 为O 的内接四边形，已知BOD 110∠=，则BCD ∠的度数为____________________．12．一个正多边形的一个外角为30°，则它的内角和为_____．13．如图，四边形ABCD 内接于⊙O ，点E 在BC 的延长线上，若∠BOD ＝100°，则∠DCE ＝_____°．14．如图，四边形ABCD 是⊙O 的内接四边形，∠B＝135°，则∠AOC 的度数为_____．15．如图，点A ，B ，C ，D 在O 上，CD CB =，30CAD ∠=︒，50ACD ∠=︒，则ADB =∠_______．三、解答题16．如图，四边形ABCD 内接于O ，AC 与BD 为对角线，BCA BAD ∠=∠，过点A 作//AE BC 交CD 的延长线于点E ．求证：EC AC =．17．如图，ABC 的外角BAM ∠的平分线与它的外接圆相交于点E ，连接BE ，CE ，过点E 作//EF BC ，交CM 于点D求证：（1）BE CE =；（2）EF 为⊙O 的切线．18．如图，⊙O 外接于正方形,ABCD P 为弧AD 上一点，且1,3AP PC ==，求正方形ABCD 的边长和PB 的长．参考答案1-5 CBBCC6-10 BDCBB11．125°12．1800°13．5014．9015．70°16．证明：∵//AE BC ，∴ACB EAC ∠=∠．∵ACB BAD ∠=∠，∴EAC BAD ∠=∠，∴EAD CAB ∠=∠，∵180ADE ADC ∠+∠=︒，180ADC ABC ∠+∠=︒，∴ADE ABC =∠∠，∵180EAD ADE E ∠+∠+∠=︒，180BAC ABC ACB ∠+∠+∠=︒， ∴E ACB EAC ∠=∠=∠，∴CE CA =．17．证明：（1）∵四边形ACBE 是圆内接四边形，∴∠EAM ＝∠EBC ，∵AE 平分∠BAM ，∴∠BAE ＝∠EAM ，∵∠BAE ＝∠BCE ，∴∠BCE ＝∠EAM ，∴∠BCE ＝∠EBC ，∴BE ＝CE ；（2）如图，连接EO 并延长交BC 于H ，连接OB ，OC ，∵OB ＝OC ，EB ＝EC ，∴直线EO 垂直平分BC ，∴EO ⊥BC ，∵EF//BC ，∴EO ⊥EF ，∵OE 是⊙O 的半径，∴EF 为⊙O 的切线．18．解：连接AC ，作AE PB ⊥于点E ， 如图所示．∵四边形ABCD 是正方形，,AB BC CD AD ∴===90,45ABC D BCD ACB ︒︒∠=∠=∠=∠=， AC ∴是O 的直径，ABC 是等腰直角三角形， 90,2,APC AC ︒∴∠==22221310,AC AP PC ∴+=+= 52AB ∴== 45,,APB ACB AE PB ︒∠=∠=⊥ APE ∴是等腰直角三角形，22PE AE AP ∴=== 2222232(5)22BE AB AE ⎛⎫∴=-=-= ⎪ ⎪⎝⎭，232∴=+=+=．22PB PE BE正方形ABCD的边长为5,PB的长为22．24.4弧长和扇形面积1．下列说法中，正确的是()A．垂直于半径的直线是圆的切线B．经过半径的外端且垂直于这条半径的直线是圆的切线C．经过半径的端点且垂直于这条半径的直线是圆的切线D．到圆心的距离等于直径的直线是圆的切线2．如图，AB是⊙O的直径，MN是⊙O的切线，切点为N，如果∠MNB＝52°，则∠NOA 的度数为()A．76°B．56°C．54°D．52°3．如图所示，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C，连接BC，若∠P ＝36°，则∠B等于()A．27°B．32°C．36°D．54°4．如图，⊙O是△ABC的内切圆，则点O是△ABC的( )A．三条边的垂直平分线的交点 B．三条角平分线的交点C．三条中线的交点 D．三条高的交点5．如图，PA，PB为⊙O的切线，切点分别为A，B，PO交AB于点C，PO的延长线交⊙O于点D，下列结论不一定成立的是( )A．PA＝PB B．∠BPD＝∠APD C．AB⊥PD D．AB平分PD6．如图，从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC，则此扇形围成的圆锥的侧面积为（）A．200πcm2B．100πcm2C．100πcm2D．50πcm27．将一把直尺，含60°角的直角三角板和光盘如图摆放，点A为60°角与直尺的交点，AB ＝3，则光盘的直径是( )A．3 B．3 3 C．6 D．6 38．如图，边长为23的等边△ABC的内切圆的半径为( )A．1 B. 3 C．2 D．2 39．佳佳制作了一个圆锥形的紫绸帽子，经测量，圆锥的母线长为40cm，所用紫绸面积为360πcm2（不计接头损耗），则圆锥的底面直径为（）A．6cm B．9cm C．18cm D．36cm10．如图，已知扇形的圆心角为60°，直径为6，则图中弓形（阴影部分）的面积为（）A．6π﹣9B．6π﹣3C．D．二、填空题11．如图3，AB为⊙O的直径，圆周角∠ABC＝40°，当∠BCD＝________°时，CD为⊙O 的切线．图312．有一圆锥，它的高为8cm，底面半径为6cm，则这个圆锥的侧面积是. 13．如图，PA，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝．14．如图，已知△ABC的内切圆⊙O与BC边相切于点D，连接OB，OD.若∠ABC＝40°，则∠BOD的度数是．15．已知一个扇形的圆心角是60°，面积是6π，那么这个扇形的弧长是2π．16．如图，⊙O是ΔABC的外接圆，∠ABC＝30°，AC＝8，则优弧ABC的长为．17.边心距为3的正六边形的周长为 .三、解答题18．如图5，点O在∠APB的平分线上，⊙O与PA相切于点C.求证：直线PB与⊙O相切．19．如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝18 cm，BC＝28 cm，CA＝26 cm，求AF，BD，CE的长．20．如图，AB，BC，CD分别与⊙O相切于点E，F，G，若∠BOC＝90°，求证：AB∥CD.答案一.选择题1 2 3 4 5 6 7 8 9 10B A A B D A D AC C二.填空题11.50°12. 60π13. 76°14.70° 15. 2π 16. 17. 12三.解答题18.证明：如图，连接OC，过点O作OD⊥PB于点D.∵⊙O与PA相切于点C，∴OC⊥PA.∵点O在∠APB的平分线上，OC⊥PA，OD⊥PB，∴OD＝OC，∴直线PB与⊙O相切．19.解：根据切线长定理，得AE＝AF，BF＝BD，CE＝CD.设AF＝AE＝x cm，则CE＝CD＝(26－x)cm，BF＝BD＝(18－x)cm.∵BC＝28 cm，∴(18－x)＋(26－x)＝28.解得x＝8.∴AF＝8 cm，BD＝10 cm，CE＝18 cm.20.证明：∵∠BOC＝90°，∴∠OBC＋∠OCB＝90°.又∵BE与BF为⊙O的切线，∴BO为∠EBF的平分线．∴∠OBE＝∠OBC.同理可得∠OCB＝∠OCG.∴∠OBE＋∠OCG＝∠OBC＋∠OCB＝90°.∴∠OBC＋∠OCB＋∠OBE＋∠OCG＝180°，即∠ABF＋∠DCF＝180°.∴AB∥CD.。

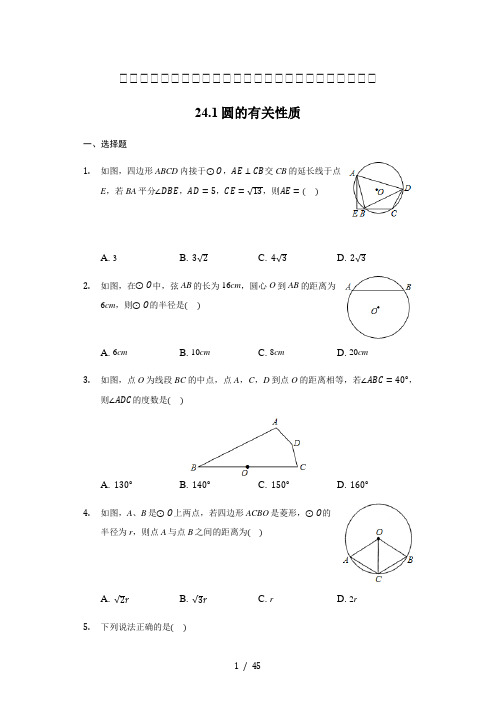
初初初初初初初初初初初初初初初初初初初初初初初初初24.1圆的有关性质一、选择题1.如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA平分∠DBE，AD=5，CE=√13，则AE =()A. 3B. 3√2C. 4√3D. 2√32.如图，在⊙O中，弦AB的长为16cm，圆心O到AB的距离为6cm，则⊙O的半径是()A. 6cmB. 10cmC. 8cmD. 20cm3.如图，点O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是()A. 130°B. 140°C. 150°D. 160°4.如图，A、B是⊙O上两点，若四边形ACBO是菱形，⊙O的半径为r，则点A与点B之间的距离为()A. √2rB. √3rC. rD. 2r5.下列说法正确的是()1/ 45A. 垂直于弦的直线平分弦所对的两条弧B. 平分弦的直径垂直于弦C. 垂直于直径平分这条直径D. 弦的垂直平分线经过圆心6.下列说法正确的是()A. 相等的圆心角所对的弧相等B. 在同圆中，等弧所对的圆心角相等C. 在同圆中，相等的弦所对的弧相等D. 相等的弦所对的弧相等7.如图，在⊙O中，半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC，若AB=8，CD=2，则EC的长度为()A. 2√15B. 8C. 2√10D. 2√138.如图所示，图中弦的条数为()A. 1条B. 2条C. 3条D. 4条9.如图，⊙O的半径为5，AB为弦，点C为AB⌢的中点，若∠ABC=30°，则弦AB的长为()A. 12B. 5 C. 5√32D. 5√310.如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为()A. 6B. 8C. 5√2D. 5√3二、填空题11.如图，在⊙O中，AB、AC是互相垂直的两条弦，OD⊥AB于点D，OE⊥AC于点E，且AB=8cm，AC=6cm，那么⊙O的半径OA长为______．12.如图，AB是⊙O的直径，C、D为半圆的三等分点，CE⊥AB于点E，∠ACE的度数为______．13.如图，AB是⊙O的直径，点D在⊙O上，∠BOD=130°，AC//OD交⊙O于C，连接BC，则∠B=________．14.如图，CD是⊙O的直径，CD=4，∠ACD=20°，点B为弧AD的中点，点P是直径CD上的一个动点，则PA+PB的3/ 45最小值为______．三、计算题15.⊙O中，直径AB和弦CD相交于点E，已知AE=1cm，EB=5cm，且∠DEB=60°，求CD的长．四、解答题16.如图，AB是⊙O的直径，点C为BD⌢的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．(1)求证：△BFG≌△CDG；(2)若AD=BE=2，求BF的长．17.如图，已知A，B，C，D是⊙O上的四个点，AB=BC，BD交AC于点E，连接CD，AD.求证：DB平分∠ADC．18.如图所示，已知⊙O′与平面直角坐标系交于A，O，B三点，点C在⊙O′上，点A的坐标为(0,2)，∠COB=45°，∠OBC= 75°，求⊙O′的直径．5/ 45答案和解析1.【答案】D【解析】解：连接AC，如图，∵BA平分∠DBE，∴∠1=∠2，∵∠1=∠CDA，∠2=∠3，∴∠3=∠CDA，∴AC=AD=5，∵AE⊥CB，∴∠AEC=90°，∴AE=√AC2−CE2=√52−(√13)2=2√3．故选：D．连接AC，如图，根据圆内接四边形的性质和圆周角定理得到∠1=∠CDA，∠2=∠3，从而得到∠3=∠CDA，所以AC=AD=5，然后利用勾股定理计算AE的长．本题考查了圆内接四边形的性质：圆内接四边形的对角互补．圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).也考查了勾股定理．2.【答案】B【解析】解：过点O作OE⊥AB于点E，连接OC，∵弦AB的长为16cm，圆心O到AB的距离为6cmAB=8cm，∴OE=6cm，AE=12在Rt△AOE中，根据勾股定理得，OA=√OE2+AE2=10cm故选：B．过点O作OE⊥AB于点E.根据垂径定理和勾股定理求解．本题考查了垂径定理和勾股定理的综合应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．【解析】解：由题意得到OA=OB=OC=OD，作出圆O，如图所示，∴四边形ABCD为圆O的内接四边形，∴∠ABC+∠ADC=180°，∵∠ABC=40°，∴∠ADC=140°，故选：B．根据题意得到四边形ABCD共圆，利用圆内接四边形对角互补即可求出所求角的度数．此题考查了圆内接四边形的性质，熟练掌握圆内接四边形的性质是解本题的关键．4.【答案】B【解析】解：连接AB，与OC交于点D，如图所示：∵四边形ACBO为菱形，∴OA=OB=AC=BC，OC⊥AB，又OA=OC=OB，∴△AOC和△BOC都为等边三角形，AD=BD，在Rt△AOD中，OA=r，∠AOD=60°，r，∴AD=OAsin60°=√32则AB=2AD=√3r.故选：B．连接AB，与OC交于点D，由ACBO为菱形，根据菱形的性质得到对角线互相垂直，且四条边相等，再由半径相等得到三角形AOC与三角形BOC都为等边三角形，同时得到AD=BD，在直角三角形AOD中，由OA=r，∠AOD为60°，利用余弦函数定义及特殊角的三角函数值求出AD的长，即可求出AB的长．此题考查了菱形的性质，等边三角形的判定与性质，垂径定理，以及锐角三角函数定义，熟练掌握性质及定理是解本题的关键．7/ 45【解析】解：A、垂直于弦的直径平分弦所对的两条弧，所以A选项错误；B、平分弦(非直径)的直径垂直于弦，所以B选项错误；C、垂直于直径的弦被这条直径平分，所以C选项错误；D、弦的垂直平分线经过圆心，所以D选项正确．故选：D．根据垂径定理对A、C进行判断；根据垂径定理的推论对B、D进行判断．本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；弦的垂直平分线经过圆心，并且平分弦所对的两条弧；平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．6.【答案】B【解析】解：A、错误．在同圆或等圆中，相等的圆心角所对的弧相等，本选项不符合题意．B、正确．C、错误．弦所对的弧有两个，不一定相等，本选项不符合题意．D、错误．相等的弦所对的弧不一定相等．故选：B．根据圆心角，弧，弦之间的关系一一判断即可．本题考查圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．7.【答案】D【解析】【分析】此题考查了圆周角定理、垂径定理、勾股定理以及三角形中位线的性质．注意准确作出辅助线是解此题的关键．首先连接BE，由⊙O的半径OD⊥弦AB于点C，AB=8，CD=2，根据垂径定理可求得AC=BC=4，然后设OA=R，利用勾股定理可得方程：42+(R−2)2=R2，则可求得半径的长，继而利用三角形中位线的性质，求得BE的长，又由AE是直径，可得∠B=90°，继而求得答案．【解答】解：如图，连接BE，设⊙O的半径为R，∵OD⊥AB，∴AC=BC=12AB=12×8=4，在Rt△AOC中，OA=R，OC=R−CD=R−2，由勾股定理，得OC2+AC2=OA2，∴(R−2)2+42=R2，解得R=5，∴OC=5−2=3，∵O是AE的中点，C是AB的中点，∴OC是三角形ABE的中位线，∴BE=2OC=6，∵AE为⊙O的直径，∴∠ABE=90∘，在Rt△BCE中，CE=√BC2+BE2=2√13．故选D．8.【答案】B【解析】【分析】本题考查了圆的有关概念，熟记连接圆上任意两点的线段叫弦是解题的关键．弦是连接圆上任意两点的线段，根据定义作答．【解答】解：由图可知，点A、B、D、C是⊙O上的点，9/ 45图中的弦有AB 、DC 一共2条．故选B ．9.【答案】D【解析】【分析】此题考查圆周角定理，垂径定理，勾股定理，含30°直角三角形有关知识，连接OC 、OA ，利用圆周角定理得出∠AOC =60°，再利用垂径定理得出AB 即可．【解答】解：连接OC 、OA ，∵∠ABC =30°，∴∠AOC =60°，∵AB 为弦，点C 为AB⏜的中点， ∴OC ⊥AB ，∴∠OAB =30°，在Rt △OAE 中，∵AO =5，∴OE =2.5，∴AE =√AO 2−OE 2=√52−(52)2=5√32， ∴AB =5√3，故选D ．10.【答案】B【解析】【分析】本题主要考查圆心角定理，解题的关键是掌握圆心角定理和圆周角定理．延长AO 交⊙O 于点E ，连接BE ，由∠AOB +∠BOE =∠AOB +∠COD 知∠BOE =∠COD ，据此可得BE=CD=6，在Rt△ABE中利用勾股定理求解可得．【解答】解：如图，延长AO交⊙O于点E，连接BE，则∠AOB+∠BOE=180°，又∵∠AOB+∠COD=180°，∴∠BOE=∠COD，∴BE=CD=6，∵AE为⊙O的直径，∴∠ABE=90°，∴AB=√AE2−BE2=√102−62=8，故选B．11.【答案】5cm【解析】解：连接OA，∵OD⊥AB，OE⊥AC，∴AE=12AC=12×6=3(cm)，AD=12AB=12×8=4(cm)，∠OEA=∠ODA=90°，∵AB、AC是互相垂直的两条弦，∴∠A=90°，∴四边形OEAD是矩形，∴OD=AE=3cm，在Rt△OAD中，OA=√AD2+OD2=5cm．故答案为：5cm．首先由AB、AC是互相垂直的两条弦，OD⊥AB，OE⊥AC，易证得四边形OEAD是矩形，根据垂径定理，可求得AE与AD的长，然后利用勾股定理即可求得⊙O的半径OA11/ 45长．此题考查了垂径定理，矩形的判定与性质以及勾股定理等知识．此题难度不大，解题的关键是注意数形结合思想的应用，注意特殊图形的性质的应用．12.【答案】30°【解析】解：如图，连接OC．∵AB是直径，AC⏜=CD⏜=BD⏜，∴∠AOC=∠COD=∠DOB=60°，∵OA=OC，∴△AOC是等边三角形，∴∠A=60°，∵CE⊥OA，∴∠AEC=90°，∴∠ACE=90°−60°=30°．故答案为30°想办法证明△AOC是等边三角形即可解决问题．本题考查圆周角定理、等边三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．13.【答案】40°【解析】【分析】本题主要考查圆周角定理及推论，平行线的性质，先求出∠AOD，利用平行线的性质得出∠A，再由圆周角定理求出∠B的度数即可．【解答】解：∵∠BOD=130°，∴∠AOD=50°，又∵AC//OD，∴∠A=∠AOD=50°，∵AB是⊙O的直径，∴∠C=90°，∴∠B=90°−50°=40°．故答案为40°．14.【答案】2【解析】【分析】本题考查的是轴对称−最短路线问题，解答此题的关键是找到点A的对称点，把题目的问题转化为两点之间线段最短解答．首先作A关于CD的对称点Q，连接BQ，然后根据圆周角定理、圆的对称性质和等边三角形的判定和性质解答．【解答】解：作A关于CD的对称点Q，连接CQ，BQ，BQ交CD于P，此时AP+PB=QP+PB= QB，根据两点之间线段最短，PA+PB的最小值为QB的长度，连接OQ，OB，∵点B为弧AD的中点，∴∠BOD=∠ACD=20°，∴∠QOD=2∠QCD=2×20°=40°，∴∠BOQ=20°+40°=60°．∵OB=OQ，∴△BOQ是等边三角形，13/ 45BQ=OB=12CD=2，即PA+PB的最小值为2．故答案为2．15.【答案】解：作OP⊥CD于P，连接OD，∴CP=PD，∵AE=1，EB=5，∴AB=6，∴OE=2，在Rt△OPE中，OP=OE⋅sin∠DEB=√3，∴PD=√OD2−OP2=√6，∴CD=2PD=2√6(cm)．【解析】作OP⊥CD于P，连接OD，根据正弦的定义求出OP，根据勾股定理求出PD，根据垂径定理计算．本题考查的是垂径定理，掌握垂直于弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．16.【答案】证明：(1)∵C是BC⏜的中点，∴CD⏜=BC⏜，∵AB是⊙O的直径，且CF⊥AB，∴BC⏜=BF⏜，∴CD⏜=BF⏜，∴CD=BF，在△BFG和△CDG中，∵{∠F=∠CDG∠FGB=∠DGC BF=CD，∴△BFG≌△CDG(AAS)；(2)如图，过C作CH⊥AD于H，连接AC、BC，∵CD⏜=BC⏜，∵CE⊥AB，∴CH=CE，∵AC=AC，∴Rt△AHC≌Rt△AEC(HL)，∴AE=AH，∵CH=CE，CD=CB，∴Rt△CDH≌Rt△CBE(HL)，∴DH=BE=2，∴AE=AH=2+2=4，∴AB=4+2=6，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ACB=∠BEC=90°，∵∠EBC=∠ABC，∴△BEC∽△BCA，∴BCAB =BEBC，∴BC2=AB⋅BE=6×2=12，∴BF=BC=2√3．【解析】(1)根据AAS证明：△BFG≌△CDG；(2)如图，作辅助线，构建角平分线和全等三角形，证明Rt△AHC≌Rt△AEC(HL)，得AE=AH，再证明Rt△CDH≌Rt△CBE(HL)，得DH=BE=2，计算AE和AB的长，证明△BEC∽△BCA，列比例式可得BC的长，就是BF的长．此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、三角形全等的性质和判定以及勾股定理．第二问有难度，注意掌握辅助线的作法，注意掌握数形结合思想的应用．17.【答案】证明：∵AB=BC，∴AB⏜=BC⏜，∴∠BDC=∠ADB，15/ 45【解析】本题考查了圆周角定理、圆心角、弧、弦的关系.熟练掌握圆周角定理，证出AB⏜=BC⏜是解决问题的关键.由圆心角、弧、弦的关系得出AB⏜=BC⏜，由圆周角定理得出∠BDC=∠ADB，即可得出结论．18.【答案】解：如图，连接AB．∵∠AOB=90°，∴AB是直径，∵∠C=180°−∠COB−∠OBC=180°−45°−75°=60°，∴∠OAB=∠OCB=60°，∴∠ABO=30°，∵A(0,2)，∴OA=2，∴AB=2OA=4，∴⊙O′的直径为4．【解析】本题考查圆周角定理，坐标由图形的性质，圆心角，弧，弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．如图，连接AB.首先证明AB是直径，解直角三角形求出AB即可．24.2点和圆、直线和圆的位置关系1、在矩形ABCD中，AB＝8，AD＝6，以A为圆心作圆，如果B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则圆A的半径r的取值范围是？2、试述点和圆的位置关系？17 / 453、直线和圆的公共点的数目不能超过 ，这是因为 。

人教版数学九年级上册《第二十四章圆》单元检测卷-带答案一、选择题1点P是☉O内一点,过点P的最长弦的长为20 cm,最短弦的长为12 cm,则OP 的长为( )A.6 cmB.8 cmC.10 cmD.12 cm2如图,AB是☉O的弦,AC是☉O的直径,已知AC=4,∠BAC=30°,连接BC,若D是BC的中点,则OD的长为( )A.√2B.√3C.3√22D.3√323如图,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OD=3∶5,则AB的长为()A.8B.12C.16D.2√914小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )A.2√3cmB.4√3cmC.6√3cmD.8√3cm5如图,有圆锥形粮堆,其正视图是边长为6的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是( )A.3B.3√5C.3√3D.46如图,在半径为5的☉O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )A.3B.4C.3√2D.4√2二、填空题7如图所示的是一个圆锥的轴截面,AB=AC=6,BC=4,那么这个圆锥的侧面积是.8如图,OA是☉O的半径,BC是☉O的弦,OA⊥BC于点D,AE是☉O的切线,AE交OC的延长线于点E.若∠AOC=45°,BC=2,则线段AE的长为.9如图,已知☉P 的半径为3,圆心P 在抛物线y =12x 2+x -32上运动,当☉P 与x 轴相切时,则圆心P 的坐标为 .10如图,在半径为3的☉O 中,B 是劣弧AC 的中点,连接AB 并延长到D ,使BD =AB ,连接AC ,BC ,CD ,如果AB =2,那么CD 等于 .11如图,在Rt △ABC 中,∠ACB =90°,∠ABC =60°,BC =2,若以AB 为直径画半圆,以点B 为圆心,BC 长为半径画弧,交AB 于点D ,则阴影部分面积为 .(结果保留π)三、解答题12如图,在△ABC 中.∠ACB =90°,AB =10,BC =6.(1)用直尺和圆规作出☉O,使圆心O在AC边上,并与其他两边都相切,与边BC相切于点C;(保留作图痕迹,不写作法)(2)通过作图,试说明☉O与AB相切的理由;(3)求☉O的半径.13如图,AB是☉O的直径,CD是☉O的弦,连接AC,BC,BD,∠D=30°.(1)求∠ABC的度数;(2)若AC=4√3,求BC的长.14如图1,四边形ABCD内接于☉O,AD为直径,过点C作CE⊥AB于点E,连接AC.(1)求证:∠CAD=∠ECB;⏜围成阴影部分(2)如图2,连接OC,若OC⊥CE,∠EAD=60°,AC=2√3,求AD,AC与CD的面积.15如图,以线段AB为直径作☉O,交射线AC于点C,AD平分∠CAB交☉O于点D,过点D作直线DE⊥AC于点E,交AB的延长线于点F.连接BD并延长交AC于点M.(1)求证:直线DE是☉O的切线;(2)求证:AB=AM;(3)若ME=1,∠F=30°,求BF的长.参考答案一、选择题1点P是☉O内一点,过点P的最长弦的长为20 cm,最短弦的长为12 cm,则OP 的长为(B)A.6 cmB.8 cmC.10 cmD.12 cm2如图,AB是☉O的弦,AC是☉O的直径,已知AC=4,∠BAC=30°,连接BC,若D是BC的中点,则OD的长为(B)A.√2B.√3C.3√22D.3√323如图,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OD=3∶5,则AB的长为(C)A.8B.12C.16D.2√914小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为(B)A.2√3cmB.4√3cmC.6√3cmD.8√3cm5如图,有圆锥形粮堆,其正视图是边长为6的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是(B)A.3B.3√5C.3√3D.46如图,在半径为5的☉O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为(C)A.3B.4C.3√2D.4√2二、填空题7如图所示的是一个圆锥的轴截面,AB =AC =6,BC =4,那么这个圆锥的侧面积是12π .8如图,OA 是☉O 的半径,BC 是☉O 的弦,OA ⊥BC 于点D ,AE 是☉O 的切线,AE 交OC 的延长线于点E.若∠AOC =45°,BC =2,则线段AE 的长为 √2 .9如图,已知☉P 的半径为3,圆心P 在抛物线y =12x 2+x -32上运动,当☉P 与x 轴相切时,则圆心P 的坐标为 (√10-1,3)或(-√10-1,3) .10如图,在半径为3的☉O 中,B 是劣弧AC 的中点,连接AB 并延长到D ,使BD =AB ,连接AC ,BC ,CD ,如果AB =2,那么CD 等于 43 .11如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2,若以AB为直径画半圆,以点π+√3.(结果保留B为圆心,BC长为半径画弧,交AB于点D,则阴影部分面积为23π)三、解答题12如图,在△ABC中.∠ACB=90°,AB=10,BC=6.(1)用直尺和圆规作出☉O,使圆心O在AC边上,并与其他两边都相切,与边BC相切于点C;(保留作图痕迹,不写作法)(2)通过作图,试说明☉O与AB相切的理由;(3)求☉O的半径.解:(1)如图所示(2)过点O作OM⊥AB,垂足为点M.由题可知,BO是∠ABC的平分线∵∠ACB=90°,∴OC⊥BC∵BO是∠ABC的平分线,OM⊥AB∴OC=OM,∴OM是☉O的半径∴AB与☉O相切;(3)在△ABC中∵∠ACB=90°,AB=10,BC=6.∴AC=√102-62=8,∵BC,AB与☉O相切,∴BM=BC=6,∴AM=4设☉O半径为x,则OA=8-x,OM=x根据勾股定理得,x2+42=(8-x)2,解得x=3,∴☉O的半径为3.13如图,AB是☉O的直径,CD是☉O的弦,连接AC,BC,BD,∠D=30°.(1)求∠ABC的度数;(2)若AC=4√3,求BC的长.解:(1)∵点C在☉O上,AB是☉O的直径∴∠ACB=90°∵∠D=30°,∴∠A=30°∵∠A+∠ACB+∠ABC=180°∴∠ABC=180°-90°-30°=60°;(2)在Rt△ABC中,∠ACB=90°,∠A=30°AB,设BC=x,则AB=2x∴BC=12在Rt△ABC中,∠ACB=90°,由勾股定理得:AB2=AC2+BC2∵BC=x,AB=2x,AC=4√3∴x2+(4√3)2=(2x)2∵解得x=4,x=-4(舍),∴BC的长为4.14如图1,四边形ABCD内接于☉O,AD为直径,过点C作CE⊥AB于点E,连接AC.(1)求证:∠CAD=∠ECB;⏜围成阴影部分(2)如图2,连接OC,若OC⊥CE,∠EAD=60°,AC=2√3,求AD,AC与CD的面积.解:(1)∵四边形ABCD是☉O的内接四边形∴∠CBE=∠D∵AD为☉O的直径∴∠ACD=90°∴∠D+∠CAD=90°∴∠CBE+∠CAD=90°∵CE⊥AB∴∠CBE+∠BCE=90°∴∠CAD=∠BCE;(2)∵CE⊥AB,OC⊥CE∴AE∥OC∴∠COD=∠EAD=60°∵OA=OC,∠AOC=120°,AC=2√3∴OA=OC=AB=2∴AD =2OA =4在Rt △ACD 中,∠CAD =30°,∴CD =2∴AD ,AC 与CD ⏜围成阴影部分的面积为:S △AOC +S 扇形OCD =12×12×2×2√3+60π×22360 =√3+2π3. 15如图,以线段AB 为直径作☉O ,交射线AC 于点C ,AD 平分∠CAB 交☉O 于点D ,过点D 作直线DE ⊥AC 于点E ,交AB 的延长线于点F .连接BD 并延长交AC 于点M.(1)求证:直线DE 是☉O 的切线;(2)求证:AB =AM ;(3)若ME =1,∠F =30°,求BF 的长.解:(1)连接OD ,则OD =OA∴∠ODA =∠OAD∵AD 平分∠CAB∴∠OAD =∠DAC∴∠ODA =∠DAC∴OD ∥AC∵DE⊥AC∴∠ODF=∠AED=90°∵OD是☉O的半径,且DE⊥OD∴直线DE是☉O的切线.(2)∵线段AB是☉O的直径∴∠ADB=90°∴∠ADM=180°-∠ADB=90°∴∠M+∠DAM=90°,∠ABM+∠DAB=90°∵∠DAM=∠DAB∴∠M=∠ABM∴AB=AM.(3)∵∠AEF=90°,∠F=30°∴∠BAM=60°∴△ABM是等边三角形∴∠M=60°∵∠DEM=90°,ME=1∴∠EDM=30°∴MD=2ME=2∴BD=MD=2∵∠BDF=∠EDM=30°∴∠BDF=∠F∴BF=BD=2.。

2023-2024学年九年级数学上册《第二十四章圆》单元测试卷有答案(人教版)学校:___________班级：___________姓名：___________考号：___________知识点归纳1、圆在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。

固定的端点O叫做圆心，线段OA叫做半径，以点O为圆心的圆，记作⊙O，读作“圆O”。

连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。

圆上任意两点间的部分叫做圆弧，简称弧。

圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

小于半圆的弧叫做劣弧。

大于半圆的弧叫做优弧。

能够重合的两个圆叫做等圆。

在同圆或等圆中，能重合的弧叫等弧。

2、垂径定理垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。

推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；弦的垂直平分线过圆心，且平分弦对的两条弧．3、弧、弦、圆心角之间的关系定义：顶点在圆心的角叫做圆心角。

在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等；在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等。

注：在同圆或等圆中，如果两个圆心角，两条弦，两条弧、两个弦的弦心距中，有一组量相等，那么其余各组量也分别相等4、圆周角定义：顶点在圆上，并且两边都和圆相交的角叫圆周角。

圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

推论1：同弧或等弧所对的圆周角相等。

推论2：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径。

圆内接四边形的性质：圆内接四边形的对角互补。

5、点和圆的位置关系设⊙O 的半径为r ，点P 到圆心的距离为OP=d ，则有：点P 在圆外⇔d ＞r ；点P 在圆上⇔d=r ；点P 在圆内⇔d ＜r 。

性质：不在同一条直线上的三个点确定一个圆。

人教版九年级数学上册第二十四章综合测试卷03一、选择题（每小题4分，共40分）1.如图24-14，AB 是O 的直径，点C 在O 上，若40A ∠=︒，则B ∠的度数为（）A .80︒B .60︒C .50︒D .40︒2.如图24-15，AB 是O 的直径，弦CD AB ⊥，垂足为M ，下列结论不成立的是（）A .CM DM=B . BCBD =C .ACD ADC ∠=∠D .OM MD=3.如图24-16，ABC △内接于O ，OD BC ⊥于点D ，50A ∠=︒，则OCD ∠的度数是（）A .40︒B .45︒C .50︒D .60︒4.如图24-17，AB 是O 的弦，BC 与O 相切于点B ，连接OA ，OB .若70ABC ∠=︒，则A ∠等于（）A .15︒B .20︒C .30︒D .70︒5.如图24-18，半径为1的小圆在半径为9的大圆内沿大圆滚动，则小圆扫过的阴影部分的面（）A .17πB .32πC .49πD .80π6.如图24-19，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，点B 与下列格点的连线中，能够与该圆弧相切的是（）A .点0,3（）B .点2,3（）C .点5,1（）D .点6,1（）7.如图24-20，在边长为1的正方形组成的网格中，ABC △的顶点都在格点上，将ABC △绕点C 顺时针旋转60︒，则顶点A 所经过的路径长为（）A .10πB.103C .10π3D .π8.如图24-21，在半径为R 的圆内作一个内接正方形，然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依次作到第n 个内切圆，它的半径是（）A .22nR ⎛⎫ ⎪ ⎪⎝⎭B .12nR ⎛⎫⎪⎝⎭C .112n R-⎛⎫⎪⎝⎭D .122n R-⎛⎫ ⎪ ⎪⎝⎭9.小明用图24-22中所示的扇形纸片制作一个圆锥的侧面，已知扇形的半径为5 cm ，弧长是6π cm ，那么这个圆锥的高是（）A .4 cmB .6 cmC .8 cmD .2 cm10.一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图的扇形的圆心角是（）A .120︒B .180︒C .60︒D .90︒二、填空题（每小题4分，共16分）11.在圆中，30︒的圆周角所对的弦的长度为________.12.当宽为3 cm 的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图24-23所示（单位：cm ），那么该圆的半径为________cm .13.如图24-24，Rt ABC △的边BC 位于直线l 上，AC =，90ACB ∠=︒，30A ∠=︒，若Rt ABC △由现在的位置向右无滑动地翻转，当点A 第3次落在直线l 上时，点A 所经过的路线的长为________（结果用含的式子表示）.14.（2013·江苏盐城）如图24-25，在ABC △中，90BAC ∠=︒， 5 cm AB =， 2 cm AC =，将ABC △绕顶点C 按顺时针方向旋转45︒至11A B C △的位置，则线段AB 扫过区域（图中的阴影部分）的面积为________2cm .三、解答题（共44分）15.（8分）如图24-26，在O 中，直径AB 与弦CD 相交于点P ，40CAB ∠=︒，65APD ∠=︒.（1）求B ∠的大小；（2）已知6AD =，求圆心O 到BD 的距离.16.（8分）如图24-27，在ABC △中，90C ∠=︒，8AC BC +=，点O 是斜边AB 上一点，以点O 为圆心的O 分别与AC ，BC 相切于点D ，E .（1）当2AC =时，求O 的半径；（2）设AC x =，O 的半径为y ，求y 与x 的函数关系式.17.（8分）如图24-28，P 的圆心为32P -（，），半径为3，直线MN 过点50M （，）且平行于y 轴，点N 在点M 的上方.（1）在图中作出P 关于y 轴对称的'P ，根据作图直接写出'P 与直线MN 的位置关系；（2）若点N 在（1）中的'P 上，求PN 的长.18.（8分）如图24-29，在O 中，弦BC 垂直于半径OA ，垂足为点E ，D 是优弧BC 上一点，连接BD ，AD ，OC ，30ADB ∠=︒.（1）求AOC ∠的度数；（2）若弦6BC =，求图中阴影部分的面积.19.（12分）实践操作：如图24-30，ABC △是直角三角形，90ACB ∠=︒，利用直尺和圆规按下列要求作图，并在图中标明相应的字母.（保留作图痕迹，不写作法）（1）作BAC ∠的平分线，交BC 于点O ；（2）以点O 为圆心，OC 为半径作圆.综合运用：在你所作的图中，（1）判别AB 与O 的位置关系，并说明理由；（2）若5AC =，12BC =，求O 的半径.第二十四章综合测试答案解析1.【答案】C【解析】因为AB 为O 的直径，所以90C ∠=︒.因为40A ∠=︒，所以180904050B ∠=︒-︒-︒=︒.2.【答案】D【解析】根据垂径定理，得CM DM =， BCBD =，AC AD =，由AC AD =，得ACD ADC ∠=∠，而OM MD =不一定成立.3.【答案】A【解析】连接OB ，则OB OC =，因为OD BC ⊥，所以12COD BOC ∠=∠.因为BOC ∠与A ∠分别是 BC所对的圆心角和圆周角，所以0A B C ∠=∠.所以50COD A ∠=∠=︒.所以90905040OCD COD ∠=︒-∠=︒-︒=︒.故选A .4.【答案】B【解析】由同圆半径相等和切线的性质，得907020A ABO ∠=∠=︒-︒=︒.故选B.5.【答案】B 【解析】22π9π(92)81π49π32πS =⋅-⋅-=-=阴影.6.【答案】C【解析】易知圆心坐标为()2,0，进而可知点()5,1符合要求.7.【答案】C【解析】ABC △绕点C 顺时针旋转60︒，顶点A 经过的路径是以点C 为圆心，AC 为半径，圆心角为60︒的圆弧.结合图形，由勾股定理，得AC =π180n R l =，可求路径长为π3.8.【答案】A【解析】第一个内切圆的半径为号2R，第二个内切圆的半径是22R ⎛⎫ ⎪ ⎪⎝⎭，所以第n个内切圆的半径是2nR ⎛⎫⎪ ⎪⎝⎭.9.【答案】A【解析】设圆锥的高、底面圆的半径分别为h ，r ，2π6πr =，所以3r =.因为圆的母线长为5，所以圆锥的高4(cm)h ==.10.【答案】A【解析】设母线长为l ，底面半径为r ，则底面周长为2πr ，底面积为2r π，侧面积为rl π.由题知侧面积是底面积的3倍，所以3l r =.设圆心角为n ︒，则π2π180n lr =，解得120n =.11.【答案】【解析】如答图24-1，因为30BAC ∠=︒，所以60BOC ∠=︒，所以BOC △是等边三角形，所以OB OC BC ===，即这个圆的半径为.12.【答案】256【解析】如答图24-2，连接OA ，AB ，OC ，设OC 与AB 的交点为点D .在Rt OAD △中，4AD =，3OD R =-，OA R =.由勾股定理，得22234R R =-+（）.解得256R =，故该圆的半径为256.134π+【解析】斜边长度是2，第一次经过的路线长度是120π2180⨯.第二次经过的路线长度是90π3120π2180180⨯+.第三次经过的路线长度与第二次经过的路线长度相同，也是90π3120π2180180⨯+.所以当点A 第三次落在直线l上时，经过的路线长度是120π290π120π24π4π224π18018018033⎛⎫⨯⨯+⨯+=+⨯=+ ⎪ ⎪⎝⎭.14.【答案】25π8【解析】在Rt ABC △中，BC ==，扇形1CBB的面积是245π29π3608⨯=，1115252CB A S =⨯⨯=△；1245π2π3602CAA S ⨯==扇形.故111129ππ25π55828CB A ABC BCB CAA S S S S S =+--=+--=△△阴影部分扇形扇形.15.【答案】解：（1）因为APD C CAB ∠=∠+∠，所以654025C ∠=︒-︒=︒，所以25B C ∠=∠=︒.（2）如答图24-3，过点O 作OE BD ⊥于点E ，则DE BE =.又因为AO BO =，所以116322OE AD ==⨯=.所以圆心O 到BD 的距离为3.16.【答案】解：如答图24-4，连接OD ，OE ，OC.因为点D ，E 为切点，所以OD AC ⊥，OE BC ⊥，OD OE =.因为ABCAO C BC C S S S =+△△△，所以111222AC BC AC OD BC OE ⋅=⋅+⋅.（1）因为8AC BC +=，2AC =，所以6BC =.所以1112626222OD OE⨯⨯=⨯⨯+⨯⨯.而OD OE =，所以32OD =，即O 的半径为32.（2）因为8AC BC +=，AC x =，所以8BC x =-.所以111(8)(8)222x x xy x y -=+-.化简，得218y x x =-+.17.【答案】解：（1）如答图24-5，点3,2P -（）关于y 轴的对称点为'3,2P （），以点'P 为圆心，3为半径的圆即为所求， 'P 与直线MN 相交。

第二十四章圆单元检测题一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列说法中,正确的是( )A.过圆心的线段叫直径B.长度相等的两条弧是等弧C.与半径垂直的直线是圆的切线D.圆既是中心对称图形,又是轴对称图形2.已知☉O的半径为6,圆心O到直线l的距离为7,则直线l与☉O的位置关系是( )A.相离B.相交C.相切D.无法确定3.(2023自贡)如图所示,△ABC内接于☉O,CD是☉O的直径,连接BD,∠DCA=41°,则∠ABC的度数是( )第3题图A.41°B.45°C.49°D.59°4.圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )A.10πB.15πC.30πD.45π5.如图所示,☉O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的取值范围是( )第5题图A.3<OP<5B.3≤OP≤5C.4<OP<5D.4≤OP≤56.如图所示,四边形ABCD内接于☉O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )A.45°B.50°C.55°D.60°7.如图所示,☉O是△ABC的外接圆,∠BAC=60°,若☉O的半径OC为2,则弦BC的长为( )第7题图A.4B.23C.338.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )2 B.22-22 D.2-29.(2022娄底改编)如图所示,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC 的内心成中心对称,则圆中的黑色部分的面积与△ABC 的面积之比是( )第9题图3π18 B.3183π9 D.3910.(2022广大附中一模)如图所示,点A,B 的坐标分别为A(2,0), B(0,2),点C 为坐标平面内一点,BC=1,点M 为线段AC 的中点,连接OM,则OM 的最大值为( )2+1 B.2+12C.22+1D.22-12二、填空题:本大题共5小题,每小题3分,共15分.11.用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设 .12.如图所示,C为AB的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= cm.13.已知圆心角为120°的扇形的面积为12π cm2,则扇形的弧长是 cm.14.如图所示,☉O的半径为1,PA,PB是☉O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为 .第14题图15.小明很喜欢钻研问题,一次数学老师拿来一个残缺的圆形瓦片(如图所示),让小明求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量得AB的中点C到AB的距离CD=1.6 cm,AB=6.4 cm,则求得圆形瓦片所在圆的半径为 cm.第15题图三、解答题(一):本大题3小题,第16题10分,第17,18题各7分,共24分.16.(1)(2022湘潭节选)如图所示,在☉O中,直径AB与弦CD相交于点E,连接AC,BD,AD.若AD=3,∠C=30°,求☉O的半径.(2)如图所示,扇形OAB的圆心角为120°,半径OA为6 cm.若把扇形纸片OAB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.17.如图所示,四边形ABCD内接于☉O,AB=AD,∠C=110°,若点E在AD 上,求∠E的度数.18.(2022珠海一模改编)如图所示,已知AB是☉O的直径,直线CD是☉O的切线,过点A作AD⊥CD,垂足为D,直线CD与AB的延长线交于点E.当AB=2BE,且CE=3时,求AD的长.四、解答题(二):本大题3小题,每小题9分,共27分.19.(原创)综合与实践素材:一张三角形纸板.操作:如图(1)所示,将一块三角形纸板ABC,准备裁剪成一个面积最大的圆形,已知∠C=90°,BC=3,AC=4.如图(2)所示,作△ABC的内切圆☉O,切点分别为D,E,G,连接OG,OD,OE.解决问题:请求出裁剪出的最大圆形面积.20.(2022眉山改编)如图所示,AB为☉O的直径,点C是☉O上一点,CD 与☉O相切于点C,过点B作BD⊥DC,连接AC,BC.(1)求证:BC平分∠ABD;(2)若BC=23,AB=4,求阴影部分的面积.21.(2022新疆节选)如图所示,☉O是△ABC的外接圆,AB是☉O的直径,点D在☉O上,AC=CD,连接AD,延长DB交过点C的切线于点E.求证:(1)∠ABC=∠CAD;(2)BE⊥CE.五、解答题(三):本大题2小题,每小题12分,共24分.22.(2022金华)综合探究如图(1)所示,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:作法如图(2)所示.1.作直径AF.2.以F为圆心,FO为半径作圆弧,与☉O交于点M,N.3.连接AM,MN,NA.(1)求∠ABC的度数;(2)△AMN是正三角形吗?请说明理由;(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.23.(2022宁波)综合运用如图(1)所示,☉O为锐角三角形ABC的外接圆,点D在BC上,AD交BC 于点E,点F在AE上,满足∠AFB-∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连接BD,DG.设∠ACB=α.(1)用含α的代数式表示∠BFD;(2)求证:△BDE≌△FDG;(3)如图(2)所示,若AD为☉O的直径,当AB的长为2时,求AC的长.答案：一、选择题1.D2.A3.C4.B5.D6.B7.B8.B9.A 10.B二、填空题11.∠B≥90°　12.2　13.4π　14.33　15.4三、解答题(一)16.(1)解:∵∠C=∠B,∠C=30°,∴∠B=30°.∵AB是☉O的直径,AD=3,∴∠ADB=90°.∴AB=6.∴☉O的半径为3.(2)如图所示,设圆锥底面圆的半径为r,所以2πr=4π,解得r=2,在Rt△OHC中,HC=2,OC=6,所以OH=OC2-H C2=42(cm).17.解:如图所示,连接BD,∵∠C+∠BAD=180°,∠C=110°,∴∠BAD=180°-110°=70°.∵AB=AD,∴∠ABD=∠ADB.×(180°-70°)=55°.∴∠ABD=12∵四边形ABDE是☉O的内接四边形,∴∠E+∠ABD=180°.∴∠E=180°-55°=125°.18.解:如图所示,连接OC,∵直线CD为☉O的切线,∴∠OCE=90°.∵AB=2BO,AB=2BE,∴BO=BE=CO.设BO=BE=CO=x,∴OE=2x.在Rt△OCE中,根据勾股定理,得OC2+CE2=OE2,即x2+(3)2=(2x)2.∴x=1.∴AE=3,∠E=30°.∴AD=32.四、解答题(二)19.解:∵∠C=90°,BC=3,AC=4,OG=OE=OD,∴AB=32+42=5.∴S △ABC =12AC×BC=12AC×OG+12BC×OE+12AB×OD=12OG×C △ABC ,即12AC×BC=12OG×C △ABC .∴12×3×4=12×OG×(3+4+5),解得OG=1,∴裁剪出的最大圆形面积为π×12=π.20.(1)证明:连接OC,如图所示,∵CD 与☉O 相切于点C,OC 为半径,∴OC ⊥CD.∵BD ⊥CD,∴OC ∥BD.∴∠OCB=∠DBC.∵OC=OB,∴∠OCB=∠OBC.∴∠DBC=∠OBC.∴BC 平分∠ABD.(2)解:如图所示,作CE ⊥AO 于点E,∵AB是直径,AB=4,∴∠ACB=90°,OA=OC=2.在Rt△ABC中,AC=AB2-B C2=42-(23)2=2,∴AO=CO=AC=2.∴△AOC是等边三角形.∴∠AOC=60°.∵CE⊥OA,∴OE=12OA=1.∴CE=3.∴阴影部分的面积S=60×π×22360-12×2×3=2π3-3.21.证明:(1)∵AC=CD,∴∠CAD=∠ADC.∵∠ABC=∠ADC,∴∠ABC=∠CAD.(2)如图所示,连接OC,∵CE与☉O相切于点C,∴∠OCE=90°.∵四边形ADBC是圆内接四边形,∴∠CAD+∠DBC=180°.∵∠DBC+∠CBE=180°,∴∠CAD=∠CBE.∵∠ABC=∠CAD,∴∠CBE=∠ABC.∵OB=OC,∴∠OCB=∠ABC.∴∠OCB=∠CBE.∴OC∥BE.∴∠E=180°-∠OCE=90°.∴BE⊥CE.五、解答题(三)22.解:(1)∵五边形ABCDE是正五边形,∴∠ABC=(5-2)×180°=108°,5即∠ABC=108°.(2)△AMN是正三角形.理由如下:如图所示,连接ON,NF,由题意,得FN=ON=OF,∴△FON是等边三角形.∴∠NFA=60°.∴NMA=60°.同理,得∠ANM=60°,∴∠MAN=60°.∴△MAN是正三角形.(3)∵∠AMN=60°,∴∠AON=120°.×2=144°,∵∠AOD=360°5∴∠NOD=∠AOD-∠AON=144°-120°=24°.∵360°÷24°=15,∴n的值是15.23.(1)解:∵∠AFB-∠BFD=∠ACB=α,①又∵∠AFB+∠BFD=180°,②②-①,得2∠BFD=180°-α,.∴∠BFD=90°-α2,(2)证明:由(1),得∠BFD=90°-α2∵∠ADB=∠ACB=α,.∴∠FBD=180°-∠ADB-∠BFD=90°-α2∴∠BFD=∠FBD.∴DB=DF.∵FG∥AC,∴∠CAD=∠DFG.∵∠CAD=∠DBE,∴∠DFG=∠DBE.在△BDE 和△FDG 中,{DB =DF ,∠DBE =∠DFG ,BE =FG ,∴△BDE ≌△FDG(SAS).(3)解:∵△BDE ≌△FDG,∴∠FDG=∠BDE=α,DE=DG.∴∠BDG=∠BDF+∠EDG=2α.∵DE=DG,∴∠DGE=12(180°-∠FDG)=90°-α2.∴∠DBG=180°-∠BDG-∠DGE=90°-3α2.∵AD 是☉O 的直径,∴∠ABD=90°.∴∠ABC=∠ABD-∠DBG=3α2.∴AC 与AB 所对的圆心角度数之比为3∶2.∴AC 与AB 的长度之比为3∶2.∵AB =2,∴AC =3.。

初初初初初初初初初初初初初初初初初初初初初初初初初24.1圆的有关性质一、选择题1.如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA平分∠DBE，AD=5，CE=√13，则AE=()A. 3B. 3√2C. 4√3D. 2√32.如图，在⊙O中，弦AB的长为16cm，圆心O到AB的距离为6cm，则⊙O的半径是()A. 6cmB. 10cmC. 8cmD. 20cm3.如图，点O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是()A. 130°B. 140°C. 150°D. 160°4.如图，A、B是⊙O上两点，若四边形ACBO是菱形，⊙O的半径为r，则点A与点B之间的距离为()A. √2rB. √3rC. rD. 2r5.下列说法正确的是()A. 垂直于弦的直线平分弦所对的两条弧B. 平分弦的直径垂直于弦C. 垂直于直径平分这条直径D. 弦的垂直平分线经过圆心6.下列说法正确的是()A. 相等的圆心角所对的弧相等B. 在同圆中，等弧所对的圆心角相等C. 在同圆中，相等的弦所对的弧相等D. 相等的弦所对的弧相等7.如图，在⊙O中，半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC，若AB=8，CD=2，则EC的长度为()A. 2√15B. 8C. 2√10D. 2√138.如图所示，图中弦的条数为()A. 1条B. 2条C. 3条D. 4条9.如图，⊙O的半径为5，AB为弦，点C为AB⌢的中点，若∠ABC=30°，则弦AB的长为()A. 12B. 5 C. 5√32D. 5√310.如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为()A. 6B. 8C. 5√2D. 5√3二、填空题11.如图，在⊙O中，AB、AC是互相垂直的两条弦，OD⊥AB于点D，OE⊥AC于点E，且AB=8cm，AC=6cm，那么⊙O的半径OA长为______．12.如图，AB是⊙O的直径，C、D为半圆的三等分点，CE⊥AB于点E，∠ACE的度数为______．13.如图，AB是⊙O的直径，点D在⊙O上，∠BOD=130°，AC//OD交⊙O于C，连接BC，则∠B=________．14.如图，CD是⊙O的直径，CD=4，∠ACD=20°，点B为弧AD的中点，点P是直径CD上的一个动点，则PA+PB的最小值为______．三、计算题15.⊙O中，直径AB和弦CD相交于点E，已知AE=1cm，EB=5cm，且∠DEB=60°，求CD的长．四、解答题16.如图，AB是⊙O的直径，点C为BD⌢的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．(1)求证：△BFG≌△CDG；(2)若AD=BE=2，求BF的长．17.如图，已知A，B，C，D是⊙O上的四个点，AB=BC，BD交AC于点E，连接CD，AD.求证：DB平分∠ADC．18.如图所示，已知⊙O′与平面直角坐标系交于A，O，B三点，点C在⊙O′上，点A的坐标为(0,2)，∠COB=45°，∠OBC= 75°，求⊙O′的直径．答案和解析1.【答案】D【解析】解：连接AC，如图，∵BA平分∠DBE，∴∠1=∠2，∵∠1=∠CDA，∠2=∠3，∴∠3=∠CDA，∴AC=AD=5，∵AE⊥CB，∴∠AEC=90°，∴AE=√AC2−CE2=√52−(√13)2=2√3．故选：D．连接AC，如图，根据圆内接四边形的性质和圆周角定理得到∠1=∠CDA，∠2=∠3，从而得到∠3=∠CDA，所以AC=AD=5，然后利用勾股定理计算AE的长．本题考查了圆内接四边形的性质：圆内接四边形的对角互补．圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).也考查了勾股定理．2.【答案】B【解析】解：过点O作OE⊥AB于点E，连接OC，∵弦AB的长为16cm，圆心O到AB的距离为6cmAB=8cm，∴OE=6cm，AE=12在Rt△AOE中，根据勾股定理得，OA=√OE2+AE2=10cm故选：B．过点O作OE⊥AB于点E.根据垂径定理和勾股定理求解．本题考查了垂径定理和勾股定理的综合应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．【解析】解：由题意得到OA=OB=OC=OD，作出圆O，如图所示，∴四边形ABCD为圆O的内接四边形，∴∠ABC+∠ADC=180°，∵∠ABC=40°，∴∠ADC=140°，故选：B．根据题意得到四边形ABCD共圆，利用圆内接四边形对角互补即可求出所求角的度数．此题考查了圆内接四边形的性质，熟练掌握圆内接四边形的性质是解本题的关键．4.【答案】B【解析】解：连接AB，与OC交于点D，如图所示：∵四边形ACBO为菱形，∴OA=OB=AC=BC，OC⊥AB，又OA=OC=OB，∴△AOC和△BOC都为等边三角形，AD=BD，在Rt△AOD中，OA=r，∠AOD=60°，r，∴AD=OAsin60°=√32则AB=2AD=√3r.故选：B．连接AB，与OC交于点D，由ACBO为菱形，根据菱形的性质得到对角线互相垂直，且四条边相等，再由半径相等得到三角形AOC与三角形BOC都为等边三角形，同时得到AD=BD，在直角三角形AOD中，由OA=r，∠AOD为60°，利用余弦函数定义及特殊角的三角函数值求出AD的长，即可求出AB的长．此题考查了菱形的性质，等边三角形的判定与性质，垂径定理，以及锐角三角函数定义，熟练掌握性质及定理是解本题的关键．【解析】解：A、垂直于弦的直径平分弦所对的两条弧，所以A选项错误；B、平分弦(非直径)的直径垂直于弦，所以B选项错误；C、垂直于直径的弦被这条直径平分，所以C选项错误；D、弦的垂直平分线经过圆心，所以D选项正确．故选：D．根据垂径定理对A、C进行判断；根据垂径定理的推论对B、D进行判断．本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；弦的垂直平分线经过圆心，并且平分弦所对的两条弧；平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．6.【答案】B【解析】解：A、错误．在同圆或等圆中，相等的圆心角所对的弧相等，本选项不符合题意．B、正确．C、错误．弦所对的弧有两个，不一定相等，本选项不符合题意．D、错误．相等的弦所对的弧不一定相等．故选：B．根据圆心角，弧，弦之间的关系一一判断即可．本题考查圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．7.【答案】D【解析】【分析】此题考查了圆周角定理、垂径定理、勾股定理以及三角形中位线的性质．注意准确作出辅助线是解此题的关键．首先连接BE，由⊙O的半径OD⊥弦AB于点C，AB=8，CD=2，根据垂径定理可求得AC=BC=4，然后设OA=R，利用勾股定理可得方程：42+(R−2)2=R2，则可求得半径的长，继而利用三角形中位线的性质，求得BE的长，又由AE是直径，可得∠B=90°，继而求得答案．【解答】解：如图，连接BE，设⊙O的半径为R，∵OD⊥AB，∴AC=BC=12AB=12×8=4，在Rt△AOC中，OA=R，OC=R−CD=R−2，由勾股定理，得OC2+AC2=OA2，∴(R−2)2+42=R2，解得R=5，∴OC=5−2=3，∵O是AE的中点，C是AB的中点，∴OC是三角形ABE的中位线，∴BE=2OC=6，∵AE为⊙O的直径，∴∠ABE=90∘，在Rt△BCE中，CE=√BC2+BE2=2√13．故选D．8.【答案】B【解析】【分析】本题考查了圆的有关概念，熟记连接圆上任意两点的线段叫弦是解题的关键．弦是连接圆上任意两点的线段，根据定义作答．【解答】解：由图可知，点A、B、D、C是⊙O上的点，图中的弦有AB 、DC 一共2条．故选B ．9.【答案】D【解析】【分析】此题考查圆周角定理，垂径定理，勾股定理，含30°直角三角形有关知识，连接OC 、OA ，利用圆周角定理得出∠AOC =60°，再利用垂径定理得出AB 即可．【解答】解：连接OC 、OA ，∵∠ABC =30°，∴∠AOC =60°，∵AB 为弦，点C 为AB⏜的中点， ∴OC ⊥AB ，∴∠OAB =30°，在Rt △OAE 中，∵AO =5，∴OE =2.5，∴AE =√AO 2−OE 2=√52−(52)2=5√32， ∴AB =5√3，故选D ．10.【答案】B【解析】【分析】本题主要考查圆心角定理，解题的关键是掌握圆心角定理和圆周角定理．延长AO 交⊙O 于点E ，连接BE ，由∠AOB +∠BOE =∠AOB +∠COD 知∠BOE =∠COD ，据此可得BE=CD=6，在Rt△ABE中利用勾股定理求解可得．【解答】解：如图，延长AO交⊙O于点E，连接BE，则∠AOB+∠BOE=180°，又∵∠AOB+∠COD=180°，∴∠BOE=∠COD，∴BE=CD=6，∵AE为⊙O的直径，∴∠ABE=90°，∴AB=√AE2−BE2=√102−62=8，故选B．11.【答案】5cm【解析】解：连接OA，∵OD⊥AB，OE⊥AC，∴AE=12AC=12×6=3(cm)，AD=12AB=12×8=4(cm)，∠OEA=∠ODA=90°，∵AB、AC是互相垂直的两条弦，∴∠A=90°，∴四边形OEAD是矩形，∴OD=AE=3cm，在Rt△OAD中，OA=√AD2+OD2=5cm．故答案为：5cm．首先由AB、AC是互相垂直的两条弦，OD⊥AB，OE⊥AC，易证得四边形OEAD是矩AE AD OA此题考查了垂径定理，矩形的判定与性质以及勾股定理等知识．此题难度不大，解题的关键是注意数形结合思想的应用，注意特殊图形的性质的应用．12.【答案】30°【解析】解：如图，连接OC．∵AB是直径，AC⏜=CD⏜=BD⏜，∴∠AOC=∠COD=∠DOB=60°，∵OA=OC，∴△AOC是等边三角形，∴∠A=60°，∵CE⊥OA，∴∠AEC=90°，∴∠ACE=90°−60°=30°．故答案为30°想办法证明△AOC是等边三角形即可解决问题．本题考查圆周角定理、等边三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．13.【答案】40°【解析】【分析】本题主要考查圆周角定理及推论，平行线的性质，先求出∠AOD，利用平行线的性质得出∠A，再由圆周角定理求出∠B的度数即可．【解答】解：∵∠BOD=130°，又∵AC//OD，∴∠A=∠AOD=50°，∵AB是⊙O的直径，∴∠C=90°，∴∠B=90°−50°=40°．故答案为40°．14.【答案】2【解析】【分析】本题考查的是轴对称−最短路线问题，解答此题的关键是找到点A的对称点，把题目的问题转化为两点之间线段最短解答．首先作A关于CD的对称点Q，连接BQ，然后根据圆周角定理、圆的对称性质和等边三角形的判定和性质解答．【解答】解：作A关于CD的对称点Q，连接CQ，BQ，BQ交CD于P，此时AP+PB=QP+PB= QB，根据两点之间线段最短，PA+PB的最小值为QB的长度，连接OQ，OB，∵点B为弧AD的中点，∴∠BOD=∠ACD=20°，∴∠QOD=2∠QCD=2×20°=40°，∴∠BOQ=20°+40°=60°．∵OB=OQ，∴△BOQ是等边三角形，BQ=OB=1CD=2，即PA+PB的最小值为2．2故答案为2．15.【答案】解：作OP⊥CD于P，连接OD，∴CP=PD，∵AE=1，EB=5，∴AB=6，∴OE=2，在Rt△OPE中，OP=OE⋅sin∠DEB=√3，∴PD=√OD2−OP2=√6，∴CD=2PD=2√6(cm)．【解析】作OP⊥CD于P，连接OD，根据正弦的定义求出OP，根据勾股定理求出PD，根据垂径定理计算．本题考查的是垂径定理，掌握垂直于弦的直径平分这条弦，并且平分弦所对的两条弧是16.【答案】证明：(1)∵C是BC⏜的中点，∴CD⏜=BC⏜，∵AB是⊙O的直径，且CF⊥AB，∴BC⏜=BF⏜，∴CD⏜=BF⏜，∴CD=BF，在△BFG和△CDG中，∵{∠F=∠CDG∠FGB=∠DGC BF=CD，∴△BFG≌△CDG(AAS)；(2)如图，过C作CH⊥AD于H，连接AC、BC，∵CD⏜=BC⏜，∴∠HAC=∠BAC，∵CE⊥AB，∴CH=CE，∵AC=AC，∴Rt△AHC≌Rt△AEC(HL)，∴AE=AH，∵CH=CE，CD=CB，∴Rt△CDH≌Rt△CBE(HL)，∴DH=BE=2，∴AE=AH=2+2=4，∴AB=4+2=6，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ACB=∠BEC=90°，∴△BEC∽△BCA，∴BCAB =BEBC，∴BC2=AB⋅BE=6×2=12，∴BF=BC=2√3．【解析】(1)根据AAS证明：△BFG≌△CDG；(2)如图，作辅助线，构建角平分线和全等三角形，证明Rt△AHC≌Rt△AEC(HL)，得AE=AH，再证明Rt△CDH≌Rt△CBE(HL)，得DH=BE=2，计算AE和AB的长，证明△BEC∽△BCA，列比例式可得BC的长，就是BF的长．此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、三角形全等的性质和判定以及勾股定理．第二问有难度，注意掌握辅助线的作法，注意掌握数形结合思想的应用．17.【答案】证明：∵AB=BC，∴AB⏜=BC⏜，∴∠BDC=∠ADB，∴DB平分∠ADC．【解析】本题考查了圆周角定理、圆心角、弧、弦的关系.熟练掌握圆周角定理，证出AB⏜=BC⏜是解决问题的关键.由圆心角、弧、弦的关系得出AB⏜=BC⏜，由圆周角定理得出∠BDC=∠ADB，即可得出结论．18.【答案】解：如图，连接AB．∵∠AOB=90°，∴AB是直径，∵∠C=180°−∠COB−∠OBC=180°−45°−75°=60°，∴∠OAB=∠OCB=60°，∵A(0,2)，∴OA=2，∴AB=2OA=4，∴⊙O′的直径为4．【解析】本题考查圆周角定理，坐标由图形的性质，圆心角，弧，弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．如图，连接AB.首先证明AB是直径，解直角三角形求出AB即可．24.2点和圆、直线和圆的位置关系1、在矩形ABCD中，AB＝8，AD＝6，以A为圆心作圆，如果B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则圆A的半径r的取值范围是？2、试述点和圆的位置关系？3、直线和圆的公共点的数目不能超过，这是因为。

第二十四章学情评估一、选择题(每小题3分，共30分)1．如图，点A，B，C在⊙O上，∠ACB＝35°，则∠AOB的度数是() A．75° B. 70° C. 65° D. 35°(第1题)(第3题)2．若直线l与半径为10的⊙O相交，则圆心O与直线l的距离d的取值范围为()A．0≤d＜10 B．d＞10 C．d＝10 D．d≤10 3．如图，AB为⊙O的直径，∠ABC＝35°，则∠CAB的度数为() A．35°B．45°C．55°D．65°4．用一个半径为30，圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是()A．10 B．20 C．10π D．20π5．已知半径为5的⊙O是△ABC的外接圆．若∠ABC＝25°，则劣弧AC的长为()A.25π36 B.125π36 C.25π18 D.5π366．如图，BM与⊙O相切于点B，若∠MBA＝140°，则∠ACB的度数为() A．40°B．50°C．60°D．70°(第6题)(第7题)7．如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，BD＝8，AE＝2，则OF的长度是()A．3 B. 6 C．2.5 D. 58．下列圆的内接正多边形中，一条边所对的圆心角最大的图形是() A．正三角形B．正方形C．正五边形D．正六边形9．如图，△ABC中，∠A＝30°，点O是边AB上一点，以点O为圆心，以OB 为半径作圆，⊙O恰好与AC相切于点D，连接BD.若BD平分∠ABC，AD ＝2 3，则线段CD的长是()A．2 B. 3 C.32 D.32 3(第9题)(第10题)(第11题)10．如图，在平面直角坐标系xOy中，A(4，0)，B(0，3)，C(4，3)，I是△ABC 的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I′的坐标为() A．(－2，3) B．(－3，2) C．(3，－2) D．(2，－3) 二、填空题(每小题4分，共28分)11．如图，AB是⊙O的切线，点B为切点，若∠A＝30°，则∠AOB＝________．12．已知圆锥的底面圆半径为3 cm，高为4 cm，则圆锥的侧面积是________cm2. 13．如图，点A，B，C在⊙O上，∠A＝40°，∠C＝20°，则∠B＝________°.(第13题)(第14题)(第15题)14．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C＝20°，则∠CDA＝________.15．如图，已知⊙O的半径为2，△ABC内接于⊙O，∠ACB＝135°，则AB＝________．16．如图，点M，N分别是正五边形ABCDE的两边AB，BC上的点，且AM＝BN，点O是正五边形的中心，则∠MON的度数是________度．(第16题)(第17题)17．如图，AB是⊙O的弦，AB＝8，点C是⊙O上的一个动点，且∠ACB＝45°.若点M，N分别是AB，BC的中点，则MN长的最大值是________．三、解答题(一)(每小题6分，共18分)18．如图，P A，PB分别与⊙O相切于A，B两点，点C在⊙O上，已知∠C＝65°，求∠P的度数．19．如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E 在⊙O上．若∠AOD＝52°，求∠DEB的度数．20.如图，在⊙O中，弦AB＝AC，AD是⊙O的直径．求证：BD＝CD.四、解答题(二)(每小题8分，共24分)21．如图，AB是半圆O的直径，C是半圆O上的一点，CF切半圆O于点C，BD⊥CF于点D，BD与半圆O交于点E.(1)求证：BC平分∠ABD；(2)若DC＝8，BE＝4，求AB的长．22．如图，△ABC 是⊙O 的内接三角形，AB 为⊙O 的直径，AB ＝6，AD 平分∠BAC ，交BC 于点E ，交⊙O 于点D ，连接BD . (1)求证：∠BAD ＝∠CBD ；(2)若∠AEB ＝125°，求BD ︵的长(结果保留π)．23．如图，在平面直角坐标系xOy 中，以点O 为圆心的圆分别交x 轴的正半轴于点M ，交y 轴的正半轴于点N ，劣弧MN 的长为65π，直线y ＝－43x ＋4与x轴、y 轴分别交于点A ，B . (1)求证：直线AB 与⊙O 相切；(2)求图中所示的阴影部分的面积(结果用π表示)．五、解答题(三)(每小题10分，共20分)24．如图，⊙O 为Rt △ABC 的外接圆，∠ACB ＝90°，BC ＝4 3，AC ＝4，点D是⊙O 上的动点，且点C ，D 分别位于AB 的两侧． (1)求⊙O 的半径；(2)当CD ＝4 2时，求∠ACD 的度数；(3)设AD 的中点为M ，在点D 的运动过程中，线段CM 是否存在最大值？若存在，直接写出CM 的最大值；若不存在，请说明理由．25．如图，AB 是半圆O 的直径，点D 是半圆O 上一点，点C 是AD ︵的中点，连接BC ，CE ⊥AB 于点E ，过点D 的切线交EC 的延长线于点G ，连接AD ，分别交CE，CB于点P，Q，连接AC，CD.(1)求证：GP＝GD；(2)求证：P是线段AQ的中点；(3)若CD＝2，BC＝4，求⊙O的半径和CE的长．答案一、1. B 2. A 3. C 4. A 5. C 6. A 7. D 8. A 9. B10. A 点拨：过点I 作IF ⊥AC 于点F ，IE ⊥OA 于点E .∵A (4，0)，B (0，3)，C (4，3)，∴BC ＝4，AC ＝3，则AB ＝5.∵I 是△ABC 的内心，∴I 到△ABC 各边距离相等，等于其内切圆的半径，易知IF ＝1，则AE ＝1，故I 到BC 的距离也为1，故IE ＝3－1＝2，OE ＝4－1＝3，则I (3，2)．∵△ABC 绕原点逆时针旋转90°，∴I 的对应点I ′的坐标为(－2，3)，故选A. 二、11. 60° 12. 15π 13. 60 14. 125° 15. 2 2 16. 72 17. 4 2三、18. 解：连接OA ，OB .∵P A ，PB 均是⊙O 的切线，∴P A ⊥OA ，PB ⊥OB ， ∴∠P AO ＝∠PBO ＝90°.∵∠P ＋∠P AO ＋∠AOB ＋∠PBO ＝360°， ∴∠P ＝180°－∠AOB .∵∠C ＝65°，∴∠AOB ＝2∠C ＝130°， ∴∠P ＝180°－130°＝50°. 19. 解：∵OD ⊥AB ，∴AD ︵＝BD ︵.∵∠AOD ＝52°，∴∠DEB ＝12×52°＝26°.20. 证明：∵AB ＝AC ，∴AB ︵＝AC ︵，∴∠ADB ＝∠ADC .∵AD 是⊙O 的直径，∴∠B ＝∠C ＝90°， ∴∠BAD ＝∠DAC ，∴BD ︵＝CD ︵，∴BD ＝CD . 四、21. (1)证明：连接OC ，如图．∵CD 为切线，∴OC ⊥CD .∵BD ⊥DF ，∴OC ∥BD ，∴∠1＝∠3. ∵OB ＝OC ，∴∠1＝∠2，∴∠2＝∠3， ∴BC 平分∠ABD .(2)解：连接AE 交OC 于G ，如图． ∵AB 为直径，∴∠AEB ＝90°. ∵OC ∥BD ，∴OC ⊥AE ，∴AG ＝EG . 易得四边形CDEG 为矩形， ∴GE ＝CD ＝8，∴AE ＝2EG ＝16. 在Rt △ABE 中，AB ＝162＋42＝417， 即AB 的长为417.22. (1)证明：∵AD 平分∠BAC ，∴∠BAD ＝∠CAD .又∵∠CBD ＝∠CAD ，∴∠BAD ＝∠CBD . (2)解：连接OD .∵∠AEB ＝125°，∴∠AEC ＝55°. ∵AB 为⊙O 的直径，∴∠ACE ＝90°. ∴∠CAE ＝35°.∴∠DAB ＝35°. ∴∠DOB ＝70°.∴BD ︵的长为70π×3180＝76π. 23. (1)证明：如图，作OC ⊥AB 于点C .设⊙O 的半径为r .因为劣弧MN 的长为65π，所以90πr 180＝65π， 所以r ＝125.对于直线y ＝－43x ＋4， 当x ＝0时，y ＝4，则OB ＝4. 当y ＝0时，x ＝3，则OA ＝3.在Rt△AOB中，AB＝32＋42＝5.因为S△AOB ＝12OC·AB＝12OA·OB，所以5OC＝12，OC＝125，所以OC＝r，所以直线AB与⊙O相切．(2)解：因为S△AOB＝12×3×4＝6，S扇形OMN＝90×π×⎝ ⎛⎭⎪⎫1252360＝3625π，所以S阴影＝S△AOB－S扇形OMN＝6－3625π.五、24. 解：(1)∵AB是直径，∴∠ACB＝90°.∵AC＝4，BC＝4 3，∴AB＝AC2＋BC2＝42＋（4 3）2＝8，∴⊙O的半径为4.(2)如图，连接OC，OD.∵CD＝4 2，OC＝OD＝4，∴CD2＝OC2＋OD2, ∴∠COD＝90°，∴∠OCD＝45°.∵AC＝OC＝OA，∴△AOC是等边三角形，∴∠ACO＝60°，∴∠ACD＝∠ACO－∠DCO＝60°－45°＝15°.(3)存在，CM的最大值为2 3＋2.25. (1)证明：如图，连接OD，则OD⊥GD，∠OAD＝∠ODA.又由题意易知∠ODA＋∠GDP＝90°，∠EP A＋∠EAP＝90°，∠EP A＝∠GPD，∴∠GPD＝∠GDP，∴GP＝GD.(2)证明：∵AB为直径，∴∠ACB＝90°.∵CE⊥AB，∴∠CEB＝90°，11∴∠ACE ＋∠ECB ＝∠ABC ＋∠ECB ＝90°， ∴∠ACE ＝∠ABC .∵点C 是AD ︵的中点，∴AC ︵＝CD ︵.∴∠ABC ＝∠CAD ， ∴∠ACE ＝∠CAD ，∴PC ＝P A .∵∠ACB ＝90°，∴∠CQA ＋∠CAP ＝∠ACE ＋∠PCQ ＝90°， ∴∠PCQ ＝∠CQA ，∴PC ＝PQ ，∴P A ＝PQ ，即P 是线段AQ 的中点．(3)解：∵AC ︵＝CD ︵，∴CD ＝AC .∵CD ＝2，∴AC ＝2.∵∠ACB ＝90°，∴AB ＝22＋42＝2 5.故⊙O 的半径为 5.∵S △ABC ＝12×CE ×AB ＝12×AC ×BC ，∴2 5CE ＝2×4，∴CE ＝4 55.。