菱形导学案

菱形的性质与判定 导学案第三课时一、学习准备：知识梳理1：菱形的定义： 菱形的性质： （边） （角）（对角线） （对称性）菱形的面积等于 ．知识梳理2：如图，小聪在作线段AB 的垂直平分线时，他是这样操作的：分别以A 和B 为圆心，大于1,2AB 的长为半径画弧，两弧相交于C 、D ，则直线CD 即为所求．根据他的作图方法可知四边形ADBC 一定是．．． 形，你判定的理由是： ． 归纳：二.学习目标：1．理解菱形的定义， 掌握菱形的性质和判定；2．能运用菱形的性质和判定进行简单的计算与证明． 三．自学提示： （一）自主学习：Ⅰ.菱形两条对角线、边长之间的关系：1. 如图所示，在菱形ABCD 中，两条对角线AC ＝6，BD ＝8，则： ①此菱形的边长为 ．周长为 ． ②此菱形的面积为 ．③此菱形对角线的交点O 到AB 的距离为 ．④菱形内部(包括边界)任取一点P ，使△ACP 的面积大于6 cm 2的概率为 ． 2. 已知菱形的边长是5cm ，一条对角线长为8cm ，则另一条对角线长为___ ___cm ． 3． 菱形ABCD 的周长为40cm ，两条对角线AC :BD =4:3，那么对角线AC =_____cm ，BD =_____cm ．4．若一个菱形的边长为2，则这个菱形两条对角线长的平方和为 ． （二）合作探究： 有一个内角为60°的菱形：1. 如图如图所示，在菱形ABCD 中，若AB ＝6，∠DAC ＝60°则：的平行四边形是菱形 的四边形是菱形①BD ＝ ． ②AC ＝ ． ③S 菱形ABCD ＝ ．归纳：有一个内角为60°的菱形，短的对角线等于 ；长的对角线等于 ． 2. 菱形的两邻角之比为1:2，边长为2，则菱形的面积为__________． 四、学习小结： 五、夯实基础：3. 已知：如图，菱形ABCD 中，∠B =60°，AB =4，则以AC 为边长的正方形ACEF 的周长为4．(11 南京)如图，菱形ABCD 的边长是2㎝，E 是AB 中点，且DE ⊥AB ，则S菱形ABCD=cm 2．5．(10 荷泽) 如图，菱形ABCD 中，∠B ＝60°，AB ＝2㎝，E 、F 分别是BC 、CD 的中点，连结AE 、EF 、AF ，则△AEF 的周长为 cm ．六、能力提升：已知：如图，AD 平分∠BAC ，DE ∥AB ，DF ∥AC ． 试判断四边形AFED 的形状，并加以证明．布置作业：【评价反思】自我 评价 反思学习态度 A B C D 学习效果 A B C D 合作情况 ABCD尚需改进第3题图 第4题图 第5题图。

初一数学导学案 编号：01 使用时间：2012-3-01 编制人：赵春梅 审核人： 领导签字： 班级： 小组： 姓名： 教师评价：第 1 页 共 2 页 第 2页 共2页巩固练习1．下列条件中，不能判定四边形ABCD为菱形的是（）．A．AC⊥BD，AC与BD互相平分 B．AB=BC=CD=DAC．AB=BC，AD=CD，且AC⊥BD D．AB=CD，AD=BC，AC⊥BD2．已知点A、B、C、D在同一平面内，下面列有6个条件：①AB∥CD，②AB=•CD，•③BC ∥CD，④BC=AD，⑤AC⊥BD，⑥AC平分∠DAB与∠DCB．从这6个条件中选出（•直接填写序号）___________3个，能使四边形ABCD是菱形．3．已知：如图，在平行四边形ABCD中，O为AC的中点，过点O作AC的垂线，与AD、BC 相交于点E、F，求证：四边形AFCE是菱形．（2008年四川省宜宾市）已知:如图,菱形ABCD中, E，F分别是CB，CD上的点，且BE=DF.(1)求证:AE=AF.(2)若∠B=60°,点E，F分别为BC和CD的中点，求证:△AEF为等边三角形.（2008年江苏省无锡市）如图，四边形中，，平分，交于．（1）求证：四边形是菱形；（2）若点是的中点，试判断的形状，并说明理由．已知：如图，四边形ABCD是菱形，∠ABC=30°，求证：AB2=AC·BD．如图8，在平行四边形ABCD 中，分别为边的中点，连接．（1）求证：．（5分）（2）若，则四边形是什么特殊四边形？请证明你的结论．（5分）【课堂小结】1.知识方面： _______________________________________ 。

2.数学思想方法：。

OBA E DFBACD第 3 页共 4 页第 4页共4页。

22.5 菱形的性质（1）导学案学习目标1.理解并掌握菱形的性质，会用性质进行相关的证明和计算;2.会运用菱形知识解决具体问题．一、新知探究：1.在平行四边形中，如果内角大小保持不变，仅改变边的长度，请仔细观察和思考，在这变化过程中，哪些关系没变？如果改变了边的长度，使两邻边相等，那么这个平行四边形成为怎样的四边形？由此可以得到： 叫做菱形。

所以菱形是特殊的平行四边形，它具有平行四边形的所有性质。

平行四边形的性质：○1边：__________○2角：___________; ○3对角线：____________; ○4对称性________2．动手操作：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下。

想一想，（1）阴影部分展开后，得到的四边形ABCD 是平行四边形吗？为什么？邻边AB 与CD 有怎样的数量关系？四边形ABCD 是菱形吗？为什么？（2）四边形ABCD 是轴对称图形吗？如果是轴对称图形，那么它有几条对称轴，都是哪些直线？______________________________________________________________________________ 结论：菱形即是________对称图形，又是________对称图形。

对称轴是________________（3）如图，四边形ABCD 是菱形，那么它的四条边有怎样的数量关系？如何证明这个结论？结论：______________________________证明：（4）两条对角线AC ，BD 有什么特定的位置关系？如何证明这个结论？ 结论：______________________________证明：（5）图中哪些角相等？我们得到什么结论？如何证明这个结论？ 结论：______________________________ 证明：二、归纳总结： 菱形的性质：（结合图形，写出符号语言） ○1边：菱形的两组对边 ，四条边都 。

教师学科教案[20 - 20学年度第—学期]任教学科：________________ 任教年级：________________ 任教老师：________________xx市实验学校19.3 菱形（1）、学习准备:1、_____________________________________________ 叫做平行四边形。

2、平行四边形的对边____________________ ,对角_____________________邻角________ ，对角线_____________________ 。

二、学习目标：1 •掌握菱形概念，知道菱形与平行四边形的关系.2 .理解并掌握菱形的定义及性质1和性质23、会用这些性质进行有关的论证和计算，会计算菱形的面积。

三、学习过程：活动1:看一看、做一做、想一想四边形的两组对边分别平行时四边形就是平行四边形，给平行四边形添加一些条件就可以得到一些特殊的平行四边形。

当平行四边形有一个角是直角时，它就变成矩形。

那么，给平行四边形加什么条件，它可以变成菱形呢？这些图形是平行四边形，但又不同于平行四边形。

用纸条做一做，然后想一想,平行四边形在什么情况下就变成这种图形？菱形定义：_____________________________________________ 叫菱形。

活动2:剪一剪、折一折：剪一个菱形活动3:折一折：菱形是轴对称图形吗？有几条对称轴?活动4:做一做、找一找观察对称轴之间有什么位置关系？找出里面相等的线段和角，并写出来活动5:筛一筛、选一选组内交流：把有关平行四边形的性质划去，剩余的文字用语言表述出来。

菱形的性质1：符号语言：菱形的性质2：符号语言：活动6:验一验、证一证组内交流，证明菱形的性质。

活动7:议一议菱形ABCD的对角线AC. BD相交于点@ .14AC -a. BD b,求菱形ABCD的面枳。

D菱形的面积四、课堂练习1•已知菱形的周长是12cm,那么它的边长是 _________ 。

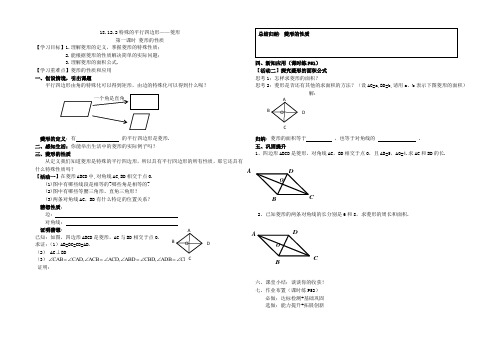
18.12.2特殊的平行四边形——菱形 第一课时 菱形的性质 【学习目标】1.理解菱形的定义，掌握菱形的特殊性质； 2.能根据菱形的性质解决简单的实际问题； 3.理解菱形的面积公式. 【学习重难点】菱形的性质和应用 一、创设情境，引出课题 平行四边形由角的特殊化可以得到矩形，由边的特殊化可以得到什么呢？ 菱形的定义：有 的平行四边形是菱形. 二、感知生活：你能举出生活中的菱形的实际例子吗？ 三、菱形的性质 从定义我们知道菱形是特殊的平行四边形，所以具有平行四边形的所有性质，那它还具有什么特殊性质吗？ 【活动一】在菱形ABCD 中,对角线AC,BD 相交于点O. (1)图中有哪些线段是相等的?哪些角是相等的? (2)图中有哪些等腰三角形、直角三角形？ (3)两条对角线AC ，BD 有什么特定的位置关系？ 猜想性质： 边：
证明猜想
求证：（1）（2） AC ⊥（3）CAB ∠
证明： 四、新知应用（课时练P51）
【活动二】探究菱形的面积公式
思考1：怎样求菱形的面积？
思考2：菱形是否还有其他的求面积的方法？（设AC=a,BD=b,请用a 、b 表示下图菱形的面积）
归纳：菱形的面积等于 ，也等于对角线的 .
五、巩固提升
1、四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，且AB=5，AO=4.求AC 和BD 的长.
2、已知菱形的两条对角线的长分别是6和8，求菱形的周长和面积.
六、课堂小结：谈谈你的收获！
七、作业布置（课时练P52）
必做：达标检测+基础巩固
选做：能力提升+拓展创新
O C B
D A O
C B
D A。

3.菱形一、基础知识梳理1. 菱形的判定定理：①四条边都相等的四边形是菱形。

②有一组邻边相等的平行四边形是菱形。

③对角线互相垂直的平行四边形是菱形。

④对角线互相垂直且平分的四边形是菱形。

2. 菱形的性质定理：①菱形四条边都相等。

②菱形对角线互相垂直且平分，并且每条对角线平分一组对角。

3. 菱形的对称性：菱形既是轴对称图形又是中心对称图形。

4. 菱形的面积：平行四边形面积法则适用于求平行面积。

两条对角线的乘积的一半。

二、典型例题2.1典型例题---菱形的基本性质例1、已知：如图所示，在菱形ABCD中，AE CD⊥，且AE=OD，求∠ADC 的度数。

AB O DEC推广1、在菱形ABCD中，已知∠ADC=120°，AC=312cm。

求BD的长；求菱形ABCD的面积。

推广2、若菱形的周长是16，两领角的度数比为1:2，则该菱形的面积是多少？例2、边长为1的菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形11DACC,使∠ACD1=60°；连接1AC，再以1AC为边做第三个菱形221DCAC，使∠12ACD =60°；……按此规律所作的第n个菱形的边长为多少？推广1、在菱形ABCD中，AE⊥BC于点E；AF⊥CD于点F；且E，F分别是BC，CD的中点，求∠EAF。

推广2、在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DE，则∠CDF等于？2.2典型例题---菱形的判定例1、△ABC中，AB=AC，AD是∠BAC的平分线，E为AD延长线上一点，CF∥BE交AD于F，连接BF、CE，求证：平行四边形BECF是菱形。

推广1、平行四边形ABCD，AC为对角线，EF垂直平分AC交AD与E点，交BC于F点；证明：四边形AFCE是菱形.E4、正方形并且每条对角线平分一组对角。

12：1.3、正方形的判定定理：（1）有一组邻边相等的矩形是正方形。

学习笔记记录区_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________人教版初中数学八年级下册18.2.4菱形的判定导学案一、学习目标：1.经历菱形判定定理的探究过程，掌握菱形的判定定理．2.会用这些菱形的判定方法进行有关的证明和计算.重点：菱形的判定定理的探究.难点：菱形的性质与判定的综合应用.二、学习过程：课前检测忆一忆1.菱形的定义：_____________________________________________.2.菱形的性质：________________________________________________________________________________________.合作探究探究：用一长一短两根细木条，在它们的中点处固定一个小钉，做成一个可转动的十字架，四周围上一根橡皮筋，做成一个四边形.转动木条，这个四边形什么时候变成菱形呢？_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________猜想：__________________________________________.已知：如图，在□ABCD 中，对角线AC、BD 相交于O 点，且BD⊥AC.求证：□ABCD是菱形.思考：我们知道，菱形的四条边相等.反过来，四条边相等的四边形是菱形吗？已知：如图，四边形ABCD，AB=BC=CD=AD.求证：四边形ABCD是菱形.【归纳】菱形的判定定理1：__________________________________________.菱形的判定定理2：__________________________________________._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________定理1几何符号语言：∵_________________________,∴_________________________.定理2几何符号语言：∵_________________________,∴_________________________.典例解析例1.如图，□ABCD 的对角线AC、BD 交于点O，且AB=5，AO=4，BO=3.求证：□ABCD是菱形.【针对练习】一个平行四边形的一条边长是9，两条对角线的长分别是12和56，这是一个特殊的平行四边形吗？为什么？求出它的面积.例2.如图，两张等宽的纸条交叉叠放在一起，重合的四边形ABCD 是一个菱形吗？为什么？_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________例3.如图,矩形ABCD 的对角线AC 的垂直平分线与边AD、BC 分别交于点E、F.求证：四边形AFCE是菱形．【针对练习】如图,在△ABC 中,AD 是角平分线,点E、F 分别在AB、AD 上,且AE=AC,EF=ED.求证：四边形CDEF是菱形.例4.如图，在▱ABCD 中，AD >AB ，∠ABC 的平分线交AD 于点F ，EF ∥AB 交BC 于点E ．(1)求证：四边形ABEF 是菱形；(2)若AB =5，AE =6，▱ABCD 的面积为36，求BC 的长．_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________【针对练习】如图，在平行四边形ABCD 中，对角线AC，BD 交于点O，过点O 作EF⊥BD，交AD 于点E，交BC 于点F，连接EB，DF．(1)求证：四边形EBFD 为菱形；(2)若∠BAD =105°，∠DBF =2∠ABE ，求∠ABE的度数．学习笔记记录区_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________达标检测1.平行四边形ABCD 中，AC，BD 是两条对角线，如果添加一个条件，即可推出平行四边形ABCD 是菱形，以下哪个条件不符合要求()A.AC⊥BDB.AC=BDC.AB=BCD.BC=CD2.顺次连接四边形ABCD 各边的中点所得的四边形是菱形，则四边形ABCD 一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形3.如图，AD 是△ABC 的中线，四边形ADCE 是平行四边形，增加下列条件，能判定□ADCE 是菱形的是()A.∠BAC=90°B.∠DAE=90°C.AB=ACD.AB=AE4.如图，已知线段AB，分别以A，B 为圆心，大于12AB 同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是()A.AB 平分∠CADB.CD 平分∠ACBC.AB ⊥CDD.AB=CD_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________5.如图，将等边三角形ABC 沿射线BC 向右平移到△DCE 的位置，连接AD，BD，则下列结论:①AD=BC；②BD，AC 互相平分；③四边形ACED是菱形.其中正确的是___________.6.一边长为5的平行四边形的两条对角线的长分别为24和26，则平行四边形的面积是_______.7.过矩形ABCD 的对角线AC 的中点O 作EF⊥AC，交BC 边于点E，交AD 边于点F，分别连接AE、CF.若AB=3，∠DCF=30°，则EF 的长为______.8.如图，在△ABC 中，AD 平分∠BAC，DF//AB，DE//AC.求证:四边形AEDF 是菱形._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________9.如图，在矩形ABCD 中，E，F，G，H 分别是AB，BC，CD，AD 的中点.求证:四边形EFGH是菱形.10.如图，△ABC 中，AC 的垂直平分线MN 交AB 于点D，交AC 于点O，CE//AB 交MN 于E，连接AE、CD.(1)求证:AD=CE;(2)填空:四边形ADCE的形状是_______，并说明理由.学习笔记记录区_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________11.如图，四边形ABCD 是菱形，∠BAD=60°，点H 为对角线AC 的中点，点E 在AB 的延长线上，CE⊥AB，点F 在AD 的延长线上，CF⊥AD.(1)求证:四边形CEHF 是菱形;(2)若四边形CEHF 的面积为18,求菱形ABCD的面积.。

《菱形的认识》导学案菱形的认识导学案一、认识菱形1. 定义菱形是一种特殊的四边形，具有以下特点：- 四条边相等，即AB = BC = CD = DA- 对角线相互垂直且相等，即AC ⊥ BD，AC = BD 2. 性质菱形具有以下性质：- 菱形的对角线相互垂直且相等- 菱形的对角线平分菱形的内角- 菱形的每条边都平分菱形的内角- 菱形的每个内角都是直角二、菱形的构造与判定1. 构造菱形的方法菱形可以通过以下方法进行构造：- 方法一：已知菱形的一个角度和一条边长，可以利用正弦定理、余弦定理等三角函数关系进行计算和绘制。

- 方法二：已知菱形的对角线长度，可以利用勾股定理和三角形的性质求解。

- 方法三：已知菱形的两条边长，可以利用几何等式和菱形的性质进行计算和绘制。

2. 判定一个四边形是否为菱形要判定一个四边形是否为菱形，可以使用以下方法：- 方法一：检查四边形的四条边是否相等，若相等则有可能是菱形，需进一步验证其他性质。

- 方法二：检查四边形的对角线是否相等，若相等则有可能是菱形，需进一步验证其他性质。

- 方法三：检查四边形的内角是否为直角，若四个内角都为直角，则为菱形。

- 方法四：检查四边形的对角线是否相互垂直，若相互垂直，则为菱形。

三、菱形在几何图形中的应用菱形在几何图形中有广泛的应用，例如：- 作为宝石、切割草坪等的装饰图案。

- 作为棋盘格的基本图案。

- 作为某些建筑物的外观设计元素。

- 用于设计图案、标志等的基本形状。

四、小结通过本次导学案的学习，我们对菱形的定义、性质、构造与判定以及在几何图形中的应用有了更深入的认识。

菱形在几何学中具有许多重要的性质和用途，对于几何学的学习和实际应用都有着重要意义。

菱形的判定-导学案(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--菱形的判定导学案【学习目标】1．理解并掌握菱形的定义及两个判定方法；会用这些判定方法进行有关的论证和计算；2．在菱形的判定方法的探索与综合应用中，培养学生的观察能力、动手能力及逻辑思维能力．【学习重难点】菱形的两个判定方法．【学习过程】一、温故互查：1．菱形的定义：2.菱形的性质：边：__________________________;______________________________角：__________________________;______________________________对角线：______________________________________________________对称性：二、设问导读：探究一：如图，四边形是菱形吗为什么归纳：有一组邻边相等的平行四边形是菱形探究二：用一长一短两根木条，在它们的中点处固定一个小钉，做成一个可转动的十字，四周围上一根橡皮筋，做成一个四边形．转动木条，这个四边形什么时候变成菱形？通过探究，容易得到：对角线的平行四边形是菱形证明上述结论：探究三：李芳同学先画两条等长的线段AB、AD，然后分别以B、D为圆心，AB为半径画弧，得到两弧的交点C，连接BC、CD，就得到了一个四边形，猜一猜，这是什么四边形？请你画一画。

通过探究，容易得到：的四边形是菱形证明上述结论：例1. 如图，ABCD的两条对角线AC、BD相交于点O，AB= 5 ，AC=8，DB=6求证:四边形ABCD是菱形.三、自主检测1.判断题，对的画“√”错的画“×”(1).对角线互相垂直的四边形是菱形（ ）(2).一条对角线垂直另一条对角线的四边形是菱形（ ）(3)..对角线互相垂直且平分的四边形是菱形（ ）(4).对角线相等的四边形是菱形（ ）2. （2011福建省三明市，14,4分）如图，▱ABCD 中，对角形AC ，BD 相交于点O ，添加一个条件，能使▱ABCD 成为菱形．你添加的条件是（不再添加辅助线和字母3. （2011•贵港）如图所示，将两张等宽的长方形纸条交叉叠放，重叠部分是一个四边形ABCD ，若AD=6cm ，∠ABC=60°，则四边形ABCD 的面积等于四.巩固提高：1.已知：如图ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ．求证：四边形AFCE 是菱形．2.如图，在四边形ABCD 中，AB ＝CD ，M ，N ，P ，Q 分别是AD ，BC ，BD ，AC 的中点． 求证：MN 与PQ 互相垂直平分。

菱形导学案2.2菱形（二）年级：九年级学科：数学课型：新授课时间：年月日执笔：太和县马集中心校审核：马集中心校数学导学案审核组课后反思【励志语录】1、不要慨叹生活底痛苦！--慨叹是弱者...—高尔基2、成功不是将来才有的，而是从决定去做的那一刻起，持续累积而成。

3、成功需要成本，时间也是一种成本，对时间的珍惜就是对成本的的节约。

【学习目标】学法指导：仔细阅读，做到有的放矢。

1、能证明菱形的两个判定定理。

2、会用菱形的定义、判定方法判定一个四边形是菱形、有关计算。

3、培养观察能力、动手能力自学能力、计算能力、逻辑思维能力。

【重点】菱形的判定定理的探究与应用。

一、知识链接：1、什么叫做平行四边形？什么叫做菱形？2、菱形有哪些性质？3、菱形与平行四边形有什么共同之处？有什么不同之处？4、两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是菱形吗？二、教材预习学法指导：课前独学教材预习内容，总结本节课的重点、难点、注意点。

课堂再以小组为单位交流，找出还存在的问题，并在小黑板上扼要展示本节重点内容和存在的问题。

注意双色笔的使用，书写工整。

1、预习内容：自学课本99页—100页，完成P100练习1、2、3。

2、预习测试：1）从定义出发可知有的平行四边形是菱形。

除此之外，我们可以通过研究菱形性质定理的逆命题得到菱形的其他判定方法：判定定理1：的平行四边形是菱形。

或的四边形是菱形。

几何语言为：。

判定定理2：。

几何语言为：。

4）用以前学过的知识证明：判定定理1判定定理2合作探究学法指导：课前独学，解决会的，有问题的上课对子或小组交流，形成共识，进行课堂大展示。

展示时要讲清所用知识点、易错点。

展示到小黑板的题要标清所用知识点、易错点；注意双色笔的使用，字体工整。

探究点一：判定的应用下列各句判定菱形的说法是否正确？为什么？1 用两个边长为a的等边三角形纸片拼成的四边形是菱形（）2有一组邻边相等的四边形是菱形（）3对角线互相垂直的四边形是菱形（）4对角线互相平分垂直的四边形是菱形（）5一条对角线平分一组对角的四边形是菱形（）总结：（l）所给四边形添加的条件不满足三个的肯定不是菱形；（2）所给四边形添加的条件是三个独立条件，但若与判定方法不同，则需要利用定义和判定方法证明或举反例，才能下结论．探究点二：判定定理1的应用1 、（教材P109的例3）2、已知：如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．探究点三：判定定理2的应用已知：如图，△ABC中，∠ACB=90°，BE平分∠ABC，CD⊥AB与D，EH⊥AB于H，CD交BE于F．求证：四边形CEHF为菱形．探究点四：判定定理的实际应用做一做：设计一个由菱形组成的花边图案．花边的长为15 cm，宽为4 cm，由有一条对角线在同一条直线上的四个菱形组成，前一个菱形对角线的交点，是后一个菱形的一个顶点．画出花边图形．四．小结提升学法指导： 1、对照学习目标找差补缺。