实验三+霍尔位置传感器测定杨氏模量

用霍尔位置传感器测杨氏模量用霍尔位置传感器测量材料的杨氏模量利用霍尔位置传感器和弯曲法测量杨氏模量实验数据杨氏模量测量实验报告随着科技进步的蓬勃发展，微位移测量这一核心技术也日趋先进。

本次测试揭示了业界近年开发的先进霍尔位置传感器。

它通过电磁铁和集成霍尔元件之间不断变化的负载信号来测量微小的偏转。

这种控制技术主要用于杨氏弯曲法。

杨氏模量测试。

在此实验室报告中，模具的杨氏模量是使用霍尔位置传感器测量的。

合金铸铁的杨氏模量采用弯曲法测定。

除了测量铜的杨氏模量外，还要校准霍尔位置传感器以解决其精度问题。

利用霍尔位置传感器测量铁的杨氏模量等。

利用实验可以使学生增强对霍尔传感器基本原理的广泛应用、科学院新型传感器的标定、以及不同长度值的测量方法。

传感器法测量位移有什么优点霍尔位置传感器和弯曲法测量杨氏模量实验数据弯曲法测量杨氏模量实验中的主要测量值有哪些。

请计算每个环境因素的不确定性。

传感器测量位移的方法有什么特点？建议】使用千分尺时，2.使用高度计光学测量重物刀口架基线位置时，刀口架不能晃动。

4.使用霍尔位置霍尔传感器及弯曲法杨氏模量测量实验报告方法本实验在弯曲法良好基础上安装霍尔位置测量杨氏模量液态金属材料的模量。

传感器。

通过对霍尔位置传感器的输入阻抗与位移的微分关系的标定和微小位移的测量，使学生了解和掌握微小位移的非电测量新方法。

微位移测量技术也得到快速发展霍尔位置传感器标定及弯曲法测量杨氏模量误差分析SUES大学物理选修实验讲座笔记磁弯曲法测量杨氏模量及霍尔位置传感器校准随着科技进步的蓬勃发展，微挠度测量的电子技术也给经济带来了飞速的发展。

本科学实验介绍了近年来出现的新型先进霍尔位置传感器，利用负载的回波来测量电磁铁与霍尔传感器之间位置变化的微小偏移量。

该科学实验结合了电子技术测量金属梁的微小位移、霍尔位置传感器的校准和弯曲法测量铝的杨氏模量。

通过实验报告，小学生可以加深对霍尔传感器广泛应用的认识，学习新型传感器的标定、不同取值宽度的测量和不同宽度测量设备的采用。

霍尔位置传感器法杨氏模量的测定1．拉伸法测量杨氏模量
◆原理：本实验采用光杠杆放大法进行测量。

弹性杨氏模量是反映材料形变与内应力关系的物理量，实验表明，在弹性范围内，正应力（单位横截面积上垂直作用力与横截面积之比，）与线应变（物体的相对伸长）成正比，即
这个规律称为虎克定律。

式中的比例系数称为杨氏模量，单位N/m2。

◆提问：一个不规则形状的刚性材料，应该如何测量其杨氏模量？
◆提问：拉伸法测量杨氏模量，除了用光杠杆法测量钢丝的微小伸长量之外，还需要什么测量工具？
◆公式：，式中叫做光杠杆的放大倍数。

2．测量圆环的转动惯量
◆结构：三线摆是上、下两个匀质圆盘，通过三条等长的摆线（摆线为不易拉伸的细线）连接而成。

◆原理：三线摆的摆动周期与摆盘的转动惯量有一定关系，所以把待测样品放在摆盘上后，三线摆系统的摆动周期就要相应地随之改变。

这样，根据摆动周期、摆盘质量以及有关的参量，就能求出摆动系统的转动惯量。

◆公式：
◆学生在实验过程中容易出现的问题：
1．三线摆、扭摆没有调水平；
2．测量转动惯量时摆角大于5度；
3．光电门的摆放位置不是在三线摆、扭摆的摆动时平衡位置附近；
4．在拉伸法测量杨氏模量实验中，学生误将望远镜的读数看成是钢丝的伸长量。

实验名称霍尔传感器测杨氏模量【实验目的】1．了解霍尔位置传感器的结构原理、特性及使用方法。

2．学习掌握粱弯曲法测量金属板的杨氏弹性模量。

3．学会确定灵敏度的方法，并确定仪器的灵敏度。

4．掌握逐差法处理数据。

【实验仪器】霍尔位置传感器、霍尔位置传感器输出信号测量仪、游标卡尺、螺旋测微器。

【实验原理】霍尔传感器置于磁感应强度为B 的磁场中，在垂直于磁场的方向通入电流I ，则会产生霍尔效应，即在与这二者相互垂直的方向上将产生霍尔电势：IB K U H H = (5.2.1)其中H K 为霍尔传感器的灵敏度，单位为T mA mV ⋅。

如果保持通入霍尔元件的电流I 不变，而使其在一均匀梯度的磁场中移动，则输出的霍尔电势的变化量为：z dzdBIK U H H ∆=∆ (5.2.2) 其中：z ∆为位移量；dzdB为磁感应强度B 沿位移方向的梯度，为常数。

为了实现上述均匀梯度磁场，选用两块相同的磁铁。

磁铁平行相对而放，即N 极相对放置。

两磁铁之间的空隙内放入霍尔元件，并使此元件平行于磁铁，且与两磁铁的间距相等，即霍尔元件放置两磁铁空隙的中心，如图6.1所示。

若间隙中心截面的中心点A 的磁感应强度为零，霍尔元件处于该处时输出的霍尔电势应为零。

当霍尔元件偏离中心沿Z 轴发生位移，由于磁感应强度不再为零，霍尔元件也就有相应电势输出，其大小可由数字电压表读出。

一般地，将霍尔电势为零时元件所处的位置作为位移参考点。

霍尔电势与位移量之间存在一一对应的关系，当位移量较小时（小于2mm ），对应关系具有良好的线性，如图6.2所示。

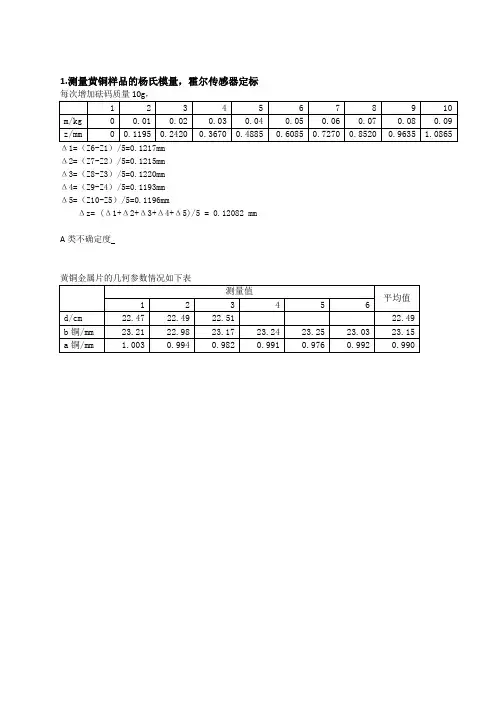
mm在粱弯曲的情况下，杨氏模量E 用下列公式计算：zb a mg d E ∆=334 (6.1)式中：d 为两刀口间的距离，a 为粱的厚度，b 为粱的宽度，m 为砝码的质量，g 为重力加速度（2792.9s m g =），z ∆为粱中心由于外力的作用而下降的距离。

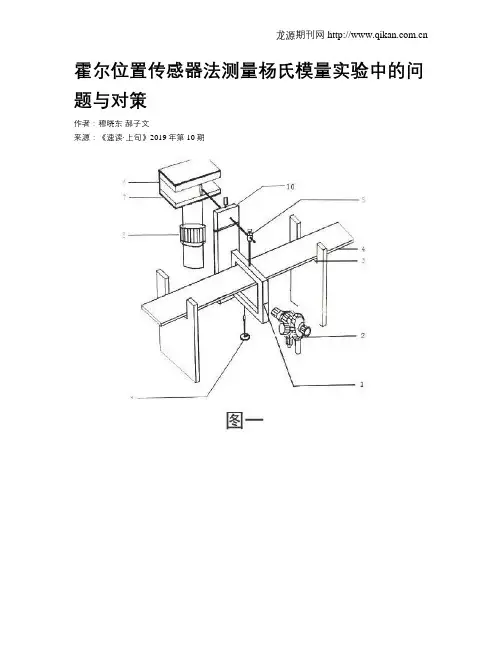
【实验装置】杨氏模量实验装置如图6.3所示。

霍耳位置传感器法测杨氏模量一、实验内容：1.了解霍耳效应及霍耳位置传感器的原理2.学会使用霍耳位置传感器法测杨氏模量二、实验仪器：杨氏模量测试仪、千分尺、游标卡尺三、实验原理：1．霍耳元件置于磁感应强度为B 的磁场中，在垂直于磁场方向通以电流I ，则与这二者平面垂直的方向上产生霍耳电势差：B I K U H ⋅⋅= （1）上式中K 为元件的霍耳灵敏度。

如果保持霍耳元件的电流I 不变，而使其在一均匀梯度的磁场中移动时，则输出的霍耳电势差变化量为：（2）杨氏模量测试仪上式中Z ∆为位移量，此式说明若dZdB 为常数时，U ∆与Z ∆成正比。

2．一段固体棒，在其两端沿轴发现施加大小相等、方向相反的外力F ，其长度L 发生改变L ∆，以S 表示横截面面积，称F/S 为胁强，相对长变L ∆/L 为胁变。

在弹性限度内，由胡克定律有：E 称为杨氏模量，其数值与材料性质有关。

在横梁受力弯曲的情况下，杨氏模量E 得测量表达式为：（3）其中：d 为两刀口之间的距离；M 为所加砝码的质量；a 为梁的厚度；b 为梁的宽度；Z ∆为梁中心由于外力作用而下降的距离；g 为重力加速度。

四、实验步骤：1．调节三维调节架的上下前后位置的调节螺丝，使传感器探测元件处于磁铁中间位置。

2．用水准器观察是否在平衡位置，若偏离可用底座螺丝调节到水平位置。

3．调节霍耳位置传感器的毫伏表。

磁铁盒可上下调节调节螺丝使磁铁上下移动，当毫伏表读数值很小时，停止调节并固定螺丝，最后调节零电位器使毫伏表读数为零。

4．调节读数显微镜，使眼睛观察十字线及分划板刻度线和数字清晰。

然后移动读数显微镜前后位置，使能清晰看到铜刀上的基线。

转动读数显微镜的鼓轮使刀口架上的基线与读数显微镜内十字刻度线重合，记下初始读数值。

5．逐次增加砝码，每次增加10.00g ，相应从读数显微镜读出梁中心的位置i Z （mm ）及毫伏表的读数i U （mv ）。

然后依次减少砝码，每次减少10.00g ，做同样的记录。

一、实验目的1. 了解霍尔位置传感器的结构原理、特性及使用方法。

2. 掌握霍尔位置传感器法测量金属板的杨氏弹性模量的实验方法。

3. 学会确定灵敏度的方法，并利用霍尔位置传感器进行杨氏模量的精确测量。

二、实验原理杨氏模量（E）是材料在弹性变形范围内应力（σ）与应变（ε）之比，即 E = σ/ε。

霍尔位置传感器是一种基于霍尔效应的传感器，它能够将微小的位移转化为电信号输出。

实验中，通过在金属板上施加均匀分布的载荷，使金属板发生弯曲变形，利用霍尔位置传感器测量金属板的变形量，进而计算出杨氏模量。

三、实验仪器与材料1. 霍尔位置传感器2. 金属板3. 载荷4. 读数显微镜5. 调节架6. 导线7. 电源8. 计算器四、实验步骤1. 将金属板放置在调节架上，确保金属板水平。

2. 将霍尔位置传感器固定在金属板上，传感器应垂直于金属板表面。

3. 通过导线将霍尔位置传感器与电源连接。

4. 调节电源，使霍尔位置传感器输出电压稳定。

5. 在金属板上施加均匀分布的载荷，使金属板发生弯曲变形。

6. 利用读数显微镜测量金属板的变形量。

7. 记录霍尔位置传感器的输出电压。

8. 重复步骤5-7，进行多次测量，取平均值。

五、数据处理1. 计算金属板的应变：ε = Δl/l0，其中Δl为金属板的变形量，l0为金属板的原始长度。

2. 计算金属板的应力：σ = F/A，其中F为载荷，A为金属板的横截面积。

3. 计算杨氏模量：E = σ/ε。

六、实验结果与分析通过实验，得到金属板的杨氏模量E的平均值为E_avg = 2.34 GPa。

与理论值相比，实验结果存在一定的误差，这可能是由于实验过程中存在测量误差、环境因素等影响。

七、实验总结1. 霍尔位置传感器法是一种简单、有效的测量杨氏模量的方法。

2. 实验过程中，要注意霍尔位置传感器的安装和调整，确保其输出电压稳定。

3. 实验结果受多种因素影响，如测量误差、环境因素等，应尽量减少这些因素的影响，以提高实验精度。

霍尔位置传感器法测杨氏模量实验报告实验报告：一、实验目的1.了解霍尔位置传感器法测量杨氏模量的原理。

2.掌握霍尔位置传感器法测量杨氏模量的实验方法。

3.测量材料的杨氏模量，加深对杨氏模量的认识。

二、实验器材1.霍尔位置传感器2.弹性体（橡胶或金属杆子）3.支架4.螺旋测微仪5.示波器6.直流电源7.电压表8.安培表三、实验原理在伸缩杆的中心填补一段塑料棒，使其成为一个弹性体，两端分别固定在两个支架上，称为悬臂梁。

然后在弹性体的表面，通过霍尔位置传感器来缓慢施加扭矩，从而引起弹性体的弯曲。

测量弯曲处的张力和应变，然后通过计算得到杨氏模量。

四、实验步骤1.将弹性体安装在支架上，利用螺旋测微仪来控制扭矩。

2.打开示波器和直流电源，将霍尔位置传感器连接到电源和示波器上。

3.将电压表和安培表连接到电路上，分别用于测量电压和电流。

4.打开电源，调节示波器和螺旋测微仪，使扭矩慢慢施加。

5.在不同的扭矩下，测量弹性体的应变和张力，记录下数据。

6.根据数据计算得到实验结果。

五、实验数据1. 霍尔传感器（v/gs）= 16.67 mV/V2. 实验质量m = 0.5 kg3. 称重表读数F = 10 N4. 弹簧钢圆柱体直径D = 9.8 mm5. 弹簧钢圆柱体长度L = 275 mm6. 以悬臂处为零点时，弹性体的长度L0 = 200 mm7. 悬臂处到霍尔位置传感器的距离L1 = 46 mm8. 扭矩T（N·m）弯曲位移δ（mm）应变ε 张力σ （MPa）伸长率ΔL/L00 0 0 0 00.05 0.9 1.805×10^-5 398325.9 0.00450.1 1.8 3.625×10^-5 796651.9 0.0090.15 2.9 5.475×10^-5 1212527 0.01450.2 4 7.3×10^-5 1599510 0.0190.25 5.2 9.8×10^-5 2010036 0.0240.3 6.5 1.27×10^-4 2443367 0.0290.35 8 1.575×10^-4 2910502 0.0340.4 9.5 1.9×10^-4 3420175 0.0390.45 11.2 2.255×10^-4 3973963 0.0440.5 13 2.625×10^-4 4571876 0.049六、实验结果分析通过实验结果，我们可以得到弹性体的应变与张力之间的关系，进而算出杨氏模量。

霍耳位置传感器法测杨氏模量一、实验目的1．了解和掌握微小位移量的非电量电测方法。

2．弯曲法测黄铜的杨氏模量。

3．对霍耳传感器进行定标,测量可锻铸铁的杨氏模量。

二、实验仪器FD-HY-I 型霍耳位置传感器测杨氏模量装置，霍耳位置传感器输出信号测量仪。

三、实验原理1．霍耳元件置于磁感应强度为B 的磁场中，在垂直于磁场方向通以电流I ，则与这二者垂直的方向上将产生霍耳电势差H U ：IB K U H 0= （1）上式中0K 为霍耳元件的灵敏度。

如果保持霍耳元件的电流I 不变，而使其在一个均匀梯度的磁场中移动时，则输出的霍耳电势差变化量为：Z dZ dBIK U H ∆=∆0 （2） 上式中Z ∆为位移量，此式说明若dZdB为常数时，U ∆与Z ∆成正比。

为实现均匀梯度的磁场，可以如图1所示两块相同的磁铁（磁铁截面积及表面磁感应强度相同）相对放置，即N 极与N 极相对，两磁铁之间留一等间距间隙，霍耳元件平行于磁铁放在该间隙的中轴上。

间隙大小要根据测量范围和测量灵敏度要求而定，间隙越小，磁场梯度就越大，灵敏度就越高。

磁铁截面要远大于霍耳元件，以尽可能的减小边缘效应影响，提高测量精确度。

若磁铁间隙内中心截面处的磁感应强度为零，霍耳元件处于该处时，输出的霍耳电势差应该为零。

当霍耳元件偏离中心沿Z 轴发生位移时，由于磁感应强度不再为零，霍耳元件也就产生相应的电势差输出，其大小可以用数字电压表测量。

由此可以将霍耳电势差为零的元件所处的位置作为位移参考零点0Z 。

霍耳电势差与位移量之间存在一一对应关系，当位移较小（< 2mm ），这一一对应关系具有良好的线性(即Z K U ∆⋅=,)0Z Z Z i -=∆)。

2．在横梁弯曲的情况下，杨氏模量E 可以用下式表示：Zb a Mgd E ∆334= （3）其中：d 为两刀口之间的距离；M 为所加砝码的质量；a 为梁的厚度；b 为梁的宽度；Z ∆为梁中心由于外力作用而下降的距离；g 为重力加速度。

《霍尔位置传感器法测量杨氏模量》实验要求与指引z 实验预习要求：（实验前完成）1、 明确本实验要求做的内容（①黄铜样品的杨氏模量Zb a Mg d E ∆⋅⋅⋅=334铜（其中ΔZ 用读数目镜测量）和对霍尔位置传感器的定标（ZUK ∆∆=）②用霍尔位置传感器测量可锻铸铁的杨氏模量Zb a Mgd E ∆⋅⋅⋅=334铁（其中ΔZ 用定标后的霍尔位置传感器测量））；2、 阅读实验原理部分，弄懂（1）什么叫霍尔效应？（2）霍尔位置传感器测量微小位移的原理（Z K Z dZdBI K U H H ∆⋅′=′∆⋅⋅⋅=∆）；（3）横梁弯曲法测量金属材料杨氏模量的原理（Zb a gM d E ∆⋅⋅⋅⋅=334，公式中各物理量的意义，其中△Z 本实验中用什么方法测量）；【注意：实验书中，（50-3）式的Z ′∆与（50-4式的Z ∆相同吗】图50-2 霍尔位置传感器法杨氏模量实验仪的结构1．铜刀架的基线 2．读数显微镜3．立柱刀口 4．横梁 5．金属杠杆（顶端装有95A 型集成霍尔传感器） 6．磁铁盒 7．磁铁（N 极相对放置） 8．调节架9．套筒螺母 10．砝3、 阅读【实验内容与步骤】，弄懂并掌握仪器的调整和测量方法和步骤；4、 阅读【注意事项】5、 写好预习报告（预先写好实验报告里的实验目的、实验仪器、实验原理（要有文字描述、有关公式）、实验主要步骤等部分以及在预习报告纸上设计画好实验数据的记录表格和做好要求做的【预备问题】的1、2、3。

z 实验测量要求1、 实验内容1（仪器调整）要求在10分钟内完成；2、 实验内容2（测量黄铜样品的杨氏模量和霍尔位置传感器的定标）要求在45分钟内完成；3、 实验内容3（用霍尔位置传感器测量可锻铸铁的杨氏模量）要求在30分钟内完成：4、 数据处理；（课后完成，写在实验报告上）按要求△Z 用逐差法数据计算，霍尔位置传感器的定标系数（霍尔位置传感器的输出灵敏度）K 要求用最小二乘法处理数据计算；5、 做思考题1、4。