高一数学模拟试题(必修三必修四)

高一数学下期期末测试试卷(考试时间:120分钟 满分:150分)一、选择题(每小题5分,共60分)在每小题给出的四个选项中,只有一个是符合题目要求的,请将正确选项的代号填在题后的括号中.)1.给出下列关系式：sin1>sin2,cos(-21)>cos 31,tan125°>tan70°, sin1213π>cos 1213π,其中正确的个数是 （ ） A 、1 B 、2 C 、3 D 、4 2.如果f(x+π)=f(-x),且f(x)= f(-x),则f(x)可能是( )A 、sin2x Bcosx C 、sin|x| D 、|sinx|3.关于函数图象的变化，正确的结论是 （ ）A 、将图象y=sin(2x-4π)向右平移4π，得图象y=sin2x B 、将图象y=sin(2x-4π)上的每一点的纵坐标不变，横坐标变为原来的21，得 图象y=sin(x-4π) C 、将图象y=f(x)按向量=(h,k)平移得图象y=f(x-h)-kD 、将图象y=f(x)先按向量平移，再按向量平移，且+=(-1,2)，则得到的图象为y=f(x+1)+24.在△ABC 中，A 、B 、C 的对边分别是a 、b 、c ，则acosB+bcosA 等于 （ ）A 、2cosCB 、2sinC C 、2b a + D 、c 5.不重合的四点A 、B 、C 、D 满足：2AB =3AC ，AB =-2BD ，则点D 分BC 之比为 （ ）A 、3B 、-3C 、31D 、-31 6.设，，是任意的非零平面向量，且两两不共线，下列命题其中正确的有 （ ）A 、①② B、②③ C、③④ D、②④7.已知OA =(-3,4),AB =(13,-4)，则AB 在OA 上的投影为 （ ）A 、11B 、-11C 、18555D 、-185558.已知AB =(3,-2), AC =(k,3)，且△ABC 为直角三角形，则实数k 的值为 （ ）A 、2B 、319C 、不存在D 、2或319 9.在△ABC 中，已知b 2-bc-2c 2=0，且a=6,cosA=87，则△ABC 的面积为 （ ） A 、215 B 、15 C 、2 D 、3 10.在△ABC 中,tanA+tanB+tanC>0,则△ABC 是( )A 、 锐角三角形B 、 钝角三角形C 、直角三角形D 、任意三角形11.已知m 、n 是夹角为60°的两个单位向量,则a =2m +n 和b =-3m +2n 的夹角为（ ）A 、30° B、60° C、120° D、150°12.在△ABC 中,sinA:sinB:sinC=2:6:(3+1),则三角形的最小内角是( )A 、60° B、45° C、30° D、以上答案都不对二、填空题(每小题4分,共16分)请将你认为正确的答案直接填在题后的横线 上.13.已知cos(4+x)=53,1217π<x<47π，则tanx=____________. 14.计算cos15°cos75°+cos 215°=_____________.15.已知△ABC 中，a=1,b=3，A=30°，则B=____________.16.在正六边形ABCDEF 中，若AB =a ，CD =b ，则CB =______________.三、解答题(本题共6个小题,共74分)解答应写出文字说明、证明过程或演算 步骤).17.(12 分) 已知△A BC 三顶点的坐标分别为A(2,1),B(0,3),C(-1,5),AD 为边BC 上的高。

高一数学下学期期末模拟考试卷（1）4. 矩形ABCD 中，对角线AC 与BD 交于点0, BC = 5e 「DC = 3e 2 ,则OC 等于（12.在地上画一正方形线框，其边长等于一枚硬币的肓径的2倍，向方框屮投掷硬币，硬币完全落在正方形外的不计, 则硬币完全落在正方形内的概率为 （ ）1. 2. 3.一、选择题：本人题共12小题，每小题5分， 1920°转化为孤度数为 A 16n 32A. —B.— 3 3C. 共60分。

在每小题给出的四个选项中,）32 —713 只有一项的符合题日要求的。

16 —713 D .根据一组数据判断是否线性相关时，应选用 A.散点图B.茎叶图C.频率分布直方图7T函数y = sin （x + —）的一个单调增区间是 D .（频率分布折线图 A.[―不0]71B. [0,-]D.1 一 一 A- — (5e. +3e ?)2 -] 一 一B. — (5ej -3e 2)1 一 一 C. 严+3e2）1 一 一D. 一 — (5e. +3e 2)25.某单位有老年人28人，中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽 取一个容量为36样木，则老年人、A. 6, 12, 18B. 7, 11, 19C. 6, 13, 17D. 7, 12, 17 7.甲乙两人下棋，甲获胜的概率为30%,甲不输的概率为70%,则甲乙两人F —盘棋，最可 能出现的情况是（ ）A.甲获胜B.乙获胜C.二人和棋D.无法判断&如图是计算丄+丄+丄+…+丄的一个程序框图，其中在判断框内应填入的条件是（）2 4 6 20A. i>10B. i<10C. i>20D. i<209. 函数y = 3 + 4sin 尢+ cos2x 的授大值是（）（ ）A. 0B. 3C. 6D. 810. 2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角 形与屮间的小正方形拼成的一人止方形，若直角三角形屮较小的锐角为&,大正方形的面积 是1,小正方形的而积是丄JlJsin 2^-cos 2 &的值等于 （ ）A. 1B. _24C. 7D. 725 252511・已知制=2血,同= 3,pq 的夹角为彳，如图，若而= 5p + 2g, AC = p- 3q 、D 为BD 的中点, 则AD 为B.C. 7D. 18cA. —B. —C. — D ■ ---------4 816 32 +龙 第二卷 （选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分。

高一数学必修3、4试题（含答案）桦甸八中2012-2013学年度下学期第二次阶段性考试高一数学试题本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分，试卷共4页，满分150分，考试时间120分钟。

第I 卷（共60分）一. 选择题：（本题包括12小题，每小题5分，共60分.每小题只有一个选项符合题意）1、sin 390?=（）A12 B 2C 2- 2、下列选项中是函数sin y x =图象的对称轴和对称中心是（）A 34x π=；(,0)2π B x π=；(,0)4π C 2x π=；(0,0) D 0x =；(0,)4π3、312,cos ,sin ,sin()513αβαβαβ==+=已知为锐角，则( ) A1665 B 5665C 98D 234、羊村村长慢羊羊决定从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊去割草，则喜羊羊和美羊羊恰好只有一只被选中的概率为( )A 310B 67C 35D 455、某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了调查社会购买力的某项指标，要从中抽取一个容量为100的样本，记作①；某学校高一年级有12名女排球运动员，要从中选出3个调查学习负担情况，记作②.那么完成上述两项调查应采用的抽样方法是( )A ①用简单随机抽样法，②用系统抽样法B ①用分层抽样法，②用简单随机抽样法C ①用系统抽样法，②用分层抽样法D ①用分层抽样法，②用系统抽样法 6、已知x 、y 的取值如下表所示：如果y 与x 呈线性相关，且线性回归方程为y ＝bx ＋132，则b ＝( )A －12B 12C －110D1107、下图给出的是计算12＋14＋16＋…＋1100的值的一个程序框图，其中判断框内应填入的条件是( )A i >100?B i ≤100?C i >50?D i ≤50? 8、设函数f (x )＝cos 2(x ＋π4)－sin 2(x ＋π4)，x ∈R ，则函数f (x )是( )A 最小正周期为π的奇函数B 最小正周期为π的偶函数C 最小正周期为π2的奇函数D 最小正周期为π2的偶函数9、下列关系式中正确的是( )A sin11°<cos10°<sin168°< p="">B sin168°<sin11°<cos10°< p="">C sin11°<sin168°<cos10°< p="">D sin168°<cos10°<="" p="">要得到函数3sin(2)3y x π=+的图象，只需将函数3sin 2y x =的图象（）A 向左平移3π个单位 B 向右平移3π个单位 C 向右平移12π个单位 D 向左平移6π个单位 11、函数y ＝sin(ωx ＋φ)(x ∈R ，ω>0,0≤φ<2π)的部分图象如图，则( )A ω＝π2，φ＝π4B ω＝π3，φ＝π6C ω＝π4，φ＝π4D ω＝π4，φ＝5π412、定义在R 上的奇函数()f x 是周期函数，其最小正周期是π且当[0,]2x π∈时，2()sin sin f x x x =+，则函数的值域（）A [1,1)- [2,2]- Ｃ [0,2] D [1,2]第II 卷（非选择题共90分）二.填空题（本大题共4小题，每小题5分，共20分。

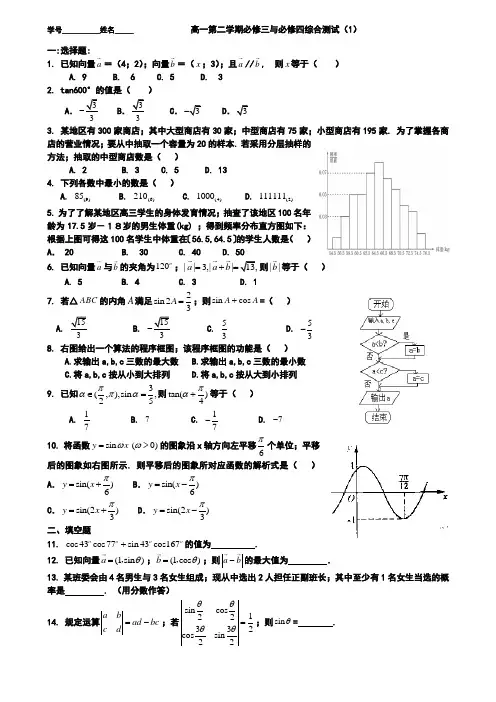
学号__________姓名_____ 高一第二学期必修三与必修四综合测试（1）一:选择题:1. 已知向量a ＝（4；2）；向量b ＝（x ；3）；且a //b , 则x 等于（ ） A. 9 B. 6 C. 5 D. 32. tan600°的值是（ ）A ．33-B ．33C ．3-D ．3 3. 某地区有300家商店；其中大型商店有30家；中型商店有75家；小型商店有195家. 为了掌握各商店的营业情况；要从中抽取一个容量为20的样本. 若采用分层抽样的方法；抽取的中型商店数是（ ）A. 2B. 3C. 5D. 13 4. 下列各数中最小的数是（ ）A. (9)85B. (6)210C. (4)1000D. (2)1111115. 为了了解某地区高三学生的身体发育情况；抽查了该地区100名年龄为17.5岁－１８岁的男生体重(kg) ；得到频率分布直方图如下：根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是（ ） A ． 20 B. 30 C. 40 D. 506. 已知向量a 与b 的夹角为120o ；||3,||13,a a b =+=则||b 等于（ ）A. 5B. 4C. 3D. 17. 若△ABC 的内角A 满足2sin 23A =；则sin cos A A +=（ ） A.153 B. 153- C. 53 D. 53- 8. 右图给出一个算法的程序框图；该程序框图的功能是（ ）A.求输出a,b,c 三数的最大数B.求输出a,b,c 三数的最小数C.将a,b,c 按从小到大排列D.将a,b,c 按从大到小排列9. 已知3(,),sin ,25παπα∈=则tan()4πα+等于（ ）A.17 B. 7 C. 17- D. 7- 10. 将函数sin (0)y x ωω=>的图象沿x 轴方向左平移6π个单位；平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是（ ） A ．sin()6y x π=+B ．sin()6y x π=-C ．sin(2)3y x π=+ D ．sin(2)3y x π=- 二、填空题11. cos43cos77sin 43cos167o o o o +的值为 . 12. 已知向量(1sin )a θ=，；(1cos )b θ=，；则a b -的最大值为．13. 某班委会由4名男生与3名女生组成；现从中选出2人担任正副班长；其中至少有1名女生当选的概率是 . （用分数作答）14. 规定运算a bad bc c d=-；若sincos122332cossin22θθθθ=；则sin θ= .15、一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ . 三、解答题16． 已知4,3a b ==；(23)(2)61a b a b -+=；（1）求a 与b 的夹角θ； （2）若(1,2)c =；且a c ⊥；试求a .17. （一）小题: 甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为12和13, 求: (1)甲、乙两人至少有一个人破译出密码的概率; (2)两人都没有破译出密码的概率.（二）小题：玻璃球盒中装有各色球12只；其中5红、4黑、2白、1绿.（1）从中取1个球, 求取得红或黑的概率；（2）从中取2个球；求至少一个红球的概率.（三）小题：若以连续掷两次骰子分别得到的点数m 、n 作为点P 的坐标(,)m n ；则点P 在圆2225x y +=外的概率是多少?18（一）小题：. 对任意正整数n ；设计一个求Ｓ＝111123n++++的程序框图；并编写出程序.（二）小题：假设关于某种设备的使用年限x 和支出的维修费用y （万元）；有以下的统计资料：（1）画出散点图； （2）求支出的维修费用y 与使用年限x 的回归方程； （3）估计使用年限为10年时；维修费用是多少？19. 已知函数1cos 222x xy =+. （1）用五点法画出它在一个周期内的闭区间上的图象； （2）说明此函数图象可由sin y x =上的图象经怎样的变换得到；（3）由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.20．设向量a ＝(sinx ；cosx)；b ＝(cosx ；cosx)；x ∈R ；函数f(x)＝()a a b +.（1）求函数f(x)的最大值与最小正周期；（2）求使不等式f(x)≥32成立的x 的取值集合.21． 下表是芝加哥1951～1981年月平均气温（华氏）：y 与x 之间的函数关系.（2）某蔬菜的种植；要求每月的平均气温不低于60华氏；试确定蔬菜在一年内种植的最长时间.学号__________姓名________ 高一第二学期·必修三与必修四综合测试题（2）一:选择题:1. sin(930)-的值是（ ）A ． 12-B ．12C ．32-D ．322 一个单位有职工160人；其中有业务员104人；管理人员32人；后勤服务人员24人；要从中抽取一个容量为20的样本；用分层抽样的方法抽取样本；则在20人的样本中应抽取管理人员人数为 （ ） A. 3 B. 4 C. 5 D. 63. 某人一次掷出两枚骰子,点数和为5的概率是（ ）A.41 B. 91 C. 361 D. 181 4．有一个数据为50的样本,其分组以及各组的频数如下:[12.5,15.5],3; [15.5,18.5],8; [18.5,21.5],9; [21.5,24.5],11; [24.4,27.5],10; [27.5,30.5],5; [30.5,33.5],4 由以上频数,估计不超过30.5的数据大约占（ ） A.10% B.92% C.5% D.30% 5. 某产品分甲、乙、丙三级；其中乙、丙两级均属次品.若生产中出现乙级品的概率为0.03；丙级品的概率为0.01；则对成品抽查一件抽得正品的概率为（ ） A ．0.99 B ．0.98 C ．0.97 D ．0.96 6. 已知α为第二象限角,那么2α是（ ） A.第一象限角 B. 第二象限角 C.第一、三象限角 D.第二、四象限7. 将十进制数111化为五进制数是（ ）A ．421（5） B. 521（5） C.423（5） D. 332（5）8. 下面为一个求10个数的平均数的程序,在横线上应填充的语句为A. i>10B.i<10C. i>=10 D i<=10 9. 一个游戏转盘上有四种颜色:红、黄、蓝、黑；并且它们所占面积的比为6：2：1：4；则指针停在红色或蓝色区域的概率为（ ）A.613 B.713 C ．413 D.101310、将函数y ＝sin(3x ＋α)的图像向右平移18π个单位；得到函数y ＝sin3x 的图像；则α=A.π6B.π18C.π6- D.π18-二、填空题11. 甲、乙两名高一男生参加投篮测试；各投篮5次；一分钟内投中次数分别如下：甲：7；8；6；8；6； 乙：7；8；7；7；6甲的方差是_______ ,乙的方差是________ ；说明 ______ 投篮更稳定.12. 一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ .13．终边落在阴影部分处（包括边界）的角的集合是_________（用弧度制表示）14．已知31tan -=α；则=-+ααααsin cos 5cos 2sin ____________. 15、关于下列各命题：①函数x y tan =在第一象限是增函数； ②函数)πy=cos2(x 4-是非奇非偶函数；③函数)πy=4sin(2x 3-的一条对称轴是πx=6； ④函数()y=3sin x +2cos x -是实数集上的偶函数其中正确命题的序号是 。

高一第二学期必修三与必修四综合测试题（3）一:选择题:1. 化简)2cos()tan()2cos(απαπαπ-++为 ( )：1A 1-B αtan C αtan -D2．tan15tan 75+o o 的值为( ) A ．2 B ． 4 C ．-4 D ．不存在3. 下面为一个求10个数的平均数的程序,在横线上应填充的语句为( )A. i>10B.i<10C. i>=10 D i<=104．从一批螺母产品中任取一个，测量其横截面直径的大小，直径小于3.98cm 的概率为0.38，直径小于4.06cm 的概率为0.30，那么直径在[3.98，4.06)范围内的概率是( )A. 0.68B. 0.38C. 0.08D. 0.625．现有五个球分别记为1，2，3，4，5，随机取出三个球放进三个盒子，每个盒子放一个球，则1或2在盒中的概率是( ) A. 1/10 B. 3/5 C.3/10 D. 9/10 6.已知ABC ∆中,D 为BC 边上的中点, 则下列等式中正确的是(A =-B =+ 0CAB AC BC ++= 2D AB AC AD +=7. 要得到函数1/2sin(2/6)y x π=+的图象，只须将函数1/2sin(/6)y x π=+的（A ）向右平移/6π个单位 （B ）向左平移/6π个单位 （C ）横坐标伸长到原来的2倍 （D ）横坐标缩短到原来的1/2倍8．设(cos ,sin ) , (cos ,sin ) , (1,0) , , (0,)a b c ααββαβπ===∈，若a c 与的夹角为θ，b c 与的夹角为ϕ，且/6θϕπ-=，则sin()αβ-的值为( ) A 2B 2C ．1/2D ．19．函数R ∈的最大值为m ，最小值为n ，则m +n =( )A ．16B ． 3+．8 D ．6+10．已知平行四边形ABCD 的3个顶点为(,),(,),(0,0)A a b B b a C-，则它的第4个顶点D 的坐标是( )A ．(2,)a b B.(,)a b a b -+ C.(,)a b b a +-D.(,)a b b a --二．填空题：11. 一个总体中共有200个个体，用简单随机抽样的方法从中抽取一个容量为20的样本，则某一特定个体被抽到的可能性是 12．当,x y ∈ [0,2]时，则01x y ≤-≤的概率为 . 13．若()2sin (01)f x x ωω=<<在区间[0,/3]π上的最大值是2，则ω=14、图中所示的是一个算法的流程图，其表达式为 15、掷两颗骰子，出现点数之和等于8的概率等于__________. 三．解答题：16题． 已知函数()2sincos /2f x x x x π=+.（1）求函数的最大值、最小值及取得最大值和最小值时自变量x 的集合. (2) 求函数的单调递增区间.17题．已知2,3a b == ;(1) 若,a b 两向量所成角2/3θπ=, 求?a b ⋅=.(2) 若,a b 两向量所成的角/3θπ=,求2a b +的大小.18题、（1）、甲乙两人约定在下午6点到7点之间于某地会面，先到者等候时间不超过一刻钟，过时即可离去，求两人能会面的概率。

高一数学第二学期必修三与必修四综合测试题（7 ）命题：方锦昌 尹秋梅易传庚一、选择题：uuur uuuruuur uuur uuur1、在 △ ABC 中， AB c ， AC b ．若点 D 知足 BD2DC ，则 AD （ ）A ． 2/3b+1/3cB ．5/3c-2/3bC ． 2/3b-1/3cD ．1/3b+2/3c2、为获得函数的图像，只要将函数 y sin 2x 的图像（）A ．向左平移 5/12 个长度单位B ．向右平移5 /12 个长度单位C ．向左平移 5 / 6 个长度单位D ．向右平移 5 / 6 个长度单位3、某校高三年级有男生 500 人，女生 400 人，为了认识该年级学生的健康状况，从男生中随意抽取25 人，从女生中随意抽取20 人进行检查 .这类抽样方法是 ()(A) 简单随机抽样法(B) 抽签法(C) 随机数表法 (D) 分层抽样法4、设 a sin5 / 7 ， b cos2 / 7 ， c tan2 /7 ，则（ ）：（ A ） a bc （ B ） a c b （ C ） b c a （D ） b a c5、 把 89 化为五进制数，则此数为()A. 322 (5)B. 323 (5)C. 324(5)D. 325 (5)6、 在区间 [ 1,1] 上任取三点，则它们到原点O 的距离平方和小于1 的概率为 ()A. π /9B. π /8C. π /6D. π /47、在区间（ 10， 20】内的所有实数中,随机取一个实数 a,则这个实数 a<13的概率是：A 、 1/3B 、1/7C 、 3/10D 、7/108、函数 ytan x sin x tan x sin x 在区间（π /2 ， 3π /2 ）内的图象是 ()yyyy3322222-o3222 -x o3 22o xo x2-2-xABCD9、已知 cos （α -π） +sin α = 4 3, 则 sin(α7π)的值是 ( )656（A ）-2 3（B ）2 3-4 4 5 5C 、 5(D)510、函数 y ＝ lncosx(- π/2 ＜ x ＜π /2 的图象是 ()二、填空：11、向量a(12)，， b (2，3) ，若向量 a b 与向量c( 4， 7) 共，．12、行右的程序框，若p＝ 0.8，出的 n＝.13、（已知a，b， c △ ABC 的三个内角A，B， C 的，向量m＝（3, 1），n＝（cosA,sinA）.若m⊥ n，且 acosB+bcosA=csinC，角 B＝ _____.14、直角坐平面上三点A(1,2)、 B(3, 2)、 C (9,7) ，若E、F段BC 的三平分点，uuur uuurAE AF =．15、从甲、乙两品种的棉花中各抽了25 根棉花的度（位：mm），果如表中所示。

高中数学习题必修4及答案篇一：人教版高一数学必修四测试题(含详细答案)高一数学考试（必修4）（特别适合按14523顺序的省份）必修4第1章三角函数（1）一、选择题：1.如果a={第一象限角}，B={锐角}，C={角度小于90°}，那么a，B和C之间的关系是（）a．b=a∩cb．b∪c=cc．acd．a=b=c2sin21200等于（）?133c?d22223.已知sin??2cos?3sin??5cos5,那么tan?的值为b．2c．（）16164.在下列函数中，最小正周期为π的偶数函数为（）A.-223D.-23x1?tan2xa.y=sin2xb.y=cosc.sin2x+cos2xd.y=21?tan2x5.转角600的端边是否有点？？4，a那么a的值是（）04b?43c?43d6.得到函数y=cos(a．向左平移x?x?)的图象，只需将y=sin的图象（）242??个单位b.同右平移个单位22c、将装置向左移动D.将装置向右移动447．若函数y=f(x)的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，再将整个图象沿x轴向左平移?1个单位，沿y轴向下平移1个单位，得到函数y=sinx的图象22Y=f（x）是（）a．y=1?1?sin(2x?)?1b.y=sin(2x?)?122221.1.c、 y=sin（2x？）？1d。

罪（2x？）？一万二千四百二十四8.函数y=sin(2x+5?)的图像的一条对轴方程是（）25.a、 x=-b.x=-c.x=d.x=42481，则下列结论中一定成立的是229.如果罪？？余弦？？（）罪恶？？2b.罪22罪？？余弦？？1d.罪？？余弦？？0c。

（）10.函数y?2sin(2x??3）形象a．关于原点对称b．关于点（－11.功能y？罪（x？a．[，0）对称c．关于y轴对称d．关于直线x=对称66?2x?r是（）??,]上是增函数b．[0,?]上是减函数22c、 [？，0]是减法函数D.[？，？]上限是一个减法函数12.功能y？（）3,2k？？a、 2k b、 2k？？，2k？？（k？z）（k？z）3.66??2??3.c、 2k3,2k（k？Z）d？2k23,2k2(kz)3二、填空：13.函数y?cos(x2)(x?[,?])的最小值是.863和2002年相同端边的最小正角度为_________015.已知sin??cos??1??,且,则cos??sin??.842如果设置一个？？x | kx?k???,k?z?，b??x|?2?x?2?，3?然后是a？b=_______________________________________三、解答题：17.认识辛克斯吗？Coxx？1和0？x？？。

高一数学 模拟试题一新人教A 版必修3高一数学水平测试模拟题一（必修3）（附答案）参考公式：用最小二乘法求线性回归方程系数公式：一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四处备选项中，只有一项是符合题目要求的）．1、算法的三种基本结构是 ( )A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2、将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( )（A ） （ B ） （ C ） （ D ）3、右面程序的输出结果为 （ ）A ． 3，4B ．7，7C ．7，8D ．7，114、已知x 、y 之间的一组数据如下：x0 1 2 3 y 8 2 6 4则线性回归方程bx a y+=ˆ所表示的直线必经过点 （ ） A ．（0，0） B ．（1.5,5） C ．（4,1.5） D ．（2,2）5、某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点，公司为了调查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为(1)；在丙地区中有20个特大型销售点，要从中抽取7个调查其销售收入和售后服务情况，记这项调查为(2)。

则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( )A 、 分层抽样法，系统抽样法B 、分层抽样法，简单随机抽样法C 、系统抽样法，分层抽样法D 、简单随机抽样法，分层抽样法6、从装有两个红球和两个黑球的口袋里任取两个球，那么互斥而不对立的两个事件是（ ）A ．“至少有一个黑球”与“都是黑球”B ．“至少有一个黑球”与“至少有一个红球”C ．“恰好有一个黑球”与“恰好有两个黑球”D ．“至少有一个黑球”与“都是红球”a=b b=a c=b b=a a=c b=a a=b a=c c=b b=aX ←3 Y ←4 X ←X ＋Y Y ←X ＋Y Print X ，Y7、下列对一组数据的分析，不正确的说法是 （ ）A 、数据极差越小，样本数据分布越集中、稳定B 、数据平均数越小，样本数据分布越集中、稳定C 、数据标准差越小，样本数据分布越集中、稳定D 、数据方差越小，样本数据分布越集中、稳定8、下列赋值语句正确的是 （ ）A ．3←+n m B. m ←1 C. 1,←n m D. 1-←m m9、如果数据n x x x ,,,21 的平均数是 x ，方差是2S ，则32,,32,3221+++n x x x 的平均数和方差分别是 （ ） A.x 与2S B.2 x ＋3 和2SC. 2 x ＋3 和 42SD. 2x ＋3 和 42S ＋12S ＋910、同室四人各写一张贺卡，先集中起来，然后每人从中任意抽取一张，则四人所抽取的都不是自己所写的贺卡的概率是（A ）41 （B ）83 （C ）241 （D ）2569 二、填空题：（本大题共6小题，每小题5分，共30分．把答案填在题中相应的横线上）．11、频率分布直方图中各小长方体的面积和为____________.12、某校有学生2000人，其中高三学生500人，为了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本，则样本中高三学生的人数为 _____________．13、有一杯1升的水,其中含有1个细菌，用一个小杯从这杯水中取出0.1升,则小杯水中含有这个细菌的概率是________________________。

高二数学必修部分测试题一、选择题（本大题共12小题，每小题５分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．0sin 390=()A ．21B ．21-C ．23 D ．23- 2．已知2tan()5αβ+=,1tan()44πβ-=,则tan()4πα+的值为() A 1223133A 4.，b 满足：|3a =，|2b =，||a b +=||a b -=()A 3D ．105.下面结论正确的是（）C.6A C 789、函数⎪⎩⎪⎨⎧+∞∈--∞∈-=--),2(,22]2,(,2211x x y x x 的值域为______________。

A 、),23(+∞- B 、]0,(-∞ C 、23,(--∞ D 、]0,2(- 10.当x>1时，不等式x+11-x ≥a 恒成立，则实数a 的取值范围是 A ．(－∞,2] B ．[2,+∞) C ．[3,+∞) D ．(－∞,3]11．已知a,b,c 成等比数列，且x,y 分别为a 与b 、b 与c 的等差中项，则y c x a +的值为（） （A ）21（B ）-2（C ）2（D ）不确定 12．已知数列{a n }的通项公式为a n =n n ++11且S n =1101-,则n 的值为（）（A ）98（B ）99（C ）100（D ）101二、填空题（本大题共4小题，每题4分，共16分，把答案填在题中横线上）13141516。

17得到y 1819（本小题满分12分）已知向量a ,b 的夹角为60,且||2a =,||1b =,(1)求a b ;(2)求||a b +.20.已知数列{a n }，前n 项和S n =2n-n 2,a n =log 5bn ，其中bn>0，求数列{bn}的前n 项和。

21（本小题满分14分）已知(3sin ,cos )a x m x =+，(cos ,cos )b x m x =-+,且()f x a b =(1)求函数()f x 的解析式;(2)当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,()f x 的最小值是－4,求此时函数()f x 的最大值,并求出相应的x 的值. 22如图如图，在底面是直角梯形的四棱锥S-ABCD ，∠ABC=90°，SA ⊥面ABCD ，SA=AB=BC=1，AD=1/2.ACAD 13.3π171)2-+x ，∴18.19.解：(1)1||||cos602112a b a b ==⨯⨯= (2)22||()a b a b +=+所以||3a b +=20.当n=1时，a 1=S 1=1当n ≥2时，a 1=S n -S n-1=3-2n ∴a n =3-2nb n =53-2n∵25155123)1(23==+-+-n n bn bn b 1=5∴{b n }是以5为首项，251为公比的等比数列。

2012—2013学年（下）期末教学质量检测高一数学（必修4）试题注意事项：1．考试时间120分钟，试题分值120分（含卷面分4分）。

2. 请将第Ⅰ卷选择题答案用2B 铅笔填涂在机读卡上，第Ⅱ卷非选择题答案填在答题纸上。

3．答题前先填好密封线内的各项内容。

第Ⅰ卷 选择题（共50分）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．的值是（ ） A ．12B ．32C ．32-D. 12-2． 在ABC △中，AB =c ，AC =b ，若点D 满足2BD DC =，则AD =（ ） A ．2133+b c B ．5233-c b C ．2133-b c D ．1233+b c 3． 一钟表的分针长10 cm ，经过15分钟，分针的端点所转过的长为A ．30 cmB ．5cmC ．π5cmD ．325πcm 4. 函数1cos ,[0,2]y x x π=-∈的大致图象是（ ）AB C D5．已知a b a ,2||,1||==与b 的夹角为600，若ka b +与b 垂直，则k 的值为A ．4-B ．4C ．43-D ．436．若()βα-cos =53,βsin =135-,且⎪⎭⎫ ⎝⎛∈2,0πα，⎪⎭⎫⎝⎛-∈0,2πβ，则sin α等于 A.6365B. 3365-C.3365D. 6365-7．与)4,3(-→a 共线的单位向量是A. )54,53(-B. )53,54(C. )54,53(-和)54,53(-D. )53,54(和)53,54(--8．函数5sin(2)2y x π=+的图像的一条对轴方程是 A ． 2x π=-B ．4x π=-C ．8x π=D ．54x π=9．把函数y ＝cos x 的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来的两倍，然后把图象向左平移π4 个单位.则所得图象表示的函数的解析式为A. y ＝2sin2xB. y ＝－2sin2xC. y ＝2cos(2x ＋π4)D. y ＝2cos(+2x 4π) 10．定义一种向量之间的⊗运算：⊗a b =c ，若()()1212,,,a a b b a =b =，则向量()1122,a b a b c =． 已知1,2,,026π⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭m n ，且点(,)P x y 在函数cos 2y x =的图象上运动，点Q 在函 数()y f x =的图象上运动，且点P 和点Q 满足：OQ OP =⊗+m n （其中O 为坐标原点），则函数()y f x =的最大值A 及最小正周期T 分别为A ．122,πB ．12,πC ．22,πD ．2,π高一数学（必修4）试题 第1页 （共4页）o | | | | | | | |2ππ23ππ221-1xy| | | | | | | |2ππ23ππ22 1 -1 xy | | | | | | | |2ππ23ππ221-1x y| | | | | | | |2ππ23ππ22 1-1xy高一数学（必修4）试题 第2页 （共4页）600sin第Ⅱ卷 非选择题（共70分，含卷面分4分）二、填空题（本大题共5小题，每小题4分，共20分。

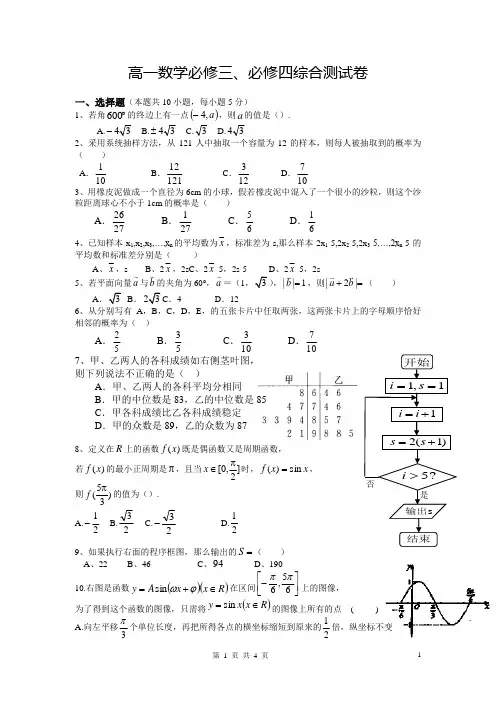
开始1,1i s ==5?i >1i i =+输出s结束否是2(1)s s =+高一数学必修三、必修四综合测试卷一、选择题（本题共10小题，每小题5分）1、若角︒600的终边上有一点()a ,4-，则a 的值是（）.A.34-B.34±C.3D.342、采用系统抽样方法，从121人中抽取一个容量为12的样本，则每人被抽取到的概率为（ ） A ．101 B ．12112 C ．123 D ．107 3、用橡皮泥做成一个直径为6cm 的小球，假若橡皮泥中混入了一个很小的沙粒，则这个沙粒距离球心不小于1cm 的概率是（ ）A ．2726 B ．271 C ．65 D ．614、已知样本x 1,x 2,x 3,…,x n 的平均数为x ，标准差为s,那么样本2x 1-5,2x 2-5,2x 3-5,…,2x n -5的平均数和标准差分别是（ ）A 、x ，sB 、2x ，2sC 、2x -5，2s-5D 、2x -5，2s 5、若平面向量a 与b 的夹角为60°，a ＝（13，||1b =，则|2|a b +=（ ）A 3B ．23C ．4D ．126、从分别写有A ，B ，C ，D ，E ，的五张卡片中任取两张，这两张卡片上的字母顺序恰好相邻的概率为（ ）A ．52 B ．53 C ．103 D ．107 7、甲、乙两人的各科成绩如右侧茎叶图， 则下列说法不正确的是（ ）A ．甲、乙两人的各科平均分相同B ．甲的中位数是83，乙的中位数是85C ．甲各科成绩比乙各科成绩稳定D ．甲的众数是89，乙的众数为878、定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当[0,2x π∈时，x x f sin )(=，则5(3f π的值为（）.A.21-B.23C.23- D.219、如果执行右面的程序框图，那么输出的S =（ ） A 、22 B 、46 C 、94 D 、19010.右图是函数()()R x x A y ∈+=ϕωsin 在区间⎥⎦⎤⎢⎣⎡-65,6ππ上的图像，为了得到这个函数的图像，只需将()R x x y ∈=sin 的图像上所有的点 ( )A.向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变B.向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 C. 向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变D .向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变二、填空题（本题共5小题，每小题5分）11、某工厂生产 A ，B ，C 三种不同型号的产品，产品数量之比依次为 2∶3∶5．现用分层抽样方法抽出一个容量为n 的样本，样本中A 种型号的产品有16件，那么此样本的容量n ＝___________．12、在扇形中，已知半径为8，弧长为12，则圆心角是 弧度，扇形面积是 . 13、已知向量a ＝(1,2)，b ＝(2，－3)．若向量c 满足(c ＋a )∥b ，c ⊥(a ＋b )，则c ＝___________．14、设方程cos 2x ＋3sin 2x ＝a ＋1在⎣⎡⎦⎤0，π2上有两个不同的实数解，则a 的取值范围是______________． 15、下列命题：（1）在△ABC 中，若B A B A cos cos sin sin =，则△ABC 是直角三角形 （2） 函数3cos 5sin 2)(2-+=x x x f 的最大值为2；（3）若3tan =α，则αααcos sin 3cos 2-的值为1；（4）若)(f x 是定义在[－1，1]上的偶函数，且在[－1，0]上是增函数，⎪⎭⎫⎝⎛∈24ππθ，，则)(cos )(sin f θθf >；（5）若锐角βα、满足βαsin cos >，则2πβα<+; 其中真命题的是 _____________ 。

高一数学试题（必修4）（特别适合按14523顺序的省份）必修4 第一章三角函数(1)一、选择题：1.已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、C关系是（）A．B=A∩C B．B∪C=C C．AC D．A=B=C2 等于（）A B C D3.已知的值为（）A．－2 B．2 C．D．－4．下列函数中，最小正周期为π的偶函数是（）A.y=sin2xB.y=cos C .sin2x+cos2x D. y=5 若角的终边上有一点，则的值是（）A B C D6．要得到函数y=cos()的图象，只需将y=sin的图象（）A．向左平移个单位 B.同右平移个单位C．向左平移个单位 D.向右平移个单位7．若函数y=f(x)的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，再将整个图象沿x轴向左平移个单位，沿y轴向下平移1个单位，得到函数y=sinx的图象则y=f(x)是（）A．y= B.y=C.y=D.8. 函数y=sin(2x+)的图像的一条对轴方程是（）A.x=-B. x=- C .x=D.x=9．若，则下列结论中一定成立的是（）A. B． C． D．10.函数的图象（）A．关于原点对称 B．关于点（－，0）对称 C．关于y轴对称 D．关于直线x=对称11.函数是（）A．上是增函数 B．上是减函数C．上是减函数D．上是减函数12.函数的定义域是（）A．B．C． D．二、填空题：13. 函数的最小值是 .14 与终边相同的最小正角是_______________15. 已知则 .16 若集合，，则=_______________________________________三、解答题：17．已知，且．a)求sinx、cosx、tanx的值．b)求sin3x – cos3x的值．18 已知，（1）求的值（2）求的值19. 已知α是第三角限的角，化简20．已知曲线上最高点为（2，），由此最高点到相邻的最低点间曲线与x轴交于一点（6，0），求函数解析式，并求函数取最小值x的值及单调区间必修4 第一章三角函数(2)一、选择题：1．已知，则化简的结果为（）A． B. C． D. 以上都不对2．若角的终边过点(-3，-2)，则( )A．sin tan＞0 B．cos tan＞0C．sin cos＞0 D．sin cot＞03 已知，，那么的值是（）A B C D4．函数的图象的一条对称轴方程是（）A． B. C. D.5．已知，,则tan2x= ( ) A． B. C. D.6．已知，则的值为（）A． B. 1 C. D. 2 7．函数的最小正周期为（）A．1 B. C. D.8．函数的单调递增区间是（）A． B.C． D.9．函数，的最大值为（）A．1 B. 2 C. D.10．要得到的图象只需将y=3sin2x的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位 D．向右平移个单位11．已知sin(+α)=，则sin(-α)值为（）A. B. — C. D. —12．若，则（）A. B. C. D.二、填空题13．函数的定义域是14．的振幅为初相为15．求值：=_______________16．把函数先向右平移个单位，然后向下平移2个单位后所得的函数解析式为________________________________三、解答题17 已知是关于的方程的两个实根，且，求的值18．已知函数，求：（1）函数y的最大值，最小值及最小正周期；（2）函数y的单调递增区间19．已知是方程的两根，且，求的值20．如下图为函数图像的一部分（1）求此函数的周期及最大值和最小值（2）求与这个函数图像关于直线对称的函数解析式必修4 第三章三角恒等变换(1)一、选择题:1.的值为 ( ）A 0BC D2.，，，是第三象限角，则（）A B C D3.设则的值是( )A B C D4. 已知，则的值为（）A B C D5.都是锐角，且，，则的值是（）A B C D6. 且则cos2x的值是（）A B C D7.在中，的取值域范围是 ( )A B C D8. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为（）A B C D9.要得到函数的图像，只需将的图像（）A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位10. 函数的图像的一条对称轴方程是（）A、 B、 C、 D、11.若是一个三角形的最小内角，则函数的值域是( )A B C D12.在中，，则等于 ( )A B C D二、填空题:13.若是方程的两根，且则等于14. .在中，已知tanA ,tanB是方程的两个实根，则15. 已知，则的值为16. 关于函数，下列命题：①若存在，有时，成立；②在区间上是单调递增；③函数的图像关于点成中心对称图像；④将函数的图像向左平移个单位后将与的图像重合．其中正确的命题序号（注：把你认为正确的序号都填上）三、解答题：17. 化简18. 求的值．19. 已知α为第二象限角，且sinα=求的值.20.已知函数，求（1）函数的最小值及此时的的集合。

高一数学必修3必修4试题含答案2篇题目1：高一数学必修3必修4试题含答案第一篇：在高中数学的学习中，必修3和必修4是两个重要的阶段。

这两个阶段涵盖了数学的基本概念和初步的应用。

为了帮助同学们更好地复习和巩固所学知识，我收集了一些必修3和必修4的试题，并附上了答案。

一、必修3试题：1. 已知函数 y = x^2 + 2x - 3，求函数的导函数。

答案：函数的导函数为 y' = 2x + 2。

2. 已知数列 {an} 的通项公式为 an = 2n^2 + 3n，求数列的前n 项和。

答案：数列的前 n 项和为 Sn = (n^4 + 2n^3 - n^2 - n) / 4。

3. 已知直线 l1 过点 A(1, 2) 和点 B(3, -1)，直线 l2 过点C(-2, 4) 和点 D(1, -3)，求直线 l1 和直线 l2 的夹角。

答案：直线 l1 的斜率为 k1 = (2 - (-1)) / (1 - 3) = -3/2；直线 l2 的斜率为 k2 = (4 - (-3)) / (-2 - 1) = 7/3。

直线 l1 和直线 l2 的夹角为 arctan((k2 - k1) / (1 + k1 * k2))。

二、必修4试题：1. 已知函数 y = x^3 + 2x^2 - 5x + 1，求函数的极值点。

答案：函数的极值点为 x = -1。

2. 已知函数 y = e^(2x) ，求函数的反函数。

答案：函数的反函数为 y = ln(x) / 2。

3. 已知数列 {an} 的通项公式为 an = 3^n + 2^n ，求数列的前 n 项和。

答案：数列的前 n 项和为 Sn = (3^(n+1) - 1) / 2。

以上是我整理的一些必修3和必修4的试题，希望对同学们的复习有所帮助。

如果还有其他问题，可以继续向我提问。

第二篇：高中数学是一个系统而复杂的学科，需要同学们在掌握了基本概念的基础上，能够进行灵活的应用。

高中数学人教版-必修三必修四测试卷(含答案)华鑫中学2011~2012学年第三次月考高一数学试卷（总分150）一、选择题：（以下每小题有且仅有一个正确答案，共40分）1、在100个产品中，一等品20个，二等品30个，三等品50个，用分层抽样的方法抽取一个容量20的样本，则二等品中A被抽取到的概率()A．等于15B．等于3 10C．等于23D．不确定2、已知点P（tanα，cosα）在第三象限，则角α的终边在（）A.第一象限B.第二象限C.第三象限D.第四象限3、已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是（）23A.2B. 1sin 2sinC.2sin1D.sin24、函数y ＝2sin(3x －π4)图象的两条相邻对称轴之间的距离是 A. π3 B. 2π3C.πD. 4π35、函数y ＝sin （π4 －2x)的单调增区间是 （ ）A.［kπ－3π8 ，kπ＋π8 ］(k ∈Z)B.［kπ＋π8 ，kπ＋5π8］(k ∈Z)C.［kπ－π8 ，kπ＋3π8］(k ∈Z)4D.［kπ＋3π8 ，kπ＋7π8］(k ∈Z)6、若,24παπ<<则（ ） A ．αααtan cos sin >> B ．αααsin tan cos >>C ．αααcos tan sin >>D ．αααcos sin tan >>7、已知函数1tan sin )(++=x b x a x f ，满足.7)5(=f 则)5(-f 的值 为 （ ） A ．5 B ．－5 C ．6 D ．－68、已知一点O 到平行四边形ABCD 的三个顶点A 、B 、C 的向量分别为a →、b →、c →,则向量等于( )A.a b c ++r r rB.a b c -+r r rC.a b c +r r r -D.a b c r r r --二、填空题（每小题5分，共7题合计35分）9、下列各数)9(85、)6(210、)4(1000、)2(111111中最小的数是____________。

高一数学第二学期必修三与必修四综合测试题（6）高一第二学期必修三与必修四综合测试题（6）一、选择题1．1920°转化为孤度数为（）A．程序：i＝1S＝1n＝0DOS＜＝500S＝S＋Ii＝i＋1n＝n＋1WENDPRINTn＋1END20(湖北16.题满分12分）已知函数f(t)=（Ⅰ）将函数g(x)化简成Asin(ωx+φ)+B（A＞0，ω＞0，φ∈[0，2π]）的形式；（Ⅱ）求函数g(x)的值域.21(08江苏高考15题)．如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于两点，已知的横坐标分别为；求的值（2）求的值。

22题、在一次抗洪抢险中，准备用射击的方法引爆一个从桥上游漂流而下的一个巨大的汽油罐。

已知现在手头只有五发子弹可用，且第一次命中油罐时只能使汽油流出；只有第二次再命中油罐时，油罐才能被引爆；又每次射击是相互不影响的，每次射击可命中油罐的概率是2/3。

（1）问油罐最终被引爆的概率会是多少？（2）如果油罐被引爆或子弹被打光则射击停止，设射击的次数为§，求§大于或等于4的概率。

综合(6)参考答案:题次12345678910答案DBDCACCCBC11．λ＝1/2；12．.13；13a=12，i=3；14．；15.34。

16解：（1）依题意知A=1；，又；即；因此；（2），，且，；；17解：（1）；（2）初三年级人数为y＋z＝2000－（373＋377＋380＋370）＝500，现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：名（3）设初三年级女生比男生多的事件为A，初三年级女生男生数记为（y，z）；由（2）知，且,基本事件空间包含的基本事件有：（245，255）、（246，254）、（247，253）、……（255，245）共11个事件A包含的基本事件有：（251，249）、（252，248）、（253，247）、(254,246)、(255,245)共5个；；18、解：（1）由函数图象的对称轴方程为（2）因为在区间上单调递增，在区间上单调递减，所以当时，去最大值1又，当时，取最小值,所以函数在区间上的值域为20题解：（Ⅰ）＝（Ⅱ）由得在上为减函数，在上为增函数，又（当），即故g(x)的值域为21解：由条件得，为锐角，故。

期末测评 高中一 年级 数学 卷、下面的程序框图输出的结果是 ．2、已知向量满足，且，则与的夹角是__________．3、关于函数F(x)=4sin(2x+π/3)(x ∈R)，有下列命题： ①由f(x 1)=f(x 2)=0可得x 1-x 2必是π的整数倍； ②y=f(x)的表达式可改写为y=4cos(2x-π/6)； ③y=f(x)的图象关于点（－π、6，0）对称； ④y=f(x)的图象关于直线x=-π/6对称。

其中正确的命题的序号是_____。

（注：把你认为正确的命题的序号都填上。

）4、从一条生产线上每隔30分钟取一件产品，共取了件，测得其尺寸后，画得其频率分布直方图如下，若尺寸在内的频数为，则尺寸在内的产品个数为 ；5、已知，且，则的值是 ．二、选择题（每空5 分，共50分）6、如下图所示的是一个算法的程序框图，它的算法功能是A ．求出a ，b ，c 三数中的最大数B ．求出a ，b ，c 三数中的最小数C ．将a ，b ，c 按从小到大排列D ．将a ，b ，c 按从大到小排列7、若样本的平均数是7，方差是2，则对于样本，下列结论中正确的是A ．平均数是13，方差是8B ．平均数是13，方差是2C．平均数是7，方差是2 D．平均数是14，方差是88、若，则等于（A）（B）（C）（D）9、函数y=cosx(o≤x≤，且x≠)的图象为10、已知函数的最小正周期为，则该函数图象A．关于直线对称B．关于点(，0)对称C．关于点(，0)对称D．关于直线对称11、已知△ABC的三个顶点A、B、C及△ABC所在平面内一点P，若，若实数，则实数等于A． B．3 C．－1 D．212、化简为A． B． C．2－D．2＋13、函数的单调增区间为A ．， B．C ．， D．14、下列命题中的真命题是A．函数内单调递增B．函数的最小正周期为2C．函数的图象是关于点（，0）成中心对称的图形D．函数的图象是关于直线x=成轴对称的图形15、已知均为锐角，则等于A． B． C．D．三、计算题（总分80分）16、(本大题满分14分)已知函数.（1）求的值；（2）求的最大值并指出相应的的取值集合.为了了解某校毕业班数学考试情况，抽取了若干名学生的数学成绩，将所得的数据经过整理后，画出频率分布直方图（如图所示）。