教材第七章习题解答

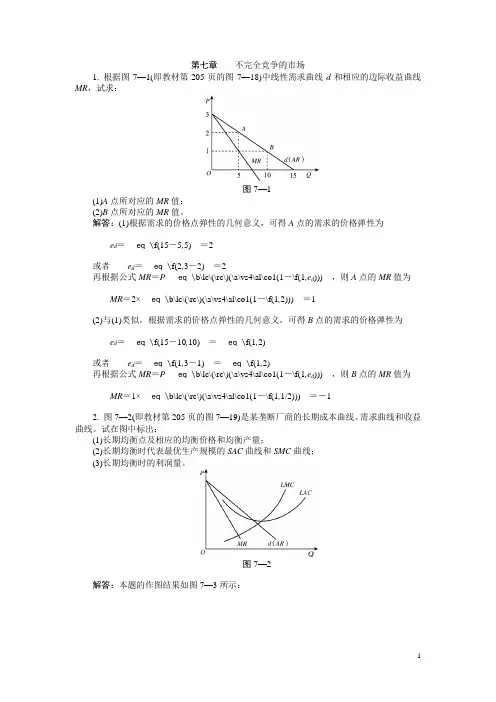
第七章不完全竞争的市场1. 根据图7—1(即教材第205页的图7—18)中线性需求曲线d和相应的边际收益曲线MR，试求：图7—1(1)A点所对应的MR值；(2)B点所对应的MR值。

解答：(1)根据需求的价格点弹性的几何意义，可得A点的需求的价格弹性为e d＝eq \f(15－5,5)＝2或者e d＝eq \f(2,3－2)＝2再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d)))，则A点的MR值为MR＝2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,2)))＝1(2)与(1)类似，根据需求的价格点弹性的几何意义，可得B点的需求的价格弹性为e d＝eq \f(15－10,10)＝eq \f(1,2)或者e d＝eq \f(1,3－1)＝eq \f(1,2)再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d)))，则B点的MR值为MR＝1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,1/2)))＝－12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。

试在图中标出：(1)长期均衡点及相应的均衡价格和均衡产量；(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线；(3)长期均衡时的利润量。

图7—2解答：本题的作图结果如图7—3所示：图7—3(1)长期均衡点为E点，因为在E点有MR＝LMC。

由E点出发，均衡价格为P0，均衡数量为Q0。

(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。

在Q0的产量上，SAC曲线和LAC曲线相切；SMC曲线和LMC曲线相交，且同时与MR曲线相交。

(3)长期均衡时的利润量由图7—3中阴影部分的面积表示，即π＝[AR(Q0)－SAC(Q0)]·Q 0。

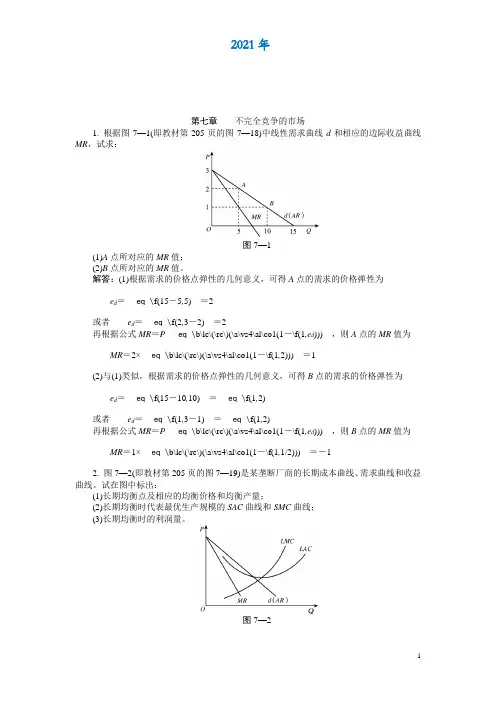
MR，试求：图7—1(1)A点所对应的MR值；(2)B点所对应的MR值。

解答：(1)根据需求的价格点弹性的几何意义，可得A点的需求的价格弹性为e d ＝eq \f(15－5,5)＝2或者e d ＝eq \f(2,3－2)＝2再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d )))，则A点的MR值为MR＝2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,2)))＝1(2)与(1)类似，根据需求的价格点弹性的几何意义，可得B点的需求的价格弹性为e d ＝eq \f(15－10,10)＝eq \f(1,2)或者e d ＝eq \f(1,3－1)＝eq \f(1,2)再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d )))，则B点的MR值为MR＝1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,1/2)))＝－12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。

试在图中标出：(1)长期均衡点及相应的均衡价格和均衡产量；(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线；(3)长期均衡时的利润量。

图7—2图7—3(1)长期均衡点为E点，因为在E点有MR＝LMC。

由E点出发，均衡价格为P0，均衡数量为Q0。

(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。

在Q0的产量上，SAC曲线和LAC曲线相切；SMC曲线和LMC曲线相交，且同时与MR曲线相交。

(3)长期均衡时的利润量由图7—3中阴影部分的面积表示，即π＝[AR(Q0)－SAC(Q0)]·Q 0。

3. 已知某垄断厂商的短期总成本函数为STC＝0.1Q3－6Q2＋140Q＋3 000，反需求函数为P＝150－3.25Q。

第七章习题答案习题7.01．下列各种情形中，P 为E 的什么点？（1）如果存在点P 的某一邻域()U P ，使得()⊂c U P E （c E 为E 的余集）； （2）如果对点P 的任意邻域()U P ，都有, ()(),C U P E U P E φφ≠≠； （3）如果对点P 的任意邻域()U P ，都有. 解 （1）P 为E 的外点；（2）P 为E 的边界点；（3）P 为E 的聚点。

2.判定下列平面点集的特征（说明是开集、闭集、区域、还是有界集、无界集等？）并分别求出它们的导集和边界.(1) (){},0≠x y y ;(2) (){}22,620≤+≤x y x y ; (3) (){}2,≤x y y x ;(4) ()(){}()(){}2222,11,24+-≥⋂+-≤x y x y x y x y .解 (1) 是开集，是半开半闭区域，是无界集，导集为2R ,边界集为(){},0=x y y ；(2)既不是开集也不是闭集，是半开半闭区域，是有界集，导集为(){}22,620≤+≤x y x y ，边界集为(){}2222,=6=20++，x y x y x y ；(3) 是闭集，是半开半闭区域，是无界集，导集为集合本身,边界集为(){}2,=x y y x ；是闭集，是闭区域，是有界集，导集为集合本身，边界集为()()(){}2222,11,24+-=+-=x y x y x y习题7.11. 设求1. 解 令,=-=yu x y v x，解得,11==--u uv x y v v，故()22,11⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭u uv f u v v v ，即()()21+,1=-u v f u v v ，所以，()()21+y ,1=-x f x y y φ≠-}){()(P E P U 22,,y f x y x y x ⎛⎫-=- ⎪⎝⎭(,).f x y2.已知函数()22,cot =+-x f x y x y xy y，试求(),f tx ty .2. 解 因为()22,cot =+-y f x y x y xy x，所以，()2222,cot ,=+-t y f tx ty tx ty txty t x即()()222,cot =+-y f tx ty t x y t xy x.3.求下列各函数的定义域 (1) 25)1(=-+z ln y xy ;(2) =z ;(3) =z(4) )0;=>>u R r(5) =u3. 解 (1)(){}2,510-+>x y yxy ；(2)(){},0->x y x y ；（3）(){}2,≥x y x y ；（4）(){}22222,<++≤x y r x y z R ；（5）(){}222,≤+x y z x y4. 求下列各极限:(1) ()()233,0,31lim →-+x y x yx y ;(2)()(,1,1ln lim→+x x y y e(3)()(,0,0lim→x y(4)()(,0,0lim→x y ;(5)()()(),0,2sin lim→x y xy x ;(6)()()()()222222,0,01cos lim→-++x y x y x y xy e.4. 解 （1）()()2333,0,31101lim 0327→--==++x y x y x y ；（2）()(()1,1,1ln ln 11lim2→+++===x x y y e e e （3）()()()(,0,0,0,0limlim→→=x y x y ()(,0,01lim4→==x y （4）()(()()),0,0,0,01limlim→→=x y x y xy xy()()),0,0=lim1=2→+x y（5）()()()()()(),0,2,0,2sin sin limlim 122→→=⋅=⋅=x y x y xy xy y x xy（6）()()()()()()()()()222222222222222,0,0,0,01cos 1cos limlim→→-+-++=⋅++x y x y x y x y x y x y xy xy eex y()()()()()()()2222222022,0,0,0,01cos 10limlim=02→→-++=⋅⋅=+x y x y x y x y xy e exy5.证明下列极限不存在: (1)()(),0,0lim→-+x y x yx y ;(2)()(),0,0lim→+-x y xyxy x y .5. (1) 解 令=y kx ,有()(),0,001limlim 1→→---==+++x y x x y x kx kx y x kx k ，k 取不同值，极限不同，故()(),0,0lim→-+x y x yx y 不存在.(2) 解令=x y()()22,0,00lim lim 1→→==+-x y x xy x xy x yx ；令2=x y()()()()22,0,02,0,0022lim lim lim 0221→→→===+-++x y y y y xy y y xy x y y y y ；01≠，故()(),0,0lim→+-x y xyxy x y不存在.6.函数=y z a 为常数）在何处间断？6. 解 因为=y z 是二元初等函数，且函数只在点集(){,x y y 上无定义，故函数在点集(){,x y y 上间断.7.用 εδ- 语言证明()(,0,0lim0→=x y .7. 证明 对0∀>ε，要使220-=≤=<ε2<ε，取=2δε<δ0-<ε，所以()(,0,0lim 0→=x y习题7.21. 设()(),sin 1arctan ,π==+-xy xz f x y e y x y 试求()1,1x f 及()1,1y f1. 解()221,sin arctan 1=+++xy x x yf x y ye y xx yyπ22=sin arctan+++xy x xy ye y y x y π.()()222,sin cos 11-=++-+xy xyy x y f x y xe y e y x x yπππ 222sin cos -=+++xyxyx x xe y e y x y πππ()()1,1,1,1∴=-=-x y f e f e2.设(),ln 2⎛⎫=+ ⎪⎝⎭y f x y x x ，求()1,0'x f ，()1,0'y f .2. 解()()222122,22--==++x yx y x f x y y x x y x x()2112,22==++y x f x y yx y x x()()11,011,02∴==，x y f f . 3.求下列函数的偏导数(1) 332=++z x y xy ，(2) ()1=+xz xy ， (3) ()222ln =+z y x y ，(4) ln tan=y z x， (5) ()222ln =+z x x y ；(6)=z (7) ()sec =z xy ；(8) ()1=+yz xy ；(9) ()arctan =-zy x y ；(10) .⎛⎫=⎪⎝⎭zx u y 3. 解 （1）2232,32z z x y y x x y ∂∂=+=+∂∂（2）因为 ()ln 1,x xy z e+=所以()()()()ln 1ln 11ln 111x x xy z xy xy e xy xy xy x xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭()()22ln 1111x x xy z x x e xy y xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭（3）()2322222222,2ln z xy z y y x y x x y y x y ∂∂==++∂+∂+（4）222222sec sec 111sec ,sec tan tan tantan y yy z y y z y x x y y y y x x x y x x x x x x x x∂∂⎛⎫⎛⎫=-=-== ⎪ ⎪∂∂⎝⎭⎝⎭ （5）()32222222222ln ,z x z x y x x y x x y y x y ∂∂=++=∂+∂+（6）z z x y ∂∂====∂∂（7）()()()()sec tan ,sec tan z z y xy xy x xy xy x y ∂∂==∂∂（8）()()22ln 1111y y xy z y y e xy x xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭()()()()ln 1ln 11ln 111y y xy z xy xy e xy xy xy y xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭ （9）()()()()()()()11222ln ,,111z z zz z z z x y z x y x y x y u u u x y z x y x y x y ------∂∂∂==-=∂∂∂+-+-+-（10）因为 ln,x z yu e=所以ln ln ln 21,,ln zzx x x z z z y y y u z x z u z x x z u x e e e x x xy y x y y y y z y y y⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂=⋅==⋅-=-= ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭4.设ln=z ，求证: 12∂∂+=∂∂z z xy x y . 4.证明 因为ln,z =所以z zx y∂∂====∂∂从而有12 z zx yx y∂∂+=+=+=∂∂5.求下列函数的二阶偏函数：(1)已知33sin sin=+z x y y x，求2∂∂∂zx y；(2)已知ln=xz y，求2∂∂∂zx y；(3)已知(ln=z x，求22∂∂z x和2∂∂∂z x y；(4)arctan=yzx求22222,,∂∂∂∂∂∂∂z z zx y x y和2∂∂∂zy x.5. 解（1）3323sin sin,3sin coszz x y y x x y y xx∂=+∴=+∂从而有223cos3coszx y y xx y∂=+∂∂（2）ln ln1,lnx xzz y y yx x∂⎛⎫=∴= ⎪∂⎝⎭从而有()()()ln1ln1ln11ln ln ln ln1xx xz yxy y y x yx y x y x--⎛⎫∂=+⋅=+⎪∂∂⎝⎭（3）(()1222 ln,zz x x yx-∂=∴===+∂从而有()()3322222222122zx y x x x yx--∂=-+=-+∂()()332222222122z x y y y x y x y --∂=-+=-+∂∂ （4）22221arctan,1y z y y z x xx x y y x ∂⎛⎫=∴=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭ 222111z x yx x y y x ∂⎛⎫=⋅= ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭从而有()()()()2222222222222222222,x y y z xy z y x x x y x y x y x y -++∂∂-===∂∂∂+++ ()()2222222222222222,z xy z x y xy x y y y x x y x y x y ⎛⎫∂-∂+--=== ⎪∂∂∂+⎝⎭++ 6. 设()ln =z y xy ，求2∂∂∂z x y 及22∂∂zy .6. 解 因为()ln ,z y xy =所以()(),ln ln 1z y y z x y xy y xy x xy x y xy∂∂===+=+∂∂从而有22211,.z z x y x y y∂∂==∂∂∂ 习题7.31. 求下列函数的全微分.(1) 2222+=-s t u s t ；(2) ()2222+=+x y xyz x y e；(3) ()arcsin0=>xz y y；(4) ⎛⎫-+ ⎪⎝⎭=y x x y z e ；1.解 （1）()()222232322222222()()22222∂--+⋅---==∂--u s s t s t s s st s t s s s t s t()()222223232222222()()22222u t s t s t t ts t ts s t s t s t ∂--+---==∂-- ()()2322222244u u st t dz ds dt ds dt s t s t s t ∂∂-∴=+=-∂∂--（2）()()()222222222222++++∂=++⋅∂x y x y xyxyx y x y yzxe x y exxy()2222222244222222+++⎛⎫--=++⋅=+ ⎪⎝⎭x y x y x y xyxyxyx y x y xe x y e x e x y x y()()()22222222222-2+++∂=++⋅∂x y x y xy xyy x x y xzye x y eyxy()()2222222222442222+++-+⎛⎫-=+⋅=+ ⎪⎝⎭x y x y x y xyxyxyy x x y y x yeey e xy xy2244442222x y xyz z x y y x dz dx dy x edx y dy x y x y xy +⎛⎫⎛⎫∂∂--∴=+=+++ ⎪ ⎪∂∂⎝⎭⎝⎭ （3）2222211∂=⋅==∂--⎛⎫yzxyyy x y x x22⎛⎫⎛⎫∂=-=-= ⎪ ⎪∂⎝⎭⎝⎭z x x yy y z zdz dx dy x y∂∂∴=+=∂∂（4）22221y x y x x y x y z y y x e e x x y x y ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-= ⎪∂⎝⎭ 22221y x y x x y x y z x x y e e y x y xy ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-+= ⎪∂⎝⎭222222y x y x x y x y z z z y x x y dz dx dy e dx e dy x y y x y xy⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭∂∂∂--∴=+==+∂∂∂ 2. 求函数2arctan1=+xz y 在1,1==x y 处的全微分.2.解()()()()()()()22222222222222222211111111111++∂++=⋅=⋅=∂++++++++y y z y y x xy y x y y xy()()()()()()22222222222222211222111111+∂-⋅--=⋅=⋅=∂++++++++y z x y xy xyx yy y x y y xy()()21,11125111z x ∂+∴==∂++ ， ()()21,12125111∂-⋅==-∂++z y ()1,12255dz dx dy ∴=- 3. 求函数22=-xyz x y 当2,1,0.02,0.01==∆=∆=x y x y 时的全微分和全增量，并求两者之差.3.解 ()()()(),, 2.02,1.011,1z z x x y y z x y z z ∆=+∆+∆-=-()()22222.02 1.0121 2.0420.6670.667021 4.08 1.0232.02 1.01⨯⨯=-=-=-=--- ()()()2223222222222--⋅∂--===-∂---y x y xy x z x y y y x x y x y x y ()()()()22322222222--⋅-∂+==∂--x x y xy y z x xy y x y x y ()2,111413z x ∂∴=-=-∂- ，()()22,182110941z y ∂+⨯==∂- ()2,11100.020.010.070.0110.00439dz ∴=-⨯+⨯=-+=00.0040.004z dz ∴∆-=-=-.*4讨论函数()()()()(),0,0,0,,0,0⎧≠⎪=⎨⎪=⎩xy x y f x y x y 在()0,0点的连续性、可导性、可微性以及其偏导函数在()0,0的连续性.4.解()()()()()(),0,0,0,0lim,lim 00,0x y x y f x y xy f →→===(),f x y ∴在()0,0点连续 又()()()00,00,0000,0limlim 0x x x f x f f x x∆→∆→∆--===∆∆ ()()()000,0,0000,0limlim 0y y y f y f f y y∆→∆→∆--===∆∆ ()()0,00,0,00x y f f ∴==.()(()(,0,0,0,0,0,00limlim limx y x y f x yf z dzρρ→∆∆→∆∆→∆∆--∆-==()()()0,0,0x y<∆∆→∆lim0z dzρρ→∆-∴=故函数(),f x y 在()0,0点可微. 由()(),0,0x y ≠时(),=-x f x yy xy()23222sinx yy xy=-+(),=-y f x y x xy ()23222xy x xy=-+()(),0,0lim 0x y y →= ，()()()()23,0,0222lim→=+x y x yy kx xy()()()33323222=lim11→==+⋅+x kx ky kx k xk ，k 不同值不同()()()23,0,0222lim→∴+x y xy xy 不存在，故()()(),0,0lim ,xx y f x y →不存在.(),x f x y ∴在()0,0点不连续，同理可证(),y f x y 在点()0,0不连续.*5.计算()2.050.99的近似值.5.解 令00,1,2,0.01,0.05yz x x y x y ===∆=∆= 则1,ln y y z z yx x x x y-∂∂==∂∂ ()()1,21,22,0z zx y ∂∂∴==∂∂ ()()()2.0521,21,20.991120.0100.0510.02 1.02∂∂∴≈+∆+∆=+⨯+⨯=+=∂∂z zx y x y*6.设有厚度为，内高为，内半径为的无盖圆柱形容器，求容器外壳体积的近似值(设容器的壁和底的厚度相同).6.解 设容器底面积半径为r ，高为h则容器体积2V r h π=22,V Vrh r r hππ∂∂==∂∂ 22∴=+dV rhdr r dh ππ002,10,0.1,0.1r cm h cm r cm h cm ==∆=∆=()()22,102,1020.10.1400.140.1 4.4∴∆≈=⋅+⋅=⨯+⨯=V dV rh r πππππ*7. 测得直角三角形两直角边的长分别为7±0.1cm 和24±0.1cm ，试求利用上述二值来计算斜边长度时的绝对误差和相对误差.0.1cm 10cm 2cm7.解 设直角三角形的直角边长分别为,x y ，则斜边z =，zz xy∂∂==∂∂由题意007,24,0.1,0.1x y x y δδ====z ∴的绝对误差为()()7,247,247240.10.10.242525∂∂=+=⨯+⨯=∂∂z x y z z x y δδδz 的相对误差()7,240.240.009625=≈zz δ 习题7.41.设，，，求. 1.解 ()3222sin 22cos 23cos 6---∂∂=⋅+⋅=⋅-⋅=-∂∂x y x y t t du z dx z dy e t e t e t t dt x dt y dt2.设，而，，求. 2.解2123∂∂=⋅+⋅=+∂∂dz z dy z dV x dx u dx V dx2341-=x3.设，，，求，. 3.解 ()()222cos 2sin ∂∂∂∂∂=⋅+⋅=-+-∂∂∂∂∂z z u z v uv v y u uv y x u x v x()()2222222cos sin sin cos cos 2cos sin sin x y y x y y x y x y y y =-+-()23sin cos cos sin x y y y y =-()()()222sin 2cos z z u z v uv v x y u uv x y y u y v y∂∂∂∂∂=+=--+-∂∂∂∂∂ ()()()2222222cos sin sin sin cos 2cos sin cos x y y x y x y x y x y y x y =--+-()()3333cos sin 2cos sin sin cos x y y x y y y y =+-+2e x y u -=sin x t =3y t =d d u tarccos()z u v =-34u x =3v x =d d zx22z u v uv =-cos u x y =sin v x y =zx ∂∂z y∂∂4.设，而，，求，. 4.解 222ln 3∂∂∂∂∂⎛⎫=⋅+⋅=⋅+- ⎪∂∂∂∂∂⎝⎭z z u z v u y u v x u x v x v x()()()2322632ln 326ln 3x y y y y x y x y x x x x +⎛⎫=+-=+-- ⎪⎝⎭5.设求5.解 ()()1wf x xy xyz y yz x ∂'=++++∂()()()()1wf x xy xyz x xz x z f x xy xyz y∂''=+++=+++∂ ()()wf x xy xyz xy xyf x xy xyz z ∂''=++=++∂6.求下列函数的一阶偏导数(其中具有一阶连续偏导数):(1)；(2)；(3)；(4).6.解 （1）()()222222∂''=-⋅=-∂z f x y x xf x y x()()()222222∂''=-⋅-=--∂zf x y y yf x y y（2）121110∂'''=+⋅=∂u f f f x y y12122211u x x f f f f y y z y z ⎛⎫∂⎛⎫''''=-+=-+ ⎪ ⎪∂⎝⎭⎝⎭122220∂⎛⎫'''=⋅+-=- ⎪∂⎝⎭u y y f f f z z z （3）1231231∂''''''=⋅+⋅+⋅=++∂uf f y f yz f yf yzf x123230∂'''''=⋅+⋅+⋅=+∂uf f x f xz xf xzf y2ln z u v =32u x y =+y v x =zx ∂∂z y∂∂(),w f x xy xyz =++,,.w w wx y z∂∂∂∂∂∂f 22()z f x y =-,x y u f y z ⎛⎫= ⎪⎝⎭(,,)u f x xy xyz =22(,e ,ln )xy u f x y x =-123300∂''''=⋅+⋅+⋅=∂uf f f xy xyf z （4）1231231122∂''''''=⋅+⋅⋅+⋅=++∂xy xyu f x f e y f xf ye f f x x x()12312202∂'''''=⋅-+⋅+⋅=-+∂xy xy uf y f e x f yf xe f y7.求下列函数的二阶偏导数，，(其中具有二阶连续偏导数):(1)，(2). 7.解（1）22121222∂''''=⋅+⋅=+∂zf xy f y xyf y f x22121222∂''''=⋅+⋅=+∂zf x f xy x f xyf y()()222211112212222222∂'''''''''∴=+⋅+⋅+⋅+⋅∂zyf xy f xy f y y f xy f y x233341111221222422yf x y f xy f xy f y f '''''''''=++++ 23341111222244yf x y f xy f y f '''''''=+++()()2222111122212222222∂''''''''''=+⋅+⋅++⋅+⋅∂∂zxf xy f x f xy yf y f x f xy x y322223111122212222422xf x yf x y f yf x y f xy f ''''''''''=+++++ 32231111222222522xf x yf x y f yf xy f ''''''''=++++()2222211122212222222∂'''''''''=+++⋅+⋅∂zx f x x f xy xf xy f x f xy y43221112222424x f x yf xf x y f '''''''=+++（2）()()222222∂''=+⋅=+∂zf x y x xf x y x()()222222∂''=+⋅=+∂zf x y y yf x y y22zx∂∂2z x y ∂∂∂22z y ∂∂f 22(,)z f x y xy =22()z f x y =+()()()()2222222222222224∂''''''∴=+++⋅=+++∂zf x y xf x y x f x y x f x y x()()22222224∂'''=+⋅=+∂∂z xf x y y xyf x y x y()()()()2222222222222224∂''''''=+++⋅=+++∂zf x y yf x y y f x y y f x y y8.设其中F 是可微函数，证明8.解()()()cos sin sin cos cos cos sin sin ux F y x x x xF y x x∂''=+--=--∂ ()sin sin cos uF y x y y∂'=-∂ ()()cos cos cos cos sin sin cos cos sin sin cos u uy x x xF y x y yF y x x x y∂∂''∴+=--+-⎡⎤⎣⎦∂∂ ()()cos cos cos cos sin sin cos cos sin sin cos cos x y x yF y x x yF y x x y ''=--+-=.习题7.51.设,φ⎛⎫= ⎪⎝⎭x y z z 其中为可微函数，求∂∂+∂∂z z x y x y . 1.解 z是,x y函数由方程xx z y φ⎛⎫= ⎪⎝⎭确定。

8.12梯形断面土渠，底宽b =3m ，边坡系数m =2，水深h =1.2m ，底坡i =0.0002，渠道受到中等养护，试求通过流量。

解： ()()1.23 1.22 6.48A h b hm =+=⨯+⨯=（m 2）232 1.28.367b b χ=+=+=+⨯=（m ）0.7745AR χ==（m ），取0.0225n =（见教材153页表6-4）∴231 6.480.7745 3.4350.0225Q n⨯===（m 3/s ）答：通过流量 3.435Q =m 3/s 。

修建混凝土砌面（较粗糙）的矩形渠道，要求通过流量Q =9.7s m /3，底坡i =0.001，试按水力最优断面设计断面尺寸。

解： 对矩形断面，水力最优断面满足2b h =。

∴22A bh h ==，24b h h χ=+=，∴2242h hR h ==∵1Q An=0.001i =，0.017n =∴23222h h ⎛⎫⋅= ⎪⎝⎭，83110.0179.7 4.14nQ h ⨯=== 1.70h =（m ）， 3.40b =（m ） 答：断面尺寸为 1.70h =m ， 3.40b =m 。

.14修建梯形断面渠道，要求通过流量Q =1s m /3，边坡系数m =1.0，底坡i =0.0022，粗糙系数n =0.03，试按不冲允许流速[]max v =0.8s m /，设计断面尺寸。

解： ∵ max 0.8v v ≤=，∴0.8QA≤，max 1 1.250.8Q A v ≥==（m 2） 又∵[]max 1v v n =≤，即[]2max 3120.502n v R i ≤== 0.366R =∴有 21.25hb mh +≥20.366≤即有2 1.253.42hb h b ⎫+≥⎪⎬+≥⎪⎭解得：2 1.870.6840h h -+=0.51.37h ⎧=⎨⎩， 2.012.455b ⎧=⎨-⎩∴ 2.00b =（m ），0.5h =（m ）答：断面尺寸为 2.00b =m ，0.5h =m 。

习题7.11.在空间直角坐标系中，指出下列各点位置的特点.()0,5,0-A ；()0,3,3-B ；()3,0,6-C ；()0,0,4D ；()7,5,0-E ；()9,0,0F .【解】A 点在y 轴上；B 点在xoy 坐标面上；C 点在zox 坐标面上；D 点在x 轴上；E 点在yoz 坐标面上；F 点在z 轴上. 2.指出下列各点所在的卦限.()1,3,2-A ；()2,1,7--B ；()1,3,2---C ；()3,2,1--D .【解】A 点在第五卦限；B 点在第三卦限；C 点在第七卦限；D 点在第六卦限. 3.自点()2,3,1--M 分别作xoy 、yoz 、zox 坐标面和x 、y 、z 坐标轴的垂线，写出各垂足的坐标，并求出点M 到上述坐标面和坐标轴的距离.【解】()2,3,1--M 在xoy 坐标面上的垂足为()0,3,1-、在yoz 坐标面上的垂足为()2,3,0-、在zox 坐标面上的垂足为()2,0,1--；()2,3,1--M 在x 轴的垂足为()0,0,1-、在y 轴的垂足为()0,3,0、在z 轴的垂足为()2,0,0-；()2,3,1--M 到x 轴的距离为()132322=-+；()2,3,1--M 到y 轴的距离为()()52122=-+-；()2,3,1--M 到z 轴的距离为()103122=+-.3.已经点()2,1,3--M .求：（1）点M 关于各坐标面对称点的坐标；（2）点M 关于各坐标轴对称点的坐标；（3）点M 关于坐标原点的对称点的坐标. 【解】（1）()2,1,3--M 关于xoy 面对称点的坐标是(),2,1,3-； ()2,1,3--M 关于yoz 面对称点的坐标是(),2,1,3---；()2,1,3--M 关于zox 面对称点的坐标是(),2,1,3-.（2）()2,1,3--M 关于x 轴对称点的坐标是(),2,1,3； ()2,1,3--M 关于y 轴对称点的坐标是(),2,1,3--；()2,1,3--M 关于z 轴对称点的坐标是(),2,1,3--.（3）()2,1,3--M 关于坐标原点的对称点的坐标是(),2,1,3-. 5.求点()5,3,4-A 到坐标原点和各坐标轴的距离.【解】 ()5,3,4-A 到坐标原点距离为()25534222=+-+；()5,3,4-A 到x 轴的距离为()345322=+-；()5,3,4-A 到y 轴的距离为415422=+； ()5,3,4-A 到z 轴的距离为()53422=-+.6.在y 轴上求与点()7,2,3-A 和()7,1,3-B 等距离的点. 【解】设所求点为()0,,0y C .据题意，有 BC AC =，即()()()()=-+-+--22270230y ()()()()22270130--+-+-y解得 23=y .所以，所求之点为.0,23,0⎪⎭⎫ ⎝⎛C 7.已知三角形ABC 的顶点坐标分别为()3,2,1A 、()3,10,7B 和()1,3,1-C ，试证明 ∠BAC 为钝角. 【解】AB 边长()()()103321017222=-+-+-==AB c ；AC 边长()()()()3312311222=-+-+--=b ； BC 边长()()()()1173110371222=-+-+--=a .由余弦定理知cos ∠BAC ()010321171032222222<⨯⨯-+=-+=bc a c b ，所以，∠BAC 为钝角.8.试在xoy 面上求一点，使它到()5,1,1-A 、()4,4,3B 和()1,6,4C 各点的距离相等. 【解】设所求点为()0,,y x D .据题意，有 CD BD AD ==，即()()()()=-+--+-2225011y x ()()()222443-+-+-z y x()()()222164-+-+-=z y x解得 5,16-==y x .所以，所求之点为().0,5,16-D习题7.21.设平行四边形ABCD 的对角线向量b BD a AC ==,，试用a ，b 表示DA CD BC AB ,,,.【解】记平行四边形ABCD 的对角线的交点为O .()b a b a BD AC OD OC DC AB -=-=-=-==2121212121；同理可求出，()b a a b OC BO BC +=+=+=212121；()a b AB CD -=-=21；()b a BC DA +-=-=21.2.已知向量n m a 23-=，n m a +=.试用向量n m ,表示b a 32-. 【解】b a 32-()()n m n m n m 733232-=+--=.3.设c b a u 2-+=，c b a v +--=3.试用向量c b a ,,表示v u 32-. 【解】v u 32-()()c b a c b a c b a 71153322-+=+----+=. 4.设ABCDEF 是一个正六边形，AF b AB a ==,，试用a ，b 表示EF DE CD BC ,,,.【解】记六边形ABCDEF 的对角线的交点为O .则四边形ABOF 、CDEO 、DEFO 及ABCO 均为平行四边形.由向量加法的平行四边形法则知，b a AF AB AO BC +=+==； b AF CD ==；a BA BA AO DE -=-===；().b a BC EF +-=-=5.设向量k a j a i a a z y x ++=,，若它满足下列条件之一：（1）a 垂直于z 轴；（2）a 垂直于xoy 面；（3）a 平行于yoz 面.那么它的坐标有什么有何特征？ 【解】（1）因为a 垂直于z 轴，故0.=k a ，即0=z a ；（2）因为a 垂直于xoy 面，故a 平行于z 轴，从而a ∥{}1,0,0=k ，所以，0==y x a a . （3）a 平行于yoz 面，故垂直于x 轴，从而.a 0=i ，所以，0=x a . 6.已知向量{}7,4,4-=AB ，它的终点坐标为()7,1,2-B ，求它的起点坐标. 【解】设起点()z y x A ,,，则{}z y x AB ----=7,1,2，根据已知条件，有77,41,42=--=--=-z y x ，解得 .0,3,2==-=z y x 所以，起点坐标为 ()0,3,2-A .7.已知向量{}1,1,6-=a ，{}0,2,1=b .求 （1）向量b a c 2-=； （2）向量c 的方向余弦； （3）向量c 的单位向量. 【解】（1）c {}{}{}{}{}{}1,3,401,41,260,4,21,1,60,2,121,1,6--=----=--=--=.（2()()26134222=-+-+=.故，⎭⎬⎫⎩⎨⎧--==261,263,2640c c ，所以，向量c 的方向余弦为.261cos ,263cos ,264cos -=-==γβα（3）.向量c 的单位向量为⎭⎬⎫⎩⎨⎧--±261,263,264.8.试确定m 和n 的值，使向量k n j i a ++-=32和k j i m b 26+-=平行. 【解】因为a ∥b ，所以2632nm =-=-，解得 .1,4-==n m9.已知向量{}12,9,8-=b 及点()7,1,2-=A ，由点A 作向量AM 34=， 且AM 与b 的方向相同.求向量AM 的坐标表达式及点M 的坐标.【解】设()z y x M ,,，则{}7,1,2-+-=z y x AM .据题意知AM ∥b 且与b 同向，因此有λ=--=+=-1279182z y x ，① 且 0>λ. ② 由①式得 λλλ127,91,82=-++=-z y x . 又已知34=，故有 ()()()341298222=++λλλ. ③③式化简得4115628922=⇒=λλ，解得 2=λ或2-=λ（舍）.所以，.17,17,18-===z y x因此AM {}24,18,16-=，()17,17,18-=M . 10.已知点()4,2,1--A 和点()z B ,2,6-9=，求z 的值. 【解】()(){}{}4,4,74,22,16+-=------=z z AB .9=，得()()9447222=++-+z ，化简得082=+z z ，解之，得 0=z 或.8-=z11.已知点()1,2,41M 和点()2,0,32M ，计算向量21M M 的模、方向余弦和方向角. 【解】{}{}1,2,112,20,4321--=---=M M ；()()2121222=+-+-=. 因为{}⎭⎬⎫⎩⎨⎧--=--==21,22,211,2,12121021M M M M .所以21M M 的方向余弦是.21cos ,22cos ,21cos =-=-=γβα 方向角为.3cos ,43,32πγπβπα===12.求与下列向量a 同方向的单位向量0a . （1）{}1,4,2-=a ；（2）k j i a ++-=32.【解】（1()21142222=+-+=，所以{}⎭⎬⎫⎩⎨⎧-=-==211,214,2121,4,22110a a .（2()14132222=++-=，所以.141,143,1421410⎭⎬⎫⎩⎨⎧-==a a 习题7.31.设向量k j i a 23--=，k j i b -+=2.求：（1）b a .；（2）b a ⨯；（3）()()b a 32⨯-；（4）()b a 2⨯；（5）向量b a ,的夹角. 【解】（1）()()()3122113.=-⨯-+⨯-+⨯=b a ；（2）k j i j b a 7521++=-=⨯；（3）()()()1836.63.2-=⨯-=-=-b a b a ；（4）()()k j i b a b a 1421022++=⨯=⨯；（5）()()14213222=-+-+=()6121222=-++=，故21236143.,cos =⨯==⎪⎪⎭⎫ ⎝⎛∧b a b a ，所以向量b a ,的夹角为 .2123arccos ,=⎪⎪⎭⎫ ⎝⎛∧b a 2.设向量a ，b ，c 为单位向量，且满足0=++c b a ①.求：a c c b b a ...++. 【解】由①式得()0.=++c b a a ；()0.=++c b a b ；()0.=++c b a c .即 0..=++c a b a ； ②0..=+c b a b ； ③0..=++b c a c ； ④ 将②、③、④相加得()03...2=+++a c c b b a所以，.23...-=++a c c b b a3.已知点()2,1,1-A ，()2,6,5-B ，()1,3,1-C 求： （1）同时与AB 及AC 垂直的单位向量； （2）ABC ∆的面积. 【解】（1）AB AC ⨯{}16,12,151612153405=++=--=k j i kj .25161215222=++=. 所以，同时与AB 及AC 垂直的单位向量为 {}⎭⎬⎫⎩⎨⎧±=±=⨯±2516,2512,25116,12,15251AC AB .（2）ABC ∆的面积225==. 4.设{}2,5,3-=a ，{}4,1,2=b ，则当实数λ与μ有什么关系时，能使b a μλ+与z 轴垂直？【解】{}μλμλμλμλ42,5,23+-++=+b a .要使b a μλ+与z 轴垂直，只须b a μλ+与{}1,0,0=k 垂直，于是有()042.=+-=+μλμλk b a ，即 .2μλ=5.设质量为100kg 的物体从点()8,1,31M 沿直线移动到点()2,4,1M ，计算重力所做的功.【解】{}6,3,21--==M M s ，{}{}980,0,01008.9,0,0=⨯-=F .所以，{}{}58806,3,2.980,0,0.=---==s F W （焦耳）.6.已知{}3,2,1-=a ，{}1,4,2-=b ，{}0,2,4=c ，b a ⨯是否与c 平行？【解】{}0,5,1005104221--=+--=--=⨯k j i j i b a ；因为c b a 52-=⨯，所以，b a ⨯与c 平行.7.求一个单位向量使其同时垂直向量{}0,1,1=a 和{}1,1,0=b .【解】{}1,1,111-=+-==⨯k j i j b a .()3111222=+-+=. 所以同时垂直向量a 和b 向量的单位向量为 {}1,1,131-±=⨯±b .习题7.41.求过点()1,0,3-且与平面012573=-+-z y x 平行的平面方程.【解】已经平面的法向量为{}5,7,3-=n .据题意知，所求平面的法向量可也取作n .所以据平面的点法式方程，所求平面即为 ()()()()0150733=--+---z y x . 化简得 04573=-+-z y x .2.求过点()6,9,20-M 且与连接坐标原点O 及0M 的线段0OM 垂直的平面方程. 【解】据题意知，所求平面的法向量可也取作{}6,9,20-==OM n .所以据平面的点法式方程，所求平面即为 ()()()()0669922=----+-z y x . 化简得 0121692=--+z y x .3.求过点()1,1,1-、()2,2,2--和()2,1,1-三点的平面方程. 【解】据平面的三点式方程，所求平面为()()()0121111121212111=---------------z y x . 即 ()()()0161913=++-+--z y x . 化简得 023=--z y x .4.求平面0522:=++-z y x π与坐标面xoy 、yoz 及zox 的夹角的余弦. 【解】平面π的法向量为{}1,2,2-=n ；xoy 面的法向量为{}1,0,0=k .由公式，平面π与xoy31=； 同理， 平面π与yoz32=； 平面π与zox32-=.5.求点()1,2,1平面01022:=-++z y x π的距离. 【解】12211012221222=++-⨯+⨯+=d .6.求两平行平面0:11=+++D Cz By Ax π与0:22=+++D Cz By Ax π之间的距离.【解】在1π上任取一点()1111,,z y x M ，则1M 到2π的距离d 就是所求1π与2π之间的距离.由点到平面的距离公式得 2222111CB A D Cz By Ax d +++++=. ①又11π∈M ，故有 0:11111=+++D Cz By Ax π，即1D Cz By Ax -=++. ②将②代入①，立得 22212CB A D D d ++-=.7.一平面通过()1,1,11M 和()11,02-M 两点，且垂直于平面0=++z y x .求该平面方程.【解】已知平面0=++z y x 的法向量为{}1,1,1=n ，{}2,0,121--=M M .据题意，可取所求平面的法向量为{}1,1,2211120121--=--=--=⨯k j i kj i n M M . 所以，所求平面方程为()()()011.11.2=-----z y x ，即 02=--z y x . 8.求满足下列条件的平面方程： （1）过点()2,1,3--和z 轴；（2）过点()2,0,4-及()7,1,5且平行于x 轴； （3）过点()3,5,2-，且平行于zox 面；（4）过点()1,0,1-且同时平行于向量k j i a ++=2，j i b -=. 【解】（1）根据题意，可设所求平面的一般式方程为 0:=+By Ax π. ① 又将点()2,1,3--的坐标代入①，得03=+-B A ，即 A B 3=. 因此，所求平面π为.03=+Ay Ax ②注意到0≠A （否则π的法向量为零向量），所以②两边除以A ，得到 03:=+y x π.（2）根据题意，可设所求平面的一般式方程为 0:=++D Cz By π. ①又将点()2,0,4-及()7,1,5的坐标分别代入①，得⎩⎨⎧=++=+-.07,02D C B D C ，故⎩⎨⎧-==.9,2C B C D . 因此，所求平面π为.029=++-C Cz Cy ②注意到0≠C （否则π的法向量为零向量），所以②两边除以C ，得到 029:=++-z y π.（3）根据题意，可设所求平面的一般式方程为 0:=+D By π. ① 又将点()3,5,2-的坐标代入①，得05=+-D B ，即 B D 5=. 因此，所求平面π为.05=+B By ②注意到0≠B （否则π的法向量为零向量），所以②两边除以B ，得到 05:=+y π.（4）根据题意，可设所求平面的一般式方程为0:=+++D Cz By Ax π. ① 其法向量为{}C B A n ,,=. 将点()1,0,1-的坐标代入①，得0=+-D C A . ② 又因为π同时平行于向量k j i a ++=2，j i b -=，故n 同时垂直于向量k j i a ++=2，j i b -=，于是有.02=++C B A ③ .0=-B A ④ ②、③、④联立得到A D A C AB 4,3,-=-== 因此①成为043:=--+A Az Ay Ax π . ⑤注意到0≠A （否则π的法向量为零向量），所以⑤两边除以A ，得到 043:=--+z y x π.9.平面在y 、z 轴上的截距分别为30，10，且与{}3,1,2=r 平行，求该平面方程. 【解】根据题意，可设所求平面的一般式方程为0:=+++D Cz By Ax π. ① 其法向量为{}C B A n ,,=.因为π在y 、z 轴上的截距分别为30，10，故π过点()0,30,0及(),10,0,0.将此两点坐标代入①得030=+D B . ② 及 010=+D C . ③ 又已知π与{}3,1,2=r 平行，故n 垂直于向量r ，于是有 032=++C B A . ④ ②、③、④联立得到B A BC BD 5,3,30-==-=. 因此①成为03035:=-++-B Bz By Bx π. ⑤注意到0≠B （否则π的法向量为零向量），所以⑤两边除以B ，得到 03035:=-++-z y x π. 10.指出下列各平面的特殊位置，并画出各平面. （1）013=-x ； （2）012=-+z y ； （3）02=+z x ； （4）135=-+z y x .【解】（1）因方程中z y ,前面的系数为零，故平面013=-x 平行于yoz 面； （2）因方程中x 前面的系数为零，故平面012=-+z y 平行于x 轴；（3）因方程中没有常数项，且y 前面的系数为零，故平面02=+z x 通过y 轴；012=-+z y 02=+z x ；（4）135=-+z y x 可化为113151=-++z y x ，故135=-+z y x 是在x 轴、y 轴、z 轴上的截距分别为51、31和1-的平面.习题7.51.用点向式方程及参数式方程表示直线⎩⎨⎧=++=+-.42,1:z y x z y x L【解】任取方程组的一组解⎪⎩⎪⎨⎧===.1,1,1z y x 则有，L 过点()1,,1,10M .可取直线的方向为{}3,1,232121121-=++-=-=⨯k j i j in n . 所以，所求直线L 的点向式方程为311121-=-=--z y x . 进一步，L 的参数式方程为⎪⎩⎪⎨⎧+=+=-=.31,1,21t z t y t x2.求过()1,2,31-P 、()2,0,12-P 两点的直线方程. 【解】可取直线的方向为 {}1,2,421-==P P s . 故所求直线为.112243-=+=--z y x 3.求过点()3,1,4-且平行于直线51123-==-z y x 的直线方程. 【解】根据题意知，可取所求直线的方向为{}5,1,2=s .故所求直线为.531124-=+=-z y x 4.求过()1,32-且垂直于平面0132=+++z y x 的直线方程.【解】可取直线的方向为 {}1,3,2=s . 故所求直线为.113322-=+=-z y x 5.求过点()2,1,00M 且与直线21111zy x =--=-垂直相交的直线方程.【解】 过点()2,1,0且与直线21111zy x =--=-垂直的平面π为()()()02210.1:=-+---z y x π.即 032:=-+-z y x π . ① 化直线21111zy x =--=-为参数式得 ⎪⎩⎪⎨⎧=-=+=.2,1,1t z t y t x ②将②代入①，有()()()032211=-+--+t t t . ③ 解得 21=t . 故直线21111z y x =--=-与平面π的交点为⎪⎭⎫⎝⎛1,21,231M . 因此所求直线的方向为⎭⎬⎫⎩⎨⎧--==1,21,2310M M s ∥{}2,1,3-.故所求直线为.221130-=-=--z y x 6. 过点()0,2,10-M 向平面012=+-+z y x 作垂线，求垂足坐标. 【解】 过点()0,2,10-M 且与平面012=+-+z y x 垂直的直线L 为.12211:--=-=+z y x L ① 化直线L 为参数式得⎪⎩⎪⎨⎧-=+=+-=.,22,1t z t y t x ②将②代入平面012=+-+z y x 方程中，得()()()012221=+--+++-t t t . ③解得 32-=t .故垂足坐标为⎪⎭⎫⎝⎛-32,32,351M .7.求直线⎩⎨⎧=-+-=-+-,0123,09335:1z y x z y x L 与⎩⎨⎧=-++=+-+.01383,02322:2z y x z y x L 的夹角θ.【解】1L 的方向为{}1,4,34323351-=-+=--=k j i j is ； 2L 的方向为{}10,5,101051083222-=+-==k j i j is ∥{}2,1,2-. 因为()()0211423.21=⨯-+-⨯+⨯=s s ，所以1L 与2L 垂直，从而2πθ=.8.求直线21121:+=-=-z y x L 与平面02:=+-z y x π的夹角θ. 【解】1L 的方向为{}2,1,2-=s ，平面π的法向量为{}2,1,1-=n . ()()7221112.=⨯+-⨯-+⨯=n s .()3212222=+-+=.()6211222=+-+=.故637sin ⨯==θ，所以，637arcsin⨯=θ.9.求过点()2,0,10-M 且垂直于平面032:=+-z y x π的直线方程. 【解】根据题意知，所求直线L 的方向向量即为平面π之法向量，即 {}3,12-=s .所以，由点向式方程知，所求直线为321021:+=--=-z y x L . 10.设平面π过直线130211:1--=-=-z y x L ，且平行于直线11122:2zy x L =-=+，求平面π的方程.【解】显然面π过点()3,,2,10M .可取面π的法向量为{}1,3,13120121-=+-==⨯=k j i j is s n . 所以，平面π的方程为()()()03.12.31.1=-+---z y x . 化简得023:=++-z y x π.11.求过点()1,2,10P 和直线⎩⎨⎧=--=-.032,6:z y x z x L 的平面π的方程.【解】直线L 的参数方程为⎪⎩⎪⎨⎧-=+-==.6,9,:x z x y x x L显然L 过点()6,9,01-P ，且L 的方向为{}1,11-=s . 根据题意，可取平面π的法向量为{}6,6,0660117110--=--=--=⨯=k j i j i s P P n ∥{}1,1,0. 所以，平面π的方程为()()()01.12.11.0=-+-+-z y x . 化简得03:=-+z y π.习题7.61.指出下列方程在平面解析几何与空间解析几何中分别表示何种几何图形.（1）1=-y x ；（2）x y 22=；（3）122=-y x ；（4）1222=+y x . 【解】（1）1=-y x 在平面解析几何中表示一条直线，在空间解析几何中表示一张平行于z 轴的平面；（2）x y 22=在平面解析几何中表示一条抛物线，在空间解析几何中表示一张抛物柱面；（3）122=-y x 在平面解析几何中表示一条双曲线，在空间解析几何中表示一张双曲柱面；（4）1222=+y x 在平面解析几何中表示一条椭圆曲线，在空间解析几何中表示一张椭圆柱面.2.写出下列曲线绕指定坐标轴旋转一周而得到的旋转曲面的方程. （1）zox 面上的抛物线x z 52=绕x 轴旋转一周； （2）xoy 面上的双曲线369422=-y x 绕y 轴旋转一周； （3）yoz 面上的直线0132=+-z y 绕z 轴旋转一周. 【解】（1）zox 面上的抛物线x z 52=绕x 轴旋转一周得到的曲面是 ()x zy 5222=+±，即x z y 522=+.（2）xoy 面上的双曲线369422=-y x 绕y 轴旋转一周得到的曲面是 ()36942222=-+±yz x ，即36494222=+-z y x .（3）yoz 面上的直线0132=+-z y 绕z 轴旋转一周而得到的曲面是 ()013222=+-+±z y x ，即()()222134-=+z y x .3.说明下列旋转曲面是怎样形成的.（1）1994222=++z y x ；（2）14222=+-z y x ；（3）1222=--z y x ； 【解】（1）1994222=++z y x 由曲线⎪⎩⎪⎨⎧==+,0,19422z y x 绕x 轴旋转一周而形成；或由曲线⎪⎩⎪⎨⎧==+,0,19422y z x 绕x 轴旋转一周而形成. （2）14222=+-z y x 由曲线⎪⎩⎪⎨⎧==-,0,1422z y x 绕y 轴旋转一周而形成；或由曲线⎪⎩⎪⎨⎧==-,0,1422x y z 绕y 轴旋转一周而形成. （3）1222=--z y x 由曲线⎩⎨⎧==-,0,122z y x 绕x 轴旋转一周而形成；或由曲线⎩⎨⎧==-,0,122y z x 绕x 轴旋转一周而形成. 4.指出下列各方程所表示的曲面.（1）14416916222=++z y x ；（2）144944222=+-z y x ；（3）z y x 729422=-； （4）16922=+z y ；（5）22z y x --=；（6）224y z x =+； （7）36249222=++z y x ；（8）444222=-+x y z . 【解】（1）原方程可化为()1169222=++y z x. 所以，原方程表示的是旋转椭球面.（2）原方程可化为1163838222=+-z y x . 所以，原方程表示的是双叶双曲面.（3）原方程可化为81822y x z -= 所以，原方程表示的是双曲抛物面，即马鞍面.（4）原方程可化为11691622=+z y . 所以，原方程表示的是椭圆柱面. （5）原方程可化为()22z y x +-=. 所以，原方程表示的是旋转抛物面. （6）原方程可化为4122z y x -=.所以，原方程表示的是双曲抛物面，即马鞍面. （7）原方程可化为11894222=++z y x . 所以，原方程表示的是椭球面.（8）原方程可化为1141222=-+x z y . 所以，原方程表示的是单叶双曲面.习题7.71.求球心在()3,2,1，半径为3的球面与平面5=z 的交线方程（写出一般式方程和参数式方程），并求出该曲线绕z 轴旋转一周而成的旋转曲面的方程.【解】（一）球心在()23,1，半径为3的球面方程为 ()()()9321222=-+-+-z y x .故球面与平面5=z 的交线的一般式方程为()()()⎩⎨⎧==-+-+-Γ.5,9321:222z z y x即()()⎩⎨⎧==-+-Γ.5,521:22z y x化为参数式方程为[]π2,0.5,sin 52,cos 51:∈⎪⎪⎩⎪⎪⎨⎧=+=+=Γt z t y t x .（二）利用公式()()()()()[][]()πθβαθθ2,0,,.,sin ,cos 2222∈∈⎪⎪⎩⎪⎪⎨⎧=+=+=t t z z t y t x y t y t x x . Γ绕z 轴旋转一周而成的旋转曲面的方程为 [][]()πθπθθ2,0,2,0.5,sin sin 54cos 5210,cos sin 54cos 5210∈∈⎪⎪⎩⎪⎪⎨⎧=++=++=t z t t y t t x .2.分别求出母线平行于x 轴、y 轴且通过曲线()()⎪⎩⎪⎨⎧=+-=++Γ2,01,162:222222z y x z y x 的柱面方程.【解】 （一）（1）、（2）联立消去x ，得 16322=-z y .所以，母线平行于x 轴且通过曲线Γ的柱面为16322=-z y . （二）（1）、（2）联立消去y ，得 162322=+z x .所以，母线平行于x 轴且通过曲线Γ的柱面为162322=+z x . 3.指出下列方程所表示的曲线.（1）⎩⎨⎧==++;3,25222x z y x （2）⎩⎨⎧==++;1,3694222y z y x（3）⎩⎨⎧-==+-;3,254222x z y x （4）⎩⎨⎧==+-+.4,08422y x z y【解】（1）表示平面3=x 上的圆周曲线1622=+z y ；（2）表示平面1=y 上的椭圆19323222=+zx ；（3）表示平面3-=x 上的双曲线141622=-y z ； （4）表示平面4=y 上的抛物线642-=x z .4.求()()⎪⎩⎪⎨⎧=++=++Γ2,21,:2222222Rz z y x R z y x 在三个坐标面上的投影曲线. 【解】 （一）（1）、（2）联立消去z 得 22243R y x =+. 所以，Γ在xoy 面上的投影曲线为⎪⎩⎪⎨⎧==+.0,43222z R y x （二）（1）、（2）联立消去y 得R z 21=. 所以，Γ在zox 面上的投影曲线为 .23.0,21R x y R z ≤⎪⎩⎪⎨⎧== （三）（1）、（2）联立消去x 得 R z 21=.所以，Γ在yoz 面上的投影曲线为.23.0,21R y x R z ≤⎪⎩⎪⎨⎧== 5.画出下列各曲面所围立体的图形. （1）0,22==z x y 及1224=++zy x ；（2）0,,222==+=z y x y x z 及1=x . 【解】略.6.求由球面224y x z --= ①和锥面()223y x z += ②所围成的立体在xoy 面上的投影区域.【解】联立①、②消去z 得 122=+y x 故Γ在xoy 面上的投影曲线为⎩⎨⎧==+.0,122z y x所以，球面和锥面所围成的立体在xoy 面上的投影区域为(){}1|,22≤+=y x y x D . 7.写出圆锥面22:y x z S +=的参数方程.【解】().20,0.,sin ,cos πθθθ≤≤+∞<<⎪⎩⎪⎨⎧===r r z r y r x习题7.81.设向量值函数()k t j t i t t r ++=sin cos ，求()t r t 4lim π→. 【解】()t r t 4lim π→k j i k t j t i t t t t 42222lim sin lim cos lim 444ππππ++=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=→→→. 2.设空间曲线C 的向量函数为(){}t t t t t r 62,34,122--+=，R t ∈.求曲线C 在与20=t 相应的点处的单位切向量.【解】因(){}64,4,2-='t t t r ，故C 相应20=t 的点处的切向量为(){}2,4,42='r .C 相应20=t 的点处的单位切向量为(){}.31,32,322,4,4612⎭⎬⎫⎩⎨⎧±=±='r 3.求曲线32,,:t z t y t x ===Γ在点)1,1,1(0M 处的切线方程和法平面方程. 【解】0M 对应参数1=t .Γ在0M 点处的切线方向为 ()()(){}|1,,='''=t t z t y t x s {}{}3,2,13,2,1|12===t t t .所以，Γ在0M 点处的切线方程为 312111-=-=-z y x . 法平面为()()()01.31.21.1=-+-+-z y x ，即 0632=-++z y x .4.在曲线32,,:t z t y t x ===Γ上求一点，使在该点处的切线平行于平面y x 2:+π4=+z .【解】平面y x 2+4=+z 的法向量为{}1,2,1=n .在Γ上任取一点()0000,,z y x M ，并设0M 对应参数0t t =.Γ在0M 点处的切线方向为()()(){}000,,t z t y t x s '''={}{}20023,2,13,2,1|0t t t t tt ===. 由题意，欲使0M 点处的切线与平面π平行，只须s 与n 垂直，为此令200341.0t t n s ++==，即0341200=++t t .解之得， 10-=t 或 310-=t .所以，所求点为()1,1,10---M 或⎪⎭⎫⎝⎛-271,91,310M .5.求曲线⎰=tu udu e x C 0cos :，t t y cos sin 2+=，t e z 31+=在0=t 处的切线方程和法平面方程.【解】参数0=t 对应曲线C 上的点()2,1,00M .C 在0M 点处的切线方向为()()(){}|,,='''=t t z t y t x s {}{}3,2,13,sin cos 2,cos |3=-==t tt e t t t e .所以，Γ在0M 点处的切线方程为 322110-=-=-z y x . 法平面为()()()02.31.20.1=-+-+-z y x ，即 0832=-++z y x .6.已知(){}t t t t r 2,1,12-+=表示空间一质点在时刻t 的位置，求质点在时刻t 的速度和加速度向量，并求质点在指定时刻1=t 的速率和运动方向.【解】（一）时刻t 的速度向量为()()()()(){}2,2,12,1,12t t t t t r t v =⎭⎬⎫⎩⎨⎧''-'+='=； 时刻t 的加速度向量为()()()()(){}{}0,2,02,2,1='''=''=t t r t a .（二）1=t 的速度为(){}2,2,11=v )32211222=++=. 1=t 的速度为(){}2,2,11=v()⎭⎬⎫⎩⎨⎧=32,32,311.复习题71.填空题（1）设b a ,为非零向量，若0.=b a ，则必有a ⊥b .（2）设b a ,为非零向量，若0=⨯b a ，则必有a ∥b .（3）若直线l 的方向向量s 与平面π的法向量n 互相平行，则直线l 与平面π必 垂直.（4）点()1,5,3P 到平面07623=+++z y x 的距离732.（5）若动()z y x M ,,到定点()5,0,0的距离等于它到x 轴的距离，则该动点的轨迹方程为25102-=-z x .（6）直线⎪⎩⎪⎨⎧+=--=+=.31,1,2t z t y t x 与平面0765=-+-z y x 的位置关系是相交但不垂直.【解】直线l 的方向向量为{}3,1,1-=s .平面的法向量为{}6,5,1-=n .因为024.≠=n s ，且s 与n s .的坐标分量不成比例， 所以直线l 与平面π相交. 2.判断题.（1）若c a b a ..=，则必有c b =.（⨯）【解】取i a =，j b =，k c =，即知上述命题是错误的 . （2）若c a b a ⨯=⨯，则必有c b =.（⨯）【解】取i a =，j b =，k c =，即知上述命题是错误的 . （3）若c a b a ..= ① 且c a b a ⨯=⨯ ② ，则必有c b =.（⨯）【解】取0=a ，j b =，k c =，即知上述命题是错误的 .【书后答案有误】. 【注意：如果假定c b a ,,均为非零向量，则上述命题是正确的，其理由如下：由①式得 ()0.=-c b a ，说明a 与c b -垂直； 由②式得 ()0=-⨯c b a ，说明a 与c b -平行.因为a 为非零向量，故c b -必为零向量，从而c b =. （4）设b a ,为非零向量，则必有a b b a ..=.（√） （5）设b a ,为非零向量，则必有a b b a ⨯=⨯..（⨯）3.已知直线⎩⎨⎧=+--=+++.03102,0123:z y x z y x l 平面024:=+-z y x π，则直线l 与平面π的位置关系为（B ）A. 平行于平面π C. 在平面π上B. 垂直于平面π D. 与平面π斜交.【解】在直线l 上任取一点⎪⎭⎫⎝⎛-0,71,7100M .直线l 的方向向量为k j i j i n n s 71428123121-+-=-=⨯=∥{}1,2,4-. 平面的法向量为{}1,2,4-=n .因为s ∥n ，所以直线l 与平面π垂直.4.设c b a u 2+-=，c b a v ---=3，试用c b a ,,表示v u 32-. 【解】v u 32-()c b a 22+-=()c b a ----33c b a 775++=.5.设点C 为线段AB 上一点，且AC CB 2=，O 为AB 外一点，记OA a =，OB b =，OC c =，试用b a ,来表示c .【解】由题意知，a b OA OB AB -=-=，a b AB AC 313131-==. 所以，a b a a b OA AC AO AC c 32313131+=+⎪⎭⎫ ⎝⎛-=+=-=.6.已知k j i a +-=32，k j i b 3+-=，j i c 2-=.计算： （1）()()b c a c b a ..-； （2）()()c b b a +⨯+. 【解】（1）()()8311312.=⨯+-⨯-+⨯=b a ； ()()8302312.=⨯+-⨯-+⨯=c a .所以，()()()()k j k j b c b c b c a c b a 24838888..--=--=-=-=-.（2）k j i j ib a +--=--=⨯581132；k j i j ic a -+=--=⨯22132；k j i j ic b -+=--=⨯362111. 所以，()()c b b b c a b a c b b a ⨯+⨯+⨯+⨯=+⨯+()k j i +--=58 ()k j i -++2 ()k j i -++36 k j --=. 【或者这样做：k j i b a 443+-=+，k j i c b 332+-=+. 所以()()c b b a +⨯+.3243k j j i--=--=】 7.已知{}2,1,2=a ，{}10,1,4-=b ，a b c λ-=，且a ⊥c ，求实数λ. 【解】{}λλλλ210,1,24----=-=a b c .因为a ⊥c ，所以 ()()()λλλ210211242.0-⨯+--⨯+-⨯==c a ，即 0927=-λ .解之得 .3=λ8.设{}1,2,3-=a ，{}2,1,1-=b ，求：（1）()()b a 72⨯；（2）i a ⨯. 【解】（1） k j i j i b a 5731123--=-=⨯{}5,7,3--=. 所以，()()b a 72⨯()b a ⨯=14{}{}70,98,425,7,314--=--=.（2）{}2,1,020001123--=--=-=⨯k j i kji i a .9.3=1=，6π=，计算：（1）b a +与b a -之间的夹角；（2）以b a 2+与b a 3-为邻边的平行四边形的面积.【解】232313,.cos .=⨯⨯=⎪⎪⎭⎫ ⎝⎛=∧b a b a . ①（1+()71232322=+⨯+===；-()11232322=+⨯-===； ()()().213 (2)2=-=-=-+b b a a b a b a设b a +与b a -之间的夹角为θ，则有()(72172cos =⨯==θ，所以72arccos =θ.（2+()1314234322=⨯+⨯+===；-()319236322=⨯+⨯-===； ()()().2916233.6..3.222-=⨯--=--=-+b b b a a a b a b a设b a 2+与b a 3-之间的夹角为θ，则有()(39293132932cos -=⨯-==b a b a θ，故 2613539291cos 1sin 22=⎪⎪⎭⎫⎝⎛-=-=θθ. 所以由三角形的面积公式知，以b a 2+与b a 3-为邻边的平行四边形的面积为.32526135313sin 2=⨯⨯=⎥⎦⎤⨯-+=θS10.已知点()0,0,1A 及()1,2,0B ，试在z 轴上求一点C ，使ABC ∆的面积最小. 【解】过点()0,0,1A 及()1,2,0B 直线l 的方向即为{}1,2,1-==AB s .l 的方程为 1211:zy x l ==--. 设点()z C ,0,0，则{}2,1,22101---=--=⨯z z ji s AC . 点C 距l 的距离为()()()6212222-+-+-==z z d 65245152+⎪⎭⎫ ⎝⎛-=z明显地，当51=z 时，d 取到最小值55254=. 所以，ABC ∆的面积最小值为 53055262155221=⨯⨯==∆S ABC . 所求点.51,0,0⎪⎭⎫ ⎝⎛C11.求过点()2,1,3--且与平面01235=-+-z y x 平行的平面方程. 【解】可取所求平面的法向量与已知平面相同，即为{}3,5,1-=n . 所以，所求平面方程为()()()0231.53.1=+++--z y x ，即 .0235=-+-z y x12.求过点()1,2,1且垂直于平面0=+y x 和05=+z y 的平面方程. 【解】可取所求平面的法向量为k j i j in n n 5501121+-==⨯=. 所以，所求平面方程为()()()0152.11.1=-+---z y x ，即 .045=-+-z y x 13.求满足下列条件的平面方程.（1）过点()2,1,1--M 和()1,1,3N 且垂直于平面0532:=-+-z y x π； （2）过点()3,3,2-M 且平行于xoy 面. 【解】（1）可取所求平面的法向量为k j i j is MN n 63122122--=-=⨯=∥{}2,1,4--. 所以，所求平面方程为()()()02.21.11.4=+-+--z y x ，即 .0924=---z y x（2）根据题意，可设所求平面的一般式方程为 .0=+D Cz将点()3,3,2-M 的坐标代入平面方程得.03=+D C 即 ()03≠-=C C D . 所以，所求平面为.03=-C Cz 化简得.03=-z14.求过点()3,0,2-且与直线⎩⎨⎧=+-+=-+-.01253,0742:z y x z y x l 垂直的平面方程.【解】直线l 的方向为k j i j in n s 111416532121++-=-=⨯=. 所以，所求平面方程为()()()03.110142.16=++-+--z y x ，即.065111416=+++-z y x15.求过点()1,3,20-M 和直线⎩⎨⎧=+-=--.062,0165:z y y x l 的平面方程. 【解】化直线l 的为参数式方程⎪⎩⎪⎨⎧+==+=.62,,165:y z y y y x l .因此直线l 过点()6,0,161M .可取所求平面的法向量为{}1,3,131531410--=--==⨯=k j i j is M M n . 所以，所求平面方程为 ()()()01.13.32.1=--+--z y x ，即.0103=---z y x 【书后答案有误】.16.求过点()1,1,1M 且与直线42135:-=+=-z y x l 平行的直线方程. 【解】根据题意知，可取所求直线的方向为{}4,2,3-=s .所以，所求直线为412131--=-=-z y x . 17.求过点()4,2,00M 且与两平面12:1=+z x π和23:2=-z y π都平行的直线方程.【解】根据题意知，可取所求直线的方向为{}1,3,232100121-=++-==⨯=k j i j in n s . 所以，所求直线为143220-=-=--z y x . 18.求下列旋转曲面方程.（1）⎩⎨⎧==.0,22x y z 绕y 轴旋转一周； （2）⎪⎩⎪⎨⎧==+.0,1422y z x 绕z 轴旋转一周.【解】（1）由公式，知⎩⎨⎧==.0,22x y z 绕y 轴旋转一周生成曲面 ()y z x 2222=+±，即 222z x y += ，为椭圆抛物面.（2）由公式，知⎪⎩⎪⎨⎧==+.0,1422y z x 绕z 轴旋转一周生成曲面 ()142222=++±z y x ，即 14222=++z y x ，为椭球面. 19.指出下列各方程所表示的是何种曲面.（1）11694222=++z y x ； （2）94322y x z +=； （3）64416222=-+z y x ； （4）3694222-=+-z y x .【解】（1）表示椭球面； （2）表示椭圆抛物面；（3）可化为164164222=-+z y x ，故（3）表示单叶双曲面； （4）可化为14369222-=-+z y x ，故（4）表示双叶双曲面. 20.求曲线⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=Γ.,1,1:2t z t t y t t x ① 对应于1=t 处的切线方程. 【解】将1=t 代入① ，得切点坐标为⎪⎭⎫ ⎝⎛1,2,21. 又切向量为()|12,1,1=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧'⎪⎭⎫ ⎝⎛+'⎪⎭⎫ ⎝⎛+=t t t t t t s ()⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+==2,1,412,1,11|122t t t t ∥{}8,4,1-.所以，曲线Γ对应于1=t 处的切线方程为8142121-=--=-z y x .。

第七章 机械能守恒定律及其守恒7.1 追寻守恒量举出生活中的一个例子，说明不同形式的机械能之间可以相互转化. 你的例子是否向我们提示，转化过程中能的总量保持不变？答:做自由落体运动的物体在下落过程中，势能不断减少，动能不断增加，在转化的过程中，动能和势能的总和不变.7.2 功1. 图7.2-8表示物体在力F 的作用下在水平面上发生了一段位移x ，分别三种情形下力F 对物体做的功. 设这三种情形下力F 和位移x 的大小都是一样的；F=10N ，x=2m. 角θ的大小如图所示.17.32J －17.32J 17.32J2. 用起重机把重量为2.0×104N 的物体匀速地提高了5m ，钢绳的拉力做了多少功？重力做了多少功？物体克服重力做了多少功？这些力做的总功是多少？拉力做功W 1＝－1×105 J ，重力做功W 2＝－1×105J ，物体克服重力功1×105J ，总功是0J3. 一位质量m=60kg 的滑雪运动员从高h=10m 的斜坡自由下滑. 如果运动员在下滑过程中受到的阻力F=50N ，斜坡的倾角θ=300，运动员滑至坡底的过程中，所受的几个力做的功各是多少？这些力做的总功是多少？重力做功:6.0×103J 支持力做功:0 阻力做功:－1.0×103J 总功:5.0×103J.4. 一个 重量为10N 的物体，在15N 的水平拉力作用下，一次在光滑水平面上移动0.5m ，另一次在粗糙水平面上移动相同的距离，粗糙面与物体间与物体间的动摩擦因数为0.2. 在这两种情况下，拉力做的功各是多少？拉力这两次做的功是否相同？各个力对物体做的总功是否相同？θ Fv乙θ＝30° θFv甲θ＝150°θ＝30°vF θ 图7.2-8解：在这两种情况下，物体所受拉力相同，移动的距离也相同，所以拉力所做的功也相同，为7.5J. 拉力做的功与是否有其他力作用在物体上没有关系，与物体的运动状态也没有关系. 光滑水平面上，各个力对物体做的总功为7.5J. 粗糙水平面上，各个力对物体做的总功为6.5N.7.3 功率1. 一台电动机工作时的功率是10kw ，要用它匀速提升2.7×104kg 的货物，提升的速度将是多大？3.7×10-2 m/s2. 一台抽水机每秒能把30kg 的水抽到10m 高的水塔上，如果不计额外功的损失，这台抽水机输出的功率是多大？如果保持这一输出功率，半小时内能做多少功？ 5.4×106J.3. 有一个力F,它在不断增大. 某人以此为条件，应用P=Fv 进行了如下推导. 根据P=Fv ，F 增大则P 增大；又根据F P v =，P 增大则v 增大；再根据vPF =，v 增大则F 减小. 这个人推导的结果与已知条件相矛盾. 他错在哪里？答：此人推导的前提不明确. 当F 增大，根据P ＝Fv 推出，P 增大的前提应是v 不变，从P v F=推出，P增大则v 增大的前提是F 不变，从P F v=推出，v 增大F 减小的前提是P 不变.4. 质量为m 的汽车在平直公路上行驶，阻力F 保持不变. 当它以速度v. 加速度a 加速前进时，发动机的实际功率正好等于额定功率，从此时开始，发动机始终在额定功率下工作. （1）汽车的加速度和速度将如何变化？说出理由. （2）如果公路足够长，汽车最后的速度是多大？解：（1）汽车的加速度减小，速度增大. 因为，此时开始发动机在额定功率下运动，即P ＝F 牵v . v 增大则F 牵减小，而F Fa m-=牵，所以加速度减小. （2）当加速度减小到零时，汽车做匀速直线运动，F牵＝F ，所以P v F=，此为汽车在功率P 下行驶的最大速度.7.4 重力势能1. 图7.4-8中的几个斜面，它们的高度相同. 倾角不同. 让质量相同的物体沿斜面从顶端运动到底端. 试根据功的定义计算沿不同斜面运动时重力做的功，以证明这个功与斜面的倾角无关.证明：设斜面高度为h ，对应于倾角为θ1. θ2. θ3的斜面长分别为l 1. l 2. l 3.由功的公式可知，在倾角为θ1的斜面，重力与位移的夹角为（12πθ-），重力所做的功为：WG ＝mg l 1cos （12πθ-）＝mg l 1sinθ1＝mgh. 同理可证，在倾角为θ2. θ3的斜面上，重力所做的功都等于mgh ，与斜面倾角无关.2. 如图7.4-9，质量为m 的足球在地面1的位置被踢出后落到地面3的位置，在空中达到的最高点2的高度为h.（1）足球由位置1运动到位置2时，重力做了多少功？足球克服重力做了多少功？足球的重力势能增加了多少？（2）足球由位置2运动到位置3时，重力做了多少功？足球重力势能减少了多少？ （3）足球由位置1运动到位置3时，重力做了多少功？足球的重力势能变化了多少？答：（1）足球由位置1运动到位置2时，重力所做的功为－mgh ，足球克服重力所做的功为mgh ，足球的重力势能增加了mgh.（2）足球由位置2运动到位置3时，重力做的功为mgh ，足球的重力势能减少了mgh. （3）足球由位置1运动到位置3时，重力做功为零，重力势能变化为零.123h图7.4-9图7.4-83. 如图7.4-10，质量m=0.5kg 的小球，从桌面以上高h 1=1.2m 的A 点下落到地面的B 点，桌面高h 2=0.8m. （1）在表格的空白外按要求填入数据.（2）如果下落时有空气阻力，表格中的数据是否应该改变？答：（1）所选择的参考平面 小球在A 点的重力势能 小球在B 点的重力势能 整个下落过程中小球重力做的功 整个下落过程中小球重力势能的变化 桌面 5.88J －3.92J 9.8J 9.8J 地面9.8J9.8J9.8J（2）如果下落过程中有空气阻力，表格中的数据不变.4. 以下说法是否正确？如果正确，说出一种可能的实际情况；如果不正确，说明这种说法为什么错.A. 物体受拉力作用向上运动，拉力做的功是1J ，但物体重力势能的增加量不是1J.B. 物体受拉力作用向上匀速运动，拉力做的功是1J ，但物体重力势能的增加量不是1J.C. 物体运动，重力做的功是-1J ，但物体重力势能的增加量不是1J.D. 没有摩擦时物体由A 沿曲线运动到B ，克服重力做的功大于1J.所选择的参考平面小球在A 点的重力势能小球在B 点的重力势能整个下落过程中小球重力做的功整个下落过程中小球重力势能的变化桌面 地面图7.4-10答：A 正确. 例如：物体在向上的拉力作用下，如果做匀加速直线运动，这时拉力的功大于重力势能的增加量. 如果物体做匀减速直线运动，这时拉力的功小于重力势能的减少量.B 错误. 物体匀速上升，拉力的大小等于重力，拉力的功一定等于重力势能的增加量.C 错误. 根据W G ＝E p1－E p2可知，重力做－1J 的功，物体势能的增加量为1J.D 错误. 重力做功只与起点和终点的位置有关，与路径无关，A. B 两点的位置不变，从A 点到B点的过程中，无论经过什么路径，重力的功都是相同的.7.7 动能和动能定理1. 改变汽车的质量和速度，都可能使汽车的动能发生改变. 在下列几种情形下，汽车的动能各是原来的几倍？A. 质量不变，速度增大到原来的2倍.B. 速度不变，质量增大到原来的2倍.C. 质量减半，速度增大到原来的4倍.D. 速度减半，质量增大到原来的4倍.答：a ．动能是原来的4倍. b ．动能是原来的2倍. c ．动能是原来的8倍. d ．动能不变.2. 把一辆汽车的速度从10km/h 加速到20km/h ，或者从50km/h 加速到60km/h ，哪种情况做的功比较多？通过计算说明.解：由动能定理W ＝E k2－E k1＝22211()2m v v -可知，在题目所述的两种情况下，第二种情况增加的动能较大，需要做的功较多.速度由10km/h 加速到20km/h 的情况下：(2221v v -)＝（202－102）（km/s ）2＝300（km/s ）2 速度由50km/h 加快到60km/h 情况下：(2221v v -)＝（602－502）（km/s ）2＝1100（km/s ）2可见，后一种情况所做的功比较多.3. 质量是2g 的子弹，以300m/s 的速度射入厚度是5cm 的木板（图7.7-4），射穿后的速度是100m/s. 子弹射穿木板的过程中受到的平均阻力是多大？你对题目中所说的“平均”一词有什么认识？解：设平均阻力为f ，根据动能定理W ＝22211122mv mv - ，有 f scos180°＝22211122mv mv -. f ＝1.6×103N ，子弹在木板中运动5cm 时，所受木板的阻力各处不同，题目所说的平均阻力是对这5cm 说的.4. 我们在第四章曾用牛顿运动定律解答过一个问题：民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面，若斜面高3.2m ，斜面长6.5m ，质量60kg 的人沿斜面滑下时所受的阻力是240N ，求人滑至底端时的速度. 请用动能定理解答本题.42m/s≈5.66m/s5、运动员把质量是500g 的足球踢出后，某人观察它在空中的飞行情况，估计上升的最大高度是10m ，在最高点的速度为20m/s. 请你根据这个估计，计算运动员踢球时对足球做的功. 150J7.8 机械能守恒定律1. 如图7.8-6，质量为m 的小球从光滑曲面上滑下. 当它到达高度为h 1的位置A 时，速度的大小为v 1，滑到高度为h 2的位置B 时，速度的大小为v2. 在由高度h 1滑到高度h 2的过程中，重力做的功为W. （1）根据动能定理列出方程，描述小球在A. B 两点间动能的关系.（2）根据重力做功与重力势能的关系，把以上方程变形，以反映出小球运动过程中机械能是守恒的.（1）小球在从A 点下落至B 点的过程中，根据动能定理W ＝ΔE k ， mg(h 1－h 2)＝22211122mv mv -（2）由mg(h 1－h 2)＝22211122mv mv -，得：mgh 1+2112mv ＝mgh 2+2212mv等式左边表示物体在A 点时的机械能，等式右边表示物体在B 点时的机械能，小球从A 点运动到B 点的过程中，机械能守恒.2. 神舟号载人飞船在发射至返回的过程中，以下哪些阶段中返回舱的机械能是守恒的？ A. 飞船升空的阶段.B. 飞船在椭圆轨道上绕地球运行的阶段.C. 返回舱在大气层以外向着地球做无动力飞行的阶段.D. 降落伞张开后，返回舱下降的阶段.答：A ．飞船升空的阶段，动力对飞船做功，飞船的机械能增加.B ．飞船在椭圆轨道上绕地球运行的阶段，只有引力对飞船做功，机械能守恒.C ．飞船在空中减速后，返回舱与轨道分离，然后在大气层以外向着地球做无动力飞行的过程中，只有引力做功，机械能守恒.D ．进入大气层并运动一段时间后，降落伞张开，返回舱下降的过程中，空气阻力做功，机械能减少.3. 把质量为0.5kg 的石块 从10m 高处以300角斜向上方抛出（图7.8-7），初速度是v 0=5m/s. 不计空气阻力.（1）石块落地时的速度是多大？请用机械能守恒定律和动能定理分别讨论. （2）石块落地时的速度的大小与下列哪些量有关，与哪些量无关？说明理由.图7.8-6A. 石块的质量B. 石块初速度的大小C. 石块初速度的仰角D. 石块抛出时的高度解：（1）石块从抛出到落地的过程中，只有重力做功，所以机械能守恒. 设地面为零势能面，根据机械能守恒定律：2201122t mv mgh mv +=，得根据动能定理：W ＝E kt －E k0，即mgh ＝ 2201122t mv mv -，v t ＝202v gh +v t ＝15m/s（2）由v t ＝202v gh +知，石块落地时速度大小与石块初速度大小和石块抛出时的高度有关，与石块的质量和石块初速度的仰角无关.4. 有一种地下铁道，车站的路轨建得高些，车辆进站时要上坡，出站时要下坡，如图7.8-8. 设坡高h 为2m ，进站车辆到达坡下的A 点时，速度为25.2km/h ，此时切断电动机的电源，车辆能不能“冲”到坡上？如果能够，到达坡上的速度是多大？列车能冲上站台, 3m/s7.9 实验：验证机械能守恒定律1. 把质量是0.2kg 的小球放在竖立的弹簧上，并把球往下按至A 的位置，如图7.9-3甲所示. 迅速松手后，弹簧把球弹起，球升至最高位置C （图丙），途中经过位置B 时弹簧正好于自由状态（图乙）. 已知B. A 的高度差为0.1m ，C. B 的高度差为0.2m ，弹簧的质量和空气的阻力均可忽略. (1) 分别说出由状态甲至状态乙. 由状态乙至状态丙的能量转化情况. (2) 状态甲中弹簧的弹性势能是多少？状态乙中小球的动能是多少？答：（1）从状态甲至状态丙过程中，弹性势能逐渐减少，动能和重力势能逐渐增大，当弹簧对小球向上的弹力大小与小球所受重力大小相等时，小球动能最大. 之后，弹性势能和动能逐渐减小，重力势能逐渐增大，当弹簧恢复到自然长度时，弹性势能为0. 之后，重力势能仍然逐渐增大，动能逐渐减小，到达C 点时，动能减少到0，重力势能达到最大.小球从状态甲运动到状态丙的过程中，机械能守恒. 故状态甲中，弹簧的弹性势能 ()()0.2100.10.20.6p AB BC E mg h h =+=⨯⨯+= J（2）小球从状态乙到状态丙的过程中，动能逐渐减少，重力势能逐渐增大.小球从状态乙到状态丙的过程中，机械能守恒，所以小球在B 点的动能与小球在C 点的势能相等. 故小球在状态乙中的动能0.2100.20.4k BC E mgh ==⨯⨯= J2. 游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来（图7.9-4）. 我们把这种情形抽象为图7.9-5的模型：弧形轨道的下端与竖直圆轨道相接，使小球从弧形轨道上端滚下，小球进入圆轨道下端后沿圆轨道运动. 实验发现，只要h 大于一定值，小球就可以顺利通过圆轨道的最高点. 如果已知圆轨道的半径为R ，h 至少要等于多大？不考虑摩擦等阻力.AB C甲乙 丙5R23、第五章第2节“问题与练习”第3题描述了一个实验. 实际做一做这个实验，用你当时得到的计算式计算钢球离开桌面的高度，按照机械能守恒定律计算钢球到达桌面的速度. 对比两种不同方法得到的速度值并尝试解释两者的差异.答：用平抛运动的知识测出的小球离开桌面时的速度要略大于小球从斜面上滚下的过程中用机械能守恒定律算出的速度，这是由于小球从斜面与桌面上运动时受到的摩擦阻力远大于小球做平抛运动时所受的空气阻力.7.10 能量守恒定律与能源1. 生活中的许多用品都可以看做能量转换器，它们把能量从一种形式转化为另一种形式. 请观察你家中的各种生活用品，分别指出它们工作时发生了哪些能量转化.答：家用电饭锅是把电能转化为内能；洗衣机是把电能转化为动能，等等.2. 三峡水力发电站是我国最大的水力发电站，平均水位落差约100m，水的流量约1.35×104m3/s. 船只通航需要约3500m3/s的流量，其余流量全部用来发电. 水流冲击全部用来发电. 水流冲击水轮机发电时，水流减少的机械能有20%转化为电能.（1）按照以上数据估算，三峡发电站的发电功率最大是多少？（2）根据你对家庭生活用电量的调查，如果三峡电站全部用于城市生活用电，它可以满足多少个百万人口城市的生活用电？（1）2.7×106kW (2)设三口之家每户的家庭生活用电功率为1kW，考虑到不是每家同时用1kW的电，我们平均每家同时用电0.5kW，则三峡发电站能供给＝5.8×106户用电，人口数为3×5.8×106＝17×106人，即可供17个百万人口城市的生活用电.3. 为了节约能源，从个人的角度讲，你能做些什么？从社会的角度讲，你能为决策者提出什么建议？。

第七章 习题及解答1. 设有一个体系，由三个定位的一维简谐振子所组成，体系能量为νh 211,这三个振子在三个固定的位置上振动,试求体系全部的微观状态数.解 对振动 νυενh )21(+=,在总能量 νενh 211=时，三个一维简谐振子可能有以下四种分布方式:（1）N 0=2, N 4=1, νενh 2120⨯=, νενh 294=， 3!2!1!31==t （2）N 0=1， N 2=2， νενh 2110⨯=, νενh 2522⨯=, 3!2!1!32==t （3）N 0=1， N 1=1, N 3=1， νενh 210=, νενh 231=， νενh 273=， 6!1!1!1!33==t （4）N 1=2， N 2=1， νενh 2321⨯=, νενh 252=， 3!2!1!34==t Ω= t 1+t 2+t 3+t 4=3+3+6+3=152。

当热力学体系的熵函数S 增加0.418J ·K —1时，体系的微观状态数增加多少？用1/∆ΩΩ表示。

解 S 1=kln Ω1， S 2=kln Ω2， S 2—S 1=kln （Ω2/Ω1)ln(Ω2/Ω1)=（S 2—S 1）/k=(0。

418J·K -1）/（1.38×10—23J ·K -1）=3。

03×10221/Ω∆Ω=（Ω2—Ω1）/Ω1=（Ω2/Ω1)-1≈Ω2/Ω1= exp （3。

03×1022）3。

在海平面上大气的组成用体积百分数可表示为：N 2（g ）为0.78,O 2(g)为0。

21,其他气体为0。

01。

设大气中各种气体都符合Bolzenmann 分布，假设大气柱在整个高度内的平均温度为220K 。

试求：这三类气体分别在海拔10km ，60km 和500km 处的分压.已知重力加速度为9.8m·s -2。

解 所用公式为p=p 0e —Mgh/RT ，其中M （空气） =29g·mol —1， M(N 2)=28g·mol —1， M （O 2)=32g·mol —1，M （其它)=［M(空气)—0。

高等数学第七章习题册答案高等数学第七章习题册答案高等数学是大学数学的一门重要课程，其中第七章涉及到的内容主要是微分方程和级数。

习题册是学生们用来巩固和提高自己数学水平的重要工具。

在这篇文章中，我将为大家提供高等数学第七章习题册的答案，希望能够帮助大家更好地理解和掌握这一章的知识。

1. 题目：求微分方程$\frac{dy}{dx}=2x+3$的通解。

解答：首先将微分方程化为标准形式$\frac{dy}{dx}-2x=3$，然后求出其齐次方程$\frac{dy}{dx}-2x=0$的通解$y_c=Ce^{2x}$，其中$C$为常数。

接下来，我们需要求出非齐次方程$\frac{dy}{dx}-2x=3$的一个特解$y_p$。

根据常数变易法，我们可以猜测特解的形式为$y_p=Ax+B$，其中$A$和$B$为待定常数。

将$y_p$代入非齐次方程，得到$\frac{d(Ax+B)}{dx}-2x=3$，整理后可得$A=2$和$B=-3$，即特解$y_p=2x-3$。

最后，将齐次方程的通解和非齐次方程的特解相加，即可得到原微分方程的通解$y=y_c+y_p=Ce^{2x}+2x-3$。

2. 题目：求微分方程$\frac{d^2y}{dx^2}-4\frac{dy}{dx}+4y=0$的通解。

解答：首先将微分方程化为特征方程$r^2-4r+4=0$，解得$r=2$，因此特征根为重根$r_1=r_2=2$。

根据特征根的重根性质，我们可以得到齐次方程的通解$y_c=(C_1+C_2x)e^{2x}$，其中$C_1$和$C_2$为常数。

接下来，我们需要求出非齐次方程的一个特解$y_p$。

根据待定系数法，我们可以猜测特解的形式为$y_p=Ae^{2x}$，其中$A$为待定常数。

将$y_p$代入非齐次方程，得到$4Ae^{2x}-4\cdot2Ae^{2x}+4Ae^{2x}=0$，整理后可得$A=0$，即特解$y_p=0$。

p317第七章习题(一) [ 2, 5, 6, 9, 15, 17, 19 ]2. 利用保域定理证明：若函数f(z)在区域D内解析，(1) 若| f(z) |在D内为常数，则f(z)在D内为常数；(2) 若Re( f(z))或Im( f(z))在D内为常数，则f(z)在D内为常数．【解】由保域定理，假若f(z)在区域D内不恒为常数，则f(D)是区域．(1) 若| f(z) |在D内为常数，则存在r ≥ 0，使得f(D) ⊆C r= { z∈ | | z | = r }．但int(C r) = ∅，故int( f(D)) = ∅，因此f(D)不是开集，因此不是区域，矛盾．(2) 若Re( f(z))在D内为常数，则存在a∈ ，使得f(D) ⊆L a= { z∈ | Re(z) = a }．但int(L a) = ∅，故int( f(D)) = ∅，因此f(D)不是开集，因此不是区域，矛盾．同理，若Im( f(z))在D内为常数，f(D)也不是区域，矛盾．故不论如何，f(z)在区域D内必恒为常数．[保区域性定理：设f(z)在区域D内解析且不恒为常数，则f(D)是区域．]5. z平面上有三个互相外切的圆周，切点之一在原点，函数w = 1/z将此三个圆周所围成的区域变成w平面上的什么区域？【解】设圆周A, B外切于原点，圆周C分别外切圆周A, B于z1, z2．由分式线性映射的保圆性，以及f(0) = ∞，知f(A), f(B)为w平面中的直线．并且因f(A), f(B)在有限z平面内无交点，f(A), f(B)为一对平行直线．因C不过原点，故f(C)为w平面中的圆周；并且，由分式线性映射的保角性，f(C)与f(A), f(B)都相切，切点分别为f(z1), f(z2)．下面的图(用sketchpad和photoshop做出，本质上是尺规作图的结果，累！)，指出圆周A, B, C的象f(A), f(B), f(C)，以及圆周A, B, C所围的区域D的象f(D)．[上面的图，我是把z平面和w平面作为一个平面来画的．因为用的是sketchpad，所以图形应该还是比较精确的．同学们可以思考：f(z) = 1/z将那三个圆所围的那个无界的(但在 ∞中是单连通的)区域变成哪个区域？]6. 如w = (az + b)/(cz + d)将单位圆周变成直线，其系数应满足什么条件？【解】首先应满足ad–bc≠ 0，以保证映射不是常值映射．其次，单位圆周上存在点α使得w(α) = ∞，这意味着cα + d = 0，因此| d | = | –cα| = | c | · | α| = | c |．反过来，若ad–bc≠ 0，| d | = | c |，则w = (az + b)/(cz + d)是分式线性映射，具有保圆性．因| –d/c | = 1，故–d/c在单位圆周上，而且w(–d/c) = ∞，故单位圆周在此映射的下的象为直线．9. 求出将圆| z – 4 i | < 2变成半平面v > u的共形映射，使得圆心变到– 4，而圆周上的点2 i变到w = 0．【解】注意到4 i和∞关于圆周| z – 4 i | = 2对称，– 4和– 4 i关于直线v = u对称；因此若分式线性映射f(z)满足f(4 i) = – 4，f(∞) = – 4 i，则f(z)将圆周| z – 4 i | = 2变成直线v = u．根据题目要求，又应有f(2 i) = 0；故可用分式线性映射的保角比性来确定共形映射w = f(z)．(w- (– 4))/(w- 0) : (– 4 i- (– 4))/(– 4 i- 0) = (z- 4 i)/(z- 2 i) : (∞- 4 i)/(∞- 2 i)；即(w- (– 4))/(w- 0) : (1 –i)/(–i) = (z- 4 i)/(z- 2 i)；所以，w = – 4i ( z– 2i)/(z- (4i + 2))．[或者，直接设f(z) = (– 4i) (z– 2i)/(z–d)，将f(4 i) = – 4代入，则– 4 = (– 4i) (4 i– 2i)/(4 i–d)，即d = 4 i +2．所以w = – 4i ( z– 2i)/(z- (4i + 2))．] 15. 求出将上半单位圆变成上半平面的共形映射，使z = 1, -1, 0分别变成w = -1, 1, ∞．【解】因f1(z) = - (z + 1)/(z- 1)把正向实轴变成正向实轴，上半平面映成上半平面，且f1(- 1) = 0，f1(0) = 1，f1(1) = ∞，故f1将实轴上的区间(0, 1)变成正实轴．由保角性，f1将上半单位圆周变成正虚轴．所以，f1将上半单位圆共形地变成第一象限．而f2(z) = z2将第一象限共形地变成上半平面．所以，f2 ◦f1将上半单位圆共形映射成上半平面，且(f2 ◦f1)(1) = ∞，(f2 ◦f1)(- 1) = 0，(f2 ◦f1)(0) = 1．注意到f1(∞) = - 1，f1(0) = 1，f1(1) = ∞；故(f1 ◦f2 ◦f1)(1) = - 1，(f1 ◦f2 ◦f1)(- 1) = 1，(f1 ◦f2 ◦f1)(0) = ∞．所以，f = f1 ◦f2 ◦f1即满足题目要求．f(z) = (f1 ◦f2 ◦f1)(z) = - ( (f2 ◦f1)(z) + 1)/( (f2 ◦f1)(z) - 1)= - ( ( f1(z)2 + 1)/( ( f1(z)2- 1)= - ( ( (- (z + 1)/(z- 1))2 + 1)/( ((- (z + 1)/(z- 1))2- 1)= - ((z + 1)2 + (z- 1)2)/( (z + 1)2 - (z- 1)2)= - 2(z2 + 1)/(4z) = (- 1/2)(z + 1/z)．17. 将扩充z平面割去1 + i到2 + 2 i的线段后剩下的区域共形映射成上半平面．【解】设割去的线段的端点分别为α, β，先做分式线性映射使得此线段变成一条以0为端点的射线(在 ∞中看成是一条以0, ∞为端点的线段)．例如可取ξ= k (z-α)/(z-β)．下面选取使当的k，使得映射将给定的线段映射成(带端点的)正实轴．为此，我们要求ξ((α + β)/2) > 0．即k (α + β)/2 -α)/(α + β)/2 -β) > 0，因此k < 0．所以，当k < 0时，ξ(z)将给定的区域映射成割去正实轴的复平面(不是扩充的)．因此，w = (k (z-α)/(z-β))1/2即为满足要求的共形映射．19. 将一个从中心起沿正实轴上的半径割开了的单位圆共形映射成单位圆，使符合条件：割缝上岸的1变成1，割缝上岸的1变成-1，0变成-i．【解】设给定的区域为D．则ξ= z1/2将D共形映射成上半单位圆 +．按第15题的论证，η = (ξ + 1)2/(ξ- 1)2将 +共形映射成上半平面 +．那么，ϕ(z) = (z1/2 + 1)2/(z1/2- 1)2将D共形映射成 +．并且，割缝上岸的1变成∞，割缝上岸的1变成0，0变成1．下面作一个分式线性映射ψ将 +共形映射成单位圆 ，并且使得ψ(∞) = 1，ψ(0) = -1，ψ(1) = -i．为满足ψ(∞) = 1，ψ(0) = -1，只要取ψ(z) = (z-α)/(z + α)；将ψ(1) = -i代入，得-i = (1 -α)/(1 + α)，即α = (1 + i)/(1 -i) = i．故ψ(z) = (z-i)/(z + i)；令f = ψ◦ϕ，则f即为满足要求的共形映射．f(z) = (ϕ(z) -i)/(ϕ(z) + i) = ((z1/2 + 1)2/(z1/2- 1)2-i)/((z1/2 + 1)2/(z1/2- 1)2 + i)= ((z1/2 + 1)2-i(z1/2- 1)2)/((z1/2 + 1)2 + i (z1/2- 1)2)= ((z + 2z1/2 + 1) -i(z - 2z1/2 + 1))/((z + 2z1/2 + 1) + i (z - 2z1/2 + 1))= ((1 -i)(z + 1) + 2(1 + i)z1/2)/((1 + i)(z + 1)+ 2(1 -i) z1/2 )= (-i) · ((z + 1) + 2i z1/2)/( (z + 1)- 2i z1/2 )．[在第17题和第19题中，我们使用了多值函数z1/2而未指明是它的哪个单值解析分支．实际上，我们是遵从了一个一般的约定：倘若未指出具体的分支，则z1/n 表示的是它的主值分支．]1. 至此，只有第六章和第七章的第二组习题尚未做完，同学们不要着急，容我慢慢做之．2. 如果还有题目，是我没有做但是同学们希望我做的，可以发Email给我，写清楚页码和题号，我将尽量满足同学们的要求．如果题目不是来自我们的教材的，一方面要打清楚，另一方面请给出题目来源：若来自书，则指明书名和作者，出版社，版次，年份；若来自互联网，则给出url；若是考研题，则指明学校，年份，最好附整个试题．3. 答疑时间定在考试前一天，上午10点开始．∀∃∅-⨯±≠≥·◦≤≡⊕⊗≅αβχδεφγηιϕκλμνοπθρστυϖωξψζ∞•︒ℵℜ℘∇∏∑⎰⊥∠ √§ψ∈∉⊆⊂⊃⊇⊄⊄∠⇒♣♦♥♠§ #↔→←↑↓⌝∨∧⋃⋂⇔⇒⇐∆∑ΓΦΛΩ∂∀m∈ +，★z∈ ∞α1, α2, ...αn lim n→∞，+n→∞∀ε > 0，∑u n，∑n≥ 1u n，m∈ ，∀ε > 0，∃δ> 0，【解】z⎰[0, 2π]l 2 dx，f(x) = (-∞, +∞)[-π, π]∑1 ≤k≤n u n，[0, 2π]。

第七章课后习题答案问题1：请简述第七章中讨论的主要概念。

答案：第七章主要讨论了[具体概念]，它涉及到[概念的详细解释]。

此概念在[相关领域或情境]中具有重要意义，因为它[解释了什么或如何应用]。

问题2：如何计算[特定数学公式或计算过程]？答案：要计算[特定数学公式或计算过程]，首先需要确定所有必要的变量。

然后，按照以下步骤进行计算：1. [第一步计算过程]2. [第二步计算过程]3. [以此类推，直至最终结果]问题3：分析[案例研究或实际情境]，并讨论其对[相关概念]的影响。

答案：在[案例研究或实际情境]中，我们可以看到[相关概念]的应用。

具体来说，[案例或情境描述]展示了[概念如何影响结果]。

通过这个案例，我们可以更好地理解[概念]在实际生活中的应用和重要性。

问题4：解释[特定术语或理论]，并给出一个例子。

答案： [特定术语或理论]是指[术语或理论的定义]。

例如，在[相关领域]中，[术语或理论]可以用来[具体应用或解释]。

一个具体的例子是[例子描述]，它清楚地展示了[术语或理论]的实际应用。

问题5： [选择题或判断题]。

答案： [正确答案]。

这个问题的答案是[正确答案]，因为[解释为什么这是正确答案]。

总结：第七章的习题涵盖了对[章节主题]的深入理解，包括理论概念、实际应用和计算技能。

通过解答这些问题，学生可以更好地掌握章节内容，并将其应用于解决实际问题。

请注意，以上内容仅为模板，具体答案需要根据实际的章节内容和习题进行定制。

如果需要针对特定章节的具体习题答案，请提供相关章节的详细内容和习题，以便我能够提供更准确的答案。

第七章：粒子在电磁场中的运动[1]证明在磁场B中，带电粒子的速度算符的各分量，满足下述的对易关系：[]zy x cq i v v B ˆ,2μ= （1） []xz y cq i v v B ˆ,2μ= （2） []y xz cq i v v B ˆ,2μ= （3） [证明]根据正则方程组：x x p H x v ∂∂== ˆ ，Φ+⎪⎭⎫ ⎝⎛-=q A c qp H 221ˆ μ ⎪⎭⎫ ⎝⎛-=x x x A c q p vˆˆ1ˆμ 同理 ⎪⎭⎫ ⎝⎛-=y y y A c q p v ˆˆ1ˆμ ()z y x p p p pˆ,ˆ,ˆˆ 是正则动量，不等于机械动量，将所得结果代入（1）的等号左方： []⎥⎦⎤⎢⎣⎡--=y y x xyxA c q p A c q p v v ˆˆ,ˆˆ1,2μ =[][][][]y x y x y x y x A A cq p A c q A p c qp pˆ,ˆˆ,ˆˆ,ˆˆ,ˆ122222μμμμ+-- （4） 正则动量与梯度算符相对应，即∇=ipˆ ，因此 []0ˆ,ˆ=y x p p又A ˆ仅与点的座标有关[]0ˆ,ˆ=yxA A[]z x y x y yxB c iq y A x A i c q x i A c q A x i c q v v 2222,,,μμμμ=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂⋅=⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫⎝⎛∂∂-= （因A B ⨯∇=ˆˆ）其余二式依轮换对称写出。

[2]利用上述对易式，求出均匀磁场中，带电粒子能量的本征值（取磁场方向为Z 轴方向） （解）设磁场沿Z 轴方向，B B B B z y x ===00矢势A ˆ 的一种可能情形是022=-=-=z y x A x B A y BA在本题的情形，哈密顿算符是：（前题）{})2(2)1(2221ˆ222222z y x z y x v v v p x c qB p y c qB p H ++=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=μμ速度算符间的对易式是：()()())5(0,)4(0,)3(,2===x z zyyxv v v v B ci q v v μ 根据（54⨯），z v 分别和x v ，y v 对易，因此z v 与22yx v v +对易，而： ()2212ˆyx v v H +=μ 与22ˆ2ˆx v H μ=有共同的本征函数，H ˆ的本征值是21ˆ,ˆH H 本征值之和。

第7章 习题解答7.1 由74290所构成的计数电路如图7.50所示，试分析它们各为几进制计数器。

图7.50 习题7.1图Q3Q3Q3Q3解：74290是异步二-五-十进制计数器，下降沿触发；CKA 是二进制计数器脉冲输入，Q 0是输出；CKB 是五进制计数器脉冲输入，Q 3Q 2Q 1是输出；异步清零端R0(1)、R0(2)和异步置9控制端R9(1)、R9(2)都是高有效。

（1）R9(1)=R9(2)=0；R0(1)=R0(2)=Q 3；CKA 无脉冲输入；CKB 接外部时钟，所以74290中只有五进制计数器工作。

设五进制计数器的初态为Q 3Q 2Q 1=000，在CLK 下降沿的作用下进行加1计数，当Q 3=1时，R0(1)=R0(2)=1，计数器异步清零，重新计数。

也就是说，该电路有效状态的转换过程是：000→001→010→011→000（由于该芯片是异步清零，所以Q 3Q 2Q 1=100是过渡状态，在011之后短暂存在）。

由此可知，该电路是四进制计数器。

（2）CKA 没有脉冲输入，CKB 接外部时钟，所以只有五进制计数器工作。

R9(1)=R9(2)=0；R0(1) =Q 1，R0(2)=Q 2；设五进制计数器的初态为Q 3Q 2Q 1=000，在CLK 下降沿的作用下进行加1计数，当Q 2=Q 1=1（即计数值变为Q 3Q 2Q 1=011）时，R0(1)=R0(2)=1，计数器异步清零，重新计数。

也就是说，该电路有效状态的转换过程是：000→001→010→000（由于该芯片是异步清零，所以Q 3Q 2Q 1=011是过渡状态，在010之后短暂存在）。

由此可知，该电路是三进制计数器。

（3）CKB=Q 0，CKA 接外部时钟，两个计数器同时工作，构成一个8421BCD 码计数器。

R9(1)=R9(2)=0；R0(1)=R0(2)=Q 3。

设计数器的初态为Q 3Q 2Q 1Q 0=0000，在CLK 下降沿的作用下按8421BCD 码进行加1计数，当Q 3=1时，R0(1)=R0(2)=1，计数器异步清零，重新计数。

习 题 七7-1 如图所示，O S O S 21=．若在O S 1中放入一折射率为n ，厚度为e 的透明介质片，求O S 1与O S 2之间的光程差．如果1S 和2S 是两个波长为λ的同相位的相干光源，求两光在O 点的相位差．[解] O S1与O S 2的几何路程相等光程差为 ()e n 1-=δ 位相差为 ()e n 122-==∆λπδλπϕ7-2 一束绿光照射到两相距 0.6mm 的双缝上，在距双缝2.5m 处的屏上出现干涉条纹．测得两相邻明条纹中心间的距离为2.27mm ，试求入射光的波长．[解] 由杨氏双缝干涉知 dD x λ=∆ 所以 5448m 10448.55.21060.01027.2733=⨯=⨯⨯⨯=∆=---D xd λÅ7-3 如图所示，在双缝干涉实验中，21SS SS =，用波长为λ的单色光照S ，通过空气后在屏幕E 上形成干涉条纹．已知点P 处为第3级干涉明条纹，求1S 和2S 到点P 的光程差．若整个装置放于某种透明液体中，点P 为第4级干涉明条纹，求该液体的折射率．[解] 1S 和2S 到P 点的光程差满足λλδ312==-=k r r整个装置放置于液体中，1S 和2S 到P 点的光程差满足()λδ412=-=r r nλλ43=n所以得到 33.134==n7-4 如习题7-1图所示，1S 和2S 是两个同相位的相干光源，它们发出波长λ＝5000Å的光波，设O 是它们中垂线上的一点，在点1S 与点O 之间插入一折射率n ＝1.50的薄玻璃，点O 恰为第4级明条纹的中心，求它的厚度e ．[解] 在O 点是第4级明条纹的中心光程差 λδ4=-=e ne所以 410414⨯=-=n e λÅ7-5 初位相相同的两相干光源产生的波长为6000Å的光波在空间某点P 相遇产生干涉，其几何路径之差为6102.1-⨯m ．如果光线通过的介质分别为空气（11=n ）、水（=2n 1.33）或松节油（=3n 1.50）时，点P 的干涉是加强还是减弱．[解] 光在折射率为n 的介质中P 点处光程差为()12r r n -=δ介质为空气时，11=n ，则()λδ2m 102.16121211=⨯=-=-=-r r r r n光程差为半波长的偶数倍，所以P 点处干涉加强． 介质为水时，=2n 1.33，则()m 106.1102.133.1661222--⨯=⨯⨯=-=r r n δ光程差介于两种情况之间，且结果与半波长的奇数倍更接近，所以P 点光强介于明暗条纹中心光强之间，且与暗条纹中心光强更接近．介质为松节油时，=3n 1.50，则()λδ3m 108.1102.15.1661233=⨯=⨯⨯=-=--r r n光程差为半波长的偶数倍，所以P 点处干涉加强．7-6 在双缝干涉实验中，用很薄的云母片（58.1=n ）覆盖在双缝的一条上，如图所示．这时屏上零级明纹移到原来第7级明纹位置上．如果入射光波5000Å，试求云母片的厚度（设光线垂直射入云母片）．[解] 原来的第7级明纹的位置满足λ721=-r r加上云母片后，光程差满足[]()012121=---=+--e n r r ne e r r所以41003.6158.15000717⨯=-⨯=-=n e λ Å7-7 用单色光源S 照射平行双缝1S 和2S 形成两相干光源．在屏上产生干涉图样，零级明条纹位于点O ，如图所示．若将缝光源S 移到S '位置，问零级明条纹向什么方向移动?若使零级明条纹移回点O ，必须在哪个缝的右边插入一薄云母片才有可能? 若以波长为5890Å的单色光，欲使移动了4个明纹间距的零级明纹移回到点O ，云母片的厚度应为多少? 云母片的折射率为1.58．[解] 零级明纹是光程差为0的位置．移动光源后光线2的光程长了，为仍保持光程差为0，必须让1的光程增加以弥补2的增加，只有在下方1才比2长，所以向下．要回到原点，即通过加片的方法使得1的光程增大，所以在1S 后加．在原点时，两光线的光程差满足()λδ41=-=e n得到 m 1006.4158.1105890414610--⨯=-⨯⨯=-=n e λ7-8 用白光作光源观察杨氏双缝干涉，设缝间距为d ，双缝与屏的距离为D ，试求能观察到的无重叠的可见光（波长范围： 4000～7600Å）光谱的级次．[解] k 级明纹的位置为dD k x λ=k 要使光谱无重叠，必须满足 ()()λm i n 1k λm a x k +≤x x 因此 ()min max 1λλ+≤k k 即 ()140007600+≤k k解得 1.1 ≤k 所以只能看到一级无重叠光谱．7-9 白色平行光垂直照射到间距为m m 0.25=d 的双缝上，在距缝cm 50处放一屏幕，若把白光（4000～7600Å）两极端波长的同级明纹间的距离叫做彩色带的宽度，试求第1级和第5级彩色带的宽度．[解] 每一级的宽度()min max min max λλ-=-=∆dDkx x x 1=k 时，()mm 72.0m 102.710400076001025.010*******21=⨯=⨯-⨯⨯⨯⨯=∆----x 5=k 时，()mm 6.3m 106.310400076001025.010505310325=⨯=⨯-⨯⨯⨯⨯=∆----x7-l0 波长为λ的单色光垂直照射在如图所示的透明薄膜上，薄膜厚度为e ．两反射光的光程差是多少?[解]薄膜上下表面的反射光均有半波损失，故没有因半波损失而产生的光程差，因此上下表面反射的光程差为e e n 60.222==δ7-11 白光垂直照射在空气中厚度为71080.3-⨯m 的肥皂膜上，肥皂膜的折射率为1.33，在可见光范围内（4000～7600Å） 哪些波长的光在反射中增强．[解] 光程差 λλδk ne =+=22 所以124-=k neλ 当1=k 时，2021612108.333.1471=-⨯⨯⨯=-λÅ 当2=k 时，同理可得67392=λÅ 当3=k 时，同理可得40433=λÅ所以在可见光范围内波长为4043 Å和6739 Å的光在反射中增强．7-12 在观察肥皂膜的反射光时，表面呈绿色（λ＝5000 Å），薄膜表面法线和视线间的夹角为450，试计算薄膜的最小厚度． [解] 两反射光的光程差为λλδk i n n e =+-=2sin 2221221=k 时对应薄膜厚度最小为m 1011.145sin 33.14105000sin 470221022122--⨯=-⨯⨯=-=in n e λ7-13 用波长连续可调的平行光垂直照射覆盖在玻璃板上的油膜，观察到5000 Å和7000 Å这两个波长的光在反射中消失．油的折射率为1.30，玻璃的折射率为1.50．求油膜的厚度．[解] 某一波长的光在反射中消失，表明光在油膜上下表面反射的光干涉相消，故光程差为 ()21222λδ+==k e n对1λ： ()2122112λ+=k e n对2λ： ()2122222λ+=k e n又因1λ与2λ之间没有其他波长的光消失，故1λ与2λ的干涉级数只可能相差一级 故112-=k k 因此575000700012121211===-+λλk k解得 31=k 22=k以31=k 代入得，()m 1073.630.141050007412710211--⨯=⨯⨯⨯=+=n k e λ7-14 波长为5500 Å的黄绿光对人眼和照像底片最敏感，要增大照像机镜头对此光的透射率，可在镜头上镀一层氟化镁 （2MgF ）薄膜． 已知氟化镁的折射率为1.38，玻璃的折射率为 1.50，求氟化镁的最小厚度．[解] 要增大波长为λ的光的透射率，则须使反射光干涉减弱．那么，光程差应满足()21222λδ+==k e n当0=k 时，e 最小，为m 1096.938.1410550048102min--⨯=⨯⨯==n e λ7-15 如图所示，用波长为λ的单色光垂直照射折射率为2n 的劈尖．图中各部分折射率的关系是1n <2n <3n ，观察反射光的干涉条纹，从劈尖顶端开始向右数第5条暗纹中心所对应的厚度是多少?[解] 因1n <2n <3n ，故在劈尖上下表面的两反射光无因半波损失引起的附加光程差，干涉暗纹应满足()21222λδ+==k e n因棱边为明纹，故从棱边开始向右数第5条暗纹对应上式中4=k所以()()2225494142412n n n k e λλλ=+⨯=+=7-16 用波长为1λ的单色光垂直照射空气劈尖，从反射光的干涉条纹中观察到劈尖装置的点A 处是暗条纹．若连续改变入射光的波长，直到波长为2λ（2λ>1λ）时，点A 将再变成暗条纹．求点 A 处空气层的厚度． [解] 空气劈尖上暗条纹处满足()21222λλδ+=+=k ne因1=n ，所以()21222λλ+=+k e ，即λk e =2 在A 处 11A 2λk e =，22A 2λk e =同一点，e 相同，又2λ>1λ，故2k <1k ，又因1λ到2λ连续可调，中间无其他波长的光干涉形成暗条纹，故112-=k k因此 122111A 212λλλλλ-==k e7-17 用波长为λ的单色光垂直照射到空气劈尖上，从反射光中观察干涉条纹，距顶点为L 处是暗条纹．使劈尖角θ连续慢慢变大，直到该点再次出现暗条纹为止，劈尖角的改变量θ∆是多少?[解] 空气劈尖干涉暗纹，光程差为 ()21222k λλδ+=+=k e劈尖角为θ时，L 处有 ()212221k 1λλ+=+k e 劈尖角为θθ∆+时，有 ()212222k 2λλ+=+k e因为劈尖角连续改变，即e 连续增大，故2k =1k +1 由上述公式得 ()λ=-12k k 2e e又 θθL L e ==sin 1k ，()()θθθθ∆+=∆+=L L e sin 2k 因此 L2λθ=∆7-18 两块长度为l0cm 的平玻璃片，一端相互接触，另一端用厚度为0.004mm 的纸片隔开形成空气劈尖．以波长为5000Å 的平行光垂直照射，观察反射光的等厚干涉条纹．在全部10cm 长度内呈现多少条明纹?[解] 设平玻璃片长为L ，纸片厚为H ，则形成的空气劈尖角为LH ==θθsin 两相邻明纹间距为 HLl 22sin 2λθλθλ===故总条数为 1610500010004.022103=⨯⨯⨯===--λH l L N7-19 为测量硅片上氧化膜的厚度，常用化学方法将薄膜的一部分腐蚀掉，使之成为劈形（又称为台阶），如图所示．用单色光垂直照射到台阶上，就出现明暗相间的干涉条纹，数出干涉条纹的数目，就可确定氧化硅薄膜的厚度．若用钠光照射，其波长λ=5893Å，在台阶上共看到5条明条纹，求膜的厚度（氧化硅的折射率2n ＝1.5，硅的折射率为3n ＝3.42）．[解] 因1n <2n < 3n ，故台阶上下表面反射光的光程差为e n 22=δ明条纹满足的条件为 λk e n =22台阶棱边为明纹，因共看到5条明纹，所以4max =k ，由明纹条件得m 1078575.1105893222101022max max--⨯=⨯⨯===n n k e λλ7-20 检查平板的平整度时，在显微镜下观察到的等厚条纹如图所示，条纹的最大畸变量为1.5条纹间距，所用光波波长为546nm ，试描述待测平面的缺陷．[解] 因每一条干涉条纹上对应的空气厚度相同，故在同一条纹上，畸变部分和平行棱边的直线部分所对应的膜厚度相等，本来离棱边越远膜的厚度越大，而现在同一条纹上，远离棱边的畸变部分厚度并不大，这说明畸变部分是凸起的，因最大畸变是为1.5条纹间距，说明最大畸变处膜厚度比非畸变时膜厚度之差e ∆对应的级数差5.1=∆k由劈尖明纹公式 λλk e =+22得 λk e ∆=∆2所以 m 101.421046.55.1277--⨯=⨯⨯=∆=∆λk e7-21 如图所示，A 、B 是两只块规（块规是两端面经过磨平抛光达到相互平行的钢质长方体）．A 的长度是标准的，B 是相同规格待校准的．A 、B 放在平台上，用一块样板平玻璃压住．（1）设垂直入射光的波长为λ=5893Å，A 、B 相隔cm 5=d ，T 与A 、 B 间的干涉条纹的间距都是0.55 mm ，试求两块规的长度差．（2）如何判断A 、B 哪一块比较长些?（3）如果T 与A 、B 间的干涉条纹间距分别为0.55 mm 和 0.3 mm ，则说明什么问题?[解] （1） 劈尖干涉，相邻条纹间距l 满足l2sin λα=所以A 、B 两只块规的高度差为m 1068.21055.0210893.51052sin 5372----⨯=⨯⨯⨯⨯⨯===∆l d d h λα （2）因空气劈尖棱边处为暗纹，所以若压平板T ，a 、c 处暗纹位置不变，则B 比A 长，若压T ，b 、d 处暗纹位置不变，则A 比B 长．（3） 设平板T 与A 、B 间形成的劈尖角分别为1α、2α．干涉条纹间距分别为1l 和2l ，则 2sin sin 2211λαα==l l已知1l >2l ，则1α<2α，B 的端面与底面不平行，且d 处向下倾斜．7-22 如图所示的观察牛顿环的装置中，设平球面透镜中心恰好和平玻璃接触，透镜球面的半径cm 400=R ，用某单色光垂直入射，观察反射光形成的牛顿环，测得第5个明环的半径是cm 30.0（1）求入射光的波长；（2）设图中OA ＝1.00cm ，求在半径为OA 的范围内可观察到的明环数．[解] （1）牛顿环明环半径公式为()2122k λR k r -=，所以()Rk r 1222k -=λ因中心为暗环，对应第5个明环5=k ，所以()5000104009103.0215222422k =⨯⨯⨯⨯=-⨯=--R r λÅ（2）因为()2122k λR k r -=，所以()5.5010541000.121217222k =⨯⨯⨯+=+≤--λR r k 所以能看到的明环数50个．7-23 用曲率半径为3.00m 的平凸透镜和平板玻璃作牛顿环实验，测得第k 级暗环半径为m m 24.4，第10+k 级暗环的半径为m m 0.6．求所用单色光的波长．[解] 牛顿环暗环半径公式为λkR r =k 故 ()λR k r 1010k +=+因此 ()()323232k 210k 1001.600.3101024.410610⨯=⨯⨯-⨯=-=--+R r r λÅ7-24 用牛顿环实验测单色光的波长．用已知波长为1λ的单色光垂直照射牛顿环装置时，测得第1和第9级暗环的半径之差为1l ；用未知单色光照射时测得第l 和第9级暗环的半径之差为2l ．求单色光的波长2λ．[解] 牛顿环暗环半径公式为 λkR r =k对1λ 11λR r = 199λR r = 所以()19119-=-λR r r又 119l r r =-， 故211⨯=λR l 同理得 222⨯=λR l因此 121222λλl l =7-25 一平凸透镜放在平板玻璃上，在反射光中观察牛顿环．当1λ＝4500Å时，测得第3级明环的半径为31006.1-⨯m ．换用红光，观测到第5级明环的半径为31077.1-⨯m ．求透镜曲率半径和红光的波长．[解] 牛顿环明环半径公式为()2122k λR k r -=，对1λ，3=k 时， 25123λR r =对2λ，5=k 时， 29225λR r =由此得 697145001006.191077.15956262123252=⨯⨯⨯⨯⨯==--λλr r Å由25123λR r =得， m 00.110450051006.12521062123=⨯⨯⨯⨯==--λr R7-26 用牛顿环干涉条纹测定凹球面的曲率半径．将已知曲率半径的平凸透镜放在待测的凹球面上，如图所示．在两曲面之间形成空气层，可以观测到环状干涉条纹．测得第4级暗环的半径4r ＝2.250cm ，已知入射光的波长λ＝5893 Å，平凸透镜的曲率半径1R ＝102.3cm ，求凹球面的曲率半径2R ．[解] 牛顿环k 级暗环条件为 ()21222λλ+=+k e 即 λk e =2由几何关系知 ()2111211212k 2e e R e R R r +=--=因为 11R e << ，故 112k 2e R r = 同理 222k 2e R r = 又 21e e e -= 联立上式得2k 1211r k R R λ-= 以 m 023.11=R ，4=k ，m 10589310-⨯=λ，m 10250.224-⨯=r ，代入得cm 8.1022=R7-27 在观察牛顿环干涉条纹的实验中，用图（a ）、（b ）、（c ）所示的装置代替平凸透镜和平玻璃组合．试画出反射光中的干涉条纹（只画暗条纹）．[解]（a ） （b ） （c ）7-28 用波长为λ的单色光源做迈克尔逊干涉仪实验，在移动反光镜2M 的过程中，视场中的干涉条纹移过k 条，求反射镜移动的距离?[解] 设反射镜移过的距离为d ，则光程差改变量为 λδk d ==∆2所以 2λk d =7-29 迈克尔逊干涉仪的一臂中放有长为100.0mm 的玻璃管，其中充有一个大气压空气，用波长为5850Å的光作光源．在把玻璃管抽成真空的过程中，发现视场中有100.0条干涉条纹从某固定点移过．求空气的折射率．[解] 设空气的折射率为n ，在由空气抽成真空的过程中，光程差改变量为()λk e n ∆=-12所以 00029.1100.10021058500.100121310=⨯⨯⨯⨯+=∆+=--e k n λ7-30 在把迈克尔逊干涉仪的可动反射镜移动0.233mm 过程中，数得条纹移动数为792，求所用光的波长．[解] 设反射镜移动距离为d ，则光程差改变 λδk d ∆==∆25884m 10884.579210233.022103=⨯=⨯⨯=∆=--k d λÅ7-31 常用雅敏干涉仪来测定气体在各种温度和压力下的折射率．干涉仪的光路如图所示．S 为光源，L 为正透镜，1G 、2G 为等厚且相互平行的玻璃板．1T 、2T 为等长的两个玻璃管，长度为l ．进行测量时，先将1T 、2T 抽空，然后把待测气体徐徐导入一管中，在E123451234512345处观察干涉条纹移动数，即可求得待测气体的折射率．设在测量某气体的折射率时，将气体慢慢放入2T 管中，从开始进气到标准状态时，在E 处共看到有98条干涉条纹移过去．所用的钠光波长λ＝5893Å （真空中），l ＝20cm ．求该气体在标准状态下的折射率．[解] 设待测气体在标准状态下的折射率为n ，则在气体导入前后，两条光路中的光程差改变为()λk l n ∆=-1所以00029.110201058939811210=⨯⨯⨯+=∆+=--l k n λ7-32 一单缝宽度4101-⨯=a m ，透镜的焦距m 5.0=f ，若分别用40001=λÅ和76002=λÅ的单色平行光垂直入射，它们的中央明条纹的宽度各是多少?[解] 一级暗纹公式为 λϕ=1sin a 而aλϕϕ==11sin所以 a f f f x λϕϕ===111tan 所以中央明纹的宽度为 af x x λ221==∆对1λ： m 1041011045.02234711---⨯=⨯⨯⨯⨯==∆a f x λ 对2λ： m 106.7101106.75.02234722---⨯=⨯⨯⨯⨯==∆a f x λ7-33 有一单缝宽m m 10.0=a ，在缝后放一焦距cm 50=f 的会聚透镜，用波长λ＝5460 Å的平行绿光垂直照射单缝，求位于透镜焦平面处的屏上的中央亮条纹的宽度．如果把此装置浸入水中，并把屏移动到透镜在水中的焦平面上，中央亮条纹的宽度变为多少?设透镜的折射率54.1='n ，水的折射率33.1=n ．（提示：透镜在水中的焦距()f nn n n f -'-'=1水） [解] （1） 中央明条纹的宽度为m 1046.51010.01046.51050223372----⨯=⨯⨯⨯⨯⨯==∆a f x λ （2） 在水中，透镜焦距为()f nn n n f -'-'=1水 所以中央明条纹的宽度为()()()()m 1040.1101.033.154.11046.550.0154.12122237---⨯=⨯⨯-⨯⨯⨯-⨯=-'-'==∆a n n f n naf x λλ水7-34 用波长λ＝7000Å的平行光垂直照射单缝，缝后放一焦距为70cm 的正透镜，在透镜焦平面处的屏上测得中央亮条纹的宽度为3100.2-⨯m ．试计算： （1）单缝的宽度．（2）当用另一单色光照射时，测得中央亮纹的宽度为3105.1-⨯m ，求此光的波长． [解]中央亮条纹宽度为 af x λ2=∆ （1）由上式可得单缝的宽度为 m 109.41021071070224372----⨯=⨯⨯⨯⨯⨯=∆=x f a λ （2）由前式可得光的波长为5250m 1025.510072105.1109.427234=⨯=⨯⨯⨯⨯⨯='∆='----f x a λÅ7-35 用平行光管把某光源发出的单色光变成平行光后垂直照射在宽度为0.308mm 的单缝上．用焦距为12.62cm 的测微目镜测得中央明条纹两侧第5级暗条纹之间的距离为x ∆＝2.414mm ．求入射光的波长．[解] 单缝衍射暗纹中心到中央亮纹中心距离为 af kx λ= 5=k 时，af x λ55= 两侧第5级暗纹之间的距离为 af x x λ1025==∆ 所以 58921062.121010414.210308.010233=⨯⨯⨯⨯⨯=∆=---f x a λÅ7-36 用波长λ＝6328Å的氦-氖激光垂直照射单缝，其夫琅禾费衍射图样的第1级极小的衍射角为50．试求单缝的宽度．[解] 单缝衍射暗纹条件为λϕk a =sin 当 1=k 时，λϕ=sin a所以 ϕλϕλ==sin a 式中 g r a d1805πϕ= 所以 m 1026.7518010328.667--⨯=⨯⨯=πa7-37 在正常照度下，人眼瞳孔的直径约为mm 2，人眼最敏感的波长为5500Å．眼前m m 250 （明视距离）处的点物在视网膜上形成艾里斑的角半径是多少? 明视距离处能够被分辨的两物点的最小距离是多少?（前房液和玻璃状液的折射率33.1=n ）[解] （1） 因人眼中玻璃状液体的折射率为n ，所以波长变为nλλ='在视网膜上形成爱里斑的角半径为rad 1052.210233.1105.522.122.122.1437---⨯=⨯⨯⨯⨯=='=nD D λλθ （2） 人眼的最小分辨角 Dλθ22.1min =设在距离L 处能分辨的最小距离为d （l d θ=），则m 104.810250102105.522.122.15337----⨯=⨯⨯⨯⨯⨯==D L d λ7-38 已知天空中两颗星对一望远镜的角距离为61084.4-⨯rad ，设它们发出光的波长为5500Å．望远镜的口径至少要多大才能分辨出这两颗星．[解] 设望远镜孔径为D ，当两星对望远镜的角距离大于其最小分辨角时方可分辨，即Dλ22.11084.46≥⨯-所以 cm 9.131084.4105.522.11084.422.1676=⨯⨯⨯=⨯≥---λD7-39 月球距地面约3.86510⨯km ，设月光按λ＝5500Å计算，问月球表面上距离多远的两点才能被直径为5.00m 的天文望远镜所分辨．[解] 设月球上两物点距离为d ，其对望远镜张角大于最小分辨角时，则能分辨该两点即DL d λ22.1≥ 所以 m 8.5100.51086.3105.522.122.187=⨯⨯⨯⨯=≥-D L d λ7-40 用波长为λ＝5893Å的钠光垂直照射光栅，测得第2级谱线的衍射角11102'︒=θ，而用待测波长的单色光照射时，测得第一级谱线的衍射角2441'︒=θ．试求光栅常数和待测光的波长．[解] 光栅方程为 ()λϕk b a =+sin 对1λ有 ()11sin λθ=+b a 对2λ有 ()222sin λθ=+b a由上两式得 546410893.51110sin 244sin 2sin sin 27002211=⨯⨯''⨯==-λθθλÅ 将1λ的数值代入得 m 1067.66-⨯=+b a7-4l 一块每毫米刻痕为500条的光栅，用钠黄光正入射，钠黄光中含有两条谱线，其波长分别为5896Å和5890Å．求在第2级光谱中这两条谱线分开的角度．[解] 光栅常数为 m 10250010163--⨯=⨯=+b a 由光栅方程可得 ()122s i nλϕ=+b a ()222sin λϕ='+b a 因此得到 ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+='-=∆b a b a 21222arcsin 2arcsin λλϕϕϕ6767043.010210890.52arcsin 10210896.52arcsin =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=----7-42 一单色平行光投射于衍射光栅，其入射方向与光栅法线夹角为θ，在和法线成︒11和︒53的方向上出现第1级光谱线，并且位于法线的两侧．求θ角的大小．为什么在法线的一侧能观察到第2级谱线，而另一侧却没有?[解]（1） 斜入射时，零级主极大在透镜的与入射光线平行的副光轴方向上．530角的衍射光线和入射光线分别在法线两侧，此衍射角应取负值，而110衍射角应取正值，所以两个第一级光谱线对应的方程分别为 ()()λθ-=-+053sin sin b a （1）()()λθ+=++011sin sin b a （2） 因此求得 3039.0sin =θ 07.17=θ（2） 设法线两侧衍射角为900时对应极大的级数分别为k 和k '在与入射光线异侧有 ()()λk b a -=-+0090sin 7.17sin （3） 在与入射光线同侧有 ()()λk b a '=++0090sin 7.17sin （4）由 （1）、（3）式相除，得 4.17.17sin 53sin 7.17sin 90sin 0000≈--=k 由 （2）、（4）式相除，得 64.27.17sin 11sin 7.17sin 90sin 0000≈++='k 由上面结果知，只有与入射光线同侧可观察到第二级谱线．7-43 一衍射光栅，每厘米有200条透光缝，每条透光缝宽为3102-⨯=a cm ，在光栅后放一焦距为m 0.1=f 的凸透镜．现以λ=6000Å单色平行光垂直照射光栅，试求： （1）透光缝的单缝衍射中央明条纹宽度；（2）在该宽度内有哪几个光栅衍射主极大?[解] （1）单缝衍射第一极小满足 λϕ=s i na （1） 中央明纹宽度为m 1061021060.122sin 2tan 2257---⨯=⨯⨯⨯⨯====∆a f f f x λϕϕ （2） 设该范围内主极大最大级数为k ，则()λϕk b a =+sin （2）由 （1）、（2）式有 5.210220010152=⨯⨯⨯=+=--a b a k 所以在此范围内能看到的主极大级数为210±±=，，k ，共5个光栅衍射主极大．7-44 试指出光栅常数()b a +为下述三种情况时，哪些级数的光谱线缺级？（1）光栅常数为狭缝宽度的两倍，即()a b a 2=+； （2）光栅常数为狭缝宽度的三倍，即()a b a 3=+；（3）光栅常数为狭缝宽度的2.5倍，即()a b a 5.2=+．[解] k 级缺级的条件为k aba k '+=() 3,2,1±±±='k （1）()a b a 2=+时，k k '=2，凡2的倍数级都缺级． （2） ()a b a 3=+时，k k '=3，凡3的倍数级都缺级． （3）()a b a 5.2=+时，k k '=5.2，凡5的倍数级都缺级．7-45 波长λ＝6000Å的单色光垂直入射到一光栅上，测得第2级主极大的衍射角为︒30，且第3级缺级．（1）光栅常数()b a +是多大？（2）透光缝可能的最小宽度是多少？（3）在屏幕上可能出现的主极大的级次是哪些？[解]（1） 由光栅方程得 ()λ230sin 0=+b a所以 m 104.21064430sin 2670--⨯=⨯⨯===+λλb a （2） 当k 级缺级时，满足 k a ba k '+=所以 k kba a '+=当1='k 时，缝宽a 最小，为 m 1083104.276--⨯=⨯=+=k b a a （3） 在屏幕上呈现的主极大的级数由最大级数和缺级情况决定． 因为 ()λφk b a =+sinmax k <4106104.276=⨯⨯=+--λba 因此 m a x k =3又因3=k 缺级，所以在屏上可能出现的级数为 2,1,0±±=k7-46 每厘米刻有400条刻痕的光栅，其透光缝5101-⨯=a m ，用波长为λ＝7000Å的光垂直照射在屏幕上可观察到多少条明条纹?[解] 光栅常数 m 105.240010152--⨯=⨯=+b a 因为 ()λϕk b a =+sinmax k <7.35107105.275=⨯⨯=+--λba 因此35max =k 缺级条件 k k k ab a k '='⨯⨯='+=--5.2101105.255所以 凡能被5整除的级数都缺级，共缺级个数为7535=='N 因此，光栅衍射在屏上呈现明条纹总数为 ()5717352=+-⨯=N7-47 以白光（波长范围4000～7600Å）垂直照射光栅，在衍射光谱中，第2级和第3级发生重叠．求第2级被重叠的范围．[解] 最小波长和最大波长分别为4000min =λ Å 7600max =λ Å第3级光谱中，min λ主极大的位置与第2级某一波长λ的主极大位置相同时，开始重叠，由光栅方程可求此波长 ()λϕ2s i n =+b a ()m i n 3s i n λϕ=+b a因此 600040002323min =⨯==λλÅ 故，第2级光谱中被重叠的光谱波长范围为 6000=λÅ~7600 Å7-48 用两米光栅摄谱仪拍摄氢原子光谱，在可见光范围内有四条谱线，如图所示．光栅上每厘米有4000条缝，光栅后的正透镜的焦距为2.00m ，在其焦平面上放一照相底片，求四条谱线在底片上的间距．[解] 光栅常数为 m 105.2400010162--⨯=⨯=+b a ∞对第一条谱线（1=k ），应用光栅方程，为()λϕ=+sin b a 对αH ， m 10563.671-⨯=λ，在底片上位置为m 543.0arcsin tan tan 1=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+==b a f f x λϕ 同理可得δγβH H H ,,三条谱线在照像底片上的位置分别为m 396.02=x m 353.03=x m 333.04=x因此 αH 与βH 之间的间距为 7m 14.01=∆x同理可得βH 与γH 之间的间距为 m043.02=∆x γH 与δH 之间的间距为 m 02.03=∆x7-49 用白光照射每毫米50条刻痕的光栅，在距光栅2m 的屏幕上观察到各色光谱，设可见光的上限波长（红光）r λ＝7800 Å，下限波长（紫光） v λ=4000 Å，试计算屏幕上第1级光谱的宽度．[解] 第一级谱线满足 ()λϕ=+s i nb a 屏幕上红光谱线的位置为 ba f f x +≈≈r1λϕ 紫光谱线的位置为 ba f f x +≈'≈v2λϕ所以第一级光谱的宽度为()()m 108.310400078001015022103v r 21---⨯=⨯-⨯⨯=-+=-=∆λλb a fx x x7-50 一光源发射红双线在波长λ＝6563 Å处，两条谱的波长差λ∆＝1.8 Å．有一光栅可以在第1级中把这两条谱线分辨出来，求光栅的最少刻线总数．[解] 光栅的分辨率为 kN R =∆=λλ所以 1.364618.16563=⨯=∆=k N λλ 即光栅最少刻线总数为3647条．7-51 一光栅宽为6cm ，每厘米有6000条刻线，在第三级光谱中，对λ＝5000 Å处，可分辨的最小波长间隔是多大?[解] 光栅的总缝数为 3600066000=⨯=N因为光栅的分辨本领为kN =∆λλ046.03600035000=⨯==∆kNλλÅ7-52 一束波长为2.96 Å的X 射线投射到晶体上，所产生的第1级衍射线偏离原入射线方向731'︒，求对应此射线的相邻两原子平面之间的距离．[解] 设掠射角为ϕ，衍射线偏离入射线的角度为θ，则2θϕ=由布拉格方程 λϕk d =sin 2 得相邻两原子平面间距为()52.52731sin296.212sin 2sin 20='⨯⨯===θλϕλk k d Å7-53 以波长为1.10Å的X 射线照射岩盐晶面，测得反射光第1级极大出现在X 射线与晶面的夹角为'3011︒处．问：（1）岩盐晶体的晶格常数d 为多大?（2）当以另一束待测的X 射线照岩盐晶面时，测得反射光第一级极大出现在X 射线与晶面的夹角为'3017︒处，求待测X 射线的波长．[解] （1） 由布拉格方程 λϕk d =sin 2 ，所以 76.25.11sin 210.1sin 20===ϕλk d Å （2） 由布拉格方程得待测X 射线的波长为66.115.17sin 76.22sin 20=⨯⨯==k d ϕλÅ7-54 一束部分偏振光垂直入射于一偏振片上，以入射光为轴旋转偏振片，测得透射光强的最大值是最小值的5倍．求部分偏振光中自然光与线偏振光强度之比．[解] 设该束部分偏振光中自然光光强为0I ，线偏振光光强为I ，透过偏振片后自然光光强变为20I ，因此光强最大时I II +=20max , 光强最小时 20m i n I I =所以22500minmaxI I I I I +== 因此 210=I I7-55 两偏振片A 、B 的透振方向成︒45角，如图所示．入射光是线偏振光，其振动方向和A 的透振方向相同．试求这束光线分别从左边入射和从右边入射时，透射光强之比．[解] 设从左右两边入射时透射光强分别为1I 和2I由马吕斯定律得从左边入射时透射光强为002012145cos I I I == 从右边入射，则00202024145cos 45cos I I I =⋅= 所以入射光从左右两边入射，透射光强之比为1:2:21=I I7-56 三个理想偏振片1P 、2P 、3P 叠放在一起，1P 与3P 的透振方向互相垂直，位于中间的2P 与1P 的透振方向间的夹角为︒30．强度为0I 的自然光垂直入射到1P 上，依次透过1P 、2P 和3P ．求通过三个偏振片后的光强．[解] 通过1P 后： 0121I I =通过2P 后： 002128330cos I I I == 通过3P 后： 0022332360cos I I I ==7-57 一束太阳光以某一入射角入射于平面玻璃上，这时反射光为完全偏振光．若透射光的折射角为︒32，试求：（1）太阳光的入射角；（2）这种玻璃的折射率．[解] 因反射光为完全偏振光，所以入射角为布儒斯特角，则 0090=+r i 0000058329090=-=-=r i由布儒斯特定律得 60.158tan tan 00===i n7-58 光从介质1射向介质2时的临界角是︒60．布儒斯特角是多大? [解] 由光的折射定律得 020190sin 60sin n n = 所以2360sin 012==n n 由布儒斯特定律 23tan 120==n n i 由此得 9.400=i7-59 如图所示的各种情况中，以线偏振光或自然光入射于两种介质的界面上．图中0i 为起偏振角， 0i i ．试画出折射光线和反射光线并标出它们的偏振状态．[解] 折射光和反射光及其偏振状态如下图7-60 如图（a ）所示，一束自然光入射在方解石的表面上，入射光线与光轴成锐角，问有几条光线从方解石透射出来? 如果把方解石切割成等厚的A 、B 两块，并平行地移动一点距离，如图（b ）所示，此时光线通过这两块方解石后，有多少条光线射出来? 如果把B 绕入射光线转过一个角度，此时将有几条光线从B 射出来?[答] （1）因入射光不沿光轴方向，也不垂直于光轴，所以在方解石中产生双折射现象，有两条光线透射出来． （2）在A 中为o 光的光线射出来入射到B ，入射面就是B 中o 光的主平面，因此光线通过B 后，只有一条光线射出，同理，在A 中为e 光的光线通过B 后也有一束光线射出，所以从B 中透射出来的仍是两束光．（3）当把B 任意转过一角度时，A 中的o 光和e 透射出来入射到B 中，各自在B 中又发生双折射现象，每条光线在B 中又分为o 光和e 光，因此，总共有四条光线从B 中射出．*7-61 如图所示，一束自然光入射到一方解石晶体上，其光轴垂直于纸面．已知方解石对o 光的折射率o n ＝1.658，对e 光的折射率为=e n 1.486．（1）如果方解石的厚度为t ＝1.0 cm ，自然光的入射角︒=45i ，求a ，b 两透射光之间的垂直距离；（2）两透射光的振动方向如何? 哪一束光在晶体中是o 光? 哪一束光在晶体中是e 光?[解]（1）由折射定律得：i r n sin sin o o = （1）i r n sin sin e e = （2） 设则,,d BC L AB ==()0e tan tan r r t L -= （3）由于 i ABC =∠，所以 i L d cos = （4）由（1）、（2）、（3）、（4）联立得43.0658.145sin sin sin 000===n i r 002.25=r 48.0486.145sin sin 0e ==r 4.28e =r ()cm 07.02.25tan 4.28tan 0.100=-⨯=Lcm 05.045cos 07.00=⨯=d即a 、b 两光线的垂直距离为cm 05.0．（2）两透射光的振动方向见图．（3）a 为e 光，b 为o 光．*7-62 设方解石对钠黄光 （5893=λÅ）和氦氖激光（63282=λÅ）的主折射率相同，把方解石切割成对上述两光的四分之一波片，其最小厚度各是多少? 6584.1o =n ，4864.1e =n ．[解] 设最小厚度分别为1e 和2e ，依题意有()41e o 1λ=-n n e ()42e o 2λ=-n n e所以 ()()m 10565.84864.16584.1410893.5477e 011--⨯=-⨯⨯=-=n n e λ ()()m 10198.94864.16584.1410328.6477e 021--⨯=-⨯⨯=-=n n e λA B C。

第七章刚体力学习题解答7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.⑴假设转动是匀加速转动，求角加速度。

⑵在此时间内，发动机转了多少转？解：⑴21260/2)12003000(/7.15s rad t===-∆∆πωβ⑵rad 27.152)60/2)(12003000(21039.26222202⨯===∆⨯--πβωωθ对应的转数=42010214.3239.262≈⨯=⨯∆πθ7.1.3 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。

求t 时刻的角速度和角加速度。

解：23212643ct bt ct bt a dtd dtd -==-+==ωθβω7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立o-xy 坐标系，原点在轴上，x 和y 轴沿水平和铅直向上的方向。

边缘上一点A 当t=0时恰好在x 轴上，该点的角坐标满足θ=1.2t+t 2 (θ:rad,t:s)。

⑴t=0时，⑵自t=0开始转45º时，⑶转过90º时，A 点的速度和加速度在x 和y 轴上的投影。

解：0.222.1==+==dtd dtd t ωθβω⑴t=0时，s m R v v y x /12.01.02.10,2.1=⨯====ωω2222/2.01.00.2/144.01.0/12.0/sm R a a s m R v a a y y n x =⨯===-=-=-=-=βτ⑵θ=π/4时,由θ=1.2t+t 2,求得t=0.47s,∴ω=1.2+2t=2.14rad/ssm R v s m R v y x /15.02/21.014.245sin /15.02/21.014.245cos =⨯⨯=︒=-=⨯⨯-=︒-=ωω222222222222/182.0)14.20.2(1.0)(45sin 45sin 45sin /465.0)14.20.2(1.0)(45cos 45cos 45cos s m R R R a s m R R R a y x -=-⨯=-︒=︒-︒=-=+⨯-=+︒-=︒-︒-=ωβωβωβωβ⑶θ=π/2时,由θ=1.2t+t 2,求得t=0.7895s,ω=1.2+2t=2.78rad/s2222/77.01.078.2/2.01.00.20/278.01.078.2s m R a s m R a v s m R v y x y x -=⨯-=-=-=⨯-=-==-=⨯-=-=ωβω7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承，以角速率ω=10rad/s 逆时针转动，求臂与铅直成45º时门中心G 的速度和加速度。