徐亚宁 信号与系统全部作业的参考答案汇编

《信号与系统》作业参考解答第一章（P16-17）1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。

证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 （m ,n 为正整数） 解：由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == （m ,n 为正整数） 1-5 试判断下列信号是否是周期信号。

若是，确定其周期。

（1）t t t f πsin 62sin 3)(+= （2）2)sin ()(t a t f =（8）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解：（1）因为t 2sin 的周期为π，而t πsin 的周期为2。

显然，使方程n m 2=π （m ,n 为正整数）成立的正整数m ,n 是不存在的，所以信号t t t f πsin 62sin 3)(+=是非周期信号。

（2）因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。

（8）由于)4/cos(k π的周期为8)4//(21==ππN ，)8/sin(k π的周期为16)8//(22==ππN ，)2/cos(k π的周期为4)2//(23==ππN ，且有16412321=⨯=⨯=⨯N N N所以，该信号是周期16=N 的周期信号。

1-10 判断下列系统是否为线性时不变系统，为什么？其中)(t f 、][k f 为输入信号，)(t y 、][k y 为零状态响应。

（1）)()()(t f t g t y = （2）)()()(2t f t Kf t y += 解：（1）显然，该系统为线性系统。

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

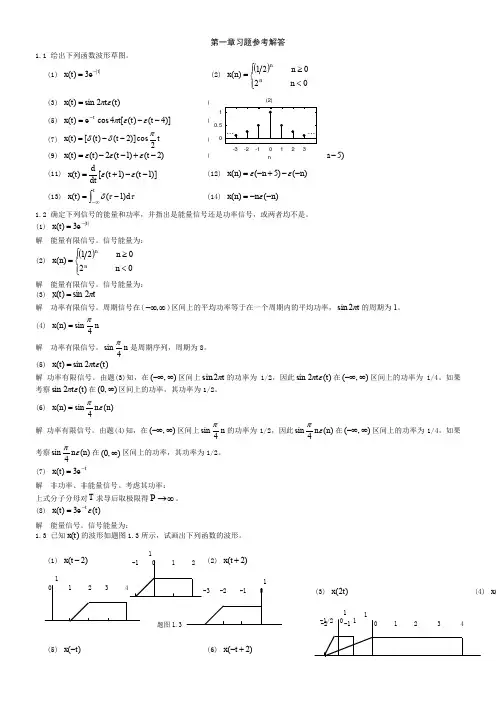
第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t et x -=解 能量有限信号。

信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：(3) t t x π2sin )(=解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

(4) n n x 4sin)(π=解 功率有限信号。

n 4sin π是周期序列，周期为8。

(5) )(2sin )(t t t x επ=解 功率有限信号。

由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。

如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。

(6) )(4sin)(n n n x επ=解 功率有限信号。

由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。

如果考察)(4sinn n επ在),0(∞区间上的功率，其功率为1/2。

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦：e e sh 2x xx --=双曲余弦：e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =，C 为常数（下同）d()d d u v u v ±=±，u 、v 为t 的函数（下同） d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式（1）等比数列123,,,,N a a a a 的通项为11n n a a q -=，q 为公比，前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑（2）等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-，d 为公差，前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰， 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰，1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭，B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰，0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑，0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑，0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤，附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤，B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1（a）确定信号、连续时间信号、非周期信号、能量信号、非因果信号。

可编辑第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t e t x -= (2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2cos )]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=t d t x ττδ)1()((14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t e t x -=解 能量有限信号。

信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：(3) t t x π2sin )(=解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

(4) n n x 4sin )(π=解 功率有限信号。

n 4sinπ是周期序列，周期为8。

(5) )(2sin )(t t t x επ= 解 功率有限信号。

由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。

如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。

(6) )(4sin )(n n n x επ=解 功率有限信号。

由题(4)知，在),(∞-∞区间上n 4sinπ的功率为1/2，因此)(4sin n n επ在),(∞-∞区间上的功率为1/4。

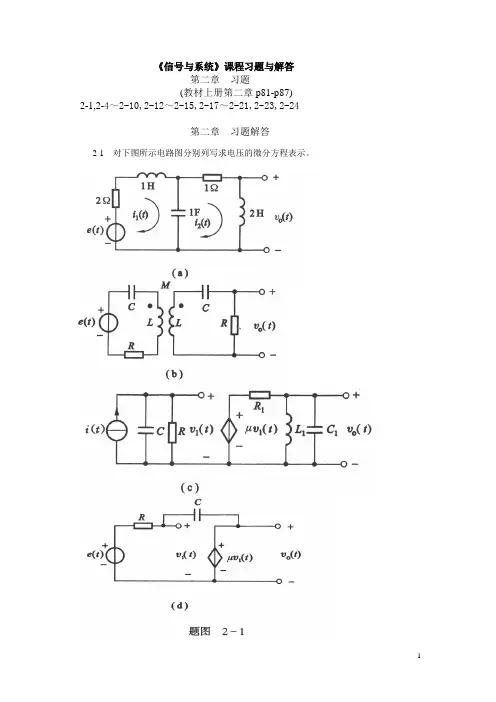
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。

图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。

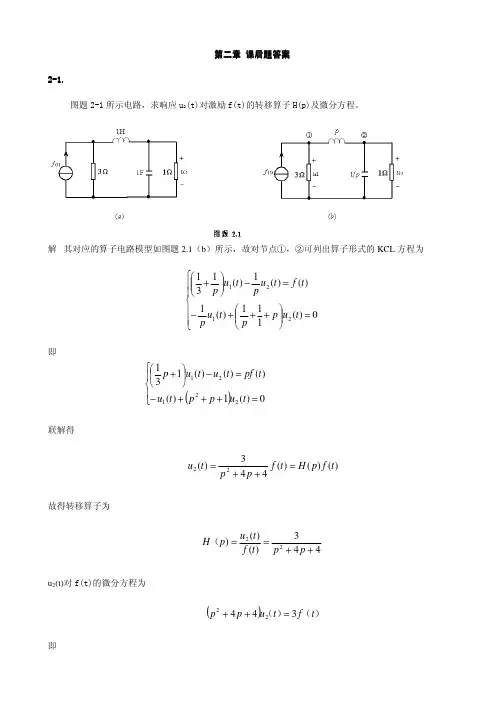
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图2.2（b）所示。

故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。

求t>0时的零输入响应i(t)和u C (t)。

解 其对应的算子电路模型如图题2.3（b）所示。

故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。

第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t et x -=解 能量有限信号。

信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：(3) t t x π2sin )(=解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

(4) n n x 4sin)(π=解 功率有限信号。

n 4sin π是周期序列，周期为8。

(5) )(2sin )(t t t x επ=解 功率有限信号。

由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。

如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。

(6) )(4sin)(n n n x επ=解 功率有限信号。

由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。

如果考察)(4sin n n επ在),0(∞区间上的功率，其功率为1/2。

第三章3.12 求下列信号的傅里叶变换（2）()/21U t - (4) ()2jt e t δ-- （6）()()211t e t δ--- （8）()()1U t U t --解：（2）因为 ()()/212U t U t -=-，所以 ()()21/21j U t e j ωπδωω-⎡⎤-↔+⎢⎥⎣⎦ （4）因为 ()()222jt j e t e t δδ---=-，所以，()()212j jt e t e ωδ-+--=↔ （6）因为 ()()()2111t e t t δδ---=-，所以，()()211t j e t e ωδ----↔（8）因为 ()()()33 1.5U t U t g t --=-，所以()() 1.53332j U t U t Sa eωω-⎛⎫--↔ ⎪⎝⎭3.14 已知信号()1f t 和()2f t 的带宽分别为1ω和2ω，并且12ωω>，求下列信号的带宽。

（1）()()12f t f t（2）()()12f t f t * （3）()()122f t f t +（4）()()212*f t f t（5）()()1221f t f t -（1）()()()()()12121*2f t f t F j F j F j ωωωπ↔=，根据卷积的性质可知()F j ω 带宽为12ωω+；（2）因为()()()()()1212f t f t F j F j F j ωωω*↔=，所以()F j ω的带宽为2ω； (3)因为()()()()()121222f t f t F j F j F j ωωω=↔=+，所以()F j ω的带宽为1ω；（4）因为()()()()()()1221121*2f t f t F j F j F j F j ωωωωπ⎡⎤*↔=⎢⎥⎣⎦，所以()F j ω的带宽为2ω；（5）因为 ()()()()12121121*222j f t f t F j F j F j e ωωωωπ-⎡⎤⎛⎫⎡⎤-↔=⎪⎢⎥⎣⎦⎝⎭⎣⎦ ，所以()F j ω的带宽为122ωω+。