八年级下册测试题

八年级下册物理第八章测试题附答案第八章测试题一、填空题1.正确认识力和运动的关系，推翻“力是维持物体运动的原因”的物理学家是XXX，建立惯性定律的物理学家是XXX。

2.一切物体在没有受到外力的时候，总保持匀速直线运动状态或静止状态，这就是牛顿第一定律。

3.重N的直升飞机，悬停在空中，则直升飞机受到的空气作用力是N，方向向上，若直升飞机做匀速直线飞行，则直升飞机受到的是平衡力。

4.同学们骑自行车上学，当停止用力蹬脚踏时，自行车仍然能向前运动，这是由于惯性的缘故；但自行车运动会越来越慢，最后停下来，这是由于自行车受到了摩擦力的作用。

5.一位乘客站在匀速直线行驶的轮船甲板上，他受到的重力和支持力是一对平衡力，与甲板的摩擦力是0N（不考虑空气阻力）。

6.一个重为50N的物体沿水平路面做匀速直线运动，需加10N的水平拉力，则它在运动时受到的摩擦力为10N；若将该物体用绳悬挂起来，物体静止时绳对物体的拉力为50N；若使物体竖直向下匀速运动，则向上的拉力应为50N。

7.用弹簧测力计拉着重200N的物体在水平桌面上做匀速直线运动，当速度为4m/s时，弹簧测力计的示数为20N，若速度为1m/s时，该物体受到的摩擦力为10N，合力为190N，若将拉力增大，当弹簧测力计的示数变为30N时，物体受到的摩擦力为20N，此时物体受到的合力为220N。

8.空降兵在降落伞打开后的一段时间内将匀速下落，它的体重为650N，伞重200N，若人受到的阻力忽略不计，则伞对人的拉力为850N，伞受到的阻力为0N。

9.物体受到同一直线上两个力的作用，已知其中一个力的大小为60N，方向向西，它们的合力方向向东，大小为20N，则另一个力的大小是40N，方向向西。

10.如图1所示，水平地面上有甲、乙两个物体叠放在一起。

已知甲物体的质量为4kg，乙物体的质量为6kg。

有一大小为10N的水平向左的拉力F作用在乙物体上后，甲、乙两物体仍保持静止状态。

八年级数学下册第三章《图形与坐标》测试题-湘教版（含答案）一．选择题1．当2＜m＜3时，点P（m﹣2，m﹣3）在第（）A．一象限B．二象限C．三象限D．四象限2．在直角坐标系中，M（﹣3，4），M到x、y轴的距离与M′到x、y轴的距离相等，则M′的坐标不可能为（）A．（﹣3，﹣4）B．（3，4）C．（3，﹣4）D．（3，0）3．若点（a，﹣3）与点（2，b）关于y轴对称，则a，b的值为（）A．a＝2，b＝3B．a＝2，b＝﹣3C．a＝﹣2，b＝﹣3D．a＝﹣2，b＝3 4．在平面直角坐标系中，点Q（﹣1，3）向右平移3个单位长度后的坐标为（）A．（﹣1，0）B．（﹣1，6）C．（2，3）D．（2，6）5．如果点A（2，﹣3）和点B关于原点对称，则点B的坐标为（）A．（﹣2，3）B．（﹣2，﹣3）C．（2，﹣3）D．（2，3）6．如图，一个动点P在平面直角坐标系中按箭头所示方向做折线运动，即第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1），…，按这样的运动规律，经过第2013次运动后，动点P的坐标是（）A．（2012，1）B．（2012，2）C．（2013，1）D．（2013，2）7．在y轴上，与点A（3，﹣2）的距离等于3的点有（）A．1个B．2个C．4个D．0个8．如图，在直角坐标系中，▱OABC的顶点A为（1，3）、C为（5，0），则B的坐标为（）A．（6，3）B．（5，5）C．（4，3）D．无法确定9．如图，△AOB关于x轴对称图形△A′OB，若△AOB内任意一点P的坐标是（a，b），则△A′OB中的对应点Q的坐标是（）A．（a，b）B．（﹣a，b）C．（﹣a，﹣b）D．（a，﹣b）10．根据指令[s，A]（s≥0，0°≤A＜360°）机器人在平面上能完成如下动作：先在原地顺时针旋转角度A，再朝其面对的方向沿直线行走距离s．现在机器人在平面直角坐标系的原点，且面对y轴的负方向，为使其移动到点（﹣3，0），应下的指令是（）A．[3，90°]B．[90°，3]C．[﹣3，90°]D．[3，270°]二．填空题11．已知点A（2，3）在第一象限，则与点A关于x轴对称的点的坐标为，与点A 关于y轴对称的点的坐标为，与点A关于原点对称的点的坐标为．12．若点A（﹣1，a），B（b，2）两点关于y轴对称，则a＝，b＝．13．点P（1，2）关于点Q（﹣1，1）的对称点的坐标为．14．定义：在平面直角坐标系内，对于点P（x，y），我们把Q（﹣y+1，x+3）叫做它的伴随点．如点（2，1）的伴随点为（﹣1+1，2+3），即（0，5）．若点M的伴随点坐标为（﹣5，3），则点M的坐标为．15．将点N（﹣1，2）向右平移3个单位，再向下平移4个单位后，其坐标变为．16．坐标系中M（﹣3，2），N（3，2）之间距离是．17．点M（﹣3，5）关于直线x＝1对称的点M′的坐标为．18．如图，规定列号写在前面，行号写在后面，如用数对的方法，棋盘中“帅”与“卒”的位置可分别表示为（e，4）和（g，3），则“马”的位置可表示为．19．在x轴上与点（0，﹣2）距离是4个单位长度的点有．20．如图，直线OD与x轴所夹的锐角为30°，OA1的长为1，△A1A2B1，△A2A3B2，△A3A4B3，…，△A n A n+1B n均为等边三角形，点A1，A2，A3，…，A n+1在x轴的正半轴上依次排列，点B1，B2，B3，…，B n在直线OD上依次排列，那么B2020的坐标为．三．解答题21．自然数按如图规律排列，14这个数位于第4行，第3列，记作（4，3），那么124这个数记作什么？…12510……43611……98712…．…16151413…………………．22．已知平面直角坐标系中，点P（1﹣a，2a﹣5）到两坐标轴的距离相等，求a值并确定点P的坐标．23．已知A（0，0）、D（4，2）、E（6，6）、C（2，4），依次连接各点得到四边形ADEC，按要求绘制下列图形．（1）横坐标、纵坐标都乘以﹣1；（2）纵坐标不变，横坐标扩大为原来的2倍；（3）横坐标都加2，同时纵坐标都减5；（4）如果坐标不变，纵坐标都扩大为原来的2倍，同时再加上3，不画图，你能叙述图形的变化吗？24．点P（x+1，2x﹣1）关于原点的对称点在第一象限，试化简：|x﹣3|﹣|1﹣x|25．如图，分别说明：△ABC从（1）→（2），再从（2）→（3）…一直到（5），它的横、纵坐标依次是如何变化的？26．当m为何值时，点P（3m﹣1，m﹣2）到y轴的距离是到x轴距离的3倍？求出此时点P到原点的距离．27．已知在平面直角坐标系中，点A、B的坐标分别为：A（﹣3，4），B（4，﹣2）．（1）求点A、B关于y轴对称的点的坐标；（2）在平面直角坐标系中分别作出点A、B关于x轴的对称点M、N，顺次连接AM、BM、BN、AN，求四边形AMBN的面积．参考答案一．选择题1．解：∵2＜m＜3时，∴m﹣2＞0，m﹣3＜0，∴点P在第四象限．故选：D．2．解：∵M点的坐标为（﹣3，4），∴M到x、y轴的距离分别为4，3，而M到x、y轴的距离与M′到x、y轴的距离相等，∴M′到x、y轴的距离也为4，3，结合各选项A、B、C到x、y轴的距离分别为4，3，D到x、y轴的距离分别为0，3，故D符合题意．故选：D．3．解：∵点（a，﹣3）与点（2，6）关于y轴对称，∴a＝﹣2，b＝﹣3，故选：C．4．解：点Q（﹣1，3）向右平移3个单位长度后的坐标为（2，3）．故选：C．5．解：∵点A（2，﹣3）和点B关于原点对称，∴点B的坐标为（﹣2，3）．故选：A．6．解：∵第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1），…，∴按这样的运动规律，第几次横坐标即为几，纵坐标为：1，0，2，0，1，0，2，0 (4)个一循环，∵＝503…1，∴经过第2013次运动后，动点P的坐标是：（2013，1）．故选：C．7．解：在y轴上，与点A（3，﹣2）的距离等于3的点有（0，﹣2），即只有1个点．故选：A．8．解：由题意得AB∥x轴，那么点A和B的纵坐标相等为3，∵OC＝5，那么点B的横坐标为1+5＝6．故选：A．9．解：∵△AOB与△A'OB关于x轴对称，∴点P（a，b）关于x轴的对称点为（a，﹣b），∴点P的对应点Q的坐标是（a，﹣b）．故选：D．10．解：根据点（0，0）到点（﹣3，0），即可知机器人先顺时针转动90°，再向左平移3个单位，于是应下指令为[3，90°]．故选：A．二．填空题11．解：∵点A（2，3）在第一象限，∴与点A关于x轴对称的点的坐标为：（2，﹣3），与点A关于y轴对称的点的坐标为：（﹣2，3），与点A关于原点对称的点的坐标为：（﹣2，﹣3）．故答案为：（2，﹣3），（﹣2，3），（﹣2，﹣3）．12．解：∵点A（﹣1，a），B（b，2）两点关于y轴对称，∴b＝1，a＝2，故答案为：2；1．13．解：设点P（1，2）关于点Q（﹣1，1）的对称点的坐标为（a，b），则＝﹣1，＝1，解得：a＝﹣3，b＝0，∴点P（1，2）关于点Q（﹣1，1）的对称点的坐标为（﹣3，0），故答案为：（﹣3，0）．14．解：设点M（m，n），则它的伴随点为（﹣n+1，m+3），∵点M的伴随点坐标为（﹣5，3），∴﹣n+1＝﹣5，m+3＝3，解得，m＝0，n＝6，∴M（0，6）．故答案为（0，6）．15．解：点N（﹣1，2）向右平移3个单位，再向下平移4个单位后，其坐标为（﹣1+3，2﹣4），即：（2，﹣2），故答案为：（2，﹣2）．16．解：∵M（﹣3，2），N（3，2），∴MN∥x轴，∴MN＝3﹣（﹣3）＝3+3＝6．故答案为：6．17．解：∵点M（﹣3，5）与点N关于直线x＝1对称，而1×2﹣（﹣3）＝5，∴点M（﹣3，5）关于直线x＝1对称的点N的坐标是（5，5），故答案为（5，5）．18．解：根据题意知“马”的位置可表示为（c，3），故答案为：（c，3）．19．解：∵点在x轴上，∴点的纵坐标为0，∵距离（0，﹣2）的距离是4，∴所求点的横坐标为±＝±2，∴所求点的坐标是（2，0）或（﹣2，0）．故答案填：（2，0）或（﹣2，0）．20．解：∵△A1B1A2为等边三角形，∴∠B1A1A2＝60°，∵∠B1OA2＝30°，∴∠B1OA2＝∠A1B1O＝30°，∴OA2＝2OA1＝2，同理可得，OA n＝2n﹣1，∵∠B n OA n+1＝30°，∠B n A n A n+1＝60°，∴∠B n OA n+1＝∠OB n A n＝30°，∴B n A n＝OA n＝2n﹣1，即△A n B n A n+1的边长为2n﹣1，则可求得其高为×2n﹣1＝×2n﹣2，∴点B n的横坐标为×2n﹣1+2n﹣1＝×2n﹣1＝3×2n﹣2，∴点B n的坐标为（3×2n﹣2，×2n﹣2），∴点B2020的坐标为（3×22018，×22018）．故答案为（3×22018，×22018）．三．解答题21．解：第一单元是：1，第二单元是：2，3，4，第三单元是：5，6，7，8，9，第四单元是：10，11，12，13，14，15，16，第五单元是：17，18，19，20，21，22，23，24，25，…，所以，124在第12单元，第3个数，即第3行第12个数，∴124这个数记作（3，12）．22．解：∵点P（1﹣a，2a﹣5）到两坐标轴的距离相等，∴符合题的点P的横、纵坐标相等或互为相反数，∴|1﹣a|＝|2a﹣5|，∴1﹣a＝±（2a﹣5）解得：a＝2或a＝4，则1﹣2＝﹣1，2×2﹣5＝﹣1，1﹣4＝﹣3，2×4﹣5＝3，所以P的坐标为（﹣1，﹣1）或（﹣3，3）．23．解：（1）如图所示：四边形A′D′E′C′即为所求；（2）如图所示：四边形A″D″E″C″即为所求；（3）如图所示：四边形A1D1E1C1即为所求；（4）图形在原基础上各点向上平移纵坐标个单位后，再将整体图形向上平移3个单位．24．解：∵点P（x+1，2x﹣1）关于原点的对称点P′的坐标为（﹣x﹣1，﹣2x+1），而P′在第一象限，∴﹣x﹣1＞0，且﹣2x+1＞0，∴x＜﹣1，∴|x﹣3|﹣|1﹣x|＝﹣（x﹣3）﹣（1﹣x）＝﹣x+3﹣1+x＝2．25．解：（1）→（2）纵坐标不变，横坐标都加1，（2）→（3）横坐标不变，纵坐标都加1，（3）→（4）横、纵坐标都乘以﹣1，（4）→（5）横坐标不变，纵坐标都乘以﹣1．26．解：根据题意得到|3m﹣1|＝3|m﹣2|，两边平方，解得m＝因而P的坐标是（，﹣），则OP＝．27．解：（1）根据轴对称的性质，得A（﹣3，4）关于y轴对称的点的坐标是（3，4）；点B（4，﹣2）关于y轴对称的点的坐标是（﹣4，﹣2）．（2）根据题意：点M、N与点A、B关于x轴对称，可得M（﹣3，﹣4），N（4，2）；进而可得四边形AMBN为梯形，且AM＝8，BN＝4．故四边形AMBN的面积为•（8+4）×7＝42．。

八年级下册Unit1 What’s the matter? 测试题一、选择填空。

（15 分）1. ------ I have a headache.A. What’s the matter, Judy?B. Where are you, Judy?C. Who are you?D. What are you doing, Judy?2.He stay at home and look after mother yesterday.A.needed toB. mustC. have toD. has to3.I th ink walking is our health.A.good atB. bad atC. well inD. good for4.We should not eat junk food.A.too manyB. too muchC. many tooD. much too5.--- How is the young man?---A.He is twelve.B. He’s much better.C. He is a doctor.D. He’s Allan.6.It’s important to eat a diet.A.balancedB. balanceC. balancingD. balances7.He often has sports. , football, basketball and ping-pong.A.For an exampleB. For exampleC. For the exampleD. For a example8.You should not eat 24 hours.A.something inB. nothing forC. anything forD. everything at9.--- My m other is ill.---A.Don’t worry.B. No hurry.C. I’m sorry to hear that.D. OK.10.--- I feel stressed out. I have so much work to do every day.--- You’d better not work too hard. It’s good for you to take some , I think.A.healthB. exerciseC. lessonD. work11.If I spend more minutes on it, now I can save your leg.A.littleB. a littleC. fewD. a few12.Before she got to Canada, she didn’t hear a single English .A.speakingB. spokenC. saidD. to say13.The day before yesterday the man gave me advice.A.a goodB. such a goodC. so good aD. a piece of good14.Please the door and you get into the hall.A.close, beforeB. close, afterC. open, whileD. open, until15.Such a officer be honest, she got her money in a dishonest way.A.can’tB. may notC. shouldn’tD. mustn’t二、完形填空（10 分）Different countries have different food. If you go to 1 , you may find 2 fish and chip shops along the 3 . Fish and chips are the 4 popular fast food in England. People often5 this kind of food at shops,6 sometimes they put the food7 paper bags and take it 8 or to their work place.Chinese fast food is also 9 in England, Australia and the US, but the most popular fast food in the US is 10 . It’s very delicious.( ) 1. A. Australia B. China C. England D. the US( ) 2. A. many B. much C. little D. few( ) 3. A. roads B. streets C. ways D. rivers( ) 4. A. very B. much C. more D. most( ) 5. A. have B. take C. sell D. put( ) 6. A. for B. so C. but D. and( ) 7. A. on B. into C. away D. out of( ) 8. A. home B. office C. school D. house( ) 9. A. different B. delicious C. cheap D. popular( )10. A. pizza B. dumplings C. fried-chicken D. fish and chips三、阅读理解（20 分）AMary had some troubles, so she went to see the doctor. He was a new doctor, and did not know her. So he first asked her some questions. One of the questions was，" What is your age?"“Well...”Mary answered,“ I don’t quite remember, doctor, but I will try to think. “She thought for a while and then said, " Yes, I remember now, doctor. When I married（结婚），I was twenty-two years old, and my husband was thirty then. Now he is sixty, I know, and that is twice thirty. And so I am twice twenty- two. That is forty-four, isn’t it?"（）1. Mary went to see the doctor because＿．A. she had a headacheB. she had a feverC. she had caught a coldD. she didn't feel well（）2. At first the doctorA. asked her some questionsB. examined her carefullyC.gave her some medicineD. asked her to have a rest（）3. The doctor's first question was“”．A.You are no more than forty, are you?B. Do y ou have a fever?C. What is your age?D. Have you had any medicine?（）4. Mary .A.answered the doctor's questions at once.B.answere d the question after thinking for a w hile.C.just kept silent.D.refused to tell her age.（）5. Mary should be .A. forty-fourB. forty-fiveC. fiftyD. fifty-twoBImagine the situation. You are driving along a desert or on a mountain.You have no idea where you are. You passed the last house two hours ago.Then your car breaks down. It is night and it is cold. You have no mobilephone. What do you do? Well, next time take a GPS with you. This inventionmay be able to help you. It is a device(装置) which uses satellites (卫星) tofind the user’s position(位置). It can find your position to within 20 metres.A GPS cannot start your car, but at least you will know where you are.GPS, which means Global Positioning System, is a small radio receiver. It looks like a mobile phone. You can hold it in your hand, or put in your pocket. It is sometimes put into a watch or a telephone. We also find GPS devices in cars, planes, or boats. Some of these devices have electronic maps, so you know where you are. For example, in a city they can tell you the name of the street.There are three parts to the Global Positioning System. The first part is the receiver. You can hold it in your hand, or have it fixed into your car, plane, etc. The second part is a group of satellites orbiting the Earth. The receiver contacts at least four of the satellites and calculates(计算) its position. The thirdpart of the system is a network of ground stations. They are all over the world. They control thesatellites and make sure they are working well.Some people think that in the future the GPS will be as common as the mobile. They are bec oming cheaper and more and more accurate(精确的). There are also new uses for the GPS. Perhaps they will become like watches. Everyone will have one and you will never be lost again.6.A ccording to the passage, with the help of the GPS, people .（2）can’t be lost in a new city（3）can’t find their way in different countries（4）can learn about the culture of an unknown place（5）can spend the least time getting to another place7.We can learn from the passage that .A.t here are three parts to the GPSB.a GPS can’t be put into a watchC.a GPS can help you start your carD.t he GPS are becoming more and more expensive8.T he underlined word “They” in paragraph 3 means“”.A.ReceiversB. GPS devicesC. SatellitesD. Ground stations9.The passage is mainly about .A. the history of the GPSB. the introduction of the GPSC. the shape of the GPSD. the three parts of the GPS10. What can we infer(推断) from the passage?A.All GPS d evices have electronic maps.B.People in many countries will use the GPS for free.C.The receiver of the GPS contacts at least five of the satellites.D.The GPS will become more and more common in everyday life.四、词汇（10 分）（一）根据句子意思和首字母补全单词。

初二下册期末考试卷一、选择题1. 下列哪个城市是中国的首都？A. 上海B. 广州C. 北京D. 香港答案：C. 北京2. 太阳是在白天出来，还是在黑夜？A. 白天B. 黑夜答案：A. 白天3. 以下哪个是地球上最高的山峰？A. 珠穆朗玛峰B. 埃菲尔铁塔C. 泰山D. 长城答案：A. 珠穆朗玛峰4. 以下哪个是世界上最长的河流？A. 长江B. 尼罗河C. 雅鲁藏布江D. 澳洲河答案：B. 尼罗河5. 以下哪个是我国最大的淡水湖？A. 青海湖B. 洞庭湖C. 太湖D. 鄱阳湖答案：A. 青海湖二、填空题6. 5+7-3=？答案：97. 中国的首都是______________。

答案：北京8. 圆周率π的近似值是_______________。

答案：3.149. 太阳系中最大的行星是______________。

答案：木星10. 《三国演义》是中国古代哪位作家写的？答案：罗贯中三、解答题11. 请用自己的语言简述水的循环过程。

答案：水的循环是指地球上水源的循环过程。

首先，太阳能使地球水面的水蒸气升华，形成云层。

之后，云层聚集成云团，降下雨水或雪。

雨水渗入地下，形成地下水或地下蓄水层。

地下水又会通过井泉、河流等方式重新回到地表，进入海洋。

海洋中的水会被太阳能再次蒸发，形成云层，循环往复。

12. 请用简单的语言解释为什么太阳是地球上最重要的能源。

答案：太阳是地球上最重要的能源，因为太阳能支撑了地球上的生态系统。

太阳能提供了光和热，使植物进行光合作用，为动物提供食物。

太阳能还驱动了水循环，维持了地球上的降水和气候，保证了地球上的生物得以生存。

没有太阳能，地球上就没有生命存在的可能。

2022—2023年部编版八年级数学下册期末测试卷带答案班级： 姓名：一、选择题（本大题共10小题，每题3分，共30分）1+1的值在（ ）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间2．若点1(),6A x -，2(),2B x -，32(),C x 在反比例函数12y x=的图像上，则1x ，2x ，3x 的大小关系是（ ） A ．123x x x << B ．213x x x << C ．231x x x << D ．321x x x <<3．已知a ，b 满足方程组51234a b a b +=⎧⎨-=⎩则a+b 的值为（ ） A ．﹣4 B ．4 C ．﹣2 D ．24．如果一次函数y=kx+b （k 、b 是常数，k ≠0）的图象经过第一、二、四象限，那么k 、b 应满足的条件是（ ）A ．k ＞0，且b ＞0B ．k ＜0，且b ＞0C ．k ＞0，且b ＜0D ．k ＜0，且b ＜05．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（ ）A ．12x x ≠B ．21120x x -=C ．122x x +=D ．122x x ⋅=6．菱形不具备的性质是（ ）A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形7．已知=2{=1x y 是二元一次方程组+=8{ =1mx ny nx my -的解，则2m n -的算术平方根为（ ）A ．±2BC ．2D ．4 8．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（ ）A ．6折B ．7折C ．8折D ．9折9．如图，由四个全等的直角三角形拼成的图形，设CE a =，HG b =，则斜边BD 的长是（ ）A ．+a bB ．⋅a bC ．222a b +D ．222a b - 10．如图，一艘海轮位于灯塔P 的南偏东70°方向的M 处， 它以每小时40海里的速度向正北方向航行，2小时后到 达位于灯塔P 的北偏东40°的N 处，则N 处与灯塔P 的 距离为（ ）A ．40海里B ．60海里C ．70海里D ．80海里二、填空题（本大题共6小题，每小题3分，共18分）1．计算：123-=________．2．当m =____________时,解分式方程533x m x x -=--会出现增根． 3．分解因式：3x －x=__________．4．如图，已知函数y=x+b 和y=ax+3的图象交点为P ，则不等式x+b ＞ax+3的解集为________．5．如图：在△ABC 中，AB=13，BC=12，点D ，E 分别是AB ，BC 的中点，连接DE ，CD ，如果DE=2.5，那么△ACD 的周长是________．6．如图一个圆柱，底圆周长10cm ，高4cm ，一只蚂蚁沿外壁爬行，要从A 点爬到B 点，则最少要爬行_______cm .三、解答题（本大题共6小题，共72分）1．解方程（1）2250x x --= （2）1421x x =-+2．先化简，再求值：822224x x x x x +⎛⎫-+÷ ⎪--⎝⎭，其中12x =-．3．已知5a 2+的立方根是3，3a b 1+-的算术平方根是4，c 13分．（1）求a ，b ，c 的值；（2）求3a b c -+的平方根．4．如图，直线y =kx +b 经过点A （-5，0），B （-1，4）（1）求直线AB 的表达式；（2）求直线CE ：y =-2x -4与直线AB 及y 轴围成图形的面积；（3）根据图象，直接写出关于x 的不等式kx +b ＞-2x -4的解集．5．如图，直线l1：y1=﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2=12x+b过点P．（1）求点P坐标和b的值；（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；②求出t为多少时，△APQ的面积小于3；③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．6．某经销商从市场得知如下信息：A品牌手表B品牌手表进价（元/块）700 100他计划用4万元资金一次性购进这两种品牌手表共100块，设该经销商购进A 品牌手表x块，这两种品牌手表全部销售完后获得利润为y元．（1）试写出y与x之间的函数关系式；（2）若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案；（3）选择哪种进货方案，该经销商可获利最大；最大利润是多少元.参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、B3、B5、D6、B7、C8、B9、C10、D二、填空题（本大题共6小题，每小题3分，共18分）12、23、x （x+1）（x －1）4、x ＞15、186三、解答题（本大题共6小题，共72分）1、（1）1211x x ==（2）3x =是方程的解.2、3.3、（1）a=5，b=2，c=3 ；（2）±4.4、（1）y =x +5；（2）272；（3）x ＞-3．5、（1）b=72；（2）①△APQ 的面积S 与t 的函数关系式为S=﹣32t+272或S=32t ﹣272；②7＜t ＜9或9＜t ＜11，③存在，当t 的值为3或或9﹣或6时，△APQ 为等腰三角形．6、（1）y=140x+6000；（2）三种，答案见解析；（3）选择方案③进货时，经销商可获利最大，最大利润是13000元．。

新人教版八年级语文下册期末测试卷及答案【完整】满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列加横线字字音正确的一项是（）A．篡（cuàn）改娴（xián）熟悄（qiāo）然殚（dān）精竭虑B．教诲（huǐ）潇（xiāo）洒不辍（chuò）屏息敛（liǎn）声C．翘（qiáo）首落（luò）弟燥（zào）热锐不可当（dàng）D．镌刻（juān）仲（zhòng）裁遗嘱（zhǔ）抑（yì）扬顿挫3、下列加点成语运用不恰当的一项是( )A．就算海枯石烂．．．．，我也会朝着自己梦想的方向努力。

B．目前，住房价格一涨再涨，令购房者叹为观止．．．．。

C．你也许有困惑，而今天困惑中的探索正是明天豁然开朗．．．．的准备。

D．因为这个项目技术含量高，攻关难度大，所以涉及的研究领域至今无人问津．．．．。

4、下面句子中没有语病的一项是（）A．这种网络社交工具的广泛使用，加快了信息流通的速度和质量。

B．电视节目《爸爸去哪儿》火了，孩子们的表现给观众留下了美好而深刻的印象。

C．身在边缘之人往往能欣赏到一些不为人知的独一无二的独特景观。

D．通过他一辈子的奋斗，使他的生活状况大为改观。

5、下列各项判断与分析中，不正确的一项是( )A．我们不应该对古人读书的正确态度滥加粗暴的不讲理的非议。

(这个句子的谓语是“滥加”)B．那树有一点佝偻，露出老态，但是坚固稳定，树顶像刚炸开的焰火一样繁密。

(这句话运用拟人和比喻的修辞手法，写出那树虽老但枝繁叶茂的状态) C．“狂澜”“沉湎”“鞠躬尽瘁”“呕心沥血”(这四个词感情色彩相同) D．防止校园欺凌事件不再发生，不让戾气弥漫整个校园，是一个系统工程，需要多方面、多领域齐心协力。

(这个句子是个病句，否定不当)6、下列语句排序，最恰当的一项是（）①一个成功的实验需要的是眼光、勇气和毅力。

八年级英语下册测试卷 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-Ⅴ. 单项选择（每小题1分，共15分）从A、B、C、D四个选项中选择可以填入空白处的最佳答案。

()21. Liu Jing’s mother is very kind and she often speaks _______ a kind way.A. forB. byC. inD. of()22. Her own twelve pictures sold very well, _______ to friends and family.A. usuallyB. MostlyC. HardlyD. recently()23. I don’t like this house with only two small bedrooms. Let’s ask for _______.A. oneB. anotherC. the otherD. others()24. —Susan, I went to the 31st International Ice and Snow Festival in Harbin.—ReallyI have _______ heard about it.A. alreadyB. everC. neverD. yet()25. I forgot to take the _______ with me to Portugal, so I didn’t take any photos.A. cameraB. alarmC. reportD. record()26. Sally is interested in English. Her teacher encouraged her_______ it well.A. learnB. learningC. to learnD. learned( )27. —Linda, is that man your English teacher Mr. Huang—No, it can’t be him. He _______ Beijing for training.A. has gone toB. has been toC. was inD. goes to()28. About _______ of the students in that village go on a ropeway to cross the river to school.A. two fifthB. two fifthsC. second fiveD. second fives()29. The car is five years old but is in almost _______ condition.A. poorB. perfectC. seriousD. typical( )30. As soon as the iPhone 6 came out, _______ people couldn’t wait to buy one.A. thousandB. thousandsC. thousand ofD. thousands of()31. I got there early so tha t I _______ others’ ideas about the plan before the meeting began.A. introducedB. protectedC. collectedD. controlled()32. When I left the hospital, the doctor said to me, “Don’t be worried. You’ll be all right in _______ days.”A. a couple ofB. a kind ofC. a piece ofD. a bit of( )33. —What is the best time of day for us _______ you—Oh, any time is OK.A. visitB. to visitC. visitingD. visited()34. Health experts _______ that lots of people would have flu this winter because the weather is unusual.A. discussedB. promisedC. fearedD. advised( )35.—I haven’t been to the Bird’s Nest. What about you—_______. I am planning to go there this weekend.A. Me tooB. Me neitherC. So did ID. Neither did IⅥ. 完形（每小题1分，共10分）先通读下面的短文，掌握其大意，然后从A、B、C、D四个选项中选择可以填入空白处的最佳答案。

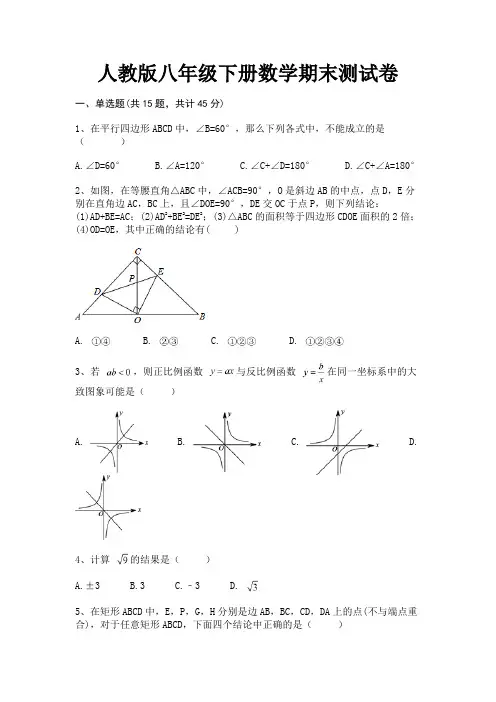
人教版八年级下册数学期末测试卷一、单选题(共15题，共计45分)1、在平行四边形ABCD中，∠B=60°，那么下列各式中，不能成立的是（）A.∠D=60°B.∠A=120°C.∠C+∠D=180°D.∠C+∠A=180°2、如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D，E分别在直角边AC，BC上，且∠DOE=90°，DE交OC于点P，则下列结论：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面积等于四边形CDOE面积的2倍；(4)OD=OE，其中正确的结论有( )A. B. C. D.3、若，则正比例函数与反比例函数在同一坐标系中的大致图象可能是（）A. B. C. D.4、计算的结果是（）A.±3B.3C.﹣3D.5、在矩形ABCD中，E，P，G，H分别是边AB，BC，CD，DA上的点(不与端点重合)，对于任意矩形ABCD，下面四个结论中正确的是（）①存在无数个四边形EFGH是平行四边形.②存在无数个四边形EFGH是矩形.③存在且仅有一个四边形EFGH是菱形.④除非矩形ABCD为正方形，否则不存在四边形EFGH是正方形.A.①②B.①②③C.①②④D.①③④6、如图为菱形ABCD与△ABE的重叠情形，其中D在BE上．若AB＝17，BD＝16，AE＝25，则DE的长度为( )A.8B.9C.11D.127、以下列各组数为边长，不能构成直角三角形的是（）A. B. C. D.8、如图，菱形ABCD的对角线BD、AC分别为2、2 ，以B为圆心的弧与AD、DC相切，则阴影部分的面积是（）A.2 ﹣πB.4 ﹣πC.4 ﹣πD.29、某射击运动员在训练中射击了10次，成绩分别是：5，8，6，8，9，7，10，9，8，10。

下列结论不正确的是( )A.中位数是8B.众数是8C.平均数是8D.方差是210、已知：∠MON，如图，小静进行了以下作图：①在∠MON的两边上分别截取OA，OB，使OA=OB；②分别以点A，B为圆心，OA长为半径作弧，两弧交于点C；③连接AC，BC，AB，OC．=4，则AB的长为（）若OC=2，S四边形OACBA.5B.4C.3D.211、两条宽度都为1的纸条，交叉重叠放在一起，且它们的交角为α，则它们重叠部分（图中阴影部分）的面积为（）A. B. C.sinα D.112、若式子有意义，则实数x的取值范围是（）A. B. 且 C. D. 且13、下列变形正确的是( )A. B. C.D.14、函数y= 中自变量x的取值范围是（）A.x≥3B.x≥﹣3C.x≠3D.x＞0且x≠315、下列各曲线表示的y与x的关系中，y不是x的函数的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，已知圆柱底面的周长为6cm，圆柱高为3cm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为________cm.17、已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD=BE=6，则AC的长等于________ .18、A，B两地之间有一条6000米长的直线跑道，小月和小华分别从A，B两地同时出发匀速跑步，相向而行，第一次相遇后，小月将自己的速度提高25%，并匀速跑步到达B点，到达后原地休息；小华匀速跑步到达A点后，立即调头按原速返回B点（调头时间忽略不计），两人距各自出发点的距离之和记为y （米），跑步时间记为x（分钟），已知y（米）与x（分钟）之间的关系如图所示，则小月到达B点后，再经过________分钟小华回到B点.19、最简二次根式与是同类最简二次根式，则b＝________.20、如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为________.21、如图，矩形OABC在第一象限，OA，OC分别于x轴，y轴重合，面积为6．矩形与双曲线y=（x＞0）交BC于M，交BA于N，连接OB，MN，若2OB=3MN，则k=________22、化简=________23、如图，已知线段，P是AB上一动点，分别以AP，BP为斜边在AB 同侧作等腰和等腰，以CD为边作正方形DCFE，连结AE，BF，当时，为________.24、如图，四边形DEFG是△ABC的内接矩形，其中D、G分别在边AB，AC上，点E、F在边BC上，DG=2DE，AH是△ABC的高，BC=20，AH=15，那么矩形DEFG 的周长是________．25、如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O, 若AB=12，EF=13,H为AB的中点,则DG＝________.三、解答题(共5题，共计25分)26、计算（结果用根号表示）（+1）（﹣2）+227、已知：正方形ABCD中，E、F分别是边CD、DA上的点，且CE=DF，AE与BF 交于点M.求证：AE=BF28、如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，求警示牌的高CD （结果精确到0.1米，参考数据：≈1.41，≈1.73）.29、如图，小巷左石两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC为0.7米，梯子顶端到地面的距离AC为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A′D为1.5米，求小巷有多宽.30、已知m＝﹣，n＝+ ，求代数式m2+mn+n2的值．参考答案一、单选题(共15题，共计45分)1、D2、D3、B4、B5、C6、D7、A8、D9、D10、B11、A12、C13、C14、A15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。

八年级语文下册第2课《回延安》测试题-部编版（含答案）学校:___________姓名：___________班级：___________考号：___________一、选择题1．给下列句子选词填空，正确的一项是()(1)手抓黄土我不放，紧紧儿________在心窝上。

(2)几回回梦里回延安，双手________定宝塔山。

(3)满心话登时说不出来，一头________在亲人怀。

A．靠抱扑B．贴搂靠C．靠绕扎D．贴搂扑2．下列对课文的理解不正确的一项是（）A．《回延安》是一首以陕北民歌“信天游”形式写成的诗歌，分为五个部分：回延安、忆延安、话延安、赞延安、祝延安。

B．诗人描绘团聚的场面时，突出了带有陕北地方特色的事物，如米酒、油馍、窑洞、红窗花等，烘托了热闹的气氛。

C．“一头扑在亲人怀”淋漓尽致地表现了诗人回到延安时无比激动的心情，可以从一个“扑”字看出来。

D．“千万条腿来千万只眼”所用的修辞手法是排比，表明变化之大，看也看不出来。

“一条条”“一座座”“一盏盏”“一排排”几句排比，在数量上运用叠词，有陕北方言的特色。

3．下列句子顺序排列恰当．．的一项是()①人们已认识到，家风是一辈又一辈先人生活的结晶，所以要向后代传递出正能量。

①古人撰写在门框上的“忠厚传家久”“持家尊古训”，就是一种传统的家风。

①俗话说：“龙生龙，凤生凤，老鼠的儿子会打洞。

”是对古今家风的一种诠释。

①家风就是家庭的风气，它是一个家庭的传统和文化。

①而今父母懂规矩，知书达理，有这样良好的文化氛围，后人自会获得很好的熏陶。

A．①①①①①B．①①①①①C．①①①①①D．①①①①①4．依次填入横线上的词语正确的一项是（）①每当夜间疲倦，正想偷懒时，仰面在灯光中黑瘦的面貌，似乎正要说出抑扬顿挫的话来。

①我母亲我最严，她是慈母兼任严父。

①我这熊熊地燃烧着的生命，我这快要使我全身炸裂的怒火，难道就不能出光明了吗？①16年后，探险家余纯顺又在那里遇难，更给罗布泊增添了几分色彩。

人 教 版 数 学 八 年 级 下 学 期期 中 测 试 卷学校________ 班级________ 姓名________ 成绩________第I 卷一、选择题：本大题共10个小题,每小题4分,共40分．在每小题给出的四个选项中,只有一项是符合题目要求的．1. 下列各式：3,2x ,32,2)2(x x +≥-其中二次根式的个数为( )A. B. C. D.2. 下列四组线段中,可以构成直角三角形的是( )A. 4,5,6B. 1.5,2,2.5C. 2,3,4D. 1,2, 3 3. 下列计算正确是( )A. 239-=B. ()233=C. ()233-=-D. 239=4. 杨伯家小院子的四棵小树E 、F 、G 、H 刚好在其四边形院子ABCD 各边的中点上,若在四边形EFGH 内种上小草,则这块草地的形状是( )A. 平行四边形B. 矩形C. 正方形D. 菱形5. 下列命题中,真命题是( )A. 对角线互相垂直的四边形是菱形B. 对角线互相垂直平分的四边形是正方形C. 对角线相等的四边形是矩形D. 对角线互相平分的四边形是平行四边形6. 如图,在▱ABCD 中,AC 、BD 为对角线,BC ＝6,BC 边上的高为4,则阴影部分的面积为( )A. 3B. 6C. 12D. 247. 如图,已知在Rt ABC 中,90,8ACB AB ∠=︒=,分别以,AC BC 为直径作半圆,面积分别记为12,S S ,则12S S +等于( )A. 2πB. 4πC. 6πD. 8π 8. 计算：()910232()3+⨯-=( ) A. 23+ B. 23- C. 23-+ D. 23--9. 用四张大小一样的长方形纸片拼成一个正方形ABCD (如图),它的面积是48,已知长方形的一边长33,AE =图中空白部分是一个正方形,则这个小正方形的周长为( )A. 23B. 43C. 83D. 310. 如图所示,在矩形ABCD 中,12,20AB AC ==,两条对角线相交于点．以OB OC 、为邻边作第个1OBB C ,对角线相交于点1A ,再以11A B 、1A C 为邻边作第个111A B C C ,对角线相交于点1O ；再以11O B 、11O C 为邻边作第个1121O B B C ……依此类推．则第个平行四边形的面积为( )A. B. C. D.第II 卷二、填空题(每题4分,满分24分,将答案填在答题纸上)11. 若二次根式x 2-有意义,则x 的取值范围是___．12. 若实数a 、b 满足240a b ++-=,则a b=_____． 13. 若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是㎝2． 14. 如图,在平行四边形ABCD 中,添加一个条件____,使平行四边形ABCD 是矩形．15. 如图,把矩形纸片ABCD 沿EF 折叠,使点落在边AD 上的点处,点落在点处,已知10,4,2AD CD B D =='=．则AE =____．16. 如图,小明在A 时测得某树的影长为2m,B 时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_____m.三、解答题(本大题共9小题,共86分．解答应写出文字说明、证明过程或演算步骤．) 17. 计算：(1)54520+- (2)()(227227)+-．18. 如图,ABCD 中,E 、F 分别在AD 、BC 上,且//EF AB .求证：EF CD =．19. 如图,在ABC 中,AB =BC ,D 、E 、F 分别是BC 、AC 、AB 边上的中点．(1)求证：四边形BDEF 是菱形．(2)若10,AB cm =求四边形BDEF 的周长．20. 如图所示的一块空地,已知4,3,90,13,AD m CD m ADC AB m ==∠=︒=12BC m =,求这块空地的面积．21. 如图所示,ABCD 是一个正方形花园,,是它的两个门,且DE CF =.要修建两条路BE 和AF ,这两条路等长吗?它们有什么位置关系?为什么?22. 问题背景：在△ABC 中,AB 、BC 、AC 三边的长分别为5、10、13,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC (即△ABC 三个顶点都在小正方形的顶点处),如图1所示．这样不需求△ABC 的高,而借用网格就能计算出它的面积．(1)请你利用上述方法求出△ABC 的面积．(2)在图2中画△DEF ,DE 、EF 、DF 三边的长分别为2、8、10①判断三角形形状,说明理由．②求这个三角形的面积．(直接写出答案)23. 如图,在四边形ABCD 中,连接AC 、BD ,已知90,ACB ADB ∠=∠=︒且点,E F 分别为AB 、CD 的中点,连接EF ．(1)求证：EF CD ⊥．(2)若26AB CD ,求EF 的长．24. 先阅读下列材料,再解决问题：我们定义一组对边平行,另一组对边不平行的四边形叫做梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线．如图,,E F 分别是梯形ABCD 的两腰AB 和CD 的中点,即EF 为梯形ABCD 的中位线．请同学们思考梯形的中位线与两底有何数量关系与位置关系?并给予证明．猜想：已知：求证：证明：25. 如图所示,在四边形ABCD 中,//,90AD BC A ∠=︒,12,21,16AB BC AD ===.动点从点出发,沿射线BC 方向以每秒个单位长度的速度运动,动点Q 同时从点出发,在线段AD 上以每秒个单位长度的速度向点运动,当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为秒．(1)填空：AQ = ；BP = ；的取值范围是 ．(2)设DPQ 的面积为,请用含的式子表示．(3)当t = 时,PD PQ =．(4)当为何值时,以点,,,P C D Q 为顶点的四边形是平行四边形．答案与解析第I卷一、选择题：本大题共10个小题,每小题4分,共40分．在每小题给出的四个选项中,只有一项是符合题目要求的．1.x≥-其中二次根式的个数为()2)A. B. C. D.[答案]C[解析][分析]根据二次根式的定义逐一进行判断即可得答案．[详解∵x2≥0,x≥-是二次根式,x≥-,∵x≥-2,∴x+2≥0,2)2)综上二次根式有三个,故选C．a≥的式子是二次根式是解题的关键．[点睛]本题考查了二次根式的判断,)02. 下列四组线段中,可以构成直角三角形的是( )A. 4,5,6B. 1.5,2,2.5C. 2,3,4D. , 3[答案]B[解析]试题分析：由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可：A、42+52=41≠62,不可以构成直角三角形,故本选项错误；B、1.52+22=6.25=2.52,可以构成直角三角形,故本选项正确；C、22+32=13≠42,不可以构成直角三角形,故本选项错误；D 、()2221233+=≠,不可以构成直角三角形,故本选项错误．故选B ．考点：勾股定理的逆定理．3. 下列计算正确的是( )A. 239-=B. ()233=C. ()233-=-D. 239=[答案]B[解析][分析]根据二次根式运算法则即可求解．[详解]A ．23-,二次根号下不能为负,故A 选项错误B ．()233=,故B 选项正确 C ．()233-=,故C 选项错误D ．233=,故D 选项错误故选：B[点睛]本题考查了二次根式的运算法则,二次根式的性质,被开方数要大于零．4. 杨伯家小院子的四棵小树E 、F 、G 、H 刚好在其四边形院子ABCD 各边的中点上,若在四边形EFGH 内种上小草,则这块草地的形状是( )A. 平行四边形B. 矩形C. 正方形D. 菱形 [答案]A[解析][分析]连接BD 、AC ,根据中位线定理可得四边形是平行四边形,即可得到结果；[详解]如图所示,连接AC 、BD ,∵E 、F 、G 、H 是四边形ABCD 各边的中点,∴∥∥EH BD FG ,12EH FG BD ==, ∴四边形EFGH 是平行四边形,故答案选A ．[点睛]本题主要考查了中点四边形的知识点,准确构造三角形,借助中位线求解是解题的关键． 5. 下列命题中,真命题的是( )A. 对角线互相垂直的四边形是菱形B. 对角线互相垂直平分的四边形是正方形C. 对角线相等的四边形是矩形D. 对角线互相平分的四边形是平行四边形[答案]D[解析][分析]根据平行四边形、矩形、菱形、正方形的判定定理进行判断即可．[详解]对角线互相垂直且平分的四边形是菱形,故A 是假命题；对角线互相垂直平分且相等的四边形是正方形,故B 是假命题；对角线相等且平分的四边形是矩形,故C 是假命题；对角线互相平分的四边形是平行四边形,故D 是真命题．故选D ．[点睛]本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．6. 如图,在▱ABCD 中,AC 、BD 为对角线,BC ＝6,BC 边上的高为4,则阴影部分的面积为( )A. 3B. 6C. 12D. 24[答案]B[解析][分析] 根据平行四边形的性质可得出阴影部分的面积为平行四边形面积的14,再由平行四边形的面积得出答案即可．[详解]∵四边形ABCD 为平行四边形,∴OA =OC ,OB =OD ,∴111646244BOC ABC ABCD S S S ===⨯⨯=, 故选：B ．[点睛]本题考查了平行四边形的面积和性质,解题的关键是掌握平行四边形的性质：对角线互相平分． 7. 如图,已知在Rt ABC 中,90,8ACB AB ∠=︒=,分别以,AC BC 为直径作半圆,面积分别记为12,S S ,则12S S +等于( )A. 2πB. 4πC. 6πD. 8π[答案]D[解析][分析]根据半圆面积公式结合勾股定理,知S 1+S 2等于以斜边为直径的半圆面积问题得解．[详解]∵在Rt ABC 中,90ACB ∠=︒,8AB =,∴22264AC BC AB +==, ∵22111228AC S AC ππ⎛⎫== ⎪⎝⎭,22211228BC S BC ππ⎛⎫== ⎪⎝⎭, ∴()2222212111188888S S AC BC AC BC AB πππππ+=+=+==． 故选：D ．[点睛]本题主要考查了勾股定理的应用,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方．8. 计算：(91022(+⨯-=( )A. 2B. 2C. 2-D. 2-[答案]B[解析][分析]逆用同底数幂的乘法法则把(102-转化成((922-⨯-,然后运用积的乘方运算法则以及平方差公式计算即可．[详解](91022(⨯99((222(=+⨯⨯ 9(222(⎡⎤=+⨯-⎣⎦2=-故选：B ．[点睛]本题考查了同底数幂的乘法,积的乘方,二次根式,平方差公式的应用,逆用同底数幂的乘法法则把()1023-转化成()()92323-⨯-是解题的关键． 9. 用四张大小一样的长方形纸片拼成一个正方形ABCD (如图),它的面积是48,已知长方形的一边长33,AE =图中空白部分是一个正方形,则这个小正方形的周长为( )A. 23B. 43C. 3D. 3[答案]C[解析] [分析] 通过正方形的面积求出边长为48,根据图形之间的联系求出空白小正方形的边长3-233即可求解．[详解]解：∵正方形ABCD 的面积是48,∴3∵3∴333∴空白小正方形的边长333∴小正方形的周长为3故选C ．[点睛]本题考查了正方形的面积与边长；解题的关键是能够观察出图形之间的联系． 10. 如图所示,在矩形ABCD 中,12,20AB AC ==,两条对角线相交于点．以OB OC 、为邻边作第个1OBB C ,对角线相交于点1A ,再以11A B 、1A C 为邻边作第个111A B C C ,对角线相交于点1O ；再以11O B 、11O C 为邻边作第个1121O B B C ……依此类推．则第个平行四边形的面积为( )A.B. C. D.[答案]C[解析][分析] 首先分别求得几个平行四边形的面积,即可得到规律：第n 个平行四边形的面积为1922n ,继而求得答案． [详解]解：∵在矩形ABCD 中,AB=12,AC=20,∴22201216-=,∴S 矩形ABCD =AB•BC=192,OB=OC ,∵以OB ,OC 为邻边作第1个平行四边形OBB 1C ,∴平行四边形OBB 1C 是菱形,OA 1是△ABC 的中位线, 可知111122OA AB OB ==, ∴112OB AB ==, ∴111116129622OBB C S BC OB ==⨯⨯=, 111111111612482222A B C C S BC OB ==⨯⨯⨯=, ∴第n 个平行四边形面积为：1922n , ∴第6个平行四边形的面积是：619232=, 故选：C ．[点睛]此题考查了平行四边形的性质以及矩形的性质,通过计算找到规律是解题的关键．第II 卷二、填空题(每题4分,满分24分,将答案填在答题纸上)11. 若二次根式x 2-有意义,则x 的取值范围是___．[答案]x 2≥[解析][详解]试题分析：根据题意,使二次根式2x -有意义,即x ﹣2≥0,解得x≥2．故答案是x≥2．[点睛]考点：二次根式有意义的条件．12. 若实数a 、b 满足240a b ++-=,则a b =_____． [答案]﹣12 [解析]根据题意得：a+2=0,b-4=0,解得：a=-2,b=4,则a b =﹣12．故答案是﹣12． 13. 若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是㎝2． [答案]24[解析]已知对角线的长度,根据菱形的面积计算公式即可计算菱形的面积．解：根据对角线的长可以求得菱形的面积,根据S=12ab=12×6×8=24cm 2, 故答案为24．14. 如图,在平行四边形ABCD 中,添加一个条件____,使平行四边形ABCD 是矩形．[答案]90A ∠=︒ (答案不唯一)[解析][分析]根据矩形的判定条件进行添加即可；[详解]根据判定条件：有一个角是90︒的平行四边形是矩形,只要有一个内角是90︒即可得出答案, 故90A ∠=︒(答案不唯一)．[点睛]本题主要考查了矩形的判定,准确理解判定条件是解题的关键．15. 如图,把矩形纸片ABCD 沿EF 折叠,使点落在边AD 上的点处,点落在点处,已知10,4,2AD CD B D =='=．则AE =____．[答案][解析][分析]根据折叠的性质可得AE=A′E ,AB=A′B′,在Rt △A′B′E 中,根据勾股定理即可得到AE 的长．[详解]∵四边形ABCD 矩形,∴AB=CD=4,∠B=90,由折叠性质可得AE=A′E ,AB=A′B′=4,∠B′A′E=∠B=90,在Rt △A′B′E 中,A′B′2+A′E 2=B′E 2,42+A′E2=(10-2-A′E)2,解得A′E=3,即AE的长为3．故答案为：3．[点睛]本题考查了折叠的性质,矩形的性质以及勾股定理的应用,熟练掌握折叠的性质是关键．16. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_____m.[答案]4[解析][分析]根据题意,画出示意图,易得：Rt△EDC∽Rt△CDF,进而可得EDDC=DCFD；即DC2=ED•FD,代入数据可得答案．[详解]如图：过点C作CD⊥EF,由题意得：△EFC是直角三角形,∠ECF=90°, ∴∠EDC=∠CDF=90°,∴∠E+∠ECD=∠ECD+∠DCF=90°,∴∠E=∠DCF,∴Rt△EDC∽Rt△CDF,有EDDC=DCFD;即DC2=EDFD,代入数据可得DC 2=16,DC =4；故答案为4.[点睛]本题考查了相似三角形的应用,能够将实际问题转化为相似三角形的问题是解题的关键.三、解答题(本大题共9小题,共86分．解答应写出文字说明、证明过程或演算步骤．) 17. 计算：(1)54520+- (2)()(227227)+-．[答案](1)25；(2)1[解析][分析](1)根据二次根式的加减运算法则计算即可；(2)根据二次根式的乘法运算法则结合平方差公式计算即可．[详解]解：()1原式53525=+- 4525=-25=．()2原式()()22227=- 87=-1=． [点睛]本题考查二次根式的运算,熟练掌握二次根式四则运算的法则是解题的关键．18. 如图,在ABCD 中,E 、F 分别在AD 、BC 上,且//EF AB .求证：EF CD =．[答案]证明见解析．[解析][分析]根据平行四边形的性质可得//,//AD BC AB CD ,再通过//EF AB 可判定四边形ABFE 是平行四边形,可得EF=CD ．[详解]证明：四边形ABCD 是平行四边形,//,//AD BC AB CD ∴//,EF AB//,EF CD ∴四边形CDEF 是平行四边形EF CD ∴=．[点睛]此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形对边平行且相等,两组对边分别平行的四边形是平行四边形．19. 如图,在ABC 中,AB =BC ,D 、E 、F 分别是BC 、AC 、AB 边上的中点．(1)求证：四边形BDEF 是菱形．(2)若10,AB cm =求四边形BDEF 的周长．[答案](1)证明见解析；(2)菱形BDEF 的周长为20cm ．[解析][分析](1)由D 、E 、F 分别是BC 、AC 、AB 边上的中点,根据三角形中位线的性质,可得EF ∥BC ,ED ∥AB ,EF=12BC ,DE=12AB ,又由AB=BC ,即可证得四边形BDEF 是菱形； (2) 由三角形中位线的性质,可求得BF 的长,进而求得周长为4BF ．[详解]解：(1)证明：D E F 、、分别是BC AC AB 、、边上的中点,// ,//,EF BC DE AB ∴ 11,22EF BC DE AB ==, 四边形BDEF 是平行四边形,又,AB BC =,DE EF ∴=平行四边形BDEF 是菱形．(2)10,AB =且是AB 边上的中点,15,2BF AB cm ∴== 由(1)知,四边形BDEF 是菱形,菱形BDEF 的周长为44520=⨯=BF cm ．故答案为：20cm ．[点睛]此题考查了菱形的判定与性质以及三角形中位线的性质．注意掌握三角形中位线定理的应用是解此题的关键．20. 如图所示的一块空地,已知4,3,90,13,AD m CD m ADC AB m ==∠=︒=12BC m =,求这块空地的面积．[答案]这块空地的面积是224m ．[解析][分析]连接AC ,先利用勾股定理求出AC ,再根据勾股定理的逆定理判定△ABC 是直角三角形,那么△ABC 的面积减去△ACD 的面积就是所求的面积．[详解]连接AC ,90ADC ∠=︒,222224325AC AD DC ∴=+=+=12,13BC m AB m ==,22222251216913AC BC AB ∴+=+===,90ACB ∴∠=︒,()211512342422ACB ACD S S m ∴-=⨯⨯-⨯⨯= 这块空地的面积是224m ．[点睛]本题考查了勾股定理、勾股定理的逆定理的应用,得到△ABC 是直角三角形是解题的关键,同时考查了直角三角形的面积公式．21. 如图所示,ABCD 是一个正方形花园,,是它的两个门,且DE CF =.要修建两条路BE 和AF ,这两条路等长吗?它们有什么位置关系?为什么?[答案]相等,BE AF ⊥,理由见解析[解析][分析]由DE =CF 可得AE =DF ,则可得△DAF ≌△ABE ,然后根据全等三角形的对应角相等可得出BE 与AF 的关系．[详解]解：BE =AF ,BE ⊥AF ；理由：∵四边形ABCD是正方形,∴AD=CD,DE=CF,∴AE=DF,又∠BAE=∠D=90°,AB=AD,∴△BAE≌△ADF∴BE=AF,∠ABE=∠F AD,∵∠ABE+∠AEB=90°,∴∠F AD+∠AEB=90°,∴BE⊥AF．故BE=AF,BE⊥AF．[点睛]本题考察了正方形的性质,全等三角形的判定与性质,主要利用了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,利用三角形全等证明相等的边是常用的方法之一,要熟练掌握并灵活运用.22. 问题背景：在△ABC中,AB、BC、AC三边的长分别为5、10、13,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC 三个顶点都在小正方形的顶点处),如图1所示．这样不需求△ABC的高,而借用网格就能计算出它的面积．(1)请你利用上述方法求出△ABC的面积．(2)在图2中画△DEF,DE、EF、DF2、810①判断三角形的形状,说明理由．②求这个三角形的面积．(直接写出答案)[答案](1)72；(2)画图见解析；①△DEF 是直角三角形,理由见解析；②2 [解析] 试题分析：(1)根据题目设置的问题背景,结合图形进行计算即可；(2)根据勾股定理,找到DE 、EF 、DF 的长分别为2、8、10,由勾股定理的逆定理可判断△DEF 是直角三角形．解：(1)S △ABC =3×3﹣12×1×2﹣12×2×3﹣12×1×3=72； (2)如图所示：∵DE =2,EF =22,DF =10,∴DE 2+EF 2=DF 2,∴△DEF 是直角三角形．△DEF 的面积=111231122132222⨯-⨯⨯-⨯⨯-⨯⨯=． 点睛：本题考查了勾股定理及作图的知识,解答本题关键是仔细理解问题背景,构图法求三角形的面积是经常用到的,同学们注意仔细掌握．23. 如图,在四边形ABCD 中,连接AC 、BD ,已知90,ACB ADB ∠=∠=︒且点,E F 分别为AB 、CD 的中点,连接EF ．(1)求证：EF CD ⊥．(2)若26AB CD ,求EF 的长．[答案](1)证明见解析；(2)332EF =．[解析][分析](1)如图(见解析),先根据直角三角形的性质可得12CE AB =,12DE AB =,从而可得CE DE =,再根据等腰三角形的判定可得CDE △是等腰三角形,然后根据等腰三角形的三线合一即可得证；(2)先分别求出CE 、CF 的长,再结合(1)的结论,利用勾股定理即可得．[详解](1)如图,连接EC 和ED点是AB 的中点,90ACB ADB ∠=∠=︒在Rt ABC 中,12CE AB = 在Rt ABD △中,12DE AB = CE DE ∴=CDE ∴是等腰三角形又点是CD 的中点,即EF 是等腰CDE △的底边CD 上的中线EF CD ∴⊥；(2)26AB CD ==3CD ∴= 由(1)已证：132CE AB == 又点是CD 的中点1322CF CD ∴== 则在Rt CEF 中,由勾股定理得：22332EF CE CF =-=．[点睛]本题考查了直角三角形的性质、等腰三角形的判定与性质、勾股定理等知识点,掌握理解等腰三角形的三线合一是解题关键．24. 先阅读下列材料,再解决问题：我们定义一组对边平行,另一组对边不平行的四边形叫做梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线．如图,,E F分别是梯形ABCD的两腰AB和CD的中点,即EF为梯形ABCD的中位线．请同学们思考梯形的中位线与两底有何数量关系与位置关系?并给予证明．猜想：已知：求证：证明：[答案]猜想：12EF AD BC；////EF AD BC；已知：如图,,E F分别是梯形ABCD的两腰AB和的中点；求证：12EF AD BC；////EF AD BC；证明见解析．[解析][分析]根据题意写出猜想、已知和求证．连接AF并延长交BC于点G,则△ADF≌△GCF,可以证得EF是△ABG 的中位线,利用三角形的中位线定理即可证得．[详解]猜想：12EF AD BC；////EF AD BC已知：如图,,E F分别是梯形ABCD的两腰AB和的中点．求证：12EF AD BC；////EF AD BC．证明：如图,连接AF并延长交BC于点G．∵AD∥BC,点F是CD中点,∴∠DAF=∠G,DF=FC,在△ADF和△GCF中,DAF G DFA CFG DF FC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△GCF (AAS ),∴AF=FG ,AD=CG ．又∵点E 是AB 中点,∴EF 是ABG 的中位线,∴EF ∥BG ,EF=12BG , 即EF ∥AD ∥BC ,EF=12(AD+BC)． [点睛]本题是通过猜想并且证明梯形的中位线定理,考查了三角形中位线定理,全等三角形的判定和性质,通过辅助线转化成三角形的中位线的问题是解题的关键．25. 如图所示,在四边形ABCD 中,//,90AD BC A ∠=︒,12,21,16AB BC AD ===.动点从点出发,沿射线BC 方向以每秒个单位长度的速度运动,动点Q 同时从点出发,在线段AD 上以每秒个单位长度的速度向点运动,当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为秒．(1)填空：AQ = ；BP = ；的取值范围是 ．(2)设DPQ 的面积为,请用含的式子表示．(3)当t = 时,PD PQ =．(4)当为何值时,以点,,,P C D Q 为顶点的四边形是平行四边形．[答案](1),2,016t t t ≤≤；(2)966S t =-；(3)163t =；(4)当5t =或373时,以点,,,P C D Q 为顶点的四边形是平行四边形．[解析][分析](1)按照路程等于速度乘以时间,求解AQ ,BP ；时间最小为0,最大为点Q 动到点D 所花费的时间；(2)通过做垂直辅助线,根据已知条件并结合三角形面积公式求解本题(3)根据等腰三角形以及矩形的性质,结合三线合一以及路程公式求解本题；(4)本题需要根据动点情况分类讨论,并结合平行四边形性质列方程求解．[详解](1)∵距离=速度时间,Q 的运动速度为1,P 的运动速度为2,运动时间为t ,∴AQ=t ,BP=2t ．∵AD=16,当点Q 运动到点D 时,动点停止运动,∴t 最大值为16,最小值为0,故016t ≤≤．(2)如图,过点作PM QD ⊥,∵//,90AD BC A ∠=︒,∴四边形ABPM 矩形,∴PM=AB=12．又∵AQ=t∴16QD t =-．()11161296622QDP S QD PM t t =••=⨯-⨯=-△． (3)由上一问可知四边形ABPM 是矩形,2AM BP t ∴==．又PD PQ =,2DM QM AM AQ BP AQ t t t ∴==-=-=-=,216AD AM DM t t =+=+=即316t =,163t ∴=． (4)当在线段BC 上时,因为平行四边形PCDQ ,则DQ PC =,∵16DQ t =-,212PC t =-,16212t t ∴-=-,解得：5t =；当在BC 延长线上时,同理：DQ=PC ,221PC t =-,16221t t ∴-=-, 解得：373t =； 综上所述：当5t =或373时,以点,,,P C D Q 为顶点的四边形是平行四边形． [点睛]本题考查几何动点问题,首先需要对运动路径有清晰理解,并且利用未知数表示未知线段,求解时具体问题具体分析,如本题主要利用面积公式,平行四边形性质求解,动点问题通常需要分类讨论．。