确定边坡最危险滑动面的计算机模拟

万方数据万方数据万方数据Bishop法自动搜索均质边坡最危险滑动面作者：李增亮， 姚勇， 曹兰柱， LI Zeng-liang， YAO Yong， CAO Lan-zhu作者单位：李增亮,LI Zeng-liang(辽宁省第四地质大队,辽宁 阜新,123000)， 姚勇,曹兰柱,YAO Yong,CAO Lan-zhu(辽宁工程技术大学资源与环境工程学院,辽宁 阜新,123000)刊名：露天采矿技术英文刊名：OPENCAST MINING TECHNOLOGY年，卷(期)：2009，(1)引用次数：0次1.刘志斌.王志宏圆弧滑坡最危险滑弧圆心位置的求解方法 19972.刘志斌.郭增涛用变尺度法求解圆弧滑坡的最危险滑面 1988(4)3.韩永春.高谦.钱洪涛毕肖普法和有限差分法应用于边坡稳定性分析[期刊论文]-山西建筑 2007(1)4.祝方才.刘杰.肖宏彬边坡稳定Bishop法的实施新方法[期刊论文]-株洲工学院学报 2005(4)5.罗勇清.周云毕肖普法确定填石路堤高边坡稳定安全系数[期刊论文]-公路与汽运 2007(3)1.学位论文成长青边坡稳定有限元分析及程序设计2007极限平衡法虽然已经在工程实践中得到了大量的应用，但是它不能很好地考虑土体的应力应变关系，对土条条间力作了各种假定，因此计算的结果并不精确，而且不能给出土体的应变信息。

有限元方法可以考虑土体的真实应力场，可以区分填筑和开挖边坡，因而应用会更广泛。

本文主要做了一下几方面的工作。

第一，完善了非圆弧滑面应力有限元程序。

边坡稳定的有限元方法，是定义了安全系数并给定一系列初始滑裂面，然后利用有限元软件比如Geo-slope和ANSYS计算得到的应力场，求解安全系数。

在确定滑面上计算点的应力张量的时候，本文采用了面积判别法，即首先对每一个四边形单元(本文全部采用四边形单元求解计算)确定其横坐标和纵坐标的范围，如果计算点在这个范围之外，就跳出对下一个单元进行判断，如果在范围内，那么计算这个点和四边形单元四个节点形成的四个三角形的面积以及四边形单元的面积，并进行求差比较。

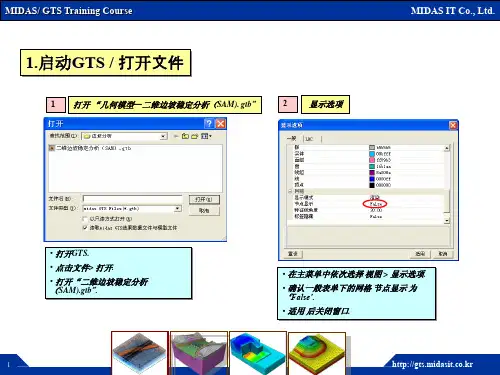
土质边坡潜在滑动面确定方法及实例0引言由凝聚性土类组成的均质或非均质土坡，一般假定它的稳定问题是平面应变问题。

大量研究表明，土质边坡的滑裂面为曲面，其中均质土坡可简化为圆弧面。

用极限平衡理论分析边坡稳定性时，无论用瑞典条分法(CFellenius}，Bishop 法，或Janbu 法，其关键在于确定潜在滑动面及其对应的最小安全系数。

如何较快地确定潜在滑动面圆心的大概位置，确定潜在滑面的形态和位置，对于土坡的稳定性评价具有重要意义1作图法1.1理论依据对于均匀土质边坡，坡面开挖后(图1)，坡面A 点处于单向应力状态，其上的作用力c σ为大主应力。

当单元体剪应力达到土体抗剪强度时就发生破坏，其潜在滑面一般通过坡脚。

破坏面与大主应力作用方向即坡面夹角为：0452ϕθ=- (1)1.2作图步骤根据上述理论分析，利用作图法确定滑面(图2)的具体步骤为:(1)根据(1)式求出θ，作直线BB ’垂直于BC ，过B 作BC ’与BB ’成θ夹角;(2)在BC 上任取点M ，作MT 与铅垂线成θ夹角，交BC ’于C 点;(3)过A 作AK 与坡面AB 成θ角;(4)在AK 与MT 上，分别从A 点和C 点起，以任意等长a 取线段AP , PU 和CL, LQ;(5)分别过P, U 作AB 平行线，过L, Q 作BC 平行线，交E 和F 点，连EF 交AK 于点S;(6)过点S 作MT 的平行线交BC ’于N;(7)过A 作AK 的垂线，过点N 作sN 的垂线，交于0点。

以0为圆心，以OA 为半径作圆弧AN 交BC 于DOAND 就是所求的潜在滑动面。

2对数螺旋线法对于土质边坡，其潜在滑动面除可为圆弧外能还可能为对数螺旋线(图3)，其方程为:k r ae θ= (2)式中a 、k 为常数; θ为螺旋线半径与水平线的夹角。

螺旋线上任一点B 的切线与过该点的半径r 的夹角为Ψ，与该半径r 垂线的夹角ϕ就是破裂面上的内摩摔角ϕ 。

文章编号:1671-2579(2007)02-0024-03基于遗传算法的高边坡最危险滑动面确定方法曾　胜(长沙理工大学,湖南长沙　410076) 摘　要:高边坡稳定性分析的关键是如何确定最危险滑动面。

传统的计算方法都是根据经验,人为地确定最危险滑动面,计算安全系数,如黄金分割法或者设定圆心、半径的步长进行逐点扫描,这些方法的精度都不高且容易陷入局部极值点。

该文引入能模拟生物进化过程的遗传优化算法来搜索边坡的最危险滑动面,通过一具体工程实例的对比计算,说明其与传统计算方法相比精度更高,适应性更强,值得推广应用。

关键词:边坡;滑动面;遗传算法;稳定收稿日期:2007-02-11作者简介:曾　胜,男,博士,副教授.E -mail :Zszs35@1　前言随着我国高速公路建设的发展,特别是近年来高速公路不断向中西部地区延伸,在高速公路修建中,不可避免地要遇到高陡边坡的工程问题。

由于高边坡失稳引起的滑坡、坍塌等现象时有发生,严重影响高速公路行车安全和正常运营。

高边坡的稳定性问题已引起了公路部门的重视。

边坡稳定分析的方法比较多,目前在工程中应用较为广泛的就是以极限平衡理论为基础的条分法,其基本思路是:假定边坡岩土体破坏是由于边坡内产生了滑动面,滑动面上的坡体服从破坏条件,假定滑动面已知,通过考虑滑动面形成的隔离体的静力平衡,判断滑动面上的滑体的稳定状态或稳定程度。

由于滑动面是人为假定的,只有求出一系列滑面发生滑动时的破坏荷载,其中最小的破坏荷载与之相对应的滑动面就是可能存在的最危险滑动面。

从中可以看出,边坡稳定性分析的关键就是先假定破裂面形状(一般为圆弧形),搜索最危险滑动面所在的位置并计算与之相对应的最小安全系数。

遗传算法是通过模拟自然界生物进化过程来搜索优化问题最优解的一种方法。

本文将遗传方法引入边坡稳定分析中,以提高边坡稳定分析的效率和精度。

2　遗传算法最优解搜索过程遗传算法(Genetic Algorit hm ,简称GA )具有智能式搜索、并行式计算和全局优化等特点,特别适合于求解目标函数的多极点问题。

确定边坡最危险滑动面的计算机模拟
易念平;吴恒;张信贵;韦珊珊
【期刊名称】《工程地质学报》
【年(卷),期】2002(010)003
【摘要】边坡稳定稳定性分析,关键是确定潜在的滑动面,目的是有利于工程安全.本文编制了二、三维计算机模拟程序,在二维模拟中提出了四种计算模式,三维模拟中考虑了空间、荷载、渗流效应,结合工程实例对边坡进行模拟并对土层抗剪强度参数进行了反演,模拟计算与实测结果吻合,模拟出的抗剪强度参数平均值与实测的抗剪强度参数标准值相当.
【总页数】5页(P326-330)
【作者】易念平;吴恒;张信贵;韦珊珊
【作者单位】广西大学土木建筑工程学院,南宁,530004;广西大学土木建筑工程学院,南宁,530004;广西大学土木建筑工程学院,南宁,530004;广西大学土木建筑工程学院,南宁,530004
【正文语种】中文
【中图分类】U416.4+4
【相关文献】
1.确定边坡最危险滑动面的几种数值方法探讨 [J], 陈绍名;张伟
2.基于断裂力学理论确定边坡最危险滑动面的方法研究与应用 [J], 张昕晔
3.土钉支护边坡最危险滑动面的确定方法 [J], 刘尧军;刘志华
4.基于跨越函数法在搜索最危险边坡滑动面的探讨 [J], 祝涓
5.受软弱结构面控制的岩石边坡最危险滑动面的确定 [J], 芮勇勤
因版权原因，仅展示原文概要，查看原文内容请购买。

土质边坡最危险滑动面的随机搜索摘要：本文基于瑞典条分法，应用MATLAB，对边坡最危险滑动面的进行搜索，该方法可以同时搜索出边坡的最小安全系数和与之相应的临界滑动面的位置。

可以应用到任意边坡几何形状，不同土质分层，伴随空隙水压力以及有外载荷的情况。

关键词：MATLAB；边坡稳定；安全系数；条分法；网格法；滑动面；Abstract: this paper, based on the Swedish slice method, the application of the MATLAB, the most dangerous of the slip plane of the slope to search for, this method can also search the minimum safety factor of the slope and the corresponding critical sliding the position. Can be applied to any slope geometric shapes, different soil layer, along with water pressure and the gap is the load.Keywords: MATLAB; The slope stability; Safety coefficient; Slice method; The grid method; Sliding surface;1概述在工程建设中常会遇到土坡稳定性问题，土坡包括天然土坡和人工土坡，天然土坡是指自然形成的山坡和江河湖海的岸坡，人工土坡则是指人工开挖基坑、基槽、路堑或填筑路堤、土坝形成的边坡。

土坡塌滑是一种常见的工程现象，土坡由于丧失稳定性而滑动，通常称为“滑坡”。

本文的目的在于使用瑞典条分法的情况下，应用软件MATLAB对最小安全系数的临界滑动面进行随机搜索，改进土坡最小安全系数搜索方法,以便比较容易的得到土坡的最小安全系数。

边坡滑裂面的搜索方法为了搜寻边坡全局意义上的临界滑动面，很多学者结合计算机模拟技术和数学优化方法提出了很多种搜索方法。

可以将这些搜索方法按照二维分析法和三维分析法进行分类。

很多优化方法从二维边坡开始研究，但由于二维边坡分析方法精度不够高，更多学者探索将二维方法应用到三维边坡中，或者提出新的优化方法。

因为极限平衡法在边坡稳定性分析中的广泛应用，很多学者将数学优化方法与极限平衡法相结合，运用到最危险滑动面的搜索之中，而且都取得了不错的效果。

目前常用的最危险滑动面搜索方法主要有：变分法，固定模式搜索法（包括区格搜索法、模式搜索法、二分法和单形体映射方法）、数学规划法（动态规划法、线性-非线性规划法）、随机搜索方法和人工智能方法（遗传算法、模拟退火算法、神经网络算法和仿生算法）等。

下面将介绍这几种搜索方法。

（1）变分法上世纪70年代，Baker和Garber（1977）等利用变分法搜索到最危险滑动面及其应力分布。

他们把滑动面看成变量，边坡的安全系数看成这些变量的泛函，再利用变分法求得使安全系数泛函F达到极小值的临界滑动面及应力分布。

该方法是一种解析方法，从数学来说是较为复杂的，尤其是难以考虑复杂的土层和地下水情况，应用范围十分有限。

（2）固定模式搜索法固定模式搜索是搜索点位置或搜索过程在搜索进行之前就已经明确限定的一种搜索方法。

属于这种搜索的搜索方法有：区格搜索法、模式搜索法、二分法和单形体映射方法。

①区格搜索法（枚举法）区格搜索法原理简单，是早期计算机辅助边坡稳定分析中常用的一种方法。

区格搜索法的基本思想是把搜索区域按一定的精度划分成满布区格形式，然后对每一个区格点计算其安全系数，取最小值点对应的滑动面为临界滑动面。

通常对于圆弧危险滑动面的确定包括划分圆弧圆心取值区域和搜索圆弧滑动面在边坡轮廓线上的交点两种途径。

该方法由于搜索点在搜索进行之前就己经确定，因此不会受安全系数函数形态的影响，也不会陷入局部极小值。

讨论滑坡体滑动面的鉴定方法1 引言滑坡体是一种常见的地质现象，多出现在地形陡峻的山区。

滑坡体在公路、铁路、水利水电工程建设中，对工程的建设和运行极为不利。

为了对滑坡体采取合理有效的处理方法，必段对滑坡体的大小及范围有一个完整的认识，对滑坡体的地质勘察工作，主要是确定滑坡体滑动面、滑坡体堆体物的主要成分，滑坡体含水程度，滑坡体稳定变形情况等。

对于大型滑坡体，确定滑动面是研究滑坡的主要任务。

滑坡体成因一般是因为岩层中存在断层、大裂隙等不良地质构造，岩层倾向与滑坡方向一致的岩层中存在软岩夹层，软岩面在地下水侵蚀作用下和山体底部受河流、人为因素冲蚀破坏应力不平衡等原因所致。

滑坡在形成过程中，滑坡体与稳定山体（岩体）相互产生摩擦作所用形成。

膨胀土是一种特殊的粘土，具有吸水软化以及失水开裂的特性。

在长期的季节性干湿风化作用、循环作用以及剥蚀作用相下，使膨胀土层中的裂隙非常发育。

另外，膨胀土层中存在各种形式的软弱结构面，例如贯通裂隙面、风化软弱面以及层间裂隙面等。

所以，在膨胀土地区修建的公路、渠道、大坝等工程常会遇到施工时边坡不稳定的情况。

例如：在云南华坪县务坪水库的引水渠和坝基在开挖过程中就发生过10处以上大小滑坡，不仅严重影响了坝基边坡和渠道的正常施工的正常运行，同时耗费了大量的治理资金。

在滑坡体处置中，滑动面位置的确定是滑坡调查、分析中的一项非常重要的任务。

对于已经发生的边坡，要先弄清滑动面位置，才能正确分析和评价边坡的稳定性状并深入了解边坡的失稳原因。

对于存在隐患的滑坡，如果弄清了滑动面位置，就能合理预测滑坡的发展趋势，同时实施有效治理。

我国目前常用确定滑动面的方法主要有三种：（1）观察法，例如通过对滑坡的形态特征及其相关要素的观察情况来确定滑动面位置。

（2）地质勘探技术法，例如采用勘探平硐和钻孔取样等手段确定滑动面。

（3）理论法，极限分析法、利用极限平衡法或有限元模拟法来搜索确定最危险滑动面的位置。