《信号与系统分析基础》第3章习题解答

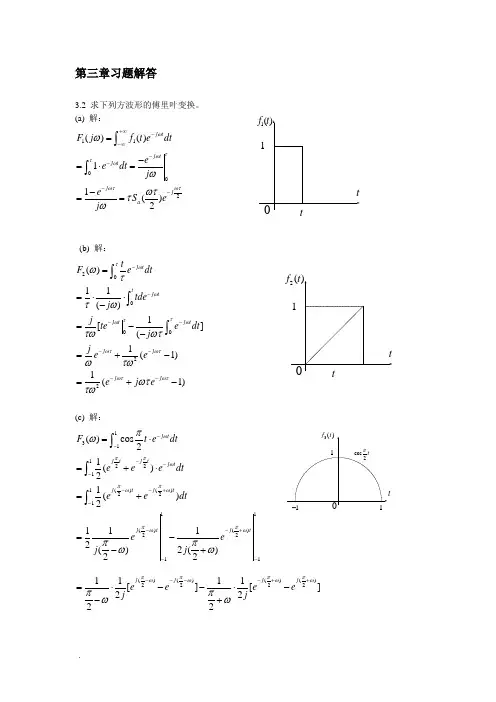
第三章习题解答3.2 求下列方波形的傅里叶变换。

(a) 解：1102()()11()2j t j t j t j j a F j f t e dt e e dt j e S e j ωτωτωωτωτωωωττω+∞--∞----=-=⋅=-==⎰⎰(b) 解：200022()11()1[](1(1)1(1)j t t j t j t j t j j j j tF e dttde j j te e dt j j e e ej eτωωττωωωτωτωτωτωττωτωωτωτωωττω--------==⋅⋅-=--=+-=+-⎰⎰⎰(c) 解：13112211()()22111()()2211()cos21()21()21112()2()22j t j t j t j t j t j t j t j tF t e dte e e dt e e dt e ej j ωππωππωωππωωπωππωω-------+---+--=⋅=+⋅=+=--+⎰⎰⎰()()()()22221111[][]2222j j j j e e e e j j ππππωωωωππωω----++=⋅--⋅--+2222sin()sin()cos ()cos ()cos 2222()()2222ππππωωωωωωπωππππωωωω-+⋅++⋅-⋅=+==-+--3.3依据上题中a,b 的结果，利用傅里叶变换的性质，求题图3.3所示各信号的傅里叶变换. (b) 解：262()()()f t g t g t =+,而()()2g t Sa τωττ↔2()6(3)2()F Sa Sa ωωω∴=+如利用3.2中(a)的结论来解，有：211'()(3)(1)f t f t f t ττ=+++，其中6,'2ττ==.3211'()()()6(3)2()j j F e F e F Sa Sa ωωττωωωωω∴=⋅+⋅=+(如()()f t F ω↔，则00()()j t f t t eF ωω±↔)(c) 解：32222()2()2(),1f t f t f t τττ=++-+= 由3.2(b)知，2221()(1)j j F e j e ωτωτωωττω--=+-32222222222222()2()2(),1112(1)2(1)222222444cos (1cos )j j j j j j j j j j F e F e F e e j e e e j e je je ωτωτωωωωωωωωωωωτωωωωωωωωωωωωωωω-----∴=+-==⋅⋅+-+⋅⋅--=+-+--=-=-3.4利用对称性求下列各函数的傅里叶变换.(2) 222(),.f t t tαα=-∞<<+∞+ 解：222t e αααω-↔+ ，由对称性，2222et αωαπα-↔+(3)2()f t444444444244()(2)(2)1(2)()21111()(2)(2)[()]*[()][()()]22282,()()0.22,()()2;26,()()f t Sa t Sa t Sa t g f t Sa t Sa t g g g g g g g g d g g d πππππππωππππππππωππωωωωππωπωωπωπωωυωππωπωωυ-=⋅↔=⋅↔=*<-*=-<<*==+<<*=⎰解：而，利用频域卷积特性，得：积分：2444246.6,()()0g g πωππππωππωωπωω-=-+=->*=⎰3.8(3) ()(2)()2()dF t f t j F d ωωω-↔-(6) (25)f t -;由1[()]()j b a F f at b e F a a ωω--=⋅，2,5,a b == 2.51(25)()22j f t e F ωω-∴-↔⋅3.9 计算下列各信号的傅里叶变换.(2) 3()2(32)()2[2()],2u t t u t t δδδ+-=+-是偶函数332232()1,1[()]().2, 3.112(32)21,()().21()2(32)()j b aj j j t F f at b e F a aa b t e e u t j u t t e j ωωωωδωδπδωωδπδωω----↔-===∴-↔⋅⋅⋅=↔+∴+-↔++ 由(7) 33(2)63(3)9[(2)(3)](2)(3)tt t e u t u t eu t e e u t e --+---+--=⋅+-⋅-33(2)23(3)31().11();(2)331(3)3t t t j t j e u t j e u t e u t e j j e u t e j αωωαωωωω---+---↔+∴↔+↔++-↔+ 同理：32(3)3(3)1[(2)(3)]()3t j j e u t u t e e j ωωω-+-+∴+--↔-+3.13 已知阶跃函数和正弦、余弦函数的傅里叶变换如下：0000001[()]()[c o s ][()()][s i n ][()()]F u t j F t F t j πδωωωπδωωδωωωπδωωδωω=+=++-=+-- 求单边正弦函数和单边余弦函数的傅里叶变换。

各章习题及答案第一章绪论1 .举例说明什么是测控？答：(1) 测控例子：为了确定一端固定的悬臂梁的固有频率，我们可以采用锤击法对梁进行激振，再利用压电传感器、电荷放大器、波形记录器记录信号波形，由衰减的振荡波形便可以计算出悬臂梁的固有频率。

（2）结论：由本例可知：测控是指确定被测对象悬臂梁的属性—固有频率的全部操作，是通过一定的技术手段—激振、拾振、记录、数据处理等，获取悬臂梁固有频率的信息的过程。

2. 测控技术的任务是什么？答：测控技术的任务主要有:通过模型试验或现场实测，提高产品质量；通过测控，进行设备强度校验，提高产量和质量；监测环境振动和噪声，找振源，以便采取减振、防噪措施；通过测控，发现新的定律、公式等；通过测控和数据采集，实现对设备的状态监测、质量控制和故障诊断。

3. 以方框图的形式说明测控系统的组成，简述主要部分的作用。

测控系统方框图如下：（2）各部分的作用如下：●传感器是将被测信息转换成某种电信号的器件；●信号的调理是把来自传感器的信号转换成适合传输和处理的形式；●信号处理环节可对来自信号调理环节的信号，进行各种运算、滤波和分析；●信号显示、记录环节将来自信号处理环节的信号显示或存贮。

●模数（A/D）转换和数模（D/A）转换是进行模拟信号与数字信号相互转换，以便用计算机处理。

4.测控技术的发展动向是什么?传感器向新型、微型、智能型方向发展；测控仪器向高精度、多功能、小型化、在线监测、性能标准化和低价格发展；参数测量与数据处理向计算机为核心发展；5. A precise optional signal source can control the output power level to within 1%. A laser is controlled by an input current to yield the power output. A microprocessor controls the input current tothe laser. The microprocessor compares the desired power level with a measured signal proportional to the laser power output obtained from a sensor. Complete the block diagram representing thisclosed-loop control system shown in Fig E1.1, identifying the output, input, and measured variables and the control device.答：6. many luxury automobiles have thermostatically controlled air-conditioning system（恒温空调系统）for the comfort of the passengers. Sketch a block diagram of an air-condition temperature on a dashboard panel（仪表盘）. Identify the function of each element of the thermostatically controlled cooling system.答：7. In the past, control systems used a human operator as part of a closed-loop control system. Sketch the block diagram of the valve control system shown in Fig. P1.2.答：8. The student-teacher learning process is inherently a feedback process intended to reduce the system error back model of the learning process and identify each block of the system.答：9. Automatic control of water level using a float level was used in the Middle East for a water clock. The water clock was used from sometime before Christ until the seventeenth century. Discuss the operation of the water clock, and establish how the float provides a feedback control that maintains the accuracy of the clock. Sketch a block diagram of the feedback system.答：第二章信号与系统分析基础1求周期方波的傅立叶级数（复指数函数形式），画出|c n|-ω和ϕ-ω图。

信号系统(第3版)习题解答《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S R S L S C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

第3章　傅里叶变换3-1 求图3-1所示对称周期矩形信号的傅里叶级数（三角形式与指数形式）。

图3-1解：（1）三角形式由图3-1可知，f(t)为奇函数，故有所以三角形式的傅里叶级数为。

（2）指数形式因所以指数形式的傅里叶级数为。

3-2 周期矩形信号如图3-2所示。

若：重复频率f=5kHz脉宽τ=20μs幅度E=10V求直流分量大小以及基波、二次和三次谐波的有效值。

图3-2解：由图3-2可知，f(x)为偶函数，且f=5kHz，得：所以直流分量为1V基波分量为1sin() 1.3910Vπ=≈二次谐波为2sin( 1.325Vπ=≈三次谐波为。

33sin() 1.2110V π=≈3-3 若周期矩形信号f 1（t ）和f 2（t ）波形如图3-2所示，f 1（t ）的参数为τ=0.5μs，T=1μs，E=1V ；f 2（t ）的参数为τ=1.5μs，T=3μs，E=3V ，分别求：（1）f 1（t ）的谱线间隔和带宽（第一零点位置）频率单位以kHz 表示；（2）f 2（t ）的谱线间隔和带宽；（3）f 1（t ）与f 2（t ）的基波幅度之比；（4）f 1（t ）基波与f 2（t ）三次谐波幅度之比。

解：由题3-2的结论可知，f(t)的傅里叶级数可表示为其中，。

（1）f 1（t ）的谱线间隔，则带宽：。

（2）f 2（t ）的谱线间隔带宽：。

（3）由题3-2可知，所以f 1（t ）的基波幅度为：f 2（t ）的基波幅度为：故。

（4）的三次谐波幅度为：故。

3-4 求图3-3所示周期三角信号的傅里叶级数并画出频谱图。

图3-3解：由图3-3可知，f(t)为偶函数，故。

bn所以的傅里叶级数可表示为()f t其幅度谱如图3-4所示。

图3-43-5 求图3-5所示半波余弦信号的傅里叶级数。

若E=10V ，f=10kHz ，大致画出幅度谱。

图3-5解：由图3-5可知，f(t)为偶函数，因而b n =0，（）；所以其傅里叶级数可表示为若E=10V ，，则幅度谱如图3-6所示。

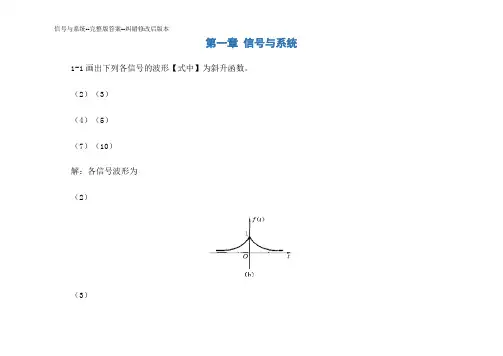
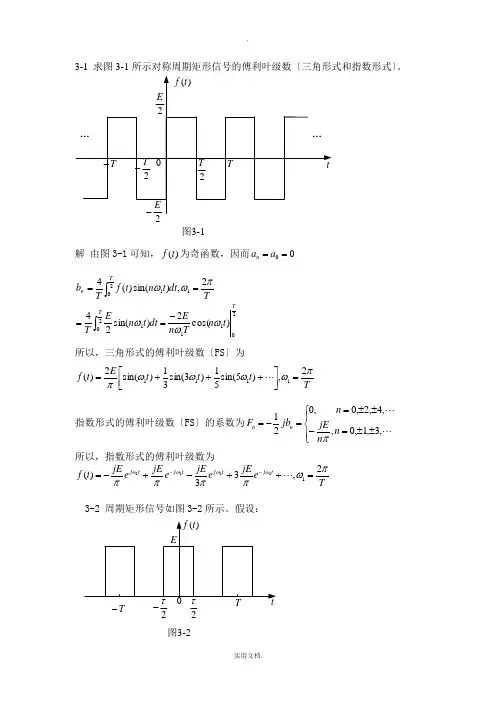
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。

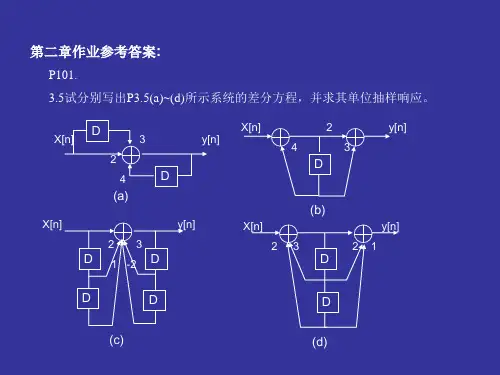
图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

假设：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕，频率单位以kHz 表示； 〔2〕)(2t f 的谱线间隔和带宽； 〔3〕)(1t f 与)(2t f 的基波幅度之比； 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。

1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。