无机材料物理性能题库(2)综述

⽆机材料物理性能课后习题答案《材料物理性能》第⼀章材料的⼒学性能1-1⼀圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉⼒，若直径拉细⾄ 2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉⼒下的真应⼒、真应变、名义应⼒和名义应变，并⽐较讨论这些计算结果。

解：由计算结果可知：真应⼒⼤于名义应⼒，真应变⼩于名义应变。

1-5⼀陶瓷含体积百分⽐为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。

若该陶瓷含有5 %的⽓孔，再估算其上限和下限弹性模量。

解：令E 1=380GPa,E 2=84GPa,V 1=,V 2=。

则有当该陶瓷含有5%的⽓孔时，将P=代⼊经验计算公式E=E 0+可得，其上、下限弹性模量分别变为 GPa 和 GPa 。

1-11⼀圆柱形Al 2O 3晶体受轴向拉⼒F ，若其临界抗剪强度τf 为135 MPa,求沿图中所⽰之⽅向的滑移系统产⽣滑移时需要的最⼩拉⼒值，并求滑移⾯的法向应⼒。

0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =?==-σ名义应⼒0851.0100=-=?=A A l l ε名义应变)(99510524.445006MPa A F T =?==-σ真应⼒)(2.36505.08495.03802211GPa V E V E E H =?+?=+=上限弹性模量)(1.323)8405.038095.0()(112211GPa E V E V E L =+=+=--下限弹性模量解：1-6试分别画出应⼒松弛和应变蠕变与时间的关系⽰意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。

解：Maxwell 模型可以较好地模拟应⼒松弛过程：Voigt 模型可以较好地模拟应变蠕变过程：以上两种模型所描述的是最简单的情况，事实上由于材料⼒学性能的复杂性，我们会⽤到⽤多个弹簧和多个黏壶通过串并联组合⽽成的复杂模型。

2.杜隆-珀替定律（元素的热容定律）：恒压下元素的原子热容为25/(K.mol);热容与温度无关奈曼-柯普定律化合物的热容定律：化合物分子热容等于构成此化合物各元素原子热容之和。

4.5.热膨胀与化学键关系：对分子晶体，分子间是弱的范德华力作用，膨胀系数大；共价键的材料如金刚石作用力很强，对高聚物沿链方向共价键连接，垂直链的方向近邻分子间是弱范德华力因此结晶高聚物和取向高聚物热膨胀有很大各向异性，高聚物热膨胀系数比金属高7.钢中A、M、F热膨胀系数大小：A＞F＞M8.Me对膨胀系数的影响：主要取决于形成K还是固溶于F中，前者使α增大后者减小。

9.金属、高聚物、无机非金属热传导大小和传导机制：热导率λ是指单位温度梯度下，单位时间内通过单位垂直面积的热量。

金属中有大量质量很轻的自由电子，能迅速传递热，无机非金属中自由电子很少，晶格振动是主要导热机制，低温声子导热（声频支格波—弹性波—声波—声子），高温时光子导热；绝缘材料声子导热；高聚物声子热传导机制在低温区，随着温度升高，λ增大；温度升至玻璃化温度时，λ出现极大值；温度高于玻璃化温度后，由于分子排列变得越来越疏松，λ也越来越小。

10.晶体中缺陷、杂质如何影响热导率：引起格波散射等效于声子平均自由程减小→↓λ11.固溶体中溶质含量、性质如何影响热导率：溶质元素的质量大小与溶剂元素相差愈大取代后结合力改变愈大，对λ影响愈大，低温时影响随T↑而↑，T高于0.5德拜温度时，与T 无关原因：低温下声子传导的平均波长远大于点缺陷的线度，不引起散射，T↑平均波长↓→接近点缺陷线度→散射达到最大，再升温散射也不变化12.抗热冲击断裂：抵抗无机材料发生瞬时断裂的性能抗热冲击损伤：抵抗材料在热冲击循环作用下表面发生开裂剥落以致最终破裂或变质的性能13.多相材料产生热应力原因：不同相有不同膨胀系数，温度变化各相膨胀收缩量不同而相互牵制产生热应力14.提高抗热冲击断裂措施：①↑材料强度σ↓弹性模量E，使σ/E↑，即提高材料的柔韧性能吸收较多的弹性应变能而不开裂，↑热稳定性②↑热导率λ，使R’↑，λ大→传热快→内外温差较快平衡，↓热应力聚集③↓热膨胀系数α④↓表面热传递系数h⑤↓产品有效厚度15.差热分析法（DTA）：在程序控制温度下将被测材料与参比物在相同条件下加热或冷却，测量试样与参比物之间温差随温度、时间的变化关系。

无机材料物理化学试题1一、填空题（每空1分，共20分）1.晶体结构中的热缺陷有 和 二类。

2.三T 图中三个T 代表 、 和 。

3.玻璃具有下列通性： 、 、 和 。

4.固体中质点扩散的推动力是 ，液－固相变过程的推动力是 ，烧结过程的推动力是 。

5.试验测得NaCl 的扩散系数与温度关系如图所 示，直线（1）属 扩散，直线（2） 属 扩散；如果提高NaCl 的纯度， 两直线的转折点向 方向移动。

6. 组成Na 2O . 1/2Al 2O 3 . 2SiO 2的玻璃中氧多面体平均非桥氧数为－－－－。

7．在硅酸盐熔体中，当以低聚物为主时，体系的粘度 、析晶能力 。

8. 写出缺陷反应式二．（10分）已知O 2溶解在FeO 晶体中形成贫铁氧化物Fe 1-X 的反应如下：试用扩散的微观理论推导Fe 2＋的扩散系数D Fe2＋与氧分压P O2的关系式。

三．（10分）写出杨德尔模型要点及动力学关系式，为什么在转化率高时出现偏差？金斯特林格主要在杨德尔模型的基础上考虑了什么影响？四 （15分）说明影响扩散的因素？五 （15分）试述熔体粘度对玻璃形成的影响？在硅酸盐熔体中，分析加入—价碱金属氧化物、二价金属氧化物或B 2O 3后熔体粘度的变化？为什么？ 六 （10分）简要说明：（1） 材料烧结时四种最基本的传质机理是什么？少量添加剂能促进烧结，其原因是什么？（2） 说明晶粒长大和二次再结晶这两种过程的主要区别，在工艺上如何防止晶FLnD 1/T(非化学计量扩logD1000/T(1)(2)−−→−−−→−322232O Y CeOZrO O La （负离子空位）。

（负离子间隙）。

∙+''++FeFe o 2Fe 2Fe V (g)＝O O 212Fe粒异常长大？ 七 （20分）分析下列相图1.划分副三角形；2.用箭头标出界线上温度下降的方向及界线的性质；3.判断化合物S 的性质；4.写出各无变量点的性质及反应式；5.分析点1、2熔体的析晶路程。

无机材料物理性能复习题、填空题1、晶体中的塑性变形有两种基本方式：滑移和孪晶。

2、一各向异性材料，弹性模量E=109pa泊松比u=o.2，则其剪切模量G=45.4 pa。

3、影响弹性模量的因素有晶体结构、温度、复相。

4、弹性模量E是一个只依赖于材料基本成份的参量，是原子间结合强度的一个标志，在工程中表征材料对弹性变形的抗力，即材料的冈【J度。

5、无机材料的热冲击损坏有两种类型：抗热冲击断裂性和抗热冲击损伤性。

6根据材料在弹性变形过程中应力和应变的响应特点，弹性可以分为理想弹性和非理想弹性两类。

7、裂纹有三种扩展方式或类型：掰开型，错开型和撕开型。

其中掰开型是低应力断裂的主要原因。

8、从对材料的形变及断裂的分析可知，在晶体结构稳定的情况下，控制强度的主要参数有三个：弹性模量，裂纹尺寸和表面能。

9、Griffith 微裂纹理论从能量的角度来研究裂纹扩展的条件,这个条件是物体内储存的弹性应变能的降低大于等于由于开裂形成两个新表面所需的表面能。

10、按照格里菲斯微裂纹理论，材料的断裂强度不是取决于裂纹的数量，而是决定于裂纹的大小，即是由最危险的裂纹尺寸或临界裂纹尺寸决定材料的断裂强度。

11、广义虎克定律适用于各向异性的非均匀材料。

12、对于中心穿透裂纹的大而薄的板，其几何形状因子Y=、13、当温度不太高时，固体材料中的热导形式主要是声子热导。

14、杜隆一伯替定律的内容是：恒压下元素的原子热容为25J/Kmol 。

15、热量是依晶格振动的格波来传递的，格波分为声频支和光频支两类。

16、固体材料的热膨胀本质是点阵结构中质点间平均距离随温度升高而增大。

17、金属材料电导的载流子是自由电子，而无机非金属材料电导的载流子可以是电子、电子空穴，或离子、离子空位。

18、晶体的离子电导可以分为离子固有电导/或本征电导和杂质电导两大类。

19、电导率的一般表达式-\j =x nqi^为，其各参数ni、qi和-h的含义分别是i载流子的浓度、载流子的电荷量、载流子的迁移率。

《材料物理性能》第一章材料的力学性能1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力，若直径拉细至2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。

解：由计算结果可知：真应力大于名义应力，真应变小于名义应变。

1-5一陶瓷含体积百分比为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。

若该陶瓷含有5 %的气孔，再估算其上限和下限弹性模量。

解：令E 1=380GPa,E 2=84GPa,V 1=0.95,V 2=0.05。

则有当该陶瓷含有5%的气孔时，将P=0.05代入经验计算公式E=E 0(1-1.9P+0.9P 2)可得，其上、下限弹性模量分别变为331.3 GPa 和293.1 GPa 。

0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =⨯==-σ名义应力0851.0100=-=∆=AA l l ε名义应变)(99510524.445006MPa A F T =⨯==-σ真应力)(2.36505.08495.03802211GPa V E V E E H =⨯+⨯=+=上限弹性模量)(1.3238405.038095.0()(112211GPa E V E V E L =+=+=--下限弹性模量1-11一圆柱形Al 2O 3晶体受轴向拉力Ff 为135 MPa,求沿图中所示之方向的滑移系统产生滑移时需要的最小拉力值，并求滑移面的法向应力。

解：1-6试分别画出应力松弛和应变蠕变与时间的关系示意图，并算出t = 0,t = ∞和t = 时的纵坐标表达式。

τ解：Maxwell 模型可以较好地模拟应力松弛过程：Voigt 模型可以较好地模拟应变蠕变过程：以上两种模型所描述的是最简单的情况，事实上由于材料力学性能的复杂性，我们会用到用多个弹簧和多个黏壶通过串并联组合而成的复杂模型。

第二章 无机材料的受力变形名义应力应力：单位面积所受的力。

σ=F/S真实应力应变：用来描述物体内部各质点之间的相对位移。

弹性形变：各向同性广义胡克定律： 体积模量弹性系数k s ：大小反映了原子间的作用力曲线在r = r 0处斜率的大小。

弹性刚度系数 大小实质上反映了原子间势能曲线极小值尖峭度的大小。

弹性系数k s 测定式架状结构石英和石英玻璃的架状结构是三维空间网络，几乎各向同性；晶体结构 双链结构、环状结构（岛状结构）、层状结构为各向异性，因材料方向不 同而差别很大。

温度：弹性常数随温度升高而降低。

并联模型：E u =V 2E 2+(1－V 2)E 1（上限）复相的弹性模量串联模型：1/E L =V 2/E 2+(1－V 2)/E 1（下限）应变松弛（或蠕变或徐变）：固体材料在恒定荷载下，变形随时间延续而缓慢增加的不平衡过程，或材料受力后内部原子由不平衡到平衡的过程。

当外力除去 后，徐变变形不能立即消失。

应力松弛（或应力弛豫）：在持续外力作用下，发生变形着的物体，在总的变形值保持不变的情况下，由于徐变变形渐增，弹性变形相应的减小，由此使物体的内部应力随时间延续而逐渐减少。

或一个体系因外界原因引起的不平衡状态逐应力和应变正应变剪切应变弹性形变机理弹性模量影响因素因为大部分固体随温度升高而发生热膨胀现象，原子间结合力减弱 因此温度对弹性刚度系数的影响，通常用弹性刚度系数的温度系数T C 表示。

应用：温度补偿材料，即一种异常的弹性性质材料（Tc 是正的)，补偿一般材料的负Tc值。

例如：低温石英有一个方向Tc 是正值，低温石英在570o C 通过四面体旋转，进行位移式相转变，变成充分膨胀的敞旷高温型石英结构。

原因：对高温石英和低温石英施加拉伸应力，前者由于Si －O －Si 键是直的，仅发生拉伸，后者除拉伸外，还有键角改变，即发生转动运动。

随着温度的增加，其刚度增加，温度系数为正值。

温度补偿材料具有敞旷结构，内部结构单位能发生较大转动的物质，这种敞旷式结构具有小的配位数。

第一章无机材料的受力形变1．形变：材料在外力的作用下发生形状与尺寸的变化2．影响弹性模量大小的因素？①化学键(本质)：共价键、离子键结合力强，弹性模量大。

分子键结合力弱，弹性模量小。

②原子间距：正应力使原子间距减小，弹性模量增大；张应力使原子间距增大，弹性模量减小。

温度升高，原子间距增大，弹性模量降低。

3．弹性模量的测定⏹静态法：采用常规三点弯曲试验加载方式；在正式读数前，在低载荷进行几次反复加载、卸载；试样尺寸有要求。

误差较大⏹动态法：三点弯曲受力，外加载荷周期性性变化，产生谐振；弯曲振动测E，扭曲振动测G；试样尺寸有要求。

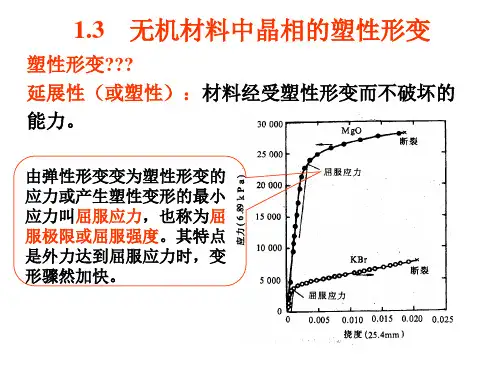
误差较小4．塑性：材料在外力去除后仍保持部分应变而不能恢复的特性5．延展性：材料发生塑性形变而不断裂（破坏）的能力6．晶体塑性形变两种基本形式：•滑移是指在剪切应力作用下晶体一部分相对于另部分发生平移滑动。

在显微镜下可观察到晶体表面出现宏观裂纹，并构成滑移带。

•孪晶是晶体材料中原子格点排列一部分与另部分呈镜像对称的现象。

镜界两侧的晶格常数可能相同、也可能不同。

7．晶体滑移的条件几何条件：滑移一般发生在晶面指数小、原子密度大的晶面（主要晶面）和晶面指数小的晶向（主要晶向）上：由于晶面指数小的面，面间距越大，原子间的作用力越小，易产生相对滑动；晶面指数小的面，原子的面密度大，滑过滑动平面使结构复原所需的位移量最小，即柏氏矢量小，也易于产生相对滑动。

静电作用因素：同号离子存在巨大的斥力，如果在滑动过程中相遇，滑动将无法实现。

8．粘度定义：使相距一定距离的两个平行平面以一定速度相对移动所需的力。

单位：Pa· s，9．影响粘度的因素？温度：一般温度升高，粘度下降。

时间：从高温状态冷却到退火点，再加热其粘度随时间增加而增加；而预先在退火点以下保持一定时间后，其粘度随时间增加而降低，但时间大大缩短。

组成：改性阳离子不同，粘度变化不同；但改性阳离子的加入，在任何温度下总会使粘度降低。

【⽆机材料物理性能】课后习题集答案解析课后习题《材料物理性能》第⼀章材料的⼒学性能1-1⼀圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉⼒，若直径拉细⾄2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉⼒下的真应⼒、真应变、名义应⼒和名义应变，并⽐较讨论这些计算结果。

解：由计算结果可知：真应⼒⼤于名义应⼒，真应变⼩于名义应变。

1-5⼀陶瓷含体积百分⽐为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。

若该陶瓷含有5 %的⽓孔，再估算其上限和下限弹性模量。

解：令E 1=380GPa,E 2=84GPa,V 1=0.95,V 2=0.05。

则有当该陶瓷含有5%的⽓孔时，将P=0.05代⼊经验计算公式E=E 0(1-1.9P+0.9P 2)0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =?==-σ名义应⼒0851.0100=-=?=A A l l ε名义应变)(99510524.445006MPa A F T =?==-σ真应⼒)(2.36505.08495.03802211GPa V E V E E H =?+?=+=上限弹性模量)(1.323)8405.038095.0()(112211GPa E V E V E L =+=+=--下限弹性模量可得，其上、下限弹性模量分别变为331.3 GPa 和293.1 GPa 。

1-11⼀圆柱形Al 2O 3晶体受轴向拉⼒F ，若其临界抗剪强度τf 为135 MPa,求沿图中所⽰之⽅向的滑移系统产⽣滑移时需要的最⼩拉⼒值，并求滑移⾯的法向应⼒。

解：1-6试分别画出应⼒松弛和应变蠕变与时间的关系⽰意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。

解：Maxwell 模型可以较好地模拟应⼒松弛过程：Voigt 模型可以较好地模拟应变蠕变过程：).1()()(0)0()1)(()1()(10=∞=-∞=-=e EEe e Et t t στεσεεεσεττ；；则有：其蠕变曲线⽅程为：./)0()(;0)();0()0((0)e (t)-t/e στσσσσσστ==∞==则有：：其应⼒松弛曲线⽅程为)(112)(1012.160cos /0015.060cos 1017.3)(1017.360cos 53cos 0015.060cos 0015.053cos 82332min 2MPa Pa N F F f =?=?=?=?=??=πσπτπτ：此拉⼒下的法向应⼒为为：系统的剪切强度可表⽰由题意得图⽰⽅向滑移以上两种模型所描述的是最简单的情况，事实上由于材料⼒学性能的复杂性，我们会⽤到⽤多个弹簧和多个黏壶通过串并联组合⽽成的复杂模型。

第一章几何结晶学基础1-1. 晶体,晶胞的定义;空间格子构造的特点;晶体的基本性质. 1-2. 参网页上的模型,运用对称要素组合定律,写出四方柱,六方柱,四方四面体,斜方双锥,六八面体,三方柱,复三方三角面体,四六面体的点群符号, 并写出其所属的晶系和晶族. 1-3. 参阅网页上的模型,请确定单型中的六八面体,复三方偏三角面体,复六方双锥,和聚型中2,3,4 号模型在晶体定向中,各晶体的晶轴分别与哪些对称轴重或晶棱方向平行? 1-4. 请写出单型三方柱,四方柱,四方双锥,六方柱,菱面体,斜方双锥各晶面的主要晶面符号. 1-5. 请写出下列聚型模型各晶面的晶面符号:1,2,3,4.两个对称面相互成1)60°,2)90°,3)45°,4)30°,可组合成什么点群? 1-6. 由两根相交的二次轴互成1)90°,2)60°,3)45°,4)30°,可以组合成什么点群? 1-7. 试在面心立方格子中画出菱面体格子一晶面在X,Y,Z 轴分别截得2,4,6 个轴单位,请写出此晶面符号. 1-8. 作图表示立方晶体的(123),(012),(421)晶面. 1-9. 在六方晶体中标出晶面(0001),(2110),(1010),(1120),(1210) 的位置. 1. 答:晶体最本质的特点是其内部的原子,离子,或原子集团在三维空间以一定周期性重复排列而成, 晶体的空间格子构造有如下特点: 结点空间格子中的点,在实际晶体中它们可以代表同种质点占有的位置,因此也称为晶体结构中的等同点位置. 行列结点在一维方向上的排列 . 空间格子中任意两个结点连接的方向就是一个行列方向.面网结点在平面上的分布构成面网.空间格子中,不在同一行列上的任意三个结点就可联成一个面网.平行六面体空间格子中的最小单位.它由六个两两平行且大小相等的面组成. 晶体的基本性质是指一切晶体所共有的性质, 这些性质完全来源于晶体的空间格子构造.晶体的基本性质主要包括以下五点: 1 ) . 自限性(自范性),指晶体在适当条件下自发形成封闭几何多面体的性质. 晶体的的多面体形态是其格子构造在外形上的反映. 暴露在空间的晶体外表, 如晶面,晶棱与角顶分别对应其晶体空间格子中的某一个面网,行列和结点. 2 ) . 结晶均一性,指同一晶体的各个不同部分具有相同的性质.因为以晶体的格子构造特点衡量,晶体不同部分质点分布规律相同,决定了晶体的均一性. 3 ) . 对称性,指晶体中的相同部分在不同方向上或不同位置上可以有规律地重复出现.这些相同部位可以是晶面,晶棱或角顶.晶体宏观上的对称性反映了其微观格子构造的几何特征. 4 ) . 各向异性,指晶体的性质因方向不同而具有差异.如云母的层状结构显示了在不同方向上的结合强度不同.从微观结构角度考虑,代表云母晶体的空间格子在不同方向上结点位置的排列不同.5 ) . 稳定性(最小内能),指在相同的热力学条件下,具有相同化学组成的晶体与气相,液相,非晶态相比,晶体具有最小内能,因此也是稳定的结构. 2. 答: 点群运用组合定律晶系晶族四方柱L 4 4L 2 5PC 1,2,3 四方中级六方中级六方柱L6 6L 2 7PC 1.2.3 四方四面体Li 4 2L 2 2P 4,5 四方中级斜方双锥3L 2 3PC 1,2,3 正交低级六八面体3L 4 4L 3 6L 25 等轴高级9PC 三方中级复三方三角面L 3 3L 2 3PC 1,2,3 体四六面体3L 4 4L 3 6L 25 等轴高级9PC 六方中级三方柱Li 6 3L 2 3P 4 3 答:略4. 答: 三方柱晶面1(2110) 晶面2( 1210) 晶面3(1120) 晶面4(0001) 晶面5(0001) 四方柱晶面1(100) 晶面2(010) 晶面3(100) 晶面4(010) 晶面5(001) 晶面6(001) 四方双锥晶面1(h0l) 晶面2(0kl) 晶面3(h0l) 晶面4(0kl) 晶面5(h0l) 晶面6(0kl) 晶面7(h0l) 晶面8(0kl) 六方柱晶面1(10l0) 晶面2(01l0) 晶面3(l100) 晶面4(l010) 晶面5(0l01) 晶面6(1l00) 晶面7(0001) 晶面8(000l) 菱面体晶面1(h00l) 晶面2(0k0l) 晶面3(h00l) 晶面4(0l0l) 晶面5(00il) 晶面6(00il) 斜方双锥晶面1(hkl) 晶面2(hkl) 晶面3(hkl) 晶面4(hkl) 晶面5(hk l ) 晶面6(hk l ) 晶面7 (hkl) 晶面8(hkl) 5. 答: 60°L33P 90°L22P 45°L44P 30°L66P 6. 答: 90°3L 2 60°L33L2 45°L 4L 30°L 6L 6 4 2 2 7. 答:略.(632) 8. 答:略9. 答:略第二章晶体化学基础和无机化合物晶体结构1-1. 晶格能与哪些因素有关?已知MgO 晶体具有氯化钠的结构型, 其晶格常数 a 为0.42nm,试计算MgO 的晶格能. 1-2. 计算具有简单立方(SC)和体心立方(BCC)结构金属(单质)晶胞的堆积密度(空间利用率). 1-3. 金属钼具有BCC 结构,其晶格常数 a 为0.3146nm,试计算钼原子的半径. 金属铬的晶格常数 a 为0.2884nm,密度为7.19g/cm3,通过计算确定铬是简单立方,体心立方还是面心立方结构.(Cr 52.00) 1-4. 在氧离子面心立方紧密堆积中,画出适合正离子填充的空隙形状和位置, 并分析八面体空隙和四面体空隙数分别与氧离子数有什么关系? 1-5. 比较面心立方最紧密堆积和六方最紧密堆积的异同点. 1-6. ThO2 具有萤石结构:Th4+离子半径为0.100nm,O2-离子半径为0.140nm,试问1)实际结构中的Th4+正离子配位数与预计配位数是否一致?2)结构是否满足鲍林规则. 1-7. 从负离子的立方密堆积出发,说明以下情况各产生什么结构类型:1)正离子填满所有四面体空隙位置;2)正离子填满一半四面体空隙位置;3)正离子填满所有八面体空隙位置. 1-8. 在萤石晶体中Ca2+半径为0.112nm,F-半径为0.131nm,求萤石晶体的堆积密度?萤石晶体a=0.547nm,求萤石的密度. 1-9. 根据教材中的萤石结构图,画出萤石晶胞的投影图,并注明Ca2+离子和F离子的标高. 1-10. 下列硅酸盐矿结构各属何种结构类型?(有Al3+离子的要说明其在结构中所处的位置): CaMg[Si2O6] Ca2Al[AlSiO7] Mg[Si4O10](OH)2 K[AlSi3O8] 1.答:因素为(1)离子的电子结构(2)离子的晶体结构类型(3)正负离子平衡距离.MgO 的晶格能为3955.5 KJ mol . 2.答:SC 堆积密度为52.36%,BCC 堆积密度为68.02%. 3.答:钼原子半径为0.1362nm.铬是体心立方BCC 结构. 4.答:四面体数:氧离子数=2:1,八面体数:氧离子数=1:1. 5.答:略. 6.答: (1)半径计算得出Th4+应为六配位,由于ThO2 为萤石结构,故不一致. (2) 不满足多面体规则,电价规则可满足. 7.答:1)反萤石结构.2)闪锌矿结构.3)NaCl 型结构. 8.答:堆积密度为60.41%,萤石的密度为 3.17g cm3. 9.答:图略. 10. 答:CaMg[Si2O6] 单链状. Ca2Al[AlSiO7] 组群状,双四面体.Al3+离子一部分位于氧八面体空隙, 另一部分位于四面体空隙. Mg[Si4O10](OH)2 层状. K[AlSi3O8] 架状.Al3+离子位于氧四面体空隙.第三章晶体的结构缺陷.3-1 方镁石(MgO)的密度是 3.58g/cm3,其晶格常数是0.42nm,计算MgO 中每个晶胞中肖特基缺陷的数目. 3-2 1)在CaF2 晶体中,弗兰克尔缺陷形成能为2.8eV,肖特基缺陷的生成能为 5.5eV, 计算在25℃和1600℃时热缺陷的浓度? 2)如果CaF2 晶体中,含有百万分之一的YF3 杂质,则在1600℃时,CaF2 晶体中是热缺陷占优势还是杂质缺陷占优势?请说明原因. 3-3 在下述晶体中,你认为何类缺陷占优势?1)用MgCl2 掺杂的NaCl;2)用Y2O3 掺杂的ZrO2;3)用YF3 掺杂的CaF2;4)在一种还原性气氛中加热的WO3. 3-4 试写出下列缺陷方程: 1) 3) 2) 4) 3-5 当ZrO2 添加到Y2O3 中,为保持结构的电中性,在形成置换型固溶体的同时, 还产生正离子空位,写出其缺陷反应方程式. 3-6 高温结构材料Al2O3 可以用ZrO2 来实现增韧,也可以用MgO 来促进Al2O3 的烧结:1)如加入0.2mol%ZrO2,试写出缺陷反应式和固溶体分子式;2)如加入0.3mol%ZrO2 和Xmol%MgO 对Al2O3 进行复合取代,试写出缺陷反应式,固溶体分子式,并求出X 值. 3-7 ZnO 属六方晶系,a=0.3242nm,c=0.5195nm,每个晶胞中含有2 个ZnO 分3 子,测得晶体密度分别为5.74,5.606g/cm ,求两种情况下各产生什么型式的固溶体? 3-8 非化学计量化合物FexO 中,Fe3+/Fe2+=0.1,求FexO 中空位浓度及x 值. 1.答:平均每个晶胞0.0082 对肖特基缺陷. 2.答:⑴T1=298K,弗兰克缺陷浓度2.21×10-24 ,肖特基缺陷浓度为1.374×10-31;T2=1873K, 弗兰克缺陷浓度 1.72×10-4,肖特基缺陷浓度为 1.4×10-5;⑵T=1600℃,热缺陷1.72×10-4,杂质缺陷1×10-6,热缺陷占优势3.答: 4.答:略5. 答: 6.答:①Al1.997Zr0.002O3 ②Zr0.003Mg0.003Al1.994O3 7.答:略8.答:Fe0.957O,空位浓度[ ]=0.0435第四章非晶态固体4-1 试分析影响熔体粘度的因素有哪些? 4-2 名词解释:晶子学说和无规则网络学说,单键强度,网络形成剂和网络变性剂4-3 玻璃的组成是13mol%Na2O,13mol%CaO,74mol%SiO2,计算非桥氧分数. 有两种不同配比的玻璃,其组成如下: 序号1 2 Na2O( mol%) 8 12 CaO( mol%) 12 8 SiO2( mol%) 80 80 试用玻璃结构参数说明两种玻璃高温下粘度的大小. 4-4 有一组二元硅酸盐熔体,其R 志变化规律如下,写出熔体一系列性质的变化规律:R = 2 , 2.5, 3, 3.5, 4 游离碱含量的变化; O/Si 比的变化; 低聚物数量; 熔体粘度; 形成玻璃的能力; 析晶能力. 4-5 什么是硼反常现象?为什么会产生硼反常现象. 1. 答:溶体组成,质点活化能,温度等. 2. 答:略. 3. 答:R 值为2.35.X 值为0.7.非桥氧分数为17.5%.两种玻璃结构参数相同,但(1)的钙含量高,所以(1)粘度大. 4.答:游离碱含量的变化增大; O/Si 比的变化增大; 低聚物数量增多; 熔体粘度递减; 形成玻璃的能力递减; 析晶能力递增. 5.答:略.第五章固体的表面与界面行为5-1 名词解释: 表面能,表面张力,吸附,接触角,晶界结构,润湿角. 5-2 试说明晶界能总小于两个相邻晶粒的表面能之和的原因. 5-3 MgO-Al2O3-SiO2 系统的低共熔物放在Si3N4 陶瓷片上,在低共熔温度下, 液相的表面张力为900×10-3N/m,而液体与固体的界面能为600×10- 3 N/m,测得接触角为70.52°. (1) (2) 求Si3N4 的表面张力; 把Si3N4 在低共熔温度下进行热处理,测试其热腐蚀的槽角为60°,求Si3N4 的晶界能. 5-4 生产氧化铅瓷件过程中需要镀银,已知1000℃时γAl2O3 s=1.0×10-3N/m, γAg L=0.92×10-3N/m,γAg L/Al2O3 s=1.77×10-3N/m,问液态银能否润湿氧化铅瓷件表面?可以用什么方法改善它们之间的润湿性? 5-5 5-6 5-7 5-8 影响润湿效果的主要因素有哪些? 大块状的石英材料经煅烧后易于破碎,这是为什么? 试说明晶粒之间的晶界应力大小对晶体性能的影响. 在真空中和在空气中将云母片剥落后再合上,会出现什么现象?说明理由? 5-9 5-10 什么是粘附功?粘附性越好是否就意味着粘附功越小,为什么? 1 克石英当它粉碎(在湿空气中)成每颗粒半径为1μm 的粉末时质量增加至 1.02 克,它的吸附水膜厚度为多少?(石英密度是2.65g/cm3) 1. 3. 答:略2. 答:略答:⑴900×10-3N/M ⑵1559×10-3N/M 4. 答:θ=147°>90°,液态银不能润湿氧化铅表面,可以通过以下方法改善它们之间的润湿性:增大瓷件表面粗糙度;设法除去表面吸附膜等. 5. 略6. 略7. 略8. 略9. 略10. 答:膜厚度为0.0177um第六章相图及其相平衡6-1 名词解释: 凝聚系统;介稳平衡;无变量点;低共熔点;双升点;双降点;液相独立析晶. 6-2 简述SiO2 的多晶转变现象,说明为什么在硅酸盐产品中SiO2 经常是以介稳状态存在. 6-3 具有不一致熔融二元化合物的二元相图(图6-11 所示),在低共熔点E 发生如下析晶过程: .已知 E 点 B 含量为20%,化合物AmBn 的 B 含量为64%.现有C1 和C2 二种配合料,已知C1 中的 B 含量为C2 中 B 含量的 1.5 倍,且在高温熔融冷却析晶时,从该二配合料中析出的初相(即到达低共熔温度前析出的第一种晶体)含量相等.试计算C1 和C2 配合料的组成. 6-4 今通过实验测得如图所示的各相图,试判断这些实验结果的正确性,若有错误,予以修正,并说明理由. 6-5 已知 A 和 B 两组份构成具有低共熔点的有限固溶体二元系统(图6-17). 试根据下列实验数据绘制概略相图: 的熔点为1000℃, 的熔点为700℃. A B 含B25%的试样在500℃完全凝固, 其中含73.3.%初相SA(B)和26.7%SA(B)+SB(A) 共生体.含B50%的试样在同一温度下凝固完毕,其中含40%初相SA(B) 和60%SA(B)+SB(A) 共生体,而SA(B)相总量占晶相总量的50%,实验数据均在达到平衡状态时测定. 6-6 试完成下图中的配料点1,2,3 的结晶路程(表明液,固相组成点的变化及其结晶过程各阶段系统中发生的相变化). 6-7 下图所示为一个三元化合物的三元相图. (1) (2) (3) (4) 判断三元化合物N 的性质; 标出边界曲线的降温方向(转熔界线用双箭头); 指出无变点K,L,M 的性质分析点1,2 的结晶路程(表明液固相组成的变化及各阶段的相变化) 6-8 如图6-43,配合料P 的液相在无变点K 发生独立析晶,最终在低共熔点 F 结束结晶.试问此时所获得的C3S,C2S,C3A 和C12A7 四种晶相的含量各为多少?,如果在F 点仍未达到平衡,残留液相能否离开F 点向其它无变点继续转移?为什么? 6-9 如图6-43,今取配合料成分恰好如无变点h 的组成,在充分平衡条件下, 问: (1) (2) (3) 加热该配合料,什么温度开始出现液相? 要使物料全部熔融,至少要加热到多高温度? 写出配合料加热到开始出现液相时和全部熔融时的反应过程. 6-10 如图6-43,若原始液相组成位于配合料圈内,并恰好在CaO 和C3S 初相区的边界曲线上: (1) (2) 说明此液相的结晶路程在缓慢冷却到无变点K 的温度1455℃时急剧冷却到室温,则最终获得哪些相? 各相含量如何? 1.答:名词解释略. 2.答:略,提示从动力学角度说明. 3.答:C1 配料组成为 A 74.1%,B 25.9%;C2 配料组成为 A 82.7%,B 17.3%. 4.答:(A)B 的熔点温度只有一个,两点应该重合.(B)液相组成不应该存在范围.(C)低共熔温度不应该是一条倾斜的直线,应该是水平的.(D)(E)均为二元系统,P 最大为3,不应该出现四相点和四相区域. 5.答:图略,提示低共熔温度线上三点的B%分别为5%,80%,95%. 6.答:略. 7.答:(1)N 为不一致熔融三元化合物.(2)略.(3)L 点位于△BNC 内部,为低共熔点, 点位于△ANB 交叉位, K 为双升点, 点位于△ANC 内部, M 为低共熔点. (4)略. 8.答:C3S,C2S,C3A 和C12A7 四种晶相的含量略,残留液相不能离开F 向其它无变量点转移,因为三元系统最多存在四相,在F 点已有四相. 9.答:(1)加热该配合料,1335 度开始出现液相.(2)要使物料全部熔融,至少要加热到2570 度.(3)略. 10. 答:最终获得C3S,C2S,玻璃相.第七章扩散与固相反应7-1 名词解释: 无序扩散,晶界扩散,表面扩散,本征扩散,非本征扩散,自扩散,互扩散,稳定扩散,不稳定扩散,扩散活化能,扩散通量. 7-2 已知CaO 的肖特基缺陷生成能为6ev,欲使Ca2+在CaO 中的扩散直至CaO 的熔点(2600 ℃)都是非本征扩散,要求三价杂质离子的浓度是多少? 7-3 设有一条内径为30mm 的厚壁管道,被厚度为0.1mm 的铁膜隔开.通过管子的一端向管内输送氮气,以保持膜片一侧氮气浓度为1 200mol/m ,而另一侧的氮气浓度为100 mol/m3.如在700℃下测得通过管道的氮气流量为 2.8×10-8mol/s,求此时氮气在铁中的扩散系数. 7-4 在二根金晶体圆棒的端点涂上示踪原子Au,并把棒的两端如图所示连接. 在920℃下加热100 小时,Au 示踪原子的扩散分布如图所示,并满足下列关系: 3 M 为实验中示踪原子总量,求此时金的自扩散系数. 7-5 试定性地分析和讨论从室温到熔融温度范围内,氯化锌添加剂(10-4mol%) 对氯化纳单晶中所有离子(Zn,Na,Cl)的扩散能力的影响. 7-6 试从扩散介质的结构,性质,晶粒尺寸,扩散物浓度,杂质等方面分析影响扩散的主要因素. 7-7 根据ZnS 烧结的数据测定了扩散系数,在450℃和563℃时,分别测得扩散系数为1.0 ×10 cm /s 和3.0×10 cm /s.(1)确定激活能和D0;(2)根据你对结构的了解, 试从运动的观点和缺陷的产生来推断激活能的含义;(3)根据ZnS 和ZnO 相互类似的特点,预测D 随硫的分压而变化的关系. 7-8 试分析碳原子在面心立方和体心立方铁八面体空隙间跳跃情况并以D=λ Pг形式写出其扩散系数(设点阵常数为a).式中λ为跃迁自由程,P 为跃迁几率,而г为跃迁频率. 7-9 指出以下概念中的错误: (1) (2) (3) 如果固体中不存在扩散流,则说明原子没有扩散; 因固体原子每次跳动方向是随机的,所以在任何情况下扩散流量为零; 晶界上原子排列混乱,不存在空位,所以以空位机制扩散的原子在晶界处无法扩散; -4 2 -4 2 (4) 间隙固溶体中溶质浓度较高,则溶质所占据的间隙越多,供扩散的空余间隙越少,即Z 值越小,越容易导致扩散系数的降低. 7-10 以空位机制进行扩散时,原子每次跳动一次就相当于空位反向跳动一次, 并未形成新的空位,而扩散活化能中却包含着空位形成能,此说法正确吗?请给出说明. 1. 2. 3. 4. 答:略答:1.1×10-5mol/m3 答:D=3.6×10 m /s 答:根据表中数据,以-ln ,求D 为2.33×10-7m2/s 对x2 作图,得一直线,求斜率K,t=360000s,D= -12 2 5. 答:低温时,以杂质扩散为主,ZnCl2 的加入对Na 离子的扩散能力有扩散作用, 而对氯离子的扩散能力影响不大,在高温条件下,本征扩散为主要形式, ZnCl2 的加入影响可忽略. 6. 略7. 答:①Q=48.9kJ,D0=0.39cm2/s ②质点处于其他质点作用的三位势阱中作周期性振动,若要摆脱其他质点的束缚,必须具有克服势阱作用的能量,这部分能量称为激活能,激活能包括迁移能和缺陷形成能. ③D∝PS2-1/4,硫分压越小,D 越大,硫分压增大,D 减小. 8. 9. 答:面心立方(fcc), = ,P= ,D= ,体心立方(bcc),D= 答:①扩散流的产生需要一个推动力,但在宏观上不存在扩散流,只要有一定温度,原子之间存在杂乱无章的自扩散. ②当有外力作用,如处于电场中,扩散流量不为零,只有在平衡状态下,扩散流量为零. ③晶界上原子所受束缚力低,其能量/振动频率搞,迁移能力强,其原子迁移到内部相党羽空位的反向扩散,不仅存在扩散,其扩散能力还比内部强. ④对扩散系数的影响可以忽略. 10.答:不正确.扩散系数是宏观值不是单个原子跳动机理的简单叠加.第八章固相反应8-1 MgO 和SiO2 固相反应生成Mg 2SiO4,反应时扩散离子是什么?写出界面反应方程. 8-2 MoO3 和CaCO3 反应时, 反应机理受到CaCO3 颗粒大小的影响. MoO3 : 当CaCO3 =1:1,MoO3 的粒径r1 为0.036mm,CaCO3 的粒径r2 为0.13mm 时,反应是扩散控制的;而当CaCO3 :MoO3=15:1,r2<0.03 时,反应由升华控制, 试解释这种现象. 8-3 试比较杨德方程和金斯特林格方程的优缺点及其适用条件. 8-4 当测量氧化铝-水化物的分解速率时,发现在等温试验期间,质量损失随时间线性增加到50%左右,超过50%时,质量损失的速率就小于线性规律.线性等温速率随温度指数地增加,温度从451℃增大到493℃时速率增大10 倍,试计算激活能,并说明这是一个扩散控制的反应?还是一般反应或是界面控制的反应. 8-5 1 平均粒径为1μm 的MgO 粉料与Al2O3 粉料以1: 摩尔比配料并均匀混合. 将原料在1300℃恒温3600h 后,有0.3mol 的粉料发生反应生成Mg Al2O4, 该固相反应为扩散控制的反应.试求在300h 后,反应完成的摩尔分数以及反应全部完成所需的时间. 答:扩散离子是Mg2+和Si4+,界面反应方程为: g 2+ +SiO4 Mg2SiO4+Si4+ Si4++4MgO Mg2SiO4+2 Mg2+ 2.答:当MoO3 的粒径r1 为0.036mm,CaCO3 的粒径r2 为0.13mm 时, CaCO3 颗粒大于MoO3,反应由扩散控制,反应速率随着CaCO3 颗粒度减小而加速,当r2<r1 时存在过量CaCO3,由于产物层变薄,扩散阻力减小,反应由MoO3 粒径升华控制, 并随着MoO3 粒径减小而加剧. 3.答:略. 4.答:1):. 由阿累尼乌斯公式: K=Aexp(-Q/RT)得: Q=R In k2/k1 (T1T2/T2-T1)=In10 *R*776*724/(493-451)=257.189KJ/mol R 故反应激活能为257.189kJ/mol 2):此反应为热分解反应,反应是在反应物与产物层的界面处进行的.由题中所述,反应进行到一定程度后质量损失速率小于线性规律,由此可推测该反应由扩散控制, 即后期由于反应物表层已被先前生成的大量产物层所包裹,导致新产生的气体无法扩散到外界去,从而减缓反应进行. 5.答:由于该固相反应为扩散控制反应,且粉料可视为均状大小球形,故用金斯特林格方程得: 1-2/3G-(1-G) 2/3 =kt G1=0.3/(1+1)=0.15 代入得K=7.45×10 -7 由题中所给条件;t1=3600h 所以当t2=300h 时,G2=0.045 令G=1,则T=1/3k=4.47×10 h 5第九章相变9-1 名词解释: 一级相变,二级相变,玻璃析晶,玻璃分相,均态成核,非均态成核,马氏体相变,亚稳分解,不稳分解. 9-2 为什么成核生长机理的相变过程需要有一定的过冷或过热, 相变才能发生, 在什么情况下需要过冷, 什么情况下需要过热?一般物质具有的最大成核速率的过冷度应该如何求得? 9-3 当一个球形晶核在液态中形成时,其自由能的变化△G=4πr2γ+ 4/3 r3△GV.式中r 为球形晶核的半径;γ为液态中晶核的表面能;△GV 为单位体积晶核形成时释放的体积自由能,求临界半径rk 和临界核化自由能△Gk. 8-4 如果液态中形成一个边长为a 的立方体晶核时, 其自由能△G 将写出什么形式?求出此时晶核的临界立方体边长ak 和临界核化自由能△Gk, 并比较球状晶核时,哪一种形状的△G 值更大,为什么? 9-5由 A 向 B 转变的相变过程中, 单位体积能变化△GV 在1000℃时为-419J/cm3, 在900℃时为-2093J/cm3,设A-B 间界面能为5×10-5J/ cm3,求: (1) (2) 在900℃和1000℃时的临界半径; 在1000℃进行相变时所需的能量. 9-6 试从热力学,动力学和形貌等方面比较亚稳分解和不稳分解这两种分相过程的特点. 9-9 某物质从熔体析晶,当时间分别为1s 和5s 时,测得晶相的体积分数分别为0.1%与11.8%,试用Vβ/V=1-exp(-Ktn)式计算Avrami 指数及其速率常数K. 9-10 如果直径为20μm 的液滴,测得成核速率IV=10 S cm ,如果锗能够过冷227℃,试计算锗的晶-液界面能?(TM=1231K,△H=34.8kJ/mol,ρ =5.35g/cm ) 9-11 举例说明相变理论在科学研究和生产实际中的应用. 1. 2. 答:略答: ,当,过热,过冷度为扩散活化能. 3. 4. 答: 答: , , ,显然立方体晶核形成, ,球形晶核较大. ,过冷;当, 3 -1 -1 -3 5. 答:900℃, ×10-17J =4.778, 1000℃, =2.387nm, 6. 9. 10. 11. 答:略答:n=3,K=10-3 答: 答:略第十章烧结过程10-1 名词解释: 熔融温度,烧结温度,烧结,烧成,液相烧结,固相烧结,晶粒生长,二次再结晶,晶粒极限尺寸,晶粒平均尺寸. 10-2 烧结的模型主要有哪几种?各适用于哪些典型的传质过程? 10-3 若固-气界面能为0.1J/m ,如果用直径为1μm 的粒子组成压块的体积为1cm ,试计算由烧结推动力而产生的能量是多少? 10-4 设有粉料粒度为5μm,若经2h 烧结后,x/r=0.1.如果不考虑晶粒的生长,若烧结至x/r=0.2.并分别通过蒸发-凝聚;体积扩散;粘性流动; 溶解-沉淀传质,则各需要多少时间?若烧结8h,则各传质过程的颈部增长x/r 又是多少? 10-5 如上题粉料的粒度改为16μm,烧结至x/r=0.2,各传质需要多少时间? 若烧结时间为8h,各个过程的x/r 又是多少?从两题计算的结果,讨论粒度与烧结时间对四种传质过程的影响程度? 10-6 下列过程中, 哪些能使烧结强度增加, 而不产生致密化过程?试说明理由.(1) 蒸发-凝聚(2)体积扩散(3)粘性流动(4)晶界扩散(5)表面扩散(6)溶解-沉淀. 10-7 制造透明Al2O3 材料时, 原始粉料粒度为2μm, 烧结至最高温度保温0.5h, 测得晶粒尺寸10μm,试问若保温时间为2h,晶粒尺寸多大?为抑制晶粒生长加入0.1%MgO,此时若保温时间为2h,晶粒尺寸又有多大? 10-8 晶界遇到夹杂物时会出现几种情况,从实现致密化目的考虑,晶界应该如何移动?怎样控制? 10-9 在烧结时,晶粒生长能够促进坯体致密化吗?晶粒生长会影响烧结速率吗?试说明之. 10-10 影响烧结的因素有哪些?最易控制的因素是哪几个? 1.答:名词解释略. 2.答:略. 3.答:烧结推动力而产生的能量是0.6J.提示,先算出粒子个数,再算出气固界面消失的面积. 4.答:根据查得各传质方式公式可得: 时间分别为16h,64h,8h,128h,若只烧结8h,则X/R 分别为0.1×41/3,0.1×4 1/5,0.2,0.1×41/6. 5.答:略6.答:略. 7.答:略3 2。

/register.php?invitecode=7db8407acaii1hHt名词解释【力学】牛顿流体：受力后极易变形，剪切力跟速度梯度成正比符合牛顿定律的的流体；粘性系数：粘性：液体在流动时，在其分子间产生摩擦的性质，粘性大小用粘度表示，是用来表征液体性质相关的阻力因子；热稳定系数：材料承受温度急剧变化而不致破坏的能力，又称抗热震性；热冲击断裂性：材料发生瞬间断裂，抵抗这类破坏的性能；抗热冲击损伤性：热冲击循环作用下，材料表面开裂、剥落并不断扩展，最终破裂或变质，抵抗这类破坏的性能；静态疲劳(亚临界生长)：裂纹在使用应力下，随着时间的推移而缓慢扩展，这种缓慢扩展也称亚临界生长或静态疲劳；动态疲劳：材料在循环应力或渐增应力作用下的延时破坏；Griffith微裂纹理论：实际材料中总存在许多的细小裂纹或缺陷，在外力作用下这些裂纹和缺陷附近产生应力集中现象，当应力达到一定程度时，裂纹就开始扩展而导致断裂，故断裂不是两部分晶体同时沿整个界面拉断，而是裂纹扩展的结果；【热学】声子：晶格振动能量的量子化单元hw称为声子，h为普朗克常数，w 为晶格振动的角频率，对应每一次晶格热振动，晶体内部产生或吸收一个声子，声子是虚拟粒子，是原子激发的形态之一；格波：晶格中的所有原子以相同频率振动而形成的波，或某一个原子在平衡位置附近的振动是以波的形式在晶体中传播形成的波；晶格热振动：晶体中原子以平衡位置为中心不停地振动，是产生热容、热膨胀等现象的物理基础；热膨胀系数：物体由于温度改变而有胀缩现象，其变化能力以等压下，单位温度所导致的体积变化来表示；能流密度：在一定空间范围内，单位面积所取得的或单位重量能源所产生的某种能源的能量或功率，是评价能源的主要指标；热导率(热导系数)：是指单位温度梯度下，单位时间内通过单位垂直面积的热量，单位是w/m2.k；【电学】电流密度：描述电路中某点电流强弱和流动方向的物理量，矢量，大小等于单位时间内通过垂直于电流方向单位面积的电量，正电荷流动方向为正方向；电导率：介质中该量与电场强度之积等于传导电流密度；即电阻率的倒数，物理意义表示物质导电性能；载流子迁移率：载流子在单位电场作用下的平均漂移速率，即载流子在电场作用下运动速度的快慢量度，运动越快迁移率越大；半导体施主能级：一个能级被电子占用时成中性，不被电子占据时带正电；受主能级：一个能级不被电子占据时成中性，被电子占据时带负电；西贝克效应(温差电动势效应)：由于两种不同的电导体或半导体的温度差异而引起两种物质间电压差的热电现象，具体说：半导体材料的两端如果有温度差，则在较高温度区有更多的电子被激发到导带中去，但热电子趋向于扩散到较冷的区域，当这两种效应引起的化学势梯度和电场梯度相等其方向相反时，就达到稳定状态，多数载流子扩散到冷端，产生△V/△T，结果在半导体两端就产生温差电动势；【介介电性质】正温度系数效应PTC：价控型BaTiO3半导体在居里点(正方相↔立方相相变点)附近，电阻率随温度而发生突变的现象，机理是几何半导体陶瓷晶界上具有表面能级，此表面能级可捕获载流子，从而在两边晶粒内产生一层电子损耗层，形成肖特基势垒，该势垒与介电常数有关，当温度高于居里点，介电常数剧减，势垒增加，电阻率增加；压敏效应：a.指对电压变化敏感的非线性电阻效应，即在某一临界电压以下，电阻值非常之高，几乎无电流通过，超过该临界电压，电阻迅速降低，让电流流过。

一、填空硅酸盐结构：岛状结构层状结构组群状结构链状结构架状结构晶格能影响因素：离子半径离子电荷电子层构型固溶体种类:填隙型置换型决定离子晶体结构的基本因素:球体最紧密堆积配位数离子的极化电负性固溶体影响因素：离子尺寸晶体的结构类型电负性非化学计量化合物：阴离子空位型阳离子填隙型阴离子填隙型阴离子空位型位错类型:刃位错螺型位错熔融三种冷却过程：结晶化玻璃化分相玻璃冷却速率的影响因素：过冷度熔体黏度晶核形成速率晶核成长速率玻璃在熔点的黏度越高越易形成玻璃，Tg/Tm〉2/3时易形成玻璃3T图中3T：时间温度转变分子引力：定向力色散力诱导力热缺陷:弗伦克尔缺陷肖特基缺陷固体表面影响因素：表面粗糙度表面微裂纹晶界：小角度晶界大角度晶界润湿现象：附着润湿铺展润湿浸渍润湿润湿的影响因素：粗糙度吸附膜熔体黏度的影响因素:温度熔体组成扩散机制：直接易位环形易位间隙扩散准间隙扩散空位扩散由点缺陷（肖特基和弗兰克尔缺陷）引起的扩散为本征扩散，空位来源于掺杂而引起的扩散为非本征扩散。

黏附的影响因素：润湿性黏附功黏附面的张力相容性和亲和性固相反应速率：化学反应速率扩散速率烧结气氛:还原性氧化性中性固态相变：一级相变二级相变从熔体中析晶的过程分二步完成，首先是成核，然后就是晶体生长过程。

均匀成核的成核速率由受核化位垒影响的成核率因子和受原子扩散影响的成核率因子所决定的。

固体质点扩散的推动力:化学位梯度液－固相变过程的推动力：过冷度烧结过程的推动力：粉料表面能的降低二、名词解释晶格能:在0K时1mol离子化合物的各离子拆散成气体所需的能量配位数：与一个原子或离子直接相邻的原子或离子数离子极化：离子正负电荷的重心发生偏离产生偶极矩的现象同质多晶：物质在不同温度、压力等热力学条件下呈现不同的晶体结构点缺陷：在空间各方向上的尺度远小于晶体、晶粒尺度的缺陷热缺陷：由晶体内部质点热运动而形成的缺陷肖特基缺陷：原子离开平衡位置迁移至晶体表面格点位置,晶体内仅留有空隙的缺陷弗伦克尔缺陷：原子离开平衡位置进入晶格间隙形成的缺陷杂质缺陷:杂质原子进入晶格形成的结构缺陷固溶体：固体作为溶剂溶有其他数量可变的杂质原子，并形成的单一均匀的晶态固体位错：晶体的一维晶格缺陷刃位错：滑移方向与位错线垂直的位错螺位错：滑移方向与位错线平行的位错非化学计量化合物：化合物中不遵循整数比,同种物质组成在一定范围内变动的化合物晶子学说：玻璃中有大量微晶的存在，晶子仅在内部有晶体结构，晶子分散在无定形介质中，向无定形介质过渡中无明显界限无规则网络学说：原子在玻璃和晶体中都形成了连续、三维空间网络结构,它们结构单元为三面体或四面体，但玻璃中的网络无周期性和规则性单键强度：化合物解离能比化合物的配位数的商网络形成剂：单键强度〉335KJ/mol的可形成玻璃的氧化物网络变性剂：单键强度〈250KJ/mol，不能单独形成玻璃的氧化物固体表面能：产生单位新表面所消耗的等温可逆功松弛：表面表面质点通过电子云极化变形来降低表面能的过程晶界应力:在晶界上由于质点排列不规则使质点距离不均匀而形成的微观机械应力气体在固体表面的吸附：气体分子在固体表面上发生的浓集现象，物理吸附无电子转移,化学吸附有电子转移，形成化学键表面张力:由表面层分子引力不均引起的作用于物质表面使表面积缩小的力接触角：固固之间或固液之间接触时产生的夹角晶界结构：不同生长方向的晶粒在相遇时形成的具有一定特征的边界结构润湿角：固液接触时，固相水平线与液相的切线相交的夹角孪晶界：两个晶体沿一个公共晶面构成镜面对称的位向关系扩散通量:单位时间内垂直通过扩散方向x的单位面积的物质流量无序扩散：原子或离子的无规则扩散迁移运动晶界扩散：沿边界或界面发生的扩散表面扩散:在晶体表面发生的本征扩散：仅仅由本身的点缺陷作为迁移载体的扩散非本征扩散：由杂质引起的缺陷进行的扩散自扩散：纯组分晶体中，不依赖浓度梯度的扩散互扩散：两种组分扩散通量大小相等,方向相反的扩散方式稳定扩散：扩散物质的浓度不随时间变化的扩散过程不稳定扩散：扩散物质的浓度随时间变化的扩散过程扩散活化能:一级相变:临界温度下自由能关于温度、压力的一次导数不连续的一类相变二级相变：临界温度下自由能一次导数连续而二次导数不连续的一类相变玻璃析晶：当玻璃熔体冷却在析晶温度范围时，由于晶核形成速率和晶体生长速率较大而导致玻璃析出晶体的过程。

1.热容：热容是使材料温度升高1K所需的热量。

公式为C=ΔQ/ΔT=dQ/dT (J/K)；它反映材料从周围环境中吸收热量的能力，与材料的质量、组成、过程、温度有关。

在加热过程中过程不同分为定容热容和定压热容。

2.比热容：质量为1kg的物质在没有相变和化学反应的条件下升高1K所需的热量称为比热容每个物质中有两种比热容，其中c p＞c v，c v不能直接测得。

3.摩尔热容：1mol的物质在没有相变或化学反应条件下升高1K所需的能量称为摩尔热容，用Cm表示，单位为J/(mol·K)4.热容的微观物理本质：材料的各种性能（包括热容）的物理本质均与晶格热振动有关。

5.热容的实验规律：1.对于金属:2.对于无机材料（了解）1.符合德拜热容理论，但是德拜温度不同，它取决于键的强度、材料的弹性模量、熔点等。

2.对于绝大多数氧化物，碳化物，摩尔热容都是从低温时一个最低值增到到1273K左右近似于3R，温度进一步升高，摩尔热容基本没有任何变化。

3.相变时会发生摩尔热容的突变4.固体材料单位体积热容与气孔率有关，多孔材料质量越小，热容越小。

因此提高轻质隔热砖的温度所需要的热量远低于致密度的耐火砖所需的热量。

6.经典理论传统理论不能解决低温下Cv的变化，低温下热容随温度的下降而降低而下降，当温度接近0K时热容趋向于07.量子理论1.爱因斯坦模型三个假设：1.谐振子能量量子化2.每个原子是一个独立的谐振子3.所有原子都以相同的频率振动。

爱因斯坦温度：爱因斯坦模型在T >> θE 时，Cv，m=3R,与实验相符合，在低温下，T当T << θE时Cv，m比实验更快趋于0，在T趋于0时，Cv,m也趋于零。

爱因斯坦模型不足之处在于：爱因斯坦模型假定原子振动不相关，且以相同频率振动，而实际晶体中，各原子的振动不是彼此独立地以同样的频率振动，而是原子间有耦合作用，点阵波的频率也有差异。

温度低尤为明显2.德拜模型德拜在爱因斯坦的基础上，考虑了晶体间的相互作用力，原子间的作用力遵从胡克定律，固体热容应是原子的各种频率振动贡献的总和。

1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力，若直径拉细至2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。

解：根据题意可得下表由计算结果可知：真应力大于名义应力，真应变小于名义应变。

1-6试分别画出应力松弛和应变蠕变与时间的关系示意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。

解：Maxwell 模型可以较好地模拟应力松弛过程： V oigt 模型可以较好地模拟应变蠕变过程：以上两种模型所描述的是最简单的情况，事实上由于材料力学性能的复杂性，联组合而成的复杂模型。

如采用四元件模型来表示线性高聚物的蠕变过程等。

1-11一圆柱形Al 2O 3晶体受轴向拉力F ，若其临界抗剪强度τf 为135 MPa,的最小拉力值，并求滑移面的法向应力。

解：1-18 融熔石英玻璃的性能参数为：E=73 Gpa ；γ=1.56 J/m 2；理论强度σth=28 Gpa 。

如材料中存在最大长度为2μm 裂，且此内裂垂直于作用力方向，计算由此导致的强度折减系数。

2c=2μm c=1*10-6mcE c πγσ2==GPa269.010*1*14.356.1*10*73*269=-强度折减系数=1-0.269/28=0.991-20 一陶瓷三点弯曲试件，在受拉面上于跨度中间有一竖向切口如图。

如果E=380 Gpa ，μ=0.24，求K Ic 值，设极限荷载达50Kg 。

计算此材料的断裂表面能。

解 c/W=0.1, Pc=50*9.8N ,B=10, W=10，S=40 代入下式：])/(7.38)/(6.37)/(8.21)/(6.4)/(9.2[2/92/72/52/32/12/3W c W c W c W c W c BW SP K c IC +-+-==]1.0*7.381.0*6.371.0*8.211.0*6.41.0*9.2[010.0*1040*8.9*502/92/72/52/32/12/3+-+- =62*（0.917-0.145+0.069-0.012+0.0012）=1.96*0.83==1.63Pam1/2212μγ-=E K IC 28.3)10*380*2/(94.0*)10*63.1(2)1(92622==-=EK IC μγJ/m 21-22 一陶瓷零件上有一垂直于拉应力的边裂，如边裂长度为：（1）2mm;(2)0.049mm;(3)2 um, 分别求上述三种情况下的临界应力。

《材料物理性能》第一章材料的力学性能1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力，若直径拉细至2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。

解：由计算结果可知：真应力大于名义应力，真应变小于名义应变。

1-5一陶瓷含体积百分比为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。

若该陶瓷含有5 %的气孔，再估算其上限和下限弹性模量。

解：令E 1=380GPa,E 2=84GPa,V 1=0.95,V 2=0.05。

则有当该陶瓷含有5%的气孔时，将P=0.05代入经验计算公式E=E 0(1-1.9P+0.9P 2)可得，其上、下限弹性模量分别变为331.3 GPa 和293.1 GPa 。

0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =⨯==-σ名义应力0851.0100=-=∆=A A l l ε名义应变)(99510524.445006MPa A F T =⨯==-σ真应力)(2.36505.08495.03802211GPa V E V E E H =⨯+⨯=+=上限弹性模量)(1.323)8405.038095.0()(112211GPa E V E V E L =+=+=--下限弹性模量1-11一圆柱形Al 2O 3晶体受轴向拉力F ，若其临界抗剪强度τf 为135 MPa,求沿图中所示之方向的滑移系统产生滑移时需要的最小拉力值，并求滑移面的法向应力。

解：1-6试分别画出应力松弛和应变蠕变与时间的关系示意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。

解：Maxwell 模型可以较好地模拟应力松弛过程：V oigt 模型可以较好地模拟应变蠕变过程：以上两种模型所描述的是最简单的情况，事实上由于材料力学性能的复杂性，我们会用到用多个弹簧和多个黏壶通过串并联组合而成的复杂模型。