《定积分的概念》教学反思

芯衣州星海市涌泉学校教案35定积分的定义与性质一、课前检测1.221(21)x x dx ++=⎰；2.由抛物线2y x =与直线2y x =-围成的平面图形的面积为.3.用力把弹簧从平衡位置拉长10 cm,此时用的力是200N ，变力F 做的功W 为J.二、知识梳理1.定积分的概念：设函数()f x 在区间[,]a b 上有定义，将区间[,]a b 等分成n 分小区间，每个小区间长度为x ∆(x ∆=),在每个小区间上取一点，依次为12,,,,i n x x x x ，作和n S =.假设x ∆无限趋近于0(亦即n 趋向于+∞)时，n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分，记为S =，其中称为被积函数，称为积分区间，称为积分下限，称为积分上限，解读：2.微积分根本定理：对于被积函数()f x ，假设()()F x f x '=，那么()b a f x dx ⎰=. 解读：3.定积分的运算性质：⑴()b a kf x dx ⎰=；⑵[()()]b a f x g x dx ±=⎰； ⑶()b a f x dx =⎰.()a c b << 解读：4.定积分的几何意义：在区间[,]a b 上曲线与x 轴所围成图形面积的(即x 轴上方的面积减去x 轴下方的面积)；⑴当()f x 在区间[,]a b 上大于0时，()ba f x dx ⎰表示由直线,(),0x a xb a b y ==≠=和曲线所围成的曲边梯形的面积，这也是定积分的几何意义.⑵当()f x 在区间[,]a b 上小于0时，()ba f x dx ⎰表示由直线,(),0x a xb a b y ==≠=和曲线所围成的曲边梯形的面积的.⑶当()f x 在区间[,]a b 上有正有负时，()ba f x dx ⎰表示介于直线,()x a xb a b ==≠之间x 轴之上、之下相应的曲边梯形的面积的.解读：5.定积分在物理中的应用：⑴匀变速运动的路程公式，作变速直线运动的物体所经过的路程s ，等于其速度函数()v t 在时间是是区间[,]a b 上的定积分，即s =.⑵变力做功公式，一物体在变力()F x (单位：N )的作用下作直线运动，假设物体沿着与F 一样的方向从x a =挪动到()x b a b =<(单位：m )，那么力F 所作的功为W =.解读：三、典型例题分析例1求定积分⑴21⎰(2x2－)dx ；⑵32⎰(＋)2dx ；〔3〕30π⎰(sinx －sin2x)dx ；小结与拓展：变式训练：求定积分：222||x x dx --⎰；定积分的几何意义：例2求曲多边形的面积〔1〕如图，函数y ＝－x2＋2x ＋1与y ＝1相交形成一个闭合图形(图中的阴影部分)，那么该闭合图形的面积是()A ．1B.C.D ．2〔2〕函数y ＝x2与y ＝kx(k ＞0)的图象所围成的阴影部分(如下列图)的面积为，那么k ＝________.变式训练：f(x)为偶函数且60⎰f(x)dx ＝8，那么66-⎰f(x)dx 等于()A ．0B ．4C ．8D ．16小结与拓展：定积分在物理中的应用例3一质点运动时速度与时间是是的关系为v(t)＝t2－t ＋2，质点作直线运动，那么此物体在时间是是[1,2]内的位移为()A.B.C.D.变式训练：一辆汽车的速度—时间是是曲线如下列图，那么该汽车在这一分钟内行驶的路程为_______米． 小结与拓展：四、归纳与总结〔以学生为主，师生一一共同完成〕1.知识：2.思想与方法：3.易错点：4.教学反思〔缺乏并查漏〕：x 01o x y3。

矩 形 的 面积 ？
①知 识 目标 ： 了解定 积分 的实 际背景 ， 了解 “ 以直代 曲” “ 、逼 近” 的思想 方法 ； 理解 定积 分 的概念 ， 掌握 用定 义求定 积分 的方
法。
②能 力 目标 ： 通过教 学培养学 生分析 问题 ， 决实 际问题 的 解 能力 ， 培养学生运用知识 的能力 ， 培养学生归纳 、 象和概括的能 抽 力。 ③情感 目标 ： 通过定 积分概念 的学 习， 引导学 生从现实 例子 出发 ， 建立“ 分割 、 近似代替 、 和 、 求 取极 限” 的定积分思想 ， 体会数 学 中的辩证思想 。 １ 教学重点与难点 ． ２ 教 学 重 点 ： 积 分 的 基 本 思 想 方 法 ， 积 分 概 念 的形 成 过 程 。 定 定 教学难点 ： 定积分概念的理解 。 对 下面为 了讲清重点 、 难点 ， 使学生 能达到本节课 设定 的 目标 ， 再从教法和学法上谈谈 。 ２ 教学 策略 ２１ 教学手段与方法 ． 定积分 思想是较抽 象 的， 本节 以教师引 导为主 ， 学生 自主探 索为辅的方式 。在教学 中采用黑板和 多媒体相 结合 的方式 ， 发 激 学生 的学 习兴趣 ， 并加深对 “ 分割 、 近似 代替 、 求和 、 取极 限” 的理
解。 ２ 教 学对 象 与 内 容 ． ２
如 图 ２ 图 ３图 ４ 、 、 。一方面 ， 学生分组讨论 ， 具体数 ｎ ４ ｎ． 取 ＝ ，－ ６ ｎ ９ 上 台画图 ； ，＝ ， 另一方面 ， 借助多媒体 引导学生观察 、 分析 、 比 较、 归纳 ， 体会逼 近思想 。从 图 中可 以看 出 ， 小矩形 越多 ， 形面 矩 积越接近 曲边梯形 面积。将 曲边梯形 的面积转化 为矩形面积 ， 帮 助学生体会 由已知探求未 知的数学方法 ， 培养学生 的动手操作能

定积分概念的课程设计一、教学目标本节课的教学目标是让学生掌握定积分的概念及其应用。

具体来说，知识目标包括：了解定积分的定义、性质和计算方法；理解定积分在实际问题中的应用。

技能目标则要求学生能够运用定积分解决简单的问题，如计算曲线下的面积、求解弯曲物体的质心等。

情感态度价值观目标则是培养学生的数学思维能力，提高他们对数学的兴趣和自信心。

二、教学内容本节课的教学内容主要包括定积分的定义、性质和计算方法。

首先，引导学生回顾不定积分的基本概念，为学生引入定积分做铺垫。

然后，详细讲解定积分的定义，通过实例让学生理解定积分的概念。

接着，介绍定积分的性质，如线性性质、保号性等，并通过例题让学生掌握这些性质的应用。

最后，讲解定积分的计算方法，如牛顿-莱布尼茨公式、分部积分法等，并通过练习让学生熟练运用这些方法。

三、教学方法为了达到本节课的教学目标，我将采用多种教学方法相结合的方式进行教学。

首先，运用讲授法，清晰、系统地讲解定积分的概念、性质和计算方法。

其次，采用讨论法，引导学生分组讨论定积分在实际问题中的应用，激发学生的思考。

此外，还将运用案例分析法，通过分析具体案例，让学生更好地理解定积分的应用。

最后，适时进行实验法，让学生在实验中感受定积分的作用，提高他们的实践能力。

四、教学资源为了支持本节课的教学内容和教学方法的实施，我将准备以下教学资源：教材、参考书、多媒体资料、实验设备。

教材和参考书将作为主要教学资源，为学生提供系统的理论知识。

多媒体资料则用于辅助教学，以图片、动画等形式展示定积分的概念和应用，增强学生的学习兴趣。

实验设备则用于进行实验教学，让学生在实践中掌握定积分的方法。

五、教学评估为了全面、客观地评估学生的学习成果，本节课的评估方式包括平时表现、作业和考试三个部分。

平时表现主要考察学生在课堂上的参与程度、提问回答等情况，以鼓励学生积极思考和提问。

作业则包括定积分的计算练习和应用问题，以此检验学生对知识的掌握程度。

定积分与微积分基本定理复习（课堂导学案）班级：；姓名：；学习小组组；号课前准备·明确目标【目标导引】1. 学生加深对定积分与微积分基本定理相关知识的理解。

2. 学生能够利用定积分相关知识解决实际应用问题，会用微积分基本定理解决相关问题。

3. 通过小组合作的形式提升学生分析解决问题的能力。

自主学习·求知探究知识梳理教与学感悟1．定积分中，a，b分别叫做积分下限与积分上叫做积分区间，f(x)叫做被积函数，x叫做积分变量，f(x)d x∫421 x dA.176 B.143 C.136 D.116∫101－x2d＝1x，直线＋52所围成的封闭图形的面积为⎭⎫＋1x2π⎰sin2x2d(4)利用牛顿—莱布尼兹公式求出各个定积分的值；(5)计算原始定积分的值．考点二利用定积分的几何意义求定积分[例2]∫10－x2＋2x d x＝________.变式：在本例中，改变积分上限，求∫20－x2＋2x d x的值．———————————————————利用几何意义求定积分的方法(1)当被积函数较为复杂，定积分很难直接求出时，可考虑用定积分的几何意义求定积分．(2)利用定积分的几何意义，可通过图形中面积的大小关系来比较定积分值的大小．考点三：利用定积分求平面图形的面积[例3](2014·高考)由曲线y＝x，直线y＝x－2及y轴所围成的图形的面积为()A.103B．4 C.163D．6变式训练：若将“y＝x－2”改为“y＝－x＋2”，将“y轴”改为“x轴”，如何求解？———————————————————利用定积分求曲边梯形面积的步骤(1)画出曲线的草图．(2)借助图形，确定被积函数，求出交点坐标，确定积分的上、下限．(3)将“曲边梯形”的面积表示成若干个定积分的和或差．(4)计算定积分，写出答案．考点四：定积分在物理中的应用[例4]列车以72 km/h的速度行驶，当制动时列车获得加速度a＝－0.4 m/s2，问列车应在进站前多长时间，以及离车站多远处开始制动？1个定理——微积分基本定理由微积分基本定理可知求定积分的关键是求导函数的原函数，由此可知，求导与积分是互为逆运算．3条性质——定积分的性质(1)常数可提到积分号外；(2)和差的积分等于积分的和差； (3)积分可分段进行．3个注意——定积分的计算应注意的问题(1)若积分式子中有几个不同的参数，则必须分清谁是积分变量； (2)定积分式子中隐含的条件是积分上限不小于积分下限； (3)面积非负， 而定积分的结果可以为负.易误警示——利用定积分求平面图形的面积的易错点[典例] (2013·上海高考)已知函数y ＝f (x )的图象是折线段ABC ，其中A (0,0)，B ⎝⎛⎭⎫12，5，C (1,0)．函数y ＝xf (x )(0≤x ≤1)的图象与x 轴围成的图形的面积为________．[易误辨析]1．本题易写错图形面积与定积分间的关系而导致解题错误． 2．本题易弄错积分上、下限而导致解题错误，实质是解析几何的相关知识和运算能力不够致错．3．解决利用定积分求平面图形的面积问题时，应处理好以下两个问题： (1)熟悉常见曲线，能够正确作出图形，求出曲线交点，必要时能正确分割图形；(2)准确确定被积函数和积分变量．变式训练：1．由曲线y ＝x 2，y ＝x 3围成的封闭图形面积为( ) A.112 B.14 C.13D.7122．(2014·高考)设a >0.若曲线y ＝x 与直线x ＝a ，y ＝0所围成封闭图形的面积为a 2，则a ＝________.本节学习感悟：定积分与微积分基本定理（教案设计部分）设计人： 审核：吕厚杰【教学目标】1. 学生加深对定积分与微积分基本定理相关知识的理解。

§1.5.1曲边梯形的面积一、教学目标：理解求曲边图形面积的过程：分割、以直代曲、逼近，感受在其过程中渗透的思想方法. 二、教学重难点重点: 掌握过程步骤：分割、以直代曲、求和、逼近（取极限）. 难点: 对过程中所包含的基本的微积分 “以直代曲”的思想的理解. 三、教学过程： 1、创设情景我们学过如何求正方形、长方形、三角形等的面积，这些图形都是由直线段围成的。

那么，如何求曲线围成的平面图形的面积呢？这就是定积分要解决的问题。

定积分在科学研究和实际生活中都有非常广泛的应用。

本节我们将学习定积分的基本概念以及定积分的简单应用，初步体会定积分的思想及其应用价值。

一个概念：如果函数()y f x =在某一区间I 上的图像是一条连续不断的曲线，那么就把函数()y f x =称为区间I 上的连续函数．（不加说明，下面研究的都是连续函数） 2、新课讲授问题：如图，阴影部分类似于一个梯形，但有一边是曲线()y f x =的一段，我们把由直线,(),0x a x b a b y ==≠=和曲线()y f x =所围成的图形称为曲边梯形．如何计算这个曲边梯形的面积？例1：求图中阴影部分是由抛物线2y x =，直线1=x 以及x 轴所围成的平面图形的面积S 。

思考：（1）曲边梯形与“直边图形”的区别？（2）能否将求这个曲边梯形面积S 的问题转化为求“直边图形”面积的问题？ 分析：曲边梯形与“直边图形”的主要区别：曲边梯形有一边是曲线段，“直边图形”的所有边都是直线段．“以直代曲”的思想的应用．0.1把区间[]0,1分成许多个小区间，进而把区边梯形拆为一些小曲边梯形，对每个小曲边梯形“以直代取”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值，对这些近似值求和，就得到曲边梯形面积的近似值．分割越细，面积的近似值就越精确。

当分割无限变细时，这个近似值就无限逼近所求曲边梯形的面积S ．也即：用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积． 解： （1）．分割 在区间[]0,1上等间隔地插入1n -个点，将区间[]0,1等分成n 个小区间： 10,n ⎡⎤⎢⎥⎣⎦，12,n n ⎡⎤⎢⎥⎣⎦，…，1,1n n -⎡⎤⎢⎥⎣⎦记第i 个区间为1,(1,2,,)i i i n n n -⎡⎤=⎢⎥⎣⎦L ，其长度为 11i i x n n n-∆=-= 分别过上述1n -个分点作x 轴的垂线，从而得到n 个小曲边梯形，他们的面积分别记作：1S ∆，2S ∆，…，n S ∆ 显然，1nii S S ==∆∑（2）近似代替记()2f x x =，如图所示，当n 很大，即x ∆很小时，在区间1,i i n n -⎡⎤⎢⎥⎣⎦上，可以认为函数()2f x x =的值变化很小，近似的等于一个常数，不妨认为它近似的等于左端点1i n-处的函数值1i f n -⎛⎫ ⎪⎝⎭，从图形上看，就是用平行于x 轴的直线段近似的代替小曲边梯形的曲边（如图）．这样，在区间1,i i n n -⎡⎤⎢⎥⎣⎦上，用小矩形的面积i S '∆近似的代替i S ∆，即在局部范围内“以直代取”，则有 211i i i i S S f x x n n --⎛⎫⎛⎫'∆≈∆=∆=∆ ⎪ ⎪⎝⎭⎝⎭g g 211(1,2,,)i i n n n-⎛⎫== ⎪⎝⎭g L ①（3）求和由①，上图中阴影部分的面积n S 为2111111nnnn i i i i i i S S f x n n n ===--⎛⎫⎛⎫'∆=∆=∆= ⎪ ⎪⎝⎭⎝⎭∑∑∑g g=22111110n n n n n n-⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭g g L g=()22231121n n⎡⎤+++-⎣⎦L =()()312116n n n n -- =1111132n n ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭从而得到S 的近似值 1111132n S S n n ⎛⎫⎛⎫≈=-- ⎪⎪⎝⎭⎝⎭（4）取极限分别将区间[]0,1等分8，16，20，…等份（如图），可以看到，当n 趋向于无穷大时，即x ∆趋向于0时，1111132n S n n ⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭趋向于S ，从而有 1111111lim lim lim 11323nn n n n i i S S f n n n n →∞→∞→∞=-⎛⎫⎛⎫⎛⎫===--= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑g 从数值上的变化趋势：3、求曲边梯形面积的四个步骤:第一步：分割．在区间[],a b 中任意插入1n -各分点，将它们等分成n 个小区间[]1,i i x x -()1,2,,i n =L ，区间[]1,i i x x -的长度1i i i x x x -∆=-，第二步：近似代替，“以直代取”。

高中数学定积分教案【篇一：《定积分》教学设计与反思】《定积分》教学设计与反思学习目标2、通过实例体会用微积分基本定理求定积分的方法．教学重点：通过探究变速直线运动物体的速度与位移的关系，使学生直观了解微积分基本定理的含义，并能正确运用基本定理计算简单的定积分．教学难点：了解微积分基本定理的含义．一、自主学习：1．定积分的定义：，2．定积分记号：思想与步骤几何意义．3．用微积分基本定理求定积分二、新知探究新知1：微积分基本定理：背景：我们讲过用定积分定义计算定积分,但如果要计算，其计算过程比较复杂，所以不是求定积分的一般方法。

我们必须寻求计算定积分的新方法，也是比较一般的方法。

探究问题1：变速直线运动中位置函数s(t)与速度函数v(t)之间的联系设一物体沿直线作变速运动，在时刻t时物体所在位移为s(t),速度为v(t)（），则物体在时间间隔内经过的位移记为，则一方面：用速度函数v(t)在时间间隔求积分，可把位移 =另一方面：通过位移函数s（t）在的图像看这段位移还可以表示为探究问题2：位移函数s(t)与某一时刻速度函数v(t)之间的关系式为上述两个方面中所得的位移可表达为上面的过程给了我们启示上式给我们的启示：我们找到了用的原函数（即满足）的数值差来计算在上的定积分的方法。

定理如果函数是上的连续函数的任意一个原函数，则该式称之为微积分基本公式或牛顿—莱布尼兹公式。

它指出了求连续函数定积分的一般方法，把求定积分的问题，转化成求原函数的问题，是微分学与积分学之间联系的桥梁。

它不仅揭示了导数和定积分之间的内在联系，同时也提供计算定积分的一种有效方法。

例1．计算下列定积分：新知2：用定积分几何意义求下列各式定积分：若求新知3：用定积分求平面图形的面积1、计算函数在区间的积分2、计算函数在区间的积分3、求与在区间围成的图形的面积通过此题的计算你发现了什么？教学反思本课的教学设计，是在新课程标准理念指导下，根据本班学生实际情况进行设计的。

定积分的概念教学反思 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】《定积分的概念》教学反思渭南市吝店中学曹茹军本节课是高二新授课，是选修2-2第四章第一节的内容：《定积分的概念》课程内容安排为一课时。

此内容要求学生在充分认识导数的基础上，通过运用积分手段解决曲边梯形的面积问题，从而借助于几何直观体会定积分的基本思想，了解定积分的概念，能用定积分法求简单的定积分．理解掌握定积分的几何意义和性质；认识到数学知识的实用价值。

新课标要求我们在教学过程中要着重培养学生的探究、发现、创新等方面的能力。

学习的全过程需要学生的参与，学生是学习的主体和中心。

围绕这个宗旨，我在课堂内容的编排上作了一定的思考。

在内容编排上，我基本遵循由易到难的过程，从最基本的，学生所熟知的前课知识开始引入，由浅入深的引导学生加以足够地探究，使学生的发现变得自然而水到渠成。

同时对于学生可能的探究结果留有足够的空间，充分肯定学生的创新发现，对于学生考虑不到的地方加以补充、引导、完善，并留出一定课后思考得余地。

在问题设置上，尽量让学生能通过自己的努力探索独立完成，通过独立思考展示与合作探究展示相结合，让其承担起引导思考与解释的重任。

我想，一堂好的示范课，不应该只是一次简单的表演与展示，如果在上课之前反复编排到一词一句，会让学生疲惫，听课老师觉得虚假而没有了讨论与交流的兴致，这其实也是对听课老师的一种不尊重的表现。

因此我按照正常的教学进度，以便学生在课堂上有充分的暴露与发现的机会，当然这样一来对于老师的临场应变要求会更高，我想这也应该是一个合格教师的基本素养吧。

当然这节课还有一些不足之处，由于没有在课前提前向学生透漏问题，想要在课堂上反应学生的真实水平，因此学生回答问题时不够全面，导致学生回答的次数较多且有些同学比较拖沓，出现了上课前松后紧的遗憾。

我觉得这样的课堂模式导学案的设置是很重要的，在今后的教学中我会不断的完善自己的教学技能，提高自己的业务水平。

课后反思
通过本堂课设计，应该能充分调动学生的积极性，明确定积分在几何中的应用的解题原理和方法。

学生能应用定积分求出某些平面图形的面积，知道某些简单的定积分表达式的几何意义．通过学习，对“面积”的概念有较为完整的认识．知道在求平面图形的面积时，定积分是一种普通适用的方法．培养了学生应用数学的意识和能力，进一步培养逻辑思维能力，以及用定积分的基本思想解决问题的能力。

不足之处：在课堂的调控中，老师讲解仍然过多，学生的动手能力还有欠缺，学生的主题意识还有待提高。

人教高中数学微积分教案
教学内容：定积分的概念与性质
教学目标：让学生了解定积分的概念与性质，掌握定积分的计算方法，培养学生分析和解决实际问题的能力。

教学重点：定积分的概念与性质，定积分的计算方法
教学难点：定积分在实际问题中的应用
教学步骤：
一、导入：通过引入一个实际问题来引起学生的兴趣，如某物体在一段时间内的运动速度问题。

二、概念学习：介绍定积分的概念，定义定积分，讲解定积分的性质和计算方法。

三、案例分析：通过几个特定例题，让学生掌握计算定积分的方法，并引导学生运用定积分解决实际问题。

四、练习检测：布置一些定积分的计算题目和应用题目，让学生熟练掌握定积分的相关知识。

五、课堂总结：回顾定积分的概念、性质和计算方法，强调定积分在实际问题中的应用，并鼓励学生多加练习，提高解决问题的能力。

六、作业布置：布置定积分相关的作业，巩固学生的知识。

教学反思：本节课通过引入实际问题、概念学习、案例分析和练习检测等教学方法，有效地帮助学生掌握定积分的相关知识，并培养他们解决问题的能力。

在今后的教学中，需要更多地引导学生实际操作，注重实践性教学，促进学生能力的提升。

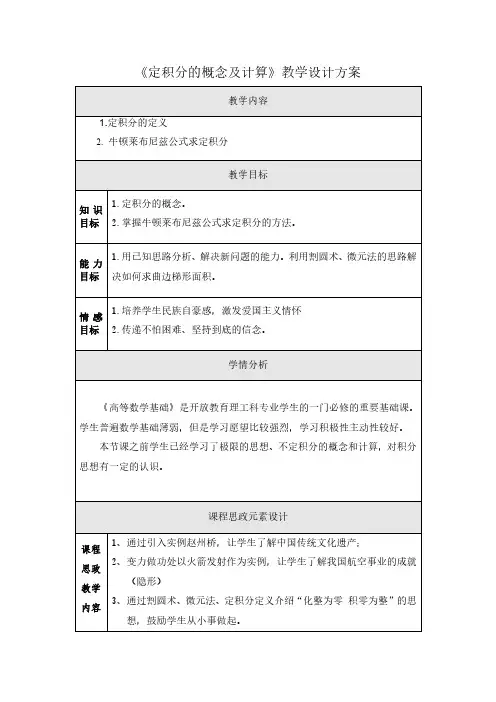
《定积分的概念及计算》教学设计方案
4、通过牛顿莱布尼兹世纪之争，传输不同途径均能达到最后目标，鼓
励学生坚持不懈
5、通过弧、弦、微分、积分概念，讲解矛盾两方面对立统一
教学方法教学举措目标1：培养学生民族自豪感，激发爱国主义情怀。

方法及措施：通过引入的实例让学生去了解中国传统工艺成就和现代航天事业的发展（介绍不易过多，引入即可，学生自己体会）
目标2：拓宽学生分析问题、解决问题的思路，进而提高解决问题的能力。

方法及措施：一是通过割圆术、微元法、定积分定义介绍“化整为零积零为整”的思想，进一步介绍这种思路方法实际应用。

二是通过牛顿、莱布尼兹世纪之争，最后的结论，让学生体会“殊途同归”，激发学生坚持不懈终将取得胜利的信心。

三是通过弧、弦、微分、积分概念，了解矛盾两方面对立统一规律。

定积分的概念一、教学目标：知识与技能：1．了解“以直代曲”、“以不变代变”的思想方法．2．会求曲边梯形的面积和汽车行驶的路程．过程与方法：通过对曲边梯形面积问题的求解及变速直线运动路程的运算，体会“以直代曲”、“以不变代变”的思想方法．情感、态度与价值：让学生探索、发现数学知识和掌握数学知识的内在规律的过程中不，不断获得成功积累愉快的体验，不断增进学习数学的兴趣，同时还通过探索这一活动培养学生善于和他人合作的精神.二、教学重点、难点重点：求曲边梯形的面积和汽车行驶的路程．难点：了解“以直代曲”、“以不变代变”的思想方法．三、教学模式与教法、学法教学模式：本课采用“探究——发现”教学模式．教师的教法：利用多媒体辅助教学，突出活动的组织设计与方法的引导．“抓三线”，即(一)知识技能线（二）过程与方法线（三）能力线.“抓两点”,即一抓学生情感和思维的兴奋点，二抓知识的切入点.学法：突出探究、发现与交流．四、教学过程（一）温故知新任何一个平面图形都有面积，其中矩形、正方形、三角形、平行四边形、梯形等平面多边形的面积，可以利用相关公式进行计算．如图所示的平面图形，是由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的，称之为曲边梯形，如何计算这个曲边梯形的面积呢？（二）探索新知探究点一 求曲边梯形的面积 思考1 如何计算下列两图形的面积？答 ①直接利用梯形面积公式求解．②转化为三角形和梯形求解．问题 如图，如何求由抛物线y ＝x 2与直线x ＝1，y ＝0所围成的平面图形的面积S? 思考2 图中的图形与我们熟悉的“直边图形”有什么区别？思考3 能否将求曲边梯形的面积问题转化为求“直边图形”的面积问题？(归纳主要步骤)答 (如图)可以通过把区间[0,1]分成许多小区间，将曲边梯形拆分为一些小曲边梯形，对每个小曲边梯形“以直代曲”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值，对这些近似值进行求和，就得到曲边梯形面积的近似值，随着拆分越来越细，近似程度会越来越好． S n ＝∑ni ＝1S i ≈∑ni ＝1(i －1n )2·Δx ＝∑n i ＝1(i －1n )2·1n (i ＝1,2，…，n )＝0·1n ＋(1n )2·1n ＋…＋(n －1n )2·1n＝1n 3[12＋22＋…＋(n －1)2]＝13(1－1n )(1－12n )． ∴S ＝lim n →∞S n ＝lim n →∞ 13(1－1n )(1－12n )＝13.求曲边梯形的面积可以通过分割、近似代替、求和、取极限四个步骤完成．思考4 在“近似代替”中，如果认为函数f (x )＝x 2在区间[i －1n ，i n ](i ＝1,2，…，n )上的值近似地等于右端点in 处的函数值f (i n )，用这种方法能求出S 的值吗？若能求出，这个值也是13吗？取任意ξi ∈[i －1n ，i n ]处的函数值f (ξi )作为近似值，情况又怎样？其原理是什么？答 以上方法都能求出S ＝13.我们解决此类问题的原理是“近似代替”和“以直代曲”，在极限状态下，小曲边梯形可以看做小矩形．例1 求由直线x ＝0，x ＝1，y ＝0和曲线y ＝x 2所围成的图形的面积．过各分点作x 轴的垂线，把曲边梯形分成n 个小曲边梯形，它们的面积分别记作ΔS 1，ΔS 2，…，ΔS n . (2)近似代替在区间[i －1n ，i n ](i ＝1,2，…，n )上，以i －1n 的函数值⎝⎛⎭⎫i －1n 2作为高，小区间的长度Δx ＝1n 作为底边的小矩形的面积作为第i 个小曲边梯形的面积，即ΔS i ≈(i －1n )2·1n .(3)求和曲边梯形的面积近似值为S ＝∑n i ＝1S i ≈∑n i ＝1(i －1n )2·1n ＝0·1n ＋(1n )2·1n ＋(2n )2·1n ＋…＋(n －1n )2·1n ＝1n 3[12＋22＋…＋(n －1)2]＝13(1－1n )(1－12n)． (4)取极限 曲边梯形的面积为 S ＝lim n →∞ 13(1－1n )(1－12n )＝13. 反思与感悟 求曲边梯形的思想及步骤：(1)思想：以直代曲、逼近；(2)步骤：分割→近似代替→求和→取极限；(3)关键：近似代替；(4)结果：分割越细，面积越精确． 跟踪训练1 求由抛物线y ＝x 2与直线y ＝4所围成的曲边梯形的面积．解 ∵y ＝x 2为偶函数，图象关于y 轴对称，∴所求曲边梯形的面积应为抛物线y ＝x 2(x ≥0)与直线x ＝0，y ＝4所围图形面积S 阴影的2倍，下面求S 阴影．由⎩⎪⎨⎪⎧y ＝x 2x ≥0y ＝4，得交点为(2,4)，如图所示，先求由直线x ＝0，x ＝2，y ＝0和曲线y ＝x 2围成的曲边梯形的面积．(1)分割将区间[0,2] n 等分，则Δx ＝2n ， 取ξi ＝2i －1n. (2)近似代替求和 S n ＝∑ni ＝12i －1n ]2·2n ＝8n 3[12＋22＋32＋…＋(n －1)2]＝83(1－1n )(1－12n)． (3)取极限S ＝lim n →∞S n ＝lim n →∞ 83(1－1n )(1－12n )＝83. ∴所求平面图形的面积为S 阴影＝2×4－83＝163.∴2S 阴影＝323，即抛物线y ＝x 2与直线y ＝4所围成的图形面积为323。

4.5.3定积分的概念一、目标导学 教学目标：1.通过求曲边梯形的面积和变速直线运动的路程，了解定积分的背景；2.借助于几何直观定积分的基本思想，了解定积分的概念，能用定积分法求简单的定积分．3.理解掌握定积分的几何意义；教学重点：定积分的概念、定积分法求简单的定积分、定积分的几何意义． 教学难点：定积分的概念、定积分的几何意义．教学过程： 二、自主探究 复习：1． 回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法，解决步骤：2．对这四个步骤再以分析、理解、归纳，找出共同点． 三、交流点拨1．定积分的概念 一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆（b ax n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式：11()()nnn i i i i b aS f x f nξξ==-=∆=∑∑如果x ∆无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。

记为：()ba S f x dx =⎰其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间，b 积分上限，a 积分下限。

说明：（1）定积分()baf x dx ⎰是一个常数，即n S 无限趋近的常数S （n →+∞时）称为()baf x dx ⎰，而不是n S ．（2）用定义求定积分的一般方法是：①分割：n 等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和：1()ni i b af nξ=-∑；④取极限：()1()lim nbi an i b af x dx f nξ→∞=-=∑⎰（3）曲边图形面积：()baS f x dx =⎰；变速运动路程21()t t S v t dt =⎰；变力做功 ()baW F r dr =⎰2．定积分的几何意义说明：一般情况下，定积分()ba f x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b ==之间各部分面积的代数和，在x 轴上方的面积取正号，在x 轴下方的面积去负号．（可以先不给学生讲）．分析：一般的，设被积函数()y f x =，若()y f x =在[,]a b 上可取负值。

科 技 教 育DOI：10.16661/ki.1672-3791.2010-5042-9427《高等数学》课堂教学中融入课程思政案例①——以《定积分的概念》为例范慧玲* 曹鸣宇 袁玉萍 张丽(黑龙江八一农垦大学理学院 黑龙江大庆 163319)摘 要：寻找每个知识点的课程思政元素是改变传统数学课的闪光点，其可以给枯燥的理论课堂带来生机，活跃学生的学习热情，使得学生在学习理论的同时树立正确的三观。

该文以高等数学中的定积分的概念为例，在设计课堂教学的过程中以问题导入的形式，引导学生思考、分析问题，将知识点和哲学思想联系在一起，以提高学生分析、解决问题的能力，逐步培养他们理论联系实际的能力。

关键词：高等数学 课程思政 定积分 教学反思中图分类号：G642 文献标识码：A 文章编号：1672-3791(2021)03(b)-0158-03Advanced Mathematics Classroom Teaching IncorporatesCurriculum Ideology and Politics Cases——Take The Concept of Definite Integral as an ExampleFAN Huiling* CAO Mingyu YUAN Yuping ZHANG Li(The College of Science of Heilongjiang Bayi Agricultural University, Daqing, Heilongjiang Province,163319 China)Abstract: Finding the ideological and political elements of the curriculum for each knowledge point is the shining point of changing the traditional mathematics class. It can bring vitality to the boring theory class, activate the students' enthusiasm for learning, and enable students to establish correct three views while learning theories. Taking the definition of definite integral as an example, this paper takes the form of asking problems during the teaching processes, it can guide the students to think and analyse problems, to link the topic with philosophical thoughts, it can improve the capacity of the students in analyzing and solving problems. It can cultivate the ability to combine theory with practice.Key Words: Advanced Mathematics; Ideological and political elements of the curriculum; Definite integral；Ref lection on teaching为了将教师思政和课堂思政以及专业思政加以落实，教师必须在高校课程方面做到对于思想政治工作①基金项目：黑龙江八一农垦大学教学研究课题《融入课程思政理念的高等数学课程改革探索与实践》（项 目编号：NDJY1925）；黑龙江省教育科学规划重点课题《“反思性实践”理念下高校教师教学评 价体系研究》阶段性成果(项目编号：GJB1319098)；黑龙江省哲学社会科学研究规划项目《老龄 化背景下黑龙江省医养结合养老产业模式与实施优化策略的研究》(项目编号：19RKE283z)。

学习数学定积分的心得体会学习数学定积分的心得体会（精选篇1）教师职业注定就是要终身学习的。

这些天陆陆续续翻看了《新课标》，也在网上看了一些专家对新课标的解读，使我受益匪浅。

《小学数学课程标准》指出：学习是一种个性化行动。

作为教师应当在课堂教学环境中创设一个有利于张扬学生个性的“场所”，让学生的个性在宽松、愉悦的氛围中得到释放，展现学生生命的活力。

然而长期以来，我们的课堂忽视了学生情感、想象、领悟等多方面的发展，我们过多地强调知识的记忆、模仿，制约了儿童的嘴巴、双手、头脑，压抑了学生的主动性和创造性，最终使学生变得机械、沉闷、缺乏童心和灵性，缺乏生命活力。

那么，面对新的课程改变的挑战，如何能让我们的小学数学课堂教学真正的活起来呢？一、使学生能成为课堂的主人，去体验数学、“玩”好数学。

《小学数学课程标准》的一个重要理念就是为学生提供做数学、“玩”数学的机会，让学生在学习过程中去体验、去经历数学。

学生有了兴趣，就会激发求知欲，形成积极的情绪，在数学中我们不断创设与学生心理需要同步的情境，唤起学习热情，让学生真切的感受到“数学真好奇”！从而产生“我也想玩一玩、试一试！”的心理。

这样的课堂教学，除了知识的传递，更多了一份情感的交流，一次思维的碰撞，使学生能萌发出一种数学真有趣，我要“玩”好数学的愿望，从而更加乐意去学习数学，在数学世界里翱翔。

二、增强学生自信、培养学生自主参与意识、参与能力。

教师的教学任务要靠教学过程来完成，实现短时、高效、省力、低耗的教学效果，关键是要优化教学过程，要在教学过程中达到优化的教学效果。

实现素质教育的目标，必须正确地处理好教与学的关系，实现教与学的最佳结合。

只有这样才能确立学生的主体地位，形成以教导学、以教促学的新局面。

1、让所有的学生都能参与教学活动，人人都要动脑、动口、动手。

需要教师们转变教学思想，摆正自己的位置，真正地还给学生主人地位，充分发扬教学民主，处理师生之间主导与主体的关系，多给学生创造动脑、动口、动手的机会。

高中数学定积分的概念教案新人教版选修一、教学目标1. 理解定积分的概念，掌握定积分的定义方法和性质。

2. 学会利用定积分解决实际问题，提高运用数学知识解决实际问题的能力。

3. 培养学生的逻辑思维能力、创新能力和合作能力。

二、教学内容1. 定积分的概念：定积分的定义、定积分的性质。

2. 定积分的计算：牛顿-莱布尼茨公式、定积分的换元法、分部积分法。

3. 定积分在实际问题中的应用。

三、教学重点与难点1. 重点：定积分的概念、性质，定积分的计算方法。

2. 难点：定积分的理解和运用，定积分的计算技巧。

四、教学方法1. 采用问题驱动法，引导学生主动探究定积分的概念和性质。

2. 利用案例分析法，让学生学会将实际问题转化为定积分问题。

3. 运用讨论法，培养学生的合作能力和创新思维。

五、教学过程1. 导入：通过生活中的实例，引导学生思考如何求解曲边图形的面积。

2. 探究定积分的概念：讲解定积分的定义，让学生理解定积分的基本思想。

3. 学习定积分的性质：引导学生通过举例，总结定积分的性质。

4. 定积分的计算：讲解牛顿-莱布尼茨公式，教授换元法和分部积分法。

5. 应用定积分解决实际问题：让学生分组讨论，选取实例进行分析。

6. 总结与反馈：对所学内容进行总结，收集学生反馈，及时调整教学方法。

六、教学评价1. 评价学生对定积分概念的理解程度，通过课堂提问、作业批改等方式进行。

2. 评价学生对定积分性质的掌握情况，通过课后练习、小测验等方式进行。

3. 评价学生运用定积分解决实际问题的能力，通过分组讨论、课堂展示等方式进行。

七、教学资源1. PPT课件：制作精美的PPT课件，展示定积分的概念、性质和计算方法。

2. 教学案例：收集与生活实际相关的案例，用于引导学生运用定积分解决实际问题。

3. 练习题库：编写一定数量的练习题，用于巩固学生对定积分的理解和运用。

八、教学进度安排1. 第1周：导入定积分的概念，讲解定积分的定义和性质。

一、先学后讲
（一）情景引入
一、定积分的实际背景1.来自曲边梯形的面积2．变速直线运动的路程
二、定积分的概念
如果 时,上述极限存在（即，这个极限值与 的分割及点 的取法均无关），则称此极限值为函数 在区间 上的定积分，记为
三、定积分的几何意义
四、定积分的性质：
（1） ；
（2） ；
（3） .
（二）经典例题
三维目标
１、知识与技能：结合实例了解积分运算的意义;理解定积分的概念及符号表示;理解求积分与求导是一对互逆的运算
２、过程与方法：掌握微积分基本定理,并会求简单的积分;
３、情感、态度与价值观：通过求曲边梯形的面积,进一步感受极限的思想,体会事物间相互转化、对立统一的辩证关系,培养辩证唯物主义观点,提高理性思维能力.
【例1】 利用定积分的定义，计算 的值.
（三）练习过关
计算下列定积分
1、 2． 3． 4. 5.
二、总结提升
教师引导，由学生自主表述，教师点评
教师引导，由学生自主表述，教师点评
教师引导，由学生先做，教师根据学生做题情况进行点评
学生自主练习，教师随堂指导，分析和讲解．
由学生自主表述，教师点评
授课题目
定积分的概念
拟1课时
第1课时
明确目标
掌握微积分基本定理,并会求简单的积分;
重点难点
重点：“以直代曲”“以不变代变”的思想方法，定积分的概念、几何意义
难点：“以直代曲”“以不变代变”的思想方法，定积分的概念．
课型
□讲授 □习题 □复习 □讨论 □其它
教 学 内 容 与 教 师 活 动 设 计
学生活动过程

定积分的概念教学目标：1.通过求曲边梯形的面积和变速直线运动的路程，了解定积分的背景；2.借助于几何直观定积分的基本思想，了解定积分的概念；3．理解掌握定积分的几何意义.教学重、难点：定积分的概念、定积分的几何意义．教学过程：一．创设情景复习：1． 回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法，2．对这四个步骤再以分析、理解、归纳，找出共同点．二．新课讲授1．定积分的概念一般地，设函数在区间上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=将区间等分成个小区间，每个小区间长度为（b a x n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式：11()()n n n i i i i b a S f x f n ξξ==-=∆=∑∑ 如果无限接近于（亦即n →+∞）时，上述和式无限趋近于常数，那么称该常数为函数在区间上的定积分。

记为：()ba S f x dx =⎰其中成为被积函数，叫做积分变量，为积分区间，积分上限，积分下限。

说明：（1）定积分()b af x dx ⎰是一个常数，即无限趋近的常数（n →+∞时）称为()ba f x dx ⎰，而不是．（2）用定义求定积分的一般方法是：①分割：等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈； ③求和：1()n i i b a f nξ=-∑； ④取极限：()1()lim nb i a n i b a f x dx f nξ→∞=-=∑⎰ （3）曲边图形面积：()baS f x dx =⎰；变速运动路程21()t t S v t dt =⎰； 变力做功 ()b a W F r dr =⎰ 2．定积分的几何意义说明：一般情况下，定积分()ba f x dx ⎰的几何意义是介于轴、函数的图形以及直线,x a xb ==之间各部分面积的代数和，在轴上方的面积取正号，在轴下方的面积去负号．（可以先不给学生讲）．分析：一般的，设被积函数()y f x =，若()y f x =在上可取负值。