机械动态仿真实验指导

实验一MATLAB基本操作一、实验目的：①通过上机实验操作，使学生熟悉MATLAB实验环境，练习MATLAB命令、m文件，进行矩阵运算、图形绘制、数据处理。

②通过上机操作，使得学生掌握Matlab变量的定义和特殊变量的含义，理解矩阵运算和数组运算的定义和规则。

③通过上机操作，使得学生掌握数据和函数的可视化，以及二维曲线、三维曲线、三维曲面的各种绘图指令。

二、实验原理与说明Matlab是Matrix 和Laboratory两词的缩写，是美国Mathworks公司推出的用于科学计算和图形处理的可编程软件，经历了基于DOS版和Windows版两个发展阶段。

三、实验设备与仪器：PC电脑，Matlab7.0仿真软件四、实验内容、方法与步骤：数组运算与矩阵运算数组“除、乘方、转置”运算符前的“.”决不能省略，否则将按矩阵运算规则进行运算；执行数组与数组之间的运算时，参与运算的数组必须同维，运算所得的结果也与参与运算的数组同维。

A=[ 1 2 3; 4 5 6; 7 8 9];B=[-1 -2 -3；-4 -5 -6；-7 -8 -9];X=A.*BY=A*Bplot用于二维曲线绘图，若格式为plot（X，Y，’s’），其中X为列向量，Y是与X等行的矩阵时，以X为横坐标，按Y的列数绘制多条曲线；若X为矩阵，Y是向量时，以Y为纵坐标按X的列数（或行数）绘制多条曲线。

参考程序如下：t=(0:pi/100:pi)'y1=sin(t)*[-1 1];y2=sin(t).*sin(9*t);plot(t,y1, 'r:', t, y2, 'b-.')axis([0 pi, -1, 1])title('Drawn by Dong-yuan GE')程序运行界面如下：plot3用于三维曲线绘制，其使用格式与plot十分相似。

参考程序如下：t=0:0.02:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z,'b-', x,y,z,'o')程序运行界面如下：mesh与surf用于三维空间网线与曲面的绘制。

机械运动控制系统的动态建模与仿真分析引言：机械运动控制系统是工业和生活中的重要组成部分，它能够实现运动控制、定位和调节等功能。

动态建模与仿真分析是理解和优化机械运动控制系统的关键步骤。

本文将介绍机械运动控制系统的动态建模方法以及仿真分析的重要性。

一、机械运动控制系统动态建模方法机械运动控制系统的动态建模是基于控制理论和动力学原理的。

常见的动态建模方法包括基于拉普拉斯变换的传递函数法和基于差分方程的状态空间法。

1. 传递函数法传递函数法是一种常用的机械运动控制系统动态建模方法。

它通过建立控制系统的输入-输出关系，描述系统的传递特性。

在这种方法中，机械运动控制系统被建模为一个线性时不变系统，可以方便地进行频域分析和控制器设计。

2. 状态空间法状态空间法是另一种常见的机械运动控制系统动态建模方法。

它通过描述系统的状态和控制量的关系，提供了系统的全局信息。

状态空间法更加适用于复杂的非线性系统，并且可以通过仿真软件进行更为准确的仿真分析。

二、动态建模与仿真分析的重要性动态建模与仿真分析是改进机械运动控制系统的关键步骤。

通过建立准确的动态模型，可以准确预测系统的响应和性能指标。

仿真分析可以帮助设计师优化控制策略和参数设置，从而提高系统的稳定性、精度和效率。

1. 预测系统性能动态建模和仿真分析可以预测机械运动控制系统的性能，并评估不同控制策略的有效性。

通过仿真分析，可以确定系统的频率响应、阻尼特性以及系统的稳定性。

这些信息对于系统设计和改进非常重要。

2. 优化控制参数仿真分析可以通过改变控制参数，找到最优的控制策略。

例如，可以通过仿真分析确定合适的控制增益、采样周期等参数，从而提高系统的响应速度和抗干扰能力。

通过优化控制参数，可以避免实际试验中的大量试错，降低成本和风险。

3. 分析故障和异常动态建模与仿真分析还可以帮助工程师识别和分析系统故障和异常情况。

通过仿真，可以模拟机械运动控制系统在不同故障条件下的响应，预测故障对系统性能的影响，并提供相应的改进方案。

机械工程师如何进行机械运动仿真机械运动仿真是现代机械工程领域的重要工具，它可以模拟和预测机械系统的运动轨迹和性能。

在设计和优化机械系统时，机械工程师可以通过运动仿真来评估不同设计方案的优劣，提高系统效率和性能。

本文将介绍机械工程师如何进行机械运动仿真。

第一步是建立模型。

机械运动仿真的第一步是建立准确的机械模型。

机械工程师需要根据实际的机械系统特性和约束，使用专业的仿真软件建立系统的数学模型。

这个模型包括机械系统的结构、零件的参数和运动学关系等。

通过建立准确的模型，机械工程师可以更好地理解和分析系统的运动行为。

第二步是选择仿真工具。

市面上有许多专业的机械运动仿真软件，机械工程师需要根据具体需求选择合适的工具。

一般而言，仿真软件应具备良好的计算精度、友好的用户界面和灵活的功能。

此外，还需注意软件是否支持导入和导出不同格式的模型文件，以便与其他设计和分析软件进行集成。

第三步是进行仿真分析。

在对机械系统进行仿真之前，机械工程师需要定义仿真参数和约束条件。

这些参数可以包括零件的材料特性、力和力矩的大小、摩擦系数等。

通过调整这些参数，机械工程师可以模拟不同工况下的机械系统行为。

同时，还需要考虑系统的约束条件，比如固定约束、转动约束等。

这些约束条件可以限制某些部件的运动自由度，使仿真结果更接近实际情况。

第四步是分析仿真结果。

仿真分析完成后，机械工程师需要对仿真结果进行详细的分析。

他们可以根据仿真结果评估机械系统的性能指标，如速度、加速度、力矩等。

此外，还可以分析零件的位移、变形和应力分布等。

通过分析仿真结果，机械工程师可以发现系统存在的问题，并进行必要的优化和改进。

最后一步是优化设计。

基于对仿真结果的分析，机械工程师可以进行优化设计。

他们可以通过改变零件的尺寸、材料或设计参数来改善系统性能。

优化设计通常采用试错法，即通过多次仿真分析和优化设计迭代，逐步优化机械系统的性能指标。

通过这样的优化过程，机械工程师可以设计出更加高效、稳定和可靠的机械系统。

机械系统动力学分析与仿真方法机械系统动力学分析与仿真方法是研究机械系统运动规律和力学特性的重要领域。

通过分析机械系统的动力学特性，可以预测机械系统的运动轨迹、力学响应和能量转换。

同时，通过仿真方法可以模拟和验证机械系统的性能，优化设计和调整参数，提高机械系统的工作效率和可靠性。

在进行机械系统动力学分析和仿真之前，首先要建立机械系统的数学模型。

这一步通常是通过力学原理和方程来描述机械系统的运动和力学特性。

数学模型可以是刚体模型、弹性模型或连续介质模型，根据具体情况选择合适的模型来描述机械系统。

同时，还需要考虑机械系统的边界条件和约束条件，确保模型的准确性和可靠性。

基于建立的数学模型，可以采用数值方法进行机械系统的动力学分析。

最常用的数值方法是有限元法，它将机械系统划分为有限个小单元，通过计算每个小单元的运动规律和力学响应，从而得到整个机械系统的动力学特性。

有限元法广泛应用于结构分析、振动分析和疲劳寿命预测等领域，是一种十分强大和有效的分析方法。

除了有限元法，还有其他数值方法可以用于机械系统的动力学分析。

比如，多体动力学方法可以有效地描述机械系统中多个刚体的运动和相互作用。

多体动力学方法可以用于对车辆、机械手臂和飞行器等动力学问题的研究。

此外，还有基于粒子的方法，如离散元法和分子动力学方法，用于对颗粒物质的运动和相互作用进行分析。

通过动力学分析，可以获取机械系统的运动规律和力学响应。

这些信息对于机械系统的设计和优化至关重要。

通过对机械系统的动力学特性进行分析，可以优化设计参数，减小不稳定性和振动问题，提高机械系统的可靠性和性能。

此外，还可以通过分析运动轨迹和能量转换，寻找机械系统的节能潜力和优化方案。

除了动力学分析，仿真方法也是研究机械系统的重要手段。

仿真方法可以通过模拟机械系统的运动和力学特性，提供对机械系统性能和行为的直观理解。

同时，还可以在仿真环境中对机械系统进行虚拟实验和测试，加快设计和验证的过程。

前言机械CAD/CAM技术这门课程是一门理论与实践结合非常紧密的课程, 经过系统的实验环节, 能够帮助学生较好地理解相关理论知识, 同时提高实际动手能力, 为将来的工程实践打好基础。

基于上述考虑, 并根据我校实际情况, 本门课程安排了分属于CAD; CAE; CAM三个不同领域的7个实验。

可达到比较全面的实验效果。

实验一将下表进行程序化处理一、编程思路: 设整型变量i为皮带型号: i＝0表示O型, I=1为A型, I=2为B型, 以此类推。

用4个一维数组a[7]、 h[7]、 a0[7]、 y0[7]分别存储V带的顶宽, 断面高、节宽和节高。

二、检索V带参数的C++语言参考程序:// sy1.cpp : 定义控制台应用程序的入口点。

#include "stdafx.h"#include <stdlib.h>#include <stdio.h>int main(int argc,char **argv){int i;float a[7]={10.0,13.0,17.0,22.0,32.0,38.0,50.0};float h[7]={6.0,8.0,10.5,13.5,19.0,23.5,30.0};float a0[7]={8.5,11.0,14.0,19.0,27.0,32.0,42.0};float y0[7]={2.1,2.3,4.1,4.8,6.9,8.3,11.0};while(1){scanf("%d",&i);if(i>=0 &&i <=6){printf("您需要查找的V带的顶宽为%f,断面高为%f,节宽为%f,节高为%f",a[i],h[i],a0[i],y0[i]);break;}else printf("您输入的V带型号不对, 请重新输入! ");}system("pause");}三、实验步骤: 如下图所示A、用Microsoft Visual Studio 作为实验环境1234输入代码并执行B、用VC++6.0作为实验环境13 4四、实验报告要求1、简述实验步骤( 要求手写) 。

机械传动系统的动态模拟与仿真机械传动系统是工程领域中常见的一种重要组成部分，它起到将力或动能从一个部件传递到另一个部件的作用。

为了准确地理解和设计机械传动系统，在实际应用之前进行动态模拟与仿真是非常重要和必要的。

动态模拟与仿真是运用计算机技术对机械系统的运动进行模拟和分析的过程。

通过建立合适的数学模型和应用计算机算法，可以预测和评估机械传动系统在不同工况下的运动特性。

这种方法不仅可以大大节省开发成本，还可以提前发现和解决潜在的问题。

首先，动态模拟与仿真可以帮助工程师准确地了解机械传动系统的动态响应。

通过建立物理模型和运用数值分析方法，可以模拟机械系统受到外部载荷作用下的响应情况。

例如，对于齿轮传动系统，我们可以通过模拟输入转矩和输出转矩的传递过程来预测各个齿轮的受力情况和系统的振动特性。

这种方式可以帮助工程师确定合适的设计参数，以保证机械系统的性能和寿命。

其次，动态模拟与仿真还可以用于预测机械传动系统的动态特性。

通过建立系统的动力学模型，工程师可以分析系统在不同工况下的运动学性能、惯性响应和振动特性等。

例如，对于涉及到高速转动的离心离合器传动系统，我们可以通过建立系统的速度-扭矩曲线，来了解系统的动态特性和通过不同参数调整来优化系统的工作效率。

此外，动态模拟与仿真可以用于优化机械传动系统的设计。

通过建立系统的动态模型和利用参数优化算法，可以快速地寻找到使系统性能最佳化的设计参数。

例如，对于涉及到润滑油膜的滚动轴承系统，我们可以通过改变润滑膜的厚度和粘性等参数，来优化系统的摩擦和磨损特性，从而延长系统的使用寿命。

最后，动态模拟与仿真还可以用于故障诊断和故障排除。

通过建立系统的故障模型和利用故障诊断算法，可以准确地识别和定位机械传动系统中的故障点。

例如，对于轴承故障，我们可以通过分析齿轮传动系统的振动信号，来判断是哪个轴承出现了故障，并及时采取相应的维修措施，以防止更严重的损坏。

综上所述，动态模拟与仿真在机械传动系统的设计和分析过程中起着重要的作用。

快速掌握动态模拟实验的操作方法动态模拟实验是一种通过计算机软件模拟真实情况下的物理实验的方法。

它不仅可以帮助学生更好地理解和掌握实验原理，还可以提高实验效率，减少实验设备和材料的使用。

下面将介绍一些快速掌握动态模拟实验的操作方法。

首先，我们需要选择一款适合自己的动态模拟实验软件。

市面上有许多种不同的软件可供选择，如MATLAB、LabVIEW等。

在选择软件时，我们可以考虑实验内容、操作界面的友好程度以及软件的稳定性等因素。

接下来，我们需要了解软件的基本操作方法。

通常，动态模拟实验软件具有类似的操作逻辑，包括建模、参数设置、仿真运行和结果分析等步骤。

在建模阶段，我们需要根据实验的要求和目的，选择合适的模型，并对模型进行参数设置。

这些参数可以包括物体的质量、形状、初始状态等。

在仿真运行阶段，我们可以通过设置仿真时间和步长等参数，进行实验的运行。

最后，在结果分析阶段，我们可以通过软件提供的数据分析工具，对实验结果进行处理和分析。

在进行动态模拟实验时，我们还需要注意一些常见的问题。

首先，模型的建立要符合实际情况，并且参数设置要准确。

如果模型和参数设置不合理，将会导致实验结果的偏差。

其次，我们需要关注仿真过程中的计算误差。

由于计算机的计算精度有限，仿真结果可能会存在一定的误差。

因此，在进行结果分析时，我们应该对结果的可靠性进行评估。

此外，我们还需要注意软件的使用限制。

不同的软件可能对计算资源、模型复杂度等方面有一定的限制，我们需要根据实际情况进行合理的选择和设置。

除了基本的操作方法，我们还可以通过学习一些高级技巧来提高动态模拟实验的效果。

例如，我们可以使用优化算法来寻找最优解，或者使用参数辨识方法来确定模型的未知参数。

这些技巧可以进一步提高实验的精度和可靠性。

总之，动态模拟实验是一种强大的工具，可以帮助我们更好地理解和掌握物理实验的原理。

通过选择合适的软件、掌握基本的操作方法，并学习一些高级技巧，我们可以快速掌握动态模拟实验的操作方法，并在实验中取得良好的效果。

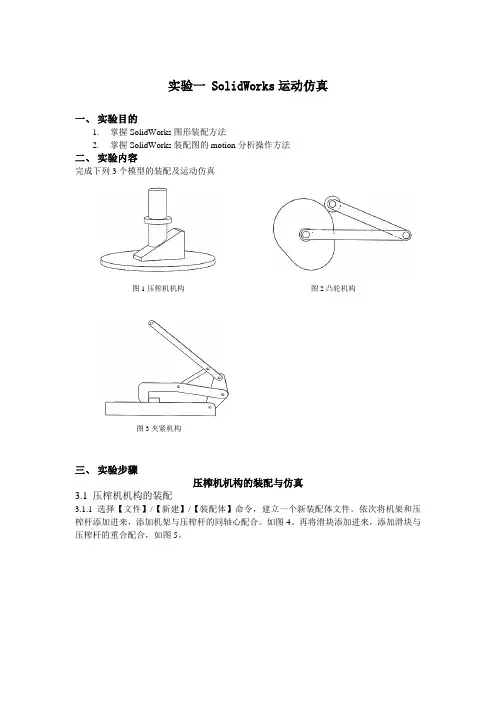
实验一 SolidWorks运动仿真一、实验目的1.掌握SolidWorks图形装配方法2.掌握SolidWorks装配图的motion分析操作方法二、实验内容完成下列3个模型的装配及运动仿真图1压榨机机构图2凸轮机构图3夹紧机构三、实验步骤压榨机机构的装配与仿真3.1 压榨机机构的装配3.1.1 选择【文件】/【新建】/【装配体】命令，建立一个新装配体文件。

依次将机架和压榨杆添加进来，添加机架与压榨杆的同轴心配合。

如图4。

再将滑块添加进来，添加滑块与压榨杆的重合配合，如图5。

图4机架与压榨杆的同轴心配合图5滑块与压榨杆的重合配合3.1.2 添加滑块端面与机架端面的重合配合，以及滑块前视基准面与机架前视基准面的重合配合（点击图形区域左边的装配体下的机架前的“+”号即可找到前视基准面）最后将滑块拖动到中间位置。

图6机架与滑块的重合配合图7机架与滑块前视基准面的重合配合3.2 压榨机机构的运动仿真3.2.1 仿真前先将“solidworks motion ”插件载入，单击工具栏中按钮“”的下三角形，选择其中的“插件”，在弹出的“插件”设置框中，选中“solidworks motion”的前后框，如下图8所示。

在装配体界面，单击左下角的【运动算例】，再在【算例类型】下拉列表中选择【motion 分析】如下图9所示。

图8载入插件图9 motin 分析3.2.2 添加实体接触：单击工具栏上的“接触按钮”，在弹出的属性管理器中【接触类型】栏内选择“实体接触”，在【选择】栏内，点击视图区中压榨杆和滑块，“材料”栏内都选择“steel (dry)”, 单击“确定”按钮“”，如下图10所示。

同理再为滑块与机架添加实体接触，参数设置与压榨杆与滑块之间的一样。

图10添加实体接触3.2.3 添加驱动力：物体对压榨杆的反作用力即为驱动力，故在压榨杆上添加一恒力即可。

单击工具栏中的“力”按钮“”，在弹出的【力/扭矩】属性管理器中，【类型】选择“力”，【方向】选择“只有作用力”，“作用零件和作用应用点”，选择压榨杆上表面，单击改变力的方向向下，【力函数】选择“常量”，大小输入50牛顿，单击确定按钮。

机械系统动态模拟与仿真研究机械系统动态模拟与仿真研究是近年来机械工程领域中备受关注的研究方向。

随着计算机技术的迅猛发展，机械系统动态模拟与仿真研究为解决机械系统设计、优化和故障诊断等问题提供了有效的手段。

本文将就机械系统动态模拟与仿真研究进行探讨。

一、动态模拟与仿真的意义和应用机械系统动态模拟与仿真研究是通过数学模型和计算机模拟技术，对机械系统的运动、力学特性和故障进行模拟和仿真，从而提供可靠的理论依据，优化设计方案，降低成本，提高性能和可靠性。

其意义主要体现在以下几个方面：首先，动态模拟与仿真可以帮助工程师快速了解机械系统的工作原理和特性。

通过建立精确的数学模型，可以清晰地展现机械系统的工作过程，提供直观的物理图像，使工程师能够更好地理解系统的工作原理，并根据仿真结果进行优化设计。

其次，动态模拟与仿真能够提高机械系统的设计效率和准确性。

通过仿真可以快速获得各种设计参数的变化对系统性能的影响，比如力学特性、运动轨迹、应力分布等，从而为设计提供量化指导，大大减少试验和优化的时间和成本。

再次，动态模拟与仿真有助于机械系统的故障诊断和优化。

通过仿真可以模拟机械系统在不同工况下的运动和响应，捕捉异常情况，并通过仿真结果进行故障诊断和根本原因分析，从而改进系统设计，提高设备可靠性和故障预测能力。

最后，动态模拟与仿真为新型机械系统的设计和优化提供了工具和方法。

在新技术、新材料不断涌现的背景下，动态模拟与仿真可以帮助工程师设计和优化具有特殊功能和复杂结构的机械系统，从而满足新应用场景和需求。

二、动态模拟与仿真的方法和技术动态模拟与仿真的研究主要依赖于计算机模拟技术和数学建模。

目前常用的模拟方法包括离散元法、多体动力学模拟、有限元分析、计算流体力学等。

离散元法是一种通过不同粒子之间的相互作用来模拟机械系统运动的方法。

它能够考虑系统中粒子之间的接触力、摩擦力和碰撞等因素，并通过数值计算模拟系统的宏观运动。

多体动力学模拟基于刚体动力学理论，通过建立刚体间的相互作用关系和动力学方程，模拟机械系统的运动和响应。

机械系统的动态仿真与分析机械系统的动态仿真与分析是一门关于机械设备运行时行为的研究领域。

通过使用先进的计算机软件和数学模型，工程师可以模拟机械系统的运动，评估其性能，并进行优化设计。

本文将介绍机械系统动态仿真与分析的重要性，方法和应用。

I. 动态仿真的重要性1. 系统性能评估动态仿真可帮助工程师全面了解机械系统的运动行为，例如速度、加速度、力和动力学特性等。

通过对系统运行状态的全面分析，工程师可以评估系统的性能，并根据仿真结果进行改进和优化。

2. 操作优化和故障排除在机械系统运行时，存在着许多因素可能影响系统的效率和稳定性。

动态仿真可以帮助工程师模拟不同操作条件下机械系统的运行情况，并找出可能存在的问题。

通过对仿真结果进行分析，工程师可以提前预测和解决潜在的故障或操作问题，从而优化机械系统的性能。

3. 节约时间和成本在过去，为了评估机械系统的性能，工程师们通常需要进行实际试验和测试，这不仅费时费力，而且成本高昂。

动态仿真可以在建立数字模型后，通过计算机软件进行模拟和分析，从而节约了试验和测试过程的时间和成本。

II. 动态仿真的方法1. 建立数学模型动态仿真需要基于机械系统的物理特性建立数学模型。

这种模型可以基于质点、刚体、弹簧、阻尼器等元素来描述机械系统的运动。

工程师需要根据系统的实际情况和需要进行模型的选择和建立。

2. 选择仿真软件为了进行动态仿真，工程师需要选择适用于机械系统的仿真软件。

一些常见的仿真软件包括ANSYS、MATLAB/Simulink、SolidWorks等。

这些软件提供了丰富的仿真工具和功能，能够对机械系统进行全面准确的仿真和分析。

3. 进行系统参数设置在进行动态仿真前，工程师需要设置模型的初始条件和系统参数。

这些参数可能包括质量、刚度系数、摩擦阻尼等。

通过合理设置参数，工程师可以获得更加准确的仿真结果。

III. 动态仿真的应用1. 新产品设计动态仿真可以帮助工程师评估新产品的运行效果，并寻找可能的改进方案。

机械设计中的动态仿真分析在当今的机械设计领域，动态仿真分析已成为一项不可或缺的重要工具。

它就像是设计师的“超级眼睛”，能够让我们在产品实际制造之前，就对其在各种工作条件下的性能和行为有一个清晰而准确的了解。

这不仅有助于减少设计失误、缩短研发周期，还能显著降低成本，提高产品的质量和可靠性。

那么，究竟什么是机械设计中的动态仿真分析呢？简单来说，它是利用计算机软件和数学模型，对机械系统的运动、受力、振动等动态特性进行模拟和预测的过程。

通过输入各种参数，如零件的几何形状、材料属性、运动规律、载荷条件等，仿真软件可以计算出系统在不同时刻的状态，生成直观的图像和数据结果。

想象一下，我们要设计一台复杂的数控机床。

如果没有动态仿真分析，我们只能依靠经验和理论计算来估计其性能。

但这样往往会存在很大的不确定性，可能导致设计出来的机床在实际运行中出现精度不足、振动过大、甚至零件损坏等问题。

而有了动态仿真分析，我们可以在虚拟环境中模拟机床的加工过程，观察刀具与工件的接触情况、机床各部件的运动轨迹和受力分布，提前发现潜在的问题，并进行针对性的优化改进。

动态仿真分析在机械设计中的应用非常广泛。

在机械传动系统的设计中，它可以帮助我们研究齿轮、皮带、链条等传动部件的动态啮合特性，评估传动效率、噪声和振动水平。

对于汽车发动机这样的复杂系统，仿真分析能够模拟气门的运动规律、活塞的往复运动以及燃烧过程，优化发动机的性能和排放。

在航空航天领域，飞机机翼的颤振分析、航天器的姿态控制等都离不开动态仿真技术的支持。

在进行动态仿真分析时，首先需要建立准确的数学模型。

这就像是为机械系统打造一个“数字替身”，模型的精度和合理性直接影响着仿真结果的准确性。

建模过程中，需要对机械系统进行合理的简化和假设，同时要考虑到各种非线性因素，如摩擦、接触、间隙等。

然后，选择合适的仿真算法和求解器也是至关重要的。

不同的算法和求解器适用于不同类型的问题，需要根据具体情况进行选择，以提高计算效率和精度。

机械运动系统的仿真与动态性能分析在工程领域中，机械运动系统的设计和优化是非常重要的一环。

而在实际工程中，由于成本和时间的限制，无法直接进行实验验证。

因此，采用仿真的方法对机械运动系统进行分析和优化，成为了一种常见的做法。

在本文中，我们将探讨机械运动系统的仿真方法以及动态性能分析的重要性。

首先，我们来讨论机械运动系统的仿真方法。

在过去，机械运动系统的仿真通常是基于传统的手工计算方法，这种方法需要大量的时间和精力，且结果往往不够准确。

随着计算机技术的快速发展，仿真软件的出现使得机械运动系统的仿真变得更加简便和高效。

目前，广泛使用的机械运动系统仿真软件有ADAMS、SIMPACK等。

这些软件提供了强大且直观的仿真环境，能够模拟机械系统的运动过程，并计算出各个部件的运动状态和力学响应。

通过调整系统的参数和优化设计，可以得到最佳的动态性能。

其次，我们来探究机械运动系统动态性能分析的重要性。

在机械系统的设计和优化过程中，动态性能的评估是不可或缺的一环。

动态性能包括机械系统的振动、冲击、稳定性等方面的指标。

通过仿真分析，可以对机械系统的动态响应进行准确的预测，从而避免在实际应用中可能出现的问题。

例如，在汽车行业中，对悬挂系统、转向系统等进行动态性能分析，可以评估车辆的驾驶稳定性和乘坐舒适性。

在航空航天领域，对飞行器的机械系统进行仿真分析，可以评估其飞行稳定性和振动性能，保证飞行的安全性和舒适性。

除了动态性能分析，机械运动系统的仿真还可以用于性能优化。

在设计过程中，通过参数调整、结构优化等方法，可以提高机械系统的性能指标，如减小能量损耗、提高运动效率等。

通过仿真分析，可以直观地展示不同设计方案的优缺点，并为工程师提供指导意见。

同时，机械运动系统的仿真还可以加速产品研发周期。

相比于实际试验，仿真分析不需要耗费大量的时间和成本，可以快速得到结果。

工程师可以通过反复仿真和优化，逐步完善设计方案，降低产品研发风险和成本。

机械设计中的动态仿真与优化方法在现代机械设计领域，动态仿真与优化方法正发挥着日益重要的作用。

它们不仅能够提高设计效率，降低成本，还能显著提升产品的性能和质量。

动态仿真是一种通过建立数学模型和计算机模拟来预测机械系统在实际运行中的行为和性能的技术。

在设计初期，设计师可以利用动态仿真软件创建虚拟的机械模型，包括零部件的几何形状、材料属性、运动关系等。

然后，通过输入各种工况条件，如载荷、速度、温度等，模拟机械系统的运动、受力和能量传递过程。

这样，设计师能够直观地了解机械系统在不同条件下的动态响应，提前发现潜在的问题，如振动过大、应力集中、运动干涉等。

与传统的设计方法相比，动态仿真具有许多显著的优势。

首先，它能够大大缩短设计周期。

在过去，为了验证一个设计方案的可行性，往往需要制造物理样机，并进行大量的实验测试，这不仅耗费时间和资金，而且一旦发现问题，修改设计的成本也很高。

而动态仿真可以在计算机上快速地进行多次模拟和优化，大大减少了设计迭代的次数。

其次，动态仿真能够提供更全面、更准确的性能评估。

它可以考虑到各种复杂的因素和边界条件，对机械系统的性能进行精细化的分析，为设计决策提供可靠的依据。

此外，动态仿真还可以帮助设计师更好地理解机械系统的工作原理和内部机制，激发创新思维，开发出更具竞争力的设计方案。

然而，要实现有效的动态仿真，需要解决一些关键问题。

首先是模型的准确性。

建立一个能够真实反映机械系统特性的数学模型是至关重要的。

这需要对机械系统的物理原理有深入的理解，准确地获取零部件的几何和材料参数，并合理地简化模型，以在计算精度和计算效率之间取得平衡。

其次是边界条件和载荷的确定。

实际工况中的边界条件和载荷往往是复杂多变的，如何准确地定义这些参数是影响仿真结果可靠性的重要因素。

此外，仿真结果的验证和校准也是必不可少的。

通过与实验数据或实际运行数据进行对比，不断修正和完善仿真模型，提高仿真的准确性和可信度。

在动态仿真的基础上，优化方法可以进一步提升机械设计的质量。

机械系统的动态建模与仿真机械系统的动态建模与仿真是现代工程领域中非常重要的一项技术。

通过建立数学模型，工程师们能够在计算机上进行仿真，预测和评估机械系统的性能。

这种技术广泛应用于机械设计、控制系统优化以及故障分析等领域。

本文将探讨机械系统动态建模与仿真的原理、方法以及在实际工程中的应用。

一、建模方法机械系统的动态建模是指将实际物理系统转化为数学模型的过程。

常用的建模方法有基于物理原理的方法和基于数据的方法。

基于物理原理的建模方法是根据机械系统的力学原理和几何关系来推导数学模型。

例如，对于一个弹簧-质量系统，可以利用胡克定律推导出弹簧的力学方程，并结合牛顿第二定律得到质点的运动方程。

这种方法的优点是模型参数具有明确的物理意义，对系统的分析更加直观，但是推导的过程相对复杂。

基于数据的建模方法是通过实验数据来建立数学模型。

在现实工程中，往往会通过传感器采集到机械系统的状态数据，例如位移、速度和加速度等。

利用这些数据，可以采用系统辨识的方法，如最小二乘法或者神经网络等，来拟合得到数学模型。

这种方法的优点是建模过程相对简单，适用于大型复杂系统，但是对实验数据的质量要求较高。

二、仿真技术机械系统的仿真是指在计算机上模拟机械系统的运行过程，以预测系统的响应和评估系统性能。

常用的仿真技术包括数值计算方法和离散事件仿真方法。

数值计算方法是基于微积分和数值解方法来求解微分方程，得到系统的状态随时间的演变。

最常用的数值解方法有欧拉法和龙格-库塔法等。

这些方法可以精确地模拟机械系统的动态特性，但是计算量较大，对计算机性能要求较高。

离散事件仿真方法是将连续时间的系统状态离散化为一系列事件，通过事件模拟系统的运行过程。

这种方法在仿真过程中只模拟系统状态发生变化的时刻，减少了计算量。

常用的离散事件仿真软件有MATLAB/Simulink和Arena等。

三、应用案例机械系统的动态建模与仿真在实际工程中有广泛的应用。

以下是一些常见的应用案例：1. 机械设计优化：在设计机械系统时，可以通过仿真对不同参数的组合进行评估，找到最优的设计方案。

机械设计中的动态仿真与分析在现代机械设计领域，动态仿真与分析已经成为了一项至关重要的技术手段。

它不仅能够帮助设计师在产品开发的早期阶段就发现潜在的问题，还能为优化设计提供有力的依据，从而大大缩短产品的研发周期，降低成本，提高产品的质量和性能。

那么，什么是机械设计中的动态仿真与分析呢？简单来说，它是通过建立机械系统的数学模型，并利用计算机软件对其在各种工况下的运动、力学特性等进行模拟和分析的过程。

动态仿真的第一步是建立模型。

这就像是为一个虚拟的机械系统创建一个数字蓝图。

设计师需要对机械系统中的各个零部件进行精确的几何建模，包括形状、尺寸、材料等属性的定义。

同时，还需要考虑零部件之间的连接方式、运动约束等关系。

这一过程需要设计师对机械系统的结构和工作原理有深入的理解，只有这样才能建立起准确、有效的模型。

模型建立好后，接下来就是赋予其物理特性。

这包括质量、惯性、弹性、阻尼等参数的设定。

这些参数的准确性直接影响到仿真结果的可靠性。

例如，对于一个旋转的轴，我们需要准确地设定其质量分布、转动惯量等参数，才能真实地反映其在运动中的动态特性。

在完成模型的建立和参数设定后，就可以开始进行仿真计算了。

计算机软件会根据设定的条件和输入的参数，模拟机械系统在不同工况下的运动和力学行为。

通过仿真，我们可以得到诸如零部件的位移、速度、加速度、受力等详细信息。

这些信息可以以图表、曲线或者动画的形式呈现出来，让设计师能够直观地了解机械系统的工作状态。

动态仿真与分析在机械设计中的应用非常广泛。

例如，在汽车设计中，通过对发动机的曲柄连杆机构进行动态仿真，可以分析其在不同转速下的受力情况，从而优化零部件的结构设计，提高发动机的可靠性和耐久性；在航空航天领域，对飞行器的起落架进行动态仿真，可以评估其在着陆过程中的冲击载荷，为设计提供改进的方向；在工业机器人的设计中，通过对机器人的运动轨迹进行仿真，可以确保其能够准确、高效地完成预定的任务，同时避免与周围环境发生碰撞。

教学机械动态仿真模型设计引言教学机械动态仿真模型设计在工程教育中起着重要作用。

通过设计模型，学生可以更深入地理解机械原理和动力学。

本文将介绍教学机械动态仿真模型的设计过程，并重点关注设计要素和实现方法。

设计要素教学机械动态仿真模型的设计需要考虑以下要素：1. 目标：首先需要明确设计模型的目标。

是帮助学生理解特定的机械原理吗？还是培养学生的工程设计能力？明确目标可以帮助设计过程更加有效。

2. 机械原理：理解机械原理是设计模型的基础。

需要选择特定的机械原理，并深入研究其工作原理和运动规律。

这样可以确保设计模型能够准确地反映机械原理。

3. 材料选择：选择合适的材料对于设计模型的成功至关重要。

需要考虑材料的强度、可塑性和成本等因素。

在选择材料时，还需要考虑到模型的使用寿命和安全性。

4. 结构设计：结构设计包括模型的尺寸、形状和连接方式等。

需要确保设计模型的结构能够支持所选机械原理的正常运行。

同时，需要考虑模型的组装和拆卸便捷性，方便学生进行实验操作。

实现方法教学机械动态仿真模型的实现方法因项目而异，但下面介绍的步骤可作为设计的参考。

1. 计划：在开始设计之前，制定一个详细的计划非常重要。

计划中应该包含设计目标、时间表、材料清单和实验步骤等。

这样可以确保设计过程有条不紊。

2. 绘制图纸：根据选定的机械原理，绘制模型的详细图纸。

图纸应包括模型的三维视图、平面图和剖视图等。

图纸可以作为设计的蓝图，帮助设计师更好地理解模型的结构。

3. 制造零件：根据图纸，使用适当的工具和设备制造模型的零件。

制造过程中需要严格按照图纸上的尺寸和要求进行操作，确保零件的精度和质量。

4. 组装模型：将零件按照图纸上的要求进行组装。

组装过程中需要注意零件的精确配合和连接方式的正确性。

组装完成后，检查模型的工作状态和运动是否符合设计要求。

5. 测试和调整：在模型制造完成后，进行测试和调整以确保其正常工作。

可以通过观察模型运动、测量运动参数等方式进行测试。

机械制造行业中的机械仿真技术使用教程机械制造行业是现代工业中的重要组成部分。

随着科技的不断进步和发展，机械仿真技术已经成为机械制造过程中不可或缺的工具。

本文将向您介绍机械仿真技术的使用教程，帮助您更好地理解和运用该技术。

第一部分：机械仿真技术的概述机械仿真技术是一种通过计算机模拟和虚拟实验的方法，来验证和分析机械系统的性能、运行方式和工作效果的技术。

它可以模拟真实的物理环境和机械装置，帮助工程师们找出系统设计中的问题并进行优化。

机械仿真技术可以应用于多个方面，例如产品设计、工艺规划、装配优化、动力传动等。

第二部分：机械仿真技术的应用领域1. 产品设计：机械仿真技术可以帮助工程师们模拟产品的结构和性能，进行真实环境下的测试和验证。

通过仿真，工程师可以发现隐藏在产品设计中的问题，进而进行改进和优化。

2. 工艺规划：在机械制造过程中，工艺规划是非常重要的一环。

机械仿真技术可以帮助工程师们模拟和分析工艺流程，优化工艺路线和设备布局，提高制造效率和质量。

3. 装配优化：机械系统的装配是一个复杂而关键的过程。

机械仿真技术可以帮助工程师们模拟和优化装配过程，避免装配错误和问题的发生，提高装配效率和准确性。

4. 动力传动：在机械制造领域中，动力传动的设计和优化对系统的运行和性能至关重要。

机械仿真技术可以帮助工程师们模拟和分析动力传动系统，找出问题并进行优化，以提高机械系统的效率和可靠性。

第三部分：机械仿真技术的使用步骤1. 确定仿真目标和需求：在使用机械仿真技术之前，首先需要明确仿真的目标和需求。

确定你想要研究和优化的机械系统的哪些方面，例如设计、工艺、装配等。

2. 数据准备和建模：机械仿真技术需要大量的数据来支持模拟和分析。

准备好所需的材料和工艺参数数据，并进行三维建模，将机械系统和环境模型化为计算机可以处理的形式。

3. 确定仿真方法和软件：根据仿真的需求和目标，选择合适的仿真方法和软件工具。

目前市场上有许多专业的机械仿真软件，例如ANSYS、SolidWorks Simulation等。