蒙氏感官,第六节,形状嵌板
- 格式:ppt
- 大小:818.50 KB
- 文档页数:10

托班蒙氏课程形状嵌板教案一、教学目标。
1. 让幼儿了解不同形状的特点和名称。
2. 培养幼儿的观察力和动手能力。
3. 帮助幼儿通过形状嵌板游戏,发展逻辑思维和空间想象能力。
二、教学重点和难点。
重点,让幼儿正确认识和使用不同形状的嵌板。
难点,引导幼儿进行形状嵌板游戏,培养其逻辑思维能力。
三、教学准备。
1. 形状嵌板,准备不同形状的嵌板,如圆形、方形、三角形、长方形等。
2. 教具,白板、彩色粉笔、幼儿绘画纸、彩色笔。
3. 教学环境,保持教室整洁,让幼儿有足够的活动空间。
四、教学过程。
1. 导入活动。
教师拿出不同形状的嵌板,让幼儿观察并说出嵌板的名称。
然后,教师提出问题,“你们知道这些形状的名称吗?我们今天要做一个有趣的游戏,看看谁能把这些形状嵌板放到正确的位置上。
”。
2. 游戏活动。
教师将形状嵌板放在白板上,然后请幼儿依次将嵌板放到正确的位置上。
在这个过程中,教师可以引导幼儿说出每个形状的名称,并让他们观察形状的特点。
如果幼儿出现错误,教师可以及时纠正并鼓励他们再试一次。
3. 拓展活动。
教师可以让幼儿用彩色笔在绘画纸上画出不同形状的图案,并在旁边写上形状的名称。
这样可以帮助幼儿巩固所学的知识,并培养他们的观察和动手能力。
4. 总结活动。
教师和幼儿一起回顾今天的学习内容,让幼儿说出自己的收获和感受。
同时,教师也可以对幼儿的表现进行肯定和鼓励,激发他们对形状嵌板游戏的兴趣。
五、教学反思。
通过这堂课的教学,我发现幼儿对形状嵌板游戏非常感兴趣,他们积极参与,并且在游戏中不断学习和进步。
但是也有一些幼儿在形状嵌板的选择和放置上存在一定困难,需要我在后续的教学中加强引导和训练。
另外,我还需要不断丰富教学内容,让幼儿在形状嵌板游戏中得到更多的启发和乐趣。
六、教学延伸。
1. 在日常生活中,教师可以引导幼儿观察周围的物体,认识不同形状的事物,如圆桌、方形窗户等。
2. 教师可以利用玩具积木和拼图等教具,让幼儿进行形状嵌板游戏的延伸练习,提高他们的空间想象能力和动手能力。

蒙氏嵌板教案教案名称:蒙氏嵌板教学教学目标:1. 认识和学习蒙氏嵌板的基本形状。
2. 培养幼儿观察、分析和解决问题的能力。
3. 发展幼儿的空间想象力和创造力。
4. 培养幼儿的手眼协调能力和精细动作能力。
5. 培养幼儿的集中注意力和自主学习的能力。
教学准备:1. 蒙氏嵌板(包括不同形状的嵌板块)。
2. 平板或桌面。
3. 绘画纸和彩色铅笔。
教学活动:活动1:认识嵌板形状1. 引导幼儿观察和描述蒙氏嵌板的不同形状,如长方形、正方形、三角形等。
2. 让幼儿用手触摸不同形状的嵌板块,感受其边角和平滑程度。
3. 让幼儿亲身体验将不同形状的嵌板块嵌入嵌板孔中,培养他们的空间认知能力。
活动2:模仿搭建1. 让幼儿观察和模仿已经搭建好的嵌板图案,了解嵌板的基本构造。
2. 引导幼儿思考如何使用不同形状的嵌板块,搭建一个与已有图案相似或相同的图案。
3. 鼓励幼儿尝试在空白的嵌板上自由搭建自己喜欢的图案,发展他们的创造力和想象力。
活动3:图案绘制1. 让幼儿利用彩色铅笔在绘画纸上模仿已搭建好的嵌板图案。
2. 鼓励幼儿自由发挥,将嵌板图案进行改编或创作,培养他们的艺术创造能力。
活动4:小组合作1. 将幼儿分成小组,每个小组至少配备一套蒙氏嵌板。
2. 引导小组合作搭建一个大型嵌板图案,让幼儿在合作中互相交流和协作,培养他们的团队合作能力。
活动5:游戏比赛1. 设计一个嵌板搭建的游戏比赛,让幼儿按照规定的时间和要求,尽快搭建出指定的图案。
2. 游戏比赛可以分为个人和小组两种形式,并设立奖励机制,鼓励幼儿积极参与。
评估方式:1. 观察幼儿的参与程度和表现,评估其对蒙氏嵌板知识和技能的掌握情况。
2. 收集幼儿完成的绘画作品,评估其对嵌板图案的理解和创作能力。
3. 观察小组合作和游戏比赛中幼儿之间的互动和表现,评估其团队合作和竞争能力。


蒙特梭利嵌板操作方法
蒙特梭利嵌板是一种教具,用来帮助儿童学习数学和几何概念。
以下是蒙特梭利嵌板的操作方法:
1. 准备工作:将嵌板放在一个平坦的表面上,并确保所有的木制几何图形都整齐地放在嵌板上。
2. 了解几何图形的属性:在使用嵌板之前,可以通过观察几何图形的形状、颜色和大小来帮助儿童理解它们的属性。
3. 选择一个学习目标:根据儿童的年龄和能力,选择一个合适的学习目标。
比如,可以选择让儿童了解和识别不同形状,或者让他们学习关于面积和周长的概念。
4. 操作嵌板:根据选定的学习目标,可以进行以下操作:
- 根据既定的模板将几何图形放在嵌板上。
- 探索几何图形的组合和分解,将它们重新排列成不同的形状。
- 使用几何图形进行比较,例如比较两个三角形的大小或两个长方形的面积。
- 创建自己的图形,通过组合不同的几何图形。
5. 引导儿童思考:在操作嵌板的过程中,引导儿童思考和提问,帮助他们探索几何概念。
例如,可以问他们如何将一个正方形分解成两个三角形,或者如何找
到不同形状的周长。
6. 清理和整理:在使用完嵌板后,将几何图形重新整理放回嵌板上,以便下次使用。
通过使用蒙特梭利嵌板,儿童可以通过实际操作和探索,深入理解数学和几何概念,培养他们的观察力、创造力和逻辑思维能力。

蒙氏描绘嵌板教案教案标题:蒙氏描绘嵌板教案教案目标:1. 帮助学生了解蒙氏描绘嵌板的概念和用途。
2. 发展学生的观察力、创造力和手眼协调能力。
3. 提高学生对几何形状和颜色的认知。
教学资源:1. 蒙氏描绘嵌板2. 彩色纸、剪刀和胶水3. 彩色铅笔或蜡笔4. 图片或实物展示几何形状教学步骤:引入活动:1. 向学生展示一些实物或图片,包括不同的几何形状,如正方形、三角形、圆形等。
2. 引导学生观察这些形状的特征,询问他们对这些形状的认知和命名。
教学活动:3. 向学生介绍蒙氏描绘嵌板,解释它是一种用于描绘几何形状和颜色的教具。
4. 向学生展示蒙氏描绘嵌板的使用方法,如如何选择合适的形状和颜色的描绘嵌板。
5. 让学生亲自尝试使用蒙氏描绘嵌板进行几何形状的描绘,鼓励他们自由组合和创造。
6. 引导学生观察和描述他们所描绘的几何形状,帮助他们加深对形状的认知。
巩固活动:7. 将学生组织成小组,每组选择一种几何形状进行描绘。
8. 学生可以使用彩色纸、剪刀和胶水制作自己的描绘嵌板,然后展示给其他小组。
9. 学生可以分享他们的创作过程和经验,相互学习和交流。
评估活动:10. 观察学生在活动中的表现,包括他们对几何形状的认知、描绘的准确性和创造性。
11. 与学生进行个别交流,了解他们对蒙氏描绘嵌板活动的理解和收获。
拓展活动:12. 鼓励学生在日常生活中观察和发现更多的几何形状,如建筑物、家具等。
13. 学生可以使用纸张、颜料或其他材料进行自由创作,展示他们对几何形状和颜色的理解和运用。
教案总结:通过蒙氏描绘嵌板教案的实施,学生将能够通过观察、描绘和创造来加深对几何形状和颜色的认知。
同时,他们还能够培养观察力、创造力和手眼协调能力。
这个教案旨在提供一个互动和有趣的学习环境,激发学生对学习的兴趣和积极性。

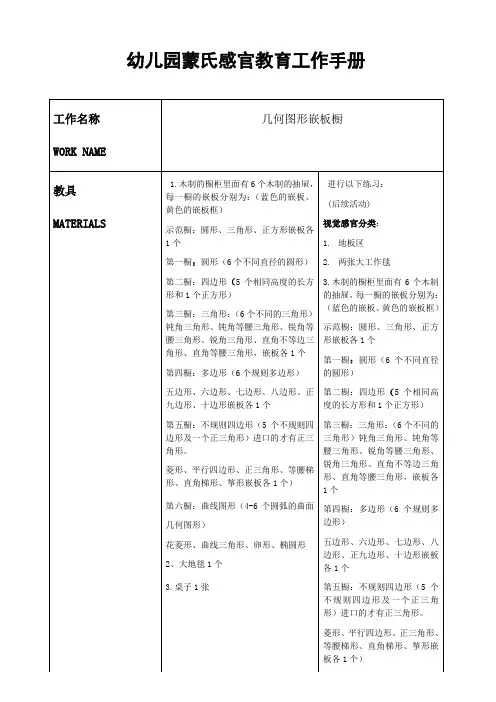
蒙氏数学教案几何图形嵌板橱
几何图形嵌板橱
【活动名称】
蒙氏训练几何图形嵌板橱
【教具准备】
几何图形嵌板图
【教学目标】
1.通过视觉和触觉的共同作用,帮助学生认识四边形(平行四边形、等腰梯形、不等边梯形)及曲线圆形(卵形、椭圆形、花边型、曲线三角形) 2.培养学生对几何图形从具体到抽象的认识。
3.加强注意力及观察力的训练。
【教学过程】
一、训练坐姿
请所有小朋友们做好,抬头挺胸、目视老师,双腿并拢,小手放在膝盖上。
二、导入
几何图形橱柜一共有六层,我们一共学习了四层,今天我们继续学习剩下的两层。
三、新授
1.请两个小朋友取来工作毯并铺好。
将第五层的抽屉拉出一点,双手抓住抽屉的两端,轻轻地放在工作毯上。
2.示范嵌板的拿法:右手3只手指(拇指、食指、中指)抓住圆柄,轻轻拿起嵌板中的一个四边形,然后放回。

蒙特梭利18件感官教具简介1.插座圆柱体适用年龄:二岁半----四岁半基本提示:配对,序列,可戴上眼罩让孩子配对,用手指触摸,探测圆穴的深浅与圆柱的大小。
错误控制:每个圆柱只能嵌入相合的圆穴。
直接目的:培养辨别大小的视觉能力间接目的:作为写字前的预备(抓握圆柱的圆柄可以作握笔的准备练习)。
培养逻辑思考能力(对应,顺序)培养敏锐的观察力。
2.粉红塔适用年龄:二岁半----六岁基本提示:和日常生活练习并行,但须先具有插座圆柱体充分练习经验,可以与棕色梯组合进行练习。
错误控制:在视觉上塔的外形显不协调直接目的:透过视觉正确地获得对三度空间差异变化的知觉。
间接目的:培养手眼协调及肌肉运动的控制,堆高时精神的抑制力及敏锐的观察力。
学习立方体的概念及数学教育的间接预备(理解十进位的准备教具)。
培养逻辑思考能力。
3.棕色梯适用年龄:二岁半----六岁基本提示:改变排列方式的序列练习,可与粉红塔合并使用。
错误控制:排列后的长方体在视觉上明显不协调。
直接目的:透过视觉的辨别在知觉上对平面及立体的差异有充分的认识。
间接目的:发展手眼及肌肉的动作协调。
培养专注的观察力。
学习长方体的概念及数学教具的间接预备(理解十进位的准备教具)。
培养逻辑思考能力(顺序性)。
4.长棒适用年龄:二岁半----六岁基本提示:练习长棒的排列方式,观察每根长棒间的差异,改变排列方式的序列练习。
错误控制:视觉上发现长短有明显不协调。
直接目的:透过视觉的辨别在知觉上对长度的差异有正确的了解。
间接目的:发展手眼及肌肉的动作协调。
隐含长度测定概念的教具,数学教育(量、基本运算、十进位等的直接预备教具)。
5.彩色圆柱体适用年龄:二岁半----五岁基本提示:尝试各种排列方式,辨别颜色对应归位,两合以上圆柱同时做垂直和水平的练习。
错误控制:圆柱规则的渐次性。
直接目的:培养视觉上对大小识别概念的再确认。
间接目的:培养手眼协调及肌肉运动的控制,堆高时精神的抑制力及敏锐的观察力与注意力。

蒙氏图形嵌板教案教案标题:蒙氏图形嵌板教案一、教学目标:1. 让学生了解蒙氏图形嵌板的基本概念和原理。
2. 培养学生的观察力、想象力和创造力。
3. 提高学生的手眼协调能力和空间认知能力。
二、教学准备:1. 蒙氏图形嵌板。
2. 各种形状的木块。
3. 黑板或白板及相应的书写工具。
4. 学生练习册。
三、教学过程:导入:1. 引入蒙氏图形嵌板的概念,向学生解释它的作用和用途。
2. 展示蒙氏图形嵌板和各种形状的木块,让学生观察并提出自己的想法。
探究活动:1. 让学生自由组合木块,尝试填满嵌板上的空白区域。
2. 引导学生观察和思考:哪些木块可以放在一起?哪些木块组合可以填满整个嵌板?3. 引导学生探索不同的组合方式,鼓励他们尝试不同的方案。
讲解与总结:1. 在学生探究的基础上,向学生介绍一些基本的嵌板组合方法和技巧。
2. 解释一些常见的图形嵌板问题,并给出解决方法。
3. 总结学生的探究成果,让他们分享自己的发现和经验。
练习与拓展:1. 分发学生练习册,让学生完成其中的练习题。
2. 设计一些拓展活动,如自由创作、团队合作等,激发学生的创造力和合作精神。
四、教学评估:1. 观察学生在探究活动中的表现,评估他们的观察力、想象力和创造力。
2. 检查学生在练习册中的答案,评估他们对嵌板组合方法和技巧的理解程度。
五、教学延伸:1. 引导学生进一步探索其他类型的图形嵌板,如数字嵌板、字母嵌板等。
2. 鼓励学生设计自己的图形嵌板问题,并与同学分享。
六、教学反思:1. 总结教学过程中的亮点和不足,思考如何改进教学策略和方法。
2. 收集学生的反馈意见,了解他们对教学内容和方式的评价,以便调整教学计划。
以上是一份关于蒙氏图形嵌板的教案,希望对您有所帮助。
如有需要,可以根据具体教学情况进行适当的调整和修改。

蒙氏铁制几何嵌板教案教案标题:蒙氏铁制几何嵌板教案教案目标:1. 介绍蒙氏铁制几何嵌板的基本概念和用途。
2. 培养学生对几何形状的认知和空间想象力。
3. 帮助学生发展解决问题和逻辑推理的能力。
4. 鼓励学生进行合作和团队合作。
教学资源:1. 蒙氏铁制几何嵌板。
2. 白板/黑板和彩色粉笔/白板标记笔。
3. 学生练习册和作业本。
4. 视频或图片展示蒙氏铁制几何嵌板的应用。
教学步骤:引入:1. 向学生介绍蒙氏铁制几何嵌板,并解释它的用途和重要性。
2. 展示一些实际应用蒙氏铁制几何嵌板的例子,如建筑设计、工程制图等。
探究:3. 向学生展示蒙氏铁制几何嵌板的各种形状,如正方形、长方形、三角形、圆形等,并解释它们的特征。
4. 通过示范,让学生亲自操作蒙氏铁制几何嵌板,尝试组合形状,形成不同的图案和结构。
5. 引导学生观察和描述他们所创建的图案和结构,帮助他们理解几何形状的属性和关系。
拓展:6. 提供一些挑战性的问题,要求学生使用蒙氏铁制几何嵌板解决,如找到不同形状的面积比较、寻找对称图形等。
7. 鼓励学生进行合作和团队合作,通过分享和讨论他们的解决方案,互相学习和提高。
巩固:8. 分发学生练习册和作业本,让学生练习使用蒙氏铁制几何嵌板解决问题,并完成相关练习和作业。
9. 定期检查学生的练习册和作业本,及时给予反馈和指导,帮助他们提高解决问题和逻辑推理的能力。
总结:10. 回顾本节课所学的内容,强调蒙氏铁制几何嵌板的重要性和应用价值。
11. 鼓励学生继续探索和应用蒙氏铁制几何嵌板,培养他们对几何形状的兴趣和创造力。
教学评估:1. 观察学生在操作蒙氏铁制几何嵌板时的表现,包括他们的准确性和创造性。
2. 检查学生的练习册和作业本,评估他们对蒙氏铁制几何嵌板的理解和应用能力。
3. 组织小组讨论和展示,评估学生在合作和团队合作中的表现。
教案扩展:1. 引导学生设计和创建自己的几何图案和结构,展示给其他同学观看和评价。

2022届安徽省淮北市高二(下)数学期末学业水平测试试题一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1. “0m <”是“函数2()log (1)f x m x x =+≥存在零点”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件2.某班有6名班干部,其中4名男生,2名女生.从中选出3人参加学校组织的社会实践活动,在男生甲被选中的情况下,女生乙也被选中的概率为 A .25B .35C .12D .233.100件产品中有6件次品,现从中不放回的任取3件产品,在前两次抽到正品的条件下第三次抽到次品的概率为( ) A .349B .198C .197D .3504.下列函数中,其图像与函数ln y x =的图像关于直线1x =对称的是 A .ln(1)y x =-B .ln(2)y x =-C .ln(1)y x =+D .ln(2)y x =+5.已知函数()()22231m m f x m m x+-=--是幂函数,且其图象与两坐标轴都没有交点,则实数(m =)A .1-B .2C .3D .2或1-6.已知函数32()312()f x x mx nx m N *=-++∈在1x =-处取得极值,对任意,()270x R f x +'∈>恒成立,则1240344035()()...()()2018201820182018f f f f ++++= A .4032 B .4034C .4035D .40367.若直线l :12x ty at=+⎧⎨=+⎩(t 为参数)经过坐标原点,则直线l 的斜率是A .2-B .1-C .1D .28.已知随机变量()2~0,X N σ,若()10.2P X>=,则()01P X <<的值为( )A .0.1B .0.3C .0.6D .0.49. “3a >”是“函数2()22f x x ax =--在区间(,2]-∞内单调递减”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不充分也必要条件10.袋中有6个不同红球、4个不同白球,从袋中任取3个球,则至少有两个白球的概率是( ). A .95B .23C .16D .1311.已知三棱锥P ABC -的体积为433,4APC π∠=,3BPC π∠=,PA AC ⊥,PB BC ⊥,且平面PAC ⊥平面PBC ,那么三棱锥P ABC -外接球的体积为( )A .43πB .23πC 123πD .323π12.已知函数211,1,(){42,1,x x f x x x x -+<=-+≥则函数()2()2xg x f x =-的零点个数为( )个A .1B .2C .3D .4二、填空题(本题包括4个小题,每小题5分,共20分)13.从混有5张假钞的20张百元钞票中任意抽取两张,将其中一张放到验钞机上检验发现是假钞,则两张都是假钞的概率是_________.14.已知命题:p R x ∀∈,cos 1x >,则p ⌝是_________________ 15.如果复数1()34aiz a R i-=∈+的实部与虚部相等,则a =_______. 16.定义函数{}()max ,f x x x λλ=-,x ∈R ,其中0λ>,符号max{,}a b 表示数,a b 中的较大者,给出以下命题: ①()f x 是奇函数;②若不等式(1)(2)1f x f x -+-≥对一切实数x 恒成立,则1λ≥③=1λ时,()()(1)(2)(100)F x f x f x f x f x =+-+-++-L 最小值是2450 ④“0xy >”是“()()()f x f y f x y +≥+”成立的充要条件 以上正确命题是__________.(写出所有正确命题的序号) 三、解答题(本题包括6个小题,共70分)17.《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表: 评分 1 2 3 4 5 6 7 8 9 10 频率0.030.020.020.030.040.050.080.150.210.36(1)求观众评分的平均数?(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用ξ表示评分为10分的人数,求ξ的分布列及数学期望.18.已知椭圆2222:1()x y C a b a b+=>的离心率为12,1F ,2F 分别是其左、右焦点,且过点(2,3)A .(1)求椭圆C 的标准方程;(2)若在直线6y x =+上任取一点P ,从点P 向12AF F ∆的外接圆引一条切线,切点为Q .问是否存在点M ,恒有PM PQ =?请说明理由.19.(6分)唐代饼茶的制作一直延续至今,它的制作由“炙”、“碾”、“罗”三道工序组成:根据分析甲、乙、丙三位学徒通过“炙”这道工序的概率分别是0.5,0.6,0.5;能通过“碾”这道工序的概率分别是0.8,0.5,0.4;由于他们平时学徒刻苦,都能通过“罗”这道工序; 若这三道工序之间通过与否没有影响,(Ⅰ) 求甲、乙、丙三位同学中恰好有一人通过“炙”这道工序的概率,(Ⅱ)设只要通过三道工序就可以制成饼茶,求甲、乙、丙三位同学中制成饼茶人数X 的分布列. 20.(6分)选修4-5:不等式选讲设函数()121f x x x =--+的最大值为m . (1)求m ;(2)若()222,,0,,2a b c a b c m ∈+∞++=,求ab bc +的最大值.21.(6分)某市要对该市六年级学生进行体育素质调查测试,现让学生从“跳绳、短跑400米、长跑1000米、仰卧起坐、游泳100米、立定跳远”6项中选择3项进行测试,其中“短跑、长跑、仰卧起坐”3项中至少选择其中1项进行测试.现从该市六年级学生中随机抽取了50名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中x y <)已知从所调查的50名学生中任选2名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为49,记ξ为这2名学生选择“短跑、长跑、仰卧起坐”的项目个数之和. (1)求x 的值;(2)求随机变量ξ的分布列和数学期望.22.(8分)现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量y 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量x 表示,数据如下表:(1)求y 关于x 的线性回归方程(计算结果精确到0.01);(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1).参考公式及数据:回归直线方程ˆˆˆybx a =+中斜率和截距的最小二乘法估计公式分别为 121(x x)(y y)ˆˆˆ,(x x)niii nii ba y bx ==--==--∑∑,其中72193,9.3,()()9.9i ii x y x x y y ===--=∑. 参考答案一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意) 1.A 【解析】显然由于21,log 0x x ≥≥,所以当m<0时,函数f( x)= m+log 2x (x≥1)存在零点;反之不成立,因为当m=0时,函数f(x)也存在零点,其零点为1,故应选A . 2.A 【解析】 【分析】根据题目可知,分别求出男生甲被选中的概率和男生甲女生乙同时被选中的概率,根据条件概率的公式,即可求解出结果. 【详解】由题意知,设“男生甲被选中”为事件A ,“女生乙被选中”为事件B ,则2536101()202C P A C ===,14361()5C P AB C ==,所以()2()()5P AB P B A P A ==,故答案选A . 【点睛】本题主要考查了求条件概率方法:利用定义计算()()()P AB P B A P A =,特别要注意()P AB 的求法. 3.A 【解析】 【分析】由已知可知100件产品中有6件次品,94件正品,设“前两次抽到正品”为事件A ,“第三次抽到次品”为事件B ,求出()P A 和()P AB ,即可求得答案. 【详解】由已知可知100件产品中有6件次品,94件正品,设“前两次抽到正品”为事件A ,“第三次抽到次品”为事件B ; 则949394936(),()100991009998P A P AB =⨯=⨯⨯ ∴()63(|)()9849P AB P B A P A === 故选:A. 【点睛】本题是一道关于条件概率计算的题目,关键是掌握条件概率的计算公式,考查了分析能力和计算能力,属于中档题. 4.B 【解析】分析:确定函数y lnx =过定点(1,0)关于x=1对称点,代入选项验证即可.详解:函数y lnx =过定点(1,0),(1,0)关于x=1对称的点还是(1,0),只有()y ln 2x =-过此点. 故选项B 正确点睛:本题主要考查函数的对称性和函数的图像,属于中档题. 5.A 【解析】 【分析】根据幂函数的定义,求出m 的值,代入判断即可. 【详解】Q 函数()()22231mm f x m m x +-=--是幂函数,211m m ∴--=,解得:2m =或1m =-,2m =时,()f x x =,其图象与两坐标轴有交点不合题意,1m =-时,()41f x x=,其图象与两坐标轴都没有交点,符合题意, 故1m =-, 故选A . 【点睛】本题考查了幂函数的定义,考查常见函数的性质,是一道常规题. 6.C 【解析】分析:根据函数()()32*312f x x mx nx m N=-++∈在1x =-处取得极值解得360m n ++=,由于*m N ∈,对任意(),270x R f x +'∈>恒成立,则0<n ,确定m n 、的值。
蒙氏感官中班几何图形嵌板橱平行四边形教案蒙氏教育的原则:
以儿童为主ー一为的是给孩子打造一个以他们为中心,让他们可以独立“做自己"的“儿童世界”。
走线——在安静的环境下让孩子进入工作。
传递工作的开展,让孩子学会基本的礼仪——“给你”“谢谢”。
老师介绍今天的工作:《几何图形嵌板橱》
教学目标:
1、通过视觉和触觉的共同作用,帮助学生认识四边形(平行四边形、等腰梯形、不等边梯形)及曲线圆形(卵形、椭圆形花边型、曲线三角形)。
2、培养学生对几何图形从具体到抽象的认识。
3、加强注意力及观察力的训练。
取工作毯。
老师为孩子示范今天的工作。
孩子动手进行操作。
丰富的教材与教具。
教具是孩子工作的材料,孩子通过“工作”,从自我重复操作练习中,建构完善的人格。
蒙氏尊重儿童的成长步调一一蒙氏科学幼教没有课表,不划分上下课时间,让儿童寻着内心的需求,自由的专心工作。
蒙特梭利认为,孩子的专心时刻如果被打断,会养成孩子虎头蛇尾的习性。
反之,这种经重复练习而延长工作的时间,则能培养孩子重要的良好习性一一专心和耐力。
蒙氏几何图形嵌板教案精品文档蒙氏几何图形嵌板教案蒙氏教案-几何图形嵌板橱第一层圆形的命名工作名称:几何图形嵌板橱第一层圆形的命名教具构成:六个圆在排序的基础上完成教学目的:认识平面几何图形,锻炼手眼协调性,控制手部肌肉的能力,为写字打基础,为学习几何体基础,培养注意力和观察力。
适应年龄:三岁以上教学过程:一、开始部分:1、教师报工作名称。
2、教师用正确的方法取教具。
二、进行部分:1、请幼儿将圆形将从大到小的顺序排序。
2、教师取出最大的圆与最小的圆。
3、教师指着最大的圆说:大圆、大圆、大圆。
教师指着最小的圆说:小圆、小圆、小圆。
4、请问小圆在哪里,请问大圆在哪里,5、请问这个是怎样的圆,请问这个是怎样的圆,三、结束部分:1、老师的工作做完了现在请小朋友来操作。
1 / 3精品文档2、收起教具并送回教具柜。
教育活动:蒙氏活动活动名称:几何图形嵌板橱——多边形活动准备:几何图形嵌板橱圆形抽屉,五个多边形。
直接目的:1、通过视觉和触觉的共同作用,帮助幼儿认识各种多边图形;2、培养幼儿对几何图形从具体到抽象的认识间接目的:1、锻炼手部肌肉的控制力;2、为读书写字做好预备工作;3、为学习平面几何作预备工作;4培养幼儿的逻辑推理能力。
活动过程:1、将第二层抽屉稍稍拉出,手握住两端慢慢地把抽屉拿出放在毯上。
2、老师坐在幼儿右侧。
3、将5个长方形嵌板一一取出散放在地毯上。
告诉幼儿“这些都是多边形”。
4、左手拿起1个五边形嵌板,翻转过来,右手中指和食指轻轻触摸圆周,在轻轻抚摸图形框内侧,边摸边说:2 / 3精品文档“五边形。
”如操作屉的操作方法,将嵌板潜入大小相同的图形框内。
5、同法,认识六边形、七边形等,将5个多边形嵌板慢慢嵌回图形框内。
6、鼓励幼儿尝试。
7、进行三段式名称练习,使幼儿认识“多边形”。
8、将圆形屉放回原处。
?3 / 3。
蒙氏三角形嵌板教案
教具构成:鱼的嵌板
教育目的:直接目的:培养孩子观察能力
间接能力:培养CCIO的能力
操作过程:
开始部分今天老师给小朋友带来了一项鱼的嵌板的工作
教学部分
1、从教具柜取出嵌板,介绍“这是一条大鱼。
”
2、右手把嵌板冲嵌板框中取出散放
3、划定范围,选中其中鱼头的嵌板
4、触摸嵌板和嵌板框
5、嵌入嵌板,“这是鱼头。
”
6、一次把嵌板嵌入进去。
结束部分我的工作做好了,感兴趣的小朋友可以尝试一下。
变化与延伸:其他动物的嵌板
适用年龄:3岁以上
错误控制:教具本身
吸引力:教具本身
成果:孩子能知道鱼的结构
活动名称:金属嵌板
教具构成:铁制嵌板、纸、笔
教育目的:
直接目的:能用手自然画出嵌板图形
间接目的:培养CCIO的能力
操作过程:
开始部分先让孩子坐在老师的两侧,“今天老师给小朋友们带来一项金属嵌板的工作。
教学部分
1、从教具柜上取下金属嵌板
2、把金属嵌板从嵌板框内取出
3、介绍嵌板图形:“小朋友们看看,这些都是哪些图形?”
4、去教具柜上取纸和笔。
5、左手拿着图形,右手拇指、食指、中指拿笔,把图形拓印在纸上。
6、其它图形按照上述步骤完成。
7、先放回笔,再放回嵌板。
8、全部画完后可把图形全部定在一起,做图形小书。
结束部分:我的工作做好了,感兴趣的小朋友可以来尝试一下。
变化与延伸:画出各种图形重叠
适用年龄:3岁以上
错误控制:教具本身
吸引力:教具本身
成果:孩子能自然地握笔书写几何图形嵌板1教案。
形状嵌板教案幼儿园一、教学目标1. 知识与技能1.能够正确辨认并说出常见的几何图形;2.能够根据图形的形态,选择正确的形状嵌板进行填充;3.能够从形状嵌板所使用的图形中,找出与其形状相同的图形。
2. 情感态度与价值观1.通过游戏学习,培养幼儿们探究、思考、动手的好习惯和兴趣;2.培养幼儿们的逻辑思维能力和空间想象能力;3.通过合作游戏,培养幼儿们的团队合作能力和互助精神。
二、教学重难点1. 主要重点1.学习几何图形,辨认识别常用图形;2.掌握使用形状嵌板填充,加深对几何图形的认识;3.通过游戏培养幼儿们的动手能力和思维能力。
2. 难点1.填充图形过程中的想象能力和思维训练;2.意识到图形的内部形态和空间分布的关系。
三、教学过程1. 导入1.引导孩子们回忆幼儿园前已学过的图形,如:圆形、正方形、矩形、三角形等;2.显示形状嵌板,提问孩子们熟知的几何图形。
2. 提高认知1.挑选一块形状嵌板进行审视,观察其形状和构造;2.确认嵌板中的每一个图形,孩子们逐一命名;3.使用形状嵌板,让孩子们练习将图形填充到相应的形状区域。
3. 游戏活动1.选择2-5种不同的形状嵌板以及相应的填充图形;2.参与者围成一圈,每个人随机发配一块形状嵌板和一些图形;3.互相询问对方手中的嵌板和图形,正确回答则得到对方的图形;4.在合理的时间内,将自己的图形分别嵌入对应形状嵌板的区域;5.参与者互相检查并确认填充是否正确,正确则记录分数;6.游戏结束后,积累分数的孩子获得奖励。
4. 拓展应用1.给孩子们一张纸,让他们在上面画出一个图形,将其切割并用形状嵌板填充;2.分组活动,让孩子们分组完成一道由多块形状嵌板组成的“大拼图”;3.挑选几块形状嵌板,让孩子们自己发配图形填充,提高自主探索能力。
四、教学评估与反馈1. 教师评估1.通过孩子们的表现辨认出学生的学习态度和学习效果;2.对于认知能力弱的孩子,可以进行个性化辅导。
2. 学生自评1.让孩子们在学习后自我检查并评估自己的学习效果;2.让孩子们分享学习过程中的所见所闻,提高学生自信心和表达能力。
蒙氏铁制嵌板操作方法
1. 准备工作:将蒙氏铁制嵌板放置在平整的桌面上,使用镊子或其它工具,将嵌板上的铁钉卸下。
2. 选嵌板:根据孩子的年龄和能力选择不同的嵌板,切勿贪图大而难,应从简单的开始,逐步提高难度。
3. 安放位置:将嵌板放置在桌面上,确保其稳定性,不易移动或倾斜。
4. 操作方法:将铁钉插到嵌板孔中,调整方向和深度,确保每只铁钉都插紧,并且与嵌板平齐。
5. 操作注意事项:操作过程中应注意手指不要被铁钉扎伤。
同时,还需注意铁钉与嵌板的插入和拔出顺序,避免铁钉被卡住或失踪。
6. 收拾清理:完成后,将铁钉按照规定归位,清洁嵌板和工具,并将其放在干燥通风的地方。
7. 升级挑战:当孩子熟练掌握基本操作后,可尝试更复杂的嵌板,提高孩子的动手能力和创造力。