经济博弈论第六章不完全信息静态博弈PPT课件
- 格式:ppt
- 大小:447.00 KB
- 文档页数:39








3 不完全信息静态博弈3.1 简介博弈论在1970年代之后逐渐进入主流经济学体系,主要是由于它在不完全信息条件下的经济分析中表现出特别的优势。
不完全信息指经济活动中一部分经济主体的某些特征对于其他主体来说是不清楚的。
如在拍卖商品或工程招投标中。
信息不完全又称为信息不对称,即其他局中人没有特定局中人清楚特定局中人自身的特征。
不完全信息静态博弈就是假定某些局中人具有其他局中人不清楚的某些特征的静态博弈。
但对于局中人本身来说,他自身的这些不为人所知的特征对于他自己来说是清楚的,因而称这些特征为局中人自己拥有的“私人信息”(private information)。
在博弈论中,习惯地将局中人的“私人信息”集中表现为局中人的支付函数特征,也就是说,局中人的私人特征将完全通过其支付函数特征表征出来,而不完全信息就表现为一些局中人不清楚另一局中人的支付函数,当然,每个局中人是完全清楚自己的支付函数的。
3.2 理论: 静态贝叶斯博弈和贝叶斯纳什均衡在假定局中人拥有私人信息的情况下,其他局中人对特定局中人的支付函数类型并不清楚,局中人不知道他在与谁博弈,在1967年前,博弈论专家认为此时博弈的结构特征是不确定的,无法进行分析。
Harsanyi (1967、1968)提出了一种处理不完全信息博弈的方法,即引入一个虚拟的局中人——“自然N ”。
N 首先行动,决定每个局中人的特征。
每个局中人知道自己的特征,但不知道其他局中人特征。
这种方法将不完全信息静态博弈变成一个两阶段动态博弈,第一个阶段是自然N 的行动选择,第二阶段是除N 外的局中人的静态博弈。
这种转换被称为“Harsanyi 转换”,它将不完全信息博弈转换为完全但不完美信息博弈。
局中人拥有的私人信息为他的“类型”,由其支付函数决定,故常将支付函数等同于类型。
用i θ表示局中人i 的一个特定类型,i H 表示局中人i 所有可能类型的集合,即i i H ∈θ,称i H 为局中人i 的类型空间,n i ,,1 =。

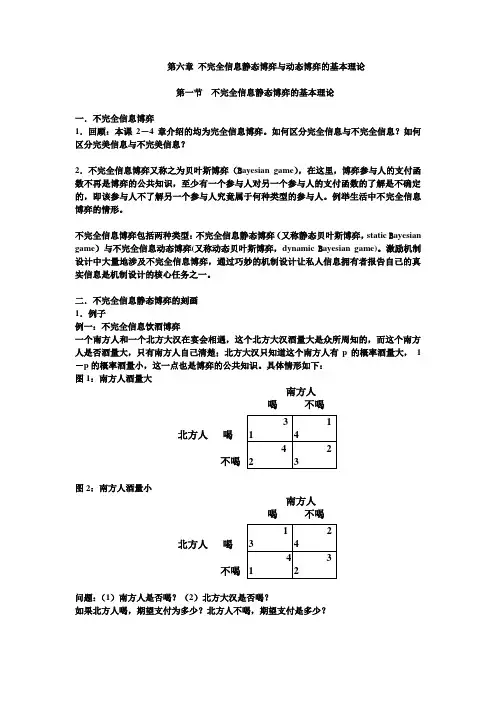
第六章不完全信息静态博弈与动态博弈的基本理论第一节不完全信息静态博弈的基本理论一.不完全信息博弈1.回顾:本课2-4章介绍的均为完全信息博弈。
如何区分完全信息与不完全信息?如何区分完美信息与不完美信息?2.不完全信息博弈又称之为贝叶斯博弈(B ayesian game),在这里,博弈参与人的支付函数不再是博弈的公共知识,至少有一个参与人对另一个参与人的支付函数的了解是不确定的,即该参与人不了解另一个参与人究竟属于何种类型的参与人。
例举生活中不完全信息博弈的情形。
不完全信息博弈包括两种类型:不完全信息静态博弈(又称静态贝叶斯博弈,static B ayesian game)与不完全信息动态博弈(又称动态贝叶斯博弈,dynamic B ayesian game)。
激励机制设计中大量地涉及不完全信息博弈,通过巧妙的机制设计让私人信息拥有者报告自己的真实信息是机制设计的核心任务之一。
二.不完全信息静态博弈的刻画1.例子例一:不完全信息饮酒博弈一个南方人和一个北方大汉在宴会相遇,这个北方大汉酒量大是众所周知的,而这个南方人是否酒量大,只有南方人自己清楚;北方大汉只知道这个南方人有p的概率酒量大,1-p的概率酒量小,这一点也是博弈的公共知识。
具体情形如下:图1:南方人酒量大南方人喝不喝北方人喝不喝图2:南方人酒量小南方人喝不喝北方人喝不喝问题:(1)南方人是否喝?(2)北方大汉是否喝?如果北方人喝,期望支付为多少?北方人不喝,期望支付是多少?例二:不完全信息古诺竞争模型(1)假设该市场上只有两家生产同一产品的企业1和2;市场均衡价格由下式决定: ()P Q a Q =-,其中12Q q q =+,1q 、2q 分别代表企业1和2提供的产量;企业1的生产成本为:111()C q cq =,这一点是博弈双方的公共知识;企业1对企业2的成本函数是不确定的,即企业2的成本函数是企业2的私人信息,企业1只知道企业2的成本函数有θ的概率为:222()h C q c q =,有1-θ的概率为222()l C q c q =,其中h l c c >,这一点也是博弈的公共知识。
