BP神经网络结构图

載师信号（期望输出信号）图1-7神经网络学习系统框图输入部接收外来的输入样本X,由训练部进行网络的权系数W调整，然后由输岀部输岀结果。

在这个过程中，期望的输出信号可以作为教师信号输入，由该教师信号与实际输出进行比较，产生的误差去控制修改权系数W学习机构可用图1—8所示的结构表示。

在图中，X，X2，…，X n，是输入样本信号，W，W，…，W是权系数。

输入样本信号X可以取离散值0”或1”输入样本信号通过权系数作用，在u产生输岀结果口WX，即有：u=B/VX =WX i +WX2 + …+WX n再把期望输岀信号丫(t)和u进行比较，从而产生误差信号e。

即权值调整机构根据误差e去对学习系统的权系数进行修改，修改方向应使误差e变小，不断进行下去，使到误差e为零，这时实际输出值u和期望输出值丫(t)完全一样，则学习过程结束。

期望辑出y图学可机构神经网络的学习一般需要多次重复训练，使误差值逐渐向零趋近，最后到达零。

则这时才会使输岀与期望一致。

故而神经网络的学习是消耗一定时期的，有的学习过程要重复很多次，甚至达万次级。

原因在于神经网络的权系数W有很多分量W，W，----W n ；也即是一个多参数修改系统。

系统的参数的调整就必定耗时耗量。

目前，提高神经网络的学习速度，减少学习重复次数是十分重要的研究课题，也是实时控制中的关键问题。

、感知器的学习算法感知器是有单层计算单元的神经网络，由线性元件及阀值元件组成。

感知器如图感知器的数学模型:v=f[加讯-e] (1-12)其中：f[.]是阶跃函数，并且有pl 2二主W凶-0工01 —1>u=SW i X^-0<O“1(1-13)9是阀值。

感知器的最大作用就是可以对输入的样本分类，故它可作分类器，感知器对输入信号的分类如下:卩，A类Y = * —B 类(1-14)1-9所示。

f [sw iX£-O]1时，输入样本称为A类；输岀为-1时，输入样本称为B类。

BP神经网络概述BP神经网络由输入层、隐藏层和输出层组成。

输入层接收外界输入的数据，隐藏层对输入层的信息进行处理和转化，输出层输出最终的结果。

网络的每一个节点称为神经元，神经元之间的连接具有不同的权值，通过权值的调整和激活函数的作用，网络可以学习到输入和输出之间的关系。

BP神经网络的学习过程主要包括前向传播和反向传播两个阶段。

前向传播时，输入数据通过输入层向前传递到隐藏层和输出层，计算出网络的输出结果；然后通过与实际结果比较，计算误差函数。

反向传播时，根据误差函数，从输出层开始逆向调整权值和偏置，通过梯度下降算法更新权值，使得误差最小化，从而实现网络的学习和调整。

BP神经网络通过多次迭代学习，不断调整权值和偏置，逐渐提高网络的性能。

学习率是调整权值和偏置的重要参数，过大或过小的学习率都会导致学习过程不稳定。

此外，网络的结构、激活函数的选择、错误函数的定义等也会影响网络的学习效果。

BP神经网络在各个领域都有广泛的应用。

在模式识别中，BP神经网络可以从大量的样本中学习特征，实现目标检测、人脸识别、手写识别等任务。

在数据挖掘中，BP神经网络可以通过对历史数据的学习，预测未来的趋势和模式，用于市场预测、股票分析等。

在预测分析中，BP神经网络可以根据历史数据，预测未来的房价、气温、销售额等。

综上所述，BP神经网络是一种强大的人工神经网络模型，具有非线性逼近能力和学习能力，广泛应用于模式识别、数据挖掘、预测分析等领域。

尽管有一些缺点，但随着技术的发展，BP神经网络仍然是一种非常有潜力和应用价值的模型。

5.4 BP神经网络的基本原理BP（Back Propagation）网络是1986年由Rinehart和McClelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。

BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)（如图5.2所示）。

5.4.1 BP神经元图5.3给出了第j个基本BP神经元（节点），它只模仿了生物神经元所具有的三个最基本也是最重要的功能：加权、求和与转移。

其中x1、x2…xi…xn分别代表来自神经元1、2…i…n的输入；wj1、wj2…wji…wjn则分别表示神经元1、2…i…n与第j个神经元的连接强度，即权值；bj 为阈值；f(·)为传递函数；yj为第j个神经元的输出。

第j个神经元的净输入值为：（5.12）其中：若视，，即令及包括及，则于是节点j的净输入可表示为：（5.13）净输入通过传递函数（Transfer Function）f (·)后，便得到第j个神经元的输出:（5.14）式中f(·)是单调上升函数，而且必须是有界函数，因为细胞传递的信号不可能无限增加，必有一最大值。

5.4.2 BP网络BP算法由数据流的前向计算（正向传播）和误差信号的反向传播两个过程构成。

正向传播时，传播方向为输入层→隐层→输出层，每层神经元的状态只影响下一层神经元。

若在输出层得不到期望的输出，则转向误差信号的反向传播流程。

通过这两个过程的交替进行，在权向量空间执行误差函数梯度下降策略，动态迭代搜索一组权向量，使网络误差函数达到最小值，从而完成信息提取和记忆过程。

5.4.2.1 正向传播设 BP网络的输入层有n个节点，隐层有q个节点，输出层有m个节点，输入层与隐层之间(·)，的权值为，隐层与输出层之间的权值为，如图5.4所示。

5.4 BP神经收集的基来源根基理之杨若古兰创作BP（Back Propagation）收集是1986年由Rinehart和McClelland为首的科学家小组提出，是一种按误差逆传播算法练习的多层前馈收集，是目前利用最广泛的神经收集模型之一.BP收集能进修和存贮大量的输入-输出模式映照关系，而无需事前揭示描述这类映照关系的数学方程.它的进修规则是使用最速降低法，通过反向传播来不竭调整收集的权值和阈值，使收集的误差平方和最小.BP神经收集模型拓扑结构包含输入层（input）、隐层(hide layer)和输出层(output layer)（如图5.2所示）.5.4.1 BP神经元图5.3给出了第j个基本BP神经元（节点），它只模仿了生物神经元所具有的三个最基本也是最次要的功能：加权、求和与转移.其中x1、x2…x i…x n分别代表来自神经元1、2…i…n的输入；w j1、w j2…w ji…w jn则分别暗示神经元1、2…i…n与第j个神经元的连接强度，即权值；b j为阈值；f(·)为传递函数；y j为第j个神经元的输出.第j个神经元的净输入值为：（5.12）其中：若视，，即令及包含及，则因而节点j的净输入可暗示为：（5.13）净输入通过传递函数（Transfer Function）f (·)后，便得到第j 个神经元的输出:（5.14）式中f(·)是单调上升函数，而且必须是有界函数，因为细胞传递的旌旗灯号不成能无穷添加，必有一最大值.5.4.2 BP收集BP算法由数据流的前向计算（正向传播）和误差旌旗灯号的反向传播两个过程构成.正向传播时，传播方向为输入层→隐层→输出层，每层神经元的形态只影响下一层神经元.若在输出层得不到期望的输出，则转向误差旌旗灯号的反向传播流程.通过这两个过程的交替进行，在权向量空间履行误差函数梯度降低计谋，动态迭代搜索一组权向量，使收集误差函数达到最小值，从而完成信息提取和记忆过程.5.4.2.1 正向传播设 BP收集的输入层有n个节点，隐层有q个节点，输出层有m个节点，输入层与隐层之间的权值为，隐层与输出层之间的权值为，如图5.4所示.隐层的传递函数为f1(·)，输出层的传递函数为f2(·)，则隐层节点的输出为（将阈值写入求和项中）：k=1,2,……q （5.15）输出层节点的输出为：j=1,2,……m （5.16）至此B-P收集就完成了n维空间向量对m维空间的近似映照.5.4.2.2 反向传播1) 定义误差函数输入个进修样本，用来暗示.第个样本输入到收集后得到输出（j=1,2,…m）.采取平方型误差函数，因而得到第p个样本的误差E p：（5.17）式中：为期望输出.对于个样本，全局误差为：（5.18）2）输出层权值的变更采取累计误差BP算法调整，使全局误差变小，即（5.19）式中：—进修率定义误差旌旗灯号为：（5.20）其中第一项：（5.21）第二项：（5.22）是输出层传递函数的偏微分.因而：（5.23）由链定理得：（5.24）因而输出层各神经元的权值调整公式为：（5.25）3）隐层权值的变更（5.26）定义误差旌旗灯号为：（5.27）其中第一项：（5.28）依链定理有：（5.29）第二项：（5.30）是隐层传递函数的偏微分.因而：（5.31）由链定理得：（5.32）从而得到隐层各神经元的权值调整公式为：（5.33）5.4.3 BP算法的改进BP算法理论具有根据可靠、推导过程严谨、精度较高、通用性较好等长处，但尺度BP算法存在以下缺点：收敛速度缓慢；容易堕入局部极小值；难以确定隐层数和隐层节点个数.在实际利用中，BP算法很难胜任，是以出现了很多改进算法.1）利用动量法改进BP算法尺度BP算法实质上是一种简单的最速降低静态寻优方法，在批改W(K)时，只按照第K步的负梯度方向进行批改，而没有考虑到之前积累的经验，即之前时刻的梯度方向，从而经常使进修过程发生振荡，收敛缓慢.动量法权值调整算法的具体做法是：将上一次权值调整量的一部分迭加到按本次误差计算所得的权值调整量上，作为本次的实际权值调整量，即：（）其中：α为动量系数，通常0＜α＜0.9；η—进修率，范围在0.001～10之间.这类方法所加的动量因籽实际上相当于阻尼项，它减小了进修过程中的振荡趋势，从而改善了收敛性.动量法降低了收集对于误差曲面局部细节的敏感性，无效的按捺了收集堕入局部极小.2）自适应调整进修速率尺度BP算法收敛速度缓慢的一个次要缘由是进修率选择不当，进修率选得太小，收敛太慢；进修率选得太大，则有可能批改过头，导致振荡甚至发散.可采取图5.5所示的自适应方法调整进修率.调整的基本指点思想是：在进修收敛的情况下，增大η，以缩短进修时间；当η偏大导致不克不及收敛时，要及时减小η，直到收敛为止.3）动量-自适应进修速率调整算法采取动量法时，BP算法可以找到更优的解；采取自适应进修速率法时，BP算法可以缩短练习时间.将以上两种方法结合起来，就得到动量-自适应进修速率调整算法.4） L-M进修规则L-M（Levenberg-Marquardt）算法比前述几种使用梯度降低法的BP 算法要快得多，但对于复杂成绩，这类方法须要相当大的存储空间.L-M(Levenberg-Marquardt)优化方法的权值调整率选为:（5.35）其中：e—误差向量；J—收集误差对权值导数的雅可比（Jacobian）矩阵；μ—标量，当μ很大时上式接近于梯度法，当μ很小时上式酿成了Gauss-Newton法，在这类方法中，μ也是自适应调整的.综合考虑，拟采取L-M进修规则和动量法分别作为神经收集的练习函数和进修函数.5.5 BP神经收集的练习计谋及结果本文借助于MATLAB神经收集工具箱来实现多层前馈BP收集（Multi-layer feed-forward backpropagation network）的色彩空间转换，免去了很多编写计算机程序的烦恼.神经收集的实际输出值与输入值和各权值和阈值有关，为了使实际输出值与收集期望输出值相吻合，可用含有必定数量进修样本的样本集和响应期望输出值的集合来练习收集.练习时仍然使用本章5.2节中所述的实测样本数据.另外，目前尚未找到较好的收集构造方法.确定神经收集的结构和权系数来描述给定的映照或迫近一个未知的映照，只能通过进修方式得到满足请求的收集模型.神经收集的进修可以理解为：对确定的收集结构，寻觅一组满足请求的权系数，使给定的误差函数最小.设计多层前馈收集时，次要偏重试验、探讨多种模型方案，在实验中改进，直到拔取一个满意方案为止，可按以下步调进行：对任何实际成绩先都只选用一个隐层；使用很少的隐层节点数；不竭添加隐层节点数，直到获得满意功能为止；否则再采取两个隐层反复上述过程.练习过程实际上是根据目标值与收集输出值之间误差的大小反复调整权值和阈值，直到此误差达到预定值为止.5.5.1 确定BP收集的结构确定了收集层数、每层节点数、传递函数、初始权系数、进修算法等也就确定了BP收集.确定这些选项时有必定的指点准绳，但更多的是靠经验和试凑.1）隐层数的确定：1998年Robert Hecht-Nielson证实了对任何在闭区间内的连续函数，都可以用一个隐层的BP收集来迫近，因此一个三层的BP收集可以完成任意的n维到m维的映照.是以我们从含有一个隐层的收集开始进行练习.2） BP收集经常使用传递函数:BP收集的传递函数有多种.Log-sigmoid型函数的输入值可取任意值，输出值在0和1之间；tan-sigmod型传递函数tansig的输入值可取任意值，输出值在-1到+1之间；线性传递函数purelin的输入与输出值可取任意值.BP收集通常有一个或多个隐层，该层中的神经元均采取sigmoid型传递函数，输出层的神经元则采取线性传递函数，全部收集的输出可以取任意值.各种传递函数如图5.6所示.只改变传递函数而其余参数均固定，用本章5.2节所述的样本集练习BP收集时发现，传递函数使用tansig函数时要比logsig函数的误差小.因而在当前的练习中隐层传递函数改用tansig函数，输出层传递函数仍选用purelin函数.3）每层节点数的确定：使用神经收集的目的是实现摄像机输出RGB色彩空间与CIE-XYZ 色空间转换，是以BP收集的输入层和输出层的节点个数分别为3.上面次要介绍隐层节点数量的确定.对于多层前馈收集来说，隐层节点数的确定是成败的关键.若数量太少，则收集所能获取的用以解决成绩的信息太少；若数量太多，不但添加练习时间，更次要的是隐层节点过多还可能出现所谓“过渡吻合”（Overfitting）成绩，即测试误差增大导致泛化能力降低，是以合理选择隐层节点数非常次要.关于隐层数及其节点数的选择比较复杂，普通准绳是：在能准确反映输入输出关系的基础上，应选用较少的隐层节点数，以使收集结构尽量简单.本论文中采取收集结构增加型方法，即先设置较少的节点数，对收集进行练习，并测试进修误差，然后逐步添加节点数，直到进修误差不再有明显减少为止.5.5.2 误差的拔取在神经收集练习过程当选择均方误差MSE较为合理，缘由如下：①尺度BP算法中，误差定义为：（5.36）每个样本感化时，都对权矩阵进行了一次点窜.因为每次权矩阵的点窜都没有考虑权值点窜后其它样本感化的输出误差是否也减小，是以将导致迭代次数添加.②累计误差BP算法的全局误差定义为：（5.37）这类算法是为了减小全部练习集的全局误差，而不针对某一特定样本，是以如果作某种点窜能使全局误差减小，其实不等于说每一个特定样本的误差也都能同时减小.它不克不及用来比较P和m分歧的收集功能.因为对于同一收集来说，P越大，E也越大； P值不异，m越大E也越大.③均方误差MSE：（5.38）其中:—输出节点的个数，—练习样本数目，—收集期望输出值，—收集实际输出值.均方误差克服了上述两种算法的缺点，所以选用均方误差算法较合理.5.5.3 练习结果练习一个单隐层的三层BP收集，根据如下经验公式选择隐层节点数[125]：（5.39）式中：n为输入节点个数，m为输出节点个数，a为1到10之间的常数.针对本论文n1取值范围为3～13.练习结果如表5.1所示.隐层节点数与误差的关系隐层神经元个数练习误差测试误差345678910111213由上表可以看出：①添加隐层节点数可以减少练习误差，但超出10当前测试误差发生动摇，即泛化能力发生变更.综合比较隐层节点数为10与12的练习误差和测试误差，决定隐层节点数选用12.②练习误差和测试误差都很大,而且收敛速度极慢（练习过程如图5.7所示），这个成绩可以通过对输出量进行归一化来解决.根据Sigmoid型传递函数输入和输出的范围，对输入变量不进行归一化处理，只对输出变量进行归一化，这是因为在输出数据请求归一化的同时，对输入数据也进行归一化的话，权值的可解释性就更差了.目标值按下式进行变更：（5.40）使目标值落在～之间，如许靠近数据变更区间端点的收集输出值就有一动摇范围，收集的功能较好.用重生成的练习样本与测试样本对隐层节点数为12的收集进行练习，得到的练习误差为×10-5，测试误差为×10-4，达到了预定的目标（练习过程如图所示）.5.6 终极练习后的神经收集结构采取三层BP收集实现摄像机输出RGB色彩空间与CIEXYZ色空间转换，其中隐层含有12个节点，传递函数采取tansig函数；输出层传递函数选用purelin函数.经过测试后结果满意，可以认为该神经收集可以用来实现这个关系映照.收集的结构如图所示：得到的BP神经收集的权值和阈值为：5.7 本章小结1) 定量地分析了用线性关系转换摄像机RGB空间到CIE-XYZ空间数据后发生的均方误差，标明CCD摄像机与尺度观察者之间有比较明显的不同，也就是说RGB与CIE-XYZ间的转换是非线性的.2) 采取MATLAB 中神经收集工具箱实现多层前馈BP收集的RGB到CIEXYZ色彩空间转换，用经过归一化的练习样本与测试样本对隐层节点数为12的三层收集进行练习，得到的练习误差为×10-5，测试误差为×10-4，结果标明经过练习的多层前馈BP收集可以满足RGB空间向CIEXYZ色彩空间转换请求，达到了预定目标.3) 确定了用于RGB和XYZ色彩空间转换的BP收集结构，并求出了该神经收集的权值和阈值.使用该收集可以定量表达食品色彩，定量比较高压加工食品色彩的变更，可以使食品色彩测定和控制实现定量化，而不再是客观性很强的模糊描述.。

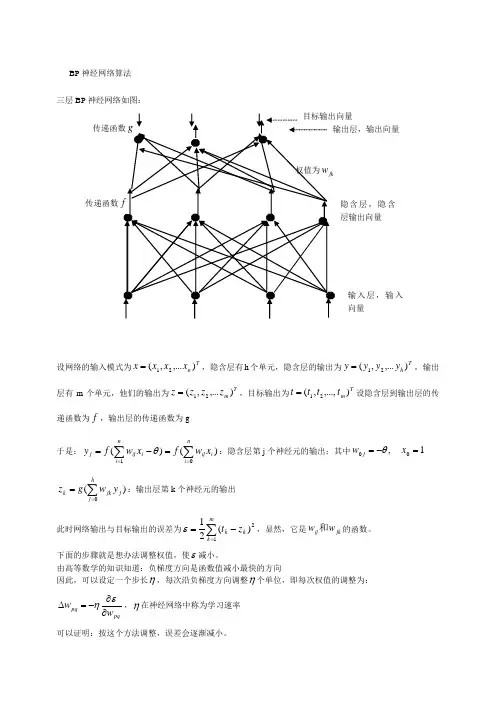
BP 神经网络算法 三层BP 神经网络如图：设网络的输入模式为Tn x x x x ),...,(21=，隐含层有h 个单元，隐含层的输出为Th y y y y ),...,(21=，输出层有m 个单元，他们的输出为Tm z z z z ),...,(21=，目标输出为Tm t t t t ),...,,(21=设隐含层到输出层的传递函数为f ，输出层的传递函数为g于是：)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ：隐含层第j 个神经元的输出；其中1,00=-=x w j θ)(0∑==hj j jk k y w g z ：输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε，显然，它是jk ij w w 和的函数。

下面的步骤就是想办法调整权值，使ε减小。

由高等数学的知识知道：负梯度方向是函数值减小最快的方向因此，可以设定一个步长η，每次沿负梯度方向调整η个单位，即每次权值的调整为：pqpq w w ∂∂-=∆εη，η在神经网络中称为学习速率 可以证明：按这个方法调整，误差会逐渐减小。

隐含层，隐含层输出向量传递函数输入层，输入向量BP 神经网络（反向传播）的调整顺序为： 1）先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0-------复合函数偏导公式若取x e x f x g -+==11)()(，则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为： 2）从输入层到隐含层的权值调整迭代公式为： 其中j u 为隐含层第j 个神经元的输入：∑==ni i ijj x wu 0注意：隐含层第j 个神经元与输出层的各个神经元都有连接，即jy ∂∂ε涉及所有的权值ij w ，因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是：因此从输入层到隐含层的权值调整迭代为公式为： 例：下表给出了某地区公路运力的历史统计数据，请建立相应的预测模型，并对给出的2010和2011年的数据，预测相应的公路客运量和货运量。