井筒问题的耦合渗流及应力分析
- 格式:doc
- 大小:188.50 KB
- 文档页数:7


渗流-应力耦合作用下边坡支护稳定性分析渗流-应力耦合作用下边坡支护稳定性分析在岩土工程领域中,边坡稳定性一直是一个重要的研究方向。
边坡工程中的稳定性问题往往涉及到多种因素,如地下水渗流、土体的力学性质等。
其中,渗流-应力耦合作用是边坡稳定性分析中的重要考虑因素之一。
本文将重点分析渗流-应力耦合作用对边坡支护稳定性的影响并进行详细讨论。
首先,我们需要了解渗流-应力耦合作用的基本概念。
渗流-应力耦合作用是指地下水渗流与土体应力状态相互影响的过程。
在边坡工程中,当地下水渗流进入土体中时,水力压力会改变土体的力学性质,从而对边坡的稳定性产生影响。
同时,土体的应力状态也会影响地下水的渗流路径和速度。
因此,边坡稳定性的分析必须考虑渗流-应力耦合作用。
接下来,我们将详细分析渗流-应力耦合作用对边坡支护稳定性的影响。
首先,渗流-应力耦合作用会导致边坡内的水力压力变化。
当地下水渗流进入边坡内部时,水位的上升会增加土体中的水力压力,从而增加边坡的自重。
这会使边坡受到更大的重力作用,从而增加了边坡的倾覆风险。
此外,水力压力的增加还可能导致边坡土体的饱和度增加,从而引起土体的液化现象,使边坡更容易失稳。
其次,渗流-应力耦合作用还会改变边坡的有效应力分布。
当地下水渗流进入边坡内部时,水力压力的增加会降低土体的有效应力,在边坡支护结构处产生更大的水平承载力和竖向支撑力。
这会增加了边坡支护结构的稳定性,防止边坡的下滑和滑动。
然而,如果渗流-应力耦合作用导致边坡土体饱和度增加,土体的强度将大大降低,对支护结构的稳定性构成威胁。
最后,我们需要采取合适的工程措施来应对渗流-应力耦合作用对边坡支护稳定性的影响。
一方面,可以通过合理设计排水系统,控制地下水的渗流路径和速度,减小渗流对边坡稳定性的影响。
另一方面,可以选择适当的支护结构,提高边坡的抗滑能力和抗液化能力,确保边坡在渗流-应力耦合作用下的稳定性。
综上所述,渗流-应力耦合作用是影响边坡支护稳定性的重要因素。

水平井井筒流态分析方法1. 引言1.1 背景介绍水平井是一种在地下水平方向钻探开采资源的钻井方式,在石油、天然气等领域被广泛应用。
相较于传统的垂直井,水平井具有钻采效率高、产量大、开采成本低等优势,因此受到了广泛关注和应用。
在水平井井筒内,流体的运动状态对井下压力、产量等参数产生了重要影响,因此需要对水平井井筒流态进行分析研究。
水平井井筒流态分析是针对水平井内流体运动特点进行的研究,旨在探讨流体在水平井井筒内的流速、压力分布等参数规律。
通过对水平井井筒流态的分析,能够更好地了解井下流体的运动状态,为提高水平井的采油效率、优化井下生产操作提供重要参考依据。
本文将对水平井井筒流态特点、分析方法进行介绍,并结合压力梯度分析、流速分析等方法,探讨水平井井筒流态的规律和特点。
通过案例分析展示水平井井筒流态分析方法在实际生产中的应用与意义。
结合现有研究成果总结观点,展望水平井井筒流态分析方法在未来的发展方向和应用前景。
1.2 研究意义水平井在油田开发中具有重要作用,井筒内的流态分析对于了解地层状态、优化生产操作具有重要意义。
水平井井筒流态研究的意义主要体现在以下几个方面:1. 安全生产:水平井井筒内的流态特点直接影响井下环境,对井筒固液分离效果、防喷溢能力等安全生产因素具有重要影响。
通过深入研究水平井的流态特点,可以有效提升井下作业的安全性。
2. 提高产能:井筒内的流态状态直接影响油气的产能,通过深入研究井筒内流体的运动规律和特性,可以有针对性地优化对应井筒的生产措施,提高产能,提升油田的整体生产水平。
3. 节约成本:对水平井井筒流态的准确分析可以帮助企业更好地控制生产成本,合理规划生产方案,减少不必要的能源浪费和设备损耗,从而降低生产成本,提高经济效益。
水平井井筒流态分析具有重要的研究意义,对于提升油田生产效率、保障安全生产、节约生产成本具有积极的意义和价值。
在未来的研究中,继续深入探究水平井井筒流态特点,不断完善分析方法,将对油田开发和生产管理带来更多的实际效益和发展机遇。






渗流应力耦合(间接耦合)在岩土结构分析中,地下水位的变化往往会造成结构的受力变化,进而引起变形。
因此在计算中需要考虑地下水位的影响。
一、原理根据太沙基(Terzaghi)原理,总应力()可以分为有效应力()和孔隙水压力()。
水不能承受剪切应力,所以有效剪切应力和总的剪切应力相等。
即总应力的表达式如下:在GTS程序中,实现应力渗流耦合(间接)是根据以上公式,首先通过渗流计算得到有效应力计算需要的孔隙水压力,然后将该孔隙水压力调入到应力分析中(包括线性非线性静力分析、施工阶段分析、边坡稳定分析等)。
二、操作过程1、线性非线性静力分析、边坡稳定分析在这两类分析中,由于不考虑施工阶段,因此程序添加了其他工况的结果(主菜单-模型-荷载)命令。
通过该命令,用户可以将渗流分析工况得到的孔隙水压力调入到应力分析中,进而计算有效应力,利用有效应力原理进行计算。
图1 其他工况的结果需要注意的是:在分析工况定义的时候,需要激活该荷载组;导入的渗流可以包括稳定流分析、非稳定流分析、施工阶段(渗流)分析的结果,其中非稳定流和施工阶段需要指定时间段。
2、施工阶段分析在施工阶段分析中,用户可以根据渗流边界的变化设定渗流工况:根据有效应力原理,首先需要得到孔隙水压力。
在GTS 施工阶段中,需要在应力分析前定义阶段类型为渗流阶段(包括稳定流和非稳定流),这样程序会根据模型以及渗流边界条件计算得到孔隙水压力,然后程序自动把每个单元的孔隙水压力调入到下一步应力计算中去。
这里需要注意的是每一步渗流必须在应力分析前。
例如:考虑降水对周围结构物的影响。
(二维分析)模型模型如上图,考虑坑周围降水(在坑周围上设置节点流量边界),以实体代表建筑物。
模型建立和边界条件不详细说明。
先说明重点说明施工阶段的定义:建筑物 基坑周围降水第一步第一步计算初始渗流场,阶段类型定义为渗流(稳态)。
第二步第二步计算自重应力场,阶段类型定义为施工。
第三步第三步计算降水引起的渗流场,阶段类型定义为渗流(稳态)。
渗流-应力耦合作用对储层裂缝发育的影响研究宋子怡;王昊;李静;孙鲁宁;张加太;刘晨【摘要】裂缝是影响储层高产、稳产的重要因素,而储层处在复杂的地质环境中,裂缝的形成和发育受众多因素的影响,研究各因素间的耦合作用对储层裂缝发育的影响,对指导油气勘探开发具有重要意义.为此,针对任丘油田任11井区雾迷山组碳酸盐岩储层进行了渗流-应力耦合作用对储层裂缝发育的影响研究.研究结果表明:未考虑渗流-应力耦合作用时,研究区最大水平主应力范围为82~100 MPa,从西南到东北逐渐增大;最小水平主应力范围为72~88 MPa,从研究区中心向西南、东北两侧逐渐递增;考虑耦合作用后,研究区最大水平主应力范围为84~102 MPa,最小水平主应力范围为76~91 MPa,最大及最小水平主应力增加.渗流-应力耦合作用后,研究区裂缝发育指数分布在0.027~1.156之间,山头顶部和近东西向断层的内部区域裂缝发育指数在0.7左右,为裂缝较发育区域;而研究区西南和东北边缘区域裂缝发育指数在0.2以下,为裂缝欠发育区域.随着耦合作用时间的增长,储层裂缝发育指数逐渐增大,在注入井和产油井附近区域的裂缝发育指数增大幅度尤为明显;储层裂缝线密度也呈增大趋势,仅产油井周围的裂缝线密度呈现为先减小后增大的趋势;未考虑耦合作用时的储层裂缝参数小于考虑耦合作用后的裂缝参数,说明仅考虑应力场进行储层裂缝预测所得结果偏小.【期刊名称】《地质力学学报》【年(卷),期】2019(025)004【总页数】9页(P483-491)【关键词】储层裂缝;渗流;应力;耦合作用【作者】宋子怡;王昊;李静;孙鲁宁;张加太;刘晨【作者单位】中海油研究总院有限责任公司, 北京100028;中国石油大学 (华东) 地质力学与工程研究所, 山东青岛266580;中国石油大学 (华东) 地质力学与工程研究所, 山东青岛266580;中国石油大学 (华东) 地质力学与工程研究所, 山东青岛266580;中国石油大学 (华东) 地质力学与工程研究所, 山东青岛266580;中国石油大学 (华东) 地质力学与工程研究所, 山东青岛266580【正文语种】中文【中图分类】TE3190 引言储层裂缝是影响储层获得高产和稳产的重要因素,储层裂缝评价是油气勘探、开采的重要工作,也是油气地质学研究的重点和难点。
文章编号:100020747(2004)0120088203热采水平井变质量流与油藏渗流的耦合数值模拟吴淑红,于立君,刘翔鹗,郭尚平(中国科学院院士)(中国石油勘探开发研究院)摘要:为真实反映水平井及近井地带的流体流动情况,需要将水平井井筒内的流动与在油藏中的渗流耦合进行油藏数值模拟。
假设“微元段”,引用“交错网格”和“等效渗透率”概念,建立了热采水平井井筒变质量流的等效渗流模型;在此基础上提出耦合井筒变质量流与油藏渗流的水平井产量公式,建立了井筒变质量流与油藏渗流耦合的数学模型。
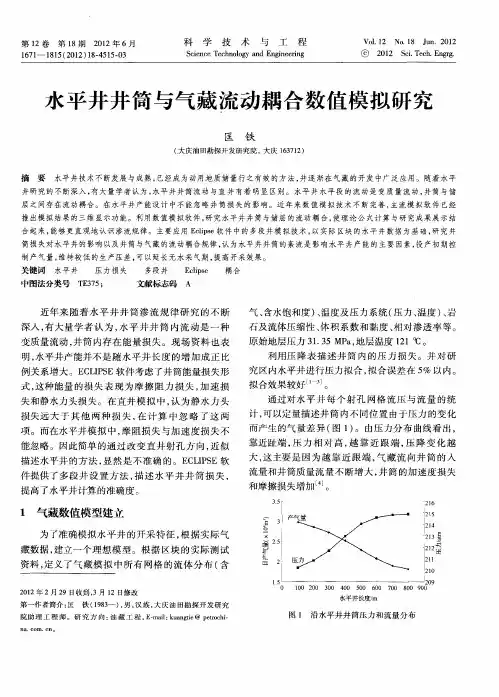
利用该模型进行热采水平井开采机理研究,认为:水平井井筒内的压降影响水平井生产动态,忽略压降将使计算的产油量和油汽比偏高;水平井所产油主要来自水平井筒的始端,在一定的油藏条件、水平井参数等情况下,每口水平井都有最优水平段长度。
图2表1参5关键词:水平井;变质量流;耦合;热采;数值模拟中图分类号:TE357.4;TE355.6 文献标识码:A 常规的热采水平井数值模拟中通常把水平井的水平井筒看作源/汇,不考虑水平井筒内流体的流动。
这样处理给计算带来了很大的方便,但是不符合实际的流动规律[1],因为在流体从油藏流入水平井井筒后再沿井筒流向生产端的过程中,不同的流入剖面对水平井筒中的流动影响不同,而井筒中的不同流动状况反过来又对油藏动态有着显著影响[2,3]。
为了更详细、准确地描述井筒和油藏的生产动态,必须综合考虑井筒内的多相流动以及油藏内的渗流情况,即耦合问题[4]。
1井筒变质量流与油藏渗流的耦合模型1.1“微元段”假设[5]将水平井筒划分为n个微元段,在保证水平井筒总流量不变的前提下,假定流入任一微元段的径向流量集中在两相邻微元段的交界面上,这样,每一微元段内的水平流动可以看作是不考虑径向流入的等质量流动。
任一微元段的流量为:Q i=Q i-1+Q r,i(1)根据假设条件,Q i在微元段i上保持不变。
1.2等效渗流模型[3]把流体在水平井筒内的流动看作是流体在多孔介质内的渗流时,其等效渗流方程为:V=-K weμd pd x(2) 令<we为井筒网格的等效孔隙度,有<we=πD2/(4ΔyΔz)单相层流时:K we=r w2/8<we单相紊流时:K we=μ2Dfρ1d p/d x<we两相流动时:K we=μm2Df tpρnsd pd x<we1.3交错网格在质量守恒方程、能量守恒方程的计算中采用一套网格(A系列),而等效渗流模型计算时采用另一套网格(B系列),这两个系列网格相互错开半个网格[5],构成交错网格。
井筒问题的耦合渗流及应力分析
摘要:如果不考虑岩石变形和流体扩散的耦合作用,孔隙介质油藏的常规渗流模型对流体的扩散解释是合理和准确的。
随着油藏越来越多的开采,流固耦合作用对流体扩散的影响是越来越显著,因此必须用多孔弹性理论来研究井筒问题的耦合渗流及应力。
本文推导了流固耦合作用下的孔隙压力、裂缝压力以及井壁围岩应力在Laplace空间的解析表达式,给出了一个模拟实例。
关键词:孔隙介质裂缝性油藏流固耦合Laplace变换
1 引言
多孔弹性理论[1~2]是用于处理饱含粘性液体的多孔介质弹性变形和孔隙流体渗流耦合问题。
它可以认为是多孔介质经典弹性理论的推广,也可以认为多孔介质经典渗流理论的推广。
孔隙中流体的存在改变了岩石的力学反应,孔隙流体扩散会导致岩石的体积变化或岩石应力状态的变化;反之岩石的应力作用也会制约或促进孔隙中流体扩散。
这种扩散-变形的耦合作用使岩石的反应具有了时间效应。
目前它不仅用于土力学中,而且广泛用于采矿工程、环境工程及石油工程。
2 孔隙-裂隙型双重孔隙介质流固耦合计算的耦合方程
由于裂缝性油藏的复杂性,即使用双重孔隙物理模型来处理,我们
也必须对其作出一些合理但有必要的假设。
对于双重孔隙介质,假设条件为:双重孔隙介质具有特征单元性质;孔隙和裂缝都是相互连通的且充满各自的空隙空间;岩石骨架是线弹性小变形材料;主生孔隙介质和次生孔隙介质中流体流速比较小,基本认为满足达西定律;主生孔隙介质和次生孔隙介质中孔隙和裂缝流体的压力、孔隙度及渗透率均不相同;主生孔隙和次生裂缝之间的流体渗流是拟稳态,用窜流函数描述;孔隙和裂缝中流体是单相;忽略流体重力和惯性力。
除了以上的假设,我们还规定孔隙流体压力和裂缝流体压力受压为正;岩石骨架受拉为正。
依据双重孔隙介质的有效应力定律、达西定律、流体-固体的质量守恒定律、本构方程、平衡方恒以及几何方程,经过数学运算可得到最终的双重孔隙介质流固耦合的微分方程,则相应的本构方程分别如下[3~5]:
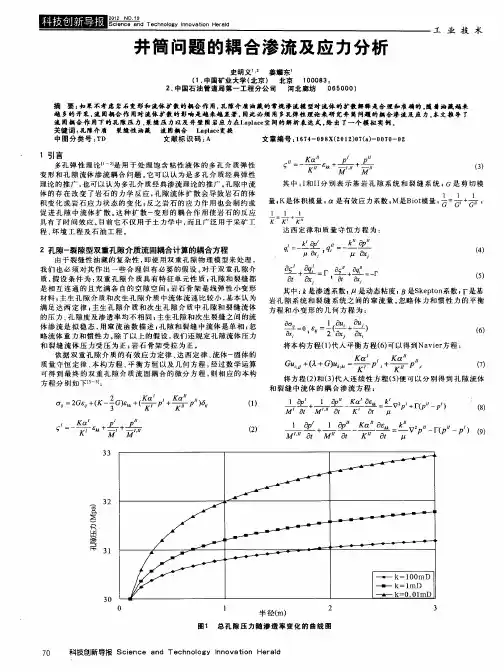
由第2本分求得耦合渗流下的孔隙压力,和耦合应力的解析或半解析解,借助Stehfest 拉普拉斯数值逆求解方法在VC++语言下编制了计算程序,模拟了各种模式下的压力和应力分布,分别如图1、图2所示。
从图1和图2中我们可以发现:孔隙压力在考虑流固耦合的情况下比不考虑流固耦合时压力下降得慢;渗透率的越大孔隙压力下降的越快,因此建立动态的渗透率模型更能接近于真实的开采。
3 结语
论文以多孔弹性理论为基础,研究了多孔介质油藏和裂缝性介质油藏下的耦合渗流问题。
本文首先建立双重孔隙介质油藏耦合渗流的
简化模型,结合油井生产分别得到了两种地层不同渗流模型孔隙或裂缝压力的半解析解或拉氏空间的解析解;其次针对耦合渗流模型进一步得到了井筒围岩应力的分布,以便更科学地制定裂缝性油藏开采方案和更好的管理油藏。
从模拟的结果可以得出以下的结论:随着泊松比的增大,孔隙压力下降越快,相应的流速越大;考虑流固耦合作用之后井筒破坏不一定发生在井壁上,并且井壁破坏具有了时间效应。
孔隙压力在考虑流固耦合的情况下比不考虑流固耦合时压力下降得慢;渗透率和泊松比越大,孔隙压力下降越快;考虑流固耦合作用坍塌破坏不一定发生在井壁。
参考文献
[1] Biot M.A.,General Theory of Three-Dimensional Consolidation.J.Appl.Phys.,1941,12:155-164.
[2] Detournay E.and Cheng A.H-D.,Fundamental of poroelasticity.Ch.5 in comprehensive rock engineering,V ol.2,Editor.Fairhurst C.,Pergamon Press,1993.
[3] Aifantis E.C.,Introducing a multi-porous medium.Developments in mechanics,1977,8:209-211.
[4] Wilson R.K.and Aifantis E.C.On the Theory of Consolidation With Double Porosity.Int.J.Eng.ci.,1982,20(9):1009-1035.
[5] Bai M.,Roegiers J.C.and Elsworth D.,Poromechanical reponse of fractured-porous rock masses.J.petroleum Science and Engineering,1995,13:155-168.
[6] Detournay E.and Cheng A.H.-D.,Poroelastic response of a borehole in a nonhydrostatic stress field. Int J Rock Mech Min Sci Geomech Abstr,1988,25:171-182.
[7] Stehfesh H.,Numerical Inversion of Laplace Transforms. Commun.ACM.,1970,13:47-49.。