弹片弹力计算

弹片弹力计算公式弹力计算公式是根据物体的质量、形状和材料的弹性特性来确定的。

以下是常见的弹力计算公式及其推导。

1.弹性力（弹簧力）计算公式：弹性力是指当物体受到外力压缩或拉伸时，恢复到原始形状时所产生的力。

对于线性弹簧，弹簧力与物体位移成正比，可以使用胡克定律来计算：F = kx其中，F为弹簧力，k为弹簧常数，x为弹簧的压缩或拉伸位移。

弹簧常数k是反应弹簧的刚度，单位是牛顿/米（N/m）。

2.可变形物体的弹性力计算公式：对于一些可变形物体，如橡胶球、固体弹性材料等，弹性力与物体的形变量成正比。

弹性力的计算公式如下：F=kΔL其中，F为弹性力，k为弹性系数，ΔL为物体的形变量。

弹性系数k 反映了物体的弹性刚度，单位为牛顿/米（N/m）。

3.万有引力和胡克定律的联合公式：当弹簧悬挂在重力场中时，弹簧力与重力的合力可以使用如下公式来计算：F_total = mg - kx其中，F_total为弹簧力和重力的合力，m为物体质量，g为重力加速度，k为弹簧常数，x为弹簧位移。

当重力和弹簧力的合力为零时，物体处于平衡状态。

4.牛顿第二定律和弹簧力的联合公式：当物体受到外力和弹簧力的合力时，根据牛顿第二定律，可以使用如下公式计算物体的加速度：F_net = ma = mg - kx其中，F_net为物体所受的合力，m为物体质量，a为物体加速度，g 为重力加速度，k为弹簧常数，x为弹簧位移。

以上是一些常见的弹力计算公式及其推导。

对于不同形状、材料和环境条件的物体，可能会有更复杂的弹力计算公式。

在实际应用中，可以根据具体情况进行适当的调整和扩展。

弹簧的弹力公式
弹簧是一种由许多物理参数决定的简单机械件，它能够在受力的情况下以一定的方式变形，从而产生弹力。

本文介绍了如何计算弹簧弹力的公式，以便正确地设计和使用。

一、定义
弹簧由多根材料丝组成，它们被螺旋地连接在一起，形成一个环状或线性的结构。

当这些结构受到外力时，可以产生弹力，使其回到原始状态。

根据物理定义，弹簧的弹力是指其受到的外力和被压缩的距离之比。

二、计算弹簧弹力的公式
计算弹簧弹力的公式是：
F = k * d
其中，F表示弹簧的弹力，单位为牛顿(N)；k表示弹簧的弹性系数，单位为牛顿/米(N/m)；d表示弹簧被压缩的距离，单位也为米(m)。

三、计算弹簧弹力的例子
假设我们有一个金属弹簧，弹簧的弹性系数为200000N/m，在垂直方向上被压缩了0.2米，则弹簧的弹力为：
F = k * d = 200000N/m * 0.2m = 40000N
四、应用
弹簧的弹力可以用于支撑负荷，如车辆和机械上的弹簧，可以支撑大量重力，具有良好的缓冲性能。

此外，弹簧还可以应用于开关装置，使机械组件在指定位置定位或改变摆动周期。

例如，它可以应用
于电子游戏机或乐器中。

五、总结
本文介绍了如何计算弹簧弹力的公式，弹力F = k * d，其中k 是弹簧弹性系数，d是弹簧被压缩的距离。

弹簧的弹力可以用于很多方面，如支撑负荷，定位和改变摆动周期等。

正确理解和使用弹簧的弹力公式，有助于准确设计弹簧，并使用它牢牢地完成各种任务。

各类弹簧弹力计算公式弹簧是一种常见的弹性元件，其具有弹力特性，用于储存和释放能量。

弹簧的弹力计算公式是根据其材料特性和几何形状来确定的。

以下是几种常见弹簧的弹力计算公式。

1.杆弹簧（线弹簧）杆弹簧是一种直线形状的弹簧，其弹力计算公式可以使用胡克定律进行描述。

胡克定律表明，弹簧的弹力与其拉伸或压缩的长度成正比，弹簧弹力的公式可以表示为：F=k*x其中，F表示弹簧的弹力，k表示弹簧的弹性系数，x表示弹簧的形变长度。

2.螺旋弹簧螺旋弹簧是一种扭转形状的弹簧，其弹力计算公式可以使用弹簧公式进行描述。

弹簧公式基于胡克定律，并考虑了螺旋形状对弹簧弹力的影响。

弹簧公式可以表示为：F=(Gd^4)/(8ND^3)其中，F表示弹簧的弹力，G表示弹簧材料的剪切模量，d表示弹簧线径，N表示弹簧的圈数，D表示弹簧的平均直径。

3.扭力弹簧扭力弹簧是一种以扭转为形变方式的弹簧，其弹力计算公式可以使用扭力弹簧公式进行描述。

扭力弹簧公式基于扭转力矩与弹簧角度的关系。

扭力弹簧公式可以表示为：T=(kφ)/L其中，T表示扭转力矩，k表示弹簧的扭力系数，φ表示弹簧的扭转角度，L表示弹簧的长度。

4.悬挂弹簧悬挂弹簧是一种用于悬挂装置的弹簧，其弹力计算公式可以根据工程需要进行设计。

常见的悬挂弹簧包括张紧弹簧和扭力挂弹簧。

对于张紧弹簧，其弹力计算公式可以表示为：F=(Gd^4)/(8Na)其中，F表示弹簧的弹力，G表示弹簧材料的剪切模量，d表示弹簧线径，N表示弹簧的圈数，a表示弹簧的平均半径。

对于扭力挂弹簧，其弹力计算公式可以表示为：F=(kφ)/R其中，F表示弹簧的弹力，k表示弹簧的扭力系数，φ表示弹簧的扭转角度，R表示弹簧的半径。

总结：以上是几种常见弹簧的弹力计算公式。

在实际设计和应用中，需要根据具体情况确定弹簧的弹性系数、形变长度、材料特性等参数，并使用相应的计算公式进行弹力计算。

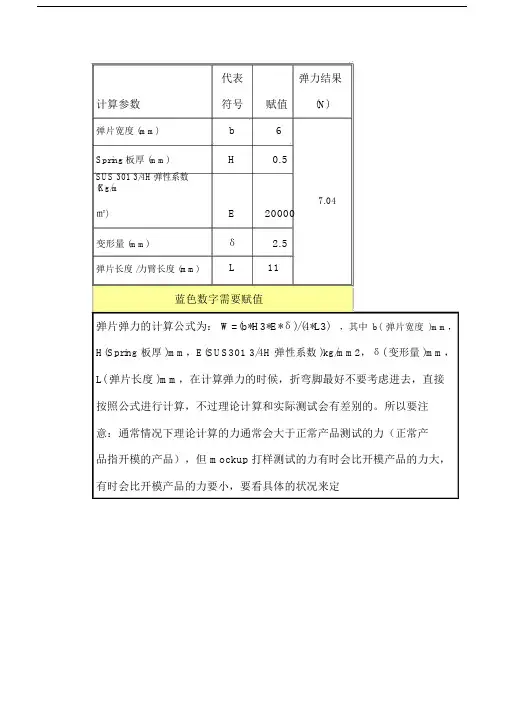
代表弹力结果
计算参数符号赋值(N)
弹片宽度 (mm) b 6
Spring板厚 (mm) H 0.5
SUS 301 3/4H弹性系数
(Kg/m
7.04
㎡) E 20000
变形量 (mm) δ 2.5
弹片长度 /力臂长度 (mm) L11
蓝色数字需要赋值
弹片弹力的计算公式为： W=(b*H3*E*δ)/(4*L3)，其中b(弹片宽度)mm，H(Spring 板厚 )mm，E(SUS301 3/4H 弹性系数 )kg/mm2，δ( 变形量 )mm，L( 弹片长度 )mm，在计算弹力的时候，折弯脚最好不要考虑进去，直接按照公式进行计算，不过理论计算和实际测试会有差别的。

所以要注
意：通常情况下理论计算的力通常会大于正常产品测试的力（正常产
品指开模的产品），但 mockup打样测试的力有时会比开模产品的力大，有时会比开模产品的力要小，要看具体的状况来定。

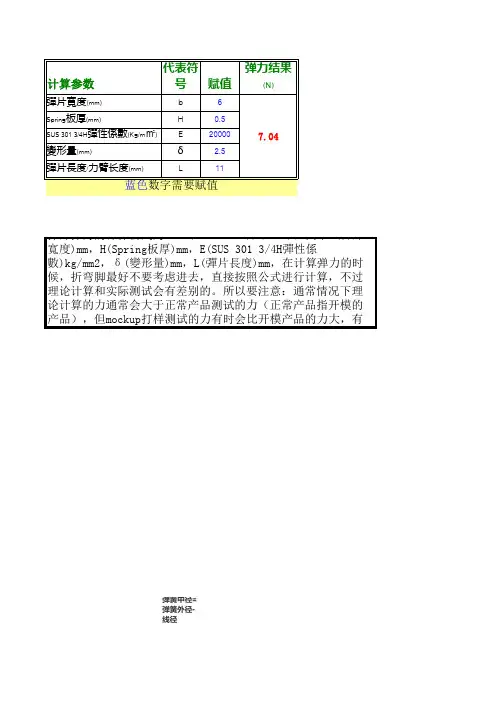
弹片弹力的计算公式为：W=(b*H3*E*δ)/(4*L3)，其中b(彈片寬度)mm，H(Spring板厚)mm E(SUS 301 3/4H彈性係數)kg/mm2，δ(變形量)mm，L(彈片長度)mm，在计算弹力的时候，脚最好不要考虑进去，直接按照公式进行计算，不过理论计算和实际测试会有差别的。

所注意：通常情况下理论计算的力通常会大于正常产品测试的力（正常产品指开模的产品）mockup打样测试的力有时会比开模产品的力大，有时会比开模产品的力要小，要看具体的来定
弹簧中径=弹簧外径-线径
寬度)mm，H(Spring板厚)mm，)mm，在计算弹力的时候，折弯和实际测试会有差别的。

所以要（正常产品指开模的产品），但产品的力要小，要看具体的状况。

弹片压力变形计算公式材料变形压力计算公式The formula between Shrapnel stress and deflectionThe deflection curve equation of Shrapnel is as following:y =-F 26EI (3l -x ) (1)The max deflection of the Shrapnel’s endpoint A :y A =-F 33EI (2) In which I stands for Z-axis moment of inertia of the Shrapnel’s Section,a b22I =⎰y 22dA =⎰⎰y-a2-b2dydZ =a 123(3)To verify the correctness of the above formula.Assume : l=10mm；a=2mm；b=0.2mm；E=210GP;F=11N Result:y A =-13.095mmThe figure is the finite element result:The deflection curve equation of Shrapnel is as following:y =-F d 22EI (1)The max deflection of the Shrapnel’s endpoint A :y A =-F d EI 2 (2) In which I stands for Z-axis moment of inertia of the Shrapnel’s Section,a b22I =⎰y 22dA =⎰⎰y-a2-b2dydZ =a 123 (3)yA =-12F d Ea 32 (4) b信用社转正申请书(1) 信用社贷款申请书样板转正申请书尊敬的领导：我于2012年3月1日成为秦安信用联社的实习员工，到今天半年试用期已满，根据信用社的规章制度，现申请转为信用社的正式员工。

弹力计算公式压力弹簧·压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；·弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；·弹簧常数公式（单位：kgf/mm）：G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，磷青铜线G=4500 ，黄铜线G=3500 d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈,钢丝材质=琴钢丝拉力弹簧拉力弹簧的k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

·初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧·弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).·弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416(a)压缩弹簧▪压缩弹簧之设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸之负荷▪弹簧常数 :以 k表示,当弹簧被压缩时,每增加1mm行程之负荷(kgf/mm).▪弹簧常数公式 :G × d4K = ————————— (kgf/mm).8 × Dm3× NcG= 线材之钢性模数琴钢线 G=8000 ,不锈钢线 G=7300 ,磷青铜线 G=4500 ,黄铜线G=3500d = 线径Do=OD =外径Di= ID = 内径Dm=MD =中心径 =Do-dN = 总圈数Nc =有效圈数=N-2▪弹簧常数计算例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,弹簧材质=琴钢线G ×d4 8000×2 4k = ——————— = —————— = 0.571 kgf/mm.8 × Dm3× Nc8×203×3.5(b)拉伸弹簧▪拉伸弹簧之 k值,与压缩弹簧计算式同.(c)扭力弹簧▪弹簧常数 :以 k 表示,当弹簧被扭转时,每增加1°扭转角之负荷 (kgf/mm).▪弹簧常数公式:E × d4k = ——————————— (kgf/mm).1167 × Dm× π× N ×RE= 线材之钢性模数∙琴钢线 E=21000 ,不锈钢线 E=19400 ,磷青铜线 E=11200 ,黄铜线 E=11200d = 线径Do=OD =外径Di= ID = 内径Dm=MD =中心径 =Do-d N = 总圈数R =负荷作用之力臂 = 3.1416。

弹力计算公式压力弹簧·压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；·弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；·弹簧常数公式（单位：kgf/mm）：G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，磷青铜线G=4500 ，黄铜线G=3500 d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈,钢丝材质=琴钢丝拉力弹簧拉力弹簧的k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

·初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧·弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).·弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416(a)压缩弹簧▪压缩弹簧之设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸之负荷▪弹簧常数 :以 k表示,当弹簧被压缩时,每增加1mm行程之负荷(kgf/mm).▪弹簧常数公式 :G × d4K = ————————— (kgf/mm).8 × Dm3× NcG= 线材之钢性模数琴钢线 G=8000 ,不锈钢线 G=7300 ,磷青铜线 G=4500 ,黄铜线G=3500d = 线径Do=OD =外径Di= ID = 内径Dm=MD =中心径 =Do-dN = 总圈数Nc =有效圈数=N-2▪弹簧常数计算例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,弹簧材质=琴钢线G ×d4 8000×2 4k = ——————— = —————— = 0.571 kgf/mm.8 × Dm3× Nc8×203×3.5(b)拉伸弹簧▪拉伸弹簧之 k值,与压缩弹簧计算式同.(c)扭力弹簧▪弹簧常数 :以 k 表示,当弹簧被扭转时,每增加1°扭转角之负荷 (kgf/mm).▪弹簧常数公式:E × d4k = ——————————— (kgf/mm).1167 × Dm× π× N ×RE= 线材之钢性模数∙琴钢线 E=21000 ,不锈钢线 E=19400 ,磷青铜线 E=11200 ,黄铜线 E=11200d = 线径Do=OD =外径Di= ID = 内径Dm=MD =中心径 =Do-d N = 总圈数R =负荷作用之力臂 = 3.1416。

基本公式：
EI
M
=
ρ
1
（弯矩与曲率的关系公式）； EI M
dx
v d =2
2（挠曲线的近似微分方程）； M 为纯弯曲时，截面的弯矩；E 为材料弹性模量；I 为横截面中性轴惯性矩；()x f v =为挠
曲线方程；ρ/1为挠曲线曲率；对于矩形截面，12
3
bt I =。

EI
l P f B 33
⋅-= 悬臂梁一端受压时的偏移量计算公式；P 为压力。

I
My
=
σ 纯弯曲时正应力计算公式，y 为考察点对中性轴的偏移量。

计算：
当知道弹片形状尺寸、材料特性和一端压紧的偏移量时，可以计算压力P ：
（对于矩形截面，12
3
bt I =
）
此时，弹片弯曲的挠曲线方程是：
)3(62
x l EI
px v --=；
由于EI Px
EI lP dx
v d +-=22 当x=0时最大，曲线曲率最大，因此，悬臂梁的固定端弯曲曲率最大。

产生最大弯曲正应力的地方是，距离中性面y=t/2的悬臂梁表面。

I
Mt 2max =
σ； 根据力矩平衡的条件，M l P =⋅ 得到弹片由于弯曲得到的最大正应力：
可以通过自由端在装配前后的偏移量得到需要的压紧力P ；另外，需要校核弯曲的最大
正应力是否超过材料的弹性许用应力的范围。

欢迎您的下载，
资料仅供参考！
致力为企业和个人提供合同协议，策划案计划书，学习资料等等
打造全网一站式需求。