导数概念及练习题

第二章 第一节 导数的概念与性质A 组一、选择题1. 设函数f (x )可导，则=--→hx f h x f h )()3(lim【 】A. 3()f x 'B.1()3f x 'C. 3()f x '-D. 1()3f x '- 2. 设函数f (x )可导，则0(1)(1)lim 2x f f x x →--=【 】A. 2(1)f 'B. 1(1)2f ' C. 2(1)f '- D. 1(1)2f '-3. 函数x y =在0=x 处的导数【 】A. 不存在B. 1C. 0D. 1-4. 设函数f (x )可导，则0(2)()limh f x h f x h →+-=【 】A. 2()f x 'B. 1()2f x 'C. 2()f x '-D. 1()2f x '-5. 设y =sinx ，则y (7)|x=0=【 】 A. 1 B. 0 C. -1 D. 2n6. 设函数f (x )可导，则0(4)()lim2h f x h f x h→--=【 】A. -4()f x 'B. 2()f x 'C. -2()f x 'D. 4()f x '7.已知函数()f x 在0x x =的某邻域内有定义，则下列说法正确的是【 】 A. 若()f x 在0x x =连续, 则()f x 在0x x =可导B. 若()f x 在0x x =处有极限, 则()f x 在0x x =连续C. 若()f x 在0x x =连续, 则()f x 在0x x =可微D. 若()f x 在0x x =可导, 则()f x 在0x x =连续8. 设[]2()(0)sin lim 4x f x f x x →-=　，则(0)f '=【 】 A. 3 B. 4 C.43D. 不存在9.设()xf x e =，则0(1)(1)limx f x f x∆→+∆-=∆【 】A. 1B. eC. 2eD. 2e10.设函数()f x 在0x 可导且0()2'=f x ，则000()(2)lim→+--=h f x h f x h h【 】A. -2B. 1C. 6D. 3 12.设()x x x f ln =，且()20='x f ，则()0x f =（ ）。

专题4.1 导数的概念、运算及导数的几何意义一、选择题1．（2019·全国高三月考（文））已知函数3()2(1)1f x x xf '=+-，则(1)f '=（ ）A ．32B ．3C ．-3D ．32-2．（2019·湖南省株洲二中高三月考（理））曲线1x y xe -=在点（1,1）处切线的斜率等于（ ）. A ．2eB ．eC ．2D ．13．（2019·河北省高三期末（理））曲线()3f x x x =-在点(1,(1))f --处的切线方程为（ ） A ．220x y ++= B ．220x y +-= C ．220x y -+=D ．220x y --=4．（2018·湖南省湖南师大附中高三一模（理））已知直线y ax =是曲线ln y x =的切线，则实数a =（ ） A ．12B ．12eC ．1eD ．21e 5．（2020·全国高三三模（文））函数()3sin 4cos f x x x =+的图象在点T (0， f (0))处的切线l 与坐标轴围成的三角形面积等于（ ） A ．43B ．53C ．73D ．836．（2019·湖南省高三期末（文））曲线()32f x x x =+-在0p 处的切线平行于直线41y x =-，则0p 点的坐标为（ ） A ．()1,0 B ．()2,8C ．()1,0和()1,4--D ．()2,8和()1,4--7．（2020·全国高三其他（理））曲线cos sin x y x =在点π,14⎛⎫⎪⎝⎭处的切线方程为（ ）. A ．π2102x y --+= B ．π2102x y ---= C ．π2102x y +-+=D ．π2102x y +--=8．（2020·黑龙江省哈九中高三三模（文））等比数列{}n a 中，12a =，84a =，函数()()()()128f x x x a x a x a =---，则()0f '=（）A ．122B ．92C ．82D ．629．（2019·汕尾市普宁华美实验学校高三期中（文））已知曲线2()ln x f x x a=+在点(1,(1))f 处的切线的倾斜角为3π4，则a 的值为（ ） A ．1B ．1-C ．12-D ．4-10．（2019·广东省普宁市华美实验学校高三开学考试（理））已知过点A （a ，0）作曲线C ：y ＝x•e x的切线有且仅有两条，则实数a 的取值范围是（ ） A ．（﹣∞，﹣4）∪（0，+∞） B ．（0，+∞） C ．（﹣∞，﹣1）∪（1，+∞） D ．（﹣∞，﹣1）二、多选题11．（2019·山东省高三月考）下列结论中不正确的是（ ） A ．若1cosy x =，则11sin y x x'=- B ．若2sin y x =，则22cos y x x '= C ．若cos5y x =，则sin 5y x '=-D ．若1sin 22y x x =，则sin 2y x x '= 12．（2020·高密市教育科学研究院高三其他）若函数()1xf x e =-与()g x ax =的图象恰有一个公共点，则实数a 可能取值为（ ） A ．2B ．0C ．1D ．1-13．（2020·山东省高三其他）已知曲线()32213f x x x ax =-+-上存在两条斜率为3的不同切线，且切点的横坐标都大于零，则实数a 可能的取值（ ） A ．196B ．3C ．103D ．9214．（2020·山东省高三其他）已知函数()ln f x x =，若()f x 在1x x =和()212x x x x =≠处切线平行，则（ ）A12= B ．12128x x <C ．1232x x +<D ．2212512x x +>三、填空题15．（2020·重庆高三其他（文））曲线32()f x x x =-在1x =处的切线方程为_____．16．（2020·河南省高三二模（理））已知函数()()2ln f x x x =-．则函数()f x 在1x =处的切线方程为___________．17．（2020·辽宁省大连二十四中高三一模（理））已知函数f （x ）=axlnx ﹣bx （a ，b ∈R ）在点（e ，f （e ））处的切线方程为y =3x ﹣e ，则a +b =_____. 18．（2020·天津高三二模）曲线1xy e x=-在点(1,(1))f 处的切线的斜率为_______，在该点处的切线方程为______.19．（2017·浙江省高三其他）已知函数3()f x x ax b =++的图象在点(1,(1))f 处的切线方程为250x y --=，则a =_______；b =_________.20．（2018·浙江省高三其他）已知曲线xy e -=，则其图像上各点处的切线斜率的取值范围为 __________；该曲线在点(0,1)处的切线方程为__________．21．（2017·北京高三期中（理））已知函数21()(2)1ax bx c x f x f x x ⎧++≥=⎨--<-⎩，其图象在点(1,(1))f 处的切线方程为__________，则它在点(3,(3))f --处的切线方程为__________． 四、解答题22．（2020·安徽省蚌埠二中高二月考（理））已知曲线32()2f x x x x =-+.(Ⅰ) 求曲线()y f x =在2x =处的切线方程； (Ⅱ) 求曲线()y f x =过原点O 的切线方程.23．（2020·山东省高二期中）（1）函数()()1sin f x x x =+的导数为()f x '，求2f π⎛⎫' ⎪⎝⎭； （2）设l 是函数1y x=图象的一条切线，证明：l 与坐标轴所围成的三角形的面积与切点无关． 24．（2020·安徽省怀宁县第二中学高二期中（理））已知函数()32f x x x =-及()y f x =上一点()1,1P -，过点P 作直线l ，使直线l 和()y f x =相切.求直线l 的方程.25．（2020·洮南市第一中学高二月考（理））已知函数()1ln 1xf x x+=-． （1）求函数()y f x =的定义域；（2）求曲线()y f x =在点()()0,0f 处的切线方程.26．（2020·湖北省高二月考）设点M 是幂函数()f x 图象上任意一点，点M 在x 轴和y 轴上的射影分别为P 、Q ，且四边形OPMQ 的面积为常数．（1）求()f x 的表达式；（2）证明：函数()f x 在点M 处的切线与坐标轴围成的面积为定值．27．（2020·河南省高二期末（理））已知函数3()16f x x x =+-（1）求曲线()y f x =在点(1,14)-处的切线的方程；（2）直线l 为曲线()y f x =的切线，且经过原点，求直线l 的方程及切点坐标.。

1．函数y ＝f (x )在x ＝x 0处的导数定义：称函数y ＝f (x )在x ＝x 0处的瞬时变化率为函数y ＝f (x )在x ＝x 0处的导数，记作f ′(x 0)或y ′|x ＝x 0，即.2．函数f (x )的导函数 称函数为f (x )的导函数．1. 基本初等函数的导数公式原函数导函数 f (x )＝c (c 为常数) f ′(x )＝0 f (x )＝x n (n ∈Q *) f ′(x )＝nx n －1 f (x )＝sin x f ′(x )＝cos x f (x )＝cos x f ′(x )＝－sin x f (x )＝a x f ′(x )＝a x ln a f (x )＝e x f ′(x )＝e x f (x )＝log a x f ′(x )＝1x ln af (x )＝ln xf ′(x )＝1x0000()()limlim x x f x x f x yxx ∆→∆→+∆-∆=∆∆00000()()()lim lim x x f x x f x yf x x x ∆→∆→+∆-∆==∆∆0()()()limx f x x f x f x x∆→+∆-=∆专题5.1 导数的概念及其意义、导数的运算2．导数的运算法则（1） [f (x )±g (x )]′＝f ′(x )±g ′(x )； （2） [f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )； （3）(g (x )≠0)． (4) 复合函数的导数复合函数y ＝f (g (x ))的导数和函数y ＝f (u )，u ＝g (x )的导数间的关系为y x ′＝y u ′·u x ′，即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积．1.函数f (x )在点x 0处的导数f ′(x 0)的几何意义是在曲线y ＝f (x )上点(x 0，f (x 0))处的切线的斜率(瞬时速度就是位移函数s (t )对时间t 的导数)．相应地，切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)．2.特别提醒：区分在点处的切线与过点处的切线（1）曲线y ＝f (x )在点P (x 0，y 0)处的切线是指P 为切点，斜率为f ′(x 0)的切线，是唯一的一条切线． （2）曲线y ＝f (x )过点P (x 0，y 0)的切线，点P 不一定是切点，切线至少有一条，切线可能有多条． 3．几类重要的切线方程(1)y ＝x －1是曲线y ＝l n x 的切线，y ＝x 是曲线y ＝l n (x ＋1)的切线，…，y ＝x ＋n 是曲线y ＝l n (x ＋n ＋1)的切线，如图1.(2)y ＝x ＋1与y ＝e x 是曲线y ＝e x 的切线，如图2. (3)y ＝x 是曲线y ＝si n x 与y ＝t an x 的切线，如图3.(4)y ＝x －1是曲线y ＝x 2－x ，y ＝x l n x 及y ＝1－1x 的切线，如图4. 由以上切线方程可得重要不等式，如l n x ≤x －1，x ＋1≤e x 等．1．奇函数的导数是偶函数，偶函数的导数是奇函数，周期函数的导数还是周期函数．2.可导函数y ＝f (x)的导数为f ′(x)，若f ′(x)为增函数，则f (x)的图象是下凹的；反之，若f ′(x)为减函数，则f (x)的图象是上凸的． 3．熟记以下结论： (1) 211()'x x=-； 2()'()()'()()'()()f x f x g x g x f x g x g x ⎡⎤⋅-⋅=⎢⎥⎣⎦(2) 21'()[]'()[()]f x f x f x =- (f (x )≠0)； (3)[af (x )±bg (x )]′＝af ′(x )±bg ′(x )．考点01 导数的概念【典例01】（2023上·北京·高三北京市第三十五中学校考阶段练习）某种新产品的社会需求量y 是时间t 的函数，记作：()y f t =．若()00f y =，社会需求量y 的市场饱和水平估计为500万件，经研究可得，()f t 的导函数()f t '满足：()()()()500f t kf t f t '=-（k 为正的常数），则函数()f t 的图像可能为（ ）【规律方法】1.根据导数的定义求函数在点处导数的方法： ①求函数的增量； ②求平均变化率；③得导数，简记作：一差、二比、三极限.2.函数y ＝f (x )的导数f ′(x )反映了函数f (x )的瞬时变化趋势，其正负号反映了变化的方向，其大小|f ′(x )|反映了变化的快慢，|f ′(x )|越大，曲线在这点处的切线越“陡”．【总结提升】1.求函数导数的一般原则如下：（1）连乘积的形式：先展开化为多项式的形式，再求导； （2）根式形式：先化为分数指数幂，再求导；（3）复杂公式：通过分子上凑分母，化为简单分式的和、差，再求导； （4）不能直接求导：适当恒等变形，转化为能求导的形式再求导．求复合函数的导数，一般是运用复合函数的求导法则，将问题转化为求基本函数的导数解决. ①分析清楚复合函数的复合关系是由哪些基本函数复合而成的，适当选定中间变量； ②分步计算中的每一步都要明确是对哪个变量求导，而其中特别要注意的是中间变量；③根据基本函数的 导数公式及导数的运算法则，求出各函数的导数，并把中间变量转换成自变量的函数； ④复合函数的求导熟练以后，中间步骤可以省略，不必再写出函数的 复合过程.3.函数的导数与导数值的区间与联系：导数是原来函数的导函数，而导数值是导函数在某一点的函数值，导数值是常数.考点03 曲线切线的斜率、倾斜角问题【典例05】（2023上·辽宁葫芦岛·高三校联考阶段练习）奇函数()()()324f x ax a x x =+-∈R 在点()()1,1f 处的切线斜率为（ ）()()1,1f 处切线方程为 ．【规律方法】以曲线上的点(x 0，f (x 0))为切点的切线方程的求解步骤： ①求出函数f (x )的导数f ′(x )； ②求切线的斜率f ′(x 0)；③写出切线方程y －f (x 0)＝f ′(x 0)(x －x 0)，并化简．考点05 求过一点的切线方程（斜率）【典例09】（2023·全国·模拟预测）过原点与曲线()2ln ,2,1,2x x f x x x ≥⎧=⎨+<⎩相切的一条切线的方程为 .【典例10】（2023下·江西萍乡·高二校联考阶段练习）已知函数()3234f x x x =--.(1)求曲线()y f x =在1x =处的切线1l 的方程； (2)求过原点O 与曲线()y f x =相切的直线2l 的方程. 【总结提升】如果已知点(x 1，y 1)不在曲线上，则设出切点(x 0，y 0)，解方程组⎩⎪⎨⎪⎧y 0＝f (x 0)，y 1－y 0x 1－x 0＝f ′(x 0)，得切点(x 0，y 0)，进而确定切线方程．求切线方程时，要注意判断已知点是否满足曲线方程，即是否在曲线上；与曲线只有一个公共点的直线不一定是曲线的切线，曲线的切线与曲线的公共点不一定只有一个．考点06 求切点坐标【典例11】（2023·高二课时练习）曲线33y x x =-+在点P 处的切线平行于直线21y x =-，则点P 的坐标【典例12】（2019·江苏·高考真题）在平面直角坐标系xOy 中，点A 在曲线y =ln x 上，且该曲线在点A 处的切线经过点（e ，1)(e 为自然对数的底数），则点A 的坐标是____. 【总结提升】已知斜率求切点：已知斜率k ，求切点(x 1，f (x 1))，即解方程f ′(x 1)＝k .考点07 切线的平行与垂直ln230x y -+=平行，则实数=a （ ）A ．ln22-B ．ln2-C ．2ln2-D ．3ln2-考点08 曲线的公切线问题【典例15】（2023下·四川绵阳·高二校考期中）若直线y kx b =+是曲线ln 2y x =+的切线，也是曲线()ln 1y x =+的切线，则k =（ ）A ．2B ．3C ．1【规律总结】1.解决此类问题通常有两种方法一是利用其中一曲线在某点处的切线与另一曲线相切，列出关系式求解；二是设公切线l 在y ＝f (x )上的切点P 1(x 1，f (x 1))，在y ＝g (x )上的切点P 2(x 2，g (x 2))，则f ′(x 1)＝g ′(x 2)＝1212()()f xg x x x --.2.处理与公切线有关的参数问题，通常根据曲线、切线、切点的三个关系列出参数的方程(组)并解出参数，建立方程(组)的依据主要是：①切点处的导数是切线的斜率；②切点在切线上；③切点在曲线上．考点09 求参数问题【典例17】（2023·海南·校联考模拟预测）已知函数()()1e xf x x =+，过点(),0P m 作曲线()y f x =的两条切线，切点分别为()(),A a f a 和()(),B b f b ，若0a b +=，则实数m =（ ）A ．0B ．1C ．2D ．3【典例18】（2023下·广东汕头·高二统考期末）已知直线(,0)y ax b a b =+∈>R 是曲线()e x f x =与曲线已知曲线的切线条数求参数范围问题时，需要明确的是，曲线存在几条切线，就会相应的有几个切点，因此就可以将切线条数问题转化为切点个数问题；也就是说抓住“切点”这个“牛鼻子”，将问题进一步转化为关于相应函数零点个数问题．考点10 导数几何意义相关的应用问题【典例19】（2022·全国·高三专题练习）已知0,0a b >>，直线y x a =+与曲线1e 21x y b -=-+相切，则下列不等式成立的是（ ） A ．18ab ≤B ．218a b+≤C D ．3a b +≤求解与导数的几何意义有关问题时应注意的两点 (1)注意曲线上横坐标的取值范围． (2)谨记切点既在切线上又在曲线上．2．（2020·北京·高考真题）为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改，设企业的污水排放量W 与时间t 的关系为()W f t =，用()()f b f a b a---的大小评价在[,]a b 这段时间内企业污水治理能力的强弱，已知整改期内，甲、乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论： ①在[]12,t t 这段时间内，甲企业的污水治理能力比乙企业强；②在2t 时刻，甲企业的污水治理能力比乙企业强； ③在3t 时刻，甲、乙两企业的污水排放都已达标；④甲企业在[][][]112230,,,,,t t t t t 这三段时间中，在[]10,t 的污水治理能力最强． 其中所有正确结论的序号是____________________．3.（2022·全国·高考真题）若曲线()e x y x a =+有两条过坐标原点的切线，则a 的取值范围是________________． 一、单选题1．（2022下·安徽滁州·高二统考期末）已知函数()2ln f x x x =-，()f x '为()f x 的导函数，则()1f '的值为（ ）A ．1-B ．0C ．1D ．22.（2023上·山东济宁·高三统考期中）若曲线()1e xy ax =+在点()0,1处的切线方程是210x y -+=，则=a（ ）． A ．3B ．2C ．1D ．03．（2023上·陕西西安·高二长安一中校考期末）若曲线2ln 1y x x =++在点(1,2)处的切线与直线10x ay +-=垂直，则实数a 的值为（ ）A ．－4B ．－3C ．4D ．34．（2023下·湖北·高二武汉市第四十九中学校联考期中）若直线0x y a ++=是曲线()314f x x bx =+-与曲线()23ln g x x x =-的公切线，则a b -=（ ）．A ．26B ．23C ．15D ．11二、多选题5．（2023下·湖南·高二期中）过点(2,6)P -作曲线3()3f x x x =-的切线，则切线方程可能是（ ）A ．30x y +=B ．24540x y --=C ．9240x y --=D ．12240x y --=匀速旋转(到OB 处为止)时，所扫过的圆内阴影部分的面积S 是时间t 的函数，它的图象大致为（ ）A ．B ．C ．D ．若把图中的圆改成如图（1）所示的半圆，正确的答案是哪个？如果改成图（2）中的三角形呢？12．（2010上·黑龙江双鸭山·高三阶段练习）已知函数()316f x x x =+-．(1)求曲线()y f x =在点()2,6-处的切线方程；(2)直线l 为曲线()y f x =的切线，且经过原点，求直线l 的方程及切点坐标．。

导数练习题大全导数是微积分中的重要概念之一，它描述了函数在某一点的变化率。

掌握导数的计算方法和性质对于解决各种问题、理解函数行为至关重要。

本文将为你提供一些导数练习题，帮助你巩固导数的概念和运用。

1. 已知函数f(x) = 3x^2 + 2x + 1，求f(x)的导函数f'(x)。

解析：为求函数f(x)的导函数，我们需要按照导数的定义对f(x)进行求导。

利用常见的导数公式，我们可以得到f'(x) = 6x + 2。

因此，f(x)的导函数为f'(x) = 6x + 2。

2. 已知函数g(x) = sin(x) + cos(x)，求g(x)的导函数g'(x)。

解析：对于g(x) = sin(x) + cos(x)，我们可以利用常见的导数公式求导。

根据导数的性质和三角函数的导数公式，我们可以得到g'(x) =cos(x) - sin(x)。

因此，g(x)的导函数为g'(x) = cos(x) - sin(x)。

3. 设函数h(x) = x^3 - 2x^2 + 3x，求h(x)的导函数h'(x)。

解析：对于h(x) = x^3 - 2x^2 + 3x，我们可以使用幂函数的导数公式进行求导。

根据导数的性质，我们可以得到h'(x) = 3x^2 - 4x + 3。

因此，h(x)的导函数为h'(x) = 3x^2 - 4x + 3。

4. 已知函数k(x) = e^x，求k(x)的导函数k'(x)。

解析：对于k(x) = e^x，其中e为自然对数的底数，我们可以利用指数函数的导数公式进行求导。

根据导数的性质和指数函数的导数公式，我们可以得到k'(x) = e^x。

因此，k(x)的导函数为k'(x) = e^x。

通过以上练习题，我们巩固了求导的方法和概念。

熟练掌握导数的计算方法可以帮助我们更好地理解函数的变化趋势和性质。

一、单项选择题1．若函数f(x)＝e x sin2x，则f′(0)等于()A．2B．1C．0D．－12.函数y＝f(x)的图象如图所示，f′(x)是函数f(x)的导函数，则下列大小关系正确的是()A．2f′(3)<f(5)－f(3)<2f′(5)B．2f′(3)<2f′(5)<f(5)－f(3)C．f(5)－f(3)<2f′(3)<2f′(5)D．2f′(5)<2f′(3)<f(5)－f(3)3．(2023·榆林模拟)已知函数f(x)＝a ln x＋x2的图象在x＝1处的切线方程为3x－y＋b＝0，则a＋b等于()A．－2B．－1C．0D．14．(2023·成都川大附中模拟)若点P是曲线y＝ln x－x2上任意一点，则点P到直线l：x＋y －4＝0距离的最小值为()B.2C．22D．42A.225．直线l与曲线y＝e x＋1和y＝e x＋1均相切，则l的斜率为()B．1C．2D．eA.126．若函数f(x)＝x2－2ax2＋ln(x＋1)的图象上不存在互相垂直的切线，则a的取值范围是() A．a≤1B．a<0C．a≥1D．a≤0二、多项选择题7．对于函数f(x)＝ln x－1，则下列判断正确的是()A．直线y＝xe2是f(x)过原点的一条切线B．f(x)关于y＝x对称的函数是y＝e x－1C．若过点(a，b)有2条直线与f(x)相切，则ln a<b＋1D．f(x)≤x－28．(2023·唐山质检)给出定义：若函数f(x)在D上可导，即f′(x)存在，且导函数f′(x)在D 上也可导，则称f(x)在D上存在二阶导函数，记f″(x)＝(f′(x))′，若f″(x)<0在D上恒成立，则称f(x)在D()A．f(x)＝sin x－cos xB．f(x)＝ln x－3xC．f(x)＝－x3＋3x－1D．f(x)＝x e－x三、填空题9．(2024·呼和浩特模拟)若曲线y＝2sin x－2cos x x－ay＋1＝0垂直，则实数a＝.10．(2023·本溪模拟)请写出与曲线y＝sin x在原点(0,0)处具有相同切线的另一个函数．11．(2023·南京模拟)若直线y＝x＋m与曲线y＝ax2和y＝ln x均相切，则a＝. 12．已知直线y＝k1x与y＝k2x(k1>k2)是曲线y＝ax＋2ln|x|(a∈R)的两条切线，则k1－k2＝.四、解答题13．已知函数f(x)的导函数为f′(x)，且满足f(x)＝2xf′(e)＋ln x.(1)求f′(e)及f(e)的值；(2)求f(x)在点(e2，f(e2))处的切线方程．14．设函数f(x)＝ax－bx，曲线y＝f(x)在点(2，f(2))处的切线方程为7x－4y－12＝0.(1)求f(x)的解析式；(2)证明曲线f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形面积为定值，并求此定值．15．已知函数f (x )＝ln x ＋x 的零点为x 0，过原点作曲线y ＝f (x )的切线l ，切点为P (m ，n )，则00e x mx 等于()A.1e B ．e C.1e 2D ．e 216．(2021·新高考全国Ⅱ)已知函数f (x )＝|e x －1|，x 1<0，x 2>0，函数f (x )的图象在点A (x 1，f (x 1))和点B (x 2，f (x 2))的两条切线互相垂直，且分别交y 轴于M ，N 两点，则|AM ||BN |的取值范围是．§3.1导数的概念及其意义、导数的计算1．A 2.A 3.B 4.C 5.B6.A 7．ACD8．BCD [对于A ，f ′(x )＝cos x ＋sin x ，f ″(x )＝－sin x ＋cos x＝－2sin当x ，f ″(x )＝－2sin ，故A 错误；对于B ，f ′(x )＝1x －3，f ″(x )＝－1x2<0B 正确；对于C ，f ′(x )＝－3x 2＋3，f ″(x )＝－6x <0C 正确；对于D ，f ′(x )＝e －x －x e －x ＝(1－x )e －x ，f ″(x )＝－e －x －(1－x )e －x ＝－(2－x )e －x ，因为x 2－x >0，所以f ″(x )＝－(2－x )e －x <0D 正确．]9．－210.y ＝x 3＋x (答案不唯一)11.14解析设直线y ＝x ＋m 与y ＝ln x 相切于点(x 0，ln x 0)，因为y ＝ln x 的导函数为y ′＝1x，所以1x 0＝1，且ln x 0＝x 0＋m ，解得x 0＝1，m ＝－1.因为直线y ＝x －1与曲线y ＝ax 2相切，联立得ax 2－x ＋1＝0，a ≠0且Δ＝1－4a ＝0，即a ＝14.12.4e解析由已知得，曲线的切线过点(0,0)，当x >0时，曲线为y ＝ax ＋2ln x ，设x 1>0，直线y ＝k 1x 在曲线上的切点为(x 1，ax 1＋2ln x 1)，y ′＝a ＋2x 1，∴切线方程为y －(ax 1＋2ln x 1)x －x 1)，又切线过点(0,0)，∴－ax 1－2ln x 1－x 1)，∴x 1＝e ，k 1＝a ＋2e；同理，当x <0时，曲线为y ＝ax ＋2ln(－x )，设x 2<0，直线y ＝k 2x 在曲线上的切点为(x 2，ax 2＋2ln(－x 2))，y ′＝a ＋2x 2，∴切线方程为y －[ax 2＋2ln(－x 2)]x －x 2)，又切线过点(0,0)，∴－ax 2－2ln(－x 2)－x 2)，∴x 2＝－e ，k 2＝a －2e，∴k 1－k 2＝4e.13．解(1)∵f (x )＝2xf ′(e)＋ln x ，∴f ′(x )＝2f ′(e)＋1x，f ′(e)＝2f ′(e)＋1e，∴f ′(e)＝－1e ，f (x )＝－2x e＋ln x ，∴f (e)＝－2e e＋ln e ＝－1.(2)∵f (x )＝－2x e＋ln x ，f ′(x )＝－2e ＋1x，∴f (e 2)＝－2e 2e ＋ln e 2＝2－2e ，f ′(e 2)＝－2e ＋1e2，∴f(x)在点(e2，f(e2))处的切线方程为y－(2－2e)－2e ＋x－e2)，即(2e－1)x＋e2y－e2＝0.14．解(1)方程7x－4y－12＝0可化为y＝74x－3，当x＝2时，y＝1 2，又∵f′(x)＝a＋b x2，a－b2＝12，＋b4＝74，＝1，＝3，∴f(x)＝x－3x.(2)设P(x0，y0)为曲线y＝f(x)上任一点，由y′＝1＋3x2知曲线在点P(x0，y0)处的切线方程为y0x－x0)．令x＝0，得y＝－6x0，∴切线与直线x＝0令y＝x，得y＝x＝2x0，∴切线与直线y＝x的交点坐标为(2x0,2x0)．∴曲线y＝f(x)在点P(x0，y0)处的切线与直线x＝0和y＝x所围成的三角形的面积S＝12|－6x0|·|2x0|＝6.故曲线y＝f(x)上任一点处的切线与直线x＝0和y＝x所围成的三角形面积为定值，且此定值为6.15．B[f′(x)＝1x＋1，切点为P(m，ln m＋m)，则切线方程为yx－m)＋ln m＋m，因为l过原点，所以0－m )＋ln m ＋m ，解得m ＝e ，则P (e ，e ＋1)，由ln x 0＋x 0＝0，可得x 0＝－ln x 0，故00e x mx ＝e x 0·0ln ex －＝e x 0·1x 0＝e.]16．(0,1)解析由题意得，f (x )＝|e x －1|－e x ，x <0，x －1，x ≥0，则f ′(x )e x ，x <0，x ，x ≥0，所以点A (x 1,1－1e x )和点B (x 2，2e x －1)，k AM ＝－1e x ，k BN ＝2e x ，所以－1e x ·2e x ＝－1，x 1＋x 2＝0，所以AM ：y －1＋1e x ＝－1e x (x －x 1)，M (0，1e x x 1－1e x ＋1)，所以|AM |=x 1|，同理|BN |·|x 2|，所以|AM ||BN |1e x ==∈(0,1)．。

桂林市卓远文化艺术培训学校专用资料导数专题知识清单及例题练习编写者： 审核者：邹俊飞一．导数的概念设0x 是函数)(x f y =定义域的一点，如果自变量x 在0x 处有增量x ∆，则函数值y 也引起相应的增量)()(00x f x x f y -∆+=∆；比值xx f x x f x y ∆-∆+=∆∆)()(00称为函数)(x f y =在点0x 到x x ∆+0之间的平均变化率；如果极限xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000存在，则称函数)(x f y =在点0x 处可导，并把这个极限叫做)(x f y =在0x 处的导数，记作)(0'x f 或0|'x x y =，即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000 说明：1. 函数f （x ）在点0x 处可导，是指0→∆x 时，x y ∆∆有极限。

如果x y∆∆不存在极限，就说函数在点x 0处不可导，或说无导数。

2.x ∆是自变量x 在0x 处的改变量，0≠∆x 时，而y ∆是函数值的改变量，可以是零。

3. 由导数的定义可知，求函数y=f （x ）在点0x 处的导数的步骤（可由学生来归纳）： （1）求函数的增量y ∆=f （0x +x ∆）－f （0x ）；（2）求平均变化率x y ∆∆=x x f x x f ∆-∆+)()(00； （3）取极限，得导数f’(0x )=x y x ∆∆→∆0lim。

例题： 利用定义求 2)(x x f =在x=2处的导数；练习：求 24)(x x f =在x=2处的导数二．导数的几何意义 （求切线方程）函数y=f （x ）在点0x 处的导数的几何意义是曲线y=f （x ）在点p （0x ，f （x 0））处的切线的斜率。

也就是说，曲线y=f （x ）在点p （0x ，f （x 0））处的切线的斜率是f’（ 0x ）。

专题4.1 导数的概念、运算及导数的几何意义（真题测试）一、单选题1. （2021·四川省叙永第一中学校高三阶段练习）对于以下四个函数：①y x =；②2y x ；③3y x =；④1y x=．在区间[]1,2上函数的平均变化率最大的是（ ） A ．①B ．②C ．③D ．④2．（2020·全国·高考真题（理））函数43()2f x x x =-的图像在点(1(1))f ，处的切线方程为（ ） A ．21y x =-- B ．21y x =-+ C ．23y x =-D ．21y x =+3．（2006·安徽·高考真题（理））若曲线4y x =的一条切线l 与直线480x y +-=垂直，则l 的方程为（ ） A ．430x y --= B ．450x y +-= C ．430x y -+= D ．430x y ++= 4．（2019·全国·高考真题（文））曲线y =2sin x +cos x 在点(π，–1)处的切线方程为（ ） A ．10x y --π-= B ．2210x y --π-= C ．2210x y +-π+=D ．10x y +-π+=5．（2016·山东·高考真题（文））若函数()y f x =的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称()y f x =具有T 性质．下列函数中具有T 性质的是（ ） A ．sin y x =B ．ln y x =C ．x y e =D ．3y x =6．（2018·全国·高考真题（文））设函数()()321f x x a x ax =+-+．若()f x 为奇函数，则曲线()y f x =在点()00，处的切线方程为( )A ．2y x =-B ．y x =-C ．2y x =D ．y x =7．（2016·四川·高考真题（文））设直线l 1，l 2分别是函数f(x)= ln ,01,{ln ,1,x x x x -<<>图象上点P 1，P­2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△PAB 的面积的取值范围是（ ） A ．(0,1)B ．(0,2)C ．(0,+∞)D ．(1,+∞)8．（2022·四川省内江市第六中学模拟预测（文））若函数()21f x x =+与()2ln 1g x a x =+的图象存在公共切线，则实数a 的最大值为（ ）A ．e 2B ．eCD ．2e二、多选题9．（2022·黑龙江·哈尔滨三中高二阶段练习）近两年为抑制房价过快上涨，政府出台了一系列以“限购、限外、限贷、限价”为主题的房地产调控政策．各地房产部门为尽快实现稳定房价，提出多种方案，其中一项就是在规定的时间T 内完成房产供应量任务S ．已知房产供应量S 与时间t 的函数关系如图所示，则在以下各种房产供应方案中，在时间[]0,T 内供应效率（单位时间的供应量）不是．．逐步提高的（ ） A ． B ．C ．D ．10．（2022·吉林·长春市第二实验中学高二期中）若曲线()sin 1f x x x =-在πx =处的切线与直线210ax y ++=互相垂直，则（ ）A ．()sin cos f x x x x '=-B ．()sin cos f x x x x '=+C ．()ππf '=-D ．2πa =-11．（2022·广东·二模）吹气球时，记气球的半径r 与体积V 之间的函数关系为r （V ），()r V '为r （V ）的导函数．已知r （V ）在03V ≤≤上的图象如图所示，若1203V V <≤≤，则下列结论正确的是（ ）A．()()()()10211021r r r r --<-- B ．()()'1'2r r > C ．()()121222r V r V V V r ++⎛⎫< ⎪⎝⎭D ．存在()012,V V V ∈，使得()()()21021r V r V r V V V --'=12．（2022·全国·高三专题练习）已知0,0a b >>，直线y x a =+与曲线1e 21x y b -=-+相切，则下列不等式成立的是（ ）A ．18ab ≤B ．218a b+≤C D ．3a b +≤三、填空题13．（2015·天津·高考真题（文））已知函数()()ln ,0,f x ax x x =∈+∞，其中a 为实数，()f x '为()f x 的导函数，若()13f '=，则a 的值为_________．14．（2015·全国·高考真题（文））已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a=________．15.（2020·全国·高考真题（文））曲线ln 1y x x =++的一条切线的斜率为2，则该切线的方程为______________. 16．（2012·浙江·高考真题（文））定义：曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l 的距离．已知曲线C 1：y ＝x 2＋a 到直线l ：y ＝x 的距离等于C 2：x 2＋(y ＋4) 2 ＝2到直线l ：y ＝x 的距离，则实数a ＝______________． 四、解答题17．（2022·浙江·高三专题练习）已知()f x '是一次函数，()()()2212x f x x f x '--=，求()f x 的解析式．18．（2021·全国·高三专题练习）已知曲线313y x =.求该曲线的过点82,3P ⎛⎫ ⎪⎝⎭的切线方程.19．（2022·全国·高三专题练习）已知曲线32y x x =+-在点0P 处的切线1l 平行于直线410x y --=，且点0P 在第三象限． (1)求0P 的坐标；(2)若直线1l l ⊥，且l 也过切点0P ，求直线l 的方程．20．（2011·陕西·高考真题（理））如图，从点1(0,0)P 作x 轴的垂线交曲线xy e =于点1(0,1)Q ，曲线在1Q 点处的切线与x 轴交于点2P ，再从2P 作x 轴的垂线交曲线于点2Q ，依次重复上述过程得到一系列点：1P ，1Q ；2P ，2Q ；；n P ，n Q 记k P 点的坐标为(,0)k x （1,2,,k n =）（1）试求k x 与1k x -的关系（2k n ≤≤） （2）求1122n n PQ P Q P Q +++21．（2022·四川·绵阳中学实验学校模拟预测（文））已知曲线()()()211ln ,2f x x x x ax b a b =+--+∈R 在1x =处的切线经过坐标原点．(1)求b 的值；(2)若()0f x ≤，求a 的取值范围．22．（2020·北京·高考真题）已知函数2()12f x x =-． （Ⅰ）求曲线()y f x =的斜率等于2-的切线方程；（Ⅱ）设曲线()y f x =在点(,())t f t 处的切线与坐标轴围成的三角形的面积为()S t ，求()S t 的最小值．专题4.1 导数的概念、运算及导数的几何意义（真题测试）一、单选题1. （2021·四川省叙永第一中学校高三阶段练习）对于以下四个函数：①y x =；①2y x ；①3y x =；①1y x=．在区间[]1,2上函数的平均变化率最大的是（ ） A ．① B ．②C ．③D ．④【答案】C 【解析】 【分析】分析求出四个函数的平均变化率，然后比较即可. 【详解】①21121y x ∆-==∆-，②41321y x ∆-==∆-，③81721y x ∆-==∆-，④1112212y x -∆==-∆-． 故选：C ．2．（2020·全国·高考真题（理））函数43()2f x x x =-的图像在点(1(1))f ，处的切线方程为（ ） A ．21y x =-- B ．21y x =-+ C ．23y x =- D ．21y x =+【答案】B 【解析】 【分析】求得函数()y f x =的导数()f x '，计算出()1f 和()1f '的值，可得出所求切线的点斜式方程，化简即可. 【详解】()432f x x x =-，()3246f x x x '∴=-，()11f ∴=-，()12f '=-， 因此，所求切线的方程为()121y x +=--，即21y x =-+. 故选：B.3．（2006·安徽·高考真题（理））若曲线4y x =的一条切线l 与直线480x y +-=垂直，则l 的方程为（ ） A ．430x y --= B ．450x y +-= C ．430x y -+= D ．430x y ++= 【答案】A 【解析】【详解】与直线480x y +-=垂直的直线l 为40x y m -+=，即4y x =在某一点的导数为4，而34y x '=，所以4y x =在(1，1)处导数为4，此点的切线为430x y --=，故选A4．（2019·全国·高考真题（文））曲线y =2sin x +cos x 在点(π，–1)处的切线方程为（ ） A ．10x y --π-= B ．2210x y --π-= C ．2210x y +-π+= D ．10x y +-π+=【答案】C 【解析】 【分析】先判定点(,1)π-是否为切点，再利用导数的几何意义求解. 【详解】当x π=时，2sin cos 1y =π+π=-，即点(,1)π-在曲线2sin cos y x x =+上．2cos sin ,y x x '=-2cos sin 2,x y πππ=∴=-=-'则2sin cos y x x =+在点(,1)π-处的切线方程为(1)2()y x --=--π，即2210x y +-π+=．故选C ．5．（2016·山东·高考真题（文））若函数()y f x =的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称()y f x =具有T 性质．下列函数中具有T 性质的是（ ） A ．sin y x = B ．ln y x = C ．x y e = D ．3y x =【答案】A 【解析】 【分析】若函数y ＝f （x ）的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则函数y ＝f （x ）的导函数上存在两点，使这点的导函数值乘积为﹣1，进而可得答案． 【详解】解：函数y ＝f （x ）的图象上存在两点，使得函数的图象在这两点处的切线互相垂直， 则函数y ＝f （x ）的导函数上存在两点，使这点的导函数值乘积为﹣1， 当y ＝sin x 时，y ′＝cos x ，满足条件；当y ＝lnx 时，y ′1x=＞0恒成立，不满足条件；当y ＝ex 时，y ′＝ex ＞0恒成立，不满足条件；当y ＝x 3时，y ′＝3x 2＞0恒成立，不满足条件； 故选A ．6．（2018·全国·高考真题（文））设函数()()321f x x a x ax =+-+．若()f x 为奇函数，则曲线()y f x =在点()00，处的切线方程为( )A ．2y x =-B ．y x =-C ．2y x =D ．y x =【答案】D 【解析】 【详解】分析：利用奇函数偶次项系数为零求得1a =，进而得到()f x 的解析式，再对()f x 求导得出切线的斜率k ，进而求得切线方程.详解：因为函数()f x 是奇函数，所以10a -=，解得1a =， 所以3()f x x x =+，2()31x f 'x =+， 所以'(0)1,(0)0f f ==，所以曲线()y f x =在点(0,0)处的切线方程为(0)'(0)y f f x -=， 化简可得y x =，故选D.7．（2016·四川·高考真题（文））设直线l 1，l 2分别是函数f(x)= ln ,01,{ln ,1,x x x x -<<>图象上点P 1，P­2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△PAB 的面积的取值范围是（ ） A ．(0,1) B ．(0,2) C ．(0,+∞) D ．(1,+∞)【答案】A 【解析】 【详解】试题分析：设()()111222,ln ,,ln P x x P x x -（不妨设121,01x x ><<），则由导数的几何意义易得切线12,l l 的斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 的方程分别为()1111ln y x x x x -=-，切线2l 的方程为()2221ln y x x x x +=--，即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭．分别令0x =得()()110,1ln ,0,1ln .A x B x -++又1l 与2l 的交点为221111112222111121211,ln .1,1,0111211PAB A B P PAB x x x x P x x S y y x S x x x x ∆∆⎛⎫-++>∴=-⋅=<=∴<< ⎪++++⎝⎭，故选A ． 8．（2022·四川省内江市第六中学模拟预测（文））若函数()21f x x =+与()2ln 1g x a x =+的图象存在公共切线，则实数a 的最大值为（ ） A ．e 2B ．e CD ．2e【答案】B 【解析】 【分析】分别设公切线与()21f x x =+和:()2ln 1C g x a x =+的切点()211,1x x +，()22,2ln 1x a x +，根据导数的几何意义列式，再化简可得2222222ln a x x x =-，再求导分析22()22ln (0)h x x x x x =-⋅>的最大值即可【详解】()2f x x '=，()2a g x x'=，设公切线与()21f x x =+的图象切于点()211,1x x +，与曲线:()2ln 1C g x a x =+切于点()22,2ln 1x a x +，∴()()2221211221212ln 1122ln 2a x x a a x x x x x x x x +-+-===--，故12a x x =，所以212211212ln 2x x x x x x x -=-，∴122222ln x x x x =-⋅，∵12a x x =，故2222222ln a x x x =-，设22()22ln (0)h x x x x x =-⋅>，则()2(12ln )h x x x '=-，∴()h x在上递增，在)+∞上递减，∴max ()e h x h ==， ∴实数a 的最大值为e 故选：B. 二、多选题9．（2022·黑龙江·哈尔滨三中高二阶段练习）近两年为抑制房价过快上涨，政府出台了一系列以“限购、限外、限贷、限价”为主题的房地产调控政策．各地房产部门为尽快实现稳定房价，提出多种方案，其中一项就是在规定的时间T 内完成房产供应量任务S ．已知房产供应量S 与时间t 的函数关系如图所示，则在以下各种房产供应方案中，在时间[]0,T 内供应效率（单位时间的供应量）不是．．逐步提高的（ ）A ． B ．C ．D ．【答案】ACD 【解析】 【分析】根据变化率的知识，结合曲线在某点处导数的几何意义，可得结果. 【详解】单位时间的供应量逐步提高时，供应量的增长速度越来越快，图象上切线的斜率随着自变量的增加会越来越大，则曲线是上升的，且越来越陡，故函数的图象应一直下凹的.则选项B 满足条件，所以在时间[0，T ]内供应效率（单位时间的供应量）不是逐步提高的是ACD 选项， 故选：ACD.10．（2022·吉林·长春市第二实验中学高二期中）若曲线()sin 1f x x x =-在πx =处的切线与直线210ax y ++=互相垂直，则（ ）A ．()sin cos f x x x x '=-B ．()sin cos f x x x x '=+C ．()ππf '=-D ．2πa =-【答案】BCD 【解析】 【分析】由已知，选项A 、选项B ，可根据给出的曲线解析式直接求导做出判断，选项C ，可将πx =带入求解出的()f x '中进行求解判断，选项D ，根据求解出的()πf '结合直线方程的斜率，利用在πx =处的切线与直线互相垂直即可列出等量关系，求解出a 的值.【详解】选项A ，已知曲线()sin 1f x x x =-，所以()sin cos f x x x x '=+，故该选项错误； 选项B ，已知曲线()sin 1f x x x =-，所以()sin cos f x x x x '=+，故该选项正确；选项C ，因为()sin cos f x x x x '=+，所以()πsin ππcos πf '=+0ππ=-=-，故该选项正确；选项D ，直线210ax y ++=的斜率为2a-，而()ππf '=-，由已知，曲线()sin 1f x x x =-在πx =处的切线与直线210ax y ++=互相垂直，所以(π)12a--=-，所以2πa =-，该选项正确； 故选：BCD.11．（2022·广东·二模）吹气球时，记气球的半径r 与体积V 之间的函数关系为r （V ），()r V '为r （V ）的导函数．已知r （V ）在03V ≤≤上的图象如图所示，若1203V V <≤≤，则下列结论正确的是（ ）A ．()()()()10211021r r r r --<-- B ．()()'1'2r r > C ．()()121222r V r V V V r ++⎛⎫< ⎪⎝⎭D ．存在()012,V V V ∈，使得()()()21021r V r V r V V V --'=【答案】BD 【解析】 【分析】 A ：设()()()()1021tan ,tan =1021r r r r αθ--=--，由图得αθ>，所以该选项错误； B:根据图象和导数的几何意义得()()12r r '>'，所以该选项正确； C:设120,3,V V == 3(3)()22r r >，所以该选项错误；D:结合图象和导数的几何意义可以判断该选项正确. 【详解】 解：A ：设()()()()1021tan ,tan =1021r r r r αθ--=--，由图得αθ>，所以tan tan ,αθ>所以()()()()10211021r r r r -->--，所以该选项错误；B:由图得图象上点的切线的斜率越来越小，根据导数的几何意义得()()12r r '>'，所以该选项正确；C:设()()1212123(3)=(0,3,),2222r V r V V V r r V V r ++⎛⎫= ⎪⎝⎭==∴，因为3()(0)2r r ->3(3)(),2r r -所以3(3)()22r r >，所以该选项错误； D:()()2121r V r V V V --表示1122(,()),(,())A V r V B V r V 两点之间的斜率，()0r V '表示00(,())C V r V 处切线的斜率，由于()012,V V V ∈，所以可以平移直线AB 使之和曲线相切，切点就是点C ,所以该选项正确. 故选：BD12．（2022·全国·高三专题练习）已知0,0a b >>，直线y x a =+与曲线1e 21x y b -=-+相切，则下列不等式成立的是（ ） A ．18ab ≤B ．218a b+≤C D ．3a b +≤【答案】AC 【解析】 【分析】利用导数的几何意义，求出a ，b 的关系，再结合均值不等式逐项分析、计算并判断作答. 【详解】设直线y x a =+与曲线1e 21x y b -=-+相切的切点为00(,)x y ， 由1e 21x y b -=-+求导得：1e x y -'=，则有01e 1x -=，解得01x =， 因此，0122y a b =+=-，即21a b +=，而0,0a b >>，对于A ，211212()2228a b ab a b +=⋅⋅≤=，当且仅当122a b ==时取“=”，A 正确；对于B ，21214(2)()448b a a b a b a b a b +=++=++≥+=，当且仅当4b a a b =，即122a b ==时取“=”，B 不正确；对于C ，因22332(2)222a a b b a b +=+++=+=，则有232≤，=4a b =时取“=”，由214a b a b+=⎧⎨=⎩得21,36a b ==，所以当21,36a b ==时，max C 正确； 对于D ，由21a b +=，0,0a b >>得，102b <<，11(,1)2a b b +=-∈，而函数3x y =在R 上单调递增，33a b +<，D 不正确. 故选：AC 三、填空题13．（2015·天津·高考真题（文））已知函数()()ln ,0,f x ax x x =∈+∞，其中a 为实数，()f x '为()f x 的导函数，若()13f '=，则a 的值为_________． 【答案】3 【解析】'()ln f x a x a =+，所以'(1)3f a ==．14．（2015·全国·高考真题（文））已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a=________． 【答案】8 【解析】 【详解】试题分析：函数ln y x x =+在(1,1)处的导数为111|1|2x x y x===+='，所以切线方程为；曲线2(2)1y ax a x =+++的导函数的为，因与该曲线相切，可令，当时，曲线为直线，与直线平行，不符合题意；当时，代入曲线方程可求得切点，代入切线方程即可求得.15.（2020·全国·高考真题（文））曲线ln 1y x x =++的一条切线的斜率为2，则该切线的方程为______________. 【答案】2y x = 【解析】 【分析】设切线的切点坐标为00(,)x y ，对函数求导，利用0|2x y '=，求出0x ，代入曲线方程求出0y ，得到切线的点斜式方程，化简即可. 【详解】设切线的切点坐标为001(,),ln 1,1x y y x x y x=++'=+， 00001|12,1,2x x y x y x ='=+===，所以切点坐标为(1,2)， 所求的切线方程为22(1)y x -=-，即2y x =. 故答案为：2y x =.16．（2012·浙江·高考真题（文））定义：曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l 的距离．已知曲线C 1：y ＝x 2＋a 到直线l ：y ＝x 的距离等于C 2：x 2＋(y ＋4) 2 ＝2到直线l ：y ＝x 的距离，则实数a ＝______________． 【答案】94【解析】 【详解】试题分析：由新定义可知，直线与曲线相离，圆的圆心到直线的距离为，此时直线与圆相离，根据新定义可知，曲线到直线的距离为，对函数求导得，令，故曲线在处的切线方程为，即，于是曲线到直线的距离为，则有，解得或，当时，直线与曲线相交，不合乎题意；当时，直线与曲线相离，合乎题意.综上所述，.四、解答题17．（2022·浙江·高三专题练习）已知()f x '是一次函数，()()()2212x f x x f x '--=，求()f x 的解析式．【答案】()2442f x x x =++【解析】 【分析】分析可知，函数()f x 为二次函数，可设()()20f x ax bx c a =++≠，根据导数的运算法则结合已知条件可得出关于a 、b 、c 的方程组，解出这三个未知数的值，即可得出函数()f x 的解析式. 【详解】由()f x '为一次函数可知()f x 为二次函数．设()()20f x ax bx c a =++≠，则()2f x ax b '=+．所以，()()()()()()222212212x f x x f x x ax b x ax bx c '--=+--++=，即()()2220a b x b c x c -+-+-=，所以，02020a b b c c -=⎧⎪-=⎨⎪-=⎩，解得442a b c =⎧⎪=⎨⎪=⎩，因此，()2442f x x x =++.18．（2021·全国·高三专题练习）已知曲线313y x =.求该曲线的过点82,3P ⎛⎫⎪⎝⎭的切线方程.【答案】123160x y --=或3320x y -+=. 【解析】 【分析】设出曲线过P 点的切线方程的切点坐标，把切点的横坐标代入到导函数中即可表示出切线的斜率，根据切点坐标和表示出的斜率，写出切线的方程，把P 的坐标带入到切线方程即可得到关于切点横坐标的方程，求出方程的解即可得到切点横坐标的值，分别代入所设的切线方程即可. 【详解】解：设切点坐标为()00,x y ，切点在曲线上，∴在点()00,x y 处切线的斜率为020x x k y x =='=.∴切线方程为()2000y y x x x -=-.又切线过点82,3P ⎛⎫ ⎪⎝⎭，且切点()00,x y 在曲线313y x =上()200030082,31,3y x x y x ⎧-=-⎪⎪∴⎨⎪=⎪⎩整理得3200340x x -+=，即()()200210x x -+=，解得02x =或01x =-.∴当02x =，083y =，即切线斜率为4时，切线的方程为123160x y --=；当01x =-，031y =-，即切线斜率为1时，切线的方程为3320x y -+=.综上，所求切线方程为123160x y --=或3320x y -+=.19．（2022·全国·高三专题练习）已知曲线32y x x =+-在点0P 处的切线1l 平行于直线410x y --=，且点0P 在第三象限． (1)求0P 的坐标；(2)若直线1l l ⊥，且l 也过切点0P ，求直线l 的方程． 【答案】(1)(1,4)--； (2)4170x y ++=. 【解析】 【分析】（1）设点000(,)P x y ，求出给定函数的导数，再利用导数的几何意义，列式计算作答. （2）求出直线l 的斜率，由（1）的结论结合直线的点斜式方程求解作答. (1)由32y x x =+-求导得：231y x '=+，设切点000(,)P x y ，而点0P 在第三象限，即000,0x y <<，依题意，20314x +=，解得：01x =-，此时，04y =-，显然点(1,4)--不在直线410x y --=上，所以切点0P 的坐标为(1,4)--. (2)直线1l l ⊥，而1l 的斜率为4，则直线l 的斜率为14-，又l 过切点0P (1,4)--，于是得直线l 的方程为14(1)4y x +=-+，即4170x y ++=，所以直线l 的方程为：4170x y ++=.20．（2011·陕西·高考真题（理））如图，从点1(0,0)P 作x 轴的垂线交曲线xy e =于点1(0,1)Q ，曲线在1Q 点处的切线与x 轴交于点2P ，再从2P 作x 轴的垂线交曲线于点2Q ，依次重复上述过程得到一系列点：1P ，1Q ；2P ，2Q ；；n P ，n Q 记k P 点的坐标为(,0)k x （1,2,,k n =）（1）试求k x 与1k x -的关系（2k n ≤≤）（2）求1122n n PQ P Q P Q +++【答案】（1）11k k x x -=-()2k n ≤≤（2）11ne e e --- 【解析】 【详解】（1）根据函数的导数求切线方程，然后再求切线与x 轴的交点坐标；（2）尝试求出通项n n P Q 的表达式，然后再求和．（1）设点1k P -的坐标是1(,0)k x -，∵x y e =，∴x y e '=， ∴111(,)k x k k Q x e---，在点111(,)k x k k Q x e ---处的切线方程是111()k k x x k y e e x x ----=-，令0y =，则11k k x x -=-（2k n ）．（2）∵10x =，11k k x x --=-，∴(1)k x k =--，∴(1)k x k k k PQ e e--==，于是有 112233n n PQ PQ PQ P Q ++++12(1)1111n k e e e ee -------=++++=-11ne e e --=-， 即112233n n PQ PQ PQ P Q ++++11ne e e --=-．21．（2022·四川·绵阳中学实验学校模拟预测（文））已知曲线()()()211ln ,2f x x x x ax b a b =+--+∈R 在1x =处的切线经过坐标原点．(1)求b 的值； (2)若()0f x ≤，求a 的取值范围． 【答案】(1)32b = (2)[)1,+∞【解析】 【分析】（1）利用导数的几何意义可求得()f x 在1x =处的切线方程，代入坐标原点即可求得b ；（2）采用分离变量的方式可得()1131ln 22a g x x x x x ⎛⎫≥=+-+ ⎪⎝⎭，利用导数可求得()g x 单调性，由此可得()max 1g x =，进而得到a 的取值范围.(1)()1ln x f x x x a x+'=+--，()11f a '∴=-，又()112f a b =--+，()f x ∴在1x =处的切线为：()()1112y a b a x ++-=--，又该切线过原点，112a b a ∴+-=-+，解得：32b =.(2)由（1）得：()()2131ln 22f x x x x ax =+--+，()f x 定义域为()0,∞+；若()0f x ≤恒成立，则1131ln 22a x x x x ⎛⎫≥+-+ ⎪⎝⎭；令()1131ln 22g x x x x x ⎛⎫=+-+ ⎪⎝⎭，则()222ln 212x x x g x x--+-'=； 令()22ln 21h x x x x =--+-，则()()221x x h x x-+'=-；210x x -+>恒成立，()0h x '∴<，()h x ∴在()0,∞+上单调递减，又()10h =，∴当()0,1x ∈时，()0h x '>；当()1,x ∈+∞时，()0h x '<；()g x ∴在()0,1上单调递增，在()1,+∞上单调递减，()()max 131122g x g ∴==-+=，1a ∴≥，即a 的取值范围为[)1,+∞.22．（2020·北京·高考真题）已知函数2()12f x x =-．（Ⅰ）求曲线()y f x =的斜率等于2-的切线方程； （Ⅱ）设曲线()y f x =在点(,())t f t 处的切线与坐标轴围成的三角形的面积为()S t ，求()S t 的最小值． 【答案】（Ⅰ）2130x y +-=，（Ⅱ）32. 【解析】 【分析】（Ⅰ）根据导数的几何意义可得切点的坐标，然后由点斜式可得结果；（Ⅱ）根据导数的几何意义求出切线方程，再得到切线在坐标轴上的截距，进一步得到三角形的面积，最后利用导数可求得最值. 【详解】（Ⅰ）因为()212f x x =-，所以()2f x x '=-，设切点为()00,12x x -，则022x -=-，即01x =，所以切点为()1,11， 由点斜式可得切线方程为：()1121y x -=--，即2130x y +-=. （Ⅱ）[方法一]：导数法显然0t ≠，因为()y f x =在点()2,12t t -处的切线方程为：()()2122y t t x t --=--， 令0x =，得212y t =+，令0y =，得2122t x t+=，所以()S t =()221121222||t t t +⨯+⋅，不妨设0t >(0t <时，结果一样)，则()423241441144(24)44t t S t t t t t++==++，所以()S t '=4222211443(848)(324)44t t t t t+-+-= 222223(4)(12)3(2)(2)(12)44t t t t t t t -+-++==， 由()0S t '>，得2t >，由()0S t '<，得02t <<， 所以()S t 在()0,2上递减，在()2,+∞上递增， 所以2t =时，()S t 取得极小值， 也是最小值为()16162328S ⨯==. [方法二]【最优解】：换元加导数法 ()()2222121121()12(0)2|2|4||t t S t t t t t ++=⋅⋅+=⋅≠．因为()S t 为偶函数，不妨设0t >，221()4S t =⋅，令a =2,0t a a =>．令412()a g a a +=，则面积为21[()]4S g a =，只需求出412()a g a a+=的最小值．34422412312()a a a a g a a a ⋅---='=()()()222223223(2a a a a a a a-++==．因为0a >，所以令()0g a '=，得a = 随着a 的变化，(),()g a g a '的变化情况如下表：所以min [()]g a g ===所以当a =2t =时，2min 1[()]324S t =⨯=． 因为[()]S t 为偶函数，当0t <时，min [()](2)(2)32S t S S =-==． 综上，当2t =±时，()S t 的最小值为32． [方法三]：多元均值不等式法同方法二，只需求出412()(0)a g a a a +=>的最小值．令4312444()a g a a a a a a +==+++≥=当且仅当34a a=，即a =所以当a =2t =时，2min 1[()]324S t =⨯=．因为()S t 为偶函数，当0t <时，min [()](2)(2)32S t S S =-==．综上，当2t =±时，()S t 的最小值为32． [方法四]：两次使用基本不等式法同方法一得到()()()()()22222222222121241646464()41616324||444tt t t S t t t t t t ++++++=≥==+++≥=+++ ,下同方法一. 【整体点评】（Ⅱ）的方法一直接对面积函数求导数，方法二利用换元方法，简化了运算，确定为最优解；方法三在方法二换元的基础上，利用多元均值不等式求得最小值，运算较为简洁；方法四两次使用基本不等式，所有知识最少，配凑巧妙，技巧性较高.60。

专题01 导数的概念及其几何意义A 组 基础巩固1.在平均变化率的定义中，自变量的增量x ∆是（ ）A ．0x ∆>B ．0x ∆<C ．0x ∆≠D ．0x ∆= 【答案】 C【解析】 x ∆可正可负但不能为零。

2．（2021·全国高二课时练习）汽车行驶的路程s 和时间t 之间的函数图象如图，在时间段[][][]011223,,,,,t t t t t t 上的平均速度分别为123,,v v v ，则三者的大小关系为（ ）A ．231v v v =<B ．123v v v <=C ．123v v v <<D ．231v v v <<【答案】C【分析】由平均变化率的几何意义判断．【详解】由题意得，123,,OA AB BC v k v k v k ===，由题图易知OA AB BC k k k <<， ∴123v v v <<，故选：C.3．（2021·全国高二单元测试）已知()y f x =的图象如图所示，则()A f x '与()B f x '的大小关系是（ ）A ．f ′(x A )＞f ′(xB ) B ．f ′(x A )＜f ′(x B )C ．f ′(x A )＝f ′(x B )D ．不能确定【答案】B【分析】根据导数的几何意义，结合图象可得答案.【详解】由导数的几何意义可知，f ′(x A )，f ′(x B )分别是切线在点A 、B 处切线的斜率， 由图象可知f ′(x A )＜f ′(x B )．故选：B4．（2021·全国高二课时练习）（多选题）为了评估某种治疗肺炎药物的疗效，现有关部门对该药物在人体血管中的药物浓度进行测量．设该药物在人体血管中药物浓度c 与时间t 的关系为()c f t =，甲、乙两人服用该药物后，血管中药物浓度随时间t 变化的关系如下图所示．给出下列四个结论正确的是（ ）A ．在1t 时刻，甲、乙两人血管中的药物浓度相同；B ．在2t 时刻，甲、乙两人血管中药物浓度的瞬时变化率相同；C ．在23[,]t t 这个时间段内，甲、乙两人血管中药物浓度的平均变化率相同；D ．在12[,]t t ，23[,]t t 两个时间段内，甲血管中药物浓度的平均变化率不相同． 【答案】ACD 【分析】理解平均变化率和瞬时变换率的意义，结合图象，判断选项. 【详解】对于A ，在1t 时刻，为两图象的交点，即此时甲、乙两人血管中的药物浓度相同，故A 正确；对于B ，甲、乙两人在2t 时刻的切线的斜率不相等，即两人的()2f t '不相同，所以甲、乙两人血管中药物浓度的瞬时变化率不相同，故B 错误；对于C ，根据平均变换率公式可知，甲、乙两人的平均变化率都是()()3232f t f t t t --，故C 正确；对于D ，在[]12,t t 时间段，甲的平均变化率是()()2121f t f t t t --，在[]23,t t 时间段，甲的平均变化率是()()3232f t f t t t --，显然不相等，故D 正确．故选：ACD 【点睛】思路点睛：本题是一道识图的实际应用问题，判断的关键是理解两个概念，瞬时变化率和平均变化率，结合导数的几何意义可知瞬时变化率就是在此点处切线的斜率，平均变化率是()()f t t f t t+-.5.（2021·全国高二单元测试）一直线运动的物体，从时间t 到t ＋Δt 时，物体的位移为Δs ，那么s t∆∆为（ ）A ．在t 时刻该物体的瞬时速度B ．当时间为Δt 时物体的瞬时速度C ．从时间t 到t ＋t ∆时物体的平均速度D ．以上说法均错误 【答案】C【分析】根据函数的平均变化率的定义判断． 【详解】根据平均变化率的概念可知， st∆∆表示从时间t 到t ＋t ∆时物体的平均速度． 故选：C ．6.（2021·全国高二单元测试）在曲线y ＝x 2＋1上取一点(1，2)及邻近一点(1＋Δx ，2＋Δy )，则y x∆∆为（ ）A ．Δx ＋12x ∆+B ．Δx －1x∆－2C ．Δx ＋2D ．2＋Δx －1x∆ 【答案】C【分析】根据平均变化率的定义计算．【详解】Δy ＝f (1＋Δx )－f （1）＝(1＋Δx )2＋1－(12＋1)＝(Δx )2＋2Δx ，∴yx∆∆＝Δx ＋2． 故选：C ．7．（2021·全国高二单元测试）酒杯的形状为倒立的圆锥(如图)，杯深8 cm ，上口宽6 cm ，水以20 cm 3/s 的流量倒入杯中，当水深为4 cm 时，水升高的瞬时变化率为________．【答案】80cm /s 9π【分析】利用体积公式计算得到1312803t h π⎛⎫= ⎪⎝⎭，再求出水深为4cm ，对应的时间为0t 的大小，最后利用导数可求瞬时变化率. 【详解】由题意，设t 时刻水面高为h ，水面圆半径为r , 则38r h =可得 3,8r h = 此时水的体积为2313364r h h ππ⨯⨯⨯= 又由题设条件知，此时的水量为20t故有3320,64t h π= 故有1312803t h π⎛⎫= ⎪⎝⎭23112801280333t h ππ-⎛⎫'=⨯⨯ ⎪⎝⎭当水深为4cm ，对应的时间为0t ，则0320t π=23312801128020333t th πππ-=⎛⎫⨯ ⎪=⨯⨯ ⎪ ⎪⎝'⎭809π= 所以当水深为4 cm 时，水升高的瞬时变化率为80cm /s 9π故答案为：80cm /s 9π【点睛】注意导数可以用来求瞬时速度、瞬时加速度等，这类问题的关键是要找到两类变量之间的关系.8．（2021·全国高二单元测试）一木块沿某一斜面自由下滑，测得下滑的距离s 与时间t 之间的函数关系为218s t =，则2t =时，木块的瞬时速度为________．【答案】12【分析】利用导数的定义可知，函数218s t =在2t =处的导数值即是木块在2t =处的瞬时速度. 【详解】解：2211()118848t t t s t t t t +∆-∆==+∆∆∆. 当2t =，且t ∆趋于0时，s t∆∆趋于12．故答案为：12. 9.如图，函数f (x )的图象是折线段ABC ,其中A ,B ,C 的坐标分别为（0，4），（2，0），（6，4），则[(0)]f f = ；0(1)(1)limx f x f x∆→+∆-∆= .【答案】 2，- 2【解析】 由图可知：f(0)=4,f(4)=2; f(x)=-2x+4,带入可得。

导数及其应用【考纲说明】1、了解导数概念的某些实际背景（如瞬时速度，加速度，光滑曲线切线的斜率等）；掌握函数在一点处的导数的定义和导数的几何意义；理解导函数的概念。

2、熟记八个基本导数公式；掌握两个函数和、差、积、商的求导法则，了解复合函数的求导法则，会求某些简单函数的导数。

3、理解可导函数的单调性与其导数的关系；了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号)；会求一些实际问题(一般指单峰函数)的最大值和最小值。

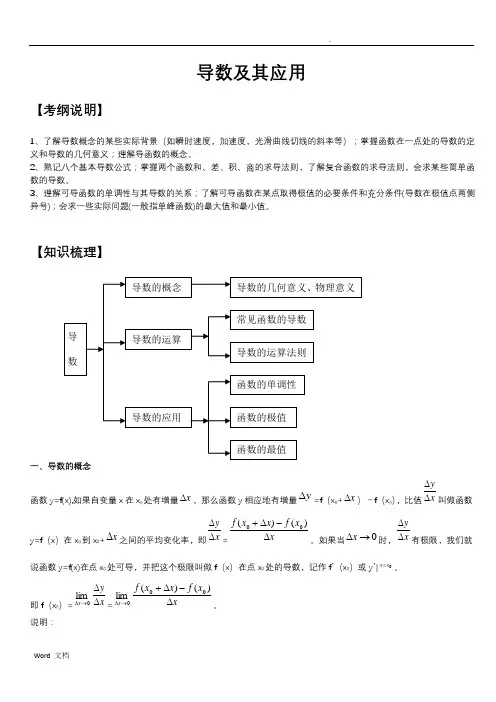
【知识梳理】一、导数的概念函数y=f(x),如果自变量x 在x 0处有增量x ∆，那么函数y 相应地有增量y ∆=f （x 0+x ∆）－f （x 0），比值x y∆∆叫做函数y=f （x ）在x 0到x 0+x ∆之间的平均变化率，即x y ∆∆=x x f x x f ∆-∆+)()(00。

如果当0→∆x 时，x y∆∆有极限，我们就说函数y=f(x)在点x 0处可导，并把这个极限叫做f （x ）在点x 0处的导数，记作f ’（x 0）或y ’|0x x =。

即f （x 0）=0lim→∆x x y∆∆=0lim →∆x x x f x x f ∆-∆+)()(00。

说明：（1）函数f （x ）在点x 0处可导，是指0→∆x 时，x y ∆∆有极限。

如果x y∆∆不存在极限，就说函数在点x 0处不可导，或说无导数。

（2）x ∆是自变量x 在x 0处的改变量，0≠∆x 时，而y ∆是函数值的改变量，可以是零。

由导数的定义可知，求函数y=f （x ）在点x 0处的导数的步骤： （1）求函数的增量y ∆=f （x 0+x ∆）－f （x 0）；（2）求平均变化率x y ∆∆=x x f x x f ∆-∆+)()(00；（3）取极限，得导数f ’(x 0)=x yx ∆∆→∆0lim。

二、导数的几何意义函数y=f （x ）在点x 0处的导数的几何意义是曲线y=f （x ）在点p （x 0，f （x 0））处的切线的斜率。

导数的概念试题及解析一、选择题1．函数在某一点的导数是( )A ．在该点的函数值的增量与自变量的增量的比B ．一个函数C ．一个常数，不是变数D ．函数在这一点到它附近一点之间的平均变化率[答案] C[解析] 由定义，f ′(x 0)是当Δx 无限趋近于0时，Δy Δx 无限趋近的常数，故应选C.2．如果质点A 按照规律s ＝3t 2运动，则在t 0＝3时的瞬时速度为( )A ．6B ．18C ．54D ．81[答案] B[解析] ∵s (t )＝3t 2，t 0＝3，∴Δs ＝s (t 0＋Δt )－s (t 0)＝3(3＋Δt )2－3·32＝18Δt ＋3(Δt )2∴Δs Δt ＝18＋3Δt .当Δt →0时，Δs Δt →18，故应选B.3．y ＝x 2在x ＝1处的导数为( )A ．2xB ．2C ．2＋ΔxD ．1 [答案] B[解析] ∵f (x )＝x 2，x ＝1，∴Δy ＝f (1＋Δx )2－f (1)＝(1＋Δx )2－1＝2·Δx ＋(Δx )2∴Δy Δx ＝2＋Δx当Δx →0时，Δy Δx →2∴f ′(1)＝2，故应选B.4．一质点做直线运动，若它所经过的路程与时间的关系为s (t )＝4t 2－3(s (t )的单位：m ，t 的单位：s)，则t ＝5时的瞬时速度为( )A ．37B ．38C ．39D ．40[答案] D[解析] ∵Δs Δt ＝4(5＋Δt )2－3－4×52＋3Δt ＝40＋4Δt ， ∴s ′(5)＝li m Δt →0 Δs Δt ＝li m Δt →0(40＋4Δt )＝40.故应选D. 5．已知函数y ＝f (x )，那么下列说法错误的是( )A ．Δy ＝f (x 0＋Δx )－f (x 0)叫做函数值的增量B.Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx叫做函数在x 0到x 0＋Δx 之间的平均变化率 C ．f (x )在x 0处的导数记为y ′D ．f (x )在x 0处的导数记为f ′(x 0)[答案] C[解析] 由导数的定义可知C 错误．故应选C.6．函数f (x )在x ＝x 0处的导数可表示为y ′|x ＝x 0，即( )A ．f ′(x 0)＝f (x 0＋Δx )－f (x 0)B ．f ′(x 0)＝li m Δx →0[f (x 0＋Δx )－f (x 0)] C ．f ′(x 0)＝f (x 0＋Δx )－f (x 0)ΔxD ．f ′(x 0)＝li m Δx →0 f (x 0＋Δx )－f (x 0)Δx[答案] D[解析] 由导数的定义知D 正确．故应选D.7．函数y ＝ax 2＋bx ＋c (a ≠0，a ，b ，c 为常数)在x ＝2时的瞬时变化率等于( )A ．4aB ．2a ＋bC ．bD ．4a ＋b [答案] D[解析] ∵Δy Δx ＝a (2＋Δx )2＋b (2＋Δx )＋c －4a －2b －c Δx＝4a ＋b ＋a Δx ，∴y ′|x ＝2＝li m Δx →0 Δy Δx ＝li m Δx →0(4a ＋b ＋a ·Δx )＝4a ＋b .故应选D. 8．如果一个函数的瞬时变化率处处为0，则这个函数的图象是( )A ．圆B ．抛物线C ．椭圆D ．直线 [答案] D[解析] 当f (x )＝b 时，f ′(x )＝0，所以f (x )的图象为一条直线，故应选D.9．一物体作直线运动，其位移s 与时间t 的关系是s ＝3t －t 2，则物体的初速度为( )A ．0B ．3C ．－2D ．3－2t[答案] B[解析] ∵Δs Δt ＝3(0＋Δt )－(0＋Δt )2Δt＝3－Δt ， ∴s ′(0)＝li m Δt →0 Δs Δt＝3.故应选B. 10．设f (x )＝1x ，则li m x →a f (x )－f (a )x －a等于( ) A ．－1a B.2aC ．－1a 2 D.1a 2[答案] C[解析] li m x →a f (x )－f (a )x －a ＝li m x →a 1x －1ax －a＝li m x →a a －x(x －a )·xa ＝－li m x →a 1ax ＝－1a 2.二、填空题11．已知函数y ＝f (x )在x ＝x 0处的导数为11，则li m Δx →0f (x 0－Δx )－f (x 0)Δx ＝________；li m x →x 0 f (x )－f (x 0)2(x 0－x )＝________.[答案] －11，－112[解析] li m Δx →0 f (x 0－Δx )－f (x 0)Δx＝－li m Δx →0 f (x 0－Δx )－f (x 0)－Δx ＝－f ′(x 0)＝－11；li m x →x 0 f (x )－f (x 0)2(x 0－x )＝－12li m Δx →0 f (x 0＋Δx )－f (x 0)Δx＝－12f ′(x 0)＝－112.12．函数y ＝x ＋1x 在x ＝1处的导数是________．[答案] 0[解析] ∵Δy ＝⎝ ⎛⎭⎪⎫1＋Δx ＋11＋Δx －⎝ ⎛⎭⎪⎫1＋11＝Δx －1＋1Δx ＋1＝(Δx )2Δx ＋1，∴Δy Δx ＝Δx Δx ＋1.∴y ′|x ＝1＝li m Δx →0 ΔxΔx ＋1＝0.13．已知函数f (x )＝ax ＋4，若f ′(2)＝2，则a 等于______．[答案] 2[解析] ∵Δy Δx ＝a (2＋Δx )＋4－2a －4Δx ＝a ，∴f ′(1)＝li m Δx →0 ΔyΔx ＝a .∴a ＝2.14．已知f ′(x 0)＝li m x →x 0 f (x )－f (x 0)x －x 0，f (3)＝2，f ′(3)＝－2，则li m x →3 2x －3f (x )x －3的值是________．[答案] 8[解析] li m x →3 2x －3f (x )x －3＝li m x →3 2x －3f (x )＋3f(3)－3f (3)x －3＝lim x →3 2x －3f (3)x －3＋li m x →3 3(f (3)－f (x ))x －3.由于f (3)＝2，上式可化为li m x →3 2(x －3)x －3－3li m x →3 f (x )－f(3)x －3＝2－3×(－2)＝8.三、解答题15．设f (x )＝x 2，求f ′(x 0)，f ′(－1)，f ′(2)．[解析] 由导数定义有f ′(x 0)＝li m Δx →0 f (x 0＋Δx )－f (x 0)Δx＝li m Δx →0 (x 0＋Δx )2－x 20Δx ＝li m Δx →0 Δx (2x 0＋Δx )Δx＝2x 0，16．枪弹在枪筒中运动可以看做匀加速运动，如果它的加速度是5.0×105m/s 2，枪弹从枪口射出时所用时间为1.6×10－3s ，求枪弹射出枪口时的瞬时速度．[解析] 位移公式为s ＝12at 2∵Δs ＝12a (t 0＋Δt )2－12at 20＝at 0Δt ＋12a (Δt )2∴Δs Δt ＝at 0＋12a Δt ，∴li m Δt →0 Δs Δt ＝li m Δt →0 ⎝ ⎛⎭⎪⎫at 0＋12a Δt ＝at 0，已知a ＝5.0×105m/s 2，t 0＝1.6×10－3s ，∴at 0＝800m/s.所以枪弹射出枪口时的瞬时速度为800m/s.17．在曲线y ＝f (x )＝x 2＋3的图象上取一点P (1,4)及附近一点(1＋Δx,4＋Δy )，求(1)Δy Δx (2)f ′(1)．[解析] (1)Δy Δx ＝f (1＋Δx )－f (1)Δx＝(1＋Δx )2＋3－12－3Δx＝2＋Δx .(2)f ′(1)＝lim Δx →0 f (1＋Δx )－f (1)Δx＝lim Δx →0(2＋Δx )＝2. 18．函数f (x )＝|x |(1＋x )在点x 0＝0处是否有导数？若有，求出来，若没有，说明理由．[解析] f (x )＝⎩⎪⎨⎪⎧ x ＋x 2 (x ≥0)－x －x 2 (x <0)Δy ＝f (0＋Δx )－f (0)＝f (Δx )＝⎩⎪⎨⎪⎧ Δx ＋(Δx )2 (Δx >0)－Δx －(Δx )2 (Δx <0)∴lim x →0＋ Δy Δx ＝lim Δx →0＋ (1＋Δx )＝1，lim Δx →0－ Δy Δx ＝lim Δx →0－ (－1－Δx )＝－1，∵lim Δx →0－ Δy Δx ≠lim Δx →0＋ Δy Δx ，∴Δx →0时，ΔyΔx 无极限．∴函数f (x )＝|x |(1＋x )在点x 0＝0处没有导数，即不可导．(x →0＋表示x 从大于0的一边无限趋近于0，即x ＞0且x 趋近于0)。

专题3.1 导数的概念及运算目录一、考纲要求1.了解导数概念的实际背景；2.通过函数图象直观理解导数的几何意义；3.能根据导数的定义求函数y ＝c (c 为常数)，y ＝x ，y ＝1x，y ＝x 2，y ＝x 3，y ＝x 的导数；4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，能求简单复合函数(仅限于形如y ＝f (ax ＋b )的复合函数)的导数；5.了解定积分的实际背景，了解定积分的基本思想，了解定积分的概念，几何意义；6.了解微积分基本定理的含义。

二、考点网络三、考情分析四、考点梳理考点1．导数的概念函数()f x 在0x x =处瞬时变化率是0000()()lim limx x f x x f x yx x∆→∆→+∆-∆=∆∆，我们称它为函数()y f x =在0x x =处的导数，记作0()f x '或0x x y ='．知识点诠释：①增量x ∆可以是正数，也可以是负，但是不可以等于0．0x ∆→的意义：x ∆与0之间距离要多近有 多近，即|0|x ∆-可以小于给定的任意小的正数；②当0x ∆→时，y ∆在变化中都趋于0，但它们的比值却趋于一个确定的常数，即存在一个常数与 00()()f x x f x y x x+∆-∆=∆∆无限接近； ③导数的本质就是函数的平均变化率在某点处的极限，即瞬时变化率．如瞬时速度即是位移在这一时 刻的瞬间变化率，即00000()()()limlimx x f x x f x yf x x x∆→∆→+∆-∆'==∆∆． 考点2．基本初等函数的导数公式考点3.导数的运算法则（1）函数和差求导法则：[()()]()()f x g x f x g x '''±=±；（2）函数积的求导法则：[()()]()()()()f x g x f x g x f x g x '''=+； （3）函数商的求导法则：()0g x ≠，则2()()()()()[]()()f x f xg x f x g x g x g x ''-=． 考点4．复合函数的导数复合函数[()]y f g x =的导数和函数()y f u =，()u g x =的导数间关系为x u x y y u '''=：重难点题型（一） 导数的定义例1．（23-24高二下·四川遂宁·阶段练习）设()f x 为可导函数，且满足0(3)lim 3(33)x f x f x∆→+∆-=∆，则曲线()y f x =在点(3,(3))f 处的切线的斜率是（ ）A ．1B ．3C ．6D ．9例2．（23-24高二下·江西萍乡·期中）已知甲､乙两个小区在[]0,t 这段时间内的家庭厨余垃圾的分出量Q 与时间t 的关系如图所示．给出下列四个结论，其中正确结论的个数为（ ）①在[]12,t t 这段时间内，甲小区比乙小区的分出量增长得慢； ②在[]23,t t 这段时间内，乙小区比甲小区的分出量增长得快； ③在2t 时刻，甲小区的分出量比乙小区的分出量增长得慢； ④乙小区在2t 时刻的分出量比3t 时刻的分出量增长得快． A ．1 B ．2C ．3D ．4例3．（24-25高三上·吉林长春·开学考试）数()f x 在R 上可导，若()23f '=，则()()232limx f x f x x∆→+∆--∆=∆ .【变式训练1】．（23-24高二上·江苏南京·期末）若0(22)(2)lim 62x f x f x∆→+∆-=∆，则()2f '=（ ）A ．32B ．6C ．3D ．3-【变式训练2】．（24-25高三·上海·课堂例题）如图，函数y =f (x )图像在点P 处的切线方程是8y x =-+，则()()55limh f h f h→+-= .【变式训练3】．（23-24高二下·山东菏泽·期中）若函数()f x 在0x x =处可导，则()()000lim4h f x h f x h h→+--=（ ） A ．()014f x ' B ．()012f x 'C ．()0f x 'D ．()02f x '重难点题型（二） 导数的运算例4．（2024高三·全国·专题练习）已知()()2024ln f x x x =+，若()0f x '=2025，则0x 等于（ ） A ．2e B ．1 C ．ln2 D ．e例5．（23-24高二下·福建福州·期末）已知函数()()21f x x x f '=-⋅，则()2f '=（ ）A ．0B ．2C ．3D ．4例6．（2024·四川绵阳·模拟预测）已知函数()sin cos f x x x =-，且()()003f x f x ='，则0sin 21cos 2x x =- .【变式训练4】．（2024·山西晋中·模拟预测）已知函数()()()()()()()234562222222f x x x x x x x x =------，则()0f '=（ ） A ．202 B ．212 C ．222 D ．232【变式训练5】．（2024·河南信阳·三模）动点P 在函数ln(4)ln y x x =--的图像上，以P 为切点的切线的倾斜角取值范围是（ ） A ．π0,4⎡⎤⎢⎥⎣⎦B ．π3π0,,π44⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭C ．π3π,24⎤⎛ ⎥⎝⎦D ．3π,π4⎡⎫⎪⎢⎣⎭【变式训练6】．（2024·江西南昌·三模）设函数()f x 的导数为()f x '，且()f x =则(1)f '= .【变式训练7】．（2024·广西柳州·模拟预测）已知()ln f x x x =，则()f x 在点()()e,e f 处的切线斜率是 ．重难点题型（三）导数的几何意义【解题方法总结】求切线方程问题的两种类型及方法(1)、求“在”曲线y ＝f (x )上一点P (x 0，y 0)处的切线方程：点P (x 0，y 0)为切点，切线斜率为k ＝f ′(x 0)，有唯一的一条切线，对应的切线方程为y －y 0＝f ′(x 0)(x －x 0)．.(2)、求“过”曲线y ＝f (x )上一点P (x 0，y 0)的切线方程：切线经过点P ，点P 可能是切点，也可能不是切点，这样的直线可能有多条，解决问题的关键是设切点，利用“待定切点法”，即： ①设切点A (x 1，y 1)，则以A 为切点的切线方程为y －y 1＝f ′(x 1)(x －x 1)；①根据题意知点P (x 0，y 0)在切线上，点A (x 1，y 1)在曲线y ＝f (x )上，得到方程组⎩⎪⎨⎪⎧y 1＝f (x 1)，y 0－y 1＝f ′(x 1)(x 0－x 1)，求出切点A (x 1，y 1)，代入方程y －y 1＝f ′(x 1)(x －x 1)，化简即得所求的切线方程． 考向1、求曲线的切线方程例7．（2023·陕西榆林·一模）曲线()e xf x x =-在0x =处的切线方程为 ．例8．（2024·四川宜宾·三模）若曲线e x y a =+的一条切线方程是1y x =-，则a =（ ）A ．2-B ．1C ．1-D ．e例9．（2023·北京东城·一模）过坐标原点作曲线2e 1x y -=+的切线，则切线方程为（ ）A ．y x =B ．2y x =C ．21e y x =D ．e y x =例10．（2024·贵州六盘水·三模）已知曲线23ln y x x =-的一条切线方程为y x m =-+，则实数m =（ ）A ．−2B ．1-C ．1D ．2【变式训练8】．（2024·湖北·模拟预测）曲线e x y =在点()0,2P 处的切线为l ，则l 在x 轴上的截距是 .【变式训练9】．（2024·陕西安康·模拟预测）若函数()3221f x x x =++，则()f x 在点()1,2P -处的切线方程为（ ）A ．10x y +-=B ．30x y ++=C ．250x y -+=D ．230x y +-=【变式训练10】．（2024·天津和平·二模）过点()0,0作曲线()2xy x =∈R 的切线，则切点的坐标为 ．【变式训练11】．（2024·山西吕梁·二模）若曲线()ln f x x =在点()00,P x y 处的切线过原点()0,0O ，则0x = .考向2、公切线例11．（2024·陕西榆林·模拟预测）已知曲线()2f x x =与()()()ln 0g x ax a =>有公共切线，则实数a 的最大值为 ．例12．（2024·广东茂名·一模）曲线ln y x =与曲线22y x ax =+有公切线，则实数a 的取值范围是（ ）A ．1,2⎛⎤-∞- ⎥⎝⎦B ．1,2⎡⎫-+∞⎪⎢⎣⎭C ．1,2⎛⎤-∞ ⎥⎝⎦D ．1,2⎡⎫+∞⎪⎢⎣⎭【变式训练12】．（2023·陕西宝鸡·模拟预测）已知曲线()e xf x x =+在点()()0,0f 处的切线与曲线()ln 1y x a =-+相切，则a = .【变式训练13】．（2023·四川绵阳·模拟预测）若函数()2f x x ax =-与函数()ln 2g x x x =+的图象在公共点处有相同的切线，则实数a =（ ）A ．2-B ．1-C ．eD ．2e -考向3、切线的条数问题例13．（2023·河南·三模）已知函数()3f x x x a =-+的图像关于原点对称，则与曲线()y f x =和214y x =+均相切的直线l 有（ ）A ．1条B ．2条C ．3条D ．4条例14．（2023·山东烟台·三模）若曲线1(0)y kx k -=<与曲线e x y =有两条公切线，则k 的值为 ．【变式训练14】．（2023·湖南衡阳·模拟预测）若曲线()(0)kf x k x=<与()e x g x =有三条公切线，则k 的取值范围为（ ）A ．1,0e ⎛⎫- ⎪⎝⎭B ．1,e⎛⎫-∞- ⎪⎝⎭C ．2,0e ⎛⎫- ⎪⎝⎭D ．2,e ⎛⎫-∞- ⎪⎝⎭【变式训练15】．（2023·河北邯郸·三模）若曲线e x y =与圆22()2x a y -+=有三条公切线，则a 的取值范围是 ．考向4、已知切线方程求参数例15．（2018·江西·一模）设e 表示自然对数的底数，函数222e e 5()2424x x a f x x ax a =+--+，当()f x 取得最小值时，则实数a 的值为 ．例16．（2015·吉林·二模）已知函数()2e xf x a =（0,e a >为自然对数的底数）的图像与直线0x =的交点为M ，函数()lnx g x a =()0a >的图像与直线0y =的交点为N ，MN 恰好是点M 到函数()ln xg x a=()0a >图像上任意一点的线段长的最小值，则实数a 的值是【变式训练16】．（2020·重庆·模拟预测）若曲线y ＝ax +2cos x 上存在两条切线相互垂直，则实数a 的取值范围是（ ）A ．[√3]B ．[﹣1，1]C ．（﹣∞，1]D ．[1]【变式训练17】．（19-20高三上·四川广安·阶段练习）已知直线2y x =与曲线()()ln f x ax b =+相切，则ab 的最大值为A ．4eB ．2eC ．eD ．2e考向5、平行、垂直与重合问题例17．（2023·四川凉山·一模）函数()21ln 2f x x a x =+在区间()1,2的图象上存在两条相互垂直的切线，则a 的取值范围为（ ）A ．()2,1-B ．()2,1--C ．()2,0-D ．()3,2--例18．（2021·四川·三模）切x 轴于点A 、对称轴平行于y 轴的抛物线和曲线y =B ，并且两曲线在B 点的切线相互垂直，A 、B 两点的横坐标分别为1、2，k 和c 是正的常数，则k 的值为 ．【变式训练18】．（2021·浙江杭州·模拟预测）函数()sin f x ax x =+的图象上存在两条相互垂直的切线，则实数a 的取值范围是（ ）A ．{}0,1B ．{}0C ．[)0,1D ．[)1,+∞【变式训练19】．（2019·江苏泰州·一模）已知函数31()4f x x x=-+，若直线1l ，2l 是函数()y f x =图象的两条平行的切线，则直线1l ，2l 之间的距离的最大值是 ．考向6、最值问题例19．（2024·四川眉山·三模）若关于x 的不等式()32ln 10x ax bx a ≤--≠恒成立，则b a的最大值为（ ）A ．21e B ．22e C ．1eD ．2e例20．（22-23高三上·河北邢台·阶段练习）二次函数222y x x -=+与()20,0y x ax b a b =-++>>在它们的一个交点处切线互相垂直，则24b a b+的最小值为 .例21．（2024·江西新余·模拟预测）（多选题）已知函数()ln f x x ax b =--，则下列说法正确的是：（ ）.A ．若1,1a b ==，则()f x 的最大值为2-B ．若1a =-，则函数()xf x 始终有且仅有1个极值点且为极小值点C ．若1ab =，则()f x 始终有且仅有1个零点D ．若()0f x ≤恒成立，则a b +的最小值为0【变式训练20】．（2024·广东江门·二模）若曲线21:C y x =与曲线2:e (0)xC y a a =>存在公切线，则a 的最大值 .【变式训练21】．（2024·福建泉州·模拟预测）若曲线2y x 与()e 0xy t t =≠恰有两条公切线，则t 的取值范围为（ ）A ．240,e ⎛⎫⎪⎝⎭B ．24,e ∞⎛⎫+ ⎪⎝⎭C ．()24,0,e ∞∞⎛⎫-⋃+ ⎪⎝⎭D ．()24,0e ∞⎧⎫-⋃⎨⎬⎩⎭【变式训练22】．（23-24高二下·河南周口·阶段练习）下列命题正确的有（ ）A ．已知函数()f x 在R 上可导，若()12f '=，则()()121lim2x f x f x→+-=B ．已知函数()()ln 21f x x =+，若()01f x '=，则012x =C ．若函数()32113f x x x =-++，则()f x 的极大值为1D ．设函数()f x 的导函数为f ′(x )，且()()232ln f x x xf x '=++，则()924f '=-1．（2024·全国·高考真题）设函数()2e 2sin 1x xf x x +=+，则曲线y =f (x )在点(0,1)处的切线与两坐标轴所围成的三角形的面积为（ ）A ．16B ．13C ．12D ．232．（2023·全国·高考真题）曲线e 1xy x =+在点e 1,2⎛⎫ ⎪⎝⎭处的切线方程为（ ）A ．e 4y x =B ．e 2y x =C ．e e 44y x =+ D ．e 3e24y x =+ 3．（2021·全国·高考真题）若过点(),a b 可以作曲线e x y =的两条切线，则（ ） A ．e b a < B ．e a b < C ．0e b a <<D ．0e a b <<4．（2020·全国·高考真题）若直线l 与曲线y x 2+y 2=15都相切，则l 的方程为（ ）A ．y =2x +1B ．y =2x +12C ．y =12x +1D ．y =12x +125．（2020·全国·高考真题）函数43()2f x x x =-的图像在点(1(1))f ，处的切线方程为（ ） A ．21y x =-- B ．21y x =-+ C ．23y x =-D ．21y x =+6．（2024·全国·高考真题）若曲线e x y x =+在点()0,1处的切线也是曲线ln(1)y x a =++的切线，则a = .7．（2022·全国·高考真题）曲线ln ||y x =过坐标原点的两条切线的方程为 ， ． 8．（2022·全国·高考真题）已知1x x =和2x x =分别是函数2()2e x f x a x =-（0a >且1a ≠）的极小值点和极大值点．若12x x <，则a 的取值范围是 ．9．（2022·全国·高考真题）若曲线()e x y x a =+有两条过坐标原点的切线，则a 的取值范围是 ． 10．（2021·全国·高考真题）曲线2x 1y x 2-=+在点()1,3--处的切线方程为 ． 11．（2024·天津·高考真题）设函数()ln f x x x =． (1)求()f x 图象上点()()1,1f 处的切线方程；(2)若()(f x a x ≥在()0,x ∈+∞时恒成立，求a 的值；(3)若()12,0,1x x ∈，证明()()121212f x f x x x -≤-． 12．（2024·全国·高考真题）已知函数3()e x f x ax a =--． (1)当1a =时，求曲线()y f x =在点()1,(1)f 处的切线方程； (2)若()f x 有极小值，且极小值小于0，求a 的取值范围． 13．（2023·全国·高考真题）已知函数()()1ln 1f x a x x ⎛⎫=++ ⎪⎝⎭．(1)当1a =-时，求曲线y =f (x )在点()()1,1f 处的切线方程． (2)若函数()f x 在(0,+∞)单调递增，求a 的取值范围． 14．（2023·天津·高考真题）已知函数()()11ln 12f x x x ⎛⎫=++ ⎪⎝⎭．(1)求曲线y =f (x )在2x =处的切线斜率； (2)求证：当0x >时，()1f x >； (3)证明：()51ln !ln 162n n n n ⎛⎫<-++≤ ⎪⎝⎭．。