Origin的非线性拟合功能

用origin拟合流变曲线流变学是研究物质在外力作用下变形和流动规律的学科。

在实际应用中，流变学被广泛应用于材料科学、化学工程、食品工业、医药等领域。

流变曲线是流变学中最基本的曲线，它描述了物质在外力作用下的变形规律。

在流变学中，常用的流变曲线包括剪切应力-剪切速率曲线、应力-应变曲线等。

本文将介绍如何使用Origin软件拟合流变曲线。

一、数据处理首先，我们需要将实验得到的流变数据导入Origin软件中。

在导入数据时，需要注意数据的格式和单位。

通常，流变数据的单位为Pa或Pa·s，而剪切速率的单位为s^-1。

在导入数据后，我们需要对数据进行处理，以便进行拟合。

具体来说，我们需要对数据进行平滑处理和去噪处理。

平滑处理可以使用Origin软件中的平滑函数进行，去噪处理可以使用滤波函数进行。

二、拟合流变曲线在数据处理完成后，我们可以开始拟合流变曲线。

在Origin软件中，拟合流变曲线可以使用非线性拟合功能进行。

具体来说，我们需要选择合适的拟合函数，并设置拟合参数的初值和范围。

常用的拟合函数包括Maxwell模型、Kelvin模型、Bingham模型等。

在选择拟合函数时，需要根据实验数据的特点进行选择。

例如，对于粘弹性流体，可以选择Maxwell模型进行拟合。

在设置拟合参数的初值和范围时，需要根据实验数据的范围进行选择。

通常，初值可以选择实验数据的平均值，范围可以选择实验数据的最大值和最小值。

在设置好拟合参数后，我们可以使用非线性拟合功能进行拟合。

拟合完成后，我们可以得到拟合曲线和拟合参数。

三、结果分析在得到拟合曲线和拟合参数后，我们可以进行结果分析。

具体来说，我们可以计算拟合曲线和实验数据之间的误差，并评估拟合结果的可靠性。

常用的误差计算方法包括均方根误差、平均绝对误差等。

在评估拟合结果的可靠性时，需要考虑拟合曲线的拟合度和拟合参数的误差范围。

四、结论在本文中，我们介绍了如何使用Origin软件拟合流变曲线。

oringe多未知数拟合曲线在Origin软件中，进行多未知数拟合曲线通常指的是使用非线性拟合（Nonlinear Fitting）功能。

非线性拟合可以用来分析和确定数据点与某个非线性方程之间的最佳拟合关系。

在Origin中，可以使用内置的拟合工具箱（Fit Tools）来进行非线性拟合。

以下是使用Origin进行多未知数非线性拟合的基本步骤：1. 打开Origin软件，并导入或创建你的数据文件。

2. 在数据表格中，确保你有足够的列来表示你的X数据和Y数据。

如果你的数据集包含多个Y变量，你可能需要对每个变量分别进行拟合。

3. 选择你的数据列，然后点击菜单栏中的“分析”（Analysis）。

4. 在下拉菜单中选择“拟合”（Fitting），然后选择“非线性拟合”（Nonlinear Fitting）。

5. 在弹出的对话框中，你可以选择不同的拟合类型，如“自定义方程”（Custom Equations）或“内置函数”（Built-in Functions）。

如果你知道你想要拟合的方程形式，可以选择“自定义方程”并输入你的方程。

如果你想要从一系列内置函数中选择，可以选择“内置函数”并从列表中选择一个。

6. 设置拟合参数。

在“拟合设置”（Fit Settings）区域，你可以设置初始参数值、拟合范围、拟合精度等。

7. 点击“开始拟合”（Start Fit）按钮，Origin将开始拟合过程，并在对话框下方显示拟合结果。

8. 查看拟合结果。

拟合结果包括最佳拟合参数、拟合曲线图、残差图等。

9. 根据需要，你可以导出拟合结果或使用拟合曲线进行进一步的分析。

请注意，非线性拟合可能需要较长的计算时间，尤其是对于复杂的数据集或方程。

此外，拟合结果的质量很大程度上取决于数据的质量和初始参数的选择。

在使用非线性拟合时，可能需要多次尝试和调整以达到满意的拟合效果。

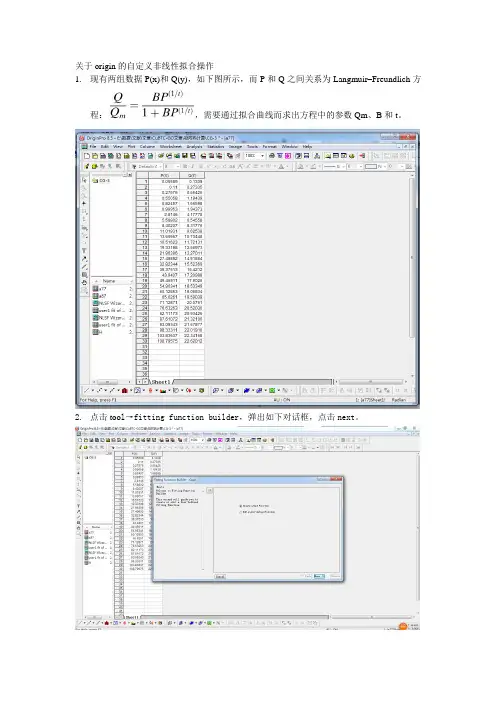
关于origin的自定义非线性拟合操作
1.现有两组数据P(x)和Q(y)，如下图所示，而P和Q之间关系为Langmuir–Freundlich方
程：，需要通过拟合曲线而求出方程中的参数Qm、B和t。

2.点击too l→fitting function builder，弹出如下对话框，点击next。

3.输入方程名称Langmuir–Freundlich，并选择origin C，如图所示，点击next。

4.输入自变量P、因变量Q和参数（Qm, B, t），如图所示，点击next。

5.将方程表达式转化为：Q=Qm*B*P^(1/t)/(1+(B*P^(1/t)))输入后，点击途中红圈所示编译
按钮。

后返回上图。

7.一直点击next，直到finish。

选中P(x)和Q(y)两列数值后点击annlysis→fitting→nonliner
curve fit→open dialog，出现下图对话框，通过category和function两个下拉菜单选择
我们刚才编辑好的方程：Langmuir–Freundlich。

由于参数的初始值系统默认均为1，这并不符合方程的收敛要求，所以需要点击红圈所示的粗拟合以便得到符合要求的参数初
始值，然后点击fit即可得到通过最小二乘法拟合出的自定义非线性曲线的各项参数值。

8.拟合后的参数值以及曲线数据等均会在同一个worbook的新sheet中展示，如下图所示。

origin 拟合曲线x数据类型Origin 是一款常用的科学数据处理和绘图软件。

对于数据拟合，Origin 支持多种方法，例如线性回归、非线性回归等。

关于x 数据类型的问题，具体的要求会取决于你要进行哪种拟合。

一般来说，Origin 支持的数据类型包括：
1. 数值型：这是最基本的数据类型，用于表示连续的数值。

例如，温度、压力、时间等。

2. 字符串型：用于表示文本数据，例如人的名字、标签等。

3. 逻辑型：用于表示真或假的数据，例如开/关、是/否等。

如果你想要对一组数据点进行拟合，通常x 轴应该是数值型数据，例如时间、距离、电压等。

如果你的x 数据是字符串型数据，例如日期，你可能需要先将它们转换为数值型数据再进行拟合。

如果你需要进行非线性拟合，你可以使用Origin 的非线性最小二乘法拟合功能。

在拟合之前，确保你的x 和y 数据都正确地输入到了Origin 中。

然后，你可以选择适合的函数形式，并调整其参数，使它们适应你的数据。

你可以查看Origin 的帮助文档或者在线教程，以了解更多关于拟合和非线性拟合的详细信息。

使用Origin进行非线性高斯拟合在数据科学和机器学习中，非线性高斯拟合是一种常见的技术，用于拟合非线性函数到实际观测数据。

它是通过最小化误差函数来确定拟合参数的过程。

在本文中，我们将介绍如何使用Origin进行非线性高斯拟合。

首先，我们需要准备数据。

在Origin中，我们可以将数据导入为一个数据集。

选择"File"菜单中的"Import"选项，然后选择要导入的数据文件。

一旦数据被导入，我们可以在Origin的工作表中看到它。

接下来，我们需要选择适当的拟合函数。

对于非线性高斯拟合，我们可以选择高斯函数作为拟合函数。

在Origin中，我们可以通过选择"Analysis"菜单中的"Peak Analysis"选项来找到高斯函数。

在"Peak Analysis"对话框中，我们可以看到各种各样的拟合函数。

选择高斯函数，并点击"OK"按钮。

接下来，我们需要在工作表中选择我们要拟合的数据。

在Origin的工作表中，我们可以使用鼠标选择数据。

选择我们要拟合的数据之后，我们可以点击工具栏上的"Peak Analysis"按钮。

这将打开"Peak Analysis"对话框。

在"Peak Analysis"对话框中，我们可以设置拟合参数的初值。

我们可以手动输入初值，或者使用"Auto Search"按钮自动初值。

一旦我们设置好初值，我们可以点击"Fit"按钮开始拟合过程。

在拟合过程完成后，我们可以在Origin的工作表中看到拟合结果。

拟合结果包括拟合参数的值、标准误差、相关系数等。

我们还可以在工作表中绘制拟合曲线和残差图。

在拟合过程完成后，我们可以对拟合结果进行分析。

我们可以计算拟合曲线上的极值点，并计算其位置和幅值。

Origin的非线性拟合功能Origin是一种科学绘图和数据分析软件，其中的非线性拟合功能是其最强大和最重要的功能之一、非线性拟合是一种数学技术，用于通过数据点来拟合非线性函数。

在科学和工程领域中，很多实际现象都对应着非线性关系，因此非线性拟合在数据分析中具有广泛的应用。

Origin的非线性拟合功能可以帮助用户通过对试验数据进行拟合，找到最佳的曲线拟合来描述数据之间的关系。

此功能通过多种拟合方法，包括非线性最小二乘法、加权非线性最小二乘法、全局拟合和多曲线拟合，提供了丰富的拟合选择。

1. 多种拟合方法：Origin提供了多种非线性拟合方法，包括Levenberg-Marquardt算法、Trust-Region算法和递归拟合等。

用户可以根据实际数据和需要选择最适合的拟合方法。

2. 自定义模型：Origin允许用户自定义拟合模型。

用户可以通过添加自定义公式和参数，构建适合自己研究的非线性模型。

这使得Origin的非线性拟合功能灵活而且可扩展。

3. 拟合统计分析：Origin的非线性拟合功能提供了丰富的统计分析工具，包括拟合参数的置信区间估计、拟合曲线的置信带计算、拟合误差分析等。

这些统计分析工具可以帮助用户评估拟合结果的可靠性。

4. 多变量拟合：Origin允许用户进行多变量非线性拟合，即同时拟合多个数据集、多个模型或多个曲线。

这种功能在研究多因素影响、复杂数据处理和模型比较等方面非常有用。

5. 拟合优化：Origin的非线性拟合功能提供了拟合优化选项，用户可以通过设置拟合参数的初始值、约束条件和拟合目标的权重等来改善拟合结果。

这些优化选项能够帮助用户更好地处理复杂数据和噪声。

6. 数据可视化：Origin的非线性拟合功能可以将拟合结果与原始数据一起绘制在图表中，方便用户直观地比较和分析拟合效果。

用户还可以使用Origin的丰富绘图工具，对拟合结果进行进一步的可视化和优化。

7. 输出和导出：Origin的非线性拟合功能可以输出拟合参数、统计分析结果和拟合曲线等信息，方便用户进行后续数据处理和报告撰写。

用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据在科学研究和实验中，数据处理是一个至关重要的环节。

通过对实验数据进行分析和拟合，可以得到对现象的更深入和准确的理解。

Origin软件是一种功能齐全且易于使用的数据分析软件，它提供了各种分析和拟合功能，包括线性拟合和非线性曲线拟合。

本文将探讨如何使用Origin软件的这两个功能来处理实验数据。

首先，我们需要明确线性拟合的概念。

线性拟合是通过一条直线来近似表示实验数据的趋势。

它通常用于分析变量之间的线性关系，并确定其相关性。

在Origin软件中，我们可以通过选择线性拟合的功能来进行这一分析。

以某个实验数据为例，我们首先打开Origin软件并加载实验数据。

然后，在图表中选择需要进行线性拟合的数据集，并点击工具栏上的“线性拟合”按钮。

Origin软件会自动计算最佳拟合直线，并在图表中显示出来。

此外，Origin软件还提供了拟合曲线的各种统计信息，如拟合趋势线的斜率、截距、相关系数和拟合误差等。

线性拟合的结果可以帮助我们推断实验数据中的相关性和趋势。

如果拟合直线的斜率为正值，并且有较高的相关系数，那么我们可以得出结论，实验数据之间存在正相关关系。

反之，如果斜率为负值，则表示实验数据之间存在负相关关系。

此外，线性拟合还可以用于预测未知数据的数值。

值得注意的是，线性拟合适用于处理线性关系较为明显的数据。

如果实验数据的分布较为复杂，并且存在非线性关系，就需要使用非线性曲线拟合功能来分析数据。

非线性曲线拟合是通过曲线来近似表示实验数据的趋势。

与线性拟合类似，非线性曲线拟合也能提供各种统计信息，如拟合曲线的拟合度、参数值、相关系数等。

使用Origin软件的非线性曲线拟合功能，可以进行多种拟合模型的选择和分析。

例如，常见的非线性模型有指数、对数、幂函数等。

我们可以根据实验数据的特点和分布选择合适的非线性模型，并进行参数估计和曲线拟合。

在origin中使用自定义公式进行非线性数据拟合在数据分析和机器学习领域，非线性数据拟合是一个常见的问题。

非线性数据是指不能通过直线来拟合的数据，因此需要使用非线性函数来拟合这些数据。

Origin软件是一个功能强大的数据分析和绘图工具，可以用于非线性数据的拟合。

在使用Origin进行非线性数据拟合之前，首先需要明确拟合的函数形式。

Origin中提供了许多常见的非线性函数供用户选择，同时也支持用户使用自定义的非线性函数进行拟合。

用户可以通过定义一个自定义的函数，并填入相应的参数，然后使用Origin提供的拟合功能对数据进行拟合。

首先，我们打开Origin，并载入需要进行非线性拟合的数据。

选择数据并选择 "Analysis -> Fitting -> Nonlinear Fit" 菜单选项，打开非线性拟合对话框。

```pythonfunc(param, x) := param(0)*x^2 + param(1)*x + param(2)```在自定义函数中，param 代表函数的参数，x 代表自变量。

用户可以根据实际情况进行参数的定义和自变量的选择。

在定义好自定义函数之后，点击 "OK" 按钮，返回到非线性拟合对话框。

在非线性拟合对话框中，可以设置需要拟合的数据范围、初始参数值等参数，然后点击 "Fit" 按钮开始进行非线性拟合。

非线性拟合完成后，Origin会给出拟合结果，并在图形界面上显示出拟合曲线。

用户可以通过拟合结果得到参数的估计值，并进行进一步的分析和处理。

除了自定义函数，Origin还提供了许多内置的非线性函数，例如指数函数、对数函数、幂函数等。

用户可以根据实际需要选择合适的函数进行拟合。

总而言之，Origin提供了强大的非线性数据拟合功能，用户可以使用自定义函数进行非线性拟合。

通过合适的函数选择和参数调整，可以得到准确的拟合结果，并进一步分析和处理拟合结果。

origin非线性拟合曲线
非线性拟合曲线是指利用给定的数据集（X,Y）进行非线性拟合曲线的计算方法，以求出最优的拟合方程，主要用于数据拟合和数据处理中。

用Origin（简称Origin）来进行非线性拟合曲线可以充分利用其强大的图像处理功能和灵活的导入导出接口。

Origin提供了方便的用户界面、函数视图和一般化的拟合功能，可以轻松完成非线性拟合曲线的计算。

Origin非线性拟合曲线的计算初步步骤如下：
第一步：打开Origin，创建一个空白的图表；
第二步：导入数据源，转换为非空白图表，例如此处以x-y对做为数据源；
第三步：点击菜单“数据”，打开“数据处理”子菜单，选择“拟合”；
第四步：选择拟合等级，点击“下一步”；
第五步：选择非线性拟合模型；
第六步：设置拟合参数并进行计算，得到拟合曲线；
第七步：右键点击拟合曲线，打开“拟合结果曲线”，显示数据点和拟合曲线；
第八步：在“拟合情况”窗口中可查看曲线拟合的详细情况。

以上就是用Origin来计算非线性拟合曲线的基本流程，Origin提供的拟合模型主要有多项式、函数、指数、对数、反比例等等，可根据实际需求选择相应的拟合模型。

Origin的强大功能和灵活的计算模型，使它在非线性拟合曲线的计算中，受到了广泛的重视。

特别是在工程及科学计算的技术中，Origin几乎是必不可少的工具。

它能够为科学研究、工程实践提供最合适的结果，以为数据拟合及处理数据提供了极大的便利性。