鲁教版初三上册数学

鲁教数学五四制九年级上册一、课程简介《鲁教数学五四制九年级上册》是山东省义务教育鲁教数学教材的一部分，适用于九年级上学期。

本教材主要内容包括代数、几何、概率与统计等数学知识，旨在培养学生的数学思维能力、解决问题的能力以及数学运算的技巧。

通过学习《鲁教数学五四制九年级上册》，学生能够系统地掌握基本的代数、几何、概率与统计等知识，为日后的学习打下坚实的基础。

二、教材结构1. 单元1：代数初步这个单元主要介绍了代数中的基本概念，如变量、系数、常数项等，并且学习了一次和二次方程的求解方法。

通过这个单元的学习，学生能够初步掌握代数运算的基本技巧。

2. 单元2：线性方程与一元一次不等式这个单元主要讲解了一元一次方程和一元一次不等式的概念与解法。

学生通过学习，能够使用代数的方法解决实际问题，并培养出逻辑思维与推理能力。

3. 单元3：图形的认识和运动这个单元主要介绍了几何中的基本概念和性质，如平行四边形、三角形、正方形等，并学习了图形的运动变换。

学生通过学习，能够认识各种几何图形，并运用几何知识解决实际问题。

4. 单元4：图形的相似这个单元主要讲解了相似图形的概念与性质，并学习了相似图形的判别方法。

学生通过学习，能够掌握相似图形之间的运算关系，并应用到实际问题中。

5. 单元5：统计与概率初步这个单元主要介绍了统计与概率的基本概念与计算方法。

学生通过学习，能够了解统计数据的收集与整理方法，以及概率的计算方法。

6. 单元6：图形的位置与方位这个单元主要讲解了图形的位置关系和方位关系。

学生通过学习，能够掌握图形在平面坐标系中的位置表示方法，并能熟练运用到实际问题中。

7. 单元7：函数初步这个单元主要介绍了函数的概念与性质，并学习了常见的一次函数和二次函数的图像特征和性质。

学生通过学习，能够理解函数的基本概念，并能够绘制和分析函数图像。

8. 单元8：一元二次方程这个单元主要讲解了一元二次方程的概念、解法和应用。

学生通过学习，能够熟练掌握二次方程的解的运算方法，并能够应用解二次方程的方法解决实际问题。

鲁教版九年级数学上册第3章《二次函数》 单元检测题一、选择题：1．抛物线y ＝2（x ﹣1）2+3的顶点坐标是（ ）A ．(1，3)B ．(3，1)C ．(﹣3，2)D ．(2，3)2．二次函数21y ax bx c =++与一次函数2y mx n =+的图象如图所示，则满2ax bx c mx n ++>+的x 的取值范围是（ ）A ．30x -<< B ．3x <-或0x > C ．3x <-或1x > D ．03x <<3．已知二次函数2y ax bx c =++的图象的对称轴为直线1x =，其图象如图所示，现有下列结论：①0abc >；①20a b +=；①420a b c -+>；①()a b m am b +≥+；①23c b <．其中正确结论的是（ ）A ．①①①B ．①①①C ．①①①D ．①①①4．根据表格对应值判断关于x 的方程ax 2＋bx ＋c ＝2的一个解x 的范围是（ ） A ．1.1＜x ＜1.2B ．1.2＜x ＜1.3C ．1.3＜x ＜1.4D ．无法判定5．便民商店经营一种商品，在销售过程中，发现一周利润y （元）与每件销售价x （元）之间的关系满足y=-2（x -20）2+1558，由于某种原因，价格只能15≤x≤22，那么一周可获得最大利润是（ ）A ．20B ．1508C ．1550D ．1558x 1.1 1.2 1.3 1.4 ax 2＋bx ＋c ﹣0.59 0.84 2.29 3.766．将抛物线y =2x 2经过怎样的平移可得到抛物线y =2(x +3)2+4（ ） A ．先向左平移3个单位，再向上平移4个单位 B ．先向左平移3个单位，再向下平移4个单位 C ．先向右平移3个单位，再向上平移4个单位 D ．先向右平移3个单位，再向下平移4个单位7．将抛物线y ＝2x 2先向右平移4个单位，再向上平移5个单位，得到的新抛物A ．4B ．3C ．2D ．1 9．把抛物线22y x bx =++的图像向右平移3个单位，再向上平移2个单位，所得到的图像的解析式为247y x x =-+，则b =（ ）A ．2B ．4C ．6D ．810．已知二次函数y ＝ax 2＋bx ＋c （a≠0）的图像如图所示，有下列5个结论：①c ＜0；①abc ＞0；①a －b ＋c ＞0；①2a －3b>0；①c －4b ＞0，你认为其中正确信息的个数有（ ）A ．2个B ．3个C ．4个D ．5个10．如图所示，二次函数y ＝ax 2+bx +c （a ≠0）的图象经过点A （﹣1，2），且与x 轴交点的横坐标分别为x 1，x 2，其中﹣2＜x 1＜﹣1，0＜x 2＜1，下列四个结论①2a ﹣b ＜0；①4a ﹣2b +c ＜0；①c ﹣a ＞2；①3a +c ＞0中，错误的个数有（ ） A ．0 B ．1 C ．2 D ．312．如图，二次函数y ＝ax 2+bx +c 的图象与y 轴正半轴相交，其顶点坐标为（12，1），下列结论：①abc ＜0；①b 2﹣4ac ＞0；①a +b ＜0；①2a +c ＜0，其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个 13．抛物线2y ax bx c =++上部分点的横坐标x ，纵坐标y 的对应值如下表： x … 2- 1- 0 1 2 …y … 15- 5- 1 3 1 … 则当14x -≤≤时，y 的取值范围是 ．14．2(1)1y x a x =+-+是关于x 的二次函数，当x 的取值范围是13x -时，y 只在=1x -时取得最大值，则实数a 的取值范围是 ．15．抛物线213222y x x =-+与x 轴交于点()1,0A x ，()2,0B x ，则AB 的长为 ． 16．将抛物线2y x 沿直线3y x =方向移动10个单位长度，若移动后抛物线的顶点在第一象限，则移动后抛物线的解析式是 ．17．将抛物线y=﹣(x ＋1)2＋3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为 ．18. 已知二次函数224y x x =-+-的图象上两点()()124,,,A y B m y ，若12y y =，则m = ．19．某电商在购物平台上销售一款小电器，其进价为45元/件，每销售一件需缴纳平台推广费5元，该款小电器每天的销售量y （件）与每件的销售价格x （元）满足函数关系：2180y x =-+．为保证市场稳定，供货商规定销售价格不得低于75元/件且不得高于90元/件．（1）写出每天的销售利润w （元）与销售价格x （元）的函数关系式；（2）每件小电器的销售价格定为多少元时，才能使每天获得的利润最大，最大是多少元？1⎛⎫两点，PAB的面积恒成立，求b的值．关于抛物线的（1）求抛物线的表达式；（2）点P是抛物线上一动点，且位于第四象限，当ABP的面积为6时，求出点P的坐标；（3）若点M在直线BH上运动，点N在x轴上运动，当以点C，M，N为顶点的三角形为等腰直角三角形时称这样的点N为“美丽点”，共有多少个“美丽点”？请直接写出当点N为“美丽点”时，CMN的面积．23．如图,设抛物线T：y=ax2+c(a> 0)与直线L:y=kx-4(k> 0)交A,B两点（点B在点A的右侧）.（1）如图，若点A（12，-52），且a+c=-1.①求抛物线T和直线L的解析式；①求①AOB的面积.（2）设点C是点B关于y轴的对称点，当点A,O,C三点共线时，求实数c的值.。

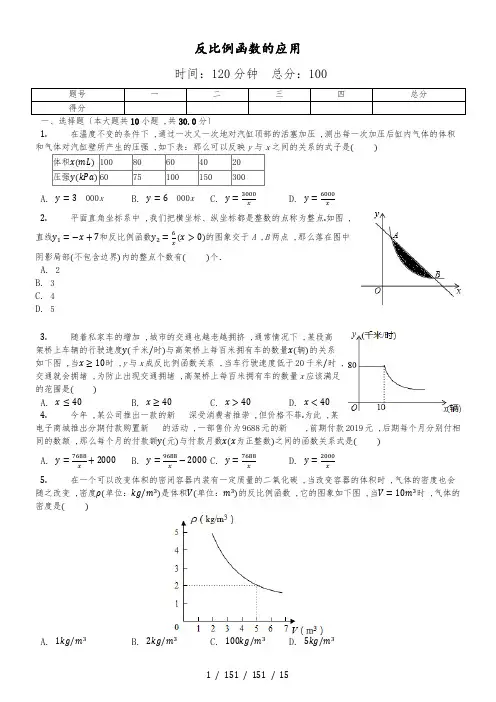
反比例函数的应用时间：120分钟总分：100题号一二三四总分得分一、选择题〔本大题共10小题 ,共30.0分〕1.在温度不变的条件下 ,通过一次又一次地对汽缸顶部的活塞加压 ,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强 ,如下表：那么可以反映y与x之间的关系的式子是()体积x(mL)10080604020压强y(kPa)6075100150300A. y=3000xB. y=6000xC. y=3000x D. y=6000x2.平面直角坐标系中 ,我们把横坐标、纵坐标都是整数的点称为整点.如图 ,直线y1=−x+7和反比例函数y2=6x(x>0)的图象交于A ,B两点 ,那么落在图中阴影局部(不包含边界)内的整点个数有()个．A. 2B. 3C. 4D. 53.随着私家车的增加 ,城市的交通也越老越拥挤 ,通常情况下 ,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如下图 ,当x≥10时 ,y与x成反比例函数关系 ,当车行驶速度低于20千米/时 ,交通就会拥堵 ,为防止出现交通拥堵 ,高架桥上每百米拥有车的数量x应该满足的范围是()A. x≤40B. x≥40C. x>40D. x<404.今年 ,某公司推出一款的新深受消费者推崇 ,但价格不菲.为此 ,某电子商城推出分期付款购置新的活动 ,一部售价为9688元的新 ,前期付款2019元 ,后期每个月分别付相同的数额 ,那么每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是()A. y=7688x +2000 B. y=9688x−2000C. y=7688xD. y=2000x5.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳 ,当改变容器的体积时 ,气体的密度也会随之改变 ,密度ρ(单位：kg/m3)是体积V(单位：m3)的反比例函数 ,它的图象如下图 ,当V=10m3时 ,气体的密度是()A. 1kg/m3B. 2kg/m3C. 100kg/m3D. 5kg/m31 / 151 / 151 / 156.如图 ,菱形ABCD的四个顶点均在坐标轴上 ,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=√3x(x>0)经过线段DC的中点E ,假设BD=4 ,那么AG的长为()A. 4√33B. √3+2 C. 2√3+1 D. 3√32+17.A是双曲线y=2x在第一象限上的一动点 ,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC ,点C在第四象限 ,点C的位置始终在一函数图象上运动 ,那么这个函数解析式为()A. y=−6xB. y=−6x(x>0)C. y=−6x(x>0)D. y=6x(x>0)8.如图 ,将直线y=x向下平移b个单位长度后得到直线l ,l与反比例函数y=kx(k>0,x>0)的图象相交于点A,与x轴相交于点B,那么OA2−OB2=10 ,那么k的值是()A. 5B. 10C. 15D. 209.在一个可以改变容积的密闭容器内 ,装有一定质量m的某种气体 ,当改变容积V时 ,气体的密度p也随之改变 ,ρ与V在一定范围内满足ρ=mv,它的图象如下图 ,那么该气体的质量m为()A. 1.4kgB. 5kgC. 7kgD. 6.4kg10.科学证实：近视眼镜的度数y(度)与镜片焦距x(m)成反比例关系 ,如果500度近视眼镜片的焦距为0.2m ,那么表示y与x函数关系的图象大致是()A. B.C. D.二、填空题〔本大题共10小题 ,共30.0分〕11.如图 ,一次函数y=kx−3(k≠0)的图象与x轴 ,y轴分别交于A ,B两点 ,与反比例函数y=12x(x>0)交于C点 ,且AB=AC ,那么k的值为______．12.如图 ,直线y=−2x+6与坐标轴相交于点A、点B,BC⊥AB ,且CDAD =43,双曲线y=kx过点C ,那么k=______．13.如果一个反比例函数图象与正比例函数y=2x图象有一个公共点A(1,a) ,那么这个反比例函数的解析式是______．14.如图 ,直线y=kx−2(k>0)与双曲线y=kx在第一象限内的交点R ,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴 ,M为垂足 ,假设△OPQ与△PRM的面积相等 ,那么k的值等于______ ．15.如下图 ,点A是双曲线y=−1x在第二象限的分支上的任意一点 ,点B、C、D分别是点A关于x轴、原点、y轴的对称点 ,那么四边形ABCD的面积是______．3 / 153 / 153 / 1516.如图 ,在平面直角坐标系中 ,正方形ABCD的顶点A、B在x轴正半轴上 ,顶点D在反比例函数y=kx的第一象限的图象上 ,CA的延长线与y轴负半轴交于点E.假设△ABE的面积为1.5 ,那么k的值为______．17.码头工人往一艘轮船上装载货物 ,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y=kx的一支).如果以5t/min的速度卸货 ,那么卸完货物需要时间是______min．18.在照明系统模拟控制电路实验中 ,研究人员发现光敏电阻值R(单位：Ω)与光照度E(单位：lx)之间成反比例函数关系 ,局部数据如下表所示：光照度E/lx0.51 1.52 2.53光敏电阻阻值R/Ω603020151210那么光敏电阻值R与光照度E的函数表达式为______．19.如图 ,一次函数y1=k1+b与反比例函数y2=k2x的图象相交于A(−1,2)、B(2,−1)两点 ,那么y2<y1时 ,x的取值范围是______ ．20.设函数y=−2x 与y=−x−1的图象的交点坐标为(a,b) ,那么1a+1b的值为______ ．三、计算题〔本大题共4小题 ,共24.0分〕21.反比例函数y=kx与一次函数y=2x+k的图象的一个交点的纵坐标是−4 ,求k的值．22.如图 ,在平面直角坐标系中 ,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点 ,与反比例函数y=m的图象交于C、D两点 ,DE⊥x轴于点E ,Cx点的坐标是(6,−1) ,DE=3．(1)求反比例函数与一次函数的解析式；(2)求△CDE的面积．23.如图 ,一次函数y1=k1x+2与反比例函数y2=k2的图象交于点A(4,m)和B(−8,−2) ,与y轴交于点Cx(1)m=______ ,k1=______ ,k2=______；(2)根据函数图象可知 ,当y1>y2时 ,x的取值范围是______；(3)过点A作AD⊥x轴于点D ,求△ABD的面积．24.如图 ,一次函数y1=−x+2的图象与反比例函数y2=m的图象交于点A(−1,3)、xB(n,−1)．(1)求反比例函数的解析式；(2)当y1>y2时 ,直接写出x的取值范围．四、解答题〔本大题共2小题 ,共16.0分〕．25.反比例函数y=4x(1)假设该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点 ,求k的值；(1≤x≤4)的图象记为曲线C1 ,将C1向左平移2个单位长度 ,得曲线C2 ,请在图中(2)如图 ,反比例函数y=4x画出C2 ,并直接写出C1平移至C2处所扫过的面积．(m≠0)的图象交于点A(3,1) , 26.如图 ,在平面直角坐标系中 ,一次函数y=kx+b与反比例函数y=mx且过点B(0,−2)．(1)求反比例函数和一次函数的表达式；(2)如果点P是x轴上一点 ,且△ABP的面积是3 ,求点P的坐标．答案和解析【答案】1. D2. B3. A4. C5. A6. A7. B8. A9. C10. B11. 3212. −1613. y=2x14. 2√215. 416. 35 / 155 / 155 / 1517. 120 18. R =30E19. x <−1或0<x <2 20. 1221. 解：由题意得：{−4=2x +k−4=kx, 解得{x =2k =−8 ,故k =−8．22. 解：(1)∵点C(6,−1)在反比例y =mx 图象上 ,∴将x =6 ,y =−1代入反比例解析式得：−1=m6 ,即m =−6 , ∴反比例解析式为y =−6x ,∵点D 在反比例函数图象上 ,且DE =3 ,即D 纵坐标为3 , 将y =3代入反比例解析式得：3=−6x ,即x =−2 , ∴点D 坐标为(−2,3) ,设直线解析式为y =kx +b ,将C 与D 坐标代入得：{−2k +b =36k+b=−1, 解得：{k =−12b =2, ∴一次函数解析式为y =−12x +2； (2)过C 作CH ⊥x 轴于点H , ∵C(6,−1) ,∴CH =1 ,对于一次函数y =−12x +2 ,令y =0 ,求得x =4 ,故A (4,0) , 由D 坐标(−2,3) ,得到E(−2,0) , ∴AE =OA +OE =6 ,∴S △CDE =S △CAE +S △DAE =12×6×1+12×6×3=12．23. 4；12；16；−8<x <0或x >424. 解：(1)把A(−1,3)代入y 2=mx 可得m =−1×3=−3 ,所以反比例函数解析式为y =−3x ；(2)把B(n,−1)代入y =−3x 得−n =−3 ,解得n =3 ,那么B(3,−1) , 所以当x <−1或0<x <3 ,y 1>y 2．25. 解：(1)解{y =kx +4y=4x得kx 2+4x −4=0 ,∵反比例函数的图象与直线y =kx +4(k ≠0)只有一个公共点 , ∴△=16+16k =0 ,∴k=−1；(2)如下图 ,C1平移至C2处所扫过的面积=2×3=6．26. 解：(1)∵反比例函数y=mx(m≠0)的图象过点A(3,1) ,∴3=m 1∴m=3．∴反比例函数的表达式为y=3x．∵一次函数y=kx+b的图象过点A(3,1)和B(0,−2)．∴{b=−23k+b=1 ,解得：{b=−2k=1 ,∴一次函数的表达式为y=x−2；(2)令y=0 ,∴x−2=0 ,x=2 ,∴一次函数y=x−2的图象与x轴的交点C的坐标为(2,0)．∵S△ABP=3 ,1 2PC×1+12PC×2=3．∴PC=2 ,∴点P的坐标为(0,0)、(4,0)．【解析】1. 解：由表格数据可得：此函数是反比例函数 ,设解析式为：y=kx,那么xy=k=6000 ,故y与x之间的关系的式子是y=6000x,应选：D．利用表格中数据得出函数关系 ,进而求出即可．此题主要考查了根据实际问题列反比例函数关系式 ,得出正确的函数关系是解题关键．2. 解：联立{y=−x+7y=6x得A(1,6) ,B(6,1) ,阴影局部即直线下方与双曲线上方的局部 ,当x=1时 ,y1=6 ,y2=6 ,其整点为(1,6) ,当x=2时 ,y1=5 ,y2=3 ,其整点为(2,3) ,(2,4) ,(2,5) ,当x=3时 ,y1=4 ,y2=2 ,其整点为(3,2) ,(3,3) ,(3,4) ,当x=4时 ,y1=3 ,y2=32,其整点为(4,2) ,(4,3) ,当x=5时 ,y1=2 ,y2=65,其整点有(5,2) ,当x=6时 ,y1=1 ,y2=1 ,其整点为(6,1) ,故落在图中阴影局部(不包含边界)内的整点个数有(2,4) ,(3,3) ,(4,2) ,应选B．根据题意 ,首先确定双曲线与直线的方程的交点 ,进而由图象可得阴影局部即直线下方与双曲线上方的局部 ,依次找x=1到6之间 ,横、纵坐标都是整数的点 ,可得答案．此题综合考查了反比例函数与一次函数的性质 ,此题难度稍大 ,综合性比拟强 ,同学们要注意对各个知识点的灵活应用．7 / 157 / 157 / 153. 解：设反比例函数的解析式为：y=kx,那么将(10,80) ,代入得：y=800x,故当车速度为20千米/时 ,那么20=800x,解得：x=40 ,故高架桥上每百米拥有车的数量x应该满足的范围是：x≤40．应选：A．利用反比例函数图象过(10,80) ,得出其函数解析式 ,再利用y=20时 ,求出x的最值 ,进而求出x的取值范围．此题主要考查了反比例函数的应用 ,根据题意得出函数解析式是解题关键．4. 解：由题意可得：y=9688−2000x =7688x．应选：C．直接利用后期每个月分别付相同的数额 ,进而得出y与x的函数关系式．此题主要考查了根据实际问题列反比例函数关系式 ,正确理解题意是解题关键．5. 解：设密度ρ与体积V的反比例函数解析式为ρ=kv ,把点(5,2)代入解ρ=kv,得k=10 ,∴密度ρ与体积V的反比例函数解析式为ρ=10v ,把v=10代入ρ=10v,得ρ=1kg/m3．应选：A．设密度ρ(单位：kg/m3)与体积V(单位：m3)的反比例函数解析式为ρ=kv,把点(5,2)代入解析式求出k ,再把v 的值代入解析式即可求出气体的密度．考查了反比例函数的应用 ,现实生活中存在大量成反比例函数的两个变量 ,解答该类问题的关键是确定两个变量之间的函数关系 ,然后利用待定系数法求出它们的关系式．6. 解：过E作y轴和x的垂线EM ,EN ,设E(b,a) ,∵反比例函数y=√3x(x>0)经过点E ,∴ab=√3 ,∵四边形ABCD是菱形 ,∴BD⊥AC ,DO=12BD=2 ,∵EN⊥x ,EM⊥y ,∴四边形MENO是矩形 ,∴ME//x ,EN//y ,∵E为CD的中点 ,∴DO⋅CO=4√3 ,∴CO=2√3 ,∴tan∠DCO=DOCO =√33,∴∠DCO=30∘ ,∵四边形ABCD是菱形 ,∴∠DAB=∠DCB=2∠DCO=60∘ ,∠1=30∘ ,AO=CO=2√3 , ∵DF⊥AB ,∴∠2=30∘ ,∴DG=AG ,设DG=r ,那么AG=r ,GO=2√3−r ,∵AD =AB ,∠DAB=60∘ ,∴△ABD是等边三角形 ,∴∠ADB=60∘ ,∴∠3=30∘ ,在Rt△DOG中 ,DG2=GO2+DO2 ,∴r2=(2√3−r)2+22 ,解得：r=4√33,∴AG=4√33,应选：A．过E作y轴和x的垂线EM ,EN ,证明四边形MENO是矩形 ,设E(b,a) ,根据反比例函数图象上点的坐标特点可得ab=√3 ,进而可计算出CO长 ,根据三角函数可得∠DCO=30∘ ,再根据菱形的性质可得∠DAB=∠DCB=2∠DCO=60∘ ,∠1=30∘ ,AO=CO=2√3 ,然后利用勾股定理计算出DG长 ,进而可得AG长．此题主要考查了反比例函数和菱形的综合运用 ,关键是掌握菱形的性质：菱形对角线互相垂直平分 ,且平分每一组对角 ,反比例函数图象上的点横纵坐标之积=k．7. 解：连接OC ,过点C作D⊥x轴 ,垂足为D．设A(a,2a) ,∵点A与点B关于原点对称 ,∴OA=OB ,∵△ABC为等边三角形 ,∴AB⊥OC ,OC=√3O ,∵AO=√a2+(2a)2 ,∴CO=√3×√a2+(2a )2=√3a2+12a2,过点C作CD⊥x轴于点D ,那么可得∠AOD=∠OCD(都是∠COD的余角) ,设点C的坐标为(x,y) ,那么tan∠AOD=tan∠OCD ,即2aa=x−y,解得：y=−a22x ,在Rt△COD中 ,CD2+OD2=OC2 ,即y2+x2=3a2+12a2,将y=−a22x代入 ,得(a4+44)x2=3(a4+4a2) ,解得：x=2√3a,y=−√3a ,那么xy=−6 ,9 / 159 / 159 / 15(x>0)．∴反比例函数的解析式为y=−6x应选：B．) ,连接OC ,那么OC⊥AB ,表示出OC ,过点C作CD⊥x轴于点D ,设出点C坐标 ,在Rt△设点A的坐标为(a,2aOCD中 ,利用勾股定理可得出x2的值 ,继而得出y与x的函数关系式．此题考查了反比例函数的综合题 ,涉及了解直角三角形、等边三角形的性质及勾股定理的知识 ,综合考察的知识点较多 ,解答此题的关键是将所学知识融会贯穿 ,注意培养自己解答综合题的能力．8. 解：直线y=x向下平移b个单位后得直线l：y=x−b ,∴B(b,0) ,(x>0)相交于点A ,∵l与函数y=kx∴x−b=k,那么x2−bx−k=0．x∴x2=bx+k．设点A的坐标为(x,x−b) ,∵OA2−OB2=x2+(x−b)2−b2=2x2−2bx=2(bx+k)−2bx=2k ,∴2k=10 ,∴k=5．应选：A．先利用函数图象“上加下减〞的平移规律 ,得出直线l的方程为y=x−b ,与反比例函数联立消去y后 ,得到关于x的方程 ,整理后得到x2=bx+k ,并令直线l方程中y=0 ,求出x的值 ,确定出B的坐标 ,得出OB2 ,设出A的坐标 ,利用勾股定理表示出OA2 ,化简OA2−OB2=2k ,由OA2−OB2=10 ,即可求出k的值．此题考查了反比例函数与一次函数的交点问题 ,一次函数的平移规律 ,利用了转化及方程的思想 ,其中得出y= x平移后直线l的方程是解此题的关键．9. 解：∵ρ=m,v∴m=ρV ,而点(5,1.4)在图象上 ,代入得m=5×1.4=7(kg)．应选C．由图象知点(5,1.4)在函数的图象上 ,根据待定系数法就可求得函数解析式.求得m的值．此题考查了反比例函数的应用 ,关键是要由点的坐标求出函数的解析式．10. 解：根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例 ,设y=k,x由于点(0.2,500)在此函数解析式上 ,∴k=0.2×500=100 ,∴y=100．x应选：B．由于近视眼镜的度数y(度)与镜片焦距x(米)成反比例 ,可设y=k,由于点(0.2,500)在此函数解析式上 ,故可先x求得k的值．此题考查了反比例函数的应用 ,解答该类问题的关键是确定两个变量之间的函数关系 ,然后利用待定系数法求出它们的关系式．11 / 1511 / 1511 / 15 11.解：作CD ⊥x 轴于D ,那么OB//CD ,在△AOB 和△ADC 中 ,{∠OAB =∠DAC ∠AOB =∠ADC =90∘AB =AC∴△AOB ≌△ADC ,∴OB =CD ,由直线y =kx −3(k ≠0)可知B(0,−3) ,∴OB =3 ,∴CD =3 ,把y =3代入y =12x (x >0)解得 ,x =4 , ∴C(4,3) ,代入y =kx −3(k ≠0)得 ,3=4k −3 ,解得k =32 ,故答案为32．作CD ⊥x 轴于D ,易得△AOB ≌△ADC ,根据全等三角形的性质得出OB =CD =3 ,根据图象上的点满足函数解析式 ,把C 点纵坐标代入反比例函数解析式 ,可得横坐标；根据待定系数法 ,可得一次函数的解析式．此题考查了反比例函数与一次函数的交点问题 ,图象上的点满足函数解析式 ,求得C 点的坐标是解题的关键． 12. 解：作CE ⊥x 轴与E ．因为AB 的解析式为y =−2x +6 ,那么A 点坐标为(3,0) ,B 点坐标为(0,6) ,∵CD AD =43 ,∴ADAC =37 , ∵DO//CE ,∴AOAE=AD AC , 即3AE =37 ,∴AE =7 ,OE =7−3=4．可知 ,C 点横坐标为−4．设BC 解析式为y =dx +b ,∵BC ⊥AB ,∴d =12 ,得到函数解析式为y =12x +b ,将B(0,6)代入解析式得 ,b =6 ,那么BC的解析式为y=12x+6．C点横坐标−4代入y=12x+6得 ,y=12×(−4)+6=4．故C点坐标为(−4,4) , 代入y=kx得 ,k=−16．故答案为−16．作CE⊥x轴与E ,构造出DO//CE ,根据CDAD =43,求出C点横坐标 ,再根据BC与AB垂直 ,求出直线BC的比例系数 ,再利用B点坐标求出一次函数BC的解析式 ,将C点横坐标代入解析式 ,即可求出C点纵坐标 ,将C点横坐标代入反比例函数解析式即可得到k的值．此题主要考查了反比例函数的性质、相互垂直的直线的比例系数的关系、待定系数法求反比例函数解析式等知识 ,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想．13. 解：将x=1代入y=2x ,得y=2 ,∴点A(1,2) ,设反比例函数解析式为y=kx,∵一个反比例函数图象与正比例函数y=2x图象有一个公共点A(1,2) ,∴2=k1．解得 ,k=2 ,即反比例函数解析式为y=2x,故答案为：y=2x．根据题意可以求得点A的坐标 ,再将点A的坐标代入反比例函数解析式即可解答此题．此题考查反比例函数与一次函数的交点问题 ,解答此题的关键是明确题意 ,找出所求问题需要的条件 ,求出相应的函数解析式．14. 解：∵y=kx−2 ,∴当x=0时 ,y=−2 ,当y=0时 ,kx−2=0 ,解得x=2k,所以点P(2k,0) ,点Q(0,−2) ,所以OP=2k,OQ=2 ,∵RM⊥x轴 ,∴△OPQ∽△MPR ,∵△OPQ与△PRM的面积相等 ,∴△OPQ与△PRM的相似比为1 ,即△OPQ≌△MPR ,∴OM=2OP=4k,RM=OQ=2 ,所以点R(4k,2) ,∵双曲线y=kx经过点R ,∴k4k=2 ,即k2=8 ,解得k1=2√2 ,k2=−2√2(舍去)．故答案为：2√2．根据△OPQ与△PRM相似以及它们面积相等 ,可以得到两三角形全等 ,再根据一次函数求出点P、Q的坐标 ,进而得到OP、OQ的长度 ,再根据三角形全等表示出点R的坐标 ,代入反比例函数表达式 ,解方程即可求得k的值．此题综合考查了一次函数和反比例函数图象的性质 ,利用三角形面积相等得到两三角形全等是解此题的突破口 ,也是解题的关键．15. 解：设A(x,y) ,∵点A是双曲线y=−1x在第二象限的分支上的任意一点 ,点B、C、D分别是点A关于x轴、原点、y轴的对称点 , ∴D(−x,y) ,B(x,−y)∵ABCD为矩形 ,∴四边形ABCD的面积为：AB×AD=2y×2x=4|xy| ,又∵点A在双曲线y=−1x上 ,∴xy=−1 ,∴四边形ABCD的面积为：4|xy|=4．故答案为：4．由题意点A在是双曲线上 ,设出A点坐标 ,在由条件对称关系 ,表示出B ,D两点坐标 ,再由矩形面积公式求出其面积．此题考查了反比例函数的性质与图象 ,还考查了点的对称问题 ,找出对称点把矩形面积表示出来．16. 解：设正方形ABCD的边长为a ,A(x,0) ,那么D(x,a) ,∵点D在反比例函数y=kx的图象上 ,∴k=xa ,∵四边形ABCD是正方形 ,∴∠CAB=45∘ ,∴∠OAE=∠CAB=45∘ ,∴△OAE是等腰直角三角形 ,∴E(0,−x) ,∴S△ABE=12AB⋅OE=12ax=1.5 ,∴ax=3 ,即k=3．故答案为：3．设正方形ABCD的边长为a ,A(x,0) ,那么D(x,a) ,再由点D在反比例函数y=kx的图象上可知 ,k=xa ,根据正方形的性质得出∠CAB的度数 ,根据对顶角相等可得出∠OAE的度数 ,进而判断出△OAE的形状 ,故可得出E点坐标 ,根据△ABE的面积为1.5即可得出k的值．此题考查的是反比例函数综合题 ,涉及到正方形的性质及反比例函数图象上点的坐标特点等相关知识 ,难度适中．17. 解：把(1.5,400)代入双曲线y=kx ,得400=k1.5,解得k=600 ,那么y与x之间的函数关系式为y=600x；当x=5时 ,y=6005=120min．故答案为：120．13 / 1513 / 1513 / 15把(1.5,400)代入双曲线y=kx,可求y与x之间的函数关系式；利用函数关系式 ,当装载速度x=5时 ,得到y=6005,即可求解．此题主要考查了反比例函数的实际应用.解题的关键是根据实际意义列出函数关系式 ,从实际意义中找到对应的变量的值 ,利用待定系数法求出函数解析式 ,再根据题意进行解答．18. 解：由题意可得：RE=30 ,那么R=30E．故答案为：R=30E．直接利用表格中数据得出RE=30 ,进而得出答案．此题主要考查了反比例函数的应用 ,正确得出RE=30是解题关键．19. 解：由图象可知 ,当−1<x<0或x>3时 ,y1<y2 ,当x<−1或0<x<2时 ,y2<y1 ,故答案为x<−1或0<x<2．根据一次函数与反比例函数图象的交点、结合图象解答即可．此题考查的是一次函数与反比例函数的交点问题 ,掌握反比例函数图象上点的坐标特征、灵活运用数形结合思想是解题的关键．20. 解：把(a,b)代入y=−2x得ab=−2 ,把(a,b)代入y=−x−1得b=−a−1 ,即a+b=−1 ,所以1a +1b=a+bab=12．故答案为12．把交点(a,b)分别代入两个解析式得到ab=−2 ,a+b=−1 ,然后把1a +1b通分得到a+bab,然后利用整体代入的方法计算．此题考查了反比例函数与一次函数的交点：求反比例函数与一次函数的交点坐标 ,把两个函数关系式联立成方程组求解 ,假设方程组有解那么两者有交点 ,方程组无解 ,那么两者无交点；两函数的交点坐标同时满足两函数解析式．21. 把y=−4代入一次函数和反比例函数 ,联立组成方程组 ,求解即可．此题考查了反比例函数和一次函数的交点问题；用到的知识点为：两个函数图象相交 ,交点的坐标都适合这两个函数解析式．22. (1)将C坐标代入反比例解析式中求出m的值 ,确定出反比例解析式 ,再由DE为3得到D纵坐标为3 ,将y=3代入反比例解析式中求出x的值 ,即为D的横坐标 ,设直线解析式为y=kx+b ,将D与C的坐标代入求出k与b的值 ,即可确定出一次函数解析式；(2)过C作CH垂直于x轴 ,由C、D的纵坐标确定出DE与CH的长 ,分别为三角形ADE与三角形ACE中AE边上的高 ,由三角形CDE的面积=三角形AED的面积+三角形AEC的面积 ,求出即可．此题考查了一次函数与反比例函数的交点问题 ,涉及的知识有：坐标与图形性质 ,待定系数法确定函数解析式 ,一次函数与坐标轴的交点 ,熟练掌握待定系数法是解此题的关键．23. 解：(1)∵一次函数y1=k1x+2与反比例函数y2=k2x的图象交于点A(4,m)和B(−8,−2) ,∴k2=(−8)×(−2)=16 ,−2=−8k1+2 ,∴k1=12,∴m=12×4+2=4；(2)∵一次函数y1=k1x+2与反比例函数y2=k2x的图象交于点A(4,4)和B(−8,−2) , ∴当y1>y2时 ,x的取值范围是−8<x<0或x>4；(3)连接BD ,由(1)知 ,y1=12x+2 ,y2=16x,∴m=4 ,点D的坐标是(4,0) ,点A的坐标是(4,4) ,点B的坐标是(−8,−2)．∴S△ABD=12AD⋅(xA横坐标−xB横坐标)=12×4×[4−(−8)]=24．故答案为：(1)4；12；16；(2)−8<x<0或x>4(1)由A与B为一次函数与反比例函数的交点 ,将B坐标代入反比例函数解析式中 ,求出k2的值 ,确定出反比例解析式 ,再将A的坐标代入反比例解析式中求出m的值 ,确定出A的坐标 ,将B坐标代入一次函数解析式中即可求出k1的值；(2)由A与B横坐标分别为4、−8 ,加上0 ,将x轴分为四个范围 ,由图象找出一次函数图象在反比例函数图象上方时x的范围即可；(3)连接BD ,三角形ABD的面积可以用AD为底边 ,高为A横坐标减去B横坐标求出 ,利用三角形的面积公式即可求出三角形ABD的面积．此题考查了反比例函数与一次函数的交点问题 ,利用了数形结合的数学思想 ,数形结合思想是数学中重要的思想方法 ,学生做题时注意灵活运用．24. (1)把A点坐标代入y2=mx可求出m的值 ,从而得到反比例函数解析式；(2)利用反比例函数解析式确定B点坐标 ,然后观察函数图象 ,写出一次函数图象在反比例函数图象上方所对应的自变量的取值范围即可．此题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标 ,把两个函数关系式联立成方程组求解 ,假设方程组有解那么两者有交点 ,方程组无解 ,那么两者无交点．25. (1)解方程组得到kx2+4x−4=0 ,由反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点 ,得到△=16+16k=0 ,求得k=−1；(2)根据平移的性质即可得到结论．此题考查了反比例函数与一次函数的交点问题 ,平移的性质 ,一元二次方程根与系数的关系 ,知道反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点时 ,△=0是解题的关键．26. (1)利用待定系数法即可求得函数的解析式；(2)首先求得AB与x轴的交点 ,设交点是C ,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标．此题考查了待定系数法求函数的解析式以及三角形的面积的计算 ,正确根据S△ABP=S△ACP+S△BCP列方程是关键．15 / 1515 / 1515 / 15。

九年级上册数学书鲁教版一、一元二次方程。

1. 定义。

- 只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程。

一般形式为ax^2+bx + c=0(a≠0)，其中a是二次项系数，b是一次项系数，c是常数项。

2. 解法。

- 直接开平方法：对于方程x^2=k(k≥0)，解得x=±√(k)。

例如方程(x -3)^2=16，则x - 3=±4，解得x = 7或x=-1。

- 配方法：将一元二次方程通过配方转化为(x + m)^2=n(n≥0)的形式再求解。

例如对于方程x^2+6x - 7 = 0，配方得(x + 3)^2=16，然后求解。

- 公式法：对于一元二次方程ax^2+bx + c = 0(a≠0)，其求根公式为x=frac{-b±√(b^2)-4ac}{2a}。

- 因式分解法：将方程化为(ax + m)(bx + n)=0的形式，则ax+m = 0或bx +n=0，进而求解。

例如方程x^2-3x+2 = 0，因式分解为(x - 1)(x - 2)=0，解得x = 1或x = 2。

3. 根的判别式。

- 对于一元二次方程ax^2+bx + c = 0(a≠0)，判别式Δ=b^2-4ac。

- 当Δ>0时，方程有两个不相等的实数根；当Δ = 0时，方程有两个相等的实数根；当Δ<0时，方程没有实数根。

4. 一元二次方程的应用。

- 增长率问题：设基数为a，平均增长率为x，增长后的量为b，则a(1 +x)^n=b（n为增长次数）。

- 面积问题：根据图形的面积关系列出一元二次方程求解，如长方形的长和宽与面积的关系等。

二、二次函数。

1. 定义。

- 形如y = ax^2+bx + c(a≠0)的函数叫做二次函数，其中a、b、c是常数，a称为二次项系数，b为一次项系数，c为常数项。

2. 图象与性质。

- 二次函数y = ax^2+bx + c(a≠0)的图象是一条抛物线。

2024年鲁教版九年级数学上学期教学计划一、教学目标：1. 了解数集、运算，掌握因子与倍数的概念，能够使用性质分拆整数。

2. 理解和运用平方根、立方根的概念和性质，能够进行有理数的开方运算。

3. 掌握实数的概念与性质，能够区分有理数和无理数。

4. 理解长方形的周长和面积之间的关系，能够计算常见图形的周长和面积。

5. 掌握统计的定义与基本概念，能够进行简单统计数据的处理与分析。

二、教学内容：1. 数集与运算(1) 数集的概念与分类(2) 自然数、整数、有理数、实数的概念与性质(3) 加、减、乘、除的运算性质2. 因子与倍数(1) 整数因子与倍数的概念与性质(2) 求解最大公因数与最小公倍数的方法3. 分式(1) 分式的概念与性质(2) 分式的简化与运算(3) 整式与分式的转化4. 根式(1) 平方根、立方根的概念与性质(2) 有理数的开方运算5. 实数与无理数(1) 实数的概念与性质(2) 有理数与无理数的区分6. 平面图形的周长和面积(1) 长方形的周长和面积(2) 正方形、三角形、梯形、圆的周长和面积7. 统计与概率(1) 统计的概念与方法(2) 统计数据的处理与分析(3) 概率的概念与计算三、教学重点：1. 数集的分类与运算性质的掌握。

2. 因子与倍数的概念与求解最大公因数与最小公倍数的方法。

3. 分式的简化与运算。

4. 有理数的开方运算。

5. 长方形及其他常见图形的周长和面积的计算。

6. 统计数据的处理与分析。

四、教学方法：1. 组织学生观察、实验、探究，培养学生独立思考和问题解决能力。

2. 结合生活实际，引导学生将数学知识运用于实际问题的解决中。

3. 运用多媒体教学手段，辅助教师进行知识讲解与演示。

4. 创设数学游戏、竞赛等情境，增加趣味性，激发学生学习兴趣。

5. 引导学生进行小组合作学习，培养学生团队合作精神。

五、教学评价：1. 定期进行阶段性评价，反馈学生的学习情况，并及时进行个别辅导。