当前位置：文档之家 › 定性资料的统计描述(3)

定性资料的统计描述(3)

  • 格式：ppt
  • 大小：1.68 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

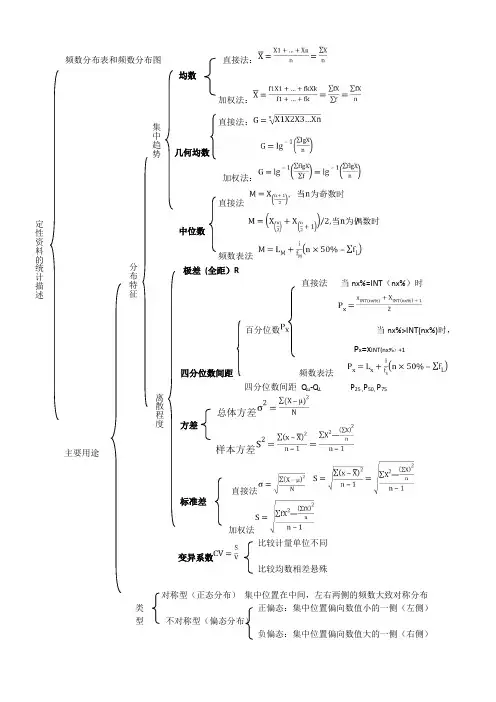
定性资料的统计描述(公式整理)

定性资料的统计描述(公式整理)

频数分布表和频数分布图 直接法：均数加权法：直接法：几何均数加权法： 直接法中位数 频数表法 极差 (全距）R直接法 当nx%=INT （nx%）时百分位数 当nx%>INT(nx%)时， P x =x INT(nx%）+1四分位数间距 频数表法四分位数间距 Q u -Q L P 25 ,P 50, P 75总体方差 样本方差直接法加权法比较计量单位不同比较均数相差悬殊对称型（正态分布） 集中位置在中间，左右两侧的频数大致对称分布 类 正偏态：集中位置偏向数值小的一侧（左侧） 型 不对称型（偏态分布）负偏态：集中位置偏向数值大的一侧（右侧）方差 标准差 变异系数 主要用途 定性资料的统计描述集中趋势离散程度分布特征集中描述 适用离散趋势适用均数 单峰对称分布资料 方差和标准差 越大，越离散 单峰对称分布资料 几何均数G对数正态分布， 观察组之间等比 变异系数CV越大，越变异不同计量单位 均数相差较大 中位数M 各种分布 不对称分布， 两端无确切值 分布不明确四分位数间距①偏态分布资料 ②两端无确切值 ③分布不明确资料概念：随机变量X 取各种值的概率称为概率分布规律，简称分布 正态分布就是一种重要的连续型随机变量的分布类型形态：呈对称钟形，在均数处最高，两侧不断降低，逐渐与横轴接近，但不与横轴相交正态分布曲线 密度函数为,分布函数，表示随机变量X 取小于或等于x 的概率①正态曲线在横轴上均数处最高。

②正态分布以均数为对中心，左右对称③正态分布有两个参数，即位置参数μ和形态参数。

特征 若固定，改变μ，曲线沿x 轴平行移动，其形态不变，若固定μ，越小，曲线越陡峭 正态分布 越大，曲线越低平，但中心在x ④正态曲线下的面积分布有规律密度函数标准正态分布(Z 分布） 分布函数标准化变换 估计总体变量值的频数分布查表过高过低均异常→双侧 应用 确定取单侧或双侧参考值 过高异常→上限 过低异常→下限 制定医学参考值范围 主要目的为减少假阳性（确诊）→99%主要目的为减少假阴性（初筛）→95% 服从正态→正态分布法不服从→百分位数法参考值范围正态分布法百分位数法确定适当的百分界限选择制定医学参考值范围方法标态 正态 面积或P -1~168.27% -1.64~1.6490% -1.96~1.96 95% -2.58~2.5899%双侧单侧双侧单侧只有上限只有下限只有上限只有下限95 P2.5~P72.5P5P9599 P0.5~P99.5P1P99。

统计习题——精选推荐

统计习题——精选推荐

卫生统计学习题第二章定量资料的统计描述1. 1985年某省农村30例6-7岁正常男童胸围（cm）测量结果如下：51.6 54.1 54.0 56.9 57.7 55.558.3 55.4 53.8 57.7 51.3 53.8 57.3 54.8 52.1 55.3 54.8 54.7 53.4 57.1 53.1 55.9 51.4 54.6 56.1 61.859.3 56.8 59.8 53.9（1）试编制以上数据的频数表，绘制直方图，概括其分布特征。

（2）用合适的统计量描述其集中趋势和离散趋势。

（3）对样本进行正态性检验第三章定性资料的统计描述1.某地通过卫生服务的基线调查得到如下资料，试作如下分析：（1）计算全人口的性别比；（2）计算育龄妇女（15~49岁）占总人口的百分比；（3）计算总负担系数；（4）计算老年人口系数某地人口构成情况年龄组（岁）男（%）女（%）年龄组（岁）男（%）女（%）0~ 4.2 4.0 45~ 2.4 2.75~ 3.2 3.1 50~ 2.1 2.410~ 4.4 4.2 55~ 1.2 2.215~ 5.5 5.3 60~ 1.3 2.420~ 5.1 5.2 65~ 1.1 1.425~ 6.0 6.1 70~ 0.8 1.230~ 4.3 4.5 75~ 0.5 0.935~ 3.2 3.3 80~ 0.2 0.540~ 2.3 2.5 85~ 0.1 0.2第四章常用概率分布1.假定虚症患者中，气虚型占30%。

现随机抽查30名虚症患者，求其中没有1名气虚型的概率、有4名气虚型的概率。

2.某溶液平均1毫升中含有大肠杆菌3个。

摇均后，随机抽取1毫升该溶液，内含大肠杆菌2个和低于2个的概率各是多少？3.某人群中12岁男童身高的分布近似正态分布，均数为144.00cm,标准差为5.77cm，试估计（1）该人群中12岁男童身高集中在哪个范围？（2）求人群中12岁男童身高的95%和99%参考值范围；（3）求人群中12岁男童身高低于140cm的概率；（4）求人群中12岁男童身高超过160cm的概率；第五章参数估计基础1.某研究表明新研制的一种安眠药比旧安眠药增加睡眠时间。

定性资料的统计描述

定性资料的统计描述
22
1. 直接法
选择人口数作标准
P' NiPi N
选择人口构成比作标准
P'
Ni N
Pi
Ni：标准年龄别 人口数
Pi：实际年龄别 ××率
N：标准人口总数
23
选择治疗人数之和作标准
直接法计算标准化治愈率（%）
病型
（1） 普通型 重型 合计
标准治 疗人数 （Ni） （2）
400 400 800(N)
38
6.已知男性的钩虫感染率高于女性。欲比较甲、乙两乡居 民的钩虫总感染率，但甲乡人口女多于男，而乙乡男多 于女，适当的比较方法是（ ）。
A.分性别进行比较 B.两个率比较的2检验 C.不具可比性，不能比较 D.对性别进行标准化后再比较 E.作两个总率差别的假设检验
39
7.要比较甲乙两厂某工种工人某种职业病患病率的高低， 采取标准化法的原理是（ ）。
p' 427 100% 53.4% 47.5% 800
24
2. 间接法（以死亡率为例）
选择年龄别死亡率作标准
P' P r P SMR n i Pi
P: 标准总死亡率 ΣniPi: 预期总死亡数
r: 实际总死亡数
r/ΣniPi (SMR) :
ni: 实际组别人口数 标准化死亡比(Standard
n i Pi
(6)=(2)(5) 51 145 115 42 353
27
原发性骨质疏松症标准化患病比SPR
城市
实际患病人数 预期患病人数
322 305
1.05
农村
实际患病人数 预期患病人数
335 353
0.95
原发性骨质疏松症标准化患病率 p’

定性资料的统计描述

定性资料的统计描述

同年内死亡人数 粗死亡率＝ 1000 0 00 当年平均人口数 1年
强度型指标（近似）
同年<1周岁死亡人数 婴儿死亡率＝ 1000 0 00 当年活产儿总数
频率型指标近似
同年孕产妇死亡数 孕产妇死亡率＝ 10万/10万 当年活产儿总数
相对比型指标
统计图表
人口统计指标
例：某医生治疗了4例支气管哮喘病患者， 其中3例有效，即报告有效率为75。
请问该说法是否正确？
某医院统计1985-1990年儿科住院病人疾病种类分 布情况见表：
表 某医院儿科住院病人疾病种类分布情况 疾病种类 先天性心脏病 病人数 250 ％ 23.8
风湿性心脏病
其它
750
2. 人时资料的描述—强度
流行病学随访研究中，不同个体被观察的时间长度各 不相同，常用人时总和表示被观察的人和时间的总和。 “强度”是流行病学、统计学术语。 ——单位时间内（如年、月、日等）某事件发 生的频率。
某事件发生的个体数 强度型指标 K （ 可能发生某事件的个体 数 时间）
强度型指标通常是指一段时间内的平均概率。如人 时发病率的分子是新发生的事件数，分母是人时 数（观察人数乘以时间）的总和，多用于大人群 长时间随访的资料。
常用的相对数指标大致有三种类型：
频率(relative frequency or proportion)
强度(intensity or rate) 相对比(relative ratio)
主要内容
1. 分类资料的描述—频率和频率分布
2. 人时资料的描述—强度
3. 复合指标—相对比 4. 相对数应用中需注意的问题
新发病例数 人时发病率 观察的人时总数 新发病例数 （折合的观察人数 （ ）单 位 时 间 的 个 数 ） 院的院内感染调查中，5031名病 人共观察了127859人日（例均25.4日），其中 有596人在医院发生感染，请计算院内感染率。

定性资料的统计描述

定性资料的统计描述

患病率
某 病 患 病 率 检 查 时 发 现 的 某 病 现 患 病 例 总 数 k 该 时 点 受 检 人 口 数
意义：
– 患病率是用以估计某病对居民危害的严重程度。
在特定人群中患病率很高的疾病有两种可能：
– 某人群得病的危险性很大； – 得病后病程很长，存活多。
死亡率和病死率
应用相对数时应注意的问题
分母一般不宜过小 不能以构成比代率 特别注意不能用构成比的动态分析代替率的
动态分析 对观察单位不等的几个率不能相加求平均率。 相对数进行比较应注意可比性 比较样本率或构成比的比较需假设检验
例1： 某医生用中西医结合疗法治疗了2例艾滋
病患者，其中1例有效，即报告有效率为 50。 请问该说法是否正确？
0.80
合计
185334 192.0
100.0
0.70
RR和OR
相对危险度(relative risk, RR) 是指暴露于某种
危险因素的观察对象的发病危险度与低暴露或非暴露 的观察对象的发病危险度之间的比值。常用于流行病 学队列研究中度量暴露的危险性大小。
比值比(odds ratio, OR)，又称优势比，是指病例
定性资料的统计描述
授课教师 朱 彩 蓉
复习
资料的两种类型
数值变量资料 分类资料(分类资料)
统计分析的内容
统计描述 统计推断
定性资料的统计描述
相对数概念 常用相对数指标 分类资料的频数表
相对数
概念：两个有关的数据或指标之比。
例：甲小学有534人，乙小学为313人， 经检查发现，甲学校患龋齿者57人， 乙 学校33人，问那所学校发现患龋齿的强 度高?

定性资料的统计描述

定性资料的统计描述

an: 报告期指标 a0:基期指标
增长速度：表示的是净增长量。
增长速度=发展速度-1
定基增长速度=定基发展速度-1
环比增长速度=环比发展速度-1
三、平均发展速度和平均增长速度
平均发展速度：各环比发展速度的几何均数， 说明某事物在一个较长时期中逐年平均增长 的程度。
平均发展速度=
n
an a0
平均增长速度：各环比增长速度的平均数， 说明某事物在一个较长时期中逐年平均增长 的程度。
如某专业杂志发文 “252例病毒性肝炎分析”
②不能用构成比的动态分析代替率的动态分析。 表 某市1980年和1990年5种传染病情况
疾病 痢疾 肝炎 流脑 麻疹 1980年
病例数 构成比（%） 病例数
1990年
构成比（%）
3604 1203 698 890 902
49.39 16.49 9.65 12.20 12.36
1、疾病统计资料来源：p40 2、疾病与死因分类 疾病命名： 第三 是给疾病起一个特定的名字，使之可区别 节 于其它疾病。(ICD-10)
疾病 统计 常用 指标
疾病分类：疾病分类是根据疾病的某些特征，按 照一定的编码规则对疾病进行统计分类的方法。

ICD是国际疾病分类英文 (International Classification
合
计
150
100.00
1
0%
33.33
20 40%
13.33 60%
26.67 80%
循环系统疾病
6.67 100%
传染病
20%
恶性肿瘤
呼吸系统疾病
消化系统疾病
某医院2001年住院病人5类疾病的死亡情况

3定性资料统计描述

3定性资料统计描述
第14页/共45页
• 例、对某大学学生吸烟状况进行调查，结 果显示该校男性大学生吸烟率为35.12%， 女性大学生吸烟率为1.58%，则该校男女 学生吸烟率之3比5.为12%： 22.23
1.58%
• 即该校男大学生吸烟率是女大学生吸烟率
的22.23倍。
第15页/共45页
• 例、体质指数(BMI)
急性传染 各区急性传染病 各区急性传染病 病发生数 发生数构成比(%) 发病率(1/万)
(3)
(4)
(5)
2433
18.9
38.21
3033
23.5
77.86
1650
12.8
23.58
1503
11.6
45.77
1282
10.0
44.67
1853
14.4
58.36
1130
8.8
73.45
12884
100.0
组的年龄构成比Ni/N乘以被标化组的组别率pi称为事 件分配发生率，分配发生率的累计就是标准化率。
第36页/共45页
三、标准组的选择
• 标准组应选择有代表性的、较稳定的、来自数量较大的人群 的指标作为标准。
• 例如世界的、全国的、全省的、本地区的或本单位历年累计的数据等；
• 也可选择相互比较的人群之一或比较人群的合并人群作为标 准。
• 例、某病两种治疗方法治愈率比较。总治
愈率的差别是由两种疗法内部的病情轻重
构成不一致造成的，而不是疗法本身有差
别。
病情 病人数
轻型
40
重型
60
合计 100
甲疗法 治愈数
36 42 78
治愈率 0.90 0.70 0.78

定性资料的统计描述

定性资料的统计描述
42.86 12.50
4
57.14 15.38
7
100.00 14.00
露露 可口可乐 百事可乐 汇源果汁
1 11 8 1
8 3 2 9
9 14 10 10
合计
24
26
50
频率指标的两个特点：
• 各组成部分之和为 1（100%）； • 某一部分所占比重增大，其它部 分会相应地减少 。
第二节 相对数指标
定性资料的统计描述
二分类变量 分类变量
定性变量
顺序变量
多分类变量
定性资料的统计描述
统计学中，定性资料的统计描 述可以做频数与频数分布，还可以 用相对数（比例/百分比、比率）来 描述和比较这类变量。
中 中 国 国 人 市 口 场 统 统 计 计 年 年 鉴 鉴
第一节 频数与频数分布
频数：各类别出现的个（例）数。
如例1：百事可乐和可口可乐市场占有率之比。
10 R＝ 0.7143 14
2. 两个率之比（相对数）
P 1 R＝ P2
如例2：甲城市300户家庭住房满意度调查中 满意率与不满意率的比较。
15% R＝ 0.4167 36%
应用相对数时的注意事项
计算相对数时，分母不宜过小，确保研究结果的 稳定性。在例数很少的情况下，尽量使用绝对数。
正确计算合计率。对观察单位数不等的几个率， 不能直接相加求其平均。 相对数的对比应注意可比性。即除了要对比的因 素外，其余的等。
【例 2 】在一项城 市住房问题的研究 中，研究人员还在 乙城市抽样调查 300 户，其中的一 个问题是：“您对 您家庭目前的住房 状况是否满意？” 1．非常不满意； 2．不满意； 3．一般； 4．满意； 5．非常满意。

统计学：定性资料的统计描述

统计学：定性资料的统计描述
发达国家较低
老年负担系数
发达国家较高
总负担系数
14岁及以下人口数 65岁及以上人口数 100% 15 ~ 64岁人口总数
发达国家较低
（3）老少比
65岁及以上的人口数 100% 14岁及以下人口数
老少比
发达国家较高
（4）性别比
性别比
男性人口数 100 女性人口数
不同年龄时期的性别比
（1）人口系数
老年（人口）系数 65岁及以上的人口数 100% 人口总数 14岁及以下人口数 100% 人口总数
发达国家较高
少儿（人口）系数
发达国家较低
（2）负担系数
少儿负担系数 14岁及以下人口数 100% 15 ~ 64岁人口总数 65岁及以上人口数 100% 15 ~ 64岁人口总数
定性资料的统计描述
( qualitative data statistical description 要求： )
1.掌握常用相对数的适用条件及应用
2.掌握医学人口常用统计指标和疾病统计常用指标 3.了解动态数列分析指标及特点
第一节
一、定性资料的构成比
定性资料的分布特征
表3-1 某医院2001年住院病人5类疾病的死亡情况
第二节
医学人口统计常用指标
一、 医学人口资料的来源 （medical population information ）
（一）人口普查
人口普查是收集资料、整理和分析一个国家或地区在某一特定时间的人口、经济和社 会资料的全过程。通常由国家政府主持，每隔5~10年进行一次。 建国以来，我国先后进 行了5次人口普查： 1953年、1964年、1982年、1990年、2000年。
1.计算相对数的分母不宜过小 2.分析时不能以构成比代替率（见表） 3.不能用构成比的动态分析代替率的动态分析（见表）

[临床医学]3定性资料的统计描述

[临床医学]3定性资料的统计描述

痢疾 肝炎 流脑 麻疹 腮腺炎 合计
3604 1203 698 890 902 7297
有人据此得出1990年和1980年相比，痢疾发病下降，肝 炎发病上升最明显的结论。
例：某班有男生50人，女生20人，男生英 语四级通过率为80％，女生四级通过率为 100％，请问该班四级通过率为多少？
答案1：90%。 答案2：85.7%
应用相对数时应注意的问题
1）分母数据一般不宜过小 2）不能以频率型指标代替强度型指标 3）正确合并估计频率（或强度）型指标 4）相对数进行比较应注意可比性 5）对相对数的统计推断
例：某医生治疗了4例支气管哮喘病患者， 其中3例有效，即报告有效率为75。
请问该说法是否正确？
某医院统计1985-1990年儿科住院病人疾病种类分 布情况见表：
例 某中学卫生科追踪了40名新生入学后吸 烟行为的情况，发现2名学生在半年时开始吸 烟，3名学生在2年时开始吸烟，其余学生在 初中三年未发生吸烟行为。问三年中吸烟的 发生率为多少？
2＋3 吸烟发生率 100％＝4.5％/人年 0.5 2＋2 3＋3 35
平均每年有4.5％的学生开始吸烟。
一、定性资料的频数分布表
表
市区 Ⅰ Ⅱ Ⅲ Ⅳ
某市某年各区急性传染病发生数及其相对数
各区与Ⅰ区 发病数之比 － 1.25 0.68 0.62 各区发生数 构成（％） 18.9 23.5 12.8 11.6 各区发病率 （1/10万） 382 779 236 458
年平均人 急性传染病 口数 发生数 636723 389540 699712 328363 2433 3033 1650 1503
表 某医院儿科住院病人疾病种类分布情况 疾病种类 病人数 ％ 先天性心脏病 风湿性心脏病 250 750 23.8 71.4

第三讲 定性资料的统计描述 卫生统计学

第三讲 定性资料的统计描述 卫生统计学

（3）负担系数（dependency ratio）：又称抚养比或抚养系数，是指 人口中非劳动年龄人数与劳动年龄人数之比。 一般以15~64岁为劳动 年龄， 14岁及以下和65岁及以上为非劳动年龄。 （4）老少比 ：指65岁及以上的老年人口与14岁及以下的少年儿童人 口之比，表示每100名少年儿童对应多少老年人，是划分人口类型的标 准之一。 （5）性别比（sex ratio）: 指男性人口与女性人口的比值。
指 标 分 子 分 母 基 数 类 型
粗死亡率
某年龄组死亡率 婴儿死亡率 新生儿死亡率 围生儿死亡率 5岁以下儿童死亡率 孕产妇死亡率 某死因死亡率 某病病死率 比例死亡比
同年内死亡人数
同年年龄组死亡人数 同年<1周岁死亡人数 同年<28天死亡人数 同年围生期死胎数+死产 数+<7天死亡人数 同年5岁以下儿童死亡数 同年孕产妇死亡数 同年内某原因死亡人数 同年某病死亡人数 同年某死因死亡数
率(frequency)指标、强度(intensity)指标和相对比
(relative ratio)指标。
例题：某年某市甲、乙两区麻疹发病儿童数分别为
100人和200人，已知两区的麻疹易感儿童数分别为 1000人和4000人，试比较区的麻疹发病情况。 甲、乙两区麻疹发病儿童数比为：100：200=1：2 甲区麻疹发病率为：（100÷1000）×100%=10% 乙区麻疹发病率为：（200÷4000）×100%=5% 甲、乙两区麻疹发病率的比为：10%：5%=2：1
注意： （1）死于所有原因的死亡率也称粗死亡率。 （2）死亡率也可按不同特征分别计算死亡专率，如按年 龄、性别、病种等计算年龄别死亡率、性别死亡率等。 （3）计算时应注意分母必须是与分子相应的人口。 （4）比较不同地区死亡率，人口构成不同时，需要先对 死亡率进行标化。

第三章 定性资料的统计描述

第三章 定性资料的统计描述

病人共观察了127859人日（例均25.4日），其中 有596人在医院发生感染，则 院内感染率=596/127859=0.0047人/人日 意味着平均每天有0.47%的病人将在医院获得感染。
（三） 相对比型指标
相对比型指标是A、B两个有联系的指标之比。
对比的两个指标可以性质相同，也可以性质不同。
公式为：相对比型指标=A指标 / B指标
30.86 37.04 24.69 6.17 0 0 1.24
71.43 46.15 166.67 16.67 0 0 10.00
合计
1621
81
100.00
49.97
第二节 死亡率的标准化 P305
一、死亡率标准化的意义和思想
比较两个总率时，若两组资料内部各小组的率有明显差
别，而且各小组内部构成也明显不同时，则不能直接比较。
动态数列的常用分析指标：
一、 绝对增长量 说明事物在一定时期所增加的绝
对数量。可分别计算累计增长量和逐年增长量。 1. 累计增长量：报告年的指标与某一固定年（基 期水平）指标之差。 2. 逐年增长量：报告年的指标与前一年指标之差。
表3-9 某大学1992~2002年本科专业招生动态变化
学生 人数 (3) 4200 4500 4800 4900 5150 5320 绝对增长量 累计 (4) 300 600 700 950 1120 逐年 (5) 300 300 100 250 170 发展速度% 定基比 (6) 100.0 107.1 114.3 116.7 122.6 126.7 环比 (7) 100.0 107.1 106.7 102.1 105.1 103.3 增长速度% 定基比 (8) 7.1 14.3 16.7 22.6 26.7 环比 (9) 7.1 6.7 2.1 5.1 3.3

第3章 定性资料的统计描述

第3章 定性资料的统计描述

某事件发生的平 均强度
二、应用相对数的注意事项
（一）计算相对数的分母不宜过小 一般来讲，观察单位数足够大时，计算的相对数 比较稳定，能够正确反映实际情况。如果观察单位太 少，直接用绝对数表示。
（二）分析时不能以构成比代替率，也不能以构成比 的动态分析代替率的动态分析。 构成比和率都是相对数，但两者又属不同的概念， 用时应注意两者的区别。
（三）计算观察单位不等的几个率的平均率时，不能将几
个率直接相加求其平均率。正确算法是将几个组的患者数
除以总检查人数。
（四）资料的对比应注意可比性 除了被研究的因素不同外，其余的因素应相同或相近， 应在相同条件下进行率和比的对比。 1. 观察对象同质、研究方法相同，观察时间等保持一 致，以保证资料的可比性。 2. 当两个总率进行比较时，如果内部构成不同，需要
第三章 定性资料的统计描述
一、相对数
相对数是两个有联系的指标之比。
常用的相对数指标：率、构成比、相对比
1、率－频率指标
定 义 公 式 常见率的计算
率的意义
（1）定义：它表示某现象发生的频率和强度。 说明某现象实际发生的例数占可能发生某现 象总数的比值。 （2）公式
率 某现象实际发生的例数 K 可能发生某现象的总数
2)人口抽样调查：与人口普查相比，人口抽样调查相对 省时省力，可以多次进行，也可以一次调查较多的项
目，或者对一个问题进行深入研究。可以在短时间内
得到调查资料和研究结果，根据样本特征推断总体的 相应特征。人口抽样调查是研究者常采用的方法之一。 3)人口登记：是指人口事件发生后随即进行登记。按照 登记人口资料的性质可以分为三类：生命事件登记、 人口迁移变动登记和户口登记。
死亡率：是指某人群在一定时间内死于某病的人

卫生统计学定性资料的统计描述

卫生统计学定性资料的统计描述


100%
例7 2004年某研究人员研究了相同年龄段的吸毒者与 非吸毒者的职业构成。
将两组人群各种职业的人数作为分子，分别除以两组 人群的调查总数，得到各种职业的构成比。
表 吸毒与非吸毒人群职业构成对比分析
构成比有两个特点：
①. 各构成比的构成总和为100％； ②. 某一部分所占比重的增减，会相应地影响其它部
卫生统计学定性资料的统计描 述
复习
资料的两种类型 定量变量资料 定性变量资料
统计分析的内容 统计描述 统计推断
统计分析
统计描述：是用统计图(表)、统计指标来描述资 料的分布规律及其数量特征。
统计推断：在医学科学研究中通常应用抽样研究 的方法，即对总体中随机抽取的部分观察单位(样 本)进行研究，然后用样本信息推断总体特征，即 统计推断。
=1.76人 / 1000人年
例4 为探讨EB病毒与鼻咽癌发病的关系, 研究者在某市进 行了EB病毒感染的抽样调查，共检查了25-57岁居民41471 人,其中38550人EB病毒抗体阴性，2921人阳性。以EB病毒 抗体阴性和阳性者分成两组,进行为期12年的队列研究，两 组分别随访了437579人年和20477人年，EB病毒抗体阴性 组发生鼻咽癌54例，阳性组57例。计算两组的累积发病率。
甲地麻疹病率 240 100% 12% 2000
乙地麻疹病率 200 100% 20% 1000
常用的相对数有率、构成比和相对比等。
1. 率
率又称频率指标或强度指标，指某现象实际发生数与 某时间点或某时间段可能发生该现象的观察单位总数 之比，用以说明某现象发生的频率或强度。
根据计算公式中分母的观察单位数是否引入时间因素， 率包括频率型和强度型/速率两类指标。

第三章定性资料的统计描述

第三章定性资料的统计描述

一、强度相对数
意义：说明某现象发生的频率或强度，又称为率。常以
百分率（%）、千分率（‰）、万分率（1/万）、十 万分率（1/10万）等表示。
计算：
某时期内发生某现象的观察单位数
率=
×比例基数
同期可能发生某现象的观察单位总数
2020年4月2日星期四
比例基数的选择主要根据习惯用法和 使计算的结果能保留1~2位整数。
可用相邻两年年末（12月31日）人口数的平均值计算年平均 人口数；也可用年中（７月１日零时）人口数代表全年的平均人 口数。
2020年4月2日星期四
徐州医学院卫生事业管理教研室
12
(二) 人口构成及其统计指标
人口学的基本特征包括年龄、性别、文化、职业等，其中 最常用来描述人口构成情况的是性别和年龄。
表3-2 人口学特征指标
指标
分子
分母
基数 指标类型
老年（人口）系数 ≥65岁人口数 人口总数
100% 频率型
少儿（人口）系数 ≤14岁人口数 人口总数
100% 频率型
总负担系数 少儿负担系数
≤14岁人口数 +≥65岁人口数
≤14岁人口数
15~64岁人口数 100% 15~64岁人口数 100%
频率型 相对比型
3、年龄组生育率(age-specific fertility rate,ASFR)又称年 龄别生育率，消除了育龄妇女内部年龄构成不同对生 育水平的影响。
2020年4月2日星期四
徐州医学院卫生事业管理教研室
21
4、终生生育率（life-time fertility rate, LTFR）说明 一批经历过整个育龄期的同龄妇女一生的实际生 育水平。
徐州医学院卫生事业管理教研室

第5章定性资料的统计描述

第5章定性资料的统计描述

第五章定性资料的统计描述在医学研究与实践中，大量资料都是按照事物的特征或属性进行分类的，这类资料称为定性资料，也称分类资料或计数资料。

如性别、HIV感染情况、病情轻重等都属于分类资料。

分类资料按类别分类计数所得到的数叫绝对数，绝对数往往不便于进行相互比较。

例如甲医院某年因某病死亡105人，同年乙医院因该病死亡185人。

但不能据此认为乙医院该病的死亡情况比甲医院严重，因为两医院因该病住院的人数不一定相等，此时需要采用相对数指标进行统计描述。

第一节常用相对数及其应用一、定性资料的频数分布与定量资料一样，定性资料也可通过编制频数分布表描述其分布特征，并通过计算一些常用的相对数指标进行统计描述和统计推断。

定性资料频数分布表又称为列联表，是用两个分类变量对同一资料进行双向分类形成的表，可用于考察两种属性的关系。

表5.1为某中学不同性别青春期少年对自身体型感觉的构成情况的列联表。

表5.1 某中学不同性别青春期少年对自身体型感觉的构成情况性别自感偏瘦正常自感偏胖男39 186 20女25 130 54列联表的横标目一般为分组变量，纵标目为结局变量。

列联表的用途主要有：1. 列出每组中各种不同结局分类后的频数。

2. 描述频数分布的特征。

3. 便于进一步对分类资料的特征进行统计描述和统计推断。

二、常用相对数指标除了用频数分布表可以全面反映定性资料的特征外，也可计算相对数指标来描述定性资料的特征。

相对数是两个有关联的数值之比，常用的相对数指标有率、构成比和相对比三种。

(一)率率是指某现象实际发生数与某时间点或某时间段可能发生该现象的观察单位总数之比，用以说明该现象发生的频率或强度。

根据计算公式中分母的观察单位总数是否引入时间因素，率包括频率和速率两类指标。

频率(frequency)计算中，分母没有引入时间因素，无时间量纲，分子是分母的一部分，其取值在0~1之间，如常见的发病率、患病率、病死率、治愈率等指标，都属于频率型指标，其实质是比例，在流行病学中也常称为累积发生率。

《医学统计学》第四章定性资料的统计描述

《医学统计学》第四章定性资料的统计描述

1、不要把构成比与率相混淆。即分析时不能以构成 比代率；这是常见的错误。
某文章作者根据上述资料认为，沙眼在20～组的患病率最高，以后随年 龄增大而减少。该作者把构成比当作率进行分析，犯了以比代率的错误。
2、使用相对数时分母不宜过小。分母过小时相对数 不稳定。
3、注意资料的可比性；
不同时期、不同地区、不同条件下的资料比较时应注意具有 可比性。
12965.2
46.3
否
265
660291.4
40.1
说明该地市区非吸烟女性饮酒者的肺癌发病率是
非吸烟女性不饮酒者的1.15倍。
3.比数比
比数比（ Odds ratio ，OR） : 常用于流行病学
中病例-对照研究资料，表示病例组和对照组中的 暴露比例与非暴露比例的比值之比，是反映疾病 与暴露之间关联强度的指标。其计算公式为
一般的，两个地方的出生率、死亡率、发病率、不同级别 医院某病的治愈率等不能直接比较。
无可比性的实例：
由表2-7可见，无论有无腋下淋巴结转移，省医院的5年生存 率均高于市医院，但从总生存率看，省医院的5年生存率低于市 医院。这不符合常理。因此，省医院与市医院的总生存率就不能 直接比较（标准化后再比）。
感谢聆听
率
某事物或现象发生的实 际数 某事物或现象发生的所 有可能数
比例基数
公式中的“比例基数”通常依据习惯而定。
需要注意的是，率在更多情况下是一个具有时间 概念的指标，即用于说明在某一段时间内某现象 发生的强度或频率，如出生率、死亡率、发病率 、患病率等，这些指标通常是指在1年时间内发 生的频率。
例4-1 某单位在2009年有3128名职工，该单位 每年对职工进行体检，在这一年新发生高血压 病人12例，则
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.发病率（强度型)
•概念：表示在观察期内，可能发生某种疾病的一 定人群中新发生该病的频率。 •计算公式： 同期内新发生某病的病例数 某病发病率= ×K
观察期内可能发生某病的平均人口数
在通常情况下，发病率的分母泛指一般平均人口数。 意义：发病率是反映某病在人群中发生频率大小的指标， 常用于衡量疾病的发生，研究疾病发生的因果关系和评价 预防措施的效果。
• 计算公式：
同期因该病死亡人数 • 某病病死率= 100% 观察期间内某病患者数
• 上式分母中患病情况不同，指标的概念也不同。 如住院病人的病死率，分母为住院人数。某一地 区某病病死率的分母则包括该地区所有患该病的 病人。故医院的病死率不能代表地区的病死率。
4.随访资料的生存率分析（频率型）
• 评价疾病防治的近期效果，一般可用治愈率、有 效率及病死率。但在研究肿瘤或研究其它预后较 差疾病的治疗效果时，则需要长期随访观察，多 用生存率来评价。 • 生存率：是指病人从某个规定时间（如发病、确 诊、开始治疗或手术时间等）开始，到某时点的 生存概率。 • 时间单位：一般以年为单位，有一年生存率，三 年、五年和十年生存率等。对于生存时间较短的 情况亦有以月或日为单位的。
卫生统计学（第五版）
数学教研室
第三节 疾病统计常用指标
疾病统计（morbidity statistics)是研 究疾病在人群中的发生、发展及流行规律 以及分布特征，阐明社会因素、自然因素 及生物因素对疾病发生发展的影响，为病
因研究、疾病防治、卫生保健工作的计划、
政策和评价提供科学依据。
一、疾病统计资料的来源
三、疾病统计指标
(一)反映疾病发生水平常用指标 1.疾病统计的计算单位 ：
●病例和病人： 一个“病人”在一定时期内（通 常指一年）可以同时患两种或两种以上的疾病或 可能一病屡患，作为两个或两个以上的病例对待。
●发病和患病：发病是指新发生某种疾病。患病 是指患有某种疾病而不管它是新发病还是老病， 只要在检查时病尚未愈，都算在内。
3.患病率（频率型）
• 概念：表示在某时点检查时可能发生某病的一定人群中 患有某病的频率。 • 计算公式：
检查时发现的某病病例 数 某病患病率 K 该时点受检人口数
其中某病病例数包括新病例和旧病例，凡患该病的一律 统计在内。同一人不应同时成为同一疾病的两个病例。
• 这一指标最适用于病程较长的疾病的统计研究，用于衡 量疾病的存在，反映某病在一定人群中的流行规模或水 平，估计医疗设施的需求量。
2. 某市有30万人口，2002年共发现2500名肺结核患者，全 年总死亡人数为3000人，其中肺结核死亡98人，要说明肺 结核死亡的严重程度，最好应用（ ）
C 北方籍战士中暑率比南方籍战士高 D 尚不能得出结论
5. 一项新是治疗方法可延长病人的生命，但不能治愈该病 A则最有可能发生的情况是（ 初死亡率 B 肺结核死亡率 ） A 该病的患病率增加 B 该病的患病率减少 C 肺结核死亡构成 D 肺结核的病死率 C 该病的发病率减少 D 该病的发病率与患病率均减少
生存率的计算方法
直接法： 观察满n年的人数中 活满n年的比率。 • 寿命表法：是应用定群 寿命表的基本原理，先 计算出随访病人活满x年 活满n年的人数 n年生存率 100% 再活下一年的死亡概率， 观察满n年的人数 然后计算出相应各阶段 优点是计算方法简单、直观，在病 的生存概率，根据概率 例较多时误差不大。缺点是当例数 乘法定律将各阶段概率 较少时，有时会出现后一年比前一 相乘而得到一定年限的 年生存率高的不合理现象，如上例 生存率。
反映疾病防治效果的指标
1.治愈率 2.某病病死率 3.生存率
1.某医院某年住院病人中胃癌患者占5%，则（） A 5%是强度指标 B 5%是频率指标
C 5%是相对比指标 D 5%说明胃癌在人群中的严重性
2. 计算麻疹疫苗接种后血清检查的阳转率，分母为（ ） A 麻疹易感人群 B 麻疹患者数
C 麻疹疫苗接种人数 D 麻疹疫苗接种后的阳转人数
（一）疾病报告和报表资料 （二）医疗卫生工作记录 （三）疾病专题调查资料
二、疾病和死因分类
• 疾病的命名（nomenclature of diseases）为了深入认识疾病， 有必要将各种不同的疾病加以命名和分类。就是要对每一 种法定疾病情况给以确切的名称， • 疾病分类（classification of diseases）是在疾病命名法的基 础上，考虑到对疾病的认识及防治需要，将一些具有共同 特性的疾病归纳在一起，加以分类。 现在国际上使用的是ICD的第十次修订本（简称ICD10）。
3.某病患者120人，其中男性114人，女性6人，分别占 95%与5%，则结论为（ ） A 该病男性易得 B 该病女性易得 C 尚不能得出结论 D 根据该资料可计算出男女性的患病率
4.某部队夏季拉练，发生中暑21例，其中北方籍战士为南 方籍战士的2.5倍，则结论为（ ） A 北方籍战士容易发生中暑 B南方籍战士容易发生中暑
时点患病率
检查人口数
10万/10万
频率型
期间患病率
时期现患疾病人数
检查人口数
10万/10万
频率型
治愈率
治愈人数
接受治疗人数
100%
频率型
生存率
活满特定时期的人 数 残疾患者人数
期初存活的人数
100%
频率型
残疾患病率
检查人数
100%
频率型
定性资料的统计描述
小结：
疾病统计
反映疾病发生水平常用指标
1.发病率 2.患病率
18
14 16
16
13
16
1978
1979 1980 1981 合计
25
36 25 46 243
23
31 23 36 213
20
29 19
16
26
16
154
120
85
66
46
33
17
某地胃癌根治术后八年生存率
术后年数(n) 1 2 3 4 5 6 7 8
存活人数
213
154
120
85
66
46
33
17
出现七、八年两年生存率均高于第 六年的生存率；因迁移等原因而失 访或死于与所研究疾病无关的其它 疾病，观察未满一年者，这些均不 能用来计算生存率，从而损失了信 息。 • 寿命表法计算生存率的优点 是可以利用截尾资料，而且 结果不会出现后一年比前一 年生存率高的不合理现象。 缺点是计算相对复杂。
某地1974～1981年胃癌根治术后随访结果
随访满 n年人数 存活率（%）
243
197
172
136
111
79
55
29
87.65
78.17

62.50
59.46
58.33
60.00
58.62
疾病统计常用指标
指标 某病发病率 分子 时期内新发生的某 病病例数 时点现患疾病人数 分母 年平均人口数×1年 基数 10万/10万 类型 强度型(近似)
(二)反映疾病防治效果的指标
1.治愈率（频率型）
接受治疗的病人中治愈的频率。 治愈率=（治愈病人数/受治病人数）×100%
2.有效率（频率型）
接受治疗的病人中治疗有效的频率 有效率=（治愈有效病人数/受治病人数）×100%
3.某病病死率（强度型)
• 概念：在规定的观察时间内，某病患者中因该病 而死亡的频率。
生 存 年 数 年份 (1) 1974 例数 (2) 29 1 (3) 28 2 (4) 25 3 (5) 23 19 4 (6) 18 5 (7) 17 6 (8) 17 7 (9) 17 8 (10)
1975
1976 1977
26
24 32
24
21 27
19
19 23
18
16 21
18
14 18