当前位置：文档之家 › 无机化学 6-2配位化合物 图文

无机化学 6-2配位化合物 图文

  • 格式：ppt
  • 大小：506.50 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

无机化学课件-配位化合物

无机化学课件-配位化合物

乙二酸根(草酸根):
O
O 2-
CC
OO
六齿配体:乙二胺四乙酸根 EDTA(Y4-)
OOC– H2C
CH2 – COO 4-
N–CH2 –CH2 –N
OOC– H2C
CH2 – COO
3.配位数:
指在配合物中直接与中心原子配合的配位 原子的数目
表示：n 特点：一般是2，4，6，8 （偶数）
单齿配体: [ Cu(NH3)4]2+
{ 3.特殊配合物
簇状配合物
π－酸配体配合物
桥基配合物：
H O （H2O）4 Fe Fe（OH2）4 O H
簇状配合物 ：
CO CO CO CO
Fe Fe
CO
CO CO
CO
CO
四、配合物的几何异构现象
几何异构体：组成相同、空间排列方式不同的物质 平面四方形空间构型的[Pt(NH3)2Cl2]，就有两
种不同的排列方式：
Cl
NH3
Pt
Cl
NH3
顺式
μ≠0 棕黄色
有抗癌活性
Cl
NH3
Pt
NH3
Cl
Байду номын сангаас
反式
μ=0 亮黄色 无抗癌活性
第二节 配合物的化学键理论
一、价键理论
（一）基本要点：
1.配合物的中心原子与配体之间是以配位键结合的： M ← L。
2.在形成配离子时，中心原子所提供的空轨道必须首 先进行杂化，形成数目相同的新杂化轨道，M以杂化 空轨道接受L提供的电子而形成σ配键。配离子的空间 构型、配位数、稳定性，主要取决于形成配位键时， M所用的杂化轨道的类型。 3.M的原子轨道杂化时，由于参加杂化的轨道能级不 同，形成的配离子可分为内轨型、外轨型。

第六章 配位化合物

第六章 配位化合物

制作:张思敬等
理学院化学系
13
Example 2
写出下列配合物的化学式：
（1）羟基· 水· 草酸根· 乙二胺合铬(Ⅲ)
（2） 氯· 硝基· 四氨合钴配阳离子(Ⅲ)
Solution
(1) [Cr(OH)(H2O)(C2O4)(en)]; (2) [Co(NH3)4(NO2)Cl]+
制作:张思敬等
理学院化学系
图6-3 [Cu(en)2]2+的结构
如果配位化合物的形成体是中性原子，配位体是CO分 子，这类配合物称为羰合物。如Ni(CO) 4, Fe(CO)5 。
制作:张思敬等
理学院化学系
7
3. 价键理论 基本要点
中心离子
中心离子（或原子）有空的价电子轨道可接受由配位 体的配原子提供的孤对电子而形成配位键。
Cu2+
H3N NH3
图6-2 [Cu(NH3)4]2+离子的结构
制作:张思敬等 理学院化学系 6
2. 特殊配合物（螯合物和羰合物）
每一个配位体只能提供一 个配位 原子的配位体称为单齿配体，而含有 两个或两个以上配位原子的配位体称 为多齿配体。能提供多齿配体的物质 称为螯合剂。由多齿配体形成的环状 结构的配合物称为螯合物，如 [Cu(en)2]2+。
{c(Cu 2+ ) / cQ }{c(NH 3 ) / cQ }4 - 14 K 解离 = = 4.78 ? 10 c{Cu(NH 3 )4 }2+ / cQ
当忽略浓度量纲时，可简化为：
c(Cu 2+ ){c(NH 3 )}4 - 14 K 解离 = = 4.78 ? 10 + c{Cu(NH 3 )2 4 }

《无机化学》第8章.配位化合物PPT课件

《无机化学》第8章.配位化合物PPT课件

配位化合物的发展趋势与展望
新材料与新能源
随着人类对新材料和新能源需求的不断增加，配位化合物有望在太 阳能电池、燃料电池等领域发挥重要作用。
生物医药领域
配位化合物在药物设计和治疗方面的应用前景广阔，有望为人类疾 病的治疗提供新的解决方案。
环境科学领域
配位化合物在处理环境污染和保护生态环境方面具有潜在的应用价值， 未来有望为环境保护做出贡献。
螯合物
由两个或更多的配位体与同一 中心原子结合而成的配合物，
形成环状结构，如： Fe(SCN)3。
命名
一般命名法
根据配位体和中心原子的名称，加上 “合”字和数字表示配位数的顺序来 命名，如：Co(NH3)5Cl。
系统命名法
采用系统命名法，将配位体名称按照 一定的顺序列出，加上“合”字和数 字表示配位数的顺序，最后加上中心 原子名称，如： (NH4)2[Co(CO3)2(NH3)4]·2H2O。
配位化合物的种类繁多，其组成和结 构取决于中心原子或离子和配位体的 性质。
配位化合物的形成条件
01
存在可用的空轨道 和孤对电子
中心原子或离子必须有可用的空 轨道，而配位体则需提供孤对电 子来形成配位键。
02
能量匹配
中心原子或离子和配位体的能量 状态需要匹配，以便形成稳定的 配位化合物。
03
空间和电子构型适 应性
中心原子或离子和配位体的空间 和电子构型需相互适应，以形成 合适的几何构型和电子排布。
02
配位化合物的组成与结构
组成
配位体
提供孤电子对与中心原子形成配位键的分子或离子。常见的配位 体有：氨、羧酸、酰胺、酸酐、醛、酮、醇、醚等。
中心原子
接受配位体提供的孤电子对形成配位键的原子。常见的中心原子有： 过渡金属元素的离子。

无机化学配位化合物PPT课件

无机化学配位化合物PPT课件

一般 配位原子的电负性值小，易给出电子对，对中心元素的 结构影响较大，可能发生重排。
4.配位数规律：
中心元素电荷 +1 +2 +3 +4
常见配位数 2 4(6) 6(4) 6(8)
5.几何异构、旋光异构
不同配体在中心元素周围空间排列位置不同产生的异构现象
H3 N
Cl
Pt
H3 N
Cl
Pt
H3 N
Cl
③同类配体：按配位原子符号的英文字母顺序排列 ；若配位原子也相同，少原子数配体在前；若原
第二节 配位化合物的结构
一、价键理论——VB法应用 Ag(NH3)2+ Zn(NH3)42+ FeF63-
1.外轨型和内轨型配合物。
Fe(CN)63-
2.低自旋和高自旋配合物。
3.中心元素的杂化类型与其电子层结构和配体中配位原子的电 负性有关。
一、碱金属、碱土金属元素结构特征及元素性质变化规律。 二、成键特征及特殊性。 三、单质在水溶液中的行为——活泼性变化规律（φ）
2021/3/12
四、重要化合物性质。
1.氧化物和氢氧化物性质知识。
⑴氧化物
①与水作用
碱性变化规律——ROH规则
②与CO2作用 ⑵氢氧化物
③氧化还原性质
①水中溶解性 ②热稳定性
2、氢化物(了解)
①结构特点
②性质
3、重要盐类
①溶解性特点；②硬水及其软化（小论文）
③对角线规则——Li与Mg的相似性
单质在空气中燃烧产物、与C、N2直接化合为碳化物和氮化物；氢 氧化物为溶解度不大的中强碱，易热分解；氯化物共价性大，能 溶2与021/有3/12机溶剂；碳酸盐、磷酸盐、氟化物等难溶等。

第六章 无机化合物

第六章 无机化合物

25
单齿配体 —含有一个配位原子的配体 -、X-等 如 NH 、 H O 、 CN 3 2 配体
多齿配体 —含两个或两个以上配位 原子的配体 如en、EDTA(乙二胺四
乙酸)
en ：
N H2CH 2CH 2 N H2

EDTA ：
26
二、配合物的组成
配 体 CN-、CO －NO2、NH3 H2O、 :ONOF-、Cl-、Br-、I-:OOC-COO:-
s表示升华; d表示分解；LiCl，ScCl3的 数据有一个温度范围，本表取平均值。
IIIA IVA VA VIA
BCl3 CCl4 NCl3 12.5 76.8 <71
AlCl3 SiCl4 PCl3 SCl4 178s 57.6 75.5 -15d
KCl CaCl2 ScCl3 TiCl4 VCl4 CrCl3 MnCl2 FeCl3 CoCl2 NiCl2 CuCl2 ZnCl2 GaCl3 GeCl4 AsCl3 SeCl4 1500s >1600 825s 136.4 148.5 1300s 1190 315d 1049 973s 933d 732 201.3 84 130.2 288d CuCl 1490
H3N Cu H3N NH3 NH3
2+ 2 SO4 21
配合物与复盐的区别
一、配位化合物的定义
复盐： [KAl(SO4)2· 12H2O] 、KCl · MgCl2 · 6H2O （NH4）2SO4 · FeSO4 · 6H2O 将其溶解于水，便可发现在水溶液中都离解为简单的组成离 子K+、Al3+、SO42-离子。
AuCl3 HgCl2 TlCl PbCl4 BiCl3

6配位化合物的结构

6配位化合物的结构

Eeg Et2g 0 10Dq 2Eeg 3Et2g 0
Eeg 6Dq0.60 Et2g 4Dq0.40
eg
d , d x2 y2 z2
6Dq 101D0Dq或 q或Δ0o
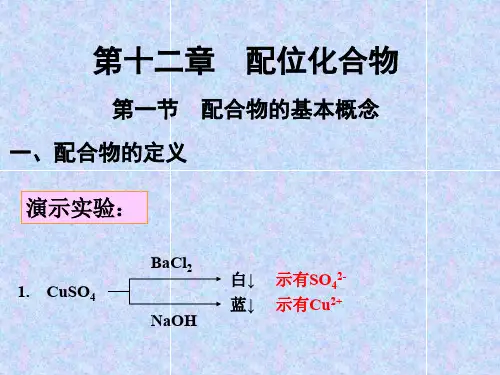
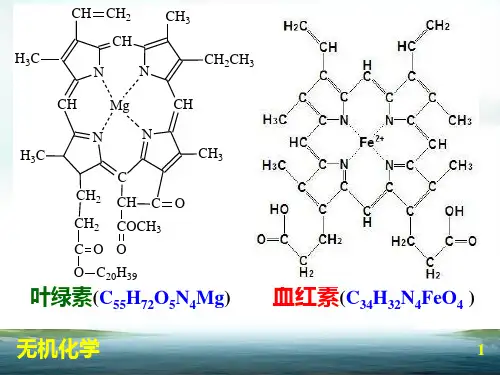
自由离子 d 轨道
Es
球形场
-4Dq
t2g dxy,dyz,dxz
正八面（Oh）场
图6-2 d 轨道在 Oh 场中的能级分裂
(2) 正四面体场中的能级分裂（Td）
A1g 1 1 1 1 1 1 1 1 1 1
x 2 y 2,z2
A2g 1 1 1 1 1 1 1 1 1 1 B1g 1 1 1 1 1 1 1 1 1 1
Rz x2 y2
B2g 1 1 1 1 1 1 1 1 1 1
xy
Eg 2 0 2 0 0 2 0 2 0 0 ( R x , R y ) , ( x z , y z )
x2 y2 z2
A2g 1 1 1 1 1 1 1 1 1 1
Eg 2 1 0 0 2 2 0 1 2 0 ( 2 z 2 x 2 y 2 , x 2 y 2 )
T1g 3 0 1 1 1 3 1 0 1 1
(R x,R y,R z)
T2g 3 0 1 1 1 3 1 0 1 1
(xz, yz,xy )
无机化学的复兴，主要源于大量新型配合物的出现， 特别是近年来广泛研究的功能配合物，原子簇化合物 （仍然存在金属与配体之间的化学键问题），使得具备 配合物化学键理论知识显得尤为重要。
6.2
晶体场理论在本质上仍然是一种静电理论，其核心思想是 中心离子d 轨道在周围配位体影响下能级发生分裂。由于中 心离子的五个d 轨道在空间的取向不同，当配体靠近 M 时， M 中的 d 轨道受到 L 负电荷的静电微扰作用，使原来简并的 d 轨道能级发生分裂。分裂的情况与晶体场的对称性（配合 物的几何构型）有关，分裂后的 d 轨道间的能量差称为分裂 能()。d 电子在分裂了的d轨道上的排布状态，决定了配位 场的光谱、磁性、稳定性、几何构型等性质。

无机化学 配位化合物PPT课件

无机化学 配位化合物PPT课件
获1913年诺贝尔化学奖
1893年苏黎世大学维尔纳 (Werner A)教授对这类化 合物本性提出了天才见解, 被后人称为维尔纳配位学 说，成为配位化学的奠基 人。维尔纳因此而获得 1913年诺贝尔化学奖。
维尔纳 (Werner, A, 1866-1919)
配位化学的奠基人—维尔纳
配位化学是当今化学学科的前沿领域之一， 配合物在医疗、药物、分离分析、染料、化学合 成等诸多方面具有极为广泛的应用。
② 配离子的解离如同弱电解质：
[Cu(NH3)4]2+
Hale Waihona Puke Cu2++4NH3
浓度非常低
+
+ [Cu(NH3)4]2+
[Cu(NH3)4]2+
Cu2+
Cu2+ 4NH3
4NH3
配离子解离出中心原子和配体，同
时，二者C重u(新O结H合)2成配离子Cu，S是动态平
衡的过程，这种平衡就叫做配位平衡。
一、稳定常数
内界
外界
离子键
➢ 配合物的解离如同强电解质：
[Cu(NH3)4]SO4→[Cu(NH3)4]2++SO42-
[ Cu (NH3)4 ]2+
中心原子 配体 配位键
➢ 配离子的解离如同弱电解质：
[Cu(NH3)4]2+
Cu2+ + 4 NH3
配合物的解离：
① 配合物的解离如同强电解质：
[Cu(NH3)4]SO4→[Cu(NH3)4]2++SO42-
Fe4[Fe(CN)6]3 [Cu(NH3)4]SO4
K2[Ag(CN)2]
[Ag(NH3)2]OH

无机化学简明教程第6章 配位化合物

无机化学简明教程第6章 配位化合物

配位数 空间 构型 四方锥 例
2 SbCl 5
5
6
三角双锥
八面体
Fe(CO)5
Fe(CN)
3 6
无机化学
19
二、配合物的磁性
磁性：物质在磁场中表现出来的性质。 磁矩： n(n 2) (B.M.)玻尔磁子 n — 未成对电子数 顺磁性：物质内部有单电子，被磁场吸引 µ > 0 , n > 0 例：O2，NO，NO2 反磁性：物质内部无单电子，被磁场排斥 µ = 0 , n =0 铁磁性：被磁场强烈吸引。例：Fe，Co，Ni
µ =3.18
µ =2.40
n=2
n=1
21
无机化学
6.3 配合物的化学键理论
一、价键理论
价键理论要点：
1、中心体M有空的价电子轨道，配位体L有孤对
电子，二者形成配位键ML；
2、中心体采取杂化轨道成键；
3、配离子空间构型与中心体的杂化类型有关。
无机化学
22
1、 配位数为 2的配合物
[Ag(NH3)2]+ Ag+的结构 [Ag(NH3)2]+的结构
原则—遵循一般无机物命名原则
1) 配合物：阴离子在前，阳离子在后； 2) 配位数目(大写) 名称(氧化数)； 配体名称 合 中心体
3) 配体间用“ · ”隔开，配体数用一、二等表示；
4) 中心体氧化数用罗马数字表示。
无机化学
15
类型
配位 酸
化学式
H[BF4]
H3[AlF6]
命名
四氟合硼(III)酸 六氟合铝(III)酸 氢氧化四氨合锌(II) 氢氧化一羟基 五水合铬(III) 四羟基合铝 (III)酸钾

无机化学 第六章 配位化合物

无机化学 第六章 配位化合物
配合物：[Cu(NH3)4](OH)2，氢氧化四氨合铜(II) 对比：NaOH氢氧化钠
总则： 服从一般无机化合物的命名原则
阴离子在前，阳离子在后;
阴离子为简单离子，则称某化某;
阴离子为复杂离子，则称某酸某;
若外界为氢离子，则缀以“酸”字;
[Co(NH3)6]3+
六氨合钴(III)离子
[Ag(NH3)2]OH
混合配体？
(1) 先无机配体，后有机配体。
[CoCl (NH3)3en]2+ 一氯 . 三氨 ·乙二胺合钴(III) 离子
(2) 先阴离子，再中性分子，后阳离子的名称。
[PtCl3NH3]三氯 . 一氨合铂(II)离子
(3) 同类配体，按配位原子元素的英文字母顺序。
[Co(NH3)5H2O]3+ 五氨 . 一水合钴(III)离子
时，则按配位原子元素符号的字母顺序排列。
2. 配合物的外界和内界的命名方法
配合物：[Cu(NH3)4] Cl2 氯化四氨合铜(II) 对比：CuCl2 氯化铜 配合物：[Cu(NH3)4]SO4 硫酸四氨合铜(II) 对比：CuSO4 硫酸铜 配合物： H2SiF6六氟合硅(IV)酸 对比：H2SO4硫酸
维尔纳配位价键理论的提出
1893年,瑞士,维尔纳（A.Werner,1866－1919）
瑞士著名化学家，苏黎世大学教 授。在科学上崇拜德国，感情上热爱 法国。在瑞士苏黎世大学学习时，他 的数学和几何学考试总是不及格，但 在他一生的科学经历中，却表现了几 何学的空间概念和丰富的想象力在化 学方面的创造性的应用。
第六章 配位化合物
配位理论产生背景和配合物的作用
我国：周朝，茜草根＋粘土或白矾 → 红色茜素染料。

大学无机化学--配位化合物ppt课件

大学无机化学--配位化合物ppt课件
12
二、配键和配位化合物分类
1. 外轨型配合物
中心原子是用最外层的ns、np或ns、np、nd组成的
杂化空轨道接受电子，与配体形成配位键.
例：[FeF6]3--中Fe3+：3d5
↑↑↑↑↑ ＿ ＿ ＿ ＿ ＿ ＿ ＿＿ ＿
3d
4s 4p
4d
sp3d2杂化，八面体构型
13
2.内轨型配合物：
配合物中心原子原有的电子层结构发生电子重排， 提供(n－1)d轨道和ns、np组成的杂化空轨道与配体 结合成配键 .
杂化类型 配位数
sp
2
sp2
3
sp3
4
dsp2
4
dsp3
5
d4s
5
Sp3d2
6
d2sp3
6
空间构型 直线形
平面三角形 正四面体
四方形 三角双锥
四方锥 八面体
实例
Ag(NH3)2+ Ag(CN)2– Cu(CN)32 – ,HgI3– Zn(NH3)42+, Cd(CN)42– Ni(CN)42–
Ni(CN)53– Fe(CO)5 TiF52–
总原则：先阴离子后阳离子，先简单后复杂
(1) 先无机配体，后有机配体。 Cis-[PtCl2(Ph3P)2] 顺－二氯 . 二(三苯基膦)合铂(II)
(2) 先阴离子，后阳离子和中性分子的名称。 K[PtCl3NH3] 三氯 . 氨合铂(II)酸钾
(3) 同类配体，按配位原子元素的英文字母顺序排列。

K
， sp，Cu（OH）2
有Cu（OH
）沉淀 2
生
成
。
29
【例2】欲完全溶解0.01mmol AgCl在1.0mL的氨 水中，则所需氨水的最低浓度是多少？ (已知AgCl的Ksp=1.56×10-10， [Ag(NH3)2+]的K稳 =1.7× 107 )

无机化学教学11章.配位化合物PPT课件

无机化学教学11章.配位化合物PPT课件
制造发光材料和显示器。
电池材料
一些配位化合物可作为电池材料， 如镍镉电池中的镉离子和镍离子
形成的配位化合物。
05
配位化合物与配合物之间的 关系
配位化合物的形成条件
配位化合物的形成需要一个中心 原子（通常为金属）和几个配位 体分子或离子，通过配位键结合。
中心原子必须有空轨道，可以接 受电子对，而配位体则提供孤对
配位化合物的颜色变化是由于电子跃迁所引起的。
详细描述
配位化合物的颜色变化是由于其组成配体和中心金属的电子跃迁所引起的。不 同的配体和金属元素会产生不同的颜色，因此可以通过观察颜色来判断配位化 合物的组成和结构。
磁性
总结词
配位化合物的磁性主要取决于其组成的金属离子和配体的性质。
详细描述
一些配位化合物具有明显的磁性，这与其组成和结构密切相关。一般来说，含有铁、钴、镍等过渡金属的配位化 合物具有明显的磁性。此外，配体的性质和配位化合物的结构也会影响其磁性。了解配位化合物的磁性对于其在 化学、物理和材料科学等领域的应用具有重要意义。
配位体
提供孤对电子与中心原子 或离子形成配位键的分子 或离子。
特性
稳定性
配位化合物具有较高的稳定性 ，主要由于配位键的形成使得
整个分子更加稳定。
多样性
配位化合物的种类繁多，可以由 不同的中心原子、配位体和配位 数组成，形成各种不同的结构。
可预测性
根据中心原子和配位体的性质 ，可以预测配位化合物的性质 和稳定性。
诊断成像
生物分析
配位化合物可用于检测生物体内的金 属离子和蛋白质等生物分子的含量和 活性。
配位化合物可用于医学影像技术，如 核磁共振成像和X射线造影剂。
在材料科学上的应用

简明无机化学配位化合物课件

简明无机化学配位化合物课件
Cu2 [ SiF6 ] 六氟合硅（IV）酸亚铜
配体前面用 二、三、四 ··· ···表示该配体的个数。
[ Co（NH3）5 H2O ] Cl3 三氯化五氨•水合钴（III）
Cu2 [ SiF6 ] 六氟合硅（IV）酸亚铜
几种不同的配体之间加 ‘ • ’ 隔开。
[ Co（NH3）5 H2O ] Cl3 三氯化五氨•水合钴（III）
而乙二胺四乙酸（用 EDTA 表示）
HOOCH2C
CH2COOH
NCH2-CH2N
HOOCH2C
CH2COOH
有 2 个 N，4 个 －OH 中的
O 均可配位。
HOOCH2C
CH2COOH
NCH2-CH2N
HOOCH2C
CH2COOH
EDTA 称多基配体。
由双基配体或多基配体形成的 配位化合物经常有环
NH2
NH2
2+
CH2 Cu
CH2
CH2
CH2
NH2
NH2
NH2
NH2
2+
CH2 Cu
CH2
CH2
CH2
NH2
NH2
两个乙二胺像蟹的双螯将 Cu2+ 钳住，形成两个环。
称这种配位化合物为螯合物。
NH2
NH2
2+
CH2 Cu
CH2
CH2
CH2
NH2
NH2
形成的环以 5 元环，6 元环 为最稳定和最常见。
—— 结构异构和空间异构。
1. 结构异构
结构异构又叫构造异构。 键联关系不同，是结构异构 的特点。 中学阶段学习过的有机化合 物的异构现象多属此类。
结构异构主要有如下几种： （1） 解离异构 （2） 配位异构 （3） 键合异构
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二、配合物的晶体场理论 1.理论要点
(1)中心原子处于负电荷的配体形成的静电场(晶体场)中;
(阴离子或极性分子）
中心原子与配体之间靠静电作用结合，形成化学键。
（2）晶体场对中心原子的空间伸展方向不同d轨道
产生排斥作用。使5个简并d轨道的发生能级分裂。
（3）d电子重新分布，系统能量降低，形成稳定配合物。
eg Δo
t2g
0.6Δo 0.4Δo
自由离子
分裂能Δo
球形场
正八面体场
吸收光谱 E= Δo = hv = hc/λ = h cv
e二重简并轨道， t三重简并轨道 eg (e1g)1表示镜面对称， t2g 2镜面反对称
g表示中心对称 Δo o八面体octahedron
3.分裂能Δo
影响分裂能的因素有：
eg
Δo
t2g
eg eg
小
大
t2g
t2g
八面体配合物的中心离子的 d电 子 在 不 同 场 强 度 的 排 布
5. 晶体场稳定化能
在配合物中，中心原子的 d 电子分布在能级 分裂的轨道上，与分布在球形场能级未发生分裂 的 d 轨道相比，能量可能降低，其能量降低值为 晶体场稳定化能（CFSE）。
八面体场： CFSE = xE(t2g) + yE(eg) + (n2-n1)P
5.92
对于ML6配合物 取决于中心原子的电子层结构和配体的性质： (1) 中心原子 (n-1)d 8-10 →外轨型配合物。 (2) 中心原子 (n-1)d 1-3 ，(n-1)d空轨道≥ 2→内轨型
(3)中心原子(n-1)d 4-7时，取决于配体。
配位原子电负性大(不易给出电子对)→外轨配合物。 配位原子电负性小(易给出孤电子对)，
Fe [Ar]
4s
4p
Fe3+ [Ar]
Fe3+ [Ar]
sp3d2（ 外 轨 型 ）
Fe3+ [Ar]
d2sp3（ 内 轨 型 ）
铁(III)离子的内轨型和外轨型电子构型
配合物的类型可通过磁矩判断
未成对电子数与磁矩 = (n(n+2) B
N
0
1
2
3
4
5
/ B 0.00
1.73
2.83
3.87 4.90
配体只影响d轨道能级分裂和d电子排布，不进入d轨道。
2. 晶体场中 d 轨道能级的分裂
中心原子放在球形对称的负电场中，负电场对5个简并d轨 道的静电排斥力是相同，d轨道的能量升高，但能级不分裂。
对于ML6配合物，6个配体位于正八面体的 6 个顶点, 形成八面体场：
八面体场
简并d轨道分裂为两组： eg轨道能量较高 dx2 y2 d z2 t2g轨道能量较低 dxy，dxz ，dyz轨道.
d电子发生重排,空出(n-1)d轨道→成内轨配合物。
价键理论的应用和局限性 价键理论可用来： 1、解释许多配合物的配位数和几何构型。 2、说明含有离域键的配合物特别稳定
[Ni(CN)4]2- 。 3、解释配离子的某些性质，如[Fe(CN)6]4-(低自旋 型配离子) 比[FeF6]3-(高自旋型配离子) 稳定。 价键理论的局限性： 1、价键理论在目前的阶段还是一个定性的理论， 不能定量地或半定量地说明配合物的性质。 2、不能解释每个配合物为何都具有自己的特征光 谱，也无法解释过渡金属配离子为何有不同的颜色。
在H2O的影响下， Fe3+
1个4s + 3个4p +2 个4d空轨道→6个sp3d2杂化轨道；
与 6个含孤对电子的H2O形成6个配位键， 形成[Fe(H2O)6] 3+，有5个单电子；外轨型高自旋化合物。
3d5
4s
4p
5d
sp3d2杂化
形成配位键
（2） 内轨配合物
中心原子的次外层(n-1)d 空轨道参与杂化。 中心原子 dsp2（平面四方形）， d2sp3杂化；
4. 八面体型配合物d电子分布
具有 d1 ~d3 构型的中心原子
eg
球形场
t2g 正八面体场
具有d4 ~ d7 构型的中心原子
eg
Δo
t2g
电子成对能P
球形场
正八面体场
当 Δo < P ，电子分占较多的轨道→高自旋配合物。 当 Δo > P，占据能量较低的 t2g 轨道→低自旋配合物。
具有d8 ~ d10 构型的中心原子
杂化类型
配合物的空间构型(p137)、稳定性、配位数、磁 矩
2. 外轨型和内轨配合物
（1） 外轨配合物 中心原子全部用最外层的空轨道
（如 ns，np，nd）进行杂化。
采 用sp， sp3， sp3d2 杂化 配位数 2， 4， 6
例如 [Fe(H2O)6] 3+ 3d54s04p04d0
*基态 Fe3+ 3d 5
（1）配体的性质：光谱化学序列.
弱场I-<Br-<S2-< Cl- < SCN- < F- <S2O32- <OH-≈ONO - < C2O42中等场配体<H2O<NCS- ≈edta 2- <NH3 < NO2-<CN-<CO强场
（2）中心原子： 电荷 正电荷多,分裂能大; 周期 第六周期副族元素>第五周期副族元素 >第四周期副族元素
第二节 配合物的化学键理论 一、配位化合物的价键理论 二、配位化合物的晶体场理论
一、配位化合物的价键理论 1.理论要点
（1）中心原子与配体通过配位键相结合。
有空轨道 孤对电子
(2) 空轨道是杂化轨道。 杂化轨道与配位原子的孤对电子的原子轨道在一定 方向上，以最大重叠方式，形成配位键。
（3）中心原子价层电子构型和配体的种类
CFSE=4E(t2g)+2E(eg) = 4×(-0.4Δo)+2×(0.6Δo) = -0.4Δo
x t2g轨道电子数 y eg轨道电子数 n2 八面体场电子对数 n1 球形场电子对数
球形
E(t2g) = - 0.4Δo
场
E(eg) = 0.6Δo
eg 0.6Δo
Δo 0.4Δo
t2g
正八面体场
如：Fe2+的6个d电子在八面体弱场中P>。，第1,2,3个电子填在
t2g轨道后，第4,5个电子填在eg轨道。第6个电子填充在t2g轨道,成对。 高自旋且有顺磁性。3d 6 ---- (t2g)4 (eg)2
配位数为 4， 6 。
例如[Fe (CN ) 6]4-
当 Fe2+ 在 CN- 影响下，Fe2+ 的5 个 3d 电子挤到
3个 3d 轨道中，采用d2sp3杂化轨道与CN -形成6个配
位键，生成[Fe (CN )
4s
4p
3d电子重排
d2sp3杂化
形成配位键
3d