数学建模第一章作业(章绍辉)

14-15(2)数学建模第一次作业注意事项：提交时间截至3月27日课前，请将电子文档发送至邮箱sxjm@。

两个题目做到一个word文档里，文档和邮件标题均以“学号+姓名”命名。

请注意提交时间(顺序会影响给分结果)。

一、(必做题)ppt的思考题(1)~(4),由学号的后两位除以4的余数来确定；二、(必做题)本文档里的题目1~5，由学号的后两位除以5的余数来确定；三、(选做题)对于“生猪价格下降1%”理解的，0.65(11%)tp=-请根据ppt课件上的过程给出相应的结果(包括图形和灵敏性分析等)。

1油污清理问题一处石油泄漏污染了200英里的太平洋海岸线，所属石油公司被责令在14天内将其清除，预期则要被处以10000美元/天的罚款。

当地的清洁队每周可以清理5英里的海岸线，耗资500美元/天，额外雇佣清洁队则要付每支清洁队18000美元的费用和500美元/天的清洁费用.(1). 为使公司的总支出最低，应该额外雇佣多少支清洁队？采用5步方法，并求出清洁费用。

(2). 讨论清洁队每周清洁海岸线长度的灵敏性。

分别考虑最优的额外雇佣清洁队的数目和公司的总支出。

(3). 讨论罚金数额的灵敏性。

分别考虑公司用来清理漏油的总天数和公司的总支出。

(4). 石油公司认为罚金过高而提出上诉。

假设处以罚金的唯一目的是为了促使石油公司及时清理泄漏的石油，那么罚金的数额是否过高？*(5). (选做题)即使一开始采取围堵措施，海浪仍导致油污以每天0.5英里的速度沿海岸线扩散，这将导致最终清理的海岸线超过200海里，请分析扩散速度对公司总支出的影响。

2报刊价格问题一家有80000订户的地方日报计划提高其订阅价格。

现在的价格为每周1.5美元，据估计如果每提高定价10美分，就会损失5000订户。

(1)采用五步法，求使利润最大的订阅价格(2)对(1)中所得结论讨论损失5000订户这一参数的灵敏性。

分别假设这个参数值为3000，4000，5000，6000或7000，计算最优订阅价格(3)设n=5000为提高定价10美分而损失的订户数，求最优订阅价格p作为n的函数关系。

数学建模章绍辉版作业 Last revised by LE LE in 2021第四章作业第二题：针对严重的交通情况，国家质量监督检验检疫局发布的国家标准，车辆驾驶人员血液中的酒精含量大于或等于20mg/100ml,小于80mg/100ml 为饮酒驾车，血液中的酒精含量大于或等于80mg/100ml 的为醉酒驾车。

下面分别考虑大李在很短时间内和较长时间内（如2个小时）喝了三瓶啤酒，多长时间内驾车就会违反新的国家标准。

1、 问题假设大李在短时间内喝下三瓶啤酒后，酒精先从吸收室（肠胃）吸收进中心室（血液和体液），然后从中心室向体外排除，忽略喝酒的时间，根据生理学知识，假设（1） 吸收室在初始时刻t=0时，酒精量立即为032D;在任意时刻，酒精从吸收室吸收进中心室的速率（吸收室在单位时间内酒精含量的减少量）与吸收室的酒精含量成正比，比例系数为1k ；（2） 中心室的容积V 保持不变；在初始时刻t=0时，中心室的酒精含量为0；在任意时刻，酒精从中心室向体外排除的速率（中心室在单位时间内酒精含量的减少量）与中心室的酒精含量成正比，比例系数为2k ；（3） 在大李适度饮酒没有酒精中毒的前提下，假设1k 和2k 都是常量，与饮酒量无关。

2、 符号说明酒精量是指纯酒精的质量，单位是毫克；酒精含量是指纯酒精的浓度，单位是毫克/百毫升； ~t 时刻（小时）；()~x t 在时刻t 吸收室（肠胃）内的酒精量（毫克）；0~D 两瓶酒的酒精量（毫克）；(t)~c 在时刻t 吸收室（血液和体液）的酒精含量（毫克/百毫升）； 2()~c t 在时刻t 中心室（血液和体液）的酒精含量（毫克/百毫升）；~V 中心室的容积（百毫升）；1~k 酒精从吸收室吸收进中心室的速率系数（假设其为常数）；2~k 酒精从中心室向体外排除的速率系数（假设其为常数）；3~k 在短时间喝下三瓶酒的假设下是指短时间喝下的三瓶酒的酒精总量除以中心室体积，即03/2D V ；而在较长时间内（2小时内）喝下三瓶酒的假设下就特指03/4D V . 3、 模型建立和求解（1） 酒是在很短时间内喝的：记喝酒时刻为0t =（小时），设(0)0c =，可用()2113212()k t k t k k c t e e k k --=--来计算血液中的酒精含量，此时12k k 、为假设中所示的常数，而033155.792D k V ⎛⎫== ⎪⎝⎭.下面用MATLAB 程序画图展示血液中酒精含量随时间变化并且利用fzero 函数和fminbnd 函数来得到饮酒驾车醉酒驾车对应的时间段，以及血液中酒精含量最高的时刻。

数学建模第一次作业院系：机电学院通信工程姓名：严宏海学号：20101003032数学建模习题11用给定的多项式，如y=x3-6x2+5x-3，产生一组数据(xi,yi，i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数)，然后用xi和添加了随机干扰的yi作的3次多项式拟合，与原系数比较。

分别作1、2、4、6次多项式拟合，比较结果，体会欠拟合、过拟合现象。

解：程序如下：x=1:0.5:10;y=x.^3-6*x.^2+5*x-3;y0=y+rand;f1=polyfit(x,y0,1)%输出多项式系数y1=polyval(f1,x);%计算各x点的拟合值plot(x,y,'+',x,y1)grid ontitle('一次拟合曲线');figure(2);f2=polyfit(x,y0,2)%2次多项式拟合y2=polyval(f2,x);plot(x,y,'+',x,y2);grid ontitle('二次拟合曲线');figure(3);f4=polyfit(x,y0,4)%4次多项式拟合y3=polyval(f4,x);plot(x,y,'+',x,y3)grid ontitle('四次拟合曲线');figure(4);f6=polyfit(x,y0,6)%6次多项式拟合y4=polyval(f6,x);plot(x,y,'+',x,y4)grid ontitle('六次拟合曲线');运行结果如下：依次为各个拟合曲线的系数（按降幂排列）f1 =43.2000 -149.0663f2 = 10.5000 -72.3000 89.8087f4 =0.0000 1.0000 -6.0000 5.0000 -2.5913f6 = 0.0000 -0.0000 0.0000 1.0000 -6.0000 5.0000-2.4199运行后，比较拟合后多项式和原式的系数，发现四次多项式系数与原系数比较接近，四次多项式的四次项系数很小。

第五章作业第一题：（1） 第三种边界条件第三种边界条件要求给定三次样条s(x)在区间[x 0,x n ]的左右端点的一阶导数0'(x )S 和'(x )a S 。

我们参考了例5.1.4在210页计算出了左右端点的一阶导数，其中0'(x )S = -3.3667、'(x )a S = 2.3333MATLAB 程序如下：x=[0,1,3,6,8,9];y=[-3.3667,3,1,2,0,2,4,2.33333];pp=csape(x,y,'complete')pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4);d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3);d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2);d3s=@(t,tj,c)6.*c(1).*ones(size(t));for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c);v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c);plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold onendtitle('第三种边界条件及其一、二、三阶导函数的图像')legend('三次样条（第三种边界条件）','样条的一阶导函数','样条的二阶导函数','样条的三阶导函数')plot([0,1,3,6,8,9],[3,1,2,0,2,4],'ko'),hold off运行结果为：pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =-0.0389 1.4056 -3.3667 3.0000-0.3514 1.2890 -0.6722 1.00000.1696 -0.8197 0.2664 2.0000-0.0848 0.7064 -0.0736 00.0678 0.1977 1.7345 2.0000所绘制的图形如下：0123456789第三种边界条件及其一、二、三阶导函数的图像结果说明：计算结果说明该三次样条的分段多项式为： S(x)= 32323232320.0389 1.4056 3.36673,010.3514(x 1) 1.289(x 1)0.6722(x 1)1,130.1696(x 3)0.8197(x 3)0.2664(x 3)2,360.0848(x 6)0.7064(x 6)0.0736(x 6),6x 80.0678(x 8)0.1977(x 8) 1.7345x x x x x x -+-+≤≤--+---+≤≤---+-+≤≤--+---≤≤-+-+(x 8)2,8x 9-+≤≤执行以下命令可以验算该三次样条在区间[0，9]的左端点x=0和右端点x=9的一阶导数分别为-3.3667和2.3333：在MATLAB 的command window 运行：[1.*pp.coefs(1,3),d1s(9,8,pp.coefs(5,:))] 运行结果为：ans =-3.3667 2.3333（2） 第四种边界条件第四种边界条件要求给定三次样条s(x)在区间[x 0,x n ]的左右端点的二阶导数0''(x )s 和''(x )n s 。

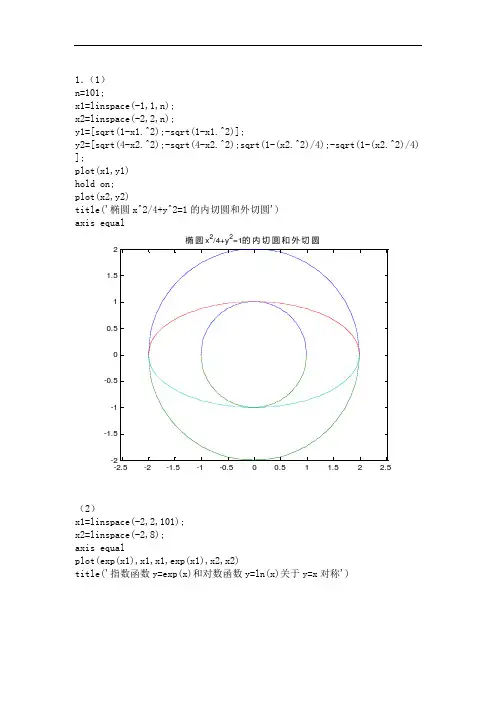
1．（1） n=101;x1=linspace(-1,1,n); x2=linspace(-2,2,n);y1=[sqrt(1-x1.^2);-sqrt(1-x1.^2)];y2=[sqrt(4-x2.^2);-sqrt(4-x2.^2);sqrt(1-(x2.^2)/4);-sqrt(1-(x2.^2)/4)];plot(x1,y1) hold on; plot(x2,y2)title('椭圆x^2/4+y^2=1的内切圆和外切圆') axis equal-2.5-2-1.5-1-0.500.51 1.52 2.5-2-1.5-1-0.500.511.52椭圆x 2/4+y 2=1的内切圆和外切圆（2）x1=linspace(-2,2,101); x2=linspace(-2,8); axis equalplot(exp(x1),x1,x1,exp(x1),x2,x2)title('指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称')-2-112345678-2-1012345678指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称（3） hold onq=input('请输入一个正整数q;') for i=1:q for j=1:i if rem(j,i)plot(j/i,1/i) end end end0.10.20.30.40.50.60.70.80.9100.050.10.150.20.250.30.350.40.450.53．代码如下：n=input('请输入实验次数n=') k=0;for i=1:nx=ceil(rand*6)+ceil(rand*6); if x ==3|x==11 k=k+1; elseif x~=2&x~=7&x~=12y= ceil(rand*6)+ceil(rand*6); while y~=x&y~=7y=ceil(rand*6)+ceil(rand*6); end if y==7k=k+1; end end end从上表可看出打赌者赢的概率大约为。

数学建模章绍辉答案【篇一：第三次数学建模作业】数科院105 刘镜韶 20102201092 数科院105 蔡秋荣 20102201166 数科院104 梁浩坤 201022011004、不妨令第k年取出奖学金后，继续存在银行的捐款余额为xk，且银行的整存整取的利率为r，奖学金的金额为d万元，则由已知可得：xk+1 =（1+r）xk－d 故：其解为数列：xk =(x0-d/r)+d/r,且x0=20万元；①奖学金金额d0.6万元，让存在银行的捐款余额每年逐步增加；②奖学金金额d=0.6万元，让存在银行的捐款余额每年保持不变；③奖学金金额d0.6万元，让存在银行的捐款余额每年逐步减少；故对于不同的情况，不妨通过编程对比xk的变化趋势；程序：n=20;r=[0.03,0.03,0.03];x=[20,20,20];d=[0.45,0.6,0.75]; fork=1:nx(k+1,:)=x(k,:).*(1+r)-d; enddisp(本金为20万时不同的奖学金下余额的变化)disp(年 0.45万元0.6万元0.75万元) disp([(0:n),x]);plot(0:n,x(:,1),k^,0:n,x(:,2),ko,0:n,x(:,3),kv) axis([-1,n+1,14,25]) legend(d=0.45,d=0.6,d=0.75,2)title(本金为20万时不同的奖学金下余额的变化) xlabel(第k年),ylabel(余额) 其命令窗口显示结果为：年 0.45万元0.6万元0.75万元 020.000020.000020.00001.000020.150020.000019.85002.000020.304520.000019.69553.000020.463620.000019.53644.000020.627520.000019.37255.000020.796420.000019.20366.000020.970320.000019.02977.000021.149420.000018.8506 8.000021.333920.000018.66619.000021.523920.000018.4761本金为20万时不同的奖学金下余额的变化10.000021.719620.000018.2804 11.000021.921220.000018.078812.000022.128820.000017.871213.000022.342720.000017.657314.000022.562920.000017.4371 15.000022.789820.000017.210216.000023.023520.000016.976517.000023.264220.000016.735818.000023.512220.000016.4878 19.000023.767520.000016.2325 第k年20.000024.030620.000015.9694当利率r=3%时，且以整存整取一年定期的形式来存入银行时；由上述图像可知：①奖学金金额d≤0.6万元时，可以永久持续下去，实现可持续发展，即用20万元本金所得的利息作为奖学金。