下载文档原格式
基于MATLAB 的信号去噪研究摘要：小波分析理论是一种新兴的信号处理理论，它在时间上和频率上都有很好的局部性，这使得小波分析非常适合于时-频分析，借助时- 频局部分析特性，小波分析理论已经成为信号去噪中的一种重要的工具。
利用小波方法去噪，是小波分析应用于实际的重要方面。
小波去噪的关键是如何选择阈值和如何利用阈值来处理小波系数，通过对小波阈值化去噪的原理介绍,运用MATLAB 中的小波工具箱，对一个含噪信号进行阈值去噪，实例验证理论的实际效果，证实了理论的可靠性。
本文简述了几种小波去噪方法，其中的阈值去噪的方法是一种实现简单、效果较好的小波去噪方法。
关键词：小波变化 滤波 去噪1. 小波去噪原理分析1.1 小波去噪原理叠加性高斯白噪声是最常见的噪声模型[6]，受到叠加性高斯白噪声“污染”的观测信号可以表示为：i i i y f z σ=+ 1,...,i n = (1.1)其中y i 为含噪信号，i f 为“纯净”采样信号，z i 为独立同分布的高斯白噪声~(0,1)iid i z N ，σ为噪声水平，信号长度为n. 为了从含噪信号y i 中还原出真实信号i f ，可以利用信号和噪声在小波变换下的不同的特性，通过对小波分解系数进行处理来达到信号和噪声分离的目的。
在实际工程应用中，有用信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号则通常表现为高频信号，所以我们可以先对含噪信号进行小波分解[7]（如进行三层分解）：321312211CD CD CD CA CD CD CA CD CA S +++=++=+= (1.2)图1.1 三层小波分解示意图其中i cA 为分解的近似部分， 为i cD 分解的细节部分，321,,i =,则噪声部分通常包含在1cD ，2cD ，3cD 中，用门限阈值对小波系数进行处理，重构信号即可达到去噪的目的。
1.2 小波去噪步骤总结去噪过程，可以分成以下三个步骤：1)对观测数据作小波分解变化[8]：z W f W y W 000∙+=σ (1.3)其中y 表示观测数据向量y 1，y 2，…y ，f 是真实信号向量f 1，f 2，…f n ，z 是高斯随机向量z 1，z 2，…z n ，其中用到了小波分解变换是线性变换的性质。
医用电子学论文摘要以小波变换的多分辨率分析为基础, 通过对体表心电信号(ECG) 及其噪声的分析, 对ECG信号中存在的基线漂移、工频干扰及肌电干扰等几种噪声, 设计了不同的小波消噪算法; 并利用MIT/BIH 国际标准数据库中的ECG 信号和程序模拟所产生的ECG 信号, 分别对算法进行了仿真与实验验证。
结果表明, 算法能有效地滤除ECG 信号检测中串入的几类主要噪声, 失真度很小, 可满足临床分析与诊断对ECG 波形的要求。
关键词: ECG 信号, 小波变换, 基线漂移, 工频干扰, 肌电干扰AbstractWe apply the multi-resolution analysis (MRA ) of wavelet transform ( WT ) , which was proposed by Mallat [ 5 ] , to suppress the three main types of noises existing in electrocardiogram ( ECG ) signals : baseline wander, power line interference and electro my ographical interference. We apply Mallat algorithm [ 4 ] to suppress the baseline wander in ECG signals. We apply the sof t-thresholding algorithm, proposed by donohoetal on the basis of MRA of WT , to suppress power line interference in ECG signals. We apply Mallat algorithm and then the algorithm proposed by Donohoetal to suppress the electro my ographical interference in ECG signals ,who sefrequency range varies f rom 5Hz to 2kHz. We performed simulations ,using both ECG signals from MIT/BIH database, and ECG signals generated via computer simulation .The results show that the algorithm can suppress the main no isesexisting in ECG signals efficiently with very little distortion, and can satisfy the requirement s of clinical analysis and diagnosis on ECG waveforms.Key words: ECG (electro cardio gram ) signal, wavelet transform , baseline wander, power line interference , electro my ographical interference目录摘要 (2)Abstract (3)目录 (4)第一章心电信号的噪声特点 (5)第二章小波分析与传统信号处理方法的比较 (5)第三章小波去噪的基本原理 (6)3.1 心电图各波特征 (6)3.2 小波变换 (6)3.3 小波分析去噪原理 (7)第四章小波去噪的基本步骤 (8)4.1 小波变换去噪的流程示意图： (8)4.2 小波除噪的具体步骤： (8)第五章小波去噪中的阈值函数和阈值的选取 (8)5.1 阈值函数 (8)5.2 阈值的选取 (9)第六章小波去噪中小波函数的选择 (10)第七章去噪效果的评价 (10)第八章程序说明及结果显示 (11)8.1 程序说明 (11)8.2 结果展示 (12)总结 (12)第一章心电信号的噪声特点心电图(elect rocardiogram , ECG) 的检测与分析, 是临床了解心脏功能状况、辅助诊断心血管疾病、评估各种治疗方法的重要手段。
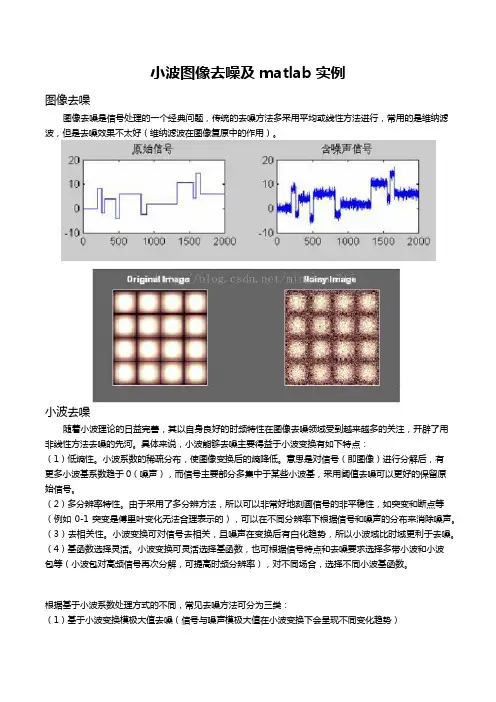
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题，传统的去噪方法多采用平均或线性方法进行，常用的是维纳滤波，但是去噪效果不太好（维纳滤波在图像复原中的作用）。
小波去噪随着小波理论的日益完善，其以自身良好的时频特性在图像去噪领域受到越来越多的关注，开辟了用非线性方法去噪的先河。
具体来说，小波能够去噪主要得益于小波变换有如下特点：（1）低熵性。
小波系数的稀疏分布，使图像变换后的熵降低。
意思是对信号（即图像）进行分解后，有更多小波基系数趋于0（噪声），而信号主要部分多集中于某些小波基，采用阈值去噪可以更好的保留原始信号。
（2）多分辨率特性。
由于采用了多分辨方法，所以可以非常好地刻画信号的非平稳性，如突变和断点等（例如0-1突变是傅里叶变化无法合理表示的），可以在不同分辨率下根据信号和噪声的分布来消除噪声。
（3）去相关性。
小波变换可对信号去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪。
（4）基函数选择灵活。
小波变换可灵活选择基函数，也可根据信号特点和去噪要求选择多带小波和小波包等（小波包对高频信号再次分解，可提高时频分辨率），对不同场合，选择不同小波基函数。
根据基于小波系数处理方式的不同，常见去噪方法可分为三类：（1）基于小波变换模极大值去噪（信号与噪声模极大值在小波变换下会呈现不同变化趋势）（2）基于相邻尺度小波系数相关性去噪（噪声在小波变换的各尺度间无明显相关性，信号则相反）（3）基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法，应用广泛，因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值，设w是小波系数的大小，wλ是施加阈值后小波系数大小，λ为阈值。
（1）硬阈值当小波系数的绝对值小于给定阈值时，令其为0，而大于阈值时，保持其不变，即：（2）软阈值当小波系数的绝对值小于给定阈值时，令其为0，大于阈值时，令其都减去阈值，即：如下图，分别是原始信号，硬阈值处理结果，软阈值处理结果。
基于MATLAB的小波分析在信号消噪中的应用摘要在信号分析与处理中信号去噪是一个常见问题，本文利用MATLAB 软件中的小波分析工具箱实现信号的去噪。
首先利用单尺度小波分解函数分解信号，并去除高频系数，再利用去噪函数处理新信号，获得了良好的去噪效果。
相比于直接利用去噪函数去噪，本文的方法减小了去噪误差，能更好的去除随机噪声。
关键字小波分解；小波重构；信号去噪；MATLAB0 引言1910年，Haar提出了最早的小波规范正交基，但当时并没有出现“小波”这个词。
1981年，Morlet对Fourier变换与加窗Fourier变换的异同、特点及函数构造做了创造性研究，首次提出了“小波分析”的概念，建立了以他的名字命名的Morlet小波，并取得巨大成功。
后来，Mallat于1987年将计算机视觉领域内的多尺度分析思想引入到小波分析中，提出多分辨率分析概念，统一了在此之前的所有正交小波基的构造，并且提出相应的分解与重构快速算法。
由于小波变换具有底熵性、多分辨率、去相关性、选基灵活性等良好特性，使小波变换在工程中得到广泛应用。
1 小波变换原理上式称为小波函数，它是由母小波经过伸缩、平移得到的函数族，可知连续小波变换是一个二元函数，它把一元函数变换成时间和频域平面上的二元函数。
同时由Parseval恒等式易得到小波变换频域的表示：通过上式可知小波变换在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，因此小波变换在时频域都有很强的表征信号局部特征的能力。
基于以上小波变换的优点，因此小波变换在信号的分析与处理中广泛应用。
2 信号去噪信号去噪是信号处理领域的一个常见问题。
传统去噪方法主要是线性滤波和非线性滤波，例如中值滤波和Wiener滤波等。
小波变换具有诸多优点因此也常利用小波变换进行信号的消噪。
MATLAB软件提供了多个阈值去噪函数，本文采用ddencmp函数获取信号去噪阈值，然后采用wdencmp实现信号去噪，并计算消噪误差。
MATLAB小波变换信号去噪引言小波变换是一种多尺度分析方法，广泛应用于信号处理领域。
由于小波变换具有良好的时频局部性质，可以将信号分解为不同频率和时间分辨率的成分，因此被广泛应用于信号去噪领域。
本文将介绍如何使用MATLAB进行小波变换信号去噪的方法。
MATLAB中的小波变换在MATLAB中，可以使用Wavelet Toolbox中的wavedec函数进行小波分解，使用wrcoef函数进行重构。
具体步骤如下：1.导入待处理的信号数据。
2.选择适当的小波基函数和分解层数。
3.使用wavedec函数对信号进行小波分解，得到分解系数。
4.根据阈值方法对分解系数进行去噪处理。
5.使用wrcoef函数对去噪后的分解系数进行重构，得到去噪后的信号。
6.分析去噪效果并进行评估。
下面将逐步详细介绍这些步骤。
选择小波基函数和分解层数小波基函数的选择在小波分析中非常重要，不同的小波基函数适用于不同类型的信号。
常用的小波基函数有Daubechies小波、Haar小波、db2小波等。
根据信号的特点和分析需求，选择合适的小波基函数是非常重要的。
在MATLAB中，可以使用wname函数查看支持的小波基函数。
可以通过比较不同小波基函数的性能指标来选择合适的小波基函数。
常见的性能指标包括频率局部化、时频局部化和误差能量。
选择分解层数时，需要根据信号的特点和噪声的程度来决定。
一般而言，分解层数越高，分解的细节系数越多，信号的时间分辨率越高，但运算量也会增加。
小波分解使用wavedec函数对信号进行小波分解。
函数的输入参数包括待分解的信号、小波基函数名称和分解层数。
函数输出包括近似系数和细节系数。
[C, L] = wavedec(x, level, wname);其中，x是待分解的信号，level是分解层数，wname是小波基函数名称。
C是包含近似系数和细节系数的向量，L是分解的长度信息。
根据分解层数，可以将分解系数划分为不同频带的系数。
完整版)小波变换图像去噪MATLAB实现本论文旨在研究数字图像的滤波去噪问题，以提高图像质量。
数字图像处理(Digital Image Processing。
DIP)是指用计算机辅助技术对图像信号进行处理的过程。
DIP技术在医疗、艺术、军事、航天等图像处理领域都有着十分广泛的应用。
然而，图像的采集、获取、编码和传输的过程中，都存在不同程度被各种噪声所“污染”的现象。
如果图像被污染得比较严重，噪声会变成可见的颗粒形状，导致图像质量的严重下降。
因此，通过一些卓有成效的噪声处理技术后，尽可能地去除图像噪声，有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。
小波变换处理应用于图像去噪外，在其他图像处理领域都有着十分广泛的应用。
小波定义为对给定函数局部化的新领域，小波可由一个定义在有限区域的函数Ψ(x)来构造，Ψ(x)称为母小波，或者叫做基本小波。
一组小波基函数，{Ψa,b(x)}，可以通过缩放和平移基本小波来生成。
当a=2j和b=ia的情况下，一维小波基函数序列定义为Ψi,j(x)=2-j2Ψ2-jx-1.函数f(x)以小波Ψ(x)为基的连续小波变换定义为函数f(x)和Ψa,b(x)的内积。
在频域上有Ψa,b(x)=ae-jωΨ(aω)。
因此，本论文以小波变换作为分析工具处理图像噪声，研究数字图像的滤波去噪问题，以提高图像质量。
当绝对值|a|减小时，小波函数在时域的宽度会减小，但在频域的宽度会增大，同时窗口中心会向|ω|增大的方向移动。
这说明连续小波的局部变化是不同的，高频时分辨率高，低频时分辨率低，这是小波变换相对于___变换的优势之一。
总的来说，小波变换具有更好的时频窗口特性。
噪声是指妨碍人或相关传感器理解或分析图像信息的各种因素。
噪声通常是不可预测的随机信号。
由于噪声在图像输入、采集、处理和输出的各个环节中都会影响，特别是在输入和采集中，噪声会影响整个图像处理过程，因此抑制噪声已成为图像处理中非常重要的一步。
基于小波分析的信号去噪一、实验目的1、掌握小波分析的原理；2、利用小波分析进行信号去噪，并编写Matlab 程序。
二、实验内容1、使用不同小波函数对信号去噪，比较消噪效果；2、采取不同分解层数对信号去噪，比较消噪效果；3、阈值设定方法对信号去噪的影响；三、实验原理小波分析方法是一种窗口大小（即窗口面积）固定但其形状可改变，时间窗和频率窗都可改变的时频局部化分析方法。
即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，所以被誉为数学显微镜。
正是这种特性，使小波变换具有对信号的自适应性。
原则上讲，传统上使用傅里叶分析的地方，都可以用小波分析取代。
小波分析优于傅里叶变换的地方是，它在时域和频域同时具有良好的局部化性质。
小波函数的定义：设()t ψ为平方可积函数，即())(2R L t ∈ψ，若其傅里叶变换()ωψ∧（()ωψ∧是()t ψ的傅里叶变换）满足∞<=⎰∧ωωωψψd C R 2)( 称()t ψ为一个基本小波或母小波（Mother Wavelet ），并称上式为小波函数的允许条件。
与标准的傅立叶变换相比，小波分析中用到的小波函数不具有唯一性，对于一个时频分析问题，如何选者最佳的小波基函数是一个重要的问题。
常用的小波函数有Haar 小波、dbN 小波、Morl 小波、Mexh 小波、Meyer 小波等，不同的小波函数对应不同的尺度函数和性能。
从下图中可以看出小波变换与傅立叶变换在时频窗口特性上有很大的不同，更显示了上述小波变换的特点。
图6-1 小波变换的时频分析窗小波变换的多分辨率分析实际上就是对一个频带信号进行低频分解，对每一步分解出来的低频部分在分解，使频率分辨率越来越高，其目的是构造一个理想的正交小波基。
小波包分析实际上就是对与多分辨率分析没有分解的高频信号也进行逐层分解，进一步提高时频分辨率。
小波分析地这些原理与特点与测控领域中的滤波原理非常相似，常常被用于信号噪声的消除。
基于MATLAB的信号去噪研究信号去噪是信号处理中的重要问题之一，它在许多领域中都扮演着重要的角色，包括通信、图像处理、生物医学工程等。
MATLAB作为一种强大的信号处理工具，提供了很多功能用于信号去噪研究。
首先，我们需要了解什么是信号去噪。
在信号中通常会包含各种噪声，这些噪声会对信号的准确性和可靠性造成影响。
信号去噪的目标是消除或减少这些噪声，以提取出原始信号的有用信息。
MATLAB提供了一系列用于信号去噪的函数和工具箱，其中最常用的是Wavelet工具箱和滤波器设计工具箱。
Wavelet工具箱中提供了多种小波变换及其逆变换函数，用于对信号进行小波变换。
小波变换在信号处理中广泛应用，它能够将信号分解成不同频率的小波系数，并可灵活地选择滤波器的尺度。
通过对小波系数进行去噪处理，可以对信号的高频噪声进行有效地去除，同时保留信号的有用信息。
滤波器设计工具箱提供了多种滤波器设计方法和函数，如低通滤波器、高通滤波器、带通滤波器等。
滤波器可以通过去除信号中的不需要的频率分量来实现去噪的效果。
在设计滤波器时，需要根据信号的特点和噪声的性质选择合适的滤波器类型和参数。
除了上述工具箱之外，MATLAB还提供了一些其他函数和工具用于信号去噪研究。
例如，通过使用统计学方法和自适应滤波算法，可以根据信号的统计特性对噪声进行建模和估计，从而实现去噪的效果。
此外，MATLAB还提供了一些图形界面工具，如信号处理工具箱和机器学习工具箱，可以帮助用户直观地理解信号去噪的过程，并进行参数调整和结果分析。
在信号去噪研究中，除了选择合适的算法和工具之外，数据预处理也是很重要的一步。
信号去噪算法对于输入数据的要求较高，因此在进行信号去噪之前，需要进行数据的预处理，如去除异常值、填充缺失值等。
总结起来，MATLAB提供了丰富的函数和工具用于信号去噪研究，包括小波变换、滤波器设计、统计方法和自适应滤波算法等。
通过使用这些工具，研究者可以选择合适的算法和参数，对信号进行去噪处理，提取出原始信号的有用信息。
基于MATLAB小波去噪方法及应用研究
摘要：在实际的计算机控制系统中，采样信号不可避免的受到各种噪声和干扰的污染，使得由采样信号辨识得到的系统模型存在偏差妨碍了系统控制精度的提高。
donoho和johnstone提出的小波去噪算法对去除高斯白噪声非常有效。
我们对此在matlab环境下做了详尽的探讨及仿真实验研究，得到一些实际应用经验，并利用傅立叶变换/反变换和小波阈值去噪方法对电厂机组调速级压力运行数据进行了去噪对比实验，结果表明小波去噪方法能取得较好的去噪效果，为后续系统模型辨识打下良好的基础。
关键词：小波分析滤波信号去噪小波去噪
中图分类号：tp301.6 文献标识码：a 文章编号：
1007-9416(2012)08-0051-03。
南京师范大学物理科学与技术学院医用电子学论文论文名称：基于小波变换的心电信号噪声消除院系：物科院专业：电路与系统*名：***学号： *********指导教师：***摘要以小波变换的多分辨率分析为基础, 通过对体表心电信号(ECG) 及其噪声的分析, 对ECG信号中存在的基线漂移、工频干扰及肌电干扰等几种噪声, 设计了不同的小波消噪算法; 并利用MIT/BIH 国际标准数据库中的ECG 信号和程序模拟所产生的ECG 信号, 分别对算法进行了仿真与实验验证。
结果表明, 算法能有效地滤除ECG 信号检测中串入的几类主要噪声, 失真度很小, 可满足临床分析与诊断对ECG 波形的要求。
关键词: ECG 信号, 小波变换, 基线漂移, 工频干扰, 肌电干扰AbstractWe apply the multi-resolution analysis (MRA ) of wavelet transform ( WT ) , which was proposed by Mallat [ 5 ] , to suppress the three main types of noises existing in electrocardiogram ( ECG ) signals : baseline wander, power line interference and electro my ographical interference. We apply Mallat algorithm [ 4 ] to suppress the baseline wander in ECG signals. We apply the sof t-thresholding algorithm, proposed by donohoetal on the basis of MRA of WT , to suppress power line interference in ECG signals. We apply Mallat algorithm and then the algorithm proposed by Donohoetal to suppress the electro my ographical interference in ECG signals ,who sefrequency range varies f rom 5Hz to 2kHz. We performed simulations ,using both ECG signals from MIT/BIH database, and ECG signals generated via computer simulation .The results show that the algorithm can suppress the main no isesexisting in ECG signals efficiently with very little distortion, and can satisfy the requirement s of clinical analysis and diagnosis on ECG waveforms.Key words: ECG (electro cardio gram ) signal, wavelet transform , baseline wander, power line interference , electro my ographical interference目录摘要 (2)Abstract (3)目录 (4)第一章心电信号的噪声特点 (5)第二章小波分析与传统信号处理方法的比较 (5)第三章小波去噪的基本原理 (6)3.1 心电图各波特征 (6)3.2 小波变换 (6)3.3 小波分析去噪原理 (7)第四章小波去噪的基本步骤 (8)4.1 小波变换去噪的流程示意图： (8)4.2 小波除噪的具体步骤： (8)第五章小波去噪中的阈值函数和阈值的选取 (8)5.1 阈值函数 (8)5.2 阈值的选取 (9)第六章小波去噪中小波函数的选择 (10)第七章去噪效果的评价 (10)第八章程序说明及结果显示 (11)8.1 程序说明 (11)8.2 结果展示 (12)总结 (12)第一章心电信号的噪声特点心电图(elect rocardiogram , ECG) 的检测与分析, 是临床了解心脏功能状况、辅助诊断心血管疾病、评估各种治疗方法的重要手段。
而体表心电信号具有较强的随机性和背景噪声, 是一种非线性、非平稳的微弱信号。
常规心电信号是mV 级信号, 频带范围是0. 05～ 100 Hz。
心电信号的噪声主要有3 类: ①工频干扰: 它是由供电网络及其设备产生的空间电磁干扰在人体的反映, 由50 Hz 及其谐波构成; ②基线漂移: 它是由测量电极的接触不良、呼吸等引起的低频干扰信号; ③肌电干扰: 它是由于人体运动、肌肉收缩而引起的, 频率在5～ 2 000 Hz 之间[1 ]。
这些噪声干扰与心电信号混杂,引起心电信号的畸变,使整个心电信号波形模糊不清,对随后的信号分析处理,尤其是计算机自动识别诊断造成误判和漏判,因此,心电信号的消噪有重要的意义。
心电信号采集过程中还有许多其它的随机噪声和环境干扰影响，如加性白噪声、极化噪声、仪器内部噪声等等。
在心电信号的干扰噪声中，0．3 Hz以下的基线漂移和肌电干扰噪声是最重要的干扰源，是心电信号处理中必须消除或抑制的噪声成分。
为了正确进行心电参数测量、波形识别和病情诊断，在低信噪微弱信号检测中必须采用抑制噪声的处理技术，提高信噪比，有利于消除心电信号的干扰传统消除干扰的算法有：FIR数字滤波、Fourier变换、基线拟合等，这些算法均存在一定的不足。
传统的信号消噪方法在处理短时低能量的瞬变信号时，经过滤波器的平滑处理，不仅信噪比得不到较大的改善，而且信号的特征信息也被模糊掉了，而这些瞬变点的位置正是心电信号最重要的信息。
由于小波分析具有良好的时频分辨特性，已成功应用于信号处理、图像处理等许多领域。
第二章小波分析与传统信号处理方法的比较处理医学信号的常用方法是以傅氏变换理论为基础的信号分析技术, 但傅氏变换存在2 个缺陷: ①它是一种纯频域变换, 只反映信号的总体谱, 而不能反映信号的局部特性; ②是当时间函数出现异常情况, 反映为一系列不连续点时, 傅立叶变换不具备奇性反演性质, 因此不能在这些有特殊意义的点上进行局布分析。
小波变换是20 世纪80 年代发展起来的一种良好的时频定位方法。
它在低频部分具有较高的频率分辨率和较低的时间分辨率, 在高频部分具有较高的时间分辨率和较低的频率分辨率。
小波分析的这些特性比较适合于处理心电信号。
第三章小波去噪的基本原理3.1 心电图各波特征一个典型的心电波形由P波、QRS波群、T波等组成，有时可看到后继的U波。
在正常情况下，这些子波按照窦房结产生的兴奋脉冲的周期而进行周期性的重复。
对于具体每个子波，都对应着心脏活动与电生理的特定阶段。
心电图诊断就是根据这几个波形的幅度大小和间隔时间来进行诊断。
连接两组波群之间的直线是心电图的基线即等电位线，如PR段和ST段，反映此时各部分心肌细胞的电位相等，体表电极上无电位差。
在心电图的临床实践中，人们积累了丰富的有关正常心电图各波段和间期正常值的数据，它们是判断病理心电图的基础。
不同波段的频率特征是不同的，各波表示的意义也不同。
3.2 小波变换小波分析方法是新出现的信号时频分析方法，具有多分辨率的特点，能够较好的处理心电信号等非平稳信号。
目前小波去噪的方法主要有小波阈值去噪和模极大值去噪。
其中模极大值法运算量大，收敛较慢。
非线性阂值法计算量小，在保持信号的奇异性的同时能够有效的去除噪声，具有广泛的适应性f4]。
因此本文利用小波阈值去噪方法，灵活利用不同的阈值函数并采用自适应阈值对心电信号进行去噪处理。
非线性阂值法即在众多的小波系数中，把绝对值较小的系数置0，而让绝对值较大的系数保留或收缩。
这样得到估计小波系数，然后利用估计小波系数直接进行信号重构，从而达到去噪的效果。
其主要分为以下三个步骤：①选取合适的小波函数对原始信号进行N 层小波分解，获得各尺度上的细节分量和近似分量。
②对l 到N 尺度上的每层细节分量选取合适的阂值，进行阈值量化处理，得到新的小波系数。
③根据小波分解的第N 层近似分量和经阂值量化处理后的第1到N 层细节分量，重构得到去噪的信号。
3.3 小波分析去噪原理在实际工程应用中，通常所分析的信号具有非线性，非平稳,并且奇异点较多的特点。
含噪的一维信号模型可表示为：其中，f(t)为真实信号，s(t)为含噪信号，e(t)为噪声， σ 为噪声标准偏差。
有用信号通常表现为低频信号或是相对比较平稳。
而噪声信号通常表现为高频信号。
利用小波对含噪的原始信号分解后，含噪部分主要集中在高频小波系数中，并且，包含有用信号的小波系数幅值较大，但数目少；而噪声对应的小波系数幅值小，数目较多。
基于上述特点，可以应用门限阈值法对小波系数进行处理。
（即对较小的小波系数置为０，较大的保留或削弱），然后对信号重构即可达到消噪的目的。
小波分解示意图：图一：小波分解示意图 )(*)()(t e t f t s σ+=1_,,1,0n t =第四章 小波去噪的基本步骤4.1 小波变换去噪的流程示意图：图二：小波去噪流程图4.2 小波除噪的具体步骤：(1) 对含噪信号进行预处理,并进行小波分解。
选择小波确定分解的层数N,然后对信号s 进行N 层分解。
(2) 小波分解的高频系数的阈值量化。
对第一层到第N 层高频系数，选择软阈值或硬阈值量化处理。
(3) 一维小波重构。
根据小波分解的第N 层低频系数和第一层到第N 层的高频系数，进行一维重构。
在上面的步骤中，最为关键的就是如何选取阈值和如何阈值量化，从某种意义上讲，它直接影响信号去噪的质量。
第五章 小波去噪中的阈值函数和阈值的选取5.1 阈值函数阈值函数分为软阈值和硬阈值两种。
(1).硬阈值(hard threshol ding)当小波系数的绝对值大于等于给定阈值时，保持不变，而小于时，令其为0。
即：为阈值。
阈值后的小波系数，为小波系数，设λλw w(2).软阈值(soft threshol ding)当小波系数的绝对值大于等于给定的阈值时，令其值为减去阈值；而小于时，令其为0．即：采用这种阈值方法去噪在实际应用中，已取得了较好的效果，但也存在着一些潜在的缺点，如硬阈值在阈值点不连续，重构可能产生一些震荡；软阈值连续，但估计的小波系数和分解的小波系数有恒定的偏差，直接影响重构信号对真实信号的逼近程度．5.2 阈值的选取阈值的选择是小波去噪和收缩最关键的一步，在去噪过程中阈值起着决定性的作用：如果太小，施加阈值后小波系数包含太多的噪声分量，达不到去噪效果；反之，则去除了有用部分，使信号失真。
