4-2 力矩 转动定律 转动惯量
- 格式:pdf
- 大小:595.99 KB
- 文档页数:21















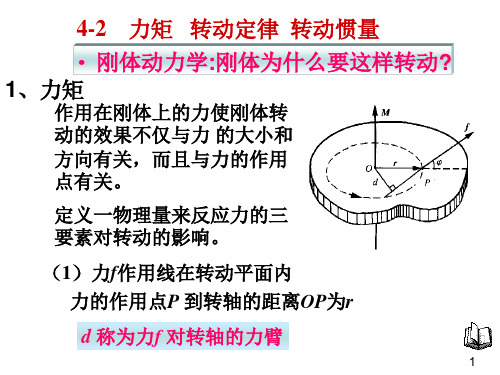
4 – 2 力矩 转动定律 转动惯量 一 力矩 v 刚体绕 O z 轴旋转 , 力 F 作用在刚体上点 P , 且在转动 v 为由点O 到力的 平面内, r 作用点 P 的径矢 . v Z F 对转轴v 的力矩 v第四章 刚体的转动v MMOv v ∑ Fi = 0 , ∑ M i = 0d v −FM = Fr sin θ = Fd: 力臂v M = r ×Fzvv rv F*dPθv Fv v ∑ Fi = 0 , ∑ M i ≠ 0v −Fv F4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动讨论 v 1)若力 F 不在转动平面内,把力分解为平行和垂 直于转轴方向的两个分量 其中 Fz r 对转轴的力 矩为零,故 F 对转轴的 力矩 v v vv v v F = Fz + F⊥ rzv v k Fzv Fθv F⊥M z k = r × F⊥ M z = rF⊥ sin θOv r2)合力矩等于各分力矩的矢量和v v v v M = M1 + M 2 + M3 + L4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动3) 刚体内作用力和反作用力的力矩互相抵消v MijOv rjv Mjidv iF ri ijj v Fji vv v M ij = −M ji4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动例1 有一大型水坝高110 m、长1000m,水深 100m,水面与大坝表面垂直,如图所示 . 求作用在大坝 上的力,以及这个力对通过大坝基点 Q 且与 x 轴平行的 力矩 . y ydAxh y O Q Odyx解 设水深h,坝长L,在坝面上取面积元 dA = Ldy 作用在此面积元上的力dF = pdA = pLdy4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动h = 100mL = 1000mydAdydF = pdA = pLdy令大气压为p0 ,则h y Op = p0 + ρg (h − y )dF = [ p0 + ρg (h − y )]Ldyhx1 2 F = ∫ [ p0 + ρg ( h − y )] L dy = p0 Lh + ρgLh 0 2代入数据,得F = 5.91× 10 N104 – 2 力矩 转动定律 转动惯量第四章 刚体的转动L = 1000m dF = [ p0 + ρg (h − y )]Ldy v dF 对通过点 Q 的轴的力矩 dM = ydFh = 100mhyhv dFdyy O Qd M = y[ p 0 + ρ g ( h − y )] L d yM = ∫ y[ p0 + ρg ( h − y )]Ldy01 1 2 3 = p0 Lh + gρLh 2 6 12 M = 2.14×10 N ⋅ m 代入数据,得4 – 2 力矩 转动定律 转动惯量 二 转动定律 1)单个质点 m 与转 轴刚性连接第四章 刚体的转动Ft = mat = mrα M = rF sin θ 2 M = rFt = mr α 2 M = mr αv MOzv rv v Ft Fm vθFnv v 质量元受外力 F ,内力 F ej ij 2 M ej + M ij = ∆m j rj α外力矩 内力矩2)刚体zOv rjv Fej∆mjv Fij4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动M ej + ∑ M ij = ∑ ∆ m j r j2α ∑j jzOQ Mij = −M ji∴∑ Mij = 0jv rjv Fej∆mj∑Mjej= ( ∑ ∆ m j r )α2 jv FijJ = ∫ r dm2定义转动惯量 转动定律J = ∑ ∆m rj2 j jM = Jα刚体定轴转动的角加速度与它所受的合外力矩成 正比 ,与刚体的转动惯量成反比 .4 – 2 力矩 转动定律 转动惯量 三 转动惯量2 j j j第四章 刚体的转动2J = ∑ ∆m r , J = ∫ r dm物理意义:转动惯性的量度 . 转动惯性的计算方法 质量离散分布刚体的转动惯量J = ∑ ∆m r = m r + m r + L2 j j 2 11 2 2 2 j质量连续分布刚体的转动惯量J = ∑∆m r = ∫ r dm2 j j 2 jdm:质量元4 – 2 力矩 转动定律 转动惯量 质量连续分布刚体的转动惯量第四章 刚体的转动J = ∑∆m r = ∫ r dm2 j j 2 jdm:质量元对质量线分布的刚体: dmλ= λdl:质量线密度对质量面分布的刚体: dmσ :质量面密度ρ:质量体密度= σdS= ρdV对质量体分布的刚体:dm第四章 刚体的转动 4 – 2 力矩 转动定律 转动惯量 例2 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 .O−l 2Ol 2rdrdr O´O´l解 设棒的线密度为 λ ,取一距离转轴 OO´ 为 处的质量元 dm = λdr dJ = r 2 dm = λr 2 drr1 3 J = 2λ ∫ r dr = λl 0 12 1 = ml 2 12l/2 2如转轴过端点垂直于棒1 2 J = λ ∫ r dr = ml 0 3l 24 – 2 力矩 转动定律 转动惯量第四章 刚体的转动解 设圆盘面密度为 σ , 在盘上取半径为 ,宽为 dr 的圆环例3 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .r圆环质量dm = σ 2π rdr2 3R ROr dr圆环对轴的转动惯量dJ = r dm = 2π σ r dr R σ 3 4 J = ∫ 2π σ r dr = π R 02而σ =m π R2所以1 2 J = mR 24 – 2 力矩 转动定律 转动惯量 注意第四章 刚体的转动转动惯量的大小取决于刚体的质量、形 状及转轴的位置 . 四 平行轴定理 质量为 m 的刚体,如果对 其质心轴的转动惯量为 J C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量dCmOJ O = J C + md21 2 圆盘对P 轴 J P = mR + mR2 的转动惯量 2PR O m4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动飞轮的质量为什么 大都分布于外轮缘?竿 子 长 些 还 是 短 些 较 安 全4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动例4 质量为 mA 的物体 A 静止在光滑水平面 上,和一质量不计的绳索相连接,绳索跨过一半径为 mB R、质量为 的圆柱形滑轮 C,并系在另一质量为 mC 的物体 B 上. 滑轮与绳索间没有滑动, 且滑轮与轴承间 的摩擦力可略去不计. 问:(1) 两物体的线加速度为多 少? 水平和竖直两段绳索的张力各为多少?(2) 物体 B从 静止落下距离 y 时, C A mA 其速率是多少?(3) mC 若滑轮与轴承间的摩 擦力不能忽略,并设 它们间的摩擦力矩为 M f 再求线加速度及 mB B 绳的张力.第四章 刚体的转动 4 – 2 力矩 转动定律 转动惯量 v A 解 (1)隔离物体分 FT1 C mA mC 别对物体A、B 及滑轮作 v 受力分析,取坐标如图, v FN v ′ FT2 运用牛顿第二定律 、转 mA FT1 动定律列方程 . v O mB B xPAv ′ FT1v PCv FCv ′ FT2mB v PB yOFT1 = mA amB g − FT2 = mB aRFT2 − RFT1 = Jαv FT2a = Rα4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动mB g a= mA + mB + mC 2 mA mB g FT1 = mA + mB + mC 2A mAv FT1CmC v ′ FT2( m A + mC 2 ) m B g FT2 = mA + mB + mC 2如令 mCmB BmA mB g FT1 = FT2 = mA + mB= 0,可得(2) B由静止出发作匀加速直线运动,下落的速率v = 2 ay =2 mB gy m A + m B + mC / 24 – 2 力矩 转动定律 转动惯量 (3) 考虑滑轮与轴承间的摩 擦力矩 M f ,转动定律第四章 刚体的转动v ′ FT1MfRFT2 − RFT1 − M f = Jα结合(1)中其它方程v FT2v FNFT1 = mA amB g − FT2 = mB av ′ FT2mBv PBRFT2 − RFT1 − M f = Jαa = RαmA v FT1 v PA4 – 2 力矩 转动定律 转动惯量第四章 刚体的转动FT1 = mA amB g − FT2 = mB aRFT2 − RFT1 − M f = JαA mAv FT1CmC v ′ FT2a = Rα mB g − M f R a= mA + mB + mC / 2mB BmA (mB g − M f / R) FT1 = mA + mB + mC / 2mB [(mA + mC 2) g + M f R] FT2 = mA + mB + mC 24 – 2 力矩 转动定律 转动惯量第四章 刚体的转动例5 一长为 l 质量为 m 匀质细杆竖直放置,其 下端与一固定铰链 O 相接,并可绕其转动 . 由于此竖 直放置的细杆处于非稳定平衡状态,当其受到微小扰 动时,细杆将在重力作用下由静止开始绕铰链O 转动 . 试计算细杆转动到与竖直线成 θ 角时的角加速度和角 速度 .v 铰链对细杆的约束力 F N作用,由转动定律得解 细杆受重力和1 mgl sin θ = Jα 24 – 2 力矩 转动定律 转动惯量第四章 刚体的转动1 mgl sin θ = Jα 2 1 2 式中 J = ml 3 3g α = sin θ 得 2l由角加速度的定义dω dω dθ dω = =ω α= dt dθ d t dθ代入初始条件积分 得3g ω dω = sin θ d θ 2l3g ω= (1− cosθ ) l。