2.1负数的引入 课件2(北京课改版七年级上)

1.1负数的引入一、教学目标1、能判断一个数是正数还是负数，能用正数或负数表示生活中具有相反意义的量．2、借助生活中的实例理解有理数的意义，体会负数引入的必要性和有理数应用的广泛性．3、培养学生积极思考，合作交流的意识和能力． 二、课时安排：1课时三、教学重点：正、负数的概念及有理数的分类． 四、教学难点：正、负数的概念及有理数的分类． 五、教学过程 （一）导入新课在数学课中我们曾经学习了自然数(如0,1,2,3，…)和分数(如 ,47,2311,53)，我们还学习了小(2.84,0.333…,0.056，…)，而且我们知道，小数只是分数的另一种形式.下面我们接着学习其他的数.（二）讲授新课 交流：1、你能举出生活中“用自然数或分数表示量的多少”的例子吗？2、你了解“光年”和“纳米”的意义吗？请设法查阅资料，了解这两个词的意义，说说1光年和1纳米的大小.你还能举出一些例子吗？ 交流：1、在我们的身边，你见到过“负数”吗？在哪里见到过？2、你怎样理解“负数”的意义？在什么情况下要用“负数”？ÊýµÄ²úÉúºÍ·¢Õ¹Àë²»¿ªÉú»îºÍÉú²úµÄÐèÒª£®ÓɼÇÊý¡¢ÅÐò£¬²úÉúÊý1£¬2£¬3£¬…Óɱíʾ“ûÓД“¿Õ딣¬²úÉúÊý0ÓÉ·ÖÎï¡¢²âÁ¿£¬²úÉú·ÖÊý£¬£¬…2131在足球比赛中，某足球队的净胜球数是“-3”(读作“负3”)；龙庆峡冰雪节时，某天的气温是“-12℃”；某精密仪器上的钛金属零件的误差一般要控制在“±0.02mm”(也就是+0.02mm 和-0.02mm)以内……可见，像“-3”，“-12”，“-0.02”，…这样的“负数”已经在我们的生活中被广泛应用了.你还能举出一些例子吗？实际上，“负数”也是用来表示一类量的多少的.这类量都有这样的共同特征：一定存在着和它们意义相反的量.例如：“净胜球数是-3”，表示的是“输了3个球”.在这里，“负数”描述的是“输球数”的多少，而“输球数”是和“赢球数”意义相反的量.思考：1、“-12℃”、“-0.02mm”也有类似的情况吗？怎样说明它们的意义？2、请举出你所了解的其他的例子来说明这种情况. （三）重难点精讲除0以外的自然数和分数，我们称它们为正整数和正分数，统称正数.为了进一步强调它们是正数，还可以在它们的前面加上一个正号“+”， 如+1，+3，+76，+3.56，+0.08， ,713,53++，“＋”号可以省略；和它们意义相反的量就用“负数”来表示，这时，在0除以外的自然数和分数的前面加上一个负号“-”，得到的数叫做负数.如－2，-7，-4.76，-0.045, ,637,95--“-”号不能省略. 我们规定：0既不是正数，也不是负数.一个数前面的“+”、“-”号叫做它的符号.“－”号读作“负”，如：“－５”读作“负５”；“＋”号读作“正”，如：“＋３”读作“正３”；“＋”号可以省略.我们原来认为，“0”表示是“没有”.在我们引入了“负数”以后，它是否又有了新的意义？这种新的意义是什么？当仓库中最后一台洗衣机运出后，仓库中洗衣机的库存量记作“0”，这时，它表示“没有”.但是当我们说“气温达到0℃时，水将结成冰”，却决不意味着那时“没有温度”，只是说那时温度恰好处于“正”、“负”之间.这说明，在引入了负数以后，“0”还表示“+”与“-”之间的分界点.你能举出其他的用“0”表示正负之间的分界点的例子吗？ 交流：1、你学过哪些数，这些数可以怎样分类？2、各类数之间有怎样的包含关系？事实上，我们知道的数可以分为整数(包括正整数、零和负整数)和分数(包括正分数和负分数)两大类.整数和分数合并在一起，统称有理数.下面介绍一种有理数的分类方法：⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 你还有其他的分类方法吗？ 典例：例1、读下列各数，指出下列各数中的正数、负数： ＋７、－９、4/3、－４.5、998.解：+7、4/3、988是正数，-9、-4.5 是负数. 跟踪训练：指出下列各数中的正数、负数：.0,109,998,5.4,31,9,7---+解：998,31,7-+是正数，109,5.4,9---是负数． 典例：例2、把下列给数填在相应的大括号里: -4,0.001,0,-1.7,15,+1.5. 正数集合｛0.001，15，+1.5…｝ 负数集合｛-4，-1.7…｝ 正整数集合｛15…｝分数集合｛0.001，-1.7，+1.5…｝ 跟踪训练：把下列各数填入相应的集合内：.18-2009135%10,67,01.0,25.1,413,101,0,31,6,9.99，，，-+-+---整数集合:{ 18,2009,67,101,0,6+-…}分数集合:{ 135%10,01.0,25.1,413,31,9.99，--+--…}正数集合:{ 2009135,67,01.0,413,6，++…}负数集合:{ 18-%10,25.1,101,31,9.99，-----…}典例：例3、如果80m 表示向东走80m ，那么-60m 表示向西走60m. 跟踪训练：1、如果水位升高3m 时水位变化记作+3m ，那么水位下降3m 时的水位变化记作 -3 m.2、月球表面的白天平均温度是零上126℃，记作 +126 ℃，夜间平均温度是零下150℃，记作 -150 ℃.（四）归纳小结通过这节课的学习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家． （五）随堂检测1、把下列各数填入相应的集合内：31215,7.25,,0,,0.32,452+--+-．正数集合：｛32.0,512,5++…｝； 负数集合：｛21,43,25.7---…｝． 2、填空：（1）如果买入100kg 大米记为＋100 kg ，那么卖出220kg 大米可记作-220千克； （2）如果－10元表示支出10元，那么＋100元表示收入100元；（3）太平洋最深处的马里亚纳海沟低于海平面11034 m ，它的海拔高度可表示为-11034m ． 六、板书设计七、作业布置课本P14 习题 1、2、3 八、教学反思。

第一章 有理数一 对有理数的认识1.1 负数的引入基础过关全练知识点1 正数和负数的意义、概念及表示 1.下列选项中具有相反意义的量是( ) A.气温上升5 ℃和零下5 ℃ B.走了100米和跑了100米 C.长大2岁和减少5千克D.顺时针旋转4圈和逆时针旋转3圈2.如果规定向东为正,向西为负,那么小明走-30米表示( ) A.小明向东走30米 B.小明向西走30米 C.小明向南走30米 D.小明向北走30米3.(2021四川乐山中考)如果规定收入为正,支出为负,且收入2元记作+2元,那么支出5元记作( ) A.5元 B.-5元C.-3元D.7元4.(2022北京十五中期中)下列各数-5、+3、-0.2、12、0、-35、-11、2.4中,负数的个数是( )A.3B.4C.5D.65.(2022北京二中期末)在一次立定跳远测试中,合格的标准是2.00 m,小明跳了2.12 m,记为+0.12 m;小敏跳了1.96 m,记为 m. 6.在7,-32,0.1,3,-2,17中,正数是 .知识点2 对0的认识7.下列关于“0”的叙述,不正确的是( ) A.0是正数与负数的分界 B.0既不是正数,也不是负数 C.0只表示没有D.0常用来表示某种量的基准8.某水库的正常水位是20米,比正常水位高记为正,比正常水位低记为负.下表是该水库今年某周的水位记录情况: 星期 一 二 三 四 五 六 日 水位变化/米+1.5-3+2.5-1.5-0.5+2.4结合表格,下列说法正确的是( ) A.本周二的水位是0米 B.本周的最高水位是2.5米 C.本周的最低水位是3米D.本周的最高水位比最低水位高5.5米 知识点3 有理数的概念及分类 9. 下列四个数中，是正整数的是( ) A.-1 B.0 C.12 D.110.（2020北京人大附中月考）下列几种说法中，正确的是（）A.有理数分为正有理数和负有理数B.整数和分数统称为有理数C.0不是有理数D.负有理数就是负整数11.（2022福建福州期中）0、-1.5、-2、3这四个数中，属于负分数的是.12.把下列各数填在相应的大括号内：-0.1，-9，5，0，+16.71，2 022，12，4，-26，-3.8，6%.-173负整数：{ …}；正有理数：{ …}；分数：{ …}.能力提升全练13.(2021山东济宁中考,1,)若盈余2万元记作+2万元,则-2万元表示()A.盈余2万元B.亏损2万元C.亏损-2万元D.不盈余也不亏损,0,1,-9四个数中,负数是()14.(2019浙江衢州中考,1,)在12A.1B.0C.1D.-9215.(2022北京师大附中期中,1,)如图是加工零件的尺寸要求,现有下列尺寸的产品(单位:mm),其中不合格的是()A.ϕ45.02B.ϕ44.9C.ϕ44.98D.ϕ45.0116.(2020湖北宜昌中考,12,)向指定方向变化用正数表示,向指定方向的相反方向变化用负数表示,“体重减少 1.5 kg”换一种说法可以叙述为“体重增加kg”.17.(2022广东东莞高埗弘正学校期中,17,)下列说法:①负分数一定是负有理数;②自然数一定是正数;③3.2是整数;④0是整数;⑤一个有理数,它不是整数就是分数,其中正确的是.(填序号)18.(2022四川绵阳期末,22,)某校七年级共有9个班级,若以每班50人为标准,超过的人数记为正数,不足的人数记为负数,则1班至9班的人数分别记为-4,-2,+3,+1,-3,-1,+2,-2,-3.(1)该校七年级一共有多少名学生?(2)若该校七年级学生平均每人为某山区学校捐款15元,求七年级学生一共捐款多少元,人数最多的班级比人数最少的班级多捐多少元.素养探究全练19.[推理能力]将一列有理数按如图所示的方式排列.回答下列问题:(1)在A处的数是正数还是负数?(2)负数排在A,B,C,D中的什么位置?(3)第2 022个数是正数还是负数?排在对应于A,B,C,D中的什么位置?答案全解全析基础过关全练1.D气温上升5 ℃和下降5 ℃是具有相反意义的量,故选项A不合题意;走了100米和跑了100米不是具有相反意义的量,故选项B不合题意;长大2岁和减少5千克并无关联,不是具有相反意义的量,故选项C 不合题意;顺时针旋转4圈和逆时针旋转3圈是一对具有相反意义的量,故选项D符合题意.故选D.2.B因为规定向东为正,向西为负,所以小明走-30米表示小明向西走30米.故选B.3.B因为规定收入为正,支出为负,且收入2元记作+2元,所以支出5元记作-5元.故选B.4.B负数有-5、-0.2、-3、-11,共4个.故选B.55.-0.04解析小敏跳了1.96 m,比标准少0.04 m,应记作-0.04 m.6.7,0.1,3,17都是正数.故填解析正数包括正整数和正分数,因此7,0.1,3,17.7,0.1,3,177.C0不仅仅表示没有,0还表示正数与负数的分界,0常用来表示某种量的基准,0既不是正数,也不是负数,故A、B、D正确,C不正确.故选C.8.D本周二的水位是20米,本周的最高水位为20+2.5=22.5(米),最低水位为20-3=17(米),本周的最高水位比最低水位高22.5-17=5.5(米),故选D.9.D-1是负整数;0是整数,但不是正整数;12是分数,不是整数;1是正整数.故选D.10.B有理数分为正有理数、负有理数和0,故A选项错误;整数和分数统称为有理数,故B选项正确;0是有理数,故C选项错误;负有理数包括负整数和负分数,故D选项错误.故选B.11.-1.5解析属于负分数的是-1.5.故填-1.5.12.负整数:{-9,-26,…}.正有理数:{512,+16.71,2022,4,6%,…}.分数:{-0.1,512,+16.71,-173,-3.8,6%,…}.能力提升全练13.B-2万元表示亏损2万元,故选B.14.D12和1是正数,0既不是正数也不是负数,-9是负数,故选D. 15.B根据题图中的数据可知,零件的直径最大为45+0.03=45.03(mm),最小为45-0.04=44.96(mm),而44.9不在该范围之内,不合格,故选B. 16.-1.5解析“体重减少1.5 kg”换一种说法可以叙述为“体重增加-1.5 kg”.故填-1.5.17.①④⑤解析小于零的有理数是负有理数,因此负分数一定是负有理数,故①正确;自然数包括0和正整数,故②错误;3.2是小数,0是整数,故③错误,④正确;整数和分数统称为有理数,因此一个有理数,它不是整数就是分数,故⑤正确.故正确的是①④⑤.18. 解析(1)根据题意可知:1班至9班的人数分别为46,48,53,51,47,49,52,48,47,∴共有46+48+53+51+47+49+52+48+47=441(名).答:该校七年级共有441名学生.(2)15×441=6 615(元).∵人数最多的班级有53名学生,人数最少的班级有46名学生,∴两个班相差53-46=7名学生,∴7×15=105(元).答:七年级学生一共捐款6 615元,人数最多的班级比人数最少的班级多捐105元.素养探究全练19. 解析通过观察发现,向上或向下的箭头所指的数是正数,向右的箭头所指的数是负数.(1)A处的数是正数.(2)负数排在B和D的位置.(3)因为2 022÷4=505……2,所以第2 022个数排在C的位置,是正数.。

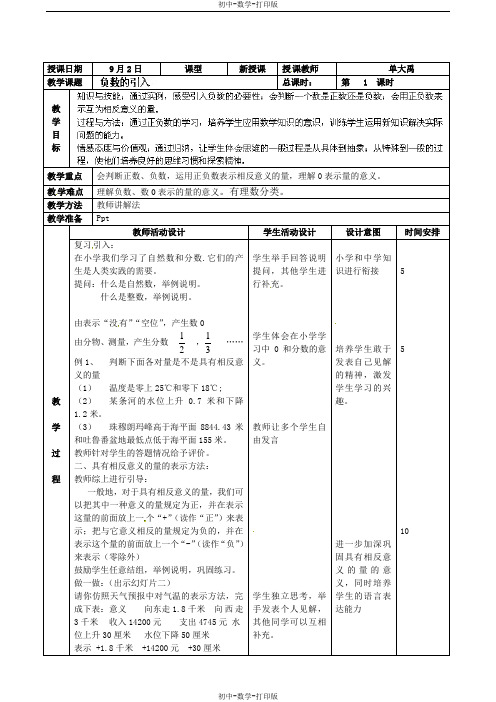
授课日期9月2日课型新授课授课教师单大禹教学课题总课时：第 1 课时教学目标教学重点会判断正数、负数，运用正负数表示相反意义的量，理解0表示量的意义。

教学难点理解负数、数0表示的量的意义。

有理数分类。

教学方法教师讲解法教学准备Ppt教学过程教师活动设计学生活动设计设计意图时间安排复习引入：在小学我们学习了自然数和分数.它们的产生是人类实践的需要。

提问：什么是自然数，举例说明。

什么是整数，举例说明。

由表示“没有”“空位”，产生数0由分物、测量，产生分数21，31……例1、判断下面各对量是不是具有相反意义的量（1）温度是零上25℃和零下18℃;（2）某条河的水位上升0.7米和下降1.2米。

（3）珠穆朗玛峰高于海平面8844.43米和吐鲁番盆地最低点低于海平面155米。

教师针对学生的答题情况给予评价。

二、具有相反意义的量的表示方法：教师综上进行引导：一般地，对于具有相反意义的量，我们可以把其中一种意义的量规定为正，并在表示这量的前面放上一个“+”（读作“正”）来表示；把与它意义相反的量规定为负的，并在表示这个量的前面放上一个“-”（读作“负”）来表示（零除外）鼓励学生任意结组，举例说明，巩固练习。

做一做：（出示幻灯片二）请你仿照天气预报中对气温的表示方法，完成下表：意义向东走1.8千米向西走3千米收入14200元支出4745元水位上升30厘米水位下降50厘米表示 +1.8千米 +14200元 +30厘米学生举手回答说明提问，其他学生进行补充。

学生体会在小学学习中0和分数的意义。

教师让多个学生自由发言学生独立思考，举手发表个人见解，其他同学可以互相补充。

小学和中学知识进行衔接培养学生敢于发表自己见解的精神，激发学生学习的兴趣。

进一步加深巩固具有相反意义的量的意义，同时培养学生的语言表达能力5510教师强调两点：1、 0既不是正数，也不是负数。

2、正数中的“+”可以省略不写。

三、巩固训练（出示幻灯片四）1、下面哪对量是具有相反意义的？（1）在知识竞赛中，加20分和扣10分。

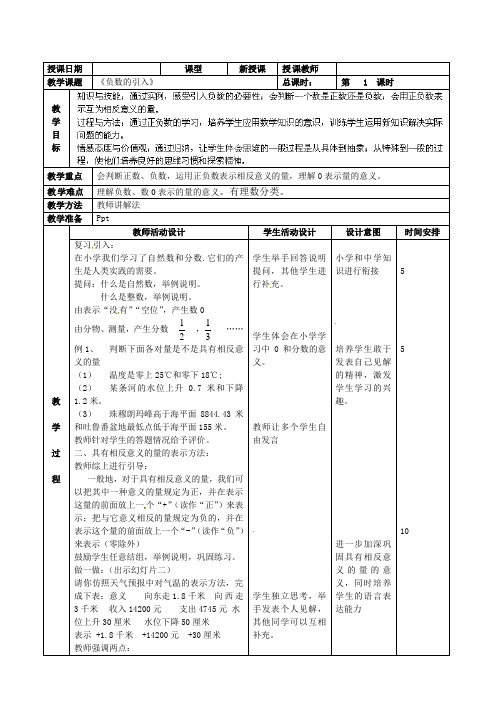
授课日期课型新授课授课教师教学课题《负数的引入》总课时：第 1 课时教学目标教学重点会判断正数、负数，运用正负数表示相反意义的量，理解0表示量的意义。

教学难点理解负数、数0表示的量的意义。

有理数分类。

教学方法教师讲解法教学准备Ppt教学过程教师活动设计学生活动设计设计意图时间安排复习引入：在小学我们学习了自然数和分数.它们的产生是人类实践的需要。

提问：什么是自然数，举例说明。

什么是整数，举例说明。

由表示“没有”“空位”，产生数0由分物、测量，产生分数21，31……例1、判断下面各对量是不是具有相反意义的量（1）温度是零上25℃和零下18℃;（2）某条河的水位上升0.7米和下降1.2米。

（3）珠穆朗玛峰高于海平面8844.43米和吐鲁番盆地最低点低于海平面155米。

教师针对学生的答题情况给予评价。

二、具有相反意义的量的表示方法：教师综上进行引导：一般地，对于具有相反意义的量，我们可以把其中一种意义的量规定为正，并在表示这量的前面放上一个“+”（读作“正”）来表示；把与它意义相反的量规定为负的，并在表示这个量的前面放上一个“-”（读作“负”）来表示（零除外）鼓励学生任意结组，举例说明，巩固练习。

做一做：（出示幻灯片二）请你仿照天气预报中对气温的表示方法，完成下表：意义向东走1.8千米向西走3千米收入14200元支出4745元水位上升30厘米水位下降50厘米表示 +1.8千米 +14200元 +30厘米教师强调两点：学生举手回答说明提问，其他学生进行补充。

学生体会在小学学习中0和分数的意义。

教师让多个学生自由发言学生独立思考，举手发表个人见解，其他同学可以互相补充。

小学和中学知识进行衔接培养学生敢于发表自己见解的精神，激发学生学习的兴趣。

进一步加深巩固具有相反意义的量的意义，同时培养学生的语言表达能力55101、 0既不是正数，也不是负数。

2、正数中的“+”可以省略不写。

三、巩固训练（出示幻灯片四）1、下面哪对量是具有相反意义的？（1）在知识竞赛中，加20分和扣10分。

北京课改版数学七年级上册1.1《负数的引入》教学设计一. 教材分析《负数的引入》是北京课改版数学七年级上册的第一节内容，主要介绍了负数的概念、性质以及负数在实际生活中的应用。

这一节内容是为学生后续学习更高级的数学知识打下基础，培养学生对数学的兴趣和思维能力。

教材通过丰富的实例和生动的图示，引导学生理解和掌握负数的概念，感受负数在现实生活中的意义。

二. 学情分析七年级的学生大多已经具备了一定的数学基础，但是对负数的概念和应用可能还比较陌生。

学生在学习这一节内容时，可能存在以下困难：1. 负数的概念比较抽象，难以理解；2. 负数与正数的区别和联系不易把握；3. 负数在实际生活中的应用场景不熟悉。

因此，在教学过程中，需要注重引导学生从实际生活中的例子出发，理解负数的概念和性质。

三. 教学目标1.理解负数的概念，掌握负数的性质；2. 能够运用负数解决实际生活中的问题；3. 培养学生的逻辑思维能力和团队协作能力。

四. 教学重难点1.负数的概念和性质；2. 负数在实际生活中的应用；3. 负数的运算规律。

五. 教学方法采用问题驱动法、案例教学法和小组合作法。

通过设置问题，引导学生主动探究负数的概念和性质；通过生活中的案例，让学生感受负数在实际生活中的应用；通过小组合作，培养学生的团队协作能力。

六. 教学准备1.准备相关的案例和实例；2. 准备教学PPT；3. 准备练习题和测试题。

七. 教学过程1.导入（5分钟）通过提问方式引导学生回顾已学的数学知识，如正数、整数、分数等，为新知识的学习做好铺垫。

接着，利用生活中气温变化等实例，引出负数的概念。

2.呈现（15分钟）利用PPT呈现负数的性质和运算规律，通过图示和实例，让学生直观地感受负数的概念。

同时，引导学生发现负数与正数的区别和联系。

3.操练（15分钟）让学生通过PPT上的练习题，巩固负数的概念和性质。

教师在旁边指导，解答学生的疑问。

4.巩固（5分钟）让学生通过PPT上的测试题，检测自己对新知识的掌握程度。