garch模型族的EVIEWS的操作

（G）ARCH模型在金融数据中的应用姓名 (括号内填学号)摘要：理解自回归异方差（ARCH）模型的概念及建立的必要性和适用的场合。

了解(G)ARCH 模型的各种不同类型，如GARCH-M 模型（GARCH in mean ），EGARCH模型 (Exponential GARCH ) 和TARCH模型 (又称GJR)。

掌握对(G)ARCH 模型的识别、估计及如何运用Eviews软件在实证研究中实现。

关键词：Garch；沪深股市1 基本概念p阶自回归条件异方程ARCH(p)模型，其定义由均值方程（1）和条件方程方程（2）给出：（1）（2）其中，表示t-1时刻所有可得信息的集合，为条件方差。

方程（2）表示误差项的方差由两部分组成：一个常数项和前p个时刻关于变化量的信息，用前p个时刻的残差平方表示(ARCH项)。

广义自回归条件异方差GARCH(p,q)模型可表示为：（3）（4）2 数据来源以上证指数和深证成份指数为研究对象，选取1997年1月2日～2002年12月31日共6年每个交易日上证指数和深证成份指数的收盘价为样本：3 描述性统计与检验3.1 描述性统计导入数据，建立工作组。

打开Eviews软件，选择“File”菜单中的“New Workfile”选项，在“Workfilefrequency”框中选择“undated or irregular”，在“Start observation”和“End observation”框中分别输入1 和1444，单击“OK”。

选择“File”菜单中的“Import--Read Text-Lotus-Excel”选项，找到要导入的名为EX6.4.xls的Excel文档完成数据导入。

生成收益率的数据列。

在Eviews窗口主菜单栏下的命令窗口中键入如下命令：genrrh=log(sh/sh(-1)) ，回车后即形成沪市收益率的数据序列rh，同样的方法可得深市收益数剧序列rz。

在对时间序列Y、X1进行回归分析时需要考虑Y与X1之间是否存在某种切实的关系，所以需要进行协整检验。

1.1利用eviews创建时间序列Y、X1 ：打开eviews软件点击file-new-workfile，见对话框又三块空白处workfile structure type处又三项选择，分别是非时间序列unstructured/undate，时间序列dated-regular frequency，和不明英语balance panel。

选择时间序列dated-regular frequency。

在date specification中选择年度，半年度或者季度等，和起始时间。

右下角为工作间取名字和页数。

点击ok。

在所创建的workfile中点击object-new object，选择series，以及填写名字如Y，点击OK。

将数据填写入内。

1.2对序列Y进行平稳性检验：此时应对序列数据取对数，取对数的好处在于可将间距很大的数据转换为间距较小的数据。

具体做法是在workfile y的窗口中点击Genr，输入logy=log(y),则生成y的对数序列logy。

再对logy序列进行平稳性检验。

点击view-United root test，test type选择ADF检验，滞后阶数中lag length选择SIC 检验，点击ok得结果如下：Null Hypothesis: LOGY has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=1)t-Statistic Prob.*Augmented Dickey-Fuller teststatistic -2.75094601716637 0.0995139988900359Test critical values: 1% level -4.297072756022265% level -3.2126963902622510% level -2.74767611540013当检验值Augmented Dickey-Fuller test statistic的绝对值大于临界值绝对值时，序列为平稳序列。

garch模型eviews均值方程GARCH模型在金融领域中被广泛应用于波动率建模和风险管理，它是根据金融资产收益率的历史数据来预测其未来波动率的一种方法。

GARCH模型的核心是建立一个波动率的均值方程，以描述波动率的长期均值和短期波动的动态调整过程。

在GARCH模型中，波动率的均值方程通常采用ARCH效应和GARCH效应的线性组合来描述。

ARCH效应指的是波动率的变化与过去的波动率变化有关，而GARCH效应则是在ARCH基础上引入了波动率残差的平方项。

这两个效应的组合可以更准确地描述金融资产收益率波动的特征。

波动率的均值方程通常可以用以下形式表示：波动率 = 常数 + 系数1 * 过去波动率 + 系数2 * 过去波动率残差的平方其中，常数代表波动率的长期均值，系数1表示波动率对过去波动率的反应程度，系数2表示波动率对过去波动率残差平方的反应程度。

通过估计这些参数，可以得到一个较为准确的波动率均值方程。

GARCH模型还可以根据实际情况引入更多的变量来建立均值方程，以提高模型的准确性。

比如，可以考虑引入其他金融指标或宏观经济变量来解释波动率的变化。

此外，还可以考虑引入时间变化的因素，比如季节性因素或周期性因素，以更好地描述波动率的动态调整过程。

在实际应用中，建立GARCH模型的关键是选择适当的历史数据和合适的模型参数。

通常需要对不同的模型进行比较，选择最优的模型来进行波动率预测。

常用的模型选择准则包括最小二乘法、极大似然法和贝叶斯信息准则等。

GARCH模型的应用广泛，可以用于金融市场的风险管理、衍生品定价、投资组合优化等方面。

通过对波动率的准确预测，可以帮助投资者更好地评估风险和收益，制定合理的投资策略。

此外，GARCH模型还可以用于金融市场的波动率分析和波动率交易等方面，为投资者提供更多的信息和决策支持。

GARCH模型的均值方程是建立波动率预测模型的核心部分，通过对过去波动率和波动率残差平方的加权组合，可以准确地描述波动率的动态调整过程。

Eviews基本操作学习（图⽰版）⽬录⽬录 (1)1、EViews简介 (3)1.1 什么是EViews (3)1.2 启动和运⾏EViews (3)1.3 EViews窗⼝ (3)1.4关闭EViews (4)2、EViews基本操作 (5)2.1⼯作⽂件与对象 (5)2.1.1⼯作⽂件 (5)2.1.2对象 (7)2.2数据处理 (10)2.2.1数据对象与样本 (10)2.2.2数据的输⼊和输出 (12)2.3图形与表格 (14)2.3.1图的创建 (14)2.3.2图的修改 (14)2.3.3多个图 (16)2.3.4图的打印和输出 (17)2.3.5表格对象 (18)2.3.6表的输出 (18)2.3.7⽂本对象 (19)3、基本回归模型 (19)3.1估计和⽅程对象 (19)3.1.1⽅程对象 (19)3.1.2在EViews中对⽅程进⾏说明 (20)3.1.3在EViews中估计⽅程 (20)3.2⽅程输出 (20)3.3⽅程操作 (22)3.3.1⽅程视图 (22)3.3.2⽅程过程 (24)3.3.3缺省⽅程 (24)4、基本检验 (24)4.1多重共线性的检验 (24)4.2异⽅差的检验 (25)4.3 ⾃相关的检验 (26)5、时间序列模型 (27)5.1时间序列平稳性的单位根检验 (27)5.1.1单位根的ADF检验 (27)5.1.2Phillips-Perron(PP)检验 (27)5.2协整 (28)6、案例分析 (29)6.1多元线性回归及多重共线性的检验 (29)6.2异⽅差的检验 (31)6.3⾃相关的检验 (34)6.4时间序列的单位根和协整检验 (36)1、EViews简介1.1什么是EViewsEViews 是在⼤型计算机的TSP (Time Series Processor)软件包基础上发展起来的新版本，是⼀组处理时间序列数据的有效⼯具，是当今世界上最流⾏的计量经济学软件之⼀。

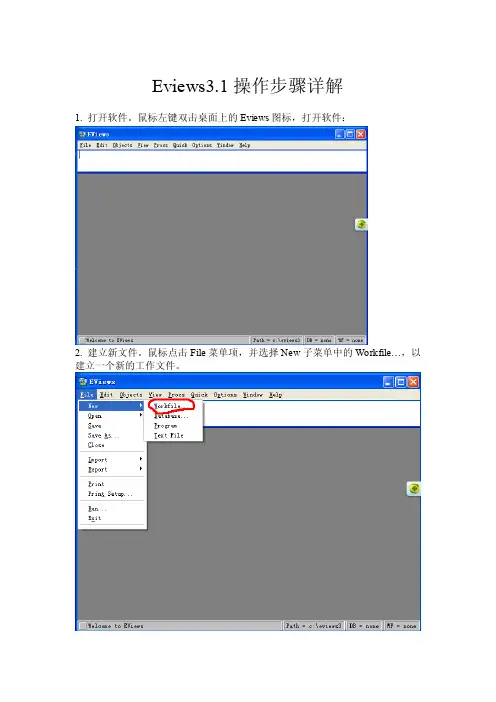
Eviews3.1操作步骤详解1. 打开软件。

鼠标左键双击桌面上的Eviews图标，打开软件：2. 建立新文件。

鼠标点击File菜单项，并选择New子菜单中的Workfile…，以建立一个新的工作文件。

3. 选择数据类型。

步骤2完成后直接将出现如下选择输入数据频率的画面：根据你将使用的数据本身频率来做相应选择。

例如，如果你要研究1980－1990年度之间的数据，那么可以选择“Annual”选项，并在Start data对应文本框内填写“1980”，以及在End data对应文本框内填写“1990”，然后点击OK按钮，完成本步骤。

4. 输入数据。

完成步骤3后，将出现如下画面：现在已经初步建立了一个新的工作文件。

接下来，需要输入需要研究的数据。

首先，将鼠标点击File菜单下面的空白处，然后给出指令“Series x”（注：单词Series 与字母x之间存在一个空格，以及你可以给变量任意你想要的名字而不一定是x），并按回车键Enter，以建立一个变量名为x的时间序列数据，显然该数据序列包含1980－1990年之间的年度数据：同样，给出指令“Series y可以建立一个变量名为y的时间序列数据。

这样，文件中就建立了变量名分别为x和y的两个时间序列型数据序列。

接下来，首先鼠标左键双击数据序列x，打开如下x数据的输入界面，然后鼠标左键点击Edit+/-选择按钮：数据输入界面被激活，出现如下画面：这表明可以直接输入数据了。

有多种方式输入数据，这里只给出最简单的方式——直接输入。

将鼠标移至NA位置，逐一输入相应年度的x数据，输入完最后一个数据后，再次点击Edit+/-按钮，确认数据输入完毕。

然后，点击关闭键，关闭整个数据输入界面：同样，对y数据序列也输入数据，这样文件中的两个数据序列都已经完成数据输入工作。

5. 一元线性回归。

点击Objects菜单：选择New Object…选项：接下来，选择Equation选项，并点击OK按钮：然后出现如下界面：在闪动的光标后输入指令：“y c x”，注意，每个字母后都是一个空格，该指令的含义是：以y为被解释变量（或应变量），以x为解释变量（或自变量），建立一个一元线性回归模型，其中字母c表示一元线性回归模型的常数项（注意，c字母被Eviews固定作为常数项的表示符号，不能任意作为他用）。

建立eviews文件
1、双击eviews
2、file\new\workfile
3、在对话框中选择unstructured
4、在上述对话框中输入样本容量和文件名（文件名可不填）
5、save as
原始数据的录入
1、双击eviews文件
2、object\new object
3、选择series
4、命名
5、点击edit+/-
6、录入数据（可以直接复制excel中的数据）
1、双击文件consp序列（即被解释变量的序列）
2、quick\estimate equation
3、在对话框依次输入：
被解释变量 c 解释变量（注意两个变量的字母表示必须一致，后面也是如此）
显示回归分析
4、view\representations
显示回归分析结果，即公式
散点图
输入数据：单击“Quick”,选择“Empty Group”,出现“Group”窗口，将第一列取
名为gdpp，第二列取名为consp，然后输入数据
（obs在1上面，在第二个obs中输入两个变量名，数据会自动录入）
（二）绘制散点图：
单击“Quick”,选择“Graph”, 在“Graph”里选择“Scatter ”,点击“OK”,出现“Series List”对话框，输入gdpp consp（有空格）,点击“OK”。

出现散点图。

如下图：
如果要模型做出来，则在下图状态下
选择view——>graph——>scatter——>scattered with regression，点击ok，即出现。