绪论授课时数：1学时一、教学内容及要求分析微波网络的研究方法；介绍微波网络概述、应用及发展前景；讲解本课程重点及学习方法。
二、教学重点与难点本课程要求掌握的先修课程中涉及的相关知识点，本课程涉及的主要重点内容，学习本课程的要求，及微波网络的工程应用。
三、作业无四、本章参考资料《电磁场与电磁波》、《微波技术基础》、《微波网络》。
五、教学后记上课后，待补充。
第一章微波网络基础授课时数：6学时一、教学内容及要求回顾交变电磁场与导波理论，介绍导波系统的电路概念，讲解场路转换的等效基础和方法（2学时），要求了解；回顾传输线理论及应用，讲解几种典型的三端口网络（接头）的性质及特性的分析过程和方法（2学时），要求掌握。
讲解微波网络中的几个基本定理：坡印亭能量定理、互易定理、福斯特电抗定理及对偶电路定理（2学时），要求掌握；二、教学重点与难点场路转换的等效基础和方法；等效电压和等效电流，模式电压和模式电流；网络的复数功率，互易网络的性质和条件，无耗网络导抗函数的性质，对偶网路满足的条件和转换关系。
三、作业教材P32：1-2；课堂讨论：利用等效电流和等效电压及传输功率，讨论波导的阻抗。
四、本章参考资料《电磁场与电磁波》、《微波技术基础》，《Microwave Engineering》。
五、教学后记上课后，待补充。
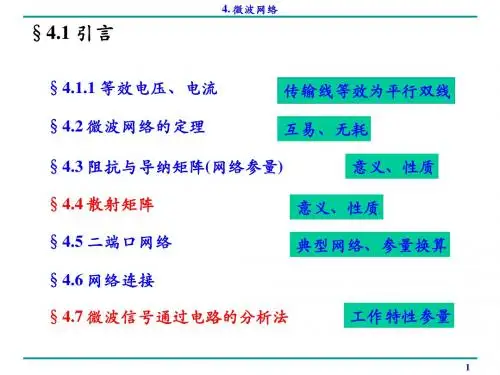
第二章微波网络特性参量授课时数：6学时一、教学内容及要求讲解微波网络固有特性参量［Z］,［Y］,［A］,［S］,［T］的定义、性质、相互间关系及求解方法（3学时），要求掌握；讲解微波网络的工作特性参量的［A］和［S］表示法（3学时），要求熟练掌握。
二、教学重点与难点微波网络固有特性电路参量：［Z］、［Y］、［A］和波参量：［S］、［T］，区分［A］和［T］及其在二端口网络级联中的应用；固有特性电路参量间的相互关系和转换；网络参量［S］的性质。
工作特性参量主要包含对象，及相应的［A］和［S］表示法。
三、作业教材P61：2-4、2-6。
