宝石学校活页课时教案(首页)
班级:高一年级科目:数学
一、基础练习
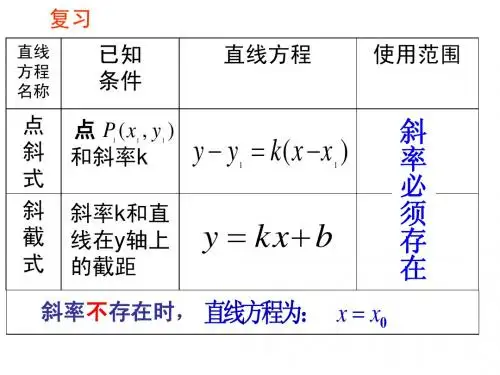
1、写出前面学过的直线方程的各种不同形式，并指出其局限性：
2、练习 根据下列条件，写出直线方程。
（1）经过点A （8，-2），斜率是12
-； （2）经过点B （4，2）,平行于x 轴；
（3）经过点P 1(3,-2),P 2(5,-4)；
（4）在x 轴上，y 轴上的截距分别是32
，-3. （5）经过点A （6，-4），斜率为43
- . 二、重点练习：
1、将下列直线方程化成一般式方程。
（1）21x 240y +-=； （2）x-2120y -=； （3）-2
110x y +-=； 提示: 一般式的直线方程要求是A 必须为正整数, 如果不是则需要通过扩倍或者
去分母化简成此形式.
2、探究：
在方程Ax+By+C=0，A 、B ，C 为何值时，方程表示的直线①平行于x 轴；②平行于y 轴；③与x 轴重合；④与y 轴重合。⑤经过坐标原点；⑥直线的斜率不存在；⑦斜率为0.
提示：分别与①1y y y =≠1（0）；②1x x x =≠1（0）
；③0y =④0x =；⑤A0+B0+C=0；⑥直线垂直于x 轴，1x x =；⑦0y x b =+对应找寻A 、B ，C 的数量关系。
解析：①0,0,0A B C =≠≠;②0,0,0A B C ≠=≠;
③0,0,0A B C =≠=;④0,0,0A B C ≠==;
⑤ A 、B 不同时为0,0C =;⑥0,0A B ≠=;⑦0,0A B =≠.
3、求下列直线的斜率以及在y 轴上的截距：
（1）3250x y +-=； （2）145
x y -=； （3）20x y += （4）7640x y -+=； 提示：利用一般式中的特殊公式C
B C A B A k -=-=-
=b ,a ,纵截距横截距来进行计算.
4、把直线l 的一般式方程260x y -+=化成斜截式和截距式。
分析：只要将直线方程化成y kx b =+的形式就可以找到直线的斜率和在y 轴上的截距；只要将6移到方程的右边,给每一项都除以-6,就可得到所求的内容。
三、难点练习：
求与直线240x y -+=平行，且过点P （3，-1）的直线的方程。
分析：把直线240x y -+=化成斜截式1y x+22=的直线的斜率k=12
故所求直线的斜率为12，设所求直线方程为1y x+c 2=，代人点P （3，-1）得c=52-，即15y x 22
=-，化成一般式得：250x y --=。 思考：能否直接从一般式出发去设所求方程。
设所求直线方程为2c 0x y -+=，代人点P （3，-1）的c=-5
结论：与直线方程Ax+By+C=0平行的直线为Ax+By+C ′=0（C ≠C ˊ） 理论迁移：
直线l 1 ：A 1x+B 1y+C 1=0（A 1、B 1都不为0）和l 2 ：A 2x+B 2y+C 2=0（A 2、B 2都不为0）探究A 1，B 1，C 1和A 2，B 2，C 2满足什么样的条件，两直线平行.
1112222
(0)A B C C A B C =≠≠. 四、课堂小结:
1、内容：直线方程的一般式的形式Ax+By+C=0（A 、B 不同时为0）；
2、重点：直线方程五种形式的相互转化，及各种形式中的一些几何量（斜率、截距等）的求解；
3、重视：分类讨论的数学思想；
4、明确：直角坐标系是把方程和直线联系起来的桥梁。
七、作业:
习题3.2 A 组 第11、8题；选做 B 组第3题.
编写人：王红卫 祖豆蔻 审核人：郑战彪 班级：17级 班 学习目标： 1、掌握直线方程的两点式、截距式、一般式以及他们之间的联系和转化； 2、根据条件熟练地求出满足已知条件的直线方程； 3、培养学生分析、比较、概括、化归的数学能力； 重点与难点： 1、直线方程的两点式、一般式； 2、对于一元二次方程表示直线方程的理解； 一、课前准备 1、一般地，如果直线l 上 ，且 ，我们就把这样的方程称为直线l 的方程。 2、如果直线l 经过000(,)p x y ，且斜率为k ，设点(,)P x y 是直线l 上任意一点，可以得到，当0x x ≠时，0 y y k x x -= -，即 （1），我们称（1）式的方程叫做直线的点斜式方程，简称点斜式。 【创设情景】 探究一 平面内，两点确定一条直线，在平面直角坐标系中，已知直线l 经过两点11122,2(,),()P x y P x y （其中0x x ≠），则直线l 的方程式什么？ 归纳总结：直线方程的两点式为 助 学 案 直线方程的两点式和一般式 第19期
例1 探究二 在坐标平面内，画直线时常选取坐标轴上的两点比较简便。在直线方程的两点式中，若12,P P 两点为坐标轴上的两点，即1P 的坐标为(),0a ,2P 的坐标为(0,b)时，直线12P P 的方程形式如何？其方程只能适用于坐标平面内怎样的直线？ 归纳总结：直线的截距式方程 例2：直线l 过点（-3，4），且在两坐标轴上的截距之和为12，求直线l 的方程
探究 三 直线方程的四种形式（点斜式、斜截式、两点式、截距式）具备怎样的特点？能否统一成一 种形式？是怎样的方程？ 归纳总结：直线方程的 一般式 1、直线方程的五种形式之间如何进行转化？ 2、直线方程各种形式中，其参数的几何意义是什么？ 3、各自的使用范围如何？ 例3 已知三角形三个顶点分别是A （-3.，0），B （2，-2），C （0,1），求这个三角形三边各自所在
编写人：王红卫 祖豆蔻 审核人：郑战彪 班级：17级 班 学习目标： 1、掌握直线方程的两点式、截距式、一般式以及他们之间的联系和转化； 2、根据条件熟练地求出满足已知条件的直线方程； 3、培养学生分析、比较、概括、化归的数学能力； 重点与难点： 1、直线方程的两点式、一般式； 2、对于一元二次方程表示直线方程的理解； 一、课前准备 1、一般地，如果直线l 上 ，且 ，我们就把这样的方程称为直线l 的方程。 2、如果直线l 经过000(,)p x y ，且斜率为k ，设点(,)P x y 是直线l 上任意一点，可以得到，当0x x ≠时，0 y y k x x -= -，即 （1），我们称（1）式的方程叫做直线的点斜式方程，简称点斜式。 【创设情景】 探究一 平面内，两点确定一条直线，在平面直角坐标系中，已知直线l 经过两点11122,2(,),()P x y P x y （其中0x x ≠），则直线l 的方程式什么？ 归纳总结：直线方程的两点式为 第19期
例1 探究二 在坐标平面内，画直线时常选取坐标轴上的两点比较简便。在直线方程的两点式中，若12,P P 两点为坐标轴上的两点，即1P 的坐标为(),0a ,2P 的坐标为(0,b)时，直线12PP 的方程形式如何？其方程只能适用于坐标平面内怎样的直线？ 归纳总结：直线的截距式方程 例2：直线l 过点（-3，4），且在两坐标轴上的截距之和为12，求直线l 的方程
探究 三 直线方程的四种形式（点斜式、斜截式、两点式、截距式）具备怎样的特点？能否统一成一 种形式？是怎样的方程？ 归纳总结：直线方程的一般式 2、直线方程各种形式中，其参数的几何意义是什么？ 3、各自的使用范围如何？ 例3 已知三角形三个顶点分别是A （-3.，0），B （2，-2），C （0,1），求这个三角形三边各自所在
直线方程的点斜式、斜截式、两点式和截距式 一、教学目标 (一)知识教学点 在直角坐标平面内，已知直线上一点和直线的斜率或已知直线上两点，会求直线的方程；给出直线的点斜式方程，能观察直线的斜率和直线经过的定点；能化直线方程成截距式，并利用直线的截距式作直线． (二)能力训练点 通过直线的点斜式方程向斜截式方程的过渡、两点式方程向截距式方程的过渡，训练学生由一般到特殊的处理问题方法；通过直线的方程特征观察直线的位置特征，培养学生的数形结合能力． (三)学科渗透点 通过直线方程的几种形式培养学生的美学意识． 二、教材分析 1．重点：由于斜截式方程是点斜式方程的特殊情况，截距式方程是两点式方程的特殊情况，教学重点应放在推导直线的斜截式方程和两点式方程上．2．难点：在推导出直线的点斜式方程后，说明得到的就是直线的方程，即直线上每个点的坐标都是方程的解；反过来，以这个方程的解为坐标的点在直线上． 的坐标不满足这个方程，但化为y-y1=k(x-x1)后，点P1的坐标满足方程． 三、活动设计 分析、启发、诱导、讲练结合． 四、教学过程 (一)点斜式 已知直线l的斜率是k，并且经过点P1(x1，y1)，直线是确定的，也就是可求的，怎样求直线l的方程(图1-24)？ 设点P(x，y)是直线l上不同于P1的任意一点，根据经过两点的斜率公式得
注意方程(1)与方程(2)的差异：点P1的坐标不满足方程(1)而满足方程(2)，因此，点P1不在方程(1)表示的图形上而在方程(2)表示的图形上，方程(1)不能称作直线l 的方程． 重复上面的过程，可以证明直线上每个点的坐标都是这个方程的解；对上面的过程逆推，可以证明以这个方程的解为坐标的点都在直线l上，所以这个方程就是过点P1、斜率为k 的直线l的方程． 这个方程是由直线上一点和直线的斜率确定的，叫做直线方程的点斜式． 当直线的斜率为0°时(图1-25)，k=0，直线的方程是y=y1． 当直线的斜率为90°时(图1-26)，直线的斜率不存在，它的方程不能用点斜式表示．但因l上每一点的横坐标都等于x1，所以它的方程是x=x1． (二)斜截式 已知直线l在y轴上的截距为b，斜率为b，求直线的方程． 这个问题，相当于给出了直线上一点(0，b)及直线的斜率k，求直线的方程，是点斜式方程的特殊情况，代入点斜式方程可得： y-b=k(x-0) 也就是
3.2.2 直线的两点式方程 三维目标 1、知识与技能 （1）掌握直线方程的两点的形式特点及适用范围； （2）了解直线方程截距式的形式特点及适用范围。 2、过程与方法 让学生在应用旧知识的探究过程中获得到新的结论，并通过新旧知识的比较、分析、 应用获得新知识的特点。 3、情态与价值观 （1）认识事物之间的普遍联系与相互转化； （2）培养学生用联系的观点看问题。 教学重点、难点： 1、 重点：直线方程两点式。 2、难点：两点式推导过程的理解。 教学过程： 一、复习准备： 1． 写出下列直线的点斜式、斜截式方程,并求直线在y 轴上的截距. ①经过点A(-2,3),斜率是-1；②经过点B(-3,0),斜率是0；③经过点() 22,C -,倾斜角是 60； 二、讲授新课： 1.直线两点式方程的教学: ① 探讨:已知直线l 经过111222(,),(,)p x y p x y (其中1212,x x y y ≠≠)两点,如何求直线的点斜 式方程? 211121 ()y y y y x x x x --=-- 两点式方程:由上述知, 经过111222(,),(,)p x y p x y (其中1212,x x y y ≠≠)两点的直线方程为 112121 y y x x y y x x --=-- ⑴, 我们称⑴为直线的两点式方程,简称两点式. 若点),(),,(222211 y x P x x P 中有21x x =，或21y y =，此时这两点的直线方程是什么？ 2．举例 例1:求过(2,1),(3,3)A B -两点的直线的两点式方程,并转化成点斜式. 练习：教材P97面1题
直线方程的两点式和一 般式 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】
编写人：王红卫 祖豆蔻 审核人：郑战彪 班级：17级 班 学习目标： 1、掌握直线方程的两点式、截距式、一般式以及他们之间的联系和转化； 2、根据条件熟练地求出满足已知条件的直线方程； 3、培养学生分析、比较、概括、化归的数学能力； 重点与难点： 1、直线方程的两点式、一般式； 2、对于一元二次方程表示直线方程的理解； 一、课前准备 1、一般地，如果直线l 上 ，且 ，我们就把这样的方程称为直线l 的方程。 2、如果直线l 经过000(,)p x y ，且斜率为k ，设点(,)P x y 是直线l 上任意一点，可以得到，当0x x ≠时，00 y y k x x -=-，即 （1），我们称（1）式的方程叫做直线的点斜式方程，简称点斜式。 【创设情景】 探究一 平面内，两点确定一条直线，在平面直角坐标系中，已知直线l 经过两点 11122,2(,),()P x y P x y （其中0x x ≠），则直线l 的方程式什么 归纳总结：直线方程的两点式为 助 学 案 直线方程的两点式和一般式 第19期
例1 探究二 在坐标平面内，画直线时常选取坐标轴上的两点比较简便。在直线方程的两点式 中，若 12 ,P P两点为坐标轴上的两点，即 1 P的坐标为(),0a,2P的坐标为(0,b)时，直线12 P P的方程形式如何其方程只能适用于坐标平面内怎样的直线 归纳总结：直线的截距式方程 例2：直线l过点（-3，4），且在两坐标轴上的截距之和为12，求直线l的方程 探究三 直线方程的四种形式（点斜式、斜截式、两点式、截距式）具备怎样的特点能否统一成一种形式是怎样的方程 归纳总结：直线方程的一般式 1、直线方程的五种形式之间如何进行转化 2、直线方程各种形式中，其参数的几何意义是什么 3、各自的使用范围如何
【课题：】直线的点斜式方程 【教学目的：】 知识目标：在直角坐标平面，已知直线上一点和直线的斜率或已知 直线上两点，会求直线的方程；给出直线的点斜式方程， 能观察直线的斜率和直线经过的定点 能力目标：通过直线的点斜式方程向斜截式方程的过渡，训练学生由 一般到特殊的处理问题方法；通过直线的方程特征观察直线的位置特征，培养学生的数形结合能力. 德育目标：通过直线方程的几种形式培养学生的美学意识. 【教学重点：】由于斜截式方程是点斜式方程的特殊情况，教学重点应放在推导直线的斜截式方程上?实质上它也是整个直线方程理论的基础。 【教学难点：】在推导出直线的点斜式方程后，说明得到的就是直线的方程，即直线上每个点的坐标都是方程的解；反过来，以这个方程的解为坐标的点在直线上. 【授课类型：】新授课 【课时安排：】1课时 【教具：】 【教学过程：】 1、复习引入： 2、讲解新课： （1）点斜式 已知直线I的斜率是k,并且经过点P i（x i, y i），直线是确定的，也就是可求的，怎样求直线I的方程（图1-24）? 设点P（x , y）是直线I上不同于R（X1, yj的任意一点，根据经过两点的斜率公式得 , y y1 k - （1） x X-| 即y-y 1=k（x-x 1）（2） 注意方程（1）与方程⑵ 的差异：点R的坐标不满足方程（1）而满足方程⑵，因此，点P1不在方程（1）表示的图形上而在方程（2）表示的图形上，方程（1）不能称作直线I的方程. 重复上面的过程，可以证明直线上每个点的坐标都是这个方程的解；对上面的过程逆推，可以证明以 这个方程的解为坐标的点都在直线I上，所以这个方程就是过点R、斜率为k的直线I的方程.（实质上 是证明了直线的方程与方程的直线的关系） 这个方程是由直线上一点和直线的斜率确定的，叫做直线方程的点斜式. 注：当直线的斜率为0°时（图1-25）, k=0,直线的方程是y=y「 当直线的斜率为90。时（图1-26）,直线的斜率不存在，它的方程不能用点斜式表示. 但因I上每一点 的横坐标都等于X i,所以它的方程是X=X i .
直线的两点式方程 【教学目标】 1.让学生掌握直线方程两点式和截距式的发现和推导过程，并能运用这两种形式求出直线的方程.培养学生数形结合的数学思想，为今后的学习打下良好的基础. 2.了解直线方程截距式的形式特点及适用范围，培养学生树立辩证统一的观点，培养学生形成严谨的科学态度和求简的数学精神. 【重点难点】 教学重点:直线方程两点式和截距式. 教学难点:关于两点式的推导以及斜率k不存在或斜率k=0时对两点式方程的讨论及变形. 【课时安排】 1课时 【教学过程】 导入新课 要学生求直线的方程，题目如下： ①A(8，-1)，B(-2，4)； ②A(6，-4)，B(-1，2)； ③A(x1，y1)，B(x2，y2)(x1≠x2). (分别找3个同学说上述题的求解过程和答案，并着重要求说求k及求解过程) 这个答案对我们有何启示？求解过程可不可以简化？我们可不可以把这种直线方程取一个什么名字呢? 推进新课 新知探究 提出问题 ①已知两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)，求通过这两点的直线方程. ②若点P1(x1,y1),P2(x2,y2)中有x1=x2或y1=y2，此时这两点的直线方程是什么？ ③两点式公式运用时应注意什么？ ④已知直线l与x轴的交点为A(a,0)，与y轴的交点为B(0,b)，其中a≠0,b≠0，求直线l的方程.
⑤a 、b 表示截距是不是直线与坐标轴的两个交点到原点的距离？ ⑥截距式不能表示平面坐标系下哪些直线？ 活动:①教师引导学生：根据已有的知识，要求直线方程，应知道什么条件？能不能把问题转化为已经解决的问题呢？在此基础上，学生根据已知两点的坐标，先判断是否存在斜率，然后求出直线的斜率，从而可求出直线方程.师生共同归纳： 已知直线上两个不同点，求直线的方程步骤： a.利用直线的斜率公式求出斜率k; b.利用点斜式写出直线的方程. ∵x 1≠x 2,k=1 212x x y y --, ∴直线的方程为y-y 1= 1212x x y y --(x-x 1). ∴l 的方程为y-y 1=1 212x x y y --(x-x 1).① 当y 1≠y 2时,方程①可以写成 121121x x x x y y y y --=--.② 由于②这个方程是由直线上两点确定的，因此叫做直线方程的两点式. 注意：②式是由①式导出的，它们表示的直线范围不同.①式中只需x 1≠x 2，它不能表示倾斜角为90°的直线的方程；②式中x 1≠x 2且y 1≠y 2，它不能表示倾斜角为0°或90°的直线的方程，但②式相对于①式更对称、形式更美观、更整齐，便于记忆.如果把两点式变成(y-y 1)(x 2-x 1)=(x-x 1)(y 2-y 1)，那么就可以用它来求过平面上任意两已知点的直线方程. ②使学生懂得两点式的适用范围和当已知的两点不满足两点式的条件时它的方程形式.教师引导学生通过画图、观察和分析，发现当x 1=x 2时，直线与x 轴垂直，所以直线方程为x=x 1；当y 1=y 2时，直线与y 轴垂直，直线方程为y=y 1. ③引导学生注意分式的分母需满足的条件. ④使学生学会用两点式求直线方程；理解截距式源于两点式，是两点式的特殊情形.教师引导学生分析题目中所给的条件有什么特点？可以用多少方法来求直线l 的方程？哪种方法更为简捷？然后求出直线方程.
直线教案直线方程的两点式和截距式教案 教学目标 1．让学生掌握直线方程两点式和截距式的发现和推导过程，并能运用这两种形式求出直线的方程． 2．通过这节课的学习，让学生学会较灵活的求直线方程的方法，能够一题多法，一题妙法． 3．培养学生的数形结合的数学思想，为今后的学习打下良好的基础． 教学重点与难点 关于两点式的推导以及斜率k不存在或斜率k=0时对两点式方程的讨论及变形，是本节课的重点和难点． 教学过程 (先回顾点斜式方程的推导过程，因为点斜式是推导两点式的基础．) 师：上节课我们学习了直线方程的点斜式，请问点斜式方程是什么？点斜式方程是怎样推导的？ 生：点斜式是y-y 1=k(x-x 1 )，x 1 ，y 1 是直线l的某一定点P1的坐标，k是这 条直线的斜率．点斜式的推导过程主要依据是直线上任意一点P(x，y)与这条直 线上一个定点P 1(x 1 ，y 1 )所确定的斜率相等，并且就是此直线 y-y 1=k(x-x 1 )． (此回答可以找两个左右的同学回答，不够的，老师再概括，一定要说清楚．) 老师再使用投影仪，要学生求直线的方程，题目如下： 1．A(8，-1)，B(-2，4)； 2．A(6，-4)，B(-1， 2)； 3．A(x 1，y 1 )，B(x 2 ，y 2 )(x 1 ≠x 2 )．
(分别找3个同学说上述题的求解过程和答案，并着重要求说求k及求解过程．) 师：请你说出上述练习的求解过程及答案． (学生Ⅰ、Ⅱ略) 生Ⅲ：首先利用直线的斜率公式求出斜率k，然后利用点斜式写出 师：这个答案对我们有何启示？求解过程可不可以简化？ 生：可以直接用上述答案作为求直线方程的公式． (老师应适时表扬该学生) 就比较对称和美观，体现了数学美．由于这个方程是由直线上两点确定的，我们可以把这种直线方程取一个什么名字？ 生：可以叫做直线方程的两点式． (教师引导学生对下述问题进行分析) 生：不同，因为后者y 1≠y 2 ，所以后者不能表示倾斜角是90°的直线． 师：这个问题提得好，但后者形式对称，整齐，便于记忆及应用，所以采用后者作为公式。 师(启发)：两点式公式里面的x 1≠x 2 ，y 1 ≠y 2 ，哪些直线不能用公式表示？
直线的两点式方程、直线的一般式方程题型全归纳 【知识梳理】 1．直线的两点式与截距式方程 2． (1)在平面直角坐标系中，对于任何一条直线，都可以用一个关于x，y的二元一次方程表示． (2)每个关于x，y的二元一次方程都表示一条直线． 3．直线的一般式方程的定义 我们把关于x，y的二元一次方程Ax＋By＋C＝0(其中A，B不同时为0)叫做直线的一般式方程，简称一般式．【常考题型】 题型一、利用两点式求直线方程 【例1】三角形的三个顶点是A(－1,0)，B(3，－1)，C(1,3)，求三角形三边所在直线的方程． 【类题通法】 求直线的两点式方程的策略以及注意点 (1)当已知两点坐标，求过这两点的直线方程时，首先要判断是否满足两点式方程的适用条件：两点的连线不平行于坐标轴，若满足，则考虑用两点式求方程． (2)由于减法的顺序性，一般用两点式求直线方程时常会将字母或数字的顺序错位而导致错误．在记忆和使用两点式方程时，必须注意坐标的对应关系． 【对点训练】 1．(1)若直线l经过点A(2，－1)，B(2,7)，则直线l的方程为________． (2)若点P(3，m)在过点A(2，－1)，B(－3,4)的直线上，则m＝________.
【例2】 直线l 过点P (43 ，2)，且与x 轴、y 轴的正半轴分别交于A 、B 两点，O 为坐标原点． (1)当△AOB 的周长为12时，求直线l 的方程． (2)当△AOB 的面积为6时，求直线l 的方程． 【类题通法】 用截距式方程解决问题的优点及注意事项 (1)由截距式方程可直接确定直线与x 轴和y 轴的交点的坐标，因此用截距式画直线比较方便． (2)在解决与截距有关或直线与坐标轴围成的三角形面积、周长等问题时，经常使用截距式． (3)但当直线与坐标轴平行时，有一个截距不存在；当直线通过原点时，两个截距均为零．在这两种情况下都不能用截距式，故解决问题过程中要注意分类讨论． 【对点训练】 2．求经过点A (－2,2)，并且和两坐标轴围成的三角形面积是1的直线方程．
直线的两点式方程 教学目标 1.让学生掌握直线方程两点式和截距式的发现和推导过程，并能运用这两种形式求出直线的方程.培养学生数形结合的数学思想，为今后的学习打下良好的基础. 2.了解直线方程截距式的形式特点及适用范围，培养学生树立辩证统一的观点，培养学生形成严谨的科学态度和求简的数学精神. 重点难点 教学重点:直线方程两点式和截距式. 教学难点:关于两点式的推导以及斜率k不存在或斜率k=0时对两点式方程的讨论及变形. 安排 1 教学过程 导入新课 要学生求直线的方程，题目如下： ①A(8，1)，B(2，4)； ②A(6，4)，B(1，2)； ③A(x1，y1)，B(x2，y2)(x1≠x2). (分别找3个同学说上述题的求解过程和答案，并着重要求说求k及求解过程) 这个答案对我们有何启示？求解过程可不可以简化？我们可不可以把这种直线方程取一个什么名字呢? 推进新课 新知探究 提出问题 ①已知两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)，求通过这两点的直线方程. ②若点P1(x1,y1),P2(x2,y2)中有x1=x2或y1=y2，此时这两点的直线方程是什么？ ③两点式公式运用时应注意什么？ ④已知直线l与x轴的交点为A(a,0)，与y轴的交点为B(0,b)，其中a≠0,b≠0，求直线l的方程. ⑤a、b表示截距是不是直线与坐标轴的两个交点到原点的距离？ ⑥截距式不能表示平面坐标系下哪些直线？
活动:①教师引导学生：根据已有的知识，要求直线方程，应知道什么条件？能不能把问题转化为已经解决的问题呢？在此基础上，学生根据已知两点的坐标，先判断是否存在斜率，然后求出直线的斜率，从而可求出直线方程.师生共同归纳： 已知直线上两个不同点，求直线的方程步骤： a.利用直线的斜率公式求出斜率k b.利用点斜式写出直线的方程. ∵x 1≠x 2,k=1 212x x y y --, ∴直线的方程为yy 1= 1212x x y y --(xx 1). ∴l 的方程为yy 1=1 212x x y y --(xx 1).① 当y 1≠y 2时,方程①可以写成 121121x x x x y y y y --=--.② 由于②这个方程是由直线上两点确定的，因此叫做直线方程的两点式. 注意：②式是由①式导出的，它们表示的直线范围不同.①式中只需x 1≠x 2，它不能表示倾斜角为90°的直线的方程；②式中x 1≠x 2且y 1≠y 2，它不能表示倾斜角为0°或90°的直线的方程，但②式相对于①式更对称、形式更美观、更整齐，便于记忆.如果把两点式变成 (yy 1)(x 2x 1)=(xx 1)(y 2y 1)，那么就可以用它来求过平面上任意两已知点的直线方程. ②使学生懂得两点式的适用范围和当已知的两点不满足两点式的条件时它的方程形式.教师引导学生通过画图、观察和分析，发现当x 1=x 2时，直线与x 轴垂直，所以直线方程为x=x 1；当y 1=y 2时，直线与y 轴垂直，直线方程为y=y 1. ③引导学生注意分式的分母需满足的条件. ④使学生学会用两点式求直线方程；理解截距式源于两点式，是两点式的特殊情形.教师引导学生分析题目中所给的条件有什么特点？可以用多少方法来求直线l 的方程？哪种方法更为简捷？然后求出直线方程. 因为直线l 经过(a ，0)和(0，b)两点，将这两点的坐标代入两点式，得 a a x b y --=--000.① 就是b y a x +=1.②
直线的两点式方程 (一)教学目标 1．知识与技能 （1）掌握直线方程的两点式的形式特点及适用范围； （2）了解直线方程截距式的形式特点及适用范围。 2．过程与方法 让学生在应用旧知识的探究过程中获得新的结论，并通过新旧知识的比较、分析、应用获得新知识的特点. 3．情态与价值观 （1）认识事物之间的普通联系与相互转化； （2）培养学生用联系的观点看问题。 （二）教学重点、难点： 1．重点：直线方程两点式。 2．难点：两点式推导过程的理解。 （三）教学设想
备选例题 例1 求经过点A (–3，4)，且在坐标轴上截距互为相反数的直线l 的方程. 【解析】当直线l 在坐标轴上截距都不为零时，设其方程为1y x a a +=-. 将A (–3，4)代入上式，有 341a a -+=-， 解得a = –7. ∴所求直线方程为x – y + 7 = 0. 当直线l 在坐标轴上的截距都为零时，设其方程为y = kx .将A (–3，4)代入方程得4 = –3k ，即k = 43 -. ∴所求直线的方程为43 y =-x ，即4x + 3y = 0.故所求直线l 的方程为x – y + 7 = 0或4x + 3y = 0. 【评析】此题运用了直线方程的截距式，在用截距时，必须注意适用条件：a 、b 存在且都不为零，否则容易漏解. 例2 如图，某地汽车客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费y （元）与行李重量x (kg)的关系用直线AB 的方程表示，试求： （1）直线AB 的方程； （2）旅客最多可免费携带多少行李？ 【解析】（1）由图知，A (60，6)，B (80，10)代入两点式可得AB 方程为x – 5y – 30
直线的两点式方程教案 一、教学目标 1、知识与技能 （1）握直线方程的两点的形式特点及适用范围； （2）了解直线方程截距式的形式特点及适用范围。 2、过程与方法 让学生在应用旧知识的探究过程中获得到新的结论，并通过新旧知识的比较、分析、应用获得新知识的特点。 3、情态与价值观 （1）认识事物之间的普遍联系与相互转化； （2）培养学生用联系的观点看问题。 二、教学重点、难点： 1、 重点：直线方程两点式。 2、难点：两点式推导过程的理解。 三、教学设想 问 题 1、利用点斜式解答如下问题： （1）已知直线l 经过两点)5,3(),2,1(21P P ,求直线l 的方程. （2）已知两点),(),,(222211y x P x x P 其中),(2121y y x x ≠≠，求通过这两点的直线方程。 设计意图 遵循由浅及深，由特殊到一般的认知规律。使学生在已有的知识基础上获得新结论，达到温故知新的目的。 师生活动 教师引导学生：根据已有的知识，要求直线方程，应知道什么条件？能不能把问题转化为已经解决的问题呢？在此基础上，学生根据已知两点的坐标，先判断是否存在斜率，然后求出直线的斜率，从而可求出直线方程： （1）)1(2 32-= -x y （2）)(11 2121x x x x y y y y ---=- 教师指出：当21y y ≠时，方程可以写成 ),(21211 211 21y y x x x x x x y y y y ≠≠--= -- 由于这个直线方程由两点确定，所以我们把它叫直线的两点式方程，简称两点式
问 题 2、 若点),(),,(222211y x P x x P 中有21x x =，或21y y =，此时这两点的直线方程是什么？ 设计意图 使学生懂得两点式的适用范围和当已知的两点不满足两点式的条件时它的方程形式。 师生活动 教师引导学生通过画图、观察和分析，发现当21x x =时，直线与x 轴垂直，所以直线方程为：1x x =；当21y y =时，直线与y 轴垂直，直线方程为：1y y =。 问 题 3、例题教学 已知直线l 与x 轴的交点为A )0,(a ，与y 轴的交点为B ),0(b ，其中0,0≠≠b a ，求直线l 的方程。 设计意图 使学生学会用两点式求直线方程；理解截距式源于两点式，是两点式的特殊情形。 师生活动 教师引导学生分析题目中所给的条件有什么特点？可以用多少方法来求直线l 的方程？那种方法更为简捷？然后由求出直线方程： 1=+ b y a x 教师指出：b a ,的几何意义和截距式方程的概念。 问 题 4、例题教学 已知三角形的三个顶点A （-5，0），B （3，-3），C （0，2），求BC 边所在直线的方程，以及该边上中线所在直线的方程。 设计意图 让学生学会根据题目中所给的条件，选择恰当的直线方程解决问题。 师生活动 教师给出中点坐标公式，学生根据自己的理解，选择恰当方法求出边BC 所在的直线方程和该边上中线所在直线方程。在此基础上，学生交流各自的作法，并进行比较。
课题：直线的两点式、截距式方程 一、学习目标： 1.掌握两点式方程并会应用其求直线方程. 2.掌握直线的截距式方程、中点坐标公式. 二、重点：两点式方程、截距式方程及其应用. 难点：截距式方程的应用. 三、学习过程： （1）复习回顾： 1.什么是直线的点斜式方程和斜截式方程？其适用范围是什么？ 2.已知直线上两点),(),,(222111y x p y x p （2121,y y x x ≠≠）如何求出这条直线方程？ （2）导读：阅读课本9795P P -,完成下列问题： 1.给定两个点),(),,(222111y x p y x p .当21x x ≠时,过这两点的直线的斜率 k = .把21p p 或作为定点，由点斜式方程可得过这两点的直线 方程为 .当21y y ≠时可得两点式方程为 . 2. 两点式方程的适用范围是什么？当时，或2121y y x x ==过这两点的 直线方程是什么？ （3）导思： 1.直线l 在x 轴上的截距的定义？直线l 在y 轴上的截距的定义？ 2.已知直线l 与x 轴的交点为A （a,0）,与y 轴的交点为B （0，b ）其 中a .0,0≠≠b 求直线l 的方程. 3.写出直线的截距式方程,其适用范围是什么？ 4.已知点的坐标为 的中点，则为p p p p y x p y x p 21222111),,(),,( 即中点坐标公式. （4）导练： 1.已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2).求BC 边所在直线的方程,以及该边上中线所在直线的方程. 2.求过点p (2,3),并且在两轴上的截距相等的直线方程. 四、达标训练 1.课本97p 1,2,3. 2.课本100p A 组 1.(4)(5)(6),4,7,8. 五、反思小结：
-1- 3.2.2直线的两点式方程 一、学习目标: 知识与技能：（1）掌握直线方程的两点的形式特点及适用范围；（2）了解直线方程截距式的形式特点及适用范围。 过程与方法：让学生在应用旧知识的探究过程中获得到新的结论，并通过新旧知识的比较、分析、应用获得新知识的特点。 情感态度与价值观：（1）认识事物之间的普遍联系与相互转化；（2）培养学生用联系的观点看问题。 二、学习重点、难点： 1、 重点：直线方程两点式。 2、难点：两点式推导过程的理解。 三、使用说明及学法指导: 注意逐字逐句仔细审题，认真思考阅读教材、独立规范作答。牢记直线方程的表达形式及解题方法规律。平行班完成学案AB 类问题. 四、知识链接： 过点),(000y x P ，斜率是k 的直线l 上的点，其坐标都满足方程)(00x x k y y -=- 它叫做直线的点斜式方程，简称点斜式。 斜截式方程：b kx y += 理解“截距”与“距离”两个概念的区别. 五、学习过程： A 问题1、利用点斜式解答如下问题： （1）已知直线l 经过两点)5,3(),2,1(21P P ,求直线l 的方程. （2）已知两点),(),,(222211y x P x x P 其中),(2121 y y x x ≠≠，求通过这两点的直线方程。 由于这个直线方程由两点确定，所以我们把它叫直线的两点式方程. B 问题2、若点),(),,(222211y x P x x P 中有21x x =，或21y y =，此时这两点的直线方程是 什么？ 例1已知直线l 与x 轴的交点为A )0,(a ，与y 轴的交点为B ),0(b ，其中0,0≠≠b a ，求直线l 的方程。
直线的两点式方程 一、教学目标 1、知识与技能：（1）掌握直线方程的两点的形式特点及适用范围； （2）了解直线方程截距式的形式特点及适用范围。 2、过程与方法 让学生在应用旧知识的探究过程中获得到新的结论，并通过新旧知识的比较、分析、应用获得新知识的特点。 3、情态与价值观 （1）认识事物之间的普遍联系与相互转化； （2）培养学生用联系的观点看问题。 二、教学重点、难点 教学重点：掌握直线的两点式方程。 教学难点：直线的两点式方程的推导过程和理解它。 三、教具 ：三角板。学具：三角尺。 四、教学过程 （一）复习导入 上节课我们学习了直线的点斜式方程，现在同学们利用点斜式解答如下问题：①已知直线l 经过两点)5,3(),2,1(21P P ,求直线l 的方程.②已知两点) ,(),,(222211y x P x x P 其中),(2121y y x x ≠≠，求通过这两点的直线方程。 学生解得：①)1(2 3 2-=-x y ；②)(112121 x x x x y y y y ---=- （二）新课讲解 1 、直线两点式方程推导 教师指出：对于上面的②当21y y ≠时，方程可以写成 ),(21211 21 121y y x x x x x x y y y y ≠≠--=-- 由于这个直线方程由两点确定，所以我们把它叫直线的两点式方程，简称两点式。 思考；若点),(),,(222211y x P x x P 中有21x x =，或21y y =，此时这两点的直线方程是什么？ 教师引导学生通过画图、观察和分析，发现当21x x =时，直线与x 轴垂直，所以直线方程为：1x x =；当21y y =时，直线与y 轴垂直，直线方程为：1y y =； 使学生懂得两点式的适用范围和当已知的两点不满足两点式的条件时它的方程形式。告诉学生经过点) ,(),,(222211y x P x x P 的所有直线的方程可以写成： 0))(())((121121=-----y y x x x x y y 2、例题讲解
直线的两点式方程 整体设计 教学分析 本节课的关键是关于两点式的推导以及斜率k不存在或斜率k=0时对两点式的讨论及变形.直线方程的两点式可由点斜式导出.若已知两点恰好在坐标轴上(非原点)，则可用两点式的特例截距式写出直线的方程.由于由截距式方程可直接确定直线与x轴和y轴的交点的坐标，因此用截距式画直线比较方便.在解决与截距有关或直线与坐标轴围成的三角形面积、周长等问题时，经常使用截距式.但当直线与坐标轴平行时，有一个截距不存在；当直线通过原点时，两个截距均为零.在这两种情况下都不能用截距式. 三维目标 1.让学生掌握直线方程两点式和截距式的发现和推导过程，并能运用这两种形式求出直线的方程.培养学生数形结合的数学思想，为今后的学习打下良好的基础. 2.了解直线方程截距式的形式特点及适用范围，培养学生树立辩证统一的观点，培养学生形成严谨的科学态度和求简的数学精神. 重点难点 教学重点:直线方程两点式和截距式. 教学难点:关于两点式的推导以及斜率k不存在或斜率k=0时对两点式方程的讨论及变形. 课时安排 1课时 教学过程 导入新课 思路1.上节课我们学习了直线方程的点斜式，请问点斜式方程是什么？点斜式方程是怎样推导的？利用点斜式解答如下问题： （1）已知直线l经过两点P1(1,2),P2(3,5),求直线l的方程. （2）已知两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)，求通过这两点的直线方程. 思路2.要学生求直线的方程，题目如下： ①A(8，-1)，B(-2，4)； ②A(6，-4)，B(-1，2)； ③A(x1，y1)，B(x2，y2)(x1≠x2). (分别找3个同学说上述题的求解过程和答案，并着重要求说求k及求解过程) 这个答案对我们有何启示？求解过程可不可以简化？我们可不可以把这种直线方程取一个什么名字呢? 推进新课 新知探究 提出问题 ①已知两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)，求通过这两点的直线方程. ②若点P1(x1,y1),P2(x2,y2)中有x1=x2或y1=y2，此时这两点的直线方程是什么？ ③两点式公式运用时应注意什么？ ④已知直线l与x轴的交点为A(a,0)，与y轴的交点为B(0,b)，其中a≠0,b≠0，求直线l 的方程. ⑤a、b表示截距是不是直线与坐标轴的两个交点到原点的距离？ ⑥截距式不能表示平面坐标系下哪些直线？ 活动:①教师引导学生：根据已有的知识，要求直线方程，应知道什么条件？能不能把问题
【课 题：】直线的点斜式方程 【教学目的：】 知识目标：在直角坐标平面，已知直线上一点和直线的斜率或已知 直线上两点，会求直线的方程；给出直线的点斜式方程， 能观察直线的斜率和直线经过的定点 能力目标：通过直线的点斜式方程向斜截式方程的过渡，训练学生由 一般到特殊的处理问题方法；通过直线的方程特征观察直 线的位置特征，培养学生的数形结合能力． 德育目标：通过直线方程的几种形式培养学生的美学意识． 【教学重点：】由于斜截式方程是点斜式方程的特殊情况，教学重点应放在 推导直线的斜截式方程上．实质上它也是整个直线方程理论 的基础。 【教学难点：】在推导出直线的点斜式方程后，说明得到的就是直线的方程， 即直线上每个点的坐标都是方程的解；反过来，以这个方程 的解为坐标的点在直线上． 【授课类型：】新授课 【课时安排：】1课时 【教 具：】 【教学过程：】 1、复习引入： 2、讲解新课： (1)点斜式 已知直线l 的斜率是k ，并且经过点P 1(x 1，y 1)，直线是确定的，也就是可求的，怎样求直线l 的方程(图1-24)？ 设点P(x ，y)是直线l 上不同于P 1(x 1，y 1)的任意一点，根据经过两点的斜率公式得 1 1x x y y k --= (1) 即y-y 1=k(x-x 1) (2) 注意方程(1)与方程(2)的差异：点P 1的坐标不满足方程(1)而满足方程(2)，因此，点P 1不在方程(1)表示的图形上而在方程(2)表示的图形上，方程(1)不能称作直线l 的方程． 重复上面的过程，可以证明直线上每个点的坐标都是这个方程的解；对上面的过程逆推，可以证明以这个方程的解为坐标的点都在直线l 上，所以这个方程就是过点P 1、斜率为k 的直线l 的方程．(实质上是证明了直线的方程与方程的直线的关系) 这个方程是由直线上一点和直线的斜率确定的，叫做直线方程的点斜式． 注：当直线的斜率为0°时(图1-25)，k=0，直线的方程是y=y 1．