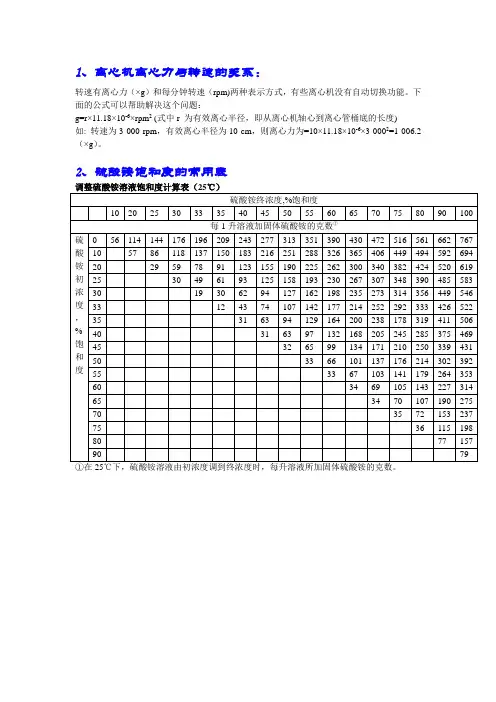
离心机转速rpm与g换算公式

工业离心机的转速计算公式工业离心机是一种常用的分离设备，广泛应用于化工、制药、食品、生物工程等领域。

它通过高速旋转的离心力将混合物中的不同成分分离出来，是生产过程中不可或缺的重要设备之一。

在使用离心机的过程中，了解离心机的转速是非常重要的，因为它直接影响到分离效果和设备的安全运行。

因此，本文将介绍工业离心机的转速计算公式及其相关知识。

首先，让我们了解一下离心机的基本原理。

离心机利用离心力将混合物中的不同成分分离出来，其原理是利用物体在旋转时受到的离心力而产生的分离效应。

当离心机高速旋转时，离心力会使得混合物中的不同成分受到不同的离心力，从而实现分离。

而离心机的转速则是影响离心力大小的重要因素之一。

工业离心机的转速通常用转每分钟（rpm）来表示，它是指离心机转动一圈所需的时间。

离心机的转速与其分离效果和设备安全运行密切相关，因此需要合理计算和控制。

在实际应用中，我们通常使用以下的转速计算公式来计算离心机的转速：n = (1.118 √(r g)) / r。

其中，n表示离心机的转速（rpm），r表示离心机半径（米），g表示重力加速度（米/秒^2）。

这个公式是根据离心力的计算公式推导而来的。

离心力的计算公式为：F = m r ω^2。

其中，F表示离心力（牛顿），m表示物体的质量（千克），r表示离心机半径（米），ω表示角速度（弧度/秒）。

根据角速度的定义，我们知道角速度与转速之间存在以下关系：ω = 2πn / 60。

将角速度的表达式代入离心力的计算公式中，可以得到：F = m r (2πn / 60)^2。

根据牛顿第二定律，离心力与加速度之间存在以下关系：F = m a。

结合以上两个公式，可以得到离心加速度与转速之间的关系：a = (4π^2 n^2 r) / (60^2)。

由于重力加速度g就是离心加速度a，因此可以得到转速与半径、重力加速度之间的关系：n = (1.118 √(r g)) / r。

通过这个转速计算公式，我们可以很方便地计算出离心机的转速。

离心机转速换算公式（rpm与g）离心力Centrifugal force (F) 离心力作为真实的力根本就不存在，在非惯性系中为计算方便假想的一个力。

请看下面的说明：向心力使物体受到指向一个中心点的吸引、或推斥或任何倾向于该点的作用。

笛卡儿把离心力解释为物体保持其“限定量”的一种趋势。

它们的区别就是，向心力是惯性参考系下的，而离心力是非惯性系中的力。

我们处理物理题时都是在惯性系下（此时牛顿定律才成立），所以一般不用离心力这个概念。

由于根本不是一个情况下的概念，我们无法对他们的方向和大小进行比较。

F=mω2rω：旋转角速度(弧度／秒) r:旋转体离旋转轴的距离(cm) m：颗粒质量相对离心力Relative centrifugal force (RCF)RCF 就是实际离心力转化为重力加速度的倍数g为重力加速度(9.80665m/s2)同为转于旋转一周等于2π弧度，因此转子的角速度以每分钟旋转的次数(每分钟转数n或r/min)表示：一般情况下，低速离心时常以r ／min来表示。

3、分离因素计算公式：RCF=F离心力／F重力= mωˆ2r/mg=ωˆ2r/g= （2*π*r/r*rpm）ˆ2*r/g =（2*π* rpm）ˆ2*r/g =（2*π）ˆ2/g * rpm^2* r 注：rpm应折换成转/秒,r转换成m=（2*π/60）ˆ2/g * rpm^2* r/100=1.119 x 10-5 x (rpm)^2 x r 换算后，rpm为r/min，r为cm例如：直径1000mm，转速1000转/分的离心机，分离因素为：RCF(1000)=(2*3.1415*16.667)^2*0.5/9.8=104.72^2*0.5/9.8=560在有关离心机的实验中，RCF(relative centrifugal field)表示相对离心场，以重力加速度g（980.66cm/s2）的倍数来表示；rpm(revolution per minute，或r/min)表示离心机每分钟的转数。

离心机之离心力G和转速rpm的换算离心原理：当含有细小颗粒的悬浮液静置时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

如红细胞，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

(浮力) 此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体质量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重，故需利用离心机产生强大的离心力，才能迫使这些微粒克服扩散沉降。

（扩散）离心就是利用离心机转子高速旋转产生的强大的离心力，加快液体中颗粒的沉降速度，把样品中不同沉降系数和浮力密度的物质分离开。

离心力(F)的大小取决于离心转头的角速度(w，r/min)和物质颗粒距离心轴的距离(r，cm)。

它们的关系是：F=rw^2为方便起见，F常用相对离心力也就是地心引力的倍数表示。

即把F值除以重力加速度g (约等于9.8m/s2 )得到离心力是重力的多少倍，称作多少个g。

例如离心机转头平均半径是6cm，当转速是60 000 r/min时，离心力=0.06*6000^2/9.8=220 000×g，表示此时作用在被离心物质上的离心力是日常地心引力的22万倍。

因此，转速r/min和离心力g值之间并不是成正比关系，还和半径有关。

同样的转速，半径大一倍，离心力(g值)也大一倍。

转速(r/min)和离心力(g值)之间的关系可用下式换算：G=1.11×(10^-5)×R×[rpm]2G为离心力，一般以g(重力加速度)的倍数来表示;10-5即：10的负五次方;[rpm]2即：转速的平方;R为半径，单位为厘米。

关于离心机及rpm单位与g(RCF)单位的换算离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 ra — 粒子旋转的加速度， m — 沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

或者用数字乘“g”来表示，例如25000×g，则表示相对离心力为25000。

相对离心力是指在离心场中，作用于颗粒的离心力相当于地球重力的倍数，单位是重力加速度“g”（980cm/sec2），此时“RCF”相对离心力可用下式计算：∴19×10－5×(rpm)2 rRCF = 1.1( rpm — revolutions per minute每分钟转数，r/min )由上式可见，只要给出旋转半径r，则RCF和rpm之间可以相互换算。

但是由于转头的形状及结构的差异，使每台离心机的离心管，从管口至管底的各点与旋转轴之间的距离是不一样的，所以在计算是规定旋转半径均用平均半径“ra v”代替：ra v=( r min＋rmax) / 2一般情况下，低速离心时常以转速“rpm”来表示，高速离心时则以“g” 表示。

计算颗粒的相对离心力时，应注意离心管与旋转轴中心的距离“r”不同，即沉降颗粒在离心管中所处位置不同，则所受离心力也不同。

因此在报告超离心条件时，通常总是用地心引力的倍数“×g”代替每分钟转数“rpm”，因为它可以真实地反映颗粒在离心管内不同位置的离心力及其动态变化。

关于离心机及rpm单位与g(rcf)单位的换算 [关键字:离心离心机离心技术离心单位离心单位的换算 rpm rcf xg贴子原创,文字内容来自网络,学习交流!离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 ra —粒子旋转的加速度， m —沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

或者用数字乘“g”来表示，例如25000×g，则表示相对离心力为25000。

相对离心力是指在离心场中，作用于颗粒的离心力相当于地球重力的倍数，单位是重力加速度“g”（980cm/sec2），此时“RCF”相对离心力可用下式计算：∴ RCF = 1.119×10－5×(rpm)2 r( rpm — revolutions per minute每分钟转数，r/min )由上式可见，只要给出旋转半径r，则RCF和rpm之间可以相互换算。

但是由于转头的形状及结构的差异，使每台离心机的离心管，从管口至管底的各点与旋转轴之间的距离是不一样的，所以在计算是规定旋转半径均用平均半径“ra v”代替：ra v=( r min＋rmax) / 2一般情况下，低速离心时常以转速“rpm”来表示，高速离心时则以“g” 表示。

计算颗粒的相对离心力时，应注意离心管与旋转轴中心的距离“r”不同，即沉降颗粒在离心管中所处位置不同，则所受离心力也不同。

离心机转速与换算公式
在有关离心机地实验中，标准地指示样本离心条件应该是用( )来衡量, 而在实际大家实验过程中, 往往习惯用即每分钟转速来表示. 为了更好地对二者进行换算,特总结下文.
即表示相对离心场，以重力加速度（）地倍数来表示；( ，或)表示离心机每分钟地转数.
与之间地换算公式为：×× ()×
其中表示离心机转轴中心与离心管中心地距离（如下图所示），单位为.由于离心管地位置由转子（）决定，因此必须由查阅相关转子地参数而得.
与地换算也可以经由下表直接读出，方法是在下图标尺上取已知地半径值和在标尺上取已知相对离心力值，这两点间线地沿长线在标尺地交点即为所要换算地值.反之亦然.。

关于离心机及rpm单位与g(RCF)单位的换算离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 ra — 粒子旋转的加速度， m — 沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

或者用数字乘“g”来表示，例如25000×g，则表示相对离心力为25000。

相对离心力是指在离心场中，作用于颗粒的离心力相当于地球重力的倍数，单位是重力加速度“g”（980cm/sec2），此时“RCF”相对离心力可用下式计算：∴19×10－5×(rpm)2 rRCF = 1.1( rpm — revolutions per minute每分钟转数，r/min )由上式可见，只要给出旋转半径r，则RCF和rpm之间可以相互换算。

但是由于转头的形状及结构的差异，使每台离心机的离心管，从管口至管底的各点与旋转轴之间的距离是不一样的，所以在计算是规定旋转半径均用平均半径“ra v”代替：ra v=( r min＋rmax) / 2一般情况下，低速离心时常以转速“rpm”来表示，高速离心时则以“g” 表示。

计算颗粒的相对离心力时，应注意离心管与旋转轴中心的距离“r”不同，即沉降颗粒在离心管中所处位置不同，则所受离心力也不同。

因此在报告超离心条件时，通常总是用地心引力的倍数“×g”代替每分钟转数“rpm”，因为它可以真实地反映颗粒在离心管内不同位置的离心力及其动态变化。

关于离心机及rpm单位与g(RCF)单位的换算离心就是利用离心机转子高速旋转产生的强大的离心力，加快液体中颗粒的沉降速度，把样品中不同沉降系数和浮力密度的物质分离开。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动。

当含有细小颗粒的悬浮液静置不动时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

象红血球大小的颗粒，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体重量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动。

离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 r a —粒子旋转的加速度， m —沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

关于离心机及rpm单位与g(RCF)单位的换算离心就是利用离心机转子高速旋转产生的强大的离心力，加快液体中颗粒的沉降速度，把样品中不同沉降系数和浮力密度的物质分离开。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动。

当含有细小颗粒的悬浮液静置不动时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

象红血球大小的颗粒，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体重量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动。

离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 r a —粒子旋转的加速度， m —沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

离心力Centrifugal force (F) 离心力作为真实的力根本就不存在，在非惯性系中为计算方便假想的一个力。

请看下面的说明：向心力使物体受到指向一个中心点的吸引、或推斥或任何倾向于该点的作用。

笛卡儿把离心力解释为物体保持其“限定量”的一种趋势。

它们的区别就是，向心力是惯性参考系下的，而离心力是非惯性系中的力。

我们处理物理题时都是在惯性系下（此时牛顿定律才成立），所以一般不用离心力这个概念。

由于根本不是一个情况下的概念，我们无法对他们的方向和大小进行比较。

F=mω2rω：旋转角速度(弧度／秒) r:旋转体离旋转轴的距离(cm) m：颗粒质量相对离心力Relative centrifugal force (RCF)RCF 就是实际离心力转化为重力加速度的倍数g为重力加速度(9.80665m/s2)同为转于旋转一周等于2π弧度，因此转子的角速度以每分钟旋转的次数(每分钟转数n或r/min)表示：一般情况下，低速离心时常以r／min来表示。

3、分离因素计算公式：RCF=F离心力／F重力= mωˆ2r/mg= ωˆ2r/g= （2*π*r/r*rpm）ˆ2*r/g =（2*π* rpm）ˆ2*r/g =（2*π）ˆ2/g * rpm^2* r注：rpm应折换成转/秒,r转换成m=（2*π/60）ˆ2/g * rpm^2* r/100=1.119 x 10-5 x (rpm)^2 x r 换算后，rpm为r/min，r为cm例如：直径1000mm，转速1000转/分的离心机，分离因素为：RCF(1000)=(2*3.1415*16.667)^2*0.5/9.8=104.72^2*0.5/9.8=560在有关离心机的实验中，RCF(relative centrifugal field)表示相对离心场，以重力加速度g （980.66cm/s2）的倍数来表示；rpm(revolution per minute，或r/min)表示离心机每分钟的转数。

离心力G和转速RPM之间的换算关系离心原理当含有细小颗粒的悬浮液静置不动时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

象红血球大小的颗粒，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体重量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动相对离心力转速r/min和离心力g值之间并不是成正比关系，还和半径有关。

同样的转速，半径大一倍，离心力(g值)也大一倍。

转速(r/min)和离心力(g值)之间的关系可用下式换算：其换算公式如下：G＝1.11×(10-5)×R×[rpm]２G为离心力，一般以ｇ（重力加速度）的倍数来表示。

10-5即：10的负五次方。

[rpm]２即：转速的平方。

R为半径，单位为厘米。

例如，离心半径为10厘米，转速为8000，其离心力为：G＝1.11×(10-5)×10×[8000]２＝7104即离心力为7104g. 而当离心力为8000g 时，其转速应为：8489即约为8500rpm。

关于离心机及rpm单位与g(RCF)单位的换算离心技术在生物科学，特别是在生物化学和分子生物学研究领域，已得到十分广泛的应用，每个生物化学和分子生物学实验室都要装备多种型式的离心机。

离心技术主要用于各种生物样品的分离和制备，生物样品悬浮液在高速旋转下，由于巨大的离心力作用，使悬浮的微小颗粒（细胞器、生物大分子的沉淀等）以一定的速度沉降，从而与溶液得以分离，而沉降速度取决于颗粒的质量、大小和密度。

基本原理:当一个粒子（生物大分子或细胞器）在高速旋转下受到离心力作用时，此离心力“F”由下式定义，即：F = m&S226;a = m&S226;ω2 ra — 粒子旋转的加速度， m — 沉降粒子的有效质量，ω—粒子旋转的角速度， r—粒子的旋转半径( cm )。

通常离心力常用地球引力的倍数来表示，因而称为相对离心力“ RCF ”。

或者用数字乘“g”来表示，例如25000×g，则表示相对离心力为25000。

相对离心力是指在离心场中，作用于颗粒的离心力相当于地球重力的倍数，单位是重力加速度“g”（980cm/sec2），此时“RCF”相对离心力可用下式计算：∴19×10－5×(rpm)2 rRCF = 1.1( rpm — revolutions per minute每分钟转数，r/min )由上式可见，只要给出旋转半径r，则RCF和rpm之间可以相互换算。

但是由于转头的形状及结构的差异，使每台离心机的离心管，从管口至管底的各点与旋转轴之间的距离是不一样的，所以在计算是规定旋转半径均用平均半径“ra v”代替：ra v=( r min＋rmax) / 2一般情况下，低速离心时常以转速“rpm”来表示，高速离心时则以“g” 表示。

计算颗粒的相对离心力时，应注意离心管与旋转轴中心的距离“r”不同，即沉降颗粒在离心管中所处位置不同，则所受离心力也不同。

因此在报告超离心条件时，通常总是用地心引力的倍数“×g”代替每分钟转数“rpm”，因为它可以真实地反映颗粒在离心管内不同位置的离心力及其动态变化。

离心机之离心力G和转速RPM之间的换算离心原理：当含有细小颗粒的悬浮液静置不动时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

象红血球大小的颗粒，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体重量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重。

所以需要利用离心机产生强大的离心力，才能迫使这些微粒克服扩散产生沉降运动。

离心就是利用离心机转子高速旋转产生的强大的离心力，加快液体中颗粒的沉降速度，把样品中不同沉降系数和浮力密度的物质分离开。

离心力(F)的大小取决于离心转头的角速度(ˉ，r/min)和物质颗粒距离心轴的距离(r，cm)。

它们的关系是：F=ˉ2 R为方便起见，F常用相对离心力也就是地心引力的倍数表示。

即把F值除以重力加速度g (约等于9.8m/s2 )得到离心力是重力的多少倍，称作多少个g。

例如离心机转头平均半径是6cm，当转速是60 000 r/min 时，离心力是240 000×g，表示此时作用在被离心物质上的离心力是日常地心引力的24万倍。

因此，转速r/min和离心力g值之间并不是成正比关系，还和半径有关。

同样的转速，半径大一倍，离心力(g值)也大一倍。

转速(r/min)和离心力(g值)之间的关系可用下式换算：G=1.11×(10^-5)×R×[rpm]2G为离心力，一般以g(重力加速度)的倍数来表示;10-5即：10的负五次方;[rpm]2即：转速的平方;R为半径，单位为厘米。

离心单位g（重力加速度）与离心机的转速之间存在换算关系。

这个关系可以通过下面的公式计算：
g = r ×(2πN/60)^2
其中，g 表示离心加速度（单位为g），r 表示离心机半径（单位为厘米），N 表示离心机的转速（单位为转/分钟）。

根据上述公式，我们可以得出转速N 与离心加速度g 之间的换算关系为：
N = √(g ×60^2 / (2π×r))
需要注意的是，这个换算关系是在假设离心机的半径保持不变的情况下得出的。

如果半径发生变化，换算关系也会随之改变。

在实际应用中，如果已知离心加速度g 和离心机半径r，可以使用上述公式计算出对应的转速N。

反之，如果已知转速N 和离心机半径r，可以使用上述公式计算出对应的离心加速度g。

这种换算关系在实验室、医学和生物学等领域中经常用于离心实验的设计和参数调整。

离心速度换算
离心速度指的是物体在旋转过程中离中心点的距离与旋转半径
的比值所得到的速度大小。

离心速度的单位是米每秒（m/s），常用于描述离心机等旋转设备中物体的离心分离速度。

离心速度的计算公式为：
V = rω
其中，V表示离心速度，r表示物体离中心点的距离，ω表示物
体的角速度（弧度/秒）。

在实际应用中，我们常常需要将离心速度从不同的单位进行换算。

下面是一些常见单位的换算关系：
1. 米每秒（m/s）与转每分钟（rpm）的换算关系为：
V(m/s) = 0.10472 × r × n
其中，n表示转速（rpm），0.10472是一个常数，r表示旋转半
径（米）。

2. 米每秒（m/s）与重力加速度（g）的换算关系为：
V(m/s) = r × g
其中，g表示地球表面的重力加速度，约为9.8米每秒的平方（m/s^2）。

需要注意的是，在进行离心分离等操作时，离心机的转速和离心加速度都需要严格控制，以确保设备运行的安全和有效性。

- 1 -。

离心机之离心力G和转速rpm的换算离心原理：当含有细小颗粒的悬浮液静置时，由于重力场的作用使得悬浮的颗粒逐渐下沉。

粒子越重，下沉越快，反之密度比液体小的粒子就会上浮。

微粒在重力场下移动的速度与微粒的大小、形态和密度有关，并且又与重力场的强度及液体的粘度有关。

如红细胞，直径为数微米，就可以在通常重力作用下观察到它们的沉降过程。

(浮力) 此外，物质在介质中沉降时还伴随有扩散现象。

扩散是无条件的绝对的。

扩散与物质的质量成反比，颗粒越小扩散越严重。

而沉降是相对的，有条件的，要受到外力才能运动。

沉降与物体质量成正比，颗粒越大沉降越快。

对小于几微米的微粒如病毒或蛋白质等，它们在溶液中成胶体或半胶体状态，仅仅利用重力是不可能观察到沉降过程的。

因为颗粒越小沉降越慢，而扩散现象则越严重，故需利用离心机产生强大的离心力，才能迫使这些微粒克服扩散沉降。

（扩散）离心就是利用离心机转子高速旋转产生的强大的离心力，加快液体中颗粒的沉降速度，把样品中不同沉降系数和浮力密度的物质分离开。

离心力(F)的大小取决于离心转头的角速度(w，r/min)和物质颗粒距离心轴的距离(r，cm)。

它们的关系是：F=rw^2为方便起见，F常用相对离心力也就是地心引力的倍数表示。

即把F值除以重力加速度g (约等于9.8m/s2 )得到离心力是重力的多少倍，称作多少个g。

例如离心机转头平均半径是6cm，当转速是60 000 r/min时，离心力=0.06*6000^2/9.8=220 000×g，表示此时作用在被离心物质上的离心力是日常地心引力的22万倍。

因此，转速r/min和离心力g值之间并不是成正比关系，还和半径有关。

同样的转速，半径大一倍，离心力(g值)也大一倍。

转速(r/min)和离心力(g值)之间的关系可用下式换算：G=1.11×(10^-5)×R×[rpm]2G为离心力，一般以g(重力加速度)的倍数来表示;10-5即：10的负五次方;[rpm]2即：转速的平方;R为半径，单位为厘米。