两点间距离公式及中点坐标公式

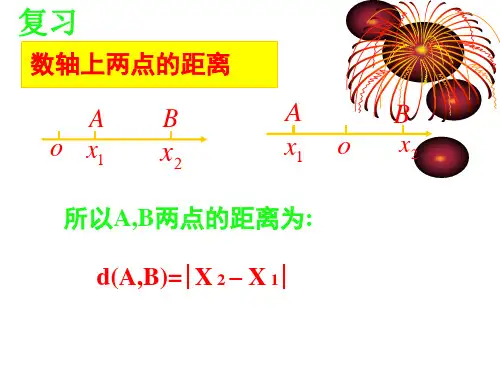
两点间距离公式中点公式Prepared on 21 November 2021两点间距离公式、中点公式教学目标：掌握两点间坐标公式、中点公式教学重点、难点：公式的应用教学过程：一、两点间距离公式：初中曾学习过数轴上两点间距离，实际就是求数轴上两点所表示的两个数的差的绝对值。

现在我们研究平面内任意两点P1（x1，y1），P2（x2，y2）间的距离。

如图，由点P1，P2分别作x轴的垂线P1M1，P2M2，与x轴分别交于点M1（x1，0），M2（x2，0）；再由点P1，P2分别作y轴的垂线P1N1，P2N2，与y轴分别交于N1（0，y1），N2（0，y2），直线P1N1，P2M2相交于Q点，则有P1Q＝M1M2＝｜x2－x1｜，Q P 2＝N 1N 2＝｜y 2－y 1｜。

由勾股定理，可得P 1P 22＝P 1Q 2＋Q P 22＝｜x 2－x 1｜2＋｜y 2－y 1｜2＝（x 2－x 1）2＋（y 2－y 1）2由此得到平面内P 1（x 1，y 1），P 2（x 2，y 2）两点间的距离公式 例1、求平面上两点A （1，-2），B （3，5）之间的距离。

解 ()()53251322=++-=AB二、中点公式平面内任意两点P 1（x 1，y 1），P 2（x 2，y 2），线段的中点，求点P 的坐标（x ，y ）.由点P 1，P 2分别作x 轴的垂线P 1M 1，P 2M 2，与x 轴分别交于点M 1（x 1，0），M 2（x 2，0），M (x ,0),则即 x x x x -=-21所以 221x x x += 类似上面方法可得因此，点21p p 之间锁链线段的中点坐标为221x x x +=，221y y y += 上式称为线段的中点公式。

例2、有一线段A B ，它的中点坐标是（4，2），端点A 坐标是（-2，3），求另一端点的坐标。

解 设另一端点B 坐标为()y x ,，由中点坐标公式可知 232,224y x +=+-= 解之得1,10==y x所以端点坐标为()1,10。

两点坐标公式和中点坐标公式
两点坐标公式指的是计算两个坐标点之间的直线距离的公式，而中点坐标公式是计算两个坐标点连线的中点坐标的公式。

1.两点坐标公式：
设两个点的坐标分别为(x1,y1)和(x2,y2)，则它们之间的直
线距离d可以使用以下公式进行计算：
d=√((x2x1)^2+(y2y1)^2)
其中"^"表示乘方运算。

这个公式的原理是根据勾股定理，通过计算两个坐标在x轴
和y轴上的差值的平方和，再开平方得到直线距离。

2.中点坐标公式：
设两个点的坐标分别为(x1,y1)和(x2,y2)，它们连线的中点
坐标为(xm,ym)，则中点坐标可以使用以下公式进行计算：
xm=(x1+x2)/2
ym=(y1+y2)/2
这个公式的原理是将两个坐标点在x轴和y轴分别做平均，
得到中点的横纵坐标。

两点间的距离公式及中点公式在我们学习数学的旅程中，有两个非常实用的宝贝，那就是两点间的距离公式和中点公式。

这两个公式就像是我们探索数学世界的秘密武器，能帮助我们解决好多有趣又有点小挑战的问题。

先来说说两点间的距离公式。

想象一下，在一个大大的平面上，有两个点 A(x1, y1) 和 B(x2, y2)，就好像是两个小伙伴在操场上站着。

那怎么算出这两个小伙伴之间的距离呢？这时候两点间的距离公式就派上用场啦，它就像是一把神奇的尺子，能告诉我们答案。

公式是：d = √[(x2 - x1)² + (y2 - y1)²] 。

给大家举个例子吧。

有一次我去公园散步，看到两个花坛，一个在坐标（3，5）的位置，另一个在（7，9）的位置。

我就想啊，这两个花坛之间的距离到底是多少呢？我马上就想到了两点间的距离公式，把数字代进去，算出来距离是√[(7 - 3)² + (9 - 5)²] = √[4² + 4²] = √32 =4√2 。

哇，一下子就知道了它们之间的距离，感觉自己就像个数学小侦探，特有成就感！再来说说中点公式。

假如还是这两个点 A(x1, y1) 和 B(x2, y2)，那它们连线的中点坐标是啥呢？中点公式告诉我们：中点坐标为（(x1 + x2) / 2, (y1 + y2) / 2）。

我想起有一次帮小朋友们分糖果。

有两个小朋友分别站在不同的位置，我想把糖果公平地放在他们中间的位置，让他们过来拿都差不多远。

这时候中点公式就帮了大忙，我算出了中点的位置，把糖果放在那里，两个小朋友都很开心，觉得特别公平。

在实际生活中，这两个公式的用处可多啦。

比如在建筑设计中，工程师要确定两个建筑物之间的距离和中间的位置；在地图导航里，计算两个地点之间的距离和中间的参考点。

所以啊，同学们可别小看这两个公式，它们虽然看起来简单，但是作用大大的。

只要我们认真掌握，就能在数学的世界里畅行无阻，解决更多的难题，发现更多的乐趣！总之，两点间的距离公式和中点公式是我们数学学习中的好帮手，让我们继续努力，用它们去探索更多未知的数学奥秘吧！。

坐标中点公式和距离公式的区别和联系在数学中，坐标中点公式和距离公式是两种常用的计算方式，用于测量和描述平面上的点之间的位置关系。

虽然它们的应用场景有所不同，但在某些方面又存在联系。

1. 坐标中点公式坐标中点公式用于确定平面上两个点的中点坐标。

假设有两个点A(x1, y1)和B(x2, y2)，我们想要找到这两个点之间的中点坐标C(x, y)。

根据坐标中点公式，中点C的横坐标可以通过以下方式计算：x = (x1 + x2) / 2中点C的纵坐标可以通过以下方式计算：y = (y1 + y2) / 2通过这个公式，可以轻松地找到任意两个点的中点坐标。

坐标中点公式常常用于计算线段的中点和图形的重心等。

2. 距离公式距离公式用于计算平面上两个点之间的距离。

假设有两个点A(x1, y1)和B(x2, y2)，我们想要计算这两个点之间的距离d。

根据距离公式，两点之间的距离d可以通过以下方式计算：d = √((x2 - x1)² + (y2 - y1)²)这个公式基于勾股定理，通过计算两点间的水平距离和垂直距离，最后使用平方根得到两点间的直线距离。

距离公式在几何学中非常重要，常用于计算线段、直角三角形、多边形等的长度。

它能够量化点与点之间的空间距离，从而帮助我们解决许多与位置和距离相关的问题。

区别与联系尽管坐标中点公式和距离公式的应用场景和计算方式有所不同，但它们之间也存在着一些联系。

首先，这两个公式都是计算平面上的点。

坐标中点公式用于计算两个点的中点坐标，而距离公式用于计算两个点之间的距离。

其次，这两个公式的计算都是基于坐标的。

坐标中点公式通过取两个点的横纵坐标的平均值来计算中点的坐标，而距离公式则使用两点的坐标差的平方和来计算距离。

最后，这两个公式都提供了一种计算平面上点的方法，能够帮助我们在几何学和数学问题中解决与点相关的计算和分析。

在实际应用中，这两个公式常常相辅相成。

例如，在分析图形的特性时，可以使用坐标中点公式找到中点，然后结合距离公式计算各个点之间的距离，从而得到关于图形的更多信息。

两点距离公式中点公式在数学的奇妙世界里，两点距离公式和中点公式就像是两个忠实的小伙伴，默默地为我们解决着各种问题。

先来说说两点距离公式吧。

假设我们有两个点，A(x₁, y₁)和 B(x₂, y₂)，那么这两点之间的距离 d 就可以通过公式d = √[(x₂ - x₁)² + (y₂- y₁)²]来计算。

这个公式看起来有点复杂，其实理解起来并不难。

我记得有一次，我们班组织了一场校园寻宝活动。

老师在校园里藏了几个“宝贝”，然后给了我们几个点的坐标，让我们通过计算两点之间的距离来找到宝贝的位置。

我和同桌小明一组，拿到的第一个点是教室门口的 A(3, 5)，第二个点是操场边的大树 B(7, 9)。

我们赶紧拿出纸和笔，按照两点距离公式开始计算。

我负责计算横坐标的差值 (7 - 3)² = 16，小明负责计算纵坐标的差值 (9 - 5)² = 16，然后我俩一起把这两个差值相加，16 + 16 = 32，再对 32 开平方，得到√32 = 4√2。

算出距离后，我们一路小跑，按照这个距离去寻找，果然在差不多的位置发现了老师藏的第一个宝贝，是一本有趣的漫画书，可把我俩高兴坏了！再聊聊中点公式。

对于两点 A(x₁, y₁)和 B(x₂, y₂)，它们的中点坐标 M((x₁ + x₂)/2, (y₁ + y₂)/2)。

这个公式在很多实际问题中都能派上用场。

有一次上美术课，老师让我们画一幅校园风景图。

我想画教学楼和校门口之间的那段路，但是不知道怎么确定路的中间位置。

这时候我就想到了中点公式。

教学楼的位置假设是 A(2, 6)，校门口是 B(8, 2)，那中点的横坐标就是 (2 + 8) / 2 = 5，纵坐标是 (6 + 2) / 2 = 4，所以路的中间位置大概就在(5, 4)这个点。

按照这个位置画出来，感觉整幅图的比例都协调多了。

在日常生活中，两点距离公式和中点公式的应用也不少呢。