东南大学可变步长计数器

自主研学的电工电子实践课程建设摘要：在国家级实验教学示范中心建设中，东南大学电工电子实验中心以电工电子实践课程改革为突破口，设计了“强化项目背景工程性、强化知识应用综合性、强化实现方法多样性、强化实践过程探索性”的一系列实验项目，构建了具有“多知识点融合、跨理论课程知识融合、已有知识与拓展知识融合、课内实验与课外研学融合”特色的电工电子实践课程。

通过案例分析、任务要求、考核规则及研学方法引导，使学生在自主选择任务要求、自主设计方案进程、自主构建实验平台、自主展示实践成果的实践进程中形成“创新意识思维、自主学习研究、项目组织规划、知识综合运用、研究探索发现、工程设计实践”的综合能力与科研素质。

关键词：课程体系；实践模式；实践环境；师资队伍；创新能力一、电工电子实践课程改革背景2000年以前，高校电工电子实验教学常常是理论课的附属。

新世纪以来，各高校纷纷独立开设了“电路实验”、“模拟电子线路实验”、“数字逻辑电路实验”等多门自成体系的实验课程。

电工电子实践课程与电路、模拟电子线路、数字逻辑电路、EDA、在系统编程技术等电工电子基础课程相配合，是工科电类专业及部分非电专业的核心基础实验课程（见图1），也是我校电工电子实验中心教学工作的主体。

随着对学生自主研学、创新设计、工程实践能力与素养要求的提高，这种电工电子基础实验教学课程体系内容、教学进程模式的不足之处越来越凸显：一是实验课程相对于理论课程独立设置，课程间知识结构壁垒制约了跨课程知识体系的综合性实验项目的开设，而现实工程实践中是很难划清知识体系的界限的。

二是受实验教学验证理论知识为主的传统影响，实验项目大都围绕知识点主观设置，实验习题化严重，解决方法单一，缺乏分析研究的空间。

学生遇到实际工程问题仍然束手无策。

三是实验教学中教师直接传授知识有余，对问题的分析过程与解决方法引导不足。

四是实验课程大都是2～3学时的相互孤立的项目，任务要求统一有余，对知识的深度与广度要求层次少有梯度，因材施教不足，实验没有深入与升华的时空条件。

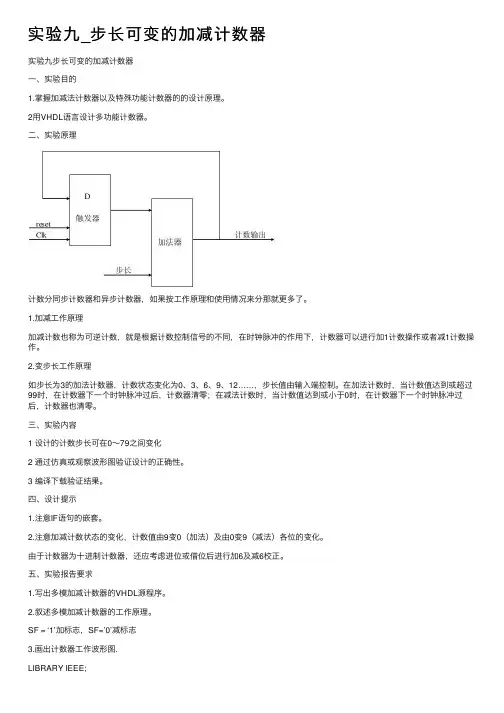
实验九_步长可变的加减计数器实验九步长可变的加减计数器⼀、实验⽬的1.掌握加减法计数器以及特殊功能计数器的的设计原理。

2⽤VHDL语⾔设计多功能计数器。

⼆、实验原理计数分同步计数器和异步计数器，如果按⼯作原理和使⽤情况来分那就更多了。

1.加减⼯作原理加减计数也称为可逆计数，就是根据计数控制信号的不同，在时钟脉冲的作⽤下，计数器可以进⾏加1计数操作或者减1计数操作。

2.变步长⼯作原理如步长为3的加法计数器，计数状态变化为0、3、6、9、12……，步长值由输⼊端控制。

在加法计数时，当计数值达到或超过99时，在计数器下⼀个时钟脉冲过后，计数器清零；在减法计数时，当计数值达到或⼩于0时，在计数器下⼀个时钟脉冲过后，计数器也清零。

三、实验内容1 设计的计数步长可在0～79之间变化2 通过仿真或观察波形图验证设计的正确性。

3 编译下载验证结果。

四、设计提⽰1.注意IF语句的嵌套。

2.注意加减计数状态的变化，计数值由9变0（加法）及由0变9（减法）各位的变化。

由于计数器为⼗进制计数器，还应考虑进位或借位后进⾏加6及减6校正。

五、实验报告要求1.写出多模加减计数器的VHDL源程序。

2.叙述多模加减计数器的⼯作原理。

SF = ‘1’加标志，SF=’0’减标志3.画出计数器⼯作波形图.LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY CHANGABLE ISPORT(CLK,RESET,SF:IN STD_LOGIC;SIZE:IN STD_LOGIC_VECTOR(6 DOWNTO 0);DO:OUT STD_LOGIC_VECTOR(6 DOWNTO 0));END ENTITY CHANGABLE;ARCHITECTURE C_SIZE OF CHANGABLE ISSIGNAL C_COUNT: STD_LOGIC_VECTOR(6 DOWNTO 0); BEGIN PROCESS(CLK,RESET,SF,SIZE)V ARIABLE TP:STD_LOGIC_VECTOR(6 DOWNTO 0); BEGINIF(RESET = '1')THENC_COUNT<=(OTHERS=>'0');ELSIF(CLK'EVENT AND CLK = '1')THENIF(SF='1')THENTP:=C_COUNT+SIZE;IF(TP>79)THENC_COUNT<=(OTHERS=>'0');ELSEC_COUNT<=C_COUNT+SIZE;END IF;ELSEIF(TP < SIZE)THENC_COUNT<=(OTHERS=>'0');ELSEC_COUNT<=C_COUNT-SIZE;END IF;END IF;END IF;DO<=C_COUNT;END PROCESS;END ARCHITECTURE C_SIZE;。

东南大学生物科学与医学工程学院虚拟仪器实验报告第二次实验实验名称：程序结构专业：生物医学工程姓名：学号：同组人员：学号：实验室: 综合楼716实验时间：10月14日评定成绩：审阅教师：一、计算n的阶乘 (3)1实验题目 (3)2实验目的 (3)3实验内容 (3)4设计方案选择、方案的优缺点。

(3)5软件设计: (3)6调试： (6)7测试结果和分析。

(6)8使用说明： (7)9结束语、总结、心得体会。

(7)二、实现加减乘除的计算器 (7)1实验题目 (7)2实验目的 (7)3实验内容 (7)4设计方案选择、方案的优缺点。

(7)5软件设计: (8)6调试： (9)7测试结果和分析 (10)8使用说明： (10)9结束语、总结、心得体会。

(10)一、计算n的阶乘1实验题目完成计算n的阶乘2实验目的①前面板数字控制器可随意输入n的值，并能显示结果(注:0!=1)。

②For循环中重复时间不少于100ms（即程序每100ms循环一次）。

3实验内容⑴学习while、For循环的使用方法。

⑵学习移位寄存器的概念，学习移位寄存器的使用。

⑶学习使用Case结构，学习添加和删除分支。

4设计方案选择、方案的优缺点。

计算n的阶乘的计算器方案选择：利用循环语句，进行数字n的阶乘运算，利用移位寄存器实现数据的传送完成数字连乘。

利用时间计时器的差值得出程序运行所用时间。

能够简洁明了的实现计算n的阶乘的功能，数据正确。

5软件设计:虚拟仪器设计步骤详细介绍。

（1）程序前面板设计：数值输入控件：名称：输入n 属性：双精度（DBL）用途：面向用户，手动输入n值数值显示控件：名称：n！的值属性：双精度（DBL）用途：显示n！运算结果名称：运行时间（ms）属性：双精度（DBL）用途：显示程序运行时间面板的布局：。

（2）框图程序设计：程序流程图：源程序：6调试：调试步骤：使用高亮执行该段程序，观察数据流的动向。

调试中问题：一开始使用整型，对于较小数值，结算结果正确，但对于较大的数值计算结果错误。

实验六步长可变的加减计数器
一、实验目的
1、掌握加减法计数器以及特殊功能计数器的设计原理；
2、用HDL语言设计多功能计数器。

二、硬件需求
EDA/SOPC实验箱一台。

三、实验原理
计数器的步长是指计数器每次的改变量。

在很多应用场合，都希望计数器的步长可变。

所谓步长可变，也就是计数器的步长是一个不定值，具体是多少是要靠外部干预的，比如外部给定其步长为5，那么该计数器每次要么增加5，要么减少5，也就是说计数器每次的改变量是5。

这种步长可变的计数器才具有一定的实际意义，比如在直接数字频率合成DDFS 中的地址累加器就是一个步长可变的递增计数器。

四、实验内容
本实验要完成的任务就是设计一个8位的计数器，步长的改变量要求从0～15，实验中用拨挡开关模块的SW1A～SW4A来作为步长改变量的输入，用按键F1来控制计数器的增减，具体要求为：当F1输入为高时，计数器为步长可变的加计数器；当F1输入为低时，计数器为步长可变的减计数器。

计数器输出的Q值用七段数码管模块来表示。

实验中计数器的时钟频率为了便于眼睛观察，同上个实验一样用1Hz的时钟。

五、实验步骤
（1）实现程序
本实验采用顶层设计
元件例化
（2）仿真波形图
从仿真波形图可以看出，LED输出波形持续变化，以设定的步长，增减计数，产生相应的七位译码值。

（3）实际结果。

一、实验目的1. 理解数字电路的基本组成和基本原理。

2. 掌握常用数字电路的分析和设计方法。

3. 提高动手实践能力，加深对数字电路理论知识的理解。

二、实验内容本次实验主要包含以下内容：1. 数字电路基础实验2. 组合逻辑电路实验3. 时序逻辑电路实验三、实验仪器与设备1. 数字电路实验箱2. 数字信号发生器3. 示波器4. 计算器5. 实验指导书四、实验原理1. 数字电路基础实验：通过实验了解数字电路的基本组成和基本原理，包括逻辑门、编码器、译码器等。

2. 组合逻辑电路实验：通过实验掌握组合逻辑电路的分析和设计方法，包括加法器、编码器、译码器、数据选择器等。

3. 时序逻辑电路实验：通过实验掌握时序逻辑电路的分析和设计方法，包括触发器、计数器、寄存器等。

五、实验步骤1. 数字电路基础实验- 连接实验箱，检查电路连接是否正确。

- 按照实验指导书的要求，进行逻辑门、编码器、译码器等电路的实验。

- 观察实验结果，分析实验现象，并记录实验数据。

2. 组合逻辑电路实验- 连接实验箱，检查电路连接是否正确。

- 按照实验指导书的要求，进行加法器、编码器、译码器、数据选择器等电路的实验。

- 观察实验结果，分析实验现象，并记录实验数据。

3. 时序逻辑电路实验- 连接实验箱，检查电路连接是否正确。

- 按照实验指导书的要求，进行触发器、计数器、寄存器等电路的实验。

- 观察实验结果，分析实验现象，并记录实验数据。

六、实验结果与分析1. 数字电路基础实验- 通过实验，验证了逻辑门、编码器、译码器等电路的基本原理和功能。

- 实验结果符合理论预期，验证了数字电路的基本组成和基本原理。

2. 组合逻辑电路实验- 通过实验，掌握了组合逻辑电路的分析和设计方法。

- 实验结果符合理论预期，验证了组合逻辑电路的基本原理。

3. 时序逻辑电路实验- 通过实验，掌握了时序逻辑电路的分析和设计方法。

- 实验结果符合理论预期，验证了时序逻辑电路的基本原理。

东南大学《微机实验及课程设计》实验报告实验五8253 计数器/定时器实验六8255 并行输入输出姓名：学号：08011专业：自动化实验室：计算机硬件技术实验时间：2012年04月27日报告时间：2013年05月15日评定成绩：审阅教师：一. 实验目的实验五：1）掌握计数器/定时器8253 的基本工作原理和编程应用方法；2）了解掌握8253 的计数器/定时器典型应用方法实验六：1）掌握8255方式0的工作原理及使用方法，利用直接输入输出进行控制显示；2）掌握8段数码管的动态刷新显示控制；3）分析掌握8255工作方式１时的使用及编程，进一步掌握中断处理程序的编写。

二. 实验内容实验五：必做：5-1 将计数器0设置为方式0，计数初值为N（小于等于0FH），用手动的方式逐个输入单脉冲，编程使计数值在屏幕上显示，并同时用逻辑笔观察OUT0电平变化。

（参考程序p63）5-2 将计数器0、1分别设置在方式3，计数初值设为1000，用逻辑笔观察OUT0电平的变化。

（参考程序p64）实验六：（1）8255方式 0：简单输入输出实验电路如图一，8255C口输入接逻辑电平开关K0～K7，编程A口输出接 LED显示电路L0～L7；用指令从 C口输入数据，再从A口输出。

图一 8255简单输入输出（2）编程将A口 L0-L7控制成流水灯，流水间隔时间由软件产生；流水方向由K0键在线控制，随时可切换；流水间隔时间也可由K4～K7键编码控制，如 0000对应停止，0001对应 1秒，1111对应 15秒,大键盘输入 ESC键退出。

（3）8段数码管静态显示:按图二连接好电路，将 8255的 A口PA0～PA6分别与七段数码管的段码驱动输入端a～ｇ相连，位码驱动输入端 S1接+5V（选中），S0、dp接地（关闭）。

编程从键盘输入一位十进制数字（0～9），在七段数码管上显示出来。

图二单管静态显示(4) 8段数码管动态显示：按图三连接好电路，七段数码管段码连接不变，位码驱动输入端S1、S0 接8255 C口的PC1、PC0。

东南大学电工电子实验中心实验报告课程名称：电路与电子线路实验1第 2 次实验实验名称：可变步长计数器的设计院（系）：专业：姓名：学号：实验室: 实验组别：同组人员：实验时间：年月日评定成绩：审阅教师：一、实验内容要求1.可变步长计数器的设计内容：实现N步长计数器●实现1/N步长计数器●N为四位二进制数，可现场设置要求：●在Multisim软件平台上设计实验电路●运行并检验实验结果二、实现方案1.N步长计数器设计方案（1）使用1个全加器和4个D触发器实现N步长加减计数器。

4个D触发器用来存储表示运算结果的4位二进制数，其D输入端分别接全加器的运算结果输出端SUM_1, SUM_2, SUM_3, SUM_4，时钟信号端CP接控制开关A。

控制开关A闭合一次，相当于加一次脉冲信号。

全加器的其中一个4位二进制数输入端A1, A2, A3, A4分别接4个D触发器的输出端Q，另一个4位二进制输入端B1, B2, B3, B4则分别接控制开关B,C,D,E。

这四个开关用于控制步长，每个开关代表着4位二进制数的一位。

设置好步长N后（通过设置控制开关B,C,D,E的闭合与断开实现），每闭合一次控制开关A，全加器将前一次的运算结果+N（二进制加法）后送到4个D触发器，因此4个D触发器的输出结果为前一次结果+N（二进制加法），从而实现了N步长加法计数器。

N步长减法计数器只需在设置步长N时取N的补码即可实现。

（2）使用1个全加器，1个二输入与门，1个二输入与非门，2个74LS47和2个七段数码管实现结果的十进制表示。

运算结果的量程为15，一个数码管用于显示结果的十位数，另一个数码管用于显示结果的个位数。

上述4个D触发器的结果Q输出到全加器的一个4位二进制数输入端，全加器的另一个4位二进制数输入端则或者输入0000，或者输入0110，具体输入哪一个要看与门输出的结果。

全加器的4个输出端接到74LS47上，该74LS47再接到显示个位数的数码管。

数字电路与系统第四次实验
04016636 项剑涛
实验1：
右移功能实验。

设计一个能够直观观察集成移位寄存器74HC194右移功能的电路，通过发光二极管的显示，展示“1000”序列右移的过程。

1.实验原理
74194芯片
2.实验电路图
3.电路实物图
4.实验验证
实验二：
广告流水灯。

用时序器件、组合器件和门电路设计一个广告流水灯，该流水灯由8个LED 组成，工作时始终为1暗7亮，且这一个暗灯循环右移。

1)写出设计过程，画出设计的逻辑电路图，按图搭接电路； 2)验证实验电路的功能；
3)将1秒连续脉冲信号加到系统时钟端，观察并记录时钟脉冲CP 、触发器的输出端Q 2、Q 1、Q 0的波形。

逻辑假设：设D 触发器的每个状态依次(地位到高位)为Q 0n , Q 1n , Q 2n。

输出依次为C=Q 2n ,B=Q 1n ,A=Q 0n 。

1
2、卡诺图
)(01)(1)
(0(1)()1n n n Q Q Q Q
Q n n +=+
C ＝Q 2n ，B ＝Q １n ，Ａ＝Q ０n
3、电路原理图连接说明，通过异步时序，使得三个触发器得到的输出可以构成三位二进制的形式，达到计数的形式000-111，对应到74138的C 、B 、A ，对应到每一个138的输出，并输出到8个灯上。

Q 1n Q 0n
４、电路原理图CP
5、硬件连接图
CP
6.实物图
7.实验验证
8.波形图。

东南⼤学电⼦测量作业答案第2章作业答案2-2 已知CD-4B 型超⾼频导纳电桥在频率⾼于1.5MHz 时，测量电容的误差为pF 5.1)%(5±±读数值求⽤该电桥分别测200pF 、30pF 、2pF 时，测量的绝对误差和相对误差，并以所得绝对误差为例，讨论仪器误差的相对部分和绝对部分对总测量误差的影响。

【解】200x=5%*200 1.511.5pFx 1.5==5% 5.75%x 20030x=5%*30 1.5 3.0pF x 1.5==5%10%x 302pF x=5%*2 1.5 1.6pFx 1.5==5%80%x 2pF pF γγγ?±±≤±?±±≤±?±±≤±?±±≤±?±±≤±?±±≤±时，时，时，以绝对误差为例，可以看出，测量值越⼤，仪器误差的相对部分对总测量误差的影响越⼤；测量值越⼩，仪器误差绝对部分对总误差的影响越⼤。

2-3对某电感进⾏了14次等精度测量，测得的数值（mH ）为L 1=20.46,L 2=20.52,L 3=20.50,L 4=20.52,L 5=20.48,L 6=20.47,L 7=20.50,L 8=20.49,L 9=20.47,L 10=20.49,L 11=20.51,L12=20.51,L 13=20.68,L 14=20.54。

试⽤莱特准则判断有⽆异常数据。

【解】141120.51(),()0.054()14i i L L mH s L mH =====∑各测量值的残差分别为v 1=-0.05,v 2=0.01,v 3=-0.01,v 4=0.01,v 5=-0.03,v 6=-0.04, v 7=-0.01,v 8=-0.02,v 9=-0.04,v 10=-0.02,v 11=0,v 12=0,v 13=0.17,v 14=0.03。

数字逻辑电路实验简易数字钟日期：2013年12月6日地点：104姓名：学号：审阅教师：得分：一、实验目的（1）掌握时序逻辑电路的一般设计过程；（2）掌握时序逻辑电路的时延分析方法，了解时序电路对时钟信号相关参数的基本要求；（3）掌握QuartusⅡ5.0的使用二、实验原理特点外引线排列图•用于快速计数的内部超前进位•用于n 位级联的进位输出•同步可编程序•有置数控制线•二极管箝位输入•直接清零•同步计数典型参数：f 工作频率=32MHzPd=93mW说明：这种同步可预置十进计数器是由四个D 型触发器和若干个门电路构成，内部有超前进位，具有计数、置数、禁止、直接（异步）清零等功能。

对所有触发器同时加上时钟，使得当计数使能输入和内部门发出指令时输出变化彼此协调一致而实现同步工作。

这种工作方式消除了非同步（脉冲时钟）计数器中常有的输出计数尖峰。

缓冲时钟输入将在时钟输入上升沿触发四个触发器。

这种计数器是可全编程的，即输出可预置到任何电平。

当预置是同步时，在置数输入上将建立一低电平，禁止计数，并在下一个时钟之后不管使能输入是何电平，输出都与建立数据一致。

清除是异步的（直接清零），不管时钟输入、置数输入、使能输入为何电平，清除输入端的低电平把所有四个触发器的输出直接置为低电平。

超前进位电路无须另加门，即可级联出n 位同步应用的计数器。

它是借助于两个计数使能输入和一个动态进位输出来实现的。

两个计数使能输入（ENP 和ENT）计数时必须是高电平，且输入ENT 必须正反馈，以便使能动态进位输出。

因而被使能的动态进位输出将产生一个高电平输出脉冲，其宽度近似等于QA 输出高电平。

此高电平溢出进位脉冲可用来使能其后的各个串联级。

使能ENP 和ENT 输入的跳变不受时钟输入的影响。

电路有全独立的时钟电路。

改变工作模式的控制输入（使能ENP、ENT 或清零）纵使发生变化，直到时钟发生为止，都没有什么影响。

计数器的功能（不管使能、不使能、置数或计数）完全由稳态建立时间和保持时间所要求的条件来决定。

一个易于系统集成的变步长反馈数字DC-DC变换模块
原钢;石寅
【期刊名称】《半导体学报：英文版》
【年(卷),期】2003(24)7
【摘要】提出了一种采用单比较器变步长反馈控制和占空比抖动方法的数字 DC- DC变换模块 .它用 6位二进制分辨率占空比的 PWM信号实现了 7位的电压分辨率 .变步长反馈控制的使用使得它具有比恒定步长方案更好的动态性能 ,而且没有过多增加控制器的复杂度 .在 1MHz的开关频率下 ,控制器自身功耗小于 0 .5 m W(不含功率开关及驱动部分 ) .由于电路的模拟部分极少 ,因此易与数字系统进行单芯片集成 .
【总页数】6页(P769-774)
【关键词】数字控制器;变步长反馈;占空比抖动
【作者】原钢;石寅
【作者单位】中国科学院半导体研究所
【正文语种】中文
【中图分类】TN492
【相关文献】
1.一种无需ADC的变步长反馈DC-DC转换器数控方式 [J], 原钢;石寅
2.双闭环反馈控制半桥DC-DC变换器设计 [J], 吴晓光;羊彦
3.易于硬件实现滤除ECG信号运动干扰的变步长LMS算法 [J], 孙见鹏;刘宏;刘滢
浩;田彤
4.电压反馈型半桥DC-DC变换器动力学特性 [J], 袁臣虎;万健如;李光叶;周海亮
5.附加电感电流线性反馈控制的级联DC-DC变换器稳定性提升方法 [J], 李虹;郭钟雅;刘晨;赵洋洋;苏文哲;张波
因版权原因，仅展示原文概要，查看原文内容请购买。

一种新型任意多模移位计数器
沈正元;肖洁;刘永旺;王志功
【期刊名称】《电气电子教学学报》
【年(卷),期】2005(027)002
【摘要】提出了一种新型移位计数器,用实例讨论了各种双模、多模移位计数器的设计.因为移位计数器的设计可查已有的反馈函数表达式,所以十分容易.这种新型移位计数器不仅可以用于在吞脉冲技术中提高前置分频器的工作速率,而且特别适宜在有较大延迟的反馈控制系统中使用.
【总页数】5页(P40-44)
【作者】沈正元;肖洁;刘永旺;王志功
【作者单位】东南大学,射频与光电集成电路研究所,江苏,南京,210096;东南大学,射频与光电集成电路研究所,江苏,南京,210096;东南大学,射频与光电集成电路研究所,江苏,南京,210096;东南大学,射频与光电集成电路研究所,江苏,南京,210096
【正文语种】中文
【中图分类】TP332.1
【相关文献】
1.一种任意进制计数器的快速设计方法探析 [J], 徐忠根;蒋琳;王洽峰;高善坤
2.粒子计数器的一种新型光学传感器设计 [J], 石鑫;韩月;丁思红;戴兵
3.任意进制移位计数器研究与实现 [J], 吕虹
4.设计任意模长二进制同步计数器的一种新方法 [J], 胡长林;周云晓
5.一种单片高速四位计数器／移位寄存器 [J], 袁博鲁
因版权原因，仅展示原文概要，查看原文内容请购买。

基于LIPM的双足机器人变步长行走规划
冯帅;孙增圻
【期刊名称】《东南大学学报：自然科学版》
【年(卷),期】2009(0)S1
【摘要】为了提高双足机器人步行运动的灵活性,提出了一种基于线性倒立摆模型的双足步行规划算法.该算法首先根据所要达到的步长,获得支撑腿切换时质心的位置;然后,根据线性倒立摆模型的运动特性,计算出质心到达上述位置所需要的时间;最后,根据该时间对摆动脚用正弦曲线进行规划,使之能够在恰当的时刻到达所需的落脚点位置进行支撑脚的切换.该算法可使双足机器人在运动中变化步长,很好地提高其步行的灵活性.通过真实机器人的实验,验证了该方法的有效性和实用性.
【总页数】4页(P121-124)
【关键词】双足机器人;步行规划;线性倒立摆模型
【作者】冯帅;孙增圻
【作者单位】清华大学智能技术与系统国家重点实验室;清华大学计算机科学与技术系
【正文语种】中文
【中图分类】TP242.6
【相关文献】
1.基于被动行走原理的双足机器人步态规划 [J], 李宏扬;孙中波;田彦涛
2.四足机器人躯干重心稳定的变步长行走研究 [J], 王恒升;邹铁庚
3.双足机器人变步长步行模式的在线生成方法 [J], 张世龙;刘国栋;潘桂彬
4.基于变质心高度策略的双足机器人变步长步态规划 [J], 周江琛; 肖晓晖
5.变刚度半被动双足机器人行走的仿人控制 [J], 张瑞;张奇志;周亚丽
因版权原因，仅展示原文概要，查看原文内容请购买。

可变步长的元胞自动机智能决策疏散模型的仿真研究张艳芳;赵宜宾;张丽娟;曾文艺【摘要】将基于模糊推理的方向选择模型和通道吸引力模型,与疏散时间模型等模块进行组合,构建了基于元胞自动机的智能决策模型.在对疏散过程的描述中引入有效通道密度概念,以使密度数值能够直观反映疏散过程各个时段通道的拥挤情况,并通过对个体变步长行进方式的执行,实现对复杂疏散行为更为合理的描述.利用变步长智能决策模型对大型超市疏散过程进行描述,仿真过程能够对个体疏散路线,通道和出口密度变化等疏散特征直观表现,对疏散时间等仿真数据分析表明模型是有效的.【期刊名称】《湘潭大学自然科学学报》【年(卷),期】2014(036)002【总页数】7页(P92-98)【关键词】元胞自动机;变步长;疏散模型;模拟仿真【作者】张艳芳;赵宜宾;张丽娟;曾文艺【作者单位】防灾科技学院基础部,北京065201;防灾科技学院基础部,北京065201;防灾科技学院基础部,北京065201;北京师范大学信息科学与技术学院,北京100875【正文语种】中文【中图分类】TP391.41元胞自动机[1](Cellular Automata,简称CA)的概念是由Von Neumann在1966年提出来的.由于其是一种时空离散的局部动力学模型，比较适用于空间和时间复杂的系统的动态模拟研究，从而被广泛应用于交通流[2]等多个领域.如果将模糊逻辑引入到经典的元胞自动机中，建立具有模糊规则的模糊元胞自动机(Fuzzy cellular automaton 简称FCA)可以解决实际问题中的信息模糊和条件不确定的问题.因此研究者对模糊元胞自动机进行了深入理论研究,如[3～5]，研究了FCA和CA的关系.FCA模型也被广泛应用于城市发展[6]、疾病预防[7]、交通流[8] 等各个领域.在人口密集场所中当突发事件发生时，积极有效的人员疏散是最大限度地减少生命财产损失的核心问题.利用元胞自动机研究疏散仿真问题是一个重要方向[9～11]，若结合元胞自动机和智能体两者优势,将元胞看作是一个智能体,理论上对疏散过程的描述将更加贴近真实情形:[12]利用智能体疏散模型对不同移动速度人员疏散情况进行了研究;[13]通过引入健康度的概念来研究火灾环境下不同速度人员的疏散情况;[14]借助规则处理和数值演算相结合的方法来控制智能体的行为特性,对疏散过程的整体特性与个体行为进行了综合研究;谢积鉴等[5]研究了行人博弈对疏散效率的影响,模拟了不同行人密度,出口宽度下疏散总时间受到的影响.上述基于智能体的疏散模型对智能体在信息处理和决策过程方面的研究还不是很系统.本文将在[16，17]的研究工作基础上,通过建立基于模糊推理的通道吸引力模型和方向选择模型,来构建模拟人员疏散的智能决策模型.文中引入有效疏散密度的概念及算法,以更直观表现疏散通道的拥挤程度. 现有疏散模型元胞的移动步长都是一个单元格长度,这与真实疏散过程有很大偏差,本文将采用变步长的元胞移动方式来更真实地反映疏散情景.进一步,本文将对变步长情况通道和出口处的密度变化,以及疏散时间进行系统研究,通过仿真和数据分析来验证模型的有效性.1 变步长的元胞自动机智能决策疏散模型元胞自动机(CA) 模型是定义在一个由具有离散、有限状态的元胞组成的元胞空间上，并按照一定的局部规则，在离散的时间维上演化的动力学系统，具有空间离散性与齐性、时间离散性、状态离散和有限性、同步性等基本特征.这里的空间是一个二维平面，按照均匀的网格划分，每个网格占据的空间为0.5 m×0.5 m.每个网格或被障碍物占据，或被人员占据，或为空.CA模型的更新规则是:第i个元胞在t+1时刻的状态由其自身及邻居在t时刻的状态共同决定. 本文元胞邻居用摩尔(Moore)型定义，与此相对应的,元胞的移动方向将有如图1所示的8个方向.下文将详细阐述通过基于模糊推理的通道吸引力模型、方向选择模型和疏散时间模型构建人员疏散的智能决策模型过程.1.1 基于模糊推理的疏散通道吸引力模型在大型公共场所中,都设有专用的疏散通道,通道上标有指示疏散方向标识,如果疏散人员对所处环境不熟悉,则在疏散路线的选择上会优先考虑疏散通道.如果周围有多条疏散通道,则疏散人员会根据所处位置到通道距离和通道上人员密度综合考虑选择哪条通道.考虑获取信息的模糊性,本文建立基于模糊推理的疏散通道吸引力模型. 智能体cell(i,j)在第k个方向对应的疏散通道吸引力pa_attraction{i,j}(k)按如下原则计算:距离通道近,且通道比较宽,人员密度小,则选择可能性大.为此取通道固有特征指数和通道上人员密度做为确定通道吸引力的两个因素.取智能体的第k个方向距最近通道距离为1d，通道宽度为cw,则第k个方向通道固有特征指数pa_feature(k)=1d/cw，将其8个方向对应特征归一化后仍记为pa_feature(k)(1,2,…,8).将特征指数分为三个模糊集PF={low,middle,high}={数值小，数值中，数值大}.隶属函数为梯型和三角形(如图2所示).在智能体的第k个方向对应最近通道上取以智能体所在行(列)为对称轴,长为7个元胞,宽为疏通宽度ch_w的区域, 计算通道密度为pa_density(k)=Np/7×ch_w,(k=1,2,…，8),其中Np表示对应区域上人员总数.将通道密度分成三个模糊集PD={low,middle,high}={数值小，数值中，数值大}.隶属函数为梯型(如图3所示).将第k(k=1,2,…，8)个方向上距智能体cell(i,j)最近的通道对其吸引力pa_attraction{i,j}(k)(作为输出)划分成5个模糊集,分别是P={NB,NM,ZO,PM,PB}={负大,负中,零,正大,正中},取模糊集隶属函数为梯形和三角形(如图4所示).构建推理规则表如表1所示,可完成第k个方向通道对智能体吸引力pa_attraction{i,j}(k)(k=1,2,…,8)的计算.表1 模糊推理规则表Tab.1 Table of the fuzzy reference ruleslowmiddlehighlowPBPMZOmiddlePMZONMhighZONMNB1.2 智能决策的方向选择模型[17]对环境熟悉的智能体在方向决策的时候主要考虑所处位置到门口的距离和选择方向上障碍物的密度两个因素,根据获取的信息具有模糊性的特点,本文沿用[17]构建的以距出口距离、目标方向密度为输入,以第k个方向移动可能性move_probability(k),(k=1,2,…，8)为输出的模糊推理模型.同时沿用[17]中的路线参考因子rout_factor来实现智能体的避障行为；沿用方向参考因子direction_factor使智能体保持路线选择方向的一致性.基于上述工作,可得智能体cekk(i,j)对第k个方向的选择可能性的计算公式如下:choice_vector{i,j}(k)=move_probability(k)×route_factor×direction_factor. (1)1.3 个体移动的速度与时间模型本文沿用[17]的速度模型:其速度大小的计算公式为:(2)其中V0=1.25 m/s，D表示视野范围内人员和障碍物密度.按每个元胞对应0.5m×0.5 m的空间划分,本文智能体每次移动步长step_length可为0.5 m或1 m.进而个体的每个时间步耗时为step_length/V s,疏散时间计算方法如下:(1) 由公式(2)计算个体疏散速度;(2) 计算疏散个体每一步实际耗时ti.该个体实际疏散时间其中n为疏散个体的个数;(3) 最终的疏散时间T=max {Ti,i=1,2,…,n}.1.4 智能决策疏散模型算法设计为了体现疏散出口对人员的吸引,本文引入出口影响因子exit_factor,其取值规则为：在距出口一定距离范围内,若第k个方向距出口的距离比现位置不远,则exit_factor(k)=1,否则exit_facto r(k)=0,(1,2,…,8).为了体现不同元胞对于同一位置的竞争能力不同,本文引入个体竞争力CP,其依然考虑身体强壮程度和等待次数两方面因素,按如下公式计算:(3)其中等待次数waite_time在下文的实例中最大取值为5;疏散人员体力值physical_strength∈{1.5,1.25,1}，分别表示体力强,中,弱;D为两相邻元胞距离,当目标元胞与现在元胞处在同一行(列)时,D=1,否则距离调节因子下文实例取reg_factor=0.8.下面通过对模型算法的描述详细阐述采用模块化结构构建变步长智能决策疏散模型的思路:步骤1：计算智能体(元胞)cell(i,j)对移动位置的选择可能性.如果人员对环境熟悉,则1.2节的方向选择模型choice_vector{i,j}(k),(k=1,2,…,8);当人员对环境不熟悉时,其头脑中对自己的先进路线及所处位置虽不及对环境熟悉的人,但还是有一定的感知的.所以当疏散人员对环境不熟悉时,则用1.1通道吸引力模型ch_grvitation{i,j}对上述模型进行修正,即choice_vector{i,j}(k)=β×choice_vector{i,j}(k)+(1-β)×ch_grvitation{i,j}(k)，k=1,2,…,8,其中β越大,表示对通道吸引力依赖越小,本文取β=0.3;如果智能体到达门口附近一定范围(本文设定距门口距离5 m以内),再用出口影响因子exit_factor 对方向选择可能性修正,即choice_vector{i,j}(k)=choice_vector{i,j}(k)×exit_factor(k)，k=1,2, (8)(4)步骤2：选择移动位置.计算智能体对周围邻居选择可能性choice_vector{i,j}(k)的最大值为cv_max及其对应的网格位置.若cv_max=0,则智能体不动;若cv_max>0,且与选择位置在同一直线上的下一个网格为空,则智能体对下一网格的选择可能性为cv_max*α,其中α为调节因子,表示个体对目标位置选择可能性随距离增加而减小,下文的仿真实例中取α=0.7,通过上述选择策略,本文可以实现人员在疏散过程中每次移动一步或两步的变速过程.当多个智能体选择同一位置格作为移动目标时,计算个体竞争力CP,竞争力大的移动,若多个智能体个体竞争力相同,则从中随机地选择一个移动到目标位置;其他人员再按上述规则选择各自邻居中的次优网格作为移动目标;若所有可选择的方向均不能作为目标位置,则智能体等待.步骤3：按照步骤2中每个智能体选择的目标位置,所有智能体同时移动,同时按照1.3的时间模型记录所有智能体的疏散时间、疏散速度等疏散过程数据.步骤4：重复上述过程直到所有智能体全部疏散完毕.2 基于变步长智能决策模型的大型超市疏散过程仿真及结果分析我们以大型仓贮超市为背景对疏散过程模拟仿真,对疏散现象进行更细致的研究.设定超市的长80 m,宽60 m,主疏散通道为3.5 m宽,其他通道大部分在1.5～2 m宽,紧急疏散通道上设有引导线,紧急出口有4个,宽度分别为3.5 m和3 m.对超市的平面空间进行均匀的网格划分,每个网格对应0.5 m×0.5 m的空间.每个时间步,每个网格可能被障碍物或智能体占有,也可能为空.对于不同体力的人员本文用三角形和圆点表示,其中对环境熟悉与不熟悉的人各占50%,每个人员所处位置在紧急疏散前随机确定.图5表示人员总数为1 100人的初始化疏散环境.应用第2节构建的疏散模型及算法,在matlab软件平台上对疏散过程进行模拟仿真.下方首先说明变步长疏散的合理性，然后利用模型对疏散过程仿真的数据来对疏散通道和出口人员密度随人数和时间的变化进行描述,通过合理的情景再现和数据分析表明模型的有效性与可行性.(1) 由于真实疏散环境中个体的行进本身是变步长,这样才使得疏散开始时个体快速向出口聚集,在出口疏散能力有限的情况下导致拥挤,使疏散时间变长.而固定步长的决策模型对上述现象不能很好地反映.在仿真人数为1 100人时,图6给出了第80时间步时固定步长(左图)和变步长(右图)模型的仿真结果对比，能够直观表现这一现象.从图6中左右出口疏散情况对比还可以看出,出口的障碍物形状及大小对于出口拥挤人群的形状会产生很大的影响,当出口没有障碍物或其尺寸较小时,人群的整体形状才会呈半圆形,否则会出现其他形状,这也与实际情况吻合.(2) 现有文献中对于疏散通道密度的计算基本上都是通过通道上现有个体数量与通道上能够容纳最大个体数量的比值来描述,此数字特征的大小并不能够完全反映通道真实的拥挤程度,比如疏散后期,虽然个体数量总和较小,但由于人员都集中于出口,所以对疏散影响还是比较大,但按现有计算方法得到的数字特征值很小.为此,本文引入有效通道疏散密度概念,其计算方法如下:如果通道上某一元胞周围一定范围(本文取2.5 m)内有行人,则此元胞被定义为有效元胞,有效通道疏散密度的数值由通道上个体总数与有效元胞总数的比值确定.有效通道疏散密度数值可以直观反映通道上个体的拥挤情况,图7给出不同人数的疏散中，通道密度随时间的变化曲线.从图中可以看出当人数大于800人时,疏散后期有效通道密度明显高于疏散中期(有效通道密度相对稳定的时期),表明当人数大于800人时,疏散后期会在出口处出现人员大量拥堵情况.(3) 由于大型公共场所疏散过程中的拥堵主要发生在出口,因此对各个出口的拥堵情况的分析可以为紧急疏散预案的制定提供很有价值的参考,图8给出了疏散环境中从左边开始的出口1到出口4在不同人数下的疏散情况对比.其中出口处人员密度这一数字特征是通过以出口为中心,以r(本文r=5 m)为半径的半圆内人员总数与这一范围内空格总数相除得到.从数据分析可得,如果不加任何疏散指示条件,个体根据自己判断选择方向,则出口1和出口4疏散过程持续时间最长.但由于出口1的障碍物尺寸较小,且没有隔离墙阻碍行人,所以人员聚集较快,高密度持续时间比较长.由于在选择出口4时,部分行人要绕过隔离墙,所以人员聚集速度不会太快,同时由于出口障碍物特点决定绝大部分行人不会选择沿靠墙的窄通道出去,所以出口密度不会太大,这有利于保持疏散速度.出口2和出口3疏散过程持续时间比较短,说明这两个出口的疏散能力没有得到充分利用,如果在疏散过程中加入疏散指示信息,充分利用这些空余的疏散能力,将会极大提高疏散效率.以上的数据分析结果将可为超市货柜摆放,应急疏散预案制定提供重要参考,以利于真正发生灾害时人员的快速疏散.(4) 大型公共场所的最佳容纳人数的确定对于控制灾害发生时的损失具有重要意义,图9给出了本文疏散环境下疏散时间(单位:s)随人数的变化趋势.由于曲线在人数为800时,疏散时间的变化率增加很快,表明此点是此疏散环境拥堵与否的分界点.当疏散人数从800增加到1 100人时,疏散时间从103.4 s提高到150.8 s,即疏散人数增加37.5%情况下,疏散时间增加了45.8%,表明超过分界点时,拥堵会变得很严重,导致疏散时间快速增加,则灾害发生时损失会大大增加.所以本超市的最佳容量是800人.上述分析表明本文所构建的变步长智能决策疏散模型,通过在个体行进步长和决策过程的模糊化两方面对已建模型的改进,使其对给定疏散环境下的紧急疏散过程的描述更加合理,同时模型的模拟仿真数据还可为大型公共场所的细节设计及相应紧急疏散预案的制定提供有价值的参考信息.3 结论与讨论在[17]的智能方向选择模型基础上,考虑真实的疏散过程中个体的行进是变速的,而且方向决策是完全智能化的,为此构建了可变步长的智能决策模型.此模型中个体方向决策的主要参考因素全部模糊化,以模糊推理机做为信息处理工具,模拟人脑的决策过程,以使对疏散过程的描述更加合理.考虑到疏散模型主要通过对疏散过程的描述来收集疏散信息,以达到为相关应急预案的制定提供有价值的参考的目的,所以引入了有效通道密度的概念,使决策者通过有效的通道密度的数值能够对疏散过程中各个阶段的拥挤情况有比较直观的了解,以使制定的应急预案在执行过程中更加有效.我们下一步将利用已建模型从两个方面对疏散过程进行深入研究:其一加入疏散指示信息,来对疏散过程进行控制,通过增加参考因素在对各种情况下的疏散过程进行仿真研究;其二,将疏散空间扩展到对立体空间,构建相应的模型,来描述楼房类建筑的疏散过程.参考文献[1] JOHN V N,ARTHUR W B.Theory of self-reproducingautomata[M].Urbana and London:University of Illinois Press,1966.[2] EZ-ZAHRAOUY H,JETTO K,BENYOUSSEF A.The effect of mixture lengths of vehicles on the traffic flow behaviour in one-dimensional ellular automaton[J].The European Physical Journal B,2004,40:111-117.[3] HEATHER B,PAOLA F.On the relationship between boolean and fuzzy cellular automata[J].Electronic Notes in Theoretical Computer Science,2009,252:5-21.[4] HEATHER B,PAOLA F.On the asymptotic behavior of fuzzy cellular automata[J].Electronic Notes in Theoretical Computer Science,2009,252:23-40.[5] CATTANEO G,FLOCCHINI P,MAURI G,et al. Cellular automata in fuzzy backgrounds[J].Physica D,1997,105:105-120.[6] YAN L,STUART R P.Modelling urban development with cellular automata incorporating fuzzy-set approaches[J].Computers, Environment and Urban Systems,2003,27:637-658.[7] JAFELICE R M, BECHARA B F Z,BARROS L C,et al.Cellular automata with fuzzy parameters in microscopic study of positive HIV individuals[J]. Mathematical and Computer Modelling,2009,50:32-44.[8] 张笑梅. 基于元胞自动机和模糊推理的交通流模型研究[D].大连：大连理工大学,2013.[9] 葛红霞,祝会兵,戴世强. 智能交通系统的元胞自动机交通流模型[J].物理学报,2005,10:4 621-4 626.[10] LI Z,YANG S B, LIU J, et al. Information based evacuation experimentand its cellular automaton simulation[J].International Journal of Modern Physics C, 2009,20(10): 1 583-1 596.[11] KAZUHIRO Y, SATOSHI K, KATSUHIRO N. Simulation for pedestrian dynamics by real-coded cellular[J]. Physics A, 2007,379: 654-660.[12] 翁文国,袁宏永,范维澄.一种基于移动机器人行为的人员疏散的元胞自动机模型[J].科学通报,2006,51(23):2 818-2 822.[13] 吕春杉,翁文国,杨锐,等.基于运动模式和元胞自动机的火灾环境下人员疏散模型[J].清华大学学报(自然科学版),2007,47(12):2 163-2 167.[14] 史健勇,任爱珠.基于智能体的大型公共建筑人员火灾疏散模型研究[J].系统仿真学报,2008,20(20):5 677-5 699.[15] 谢积鉴. 薛郁通过博弈的室内行人疏散动力学研究[J].物理学报，2012, 61(19): 194 502.[16] 赵宜宾,黄猛,张鹤翔.基于元胞自动机的多出口人员疏散模型的研究[J].系统工程学报,2012,27(4):439-445.[17] 赵宜宾,刘艳艳,张梅东,等.基于模糊元胞自动机的多出口人员疏散模型[J].自然灾害学报,2013,22(2):13-20.。