当前位置：文档之家 › 数字电路逻辑设计第3章

数字电路逻辑设计第3章

  • 格式：ppt
  • 大小：1.71 MB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)

(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
3-6
3-7
3-8
3-9
3-10
求减数的补码，然后与被减数相加即可。电路图如下：
3-11
3-12
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
3-13
(1)真值表：
（2）电路图
3-14
3-15
第四章习题
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-10
RSDRSJK RST
4-11
(1)转换真值表
1 1 0 1
1 1 1 0
1 1 1 1
1 0 1 0
0 0 0 0
0 0 0 1
0 0 1 0
00 11
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
××××
××××
××××
××××
××××
1×0×1×0×
0×0×0××1
0×0××1 1×
0×0××0×1
0××1 1×1×

数字电路第三章习题答案

数字电路第三章习题答案
S 1 S 0(A B A B )
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B
数字电路第三章习题答案
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当 电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在B、 C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
3531736半加器的设计1半加器真值表2输出函数3逻辑图输入输出被加数a加数b4逻辑符号31837ab改为用与非门实现函数表达式变换形式
3-1 分析图示电路，分别写出M=1,M=0时的逻辑函数表达式
即M＝1时，对输入取反，M＝0时不取反。
数字电路第三章习题答案
3-2 分析图示补码电路，要求写出逻辑函数表达式，列出真值表。
3-10 试用与非门设计一个逻辑选择电路。
S1、S0为选择端，A、B为数据输入端。 选择电路的功能见下表。选择电路可 以有反变量输入。
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B FS 1 S 0A B S 1 S 0(A B )S 1 S 0(A BA)B
数字电路第三章习题答案
3-5
Ai 0 0 0 0 1 1 1 1
Si Ai BiCi Ai BiCi Ai BiCi Ai BiCi

人邮社数字电路逻辑设计习题答案

人邮社数字电路逻辑设计习题答案

习题参考解答第1章基本知识1．什么是数字信号？什么是模拟信号？（注：所有蓝色标题最后均去掉！）答案：数字信号：指信号的变化在时间上和数值上都是断续的，或者说是离散的，这类信号有时又称为离散信号。

例如，在数字系统中的脉冲信号、开关状态等。

模拟信号：指在时间上和数值上均作连续变化的信号。

例如，温度、交流电压等信号。

2．数字系统中为什么要采用二进制？答案：二进制具有运算简单、物理实现容易、存储和传送方便、可靠等优点。

3．机器数中引入反码和补码的主要目的是什么？答案：将减法运算转化为加法运算，统一加、减运算，使运算更方便。

4．BCD码与二进制数的区别是什么?答案：二进制数是一种具有独立进位制的数，而BCD码是用二进制编码表示的十进制数。

5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什么？答案：两个余3码表示的十进制数相加时，对运算结果修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

为了解决四位二进制运算高位产生的进位与一位十进制运算产生的进位之间的差值。

6．奇偶检验码有哪些优点和不足？答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电路也简单。

缺点是只有检错能力，没有纠错能力，其次只能发现单错，不能发现双错。

7．按二进制运算法则计算下列各式。

答案：（1）110001 （2）110.11 （3）10000111 （4）1018．将下列二进制数转换成十进制数、八进制数和十六进制数。

答案：（1）（117）10 ，（165）8 ，（75）16（2）（0.8281）10 ，（0.65）8 ，（0.D4）16（3）（23.25）10 ，（27.2）8 ，（17. 4）169．将下列十进制数转换成二进制数、八进制数和十六进制数（精确到二进制小数点后4位）。

答案：（1）（1000001）2 ，（101）8 ，（41）16（2）（0.0100）2 ，（0.20）8 ，（0.40）16（3）（100001.0101）2 ，（41.24）8 ，（21.50）1610．写出下列各数的原码、反码和补码。

数字电路与逻辑设计PPT课件

数字电路与逻辑设计PPT课件

Cn+1 Dn
0
0
1
1
1
1
1
0
0
1
0
0
0
0
1
1
第3章 组合逻辑电路
AnBn
AnBn
An Bn
全 减
Dn
Cn 0
00 0
01 1
11 0
10 0
Cn 00 01 11 10 00 1 0 1
Cn
器
Cn+1 1 1
1
1
0
11 0 1 0
(a)
(b)
(c)
全减器框图及K图 (a) 框图; (b) Cn+1； (c) Dn
0 0 0
带编码器的MCU应用电路
3.3.2 译码器
第3章 组合逻辑电路
将二进制代码转换成不同的输出 信号的过程称为译码。常用的MSI译码器 为74HC138(3－8Line Decoder)。
② 根据输出函数表达式列出真值表。
③ 确定电路的逻辑功能。
第3章 组合逻辑电路
【例3-1】分析图所示电路，指出该电路 的逻辑功能。
Ai
＝1
＝1
Bi
Si
Ci
& ≥1
Ai Bi
∑
Si
1
Ci+1 Ci
Ci+1
(a)
(b)
解： ① 写出函数表达式。
第3章 组合逻辑电路
Si Ai Bi Ci Ci1 ( Ai Bi )Ci Ai Bi
第3章 组合逻辑电路
组合逻辑电路：任何时候的输 出仅仅取决于该时刻的输入，而与电路原 来的状态没有任何关系。输出状态随着输 入信号的改变而改变。

数字电路逻辑设计(第二版) 王毓银 电子科技大学

数字电路逻辑设计(第二版) 王毓银 电子科技大学
3.5.3 CMOS传输门
3.5.4 CMOS逻辑门电路
3.5.5 BiCMOS门电路
3.5.6 CMOS电路的正确使用方法
3.6 VHDL描述逻辑门电路
3.6.1 VHDL描述电路的基本方法
3.6.2 VHDL描述逻辑门电路
习题
第4章 组合逻辑电路
4.1 组合逻辑电路分析
6.4.1 设计给定序列信号的产生电路
6.4.2 根据序列循环长度M的要求设计发生器电路
6.5 时序逻辑电路的VHDL描述
6.5.1 移位寄存器的VHDL描述
6.5.2 计数器的VHDL描述
习题
第7章 半导体存储器
7.1 概述
7.1.1 半导体存储器的特点与应用
5.3 主从触发器
5.3.1 主从触发器基本原理
5.3.2 主从J-K触发器主触发器的一次翻转现象
5.3.3 主从J-K触发器集成单元
5.3.4 集成主从J-K触发器的脉冲工作特性
5.4 边沿触发器
5.4.1 维持一阻塞触发器
5.4.2 下降沿触发的边沿触发器
10.2.6 DAC的转换精度与转换速度
10.3 模数转换器（ADC）
10.3.1 模数转换基本原理
10.3.2 并联比较型ADC
10.3.3 逐次逼近型ADC
10.3.4 双积分型ADC
10.4 集成ADC及其应用举例
双积分型集成ADC
10.4.2 逐次逼近型集成ADC
2.1.3 真值表与逻辑函数
2.1.4 逻辑函数相等
2.1.5 三个规则
2.1.6 常用公式
2.1.7 逻辑函数的标准形式

数字电路与逻辑设计 (第四版)1--4章答案

数字电路与逻辑设计 (第四版)1--4章答案

第一章1.4（1）10101=1∗104+1∗102+1∗100（2）0.10101=1∗10−1+1∗10−3+1∗10−5（3）1010.101=1∗103+1∗101+1∗10−1+1∗10−31.5（1）(163)10=(10100011)2（2）(0.525)10=(0.100001)2（3）(41.41)10=(101001.01101000111)21.6(123)8=(1∗82+2∗8+3)10=(83)10 1.76n<(0.3)3⇒n log6<3(log3−1)⇒n<3(log3−1)log6=−2.016⇒n≤−3(8.705)10≈(12.412)61.8A(B+C+D)+BC(A̅+D̅)+D̅⇒A+A BC+D̅1.9A̅+BA+C+DA⇒A̅+B+C+D 1.10（1）F(A,B,C)|B=1&C=1=(AB+A̅C)|B=1&C=1=1（2）F(A,B,C)|A̅=1&B=1&C=1=A̅BC|A̅=1&B=1&C=1=11.11（1）1.12A̅+C ̅̅̅̅̅̅̅+D ∙(A +C ̅)(A +B )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅= 1.13（1）F =A (B̅+C +D )(B +D ̅)=ABC +A (B⨀D ) （2）F =A̅⋅B ̅+(AB +AB ̅+A ̅B )C =A ̅⋅B ̅+C （3）F =A +A ⋅B̅⋅C ̅+AC ̅D +(C ̅+D ̅)E =A +C ̅E +D ̅E （4）F =AB̅(C +D )+BC ̅+A ̅∙B ̅+A ̅C +BC +B ̅⋅C ̅⋅D ̅=A ̅+B ̅ （5）F =(A +B )(A +C )(A +C̅)=A （6）F =(A +BC̅)(A ̅+D ̅B)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B ̅+A ̅C +AD （7）F =A (A +B̅+C ̅)(A ̅+C +D )(E +C ̅⋅D ̅)=ACE +ADE 1.14（1）F (A,B,C )=∑m(2,3,6,7)=A BC +A BC +ABC +ABC =B（2）F (A,B,C,D,E )=∏M (0,4,8,12,16,20,24,28)=A ⋅B̅⋅C ⋅D ̅⋅E ̅+A ⋅B ̅⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ̅⋅C ⋅D ̅⋅E ̅+A ⋅B̅⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅=D ̅E ̅ 1.15（1）F (A,B,C )=∑m (1,3,7)=∏M (0,2,4,5,6)（2）F (A,B,C,D )=∑m(0,2,6,12,13,14)=∏M(1,3,4,5,7,8,9,10,11,15)1.16（1）F (A,B,C )=∏M(0,3,6,7)=∑m(1,2,4,5)（2）F (A,B,C,D )=∏M(0,1,2,3,4,6,12)∑m(5,7,8,9,10,11,13,14,15)1.17（1）F (A,B,C,D )=AB +A̅B ̅+CD ̅=ABC D ̅+ABC D +ABCD ̅+ABCD +A B ̅C D ̅+A B ̅C D +A B̅CD ̅+A B ̅CD +AB ̅CD ̅+A BCD ̅=∑m(0,1,2,3,6,10,12,13,14,15) （2）F (A,B,C )=(A +B )(B̅+C )=∏M(6,7,5,1)=∑m(0,2,3,4) 1.18（1）F (A,B,C )=A ⊕B +AC̅=A B +AB ̅+A C =A BC +A BC +AB ̅C +AB ̅C +A B ̅C +A BC =∑m (2,3,4,5,1)=∏M(0,6,7)（2）F (A,B,C,D )=(A +B̅+C )(A +B ̅)(A +C ̅+D ̅)(B +C ̅+D ̅)=∏M(10,11,8,9,12,4) 1.19（1）F =(AB +A B̅)(C +D )(E +C D ̅)⇒F ̅=A ⊕B +C D ̅+E ̅ （2）F =A +B +C ̅+D +E ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅⇒F ̅=A(B +C ̅+D +E ̅̅̅̅̅̅̅̅)=AB +AC +AD̅E 1.20（1）F =AB +CD +A̅C ⇒F ∗=(A +B )(C +D )(A +C )=A BC +AC +A BD （2）F =A (B̅C +BC ̅)+AC ̅⇒F ∗=(A +(B ̅+C )(B +C ))(A +C )=A +B ̅C （3）F =(A ̅+B)(B +A ̅C)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅⇒F ∗=A B +B(A +C)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅+AC 1.21（1）A ̅⊕B =A ⊕B ̅=A ⊕B ̅̅̅̅̅̅̅̅A̅⊕B =A ̅B ̅+AB =A⨀B A ⊕B̅=AB +A ̅B ̅=A⨀B A ⊕B ̅̅̅̅̅̅̅̅=A⨀B（2）A̅B ̅C +A ̅BC ̅+AB ̅C ̅+ABC =A ⊕B ⊕C A ⊕B ⊕C =(A ̅B +AB ̅)⊕C =(A ̅B +AB ̅)C +(A ̅B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅C =A BC +AB ̅C +A B ̅C +ABC （3）AB +BC +CA =(A +B)(B +C)(C +A)(A+B)(B+C)(C+A)=(B+AC)(C+A)=AB+BC+CA （4）AB̅+BC̅+CA̅=A̅B+B̅C+C̅A令：AB̅+BC̅+CA̅=K,K=1或0{A⟶A̅B⟶B̅C⟶C⇒A̅B+B̅C+C̅A=KAB̅+BC̅+CA̅=K=A̅B+B̅C+C̅A1.22（2）1.23（1）F(A,B,C,D)=∏M(1,3,5,7,13,15)=∑m(0,2,4,6,8,9,10,11,12,14)（2）F(A,B,C,D,E)=∏M(0,1,2,3,4,6,8,10,12,13,14)1.24（1）F(A,B,C,D)=∑m(3,5,6,9,12,13,14,15)+∑ϕ(0,1,7)()∑∑（4）F(A,B,C,D,E)=A̅̅̅̅̅̅（5）F(A,B,C,D)=A̅̅̅1.25̅̅12（2）F̅̅12（3）F1(A,B,C,D)=∑m(1,3,4,5,6,7,15)F2(A,B,C,D)=∑m(1,3,10,14,15)12第二章2.1关门电平V off=1.3V:保持电路输出高电平状态所允许的输入低电平的最大值开门电平V on=1.５V:保持电路输出低电平状态所允许的输入高电平的最小值≈1.4V:V off至V on这一段狭窄转折的中值阈值电压VＴ输入高电平时的抗干扰容限VＮＨ＝VＯＨmin−V on=2.4−1.5=0.9V输入低电平时的抗干扰容限VＮＬ＝V off−VＯＬmax=1.3−0.7=0.6V高电平：V OH(2.4～5.0V),标称值3.6V 低电平：V OL(0～0.7V),标称值0.3V2.2TTL与非门：高电平：V OH(2.4～5.0V),标称值3.6V 低电平：V OL(0～0.7V),标称值0.3V 关门电平V off=1.3V开门电平V on=1.５V阈值电压VＴ≈1.4V输入高电平时的抗干扰容限VＮＨ＝VＯＨmin−V on=2.4−1.5=0.9V输入低电平时的抗干扰容限VＮＬ＝V off−VＯＬmax=1.3−0.7=0.6V输出低电平的工作状态：N0L=I OLmax(驱动门)I IL(负载门)输出高电平的工作状态：N0H=I OH(驱动门)I IH(负载门)N I≤５V1:输入信号，V0:反相输出信号；V0下降到V m/2相对应于V1上升到V m/2之间的延迟时间称为导通延迟t PLHV0上升到V m/2相对应于V1下降到V m/2之间的延迟时间称为截止延时t PHLt PLH>t PHLt pd=(t PLH+t PHL)/2平均功耗小，速度快不能并联OC门方便线与逻辑，可并联，主要应用（1）实现与或非逻辑（2）电平转换（3）实现数据采集三态与非门（TSL）具有一个使能状态CMOS与非门抗干扰容限低，负载高，速度接近TTL，可并联2.3将与门、与非门的闲置端接1电平，而将或门、或非门闲置端接接0电平。

数字电路与逻辑设计复习

数字电路与逻辑设计复习
(4)给定F的或与表达式求F的标准与非-与非表达式: 由F的或与表达式→卡诺图→得到F的与或表达式→两次求反→ F的标准或非-或非表达式
第二章 逻辑函数及其简化 公式法化简
① F=(A⊕B)(B⊕C) ●A+B+A+C
解: F=[(A⊕B)(B⊕C) +A+B] ●(A+C) =[(AB+AB)(BC+BC)+A+B) ●(A+C)
第二章 逻辑函数及其简化 1 若A、B、C、D、E为某逻辑函数输入变量，函数的最大项表达式 所包含的最大项的个数不可能是： A 32 B 15 C 31 D 632 2 以下表达式中符合逻辑运算规则的是： A. C●C=C2 B. 1+1=10 C. 0﹤1 D. A+1=1 3 符合逻辑运算规则的是: A. 1×1=1 B. 1+1=10 C. 1+1=1 D. 1+1=2 4 逻辑函数F=AB+CD+BC的反函数F是:_____;对偶函数F﹡是:____; 5 逻辑代数的三个重要规则是:_________,__________,_________ 当逻辑函数有n个变量时,共有____种变量取值组合。 6 异或与同或在逻辑上正好相反，互为反函数，对吗？ 7 逻辑变量的取值，1比0大，对吗？ 8 F=A⊕B⊕C=A⊙B⊙C,对吗? 答案：1. D 2. D 3. C 4. ___ 5. ____ ____ 6. √ 7. × 8. √
第一章 绪论 1．数制的转换 (1)任意进制→十进制(按位权展开相加) (2)十进制→任意进制(除R取余,乘R取整) (3) 二进制--八进制--十六进制(中介法) (4)精度要求(1/Ri＜精度要求值) 2．常用的BCD码 有权码(8421码、2421码、5121码、631-1码) 无权码(余3码，移存码、余3循环码)。

电子技术 数字电路 第3章 组合逻辑电路

电子技术 数字电路 第3章 组合逻辑电路

是F，多数赞成时是“1”， 否则是“0”。
0111 1000 1011
2. 根据题意列出真值表。
1101 1111
（3-13）
真值表
ABCF 0000 0010 0100 0111 1000 1011 1101 1111
3. 画出卡诺图，并用卡 诺图化简：
BC A 00
00
BC 01 11 10
010
3.4.1 编码器
所谓编码就是赋予选定的一系列二进制代码以 固定的含义。
一、二进制编码器
二进制编码器的作用：将一系列信号状态编制成 二进制代码。
n个二进制代码（n位二进制数）有2n种 不同的组合，可以表示2n个信号。
（3-17）
例：用与非门组成三位二进制编码器。 ---八线-三线编码器 设八个输入端为I1I8，八种状态，
全加器SN74LS183的管脚图
14 Ucc 2an 2bn2cn-1 2cn
2sn
SN74LS183
1 1an 1bn 1cn-11cn 1sn GND
（3-39）
例：用一片SN74LS183构成两位串行进位全加器。
D2
C
D1
串行进位
sn
cn
全加器
an bn cn-1
sn
cn
全加器
an bn cn-1
1 0 1 1 1 AB
AC
F AB BC CA
（3-14）
4. 根据逻辑表达式画出逻辑图。 (1) 若用与或门实现
F AB BC CA
A
&
B
C
&
1 F
&
（3-15）
(2) 若用与非门实现

第3章-组合逻辑电路

第3章-组合逻辑电路
一、二进制译码器（最小项译码器） 输入：一组二进制代码 输出：一组与输入代码一一对应的高、低电平信号。
例：3位二进制（3线－8线）译码器框图如下所示：
图3.3.5
3线－8线译码器框图
二进制译码器可采用二极管与门阵列或三极管集 成门电路等构成。
（1）二极管与门阵列译码器电路 0(0V) 1(3V)
表3-3-4
74LS42功能表
74LS42逻辑电路图及各输出表达式如下所示：
Y 0 Y 1 Y 2 Y 3 Y 4 Y5 Y 6 Y 7 Y8 Y9 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0
Y3
Y2
Y1
Y0
§3.3 若干常用的组合逻辑电路
目前，一些常用的逻辑电路已经制成了中、小 规模集成化电路产品。
§3.3.1 编码器（Encoder）
“编码”：即为了区分一系列不同的事物，将其 中的每个事物用一个二值代码表示。 编码器的逻辑功能：把输入的每一个高、低电平 信号变成一个对应的二进制代码。
第三章
Chapter 3
组合逻辑电路
Combinational Logic Circuit
本章主要内容
第一节 第二节 第三节 概述 组合逻辑电路的分析和设计方法 若干常用组合逻辑电路
§3.3.1 编码器(Encoder) §3.3.2 译码器(Decoder) §3.3.3 数据分配器(Demultiplexer)

数字电子电路技术 第三章 SSI组合逻辑电路的分析与设计 课件

数字电子电路技术 第三章 SSI组合逻辑电路的分析与设计 课件

表3-1 例3-1真值表
第四步：确定电路的逻 辑功能。
由真值表可知，三个变
量输入Ａ，Ｂ，Ｃ，只有两
个及两个以上变量取值为1 时，输出才为1。可见电路 可实现多数表决逻辑功能。
Ａ ＢＣ F ０ ００ ０ ０ ０１ ０ ０ １０ ０ ０ １１ １ １ ００ ０ １ ０１ １
１ １０ １
21.10.2020
h
11
2. 组合逻辑电路设计方法举例。
例3-3 一火灾报警系统，设有烟感、温感和 紫外光感三种类型的火灾探测器。为了防止误报警， 只有当其中有两种或两种以上类型的探测器发出火 灾检测信号时，报警系统产生报警控制信号。设计 一个产生报警控制信号的电路。
解：(1)分析设计要求，设输入输出变量并逻辑赋值；
用方法和应用举例。
21.10.2020
h
4
３.1 SSI组合逻辑电路的分析和设计
小规模集成电路是指每片在十个门以下的集成芯片。
3.1.1 组合逻辑电路的分析方法
所谓组合逻辑电路的分析，就是根据给定的逻辑 电路图，求出电路的逻辑功能。
1. 分析的主要步骤如下： (1)由逻辑图写表达式； (2)化简表达式； (3)列真值表； (4)描述逻辑功能。
21.10.2020
h
18
对M个信号编码时，应如何确定位数N？
N位二进制代码可以表示多少个信号？
例：对101键盘编码时，采用几位二进制代码？ 编码原则：N位二进制代码可以表示2N个信号， 则对M个信号编码时，应由2N ≥M来确定位数N。
例：对101键盘编码时，采用了7位二进制代码 ASCⅡ码。27＝128＞101。
０１１１
１０００
１０１１
１１０１
１ １ １ １ 21.10.2020

电子教案数字电子技术第三章组合逻辑电路XX1

电子教案数字电子技术第三章组合逻辑电路XX1
电子教案数字电子技术第三章组合逻 辑电路XX1
3rew
演讲完毕，谢谢听讲!
再见，see you again
2020/11/28
电子教案数字电子技术第三章组合逻 辑电路XX1
•解：（1）列出真值表：
（2）由真值表写出各输出的逻辑表达式为：
电子教案数字电子技术第三章组合逻 辑电路XX1
• 重新整理 得：
• （3）由表达式 画
• 出逻辑图：
电子教案数字电子技术第三章组合逻 辑电路XX1
• （4）增加控制使能标志GS ：
• 当按下S0～ S9
• 任意一个键 时，
• GS=1，表示 有
例4.3.1 试用8选1数据选择器74151实现逻辑函数：
解：将逻辑函数转换成 最小项表达式：
=m3+m5+m6+m7 画出连线图。
电子教案数字子技术第三章组合逻 辑电路XX1
（2）当逻辑函数的变量个数大于数据选择器的地址输入变 量个数时。 例4.3.2 试用4选1数据选择器实现逻辑函数： 解：将A、B接到地址输入端，C加到适当的数据输入端。 作出逻辑函数L的真值表，根据真值表画出连线图。
按内部连接方式不同，七段数字显示器分为共阴极和共阳极两 种。
2．七段显示译码器7448 七段显示译码器7448是一种 与共阴极数字显示器配合 使用的集成译码器。
电子教案数字电子技术第三章组合逻 辑电路XX1
电子教案数字电子技术第三章组合逻 辑电路XX1
•7448的逻辑功能： （1）正常译码显示。LT=1，BI/RBO=1时，对输入为十
如果想用与非门组成半加器，则将上式用代数法变换 成与非形式：
由此画出用与非门组成的半加器。
电子教案数字电子技术第三章组合逻 辑电路XX1

数字电子技术基础(第3章) 组合逻辑分析与设计

数字电子技术基础(第3章) 组合逻辑分析与设计

第3章 组合逻辑设计
A B
&
Y
与非门的逻辑符号
L=A+B （2）或非运算：逻辑表达式为： Y A B
A 0 0 1 1 B Y 0 1 1 0 0 0 1 0 真值表
A B
≥1
Y
或非门的逻辑符号
第3章 组合逻辑设计
（3）异或运算：逻辑表达式为： Y
A 0 0 1 1 B Y 0 0 1 1 0 1 1 0 真值表
A
B F
A B
F
0 0 1 1
0 1 0 1
0 1 1 1
第3章 组合逻辑设计
功能表
开关 A 断开 断开 闭合 闭合 开关 B 断开 闭合 断开 闭合 灯Y 灭 亮 亮 亮
真值表
A 0 0 1 1
B 0 1 0 1
Y 0 1 1 1
逻辑符号 实现或逻辑的电 路称为或门。或 门的逻辑符号：
A B
≥1
第3章 组合逻辑设计
第3章 组合逻辑分析与设计
3.1 逻辑代数基础
3.2 逻辑函数的化简
3.3 组合逻辑电路的分析
3.4 组合逻辑电路的设计
3.5 VHDL硬件描述语言 3.6 基本组合逻辑电路的设计举例 3.7 组合逻辑电路中的竞争-险象
第3章 组合逻辑设计
3.1 逻辑代数基础
逻辑代数（Logic Algebra）是由英国数学家乔治· 布尔(George Boole)于1847年首先提出的，因此也称为
(A+B)(A+C)
第3章 组合逻辑设计
吸收率：
A ( A B) A B A A B A B
证明： A A B ( A A)(A B)

第3章组合逻辑电路

第3章组合逻辑电路

第3章组合逻辑电路3.1 组合逻辑电路的概述按照逻辑功能的不同特点，可以把数字电路分成两大类，一类叫做组合逻辑电路，另一类叫做时序逻辑电路。

什么叫组合逻辑电路呢？在t=a时刻有输入X1、X2、……Zn，那么在t=a时刻就有输出Z1、Z2、……Zm，每个输出都是输入X1、X2、……Zn的函数，Z1=f1（X1、X2、……Xn）Z1=f2（X1、X2、……Xn）Zm=fm（X1、X2、……Xn）从以上概念可以知道组合逻辑电路的特点就是即刻输入，即刻输出。

任何组合逻辑电路可由表达式、真值表、逻辑图和卡诺图等四种方法中的任一种来表示其逻辑功能。

3.2 组合逻辑电路的分析方法和设计方法3.2.1组合逻辑电路的分析方法分析组合逻辑电路的目的，就是要找出电路输入和输出之间的逻辑关系，分析步骤如下：（1）根据已知的逻辑电路，写出逻辑函数表达式（采用逐级写出逻辑函数表达式），最后写出该电路的输出与输入的逻辑表达式。

（2）首先对写出的逻辑函数表达式进行化简，一般系用公式法或卡诺图法。

（3）列出真值表进行逻辑功能的分析。

以上步骤可用框图表示，如图3-2所示。

图3-2 组合逻辑电路分析框图下面举例说明对组合逻辑电路的分析，掌握其基本思路及方法。

【例3-1】 分析图3-3所示电路的逻辑功能图3-3 [例3-1]逻辑电路解：（1）写出输出Z 的逻辑表达式： Z1=B A ， Z2=B AZ=21Z Z •=B A B A • （2）化简Z=B A B A •=A B +A B=A ⊕B （3）列出真值表进行逻辑功能说明 列出该函数真值表，如表3.1所示： 表3-1 [例3-1]真值表 A B Z 0 0 0 0 1 1 1 0 1 1 13.2.2组合逻辑电路的设计方法组合逻辑电路的设计步骤与分析步骤相反，设计任务就是根据逻辑功能的要求设计逻辑电路，其步骤如下：（1）首先对命题要求的逻辑功能进行分析，确定哪些是输入变量，哪些为输出函数，以及它们之间的相互逻辑关系，并对它们进行逻辑赋值。

数字逻辑电路第3章复习题

数字逻辑电路第3章复习题

一、分析题：1、试分析如下面图（a ）和图(B)所示逻辑电路，说明分别是什么逻辑功能。

（10分）.2、（10分）、试分析下图所示逻辑电路。

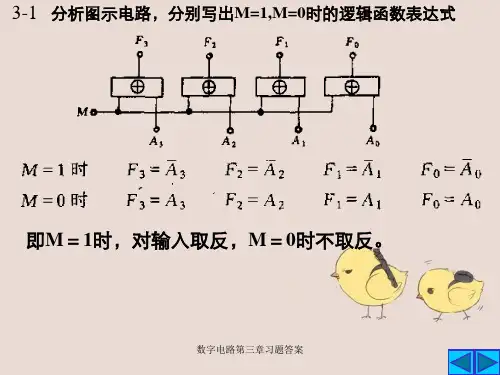
2B L =11AC&L &=1&3-1、（12分）、分析下图电路的逻辑功能。

要求写出逻辑函数表达式，画出真值表，说明电路的逻辑功能。

3-2（8分）、由译码器74138和8选1数据选择器74151组成如下图所示的逻辑电路。

X 2X 1X 0及Z 2Z 1Z 0为两个三位二进制数，试分析下图电路的逻辑功能。

（74138是3-8线译码器，74151是8选1数据选择器）。

A1&B1&&L≥1≥1≥1≥1LAB（a）（b）5Y 6D 074138D 13401A Y 7G 0Y 13D A 52D Y D A 6G D 1Y Y Y D 274201Y2BD 74151G 2A1A A 02A Y1X 02X X 10Z Z Z 24、（6分）由译码器74138和门电路组成的电路如下图所示，试写出L 1、L 2的最简表达式。

5、6、（12分）、下图所示的TTL 门电路中，要求实现下列规定的逻辑功能时，其连接有无错误？说明正确或错误的理由。

如有错误请改正。

CD AB L ⋅=1 AB L =2 C AB L +=3+V &R PC D&L CCB A 1B&A =1V CCL 2&L 3CB A ≥1（a ） (b) (c)7、（12分）、在下图（a ）（b ）（c ）中，所有的门电路都为TTL 门，设输入A 、B 、C 的波形如图（d ）所示，试分析电路的逻辑关系，写出表达式，并定量画出各输出的波形图。

BA =1V CCL 1≥1A 2L BC &≥1EN&△B C1G L 3A &ABC(a)(b)(c)(d)8、（8分）、分析下图所示电路，求输入S 1、S 0各种取值下的输出Y ，填入下表中。

蒋立平版数字逻辑电路与系统设计习题答案

蒋立平版数字逻辑电路与系统设计习题答案

蒋立平版数字逻辑电路与系统设计 第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1） （11011）2（2（10010111）2 （3） （1101101）2（4 （11111111）2 （5） （0.1001）2 （6 （0.0111）2 （7） （11.001）2 （8 （101011.11001）2题1.1 解： （1） （11011）2 =（27）10（10010111）2 =（151）10（3） （1101101）2 =（109）10 （11111111）2 =（255）10（5） （0.1001）2 =（0.5625）10 （0.0111）2 =（0.4375）10（7） （11.001）2 =（3.125）10 （101011.11001）2 =（43.78125）101.3 数。

（1） （1010111）2（110111011）2 （3） （10110.011010）2（4） （101100.110011）2 题1.3 解： （1） （1010111）2=（57）16 =（127）8（2） （110011010）2 =（19A ）16 =（632）8 （3） （10110.111010）2 =（16.E8）16 =（（4） （101100.01100001）2 =（2C.61）16 =1.5 将下列十进制数表示为8421BCD 码。

（1） （43）10 （95.12）10 （3） （67.58）10 （ （932.1）10题1.5 解：（1） （43）10 =（01000011）8421BC D（2） （95.12）10 =（10010101.00010010）8421BC D （3） （67.58）10 =（01100111.01011000）8421BC D （4） （932.1）10 =（1.7 将下列有符号的十进制数表示成补二进制数。

（1） +13 （2）−9 （3）+3 （4）−题1.7解：（1） +13 =（01101）2 （（10111）2（3） +3 =（00011）2 （（11000）21.9 用真值表证明下列各式相等。

数字电路 第3章习题课

数字电路 第3章习题课

题3-15
A B C D
F 0 0 1 1 1 1 0 0 0 0 × × × × × ×
× ×
题3-15
解： F BC D0 0
F
四选一MUX D1 1 D2 1 D3 0 E
题3-16
用74LS138和与非门实现下列逻辑函数。
Y1 ABC A( B C )
+5V
0 0 1 F3 F 5 F 61 F 7 04 F 0 0 1 0 0 1 74138 1 1 1 0 A0 1 1 12 A1 A 0 0 0 0X0 0 X1 0 X2
题3-13
试用 74138 和 74151 构成两个四位二进制数相同 比较器。其功能为两个二进制数相等时输出为 1， 否则为 0。 解：74138 和 74151 地址端均为三变量输入，要 实现四位二进制数相同比较器，必须分别用两个芯 片级联扩展输入端，并分别将待比较的两个四位二 进制数输入到扩展后的输入端，就可得到两个四位 二进制数相同时，输出为 1 的功能。逻辑图如图 3-36 所示。
1 0 B F= A B+ A B 1 1 B 0 0 0 0 1 B F= AB
G1 G0 A
A2 F F A1 MUX A0 D D D D D D D 0 1 2 3 4 5 6 D7 1 1
B
1
1 1
1 0 B F= A B+A 1 1 1 = A +B
题3-5
列出图 3-58 所示电路的真值表。图中芯片为 8421 码二-十进制译码器,输出低电平有效。
0 1
D
题3-3
解：
F F0 F4 F5 F6 F8 F10 F12 F15 F0 F4 F5 F6 F8 F10 F12 F15 (0,4,5,6,8,10,12,15)

数字电路与逻辑设计 第3讲

数字电路与逻辑设计 第3讲

真值表如下： 真值表如下：
输出 Y2 Y1 Y0 GS
1 × × × × × × × × × × × × × × × 0
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
今后会经常遇到的几种控制信号：（用来增强器件的功能） 今后会经常遇到的几种控制信号： 用来增强器件的功能） EI为使能输入端 低电平有效) 有时也称作片选信号。 为使能输入端( 1 、 EI 为使能输入端 ( 低电平有效 ) ， 有时也称作片选信号 。 就 74LS LS148 EI/CS=1 74LS148 来 说 ， 当 EI/CS=1 时 ， 该 器 件 是 不 工 作 的 ， 只 有 在 EI/CS=0时才工作。 EI/CS=0时才工作。 EO为使能输出端 低电平有效) EO只有在 EI=0 为使能输出端( 只有在EI= 2 、 EO 为使能输出端 ( 低电平有效 ) ： EO 只有在 EI=0 （ 器件在工 而且所有输入都为1 说明无有效输入） 输出为0 作），而且所有输入都为1（说明无有效输入）时，输出为0。 这时可以将该片的EO接到另一片的EI EO接到另一片的EI上 这时可以将该片的EO接到另一片的EI上（显然这一片的优先权 允许它工作（EI=0 因此实现了扩展。 低），允许它工作（EI=0）。因此实现了扩展。 3 、 GS 为 优 先 编 码 工 作 标 志 ( 低 电 平 有 效 ) ： 用 来 区 分 011111111” 此时GS= 编码器处于编码状态） GS=0 I0I1I2…I7=“011111111”（此时GS=0,编码器处于编码状态） I =“011111111 111111111” GS=1 和 I0I1I2…I7=“111111111” 的情况 （ 此时 GS=1 ， 编码器处于 I =“111111111 的情况（ 此时GS= 非编码状态） 非编码状态）。

数字电路与逻辑设计第3章组合逻辑电路

数字电路与逻辑设计第3章组合逻辑电路

（2）根据真值表，用卡诺图（图3-5 a）化简后，
可以得到该电路的逻辑函数表达式：
F AC BC AB
由于题目中没有特别要求以何种逻辑门 输出，所以可用与门和或门输出来实现 该逻辑功能，表达式形式无需转换。
（3）逻辑图 由化简后的表达式和真值 表可以看出，(图 3-5 b)即使该题的逻 辑电路图。
表 3-7 8线—3线编码器的真值表
因为任意时刻 I0 ～ I7 中只有一个值为“1”利 用约束项的知识把上述真值表化简后如表3-8 所示。
表 3-8 化简后的真值表
由真值表写出其对应的逻辑函数表达式：
Y2 I4 I5 I6 I7 I4I5I6I7 Y1 I2 I3 I6 I7 I2I3I6I7 Y0 I1 I3 I5 I7 I1I3I5I7
3) 将表达式转化成用“与非” 逻辑形式实 现的形式：
图3-9 （a）卡诺图 （b）逻辑电路
3.2 编码器
编码就是将特定的逻辑信号变换成 一组二进制的代码，而能够实现这种功 能的逻辑部件就称为编码器。编码器的 功能是将输入信号转换为对应的代码信 号，即是用输出的代码信号来表示相对 应的输入信号，以便于进行对代码进行 存储，传输及运算等处理。
FA A FB AB FC ABC FD ABCD
(3)由上述表达式可得其对应的优先编码逻辑 电路如图3-12所示。
图3-13 16线—4线优先编码器的逻辑电路
（2）根据列写出的逻辑问题的真值表，写出对应 的逻辑函数表达式。
（3）将得到的逻辑函数表达式进行变换和化简。 逻辑函数的化简可以利用我们前面所学习的代 数法或卡诺图法，从而得到逻辑函数的最简表 达式，对于一个逻辑电路，在设计时应尽可能 使用最少数量的逻辑门，逻辑门变量数也应尽 可能少用，还应根据题意变换成适当形式的表 达式。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

本章知识要点
●
● ● ●
集成电路的分类
半导体器件的开关特性 逻辑门电路 逻辑函数的实现
3
3.1 数字集成电路的分类
数字集成电路通常按照所用半导体器件的不同或者根据
集成规模的大小进行分类。
一. 根据所采用的半导体器件进行分类
根据所采用的半导体器件，分为两大类。 双极型集成电路：采用双极型半导体器件作为元件。主要 特点是速度快、负载能力强，但功耗较大、集成度较低。 单极型集成电路(MOS集成电路): 采用金属-氧化物半导体 场效应管(Metel Oxide Semiconductor Field Effect Transister)作为元件。主要特点是结构简单、制造方便、集成度 高、功耗低，但速度相对双极型较慢。
0.1V，硅管约0.5V。
正向电压 VF ≤VTH：管子截止，电阻很大、正向电流 IF 接近于 0，二极管类似于开关的断开状态 ； 正向电压 VF = VTH：管子开始导通，正向电流 IF 开始上升； 正向电压 VF ＞VTH ：管子充分导通(导通电压一般锗管约0.3V， 硅管约 0.7V，通常称为导通电压) ，电阻很小，正向电流IF 急剧增加 ，二 极管类似于开关的接通状态。
10
2． 反向特性
二极管在反向电压 VR 作用下，处于截止状态，反向电阻 很大，反向电流 IR 很小（将其称为反向饱和电流，用 IS 表示 ，通常可忽略不计），二极管的状态类似于开关断开。而且反 向电压在一定范围内变化基本不引起反向电流的变化。
使用注意事项!
● 正向导通时可能因电流过大而导致二极管烧坏。组成实 际电路时通常要串接一只电阻 R，以限制二极管的正向电流； ● 反向电压超过某个极限值时，将使反向电流IR突然猛增 ，致使二极管被击穿（通常将该反向电压极限值称为反向击穿 电压VBR），一般不允许反向电压超过此值。 11
根据设计方法和功能定义通常可分为如下3类：
1. 非定制电路（又称为标准集成电路）
2. 全定制电路（又称为专用集成电路） 3. 半定制电路
7
3.2 半导体器件的开关特性
数字电路中的晶体二极管、三极管和MOS管等器件一般是 以开关方式运用的，工作状态相当于相当于开关的“接通”与 “断开”。 数字系统中的半导体器件运用在开关频率十分高的电路中
21
当输入电压vi由-V1 跳变到+V2时，三极管从截止到开始导通所需要的时 间称为延迟时间td。 经过延迟时间td后，iC不断增大。iC上升到最大值的90%所需要的时间称 为上升时间tr 当输入电压vi由+V2跳变到-V1时，集电极电流从ICS到下降至0.9ICS所需要 的时间称为存储时间ts。 集电极电流由0.9ICS降至0.1ICS所需的时间称为下降时间tf 。
一. 非门
非门又称“反相器”。晶体三极管反相器的电路图和逻 辑符号如图 (a)和图(b)所示0
A 0 1
F 1 0
25
二.
与门
一个由二极管构成的2输入与门电路如下图所示。
A/V B/ V 0 0 0 +5 +5 0 +5 +5 F/V 0 0 0 +5
A
B
F 0 0 0 1
，研究其开关特性时，不仅要研究它们在导通与截止两种状态 下的静止特性，而且还要分析它们在导通和截止状态之间的转 变过程，即动态特性。
8
3.2.1 晶体二极管的开关特性
常见外形图
一．静态特性
静态特性是指二极管在导通和截止两种稳定状态下的特性。典型二极 管的静态特性曲线为：
9
1. 正向特性 ： 门槛电压 ( VTH )：使二极管开始导通的正向电压，一般锗管约
第
三
章
随着微电子技术的发展，人们把实现各种逻辑功能的元 器件及其连线都集中制造在同一块半导体材料小片上，并封 装在一个壳体中，通过引线与外界联系，即构成所谓的集成 电路块，通常又称为集成电路芯片。
集成门电路和触发器等逻辑器件是实现数字系统功能的
物质基础。
采用集成电路进行数字系统设计的优点： 可靠性高、可维性好、功耗低、成本低等优点，可以大 大简化设计和调试过程。 2
22
1．开通时间（ ton ） 开通时间：三极管从截止状态到饱和状态所需要的时间。 开通时间ton = 延迟时间td +上升时间tr
2. 关闭时间 （ toff ）
关闭时间 ：三极管从饱和状态到截止状态所需要的时间。 关闭时间toff =存储时间ts +下降时间tf 开通时间ton和关闭时间toff是影响电路工作速度的主要 因素。 23
3.3 逻 辑 门 电 路
实现基本逻辑运算和常用复合逻辑运算的逻辑器件统称 为逻辑门电路，它们是组成数字系统的基本单元电路。
以TTL集成逻辑门和CMOS集成逻辑为例进行介绍。 要求：重点掌握集成逻辑门电路的功能和外部特性，以 及器件的使用方法。对其内部结构和工作原理只要求作一般 了解。
24
3.3.1 简单逻辑门电路
2. 开通时间
开通时间：二极管从反向截止到正向导通的时间称为开 通时间。 由于 PN 结在正向电压作用下空间电荷区迅速变窄，正 向电阻很小，因而它在导通过程中及导通以后，正向压降都 很小，故电路中的正向电流IF ≈VF/R。而且加入输入电压VF 后，回路电流几乎是立即达到IF的最大值。 即：二极管的开通时间很短，对开关速度影响很小，相 对反向恢复时间而言几乎可以忽略不计。 16
4
双极型集成电路分为： 晶体管-晶体管逻辑电路TTL(Transistor Transistor
Logic) 发射极耦合逻辑电路(Emitter Coupled Logic) 集成注入逻辑电路I2L(Integrated Injection Logic) ┊ TTL电路的“性能价格比”较佳，应用最广泛。 MOS集成电路分为： PMOS( P-channel Metel Oxide Semiconductor) NMOS(N-channel Metel Oxide Semiconductor) CMOS(Complement Metal Oxide Semiconductor) ┊ CMOS 电路应用较普遍，因为它不但适用于通用逻电 路的设计，而且综合性能好 。 5
1. 反向恢复时间
反向恢复时间：二极管从正向导通到反向截止所需要的 时间称为反向恢复时间。
当作用在二极管两端的电压由正向导通电压VF 转为反向
截止电压 VR 时，在理想情况下二极管应该立即由导通转为截 止，电路中只存在极小的反向电流。
实际情况如何呢？ 13
实际过程如图所示：
ts — 称为存储时间； tt — 称为渡越时间； tre= ts+tt —称为反
0 0 0 1 1 0 1 1
26
三.
或门
一个由二极管构成的2输入或门电路如下图所示。
A/V B/ V 0 0 0 +5 +5 0 +5 +5 F/V 0 +5 +5 +5
A
B
F 0 1 1 1
0 0 0 1 1 0 1 1
27
3.3.2 TTL 集成逻辑门电路
TTL(Transistor Transistor Logic)电路是晶体管- 晶体 管逻辑电路的简称。60年代问世，经过对电路结构和工艺
3.2.2
晶体三极管的开关特性
各种不同三极管的实物图
17
一．静态特性 晶体三极管由集电结和发射结两个 PN 结构成。三极管 有截止、放大、饱和3种工作状态。 一个用 NPN 型共发射极晶体三极管组成的简单电路及 其输出特性曲线如下图所示。
18
电路工作特点：
1. 截止状态 vI≤0，两个PN结均为反偏，iB≈0,iC ≈0,vCE ≈VCC。三极管呈 现高阻抗，类似于开关断开。 2. 放大状态 vI＞ VTH ，发射结正偏，集电结反偏，iC =βiB 。 3. 饱和状态 vB ＞ VTH，并达到一定值 ，两个PN结均为正偏，iB ≥IBS(基极 临界饱和电流) ≈VCC/βRc ,此时iC = ICS(集电极饱和电流)≈VCC/Rc。三 极管呈现低阻抗，类似于开关接通。 19
※ 当有输入端接低电平(0.3V)时：输入端为低的发射结 导通，使T1的基极电位vb1=0.3V+0.7V=1V。该电压作用于T1的 集电结和T2、T4的发射结上，不可能使T2和T4导通，即T2、T4均 截止。
该电路可按 图中虚线划分为三部分：
输入级—— 由多发射极晶体管T1和电阻R1组成； 中间级—— 由晶体管T2和电阻R2、R3组成； 输出级—— 由晶体管T3、T4、D4和电阻R4、R5组成。 29
(2) 工作原理
※ 输入端全部接高电平(3.6V)：电源Vcc通过R1和T1的集电 结向T2提供足够的基极电流，使T2饱和导通。T2的发射极电流在 R3 上产生的压降又使 T4 饱和导通，输出为低电平(≈0.3V)。 此时，T1的基极电压 vb1=vbc1+vbe2+vbe4≈ 2.1V；T2的集电 极电压vc2 = vces2+vbe4≈0.3V+0.7V≈1V,该值不足以使T3和D4导 通,故D4截止。 实现了“输入全高 ，输出为低”的逻辑关系。 30
的不断改进，性能得到不断改善，至今仍被广泛应用于各 种逻辑电路和数字系统中。 TTL电路的功耗大、线路较复杂，使其集成度受到一 定的限制，故广泛应用于中小规模逻辑电路中。 下面，对几种常见TTL门电路进行介绍，重点讨论TTL与 非门。
28
一. 典型TTL与非门
1. 电路结构及工作原理
(1) 电路结构 典型TTL与非门电路 图及相应逻辑符号如右 图所示。
二．根据集成电路规模的大小进行分类
根据一片集成电路芯片上包含的逻辑门个数或元件个数 ，分为 SSI 、MSI 、LSI 、VLSI。 1. SSI (Small Scale Integration : 逻辑门数小于10 门(或 元件数小于100个)；